Effects of Community Connectivity on the Spreading Process of Epidemics
Abstract
1. Introduction
2. Community Network Model
3. Infectious Disease Dynamics Model and Analysis
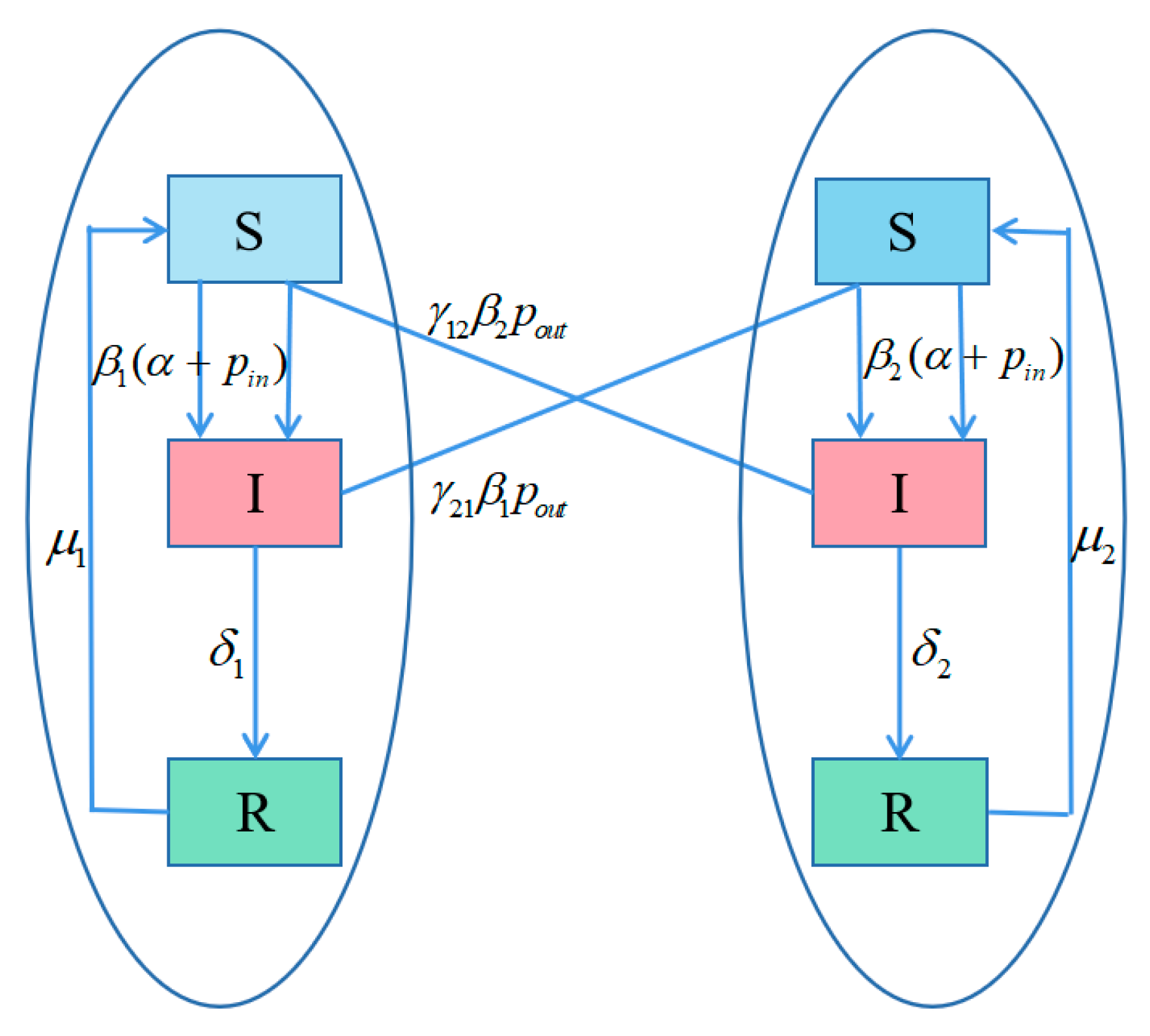
3.1. Model Description
3.2. The Basic Reproduction Number
4. The Impact of Community Structure on the Spreading of Infectious Diseases
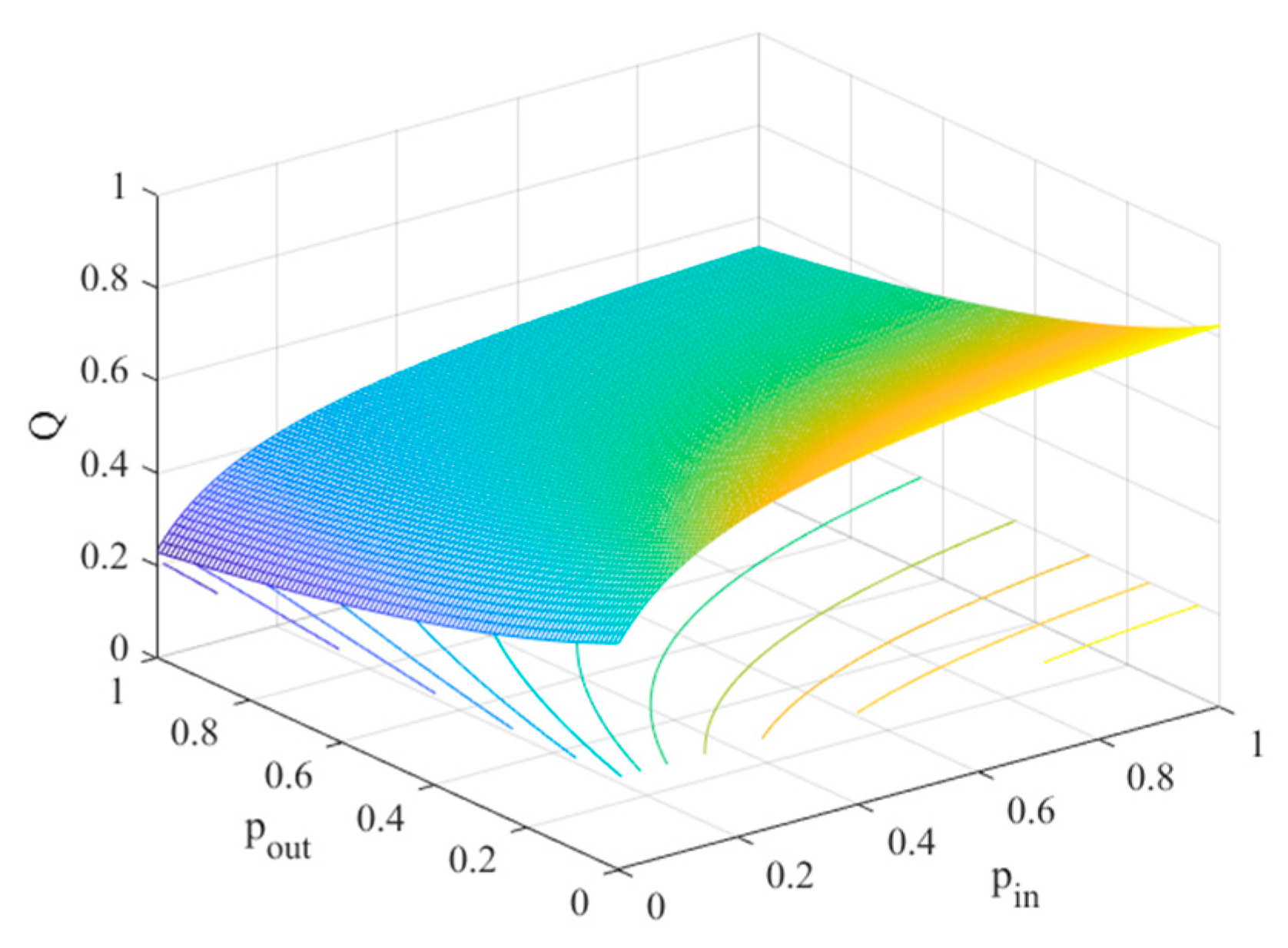
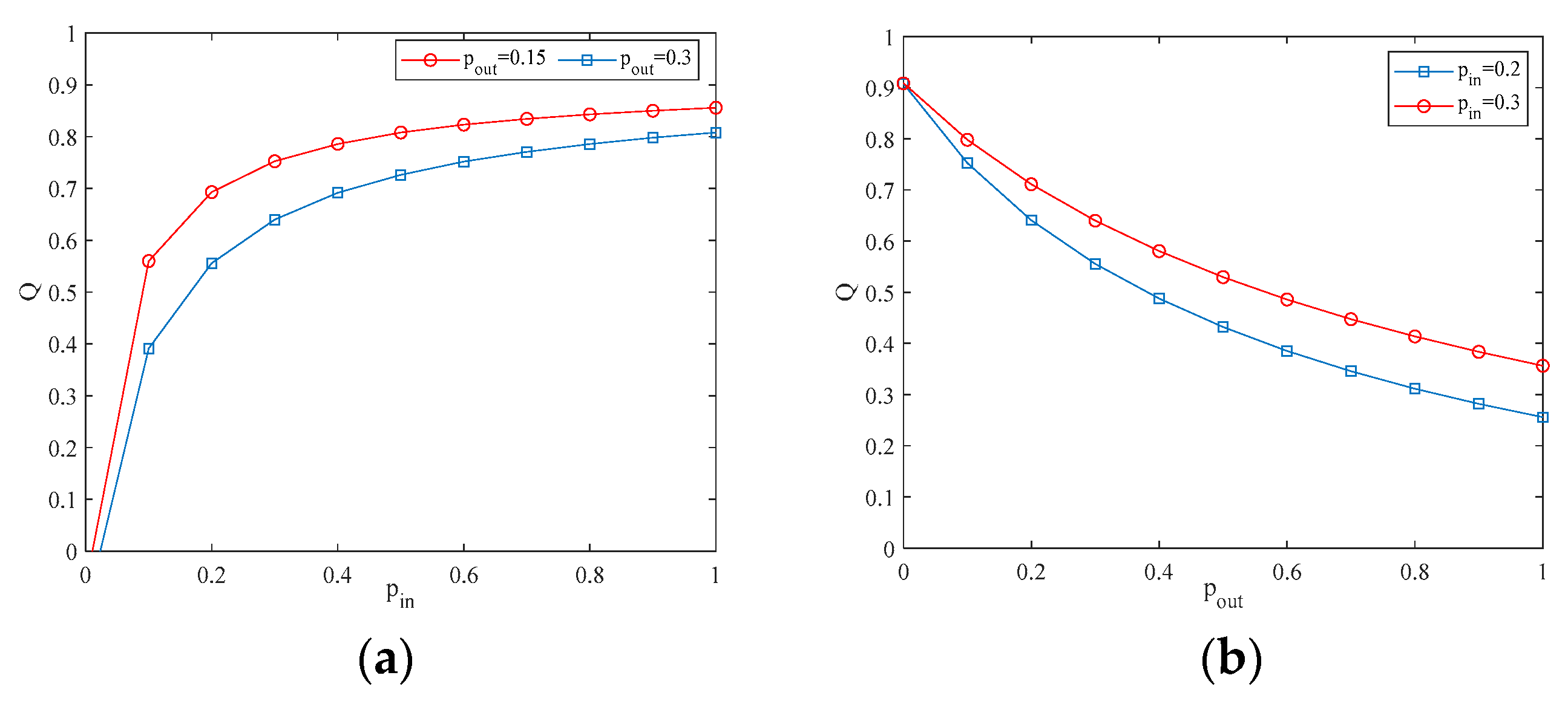
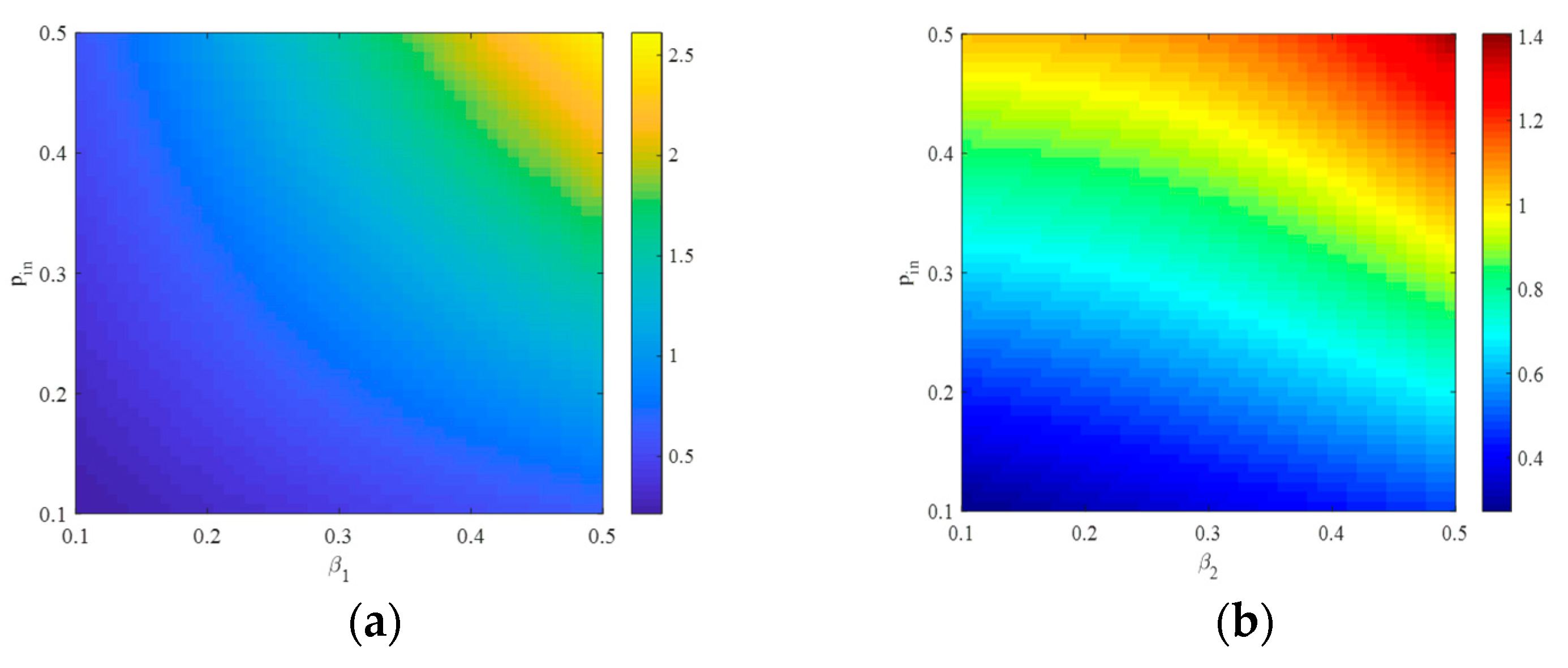
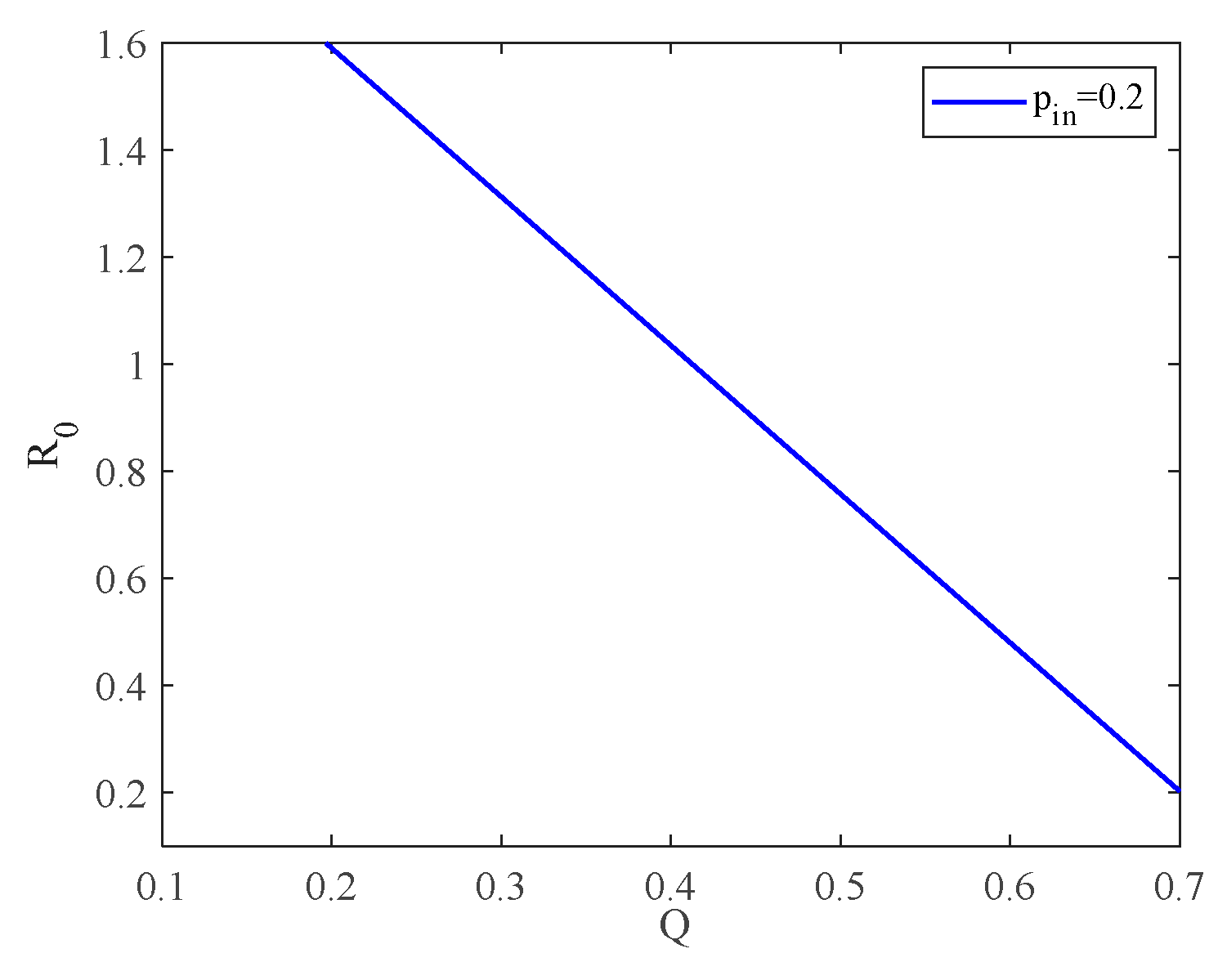
4.1. The Influence of the Connection Rate on the Basic Reproduction Number
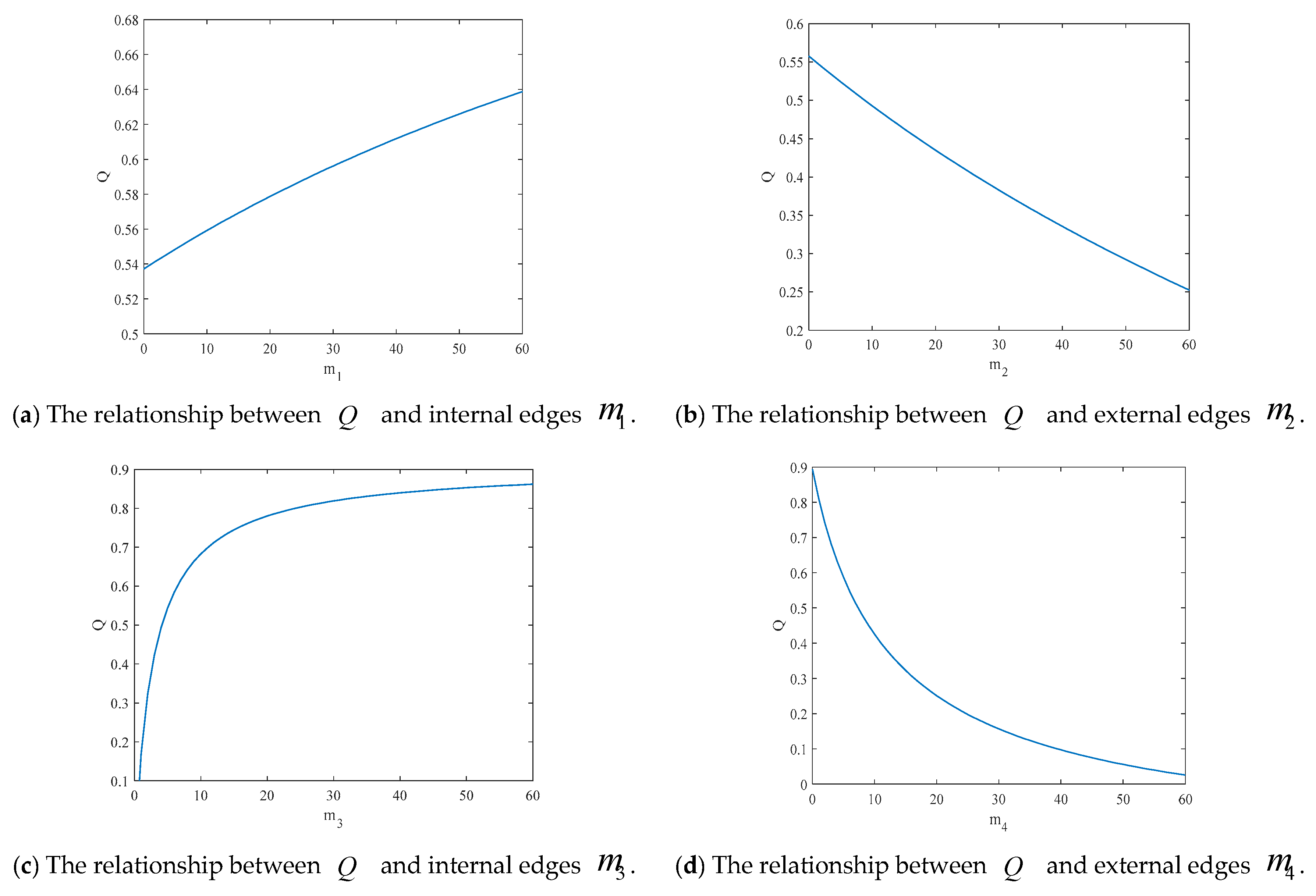
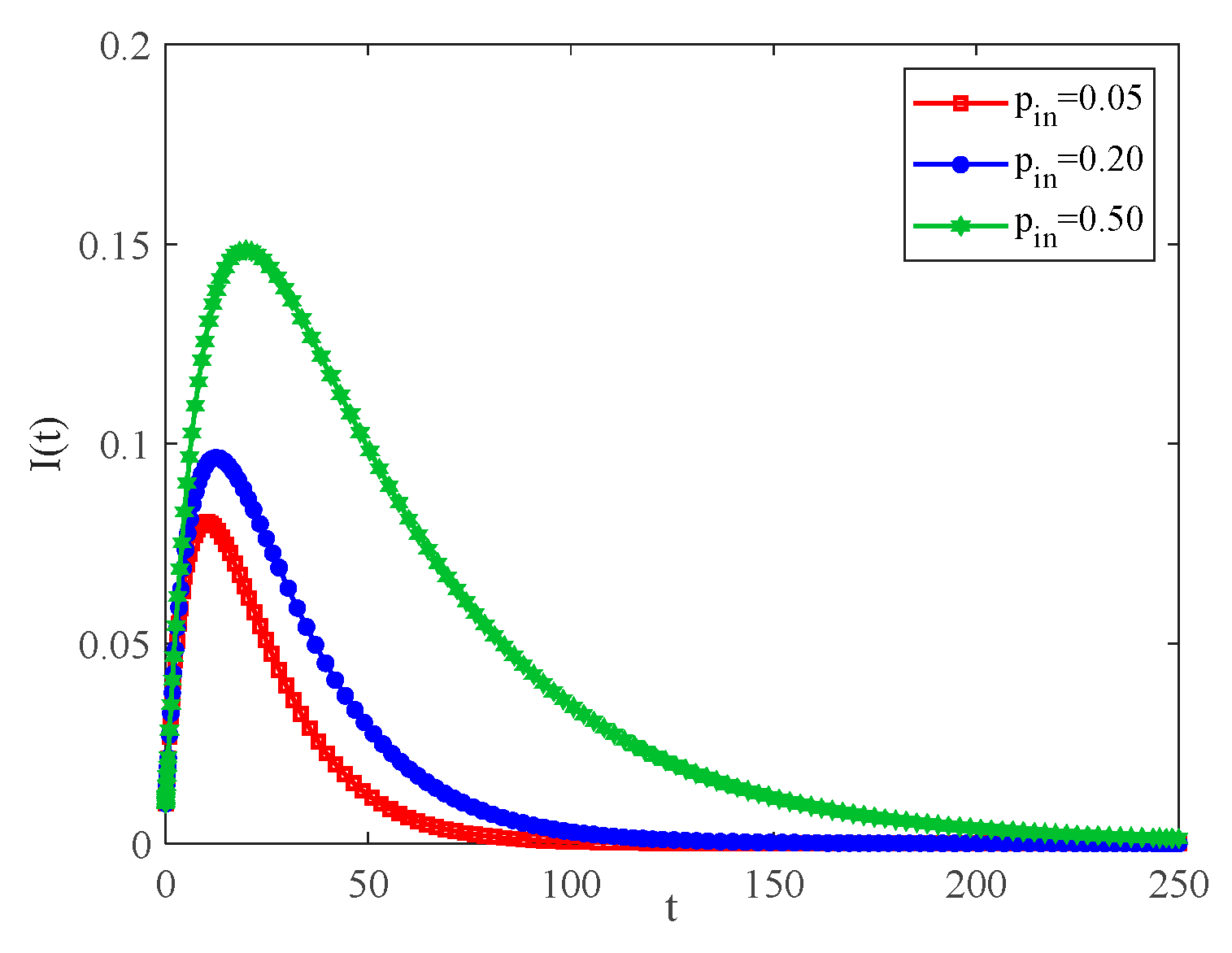
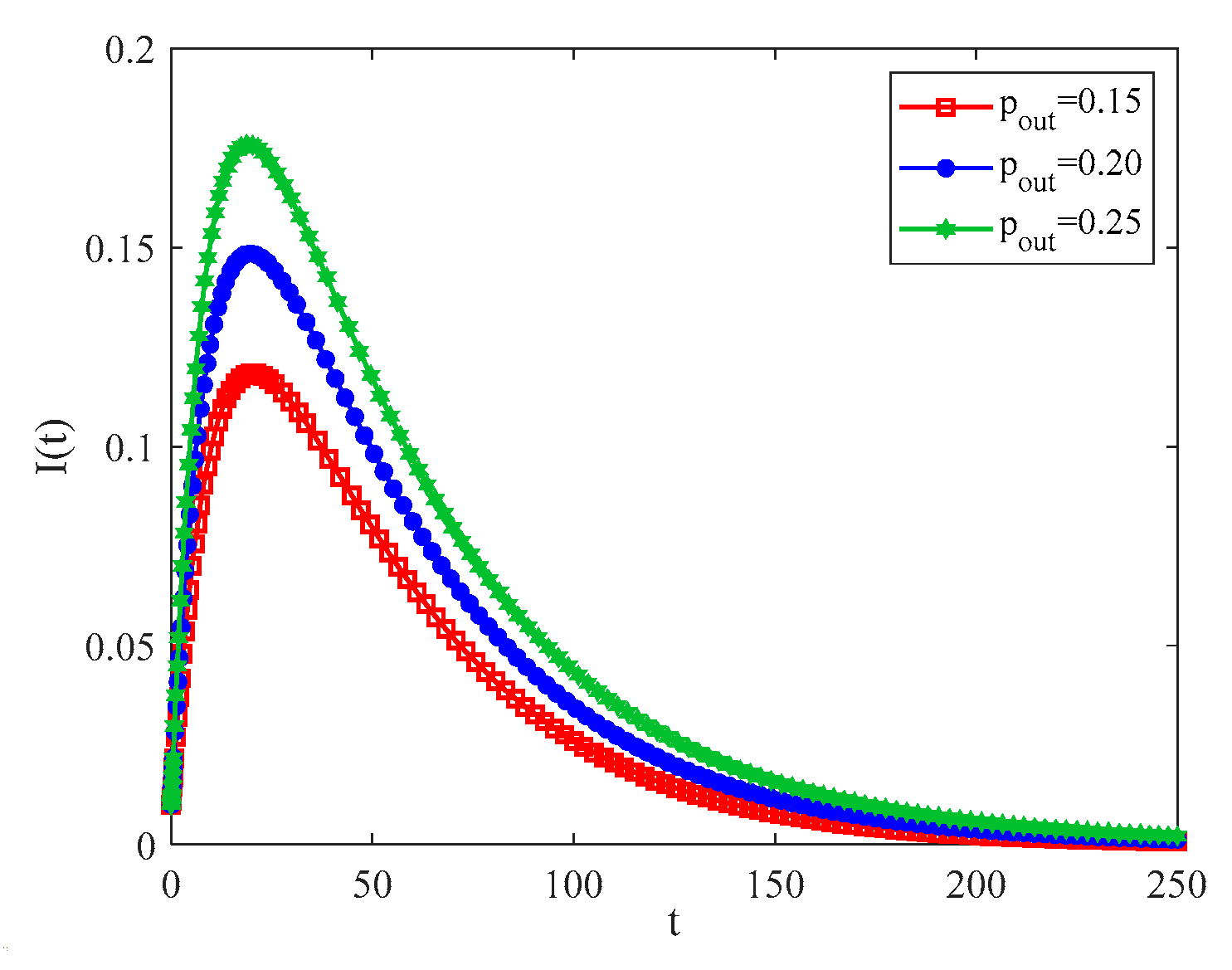
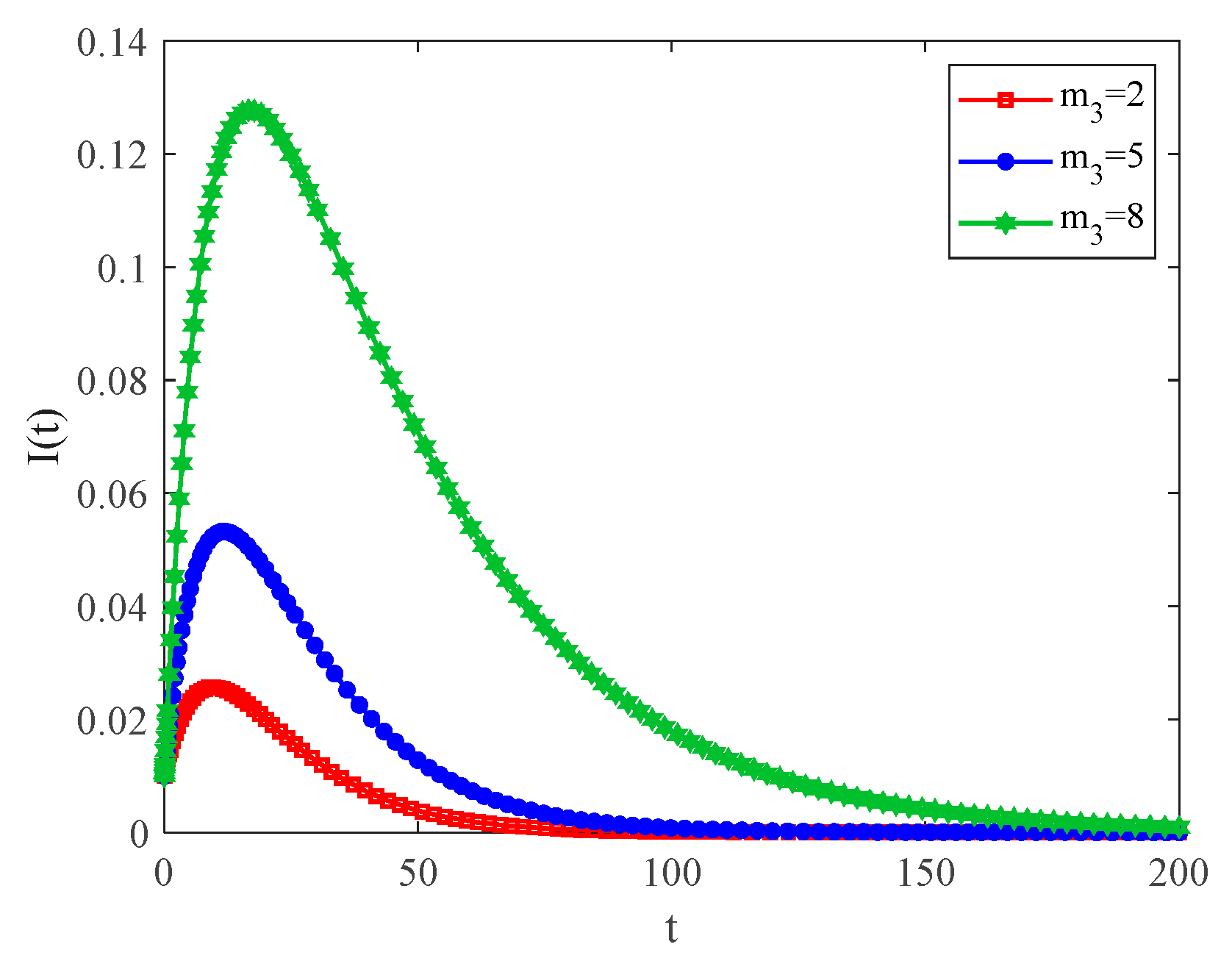
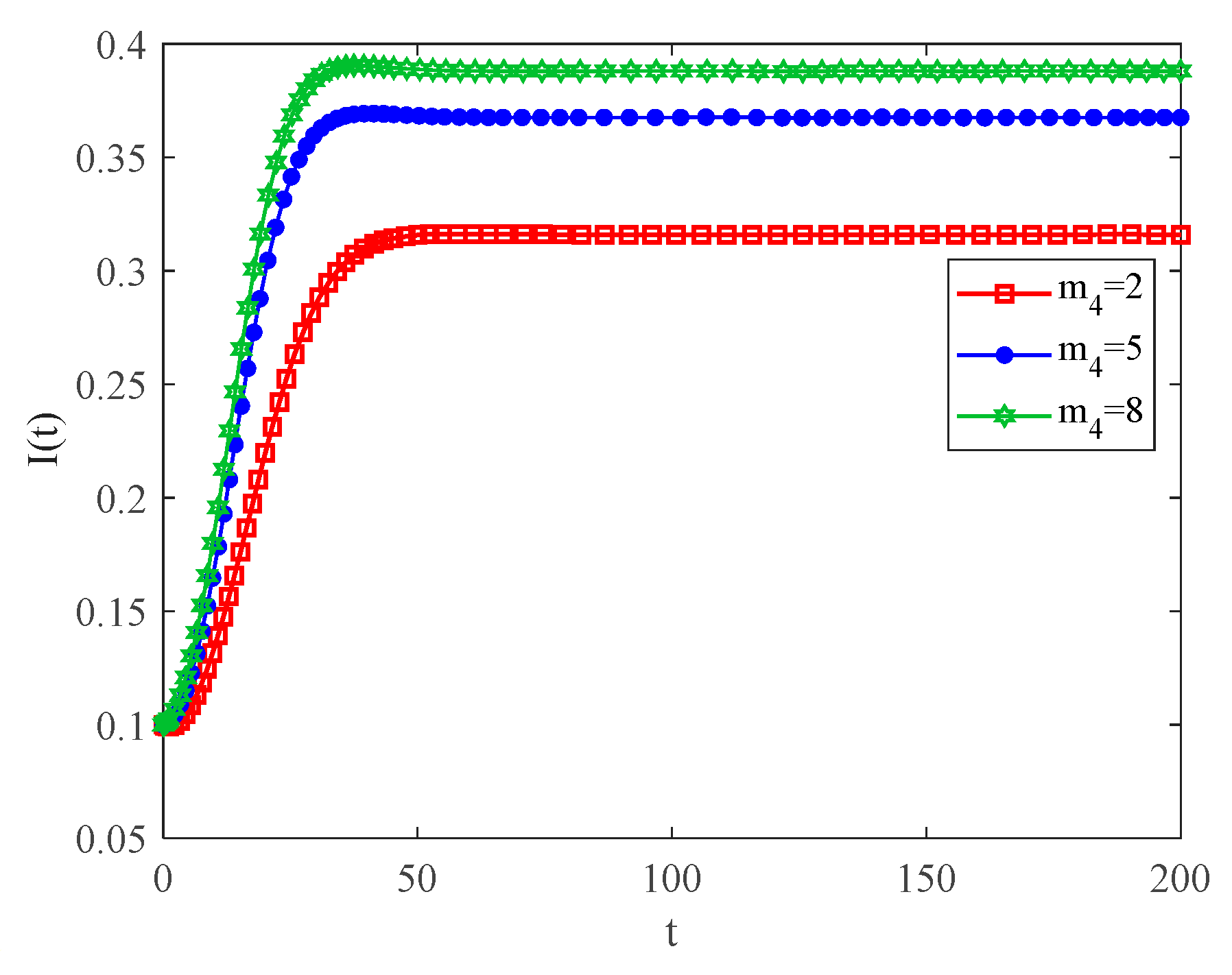
4.2. The Influence of the Connection Rate and Connected Edges on Infection Density
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, Y.W.; Song, Y.R.; Jiang, G.P. Global dynamics of a novel multi-group model for computer worms. Chin. Phys. B 2013, 22, 040204. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Song, H.T.; Wang, R.F.; Liu, S.Q.; Jin, Z.; He, D. Global stability and optimal control for a COVID-19 model with vaccination and isolation delays. Results Phys. 2022, 42, 106011. [Google Scholar] [CrossRef] [PubMed]
- Borge-Hohhoefer, J.; Meloni, S.; Goncalves, B.; Moreno, Y. Emergence of influential spreaders in modified rumor models. J. Stat. Phys. 2013, 151, 383–393. [Google Scholar] [CrossRef]
- Zhao, L.J.; Wang, Q.; Chen, J.J.; Chen, Y.; Wang, J.; Huang, W. Rumor spreading model with consideration of forgetting mechanism: A case of online blogging Live Journal. Physica A 2011, 390, 2619–2625. [Google Scholar] [CrossRef]
- Carvalho, S.A. Modeling and analysis of dengue epidemic: Control methods and vaccination strategies. Theory Biosci. 2019, 138, 223–239. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2000, 86, 3200–3203. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic spreading in finite size scale-free networks. Phys. Rev. E 2002, 65, 035108. [Google Scholar] [CrossRef]
- Dickison, M.; Havlin, S.; Stanley, H.E. Epidemics on interconnected networks. Phys. Rev. E 2012, 85, 066109. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Huang, T.; Guo, Z.X.; He, Z.G. Complex-network-based traffic network analysis and dynamics: A comprehensive review. Phys. A Stat. Mech. Its Appl. 2022, 607, 128063. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Huang, W.; Li, C.G. Epidemic spreading in scale-free networks with community structure. J. Stat. Mech. Theory Exp. 2007, 2007, P01014. [Google Scholar] [CrossRef]
- Zhang, J.P.; Jin, Z. Epidemic spreading on complex networks with community structure. Appl. Math. Comput. 2012, 219, 2829–2838. [Google Scholar] [CrossRef]
- Chen, J.; Hu, M.B.; Li, M. Traffic-driven epidemic spreading in multiplex networks. Phys. Rev. E 2020, 101, 012301. [Google Scholar] [CrossRef]
- Li, J.X.; Wang, J.; Jin, Z. SIR dynamics in random networks with communities. J. Math. Biol. 2018, 77, 1117–1151. [Google Scholar] [CrossRef]
- Wang, S.F.; Gong, M.G.; Liu, W.F.; Wu, Y. Preventing epidemic spreading in networks by community detection and memetic algorithm. Appl. Soft Comput. J. 2020, 89, 106–118. [Google Scholar] [CrossRef]
- Arenas, A.; Cota, W.; Gomez-Gardenes, J.; Gomez, S.; Granell, C.; Matamalas, J.T.; Soriano-Panos, D.; Steinegger, B. Derivation of the effective reproduction number R for COVID-19 in relation to mobility restrictions and confinement. medRxiv 2020, 11, 2020-04. [Google Scholar]
- Matamalas, J.T.; Arenas, A.; Gomez, S. Effective approach to epidemic containment using link equations in complex networks. Sci. Adv. 2018, 4, eaau4212. [Google Scholar] [CrossRef]
- Zhua, P.C.; Wang, X.; Zhi, Q.; Ma, J.Z.; Guo, Y.M. Analysis of epidemic spreading process in multi-communities. Chaos Solitons Fractals 2018, 109, 231–237. [Google Scholar] [CrossRef]
- Fu, X.H.; Song, Q.L.; Li, S.Q.; Shen, Y.; Yue, S. Dynamic changes in bacterial community structure are associated with distinct priming effect patterns. Soil Biol. Biochem. 2022, 169, 108671. [Google Scholar] [CrossRef]
- Shao, F.; Jiang, G.P. Traffic driven epidemic spreading in homogeneous networks with community structure. J. Netw. 2012, 7, 850–855. [Google Scholar] [CrossRef]
- Gong, Y.W.; Song, Y.R.; Jiang, G.P. Time-varying human mobility patterns with metapopulation epidemic dynamics. Physica 2013, 392, 4242–4251. [Google Scholar] [CrossRef] [PubMed]
- Saramfiki, J.; Kaski, K. Modelling development of epidemics with dynamic small world networks. J. Theor. Biol. 2005, 234, 413–421. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.X.; Zhang, J.G.; An, X.L.; Nan, M.; Qiao, S. Stability and Hopf bifurcation analysis of flux neuron model with double time delays. J. Appl. Math. Comput. 2022, 68, 4017–4050. [Google Scholar] [CrossRef]
- Torri, G.; Giacometti, R. Financial contagion in banking networks with community structure. Commun. Nonlinear Sci. Numer. Simul. 2022, 117, 106924. [Google Scholar] [CrossRef]
- Liu, Z.H.; Hu, B.B. Epidemic spreading in community networks. Europhys. Lett. 2005, 72, 315–321. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Salathe, M.; Jones, J.H. Dynamics and control of diseases in networks with community structure. PLoS Comput. Biol. 2010, 6, 1000736. [Google Scholar] [CrossRef]
- Stegehuis, C. Epidemic spreading on complex networks with community structures. Sci. Rep. 2016, 6, 29748. [Google Scholar] [CrossRef]
- Young, J.-G.; Hébert-Dufresne, L.; Allard, A.; Dubé, L.J. Growing networks of overlapping communities with internal structure. Phys. Rev. E 2016, 94, 022317. [Google Scholar] [CrossRef]
- Li, C.C.; Jiang, G.P.; Song, Y.R.; Xia, L.L.; Li, Y.W.; Song, B. Modeling and analysis of epidemic spreading on community networks with heterogeneity. J. Parallel Distrib. Comput 2018, 119, 136–145. [Google Scholar] [CrossRef]
- Xu, Z.P.; Li, K.Z.; Sun, M.F.; Fu, X.C. Interaction between epidemic spread and collective behavior in scale-free networks with community structure. J. Theor. Biol. 2019, 462, 122–133. [Google Scholar] [CrossRef]
- Dansu, E.J.; Seno, H. A model for epidemic dynamic in a community with visitor subpopulation. J. Theor. Biol. 2019, 478, 115–127. [Google Scholar] [CrossRef]
- Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]


| Parameter | Explanation |
|---|---|
| Infection rate in the community | |
| Probability of nodes being connected in the inner community at the initial moment | |
| Probability of nodes being connected in the inner community at each time step | |
| Probability of nodes being connected in the outer community at each time step | |
| Recovery rate of infected in the community | |
| Probability of recovered reverting to susceptible | |
| Coefficient factor affecting the infection rate in the outer community |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Gu, Z.; Yang, L. Effects of Community Connectivity on the Spreading Process of Epidemics. Entropy 2023, 25, 849. https://doi.org/10.3390/e25060849
Gao Z, Gu Z, Yang L. Effects of Community Connectivity on the Spreading Process of Epidemics. Entropy. 2023; 25(6):849. https://doi.org/10.3390/e25060849
Chicago/Turabian StyleGao, Zhongshe, Ziyu Gu, and Lixin Yang. 2023. "Effects of Community Connectivity on the Spreading Process of Epidemics" Entropy 25, no. 6: 849. https://doi.org/10.3390/e25060849
APA StyleGao, Z., Gu, Z., & Yang, L. (2023). Effects of Community Connectivity on the Spreading Process of Epidemics. Entropy, 25(6), 849. https://doi.org/10.3390/e25060849





