Self-Organizing Interval Type-2 Fuzzy Neural Network Compensation Control Based on Real-Time Data Information Entropy and Its Application in n-DOF Manipulator
Abstract
1. Introduction
- (1)
- Most of the previous studies are aimed at suppressing or compensating for a certain type of interference [26,27,28,29]. However, as a multi-coupling complex system with fast state change, the manipulator system has multiple types of disturbances in the movement process, and the information entropy of real-time data in the control process is high, and most of the disturbances are time-varying random disturbances [30].
- (2)
- While pursuing high precision, previous studies usually inevitably increase the complexity of the control algorithm and increase the time complexity of the control system calculation [31,32,33], thus making the response time to significantly longer. In the n-DOF manipulator control system, the state response speed is very fast and the controller response speed is very high. It is difficult for the existing research to be competent in this kind of control work.
- (3)
- In the existing research of the fuzzy self-organizing control framework, the initial rules and structure of fuzzy neural network have a great influence on the control effect [34,35]. The fuzzy neural network usually is self-organized in the control process after setting one or several good initial rules. However, in complex object control, it is usually impossible to set a suitable initial rule in advance, and the network needs to learn by itself from the first rule.
- (1)
- An error compensation algorithm for a n-DOF manipulator is proposed, which compensates various types of error perturbations in various mechanisms by directly comparing input and output errors, and reduces the computational complexity of data-driven fuzzy algorithms when the amount of real-time data and information entropy are large. At the same time, the stability of the closed-loop control systems are proved by Lyapunov stability theory, and the simulation also confirms its effect.
- (2)
- A fuzzy network structure self-organization method and parameter self-adaptation method are proposed for the control object with high real-time requirements of electromechanical system. The time complexity and response time of this method can meet the requirements of real-time control.
- (3)
- A fuzzy rule self-organizing increase and decrease index function is proposed. This function does not need the overall information of the data set (such as the overall variance, mean, etc., of the data set) nor does it need to store the previous data information. It only needs the current data information at each moment to guide the self-organizing network to achieve reasonable rule increase and decrease. At the same time, this paper explains the reason why the function is suitable for fuzzy self-organizing network from the theoretical structure level of the function.
2. Modeling of the Robotic Arm
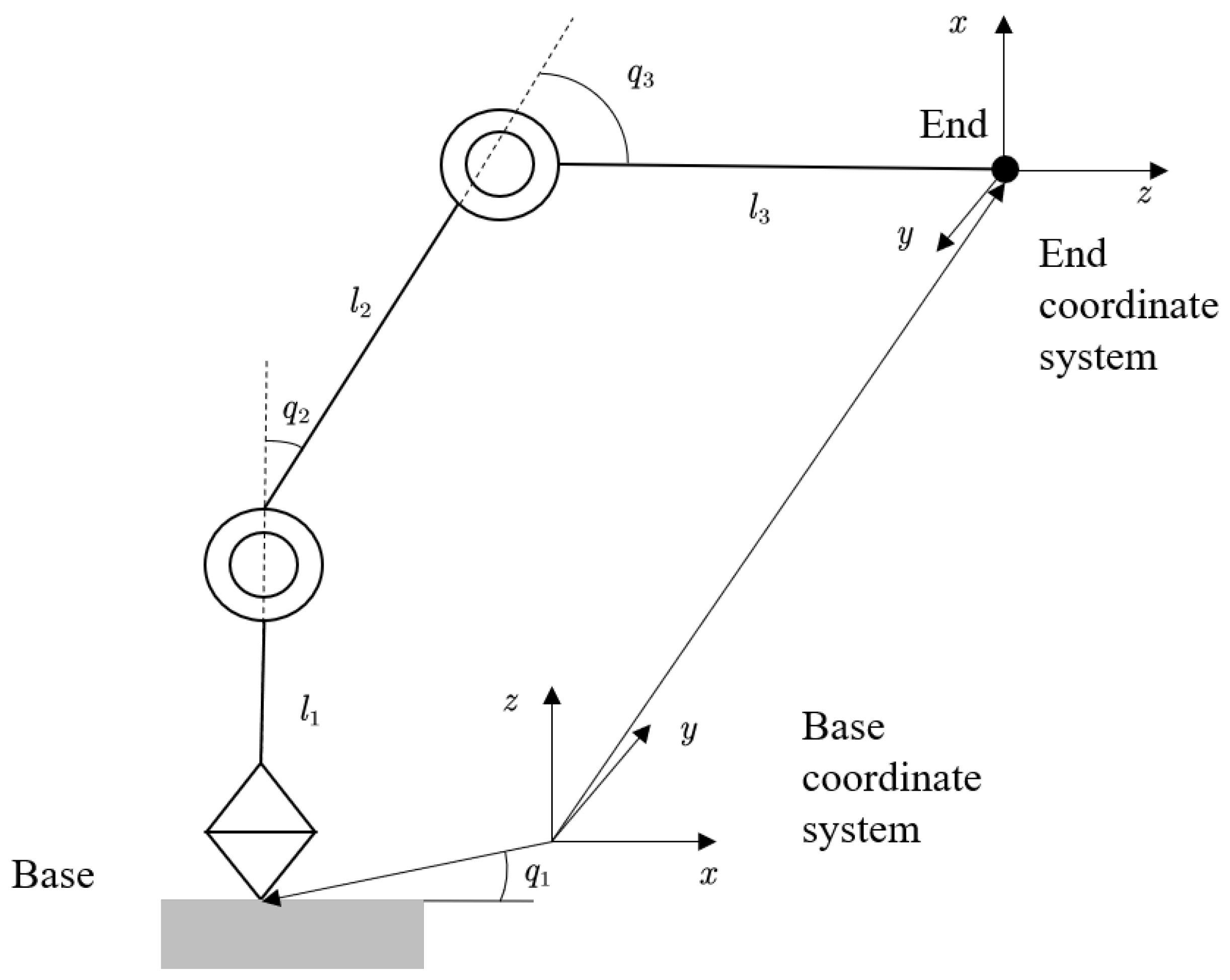
2.1. Kinematic Modeling of the Manipulator
2.2. Dynamic Modeling of the Manipulator
- (1)
- The inertia matrix H is a symmetric positive definite matrix and bounded, that is
- (2)
- is an obliquely symmetric matrix, that is
3. Design of Robotic Arm Controller
3.1. Design of Sliding Mode Controller
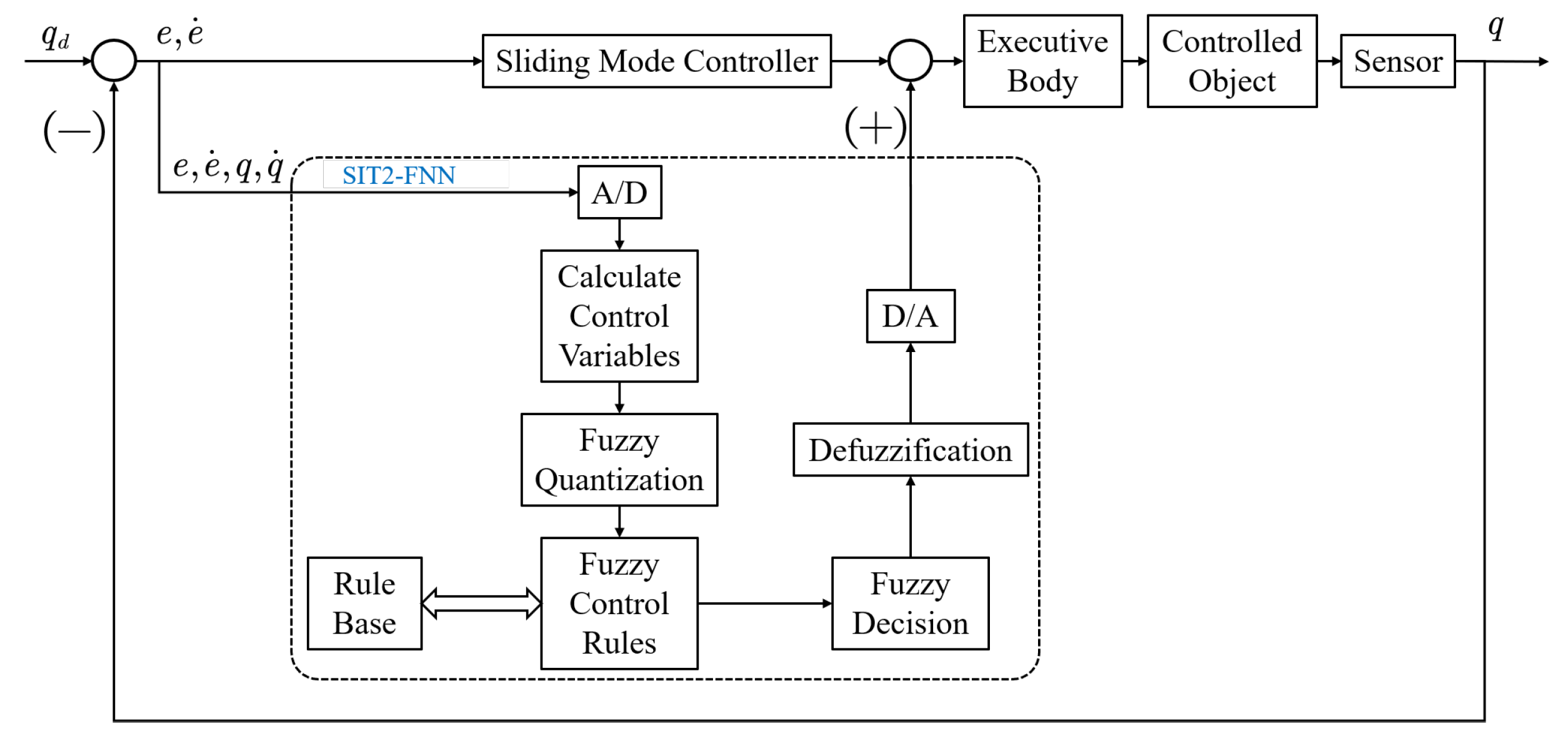
3.2. Design of Self-Organizing Interval Type-2 Fuzzy Error Compensation Controller (T2-SOFNNEC)
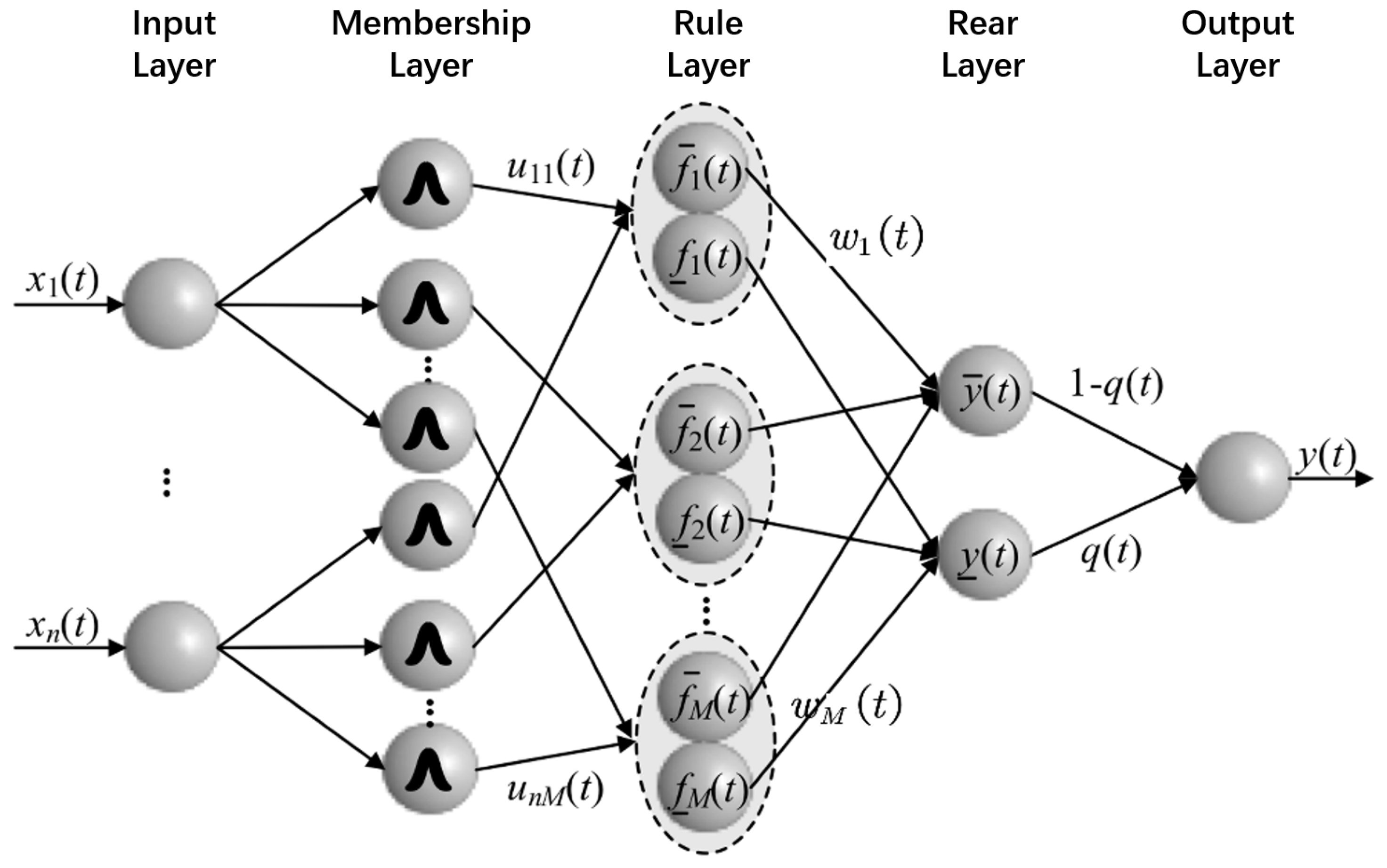
- (1)
- Input layer: The input layer is the transmission of the reference input, and each neuron represents an input dimension.
- (2)
- Membership layer: Each neuron in the membership layer represents the antecedent of a fuzzy rule, and each membership function takes the Gaussian function as the basis function, which can be expressed asAmong them, represents the center of the jth rule input in the ith dimension, represents the width of the jth rule input in the ith dimension, and represents the half interval width of the membership function.
- (3)
- Rule layer: The value of each neuron in the rule layer is normalized by the corresponding membership degrees of all inputs, which can be expressed as
- (4)
- Consequent layer: The output of the consequent layer is calculated by multiplying the rule value by the weight:
- (5)
- Output layer: The function of the output layer is to downgrade the interval type-2 fuzzy system, and its output value is the product of the consequent value and the proportional coefficient:
- (1)
- Estimation error
- (2)
- Experience error
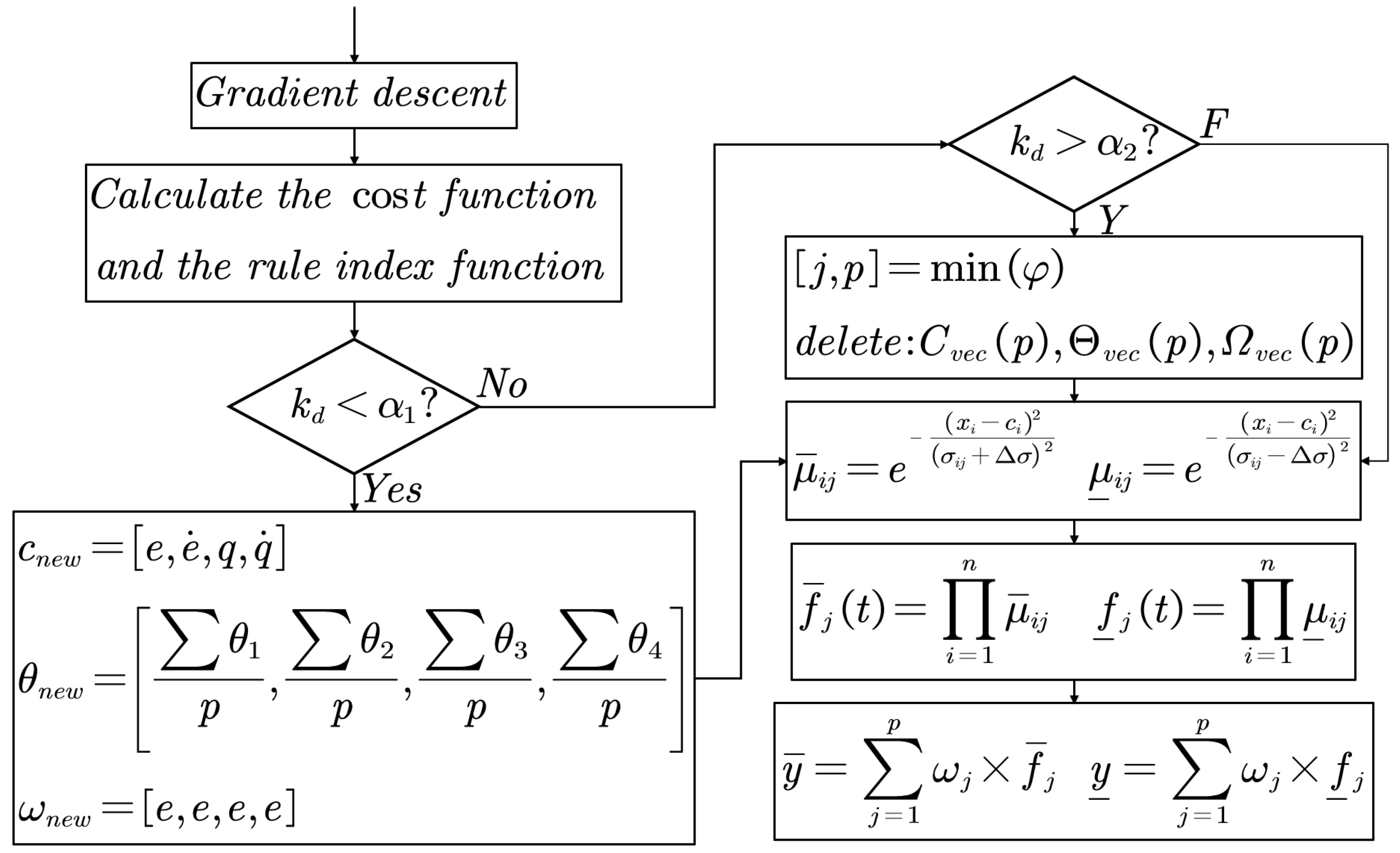
- (3)
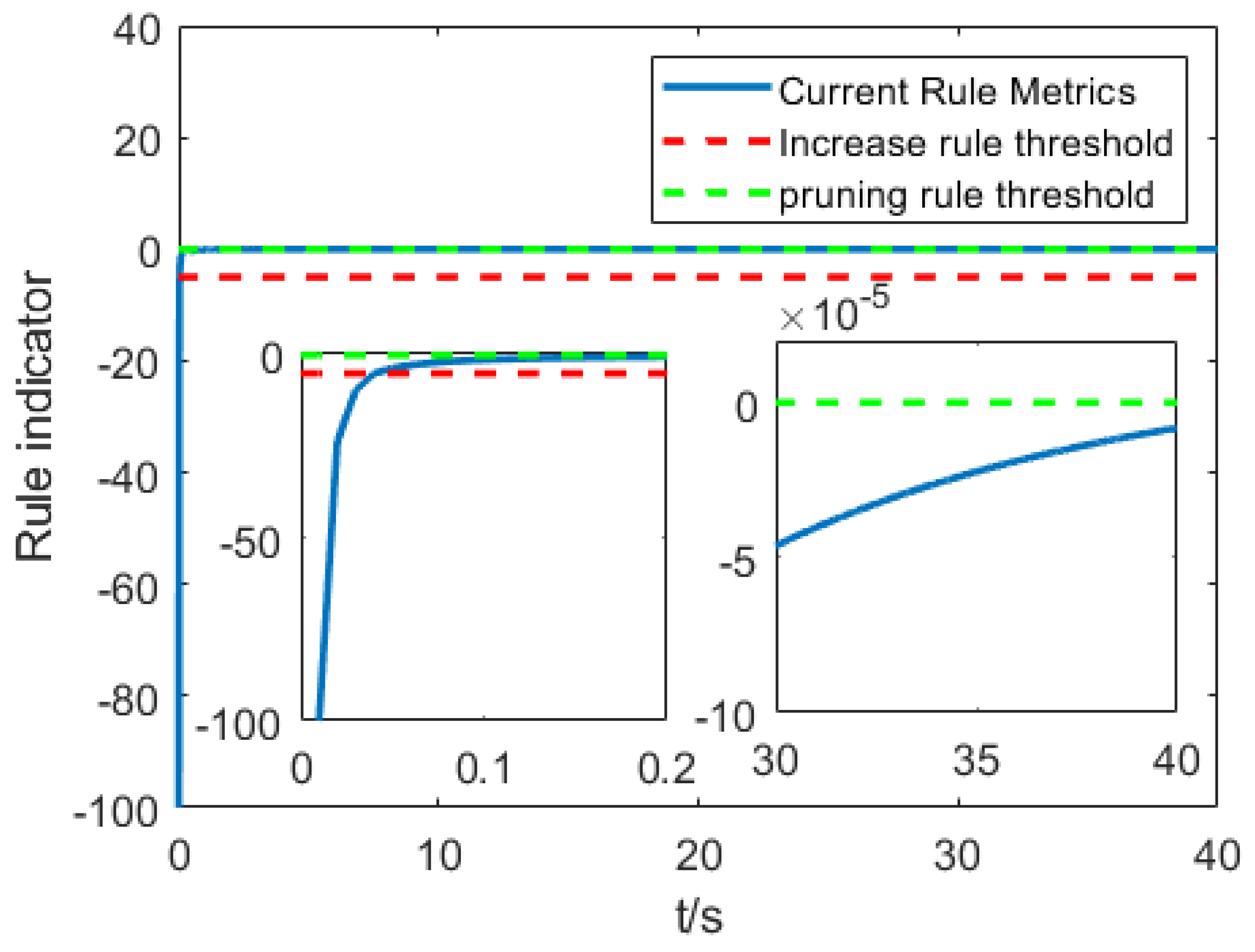
- Rule increase and decrease function
- (4)
- Rule growth stage
- (5)
- Rule deletion stage
- (6)
- Parameter optimization stage
4. Stability Analysis
4.1. Stability Analysis of Sliding-Mode Control Loop
4.2. Stability Analysis of Self-Organized Growth Stage
4.3. Stability Analysis of Self-Organizing Cut-Out Stage
5. Simulation
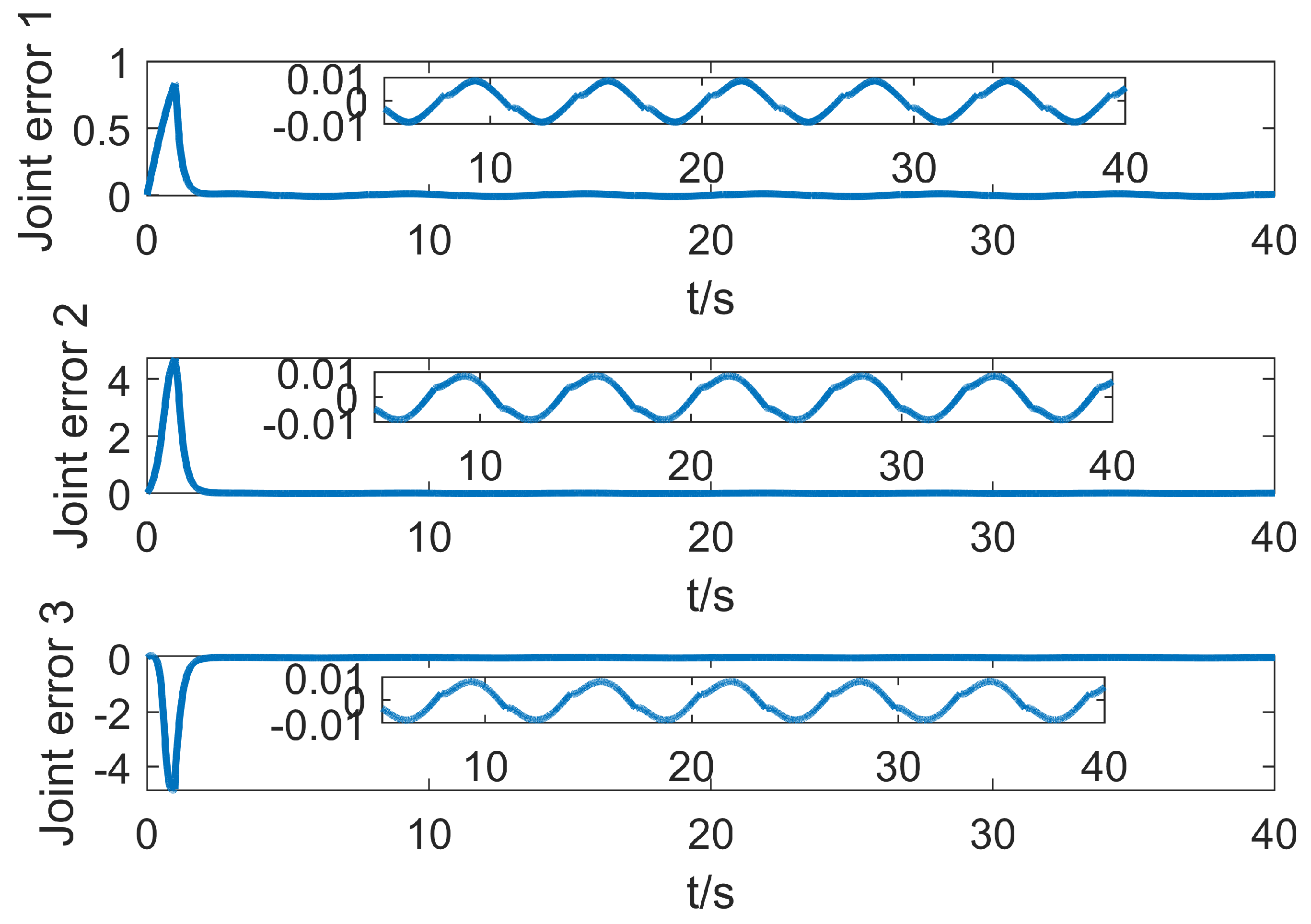
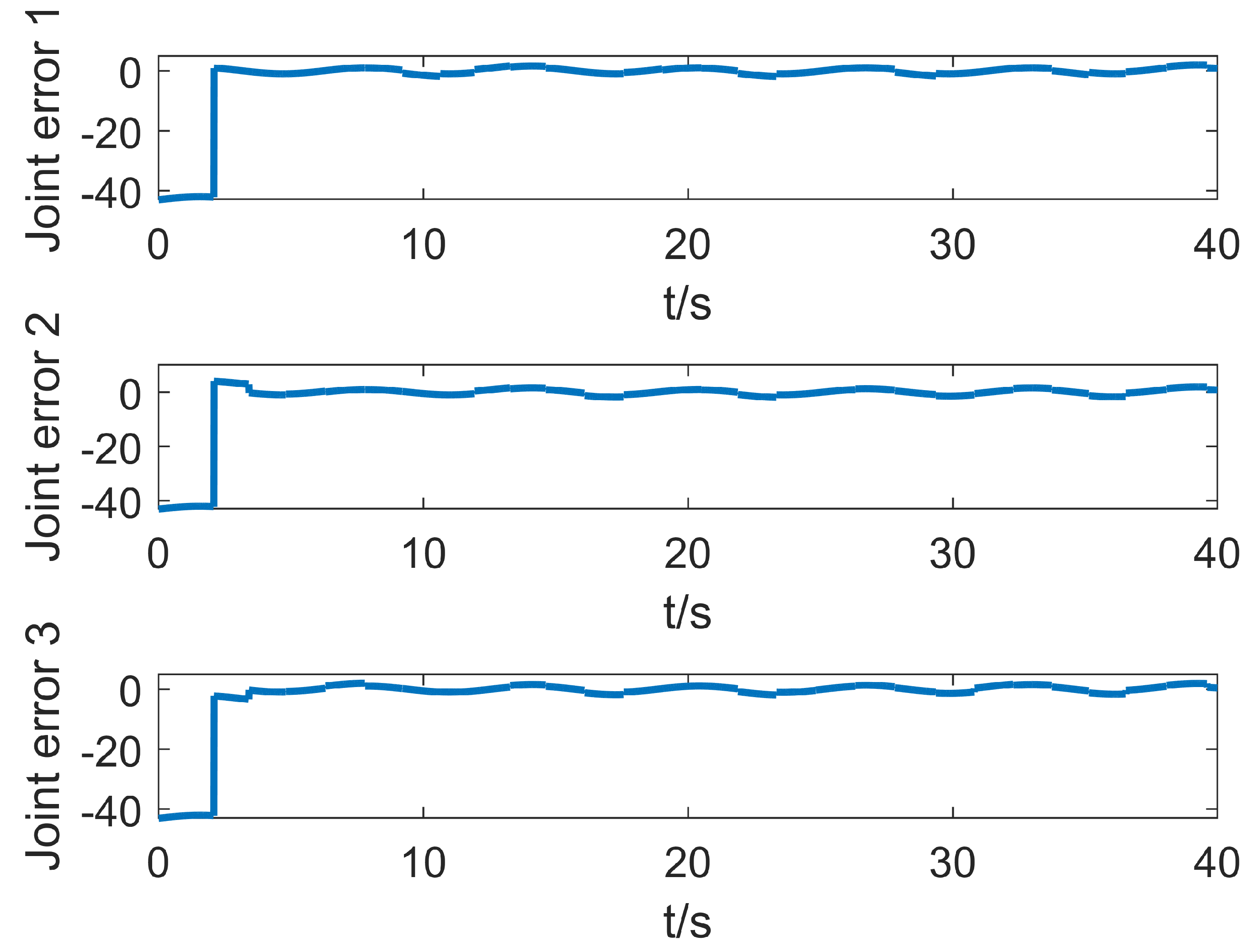
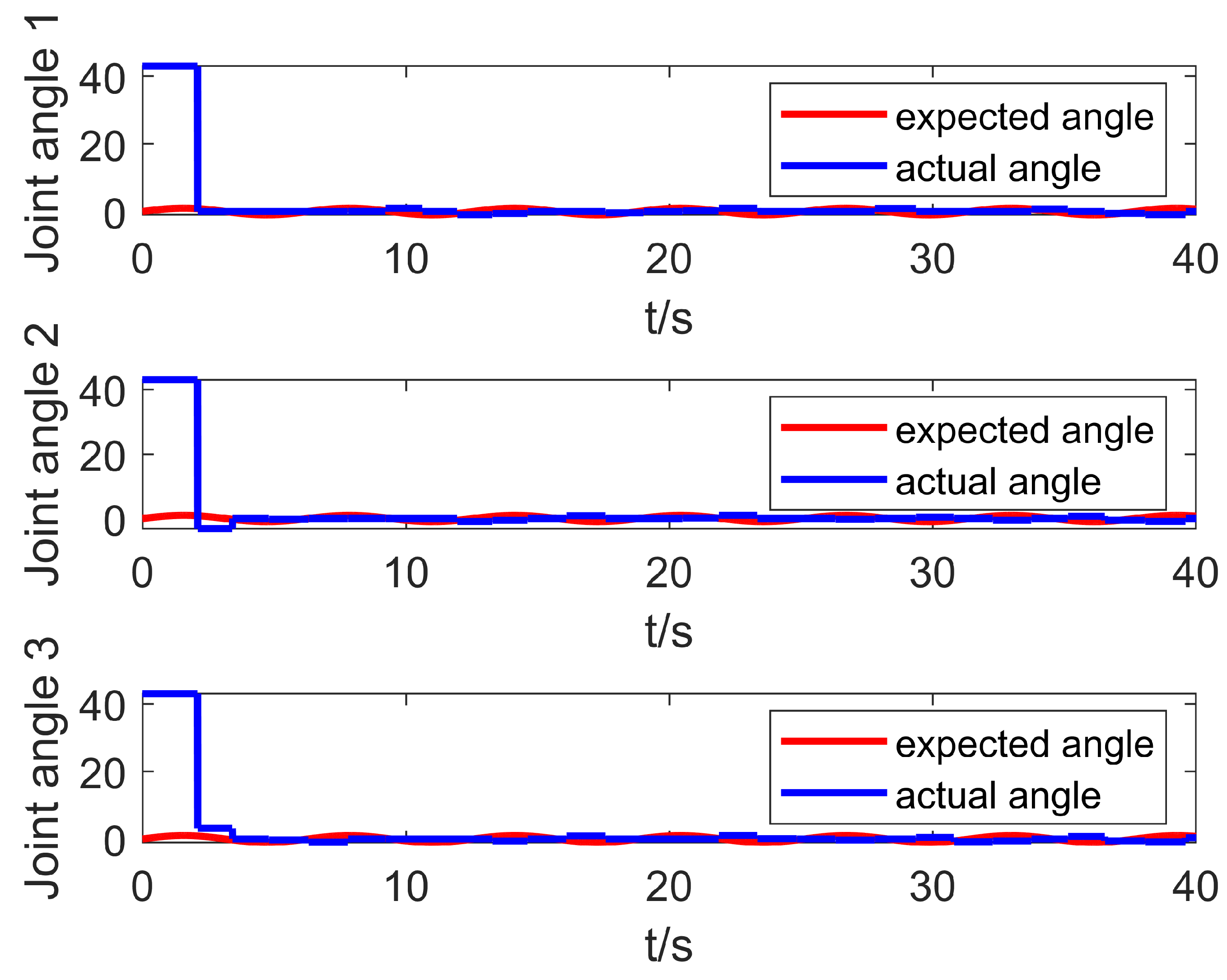
5.1. Simulation with Base Jitter
5.2. Simulation with Base Jitter and Signal Interference
5.3. Simulation with Base Jitter, Signal Interference, and Time Delay
5.4. Coppeliasim-MATLAB Co-Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| The th term of the centrifugal force matrix | |
| C | Centrifugal force matrix |
| The center of the jth rule | |
| e | Control-error signal |
| The upper output of the rule layer | |
| The lower output of the consequent layer | |
| Force of friction | |
| F | Static and dynamic friction matrix |
| The ith gravitational vector | |
| G | Gravitational vector matrix |
| The th term of the inertial matrix | |
| H | Inertial matrix |
| The index function | |
| The length of the ith arm | |
| Expected angle | |
| The actual angle of the ith joint | |
| The upper output of the consequent layer | |
| The lower output of the consequent layer | |
| y | The output of the FNN |
| The parameter of rule adaptive | |
| The width of the jth rule | |
| The uncertain disturbance term caused by modeling error and external interference | |
| The value of Upper membership function | |
| The value of Lower membership function | |
| Estimation error | |
| Experience error | |
| Control moment |
References
- Qin, B.; Luo, Q.; Luo, Y.; Zhang, J.; Liu, J.; Cui, L. Research and Application of Key Technologies of Edge Computing for Industrial Robots. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; Volume 1, pp. 2157–2164. [Google Scholar]
- Kumar, S.; Savur, C.; Sahin, F. Dynamic awareness of an industrial robotic arm using time-of-flight laser-ranging sensors. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 2850–2857. [Google Scholar]
- Yang, J.; Zhang, G.; Wang, L.; Wang, J.; Wang, H. Multi-degree-of-freedom joint nonlinear motion control with considering the friction effect. In Proceedings of the 2021 IEEE 19th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 21–23 January 2021; pp. 000211–000216. [Google Scholar]
- Zhao, M.; Anzai, T.; Shi, F.; Chen, X.; Okada, K.; Inaba, M. Design, modeling, and control of an aerial robot dragon: A dual-rotor-embedded multilink robot with the ability of multi-degree-of-freedom aerial transformation. IEEE Robot. Autom. Lett. 2018, 3, 1176–1183. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, C.; Wang, J. Trajectory optimization and closed-loop feedback control of multi-degree-of-freedom robot. In Proceedings of the 2021 IEEE International Conference on Emergency Science and Information Technology (ICESIT), Chongqing, China, 22–24 November 2021; pp. 11–14. [Google Scholar]
- Yan, W.; Liu, Y.; Lan, Q.; Zhang, T.; Tu, H. Trajectory planning and low-chattering fixed-time nonsingular terminal sliding mode control for a dual-arm free-floating space robot. Robotica 2022, 40, 625–645. [Google Scholar] [CrossRef]
- Li, F.; Peng, H.; Yang, H.; Kan, Z. A symplectic kinodynamic planning method for cable-driven tensegrity manipulators in a dynamic environment. Nonlinear Dyn. 2021, 106, 2919–2941. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, C.; Cao, H.; Dian, S.; Xie, X. Multiobjective Optimization Design of Interpretable Evolutionary Fuzzy Systems With Type Self-Organizing Learning of Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2023, 31, 1638–1652. [Google Scholar] [CrossRef]
- Wang, W.; Tian, W.; Liao, W.; Li, B.; Hu, J. Error compensation of industrial robot based on deep belief network and error similarity. Robot. Comput.-Integr. Manuf. 2022, 73, 102220. [Google Scholar] [CrossRef]
- Khorashadizadeh, S.; Sadeghijaleh, M. Adaptive fuzzy tracking control of robot manipulators actuated by permanent magnet synchronous motors. Comput. Electr. Eng. 2018, 72, 100–111. [Google Scholar] [CrossRef]
- Urrea, C.; Kern, J.; Alvarado, J. Design and evaluation of a new fuzzy control algorithm applied to a manipulator robot. Appl. Sci. 2020, 10, 7482. [Google Scholar] [CrossRef]
- Fateh, S.; Fateh, M.M. Adaptive fuzzy control of robot manipulators with asymptotic tracking performance. J. Control. Autom. Electr. Syst. 2020, 31, 52–61. [Google Scholar] [CrossRef]
- Klimchik, A.; Pashkevich, A. Robotic manipulators with double encoders: Accuracy improvement based on advanced stiffness modeling and intelligent control. IFAC-PapersOnLine 2018, 51, 740–745. [Google Scholar] [CrossRef]
- Bagheri, M.; Naseradinmousavi, P.; Krstić, M. Feedback linearization based predictor for time delay control of a high-DOF robot manipulator. Automatica 2019, 108, 108485. [Google Scholar] [CrossRef]
- Hu, S. Sliding Mode Control of Nonlinear Multi Joint Robot System; National Defense Industry Press: Beijing, China, 2015. [Google Scholar]
- Yang, Q.; Saeedifard, M.; Perez, M.A. Sliding mode control of the modular multilevel converter. IEEE Trans. Ind. Electron. 2018, 66, 887–897. [Google Scholar] [CrossRef]
- Mei, K.; Ding, S.; Chen, X. Fuzzy non-singular terminal sliding mode controller design for nonlinear systems with input saturation. Int. J. Fuzzy Syst. 2020, 22, 2271–2283. [Google Scholar] [CrossRef]
- Khan, M.U.; Kara, T. Adaptive type-2 neural fuzzy sliding mode control of a class of nonlinear systems. Nonlinear Dyn. 2020, 101, 2283–2297. [Google Scholar] [CrossRef]
- Elleuch, I.; Khedher, A.; Othman, K.B. State and faults estimation based on proportional integral sliding mode observer for uncertain Takagi–Sugeno fuzzy systems and its application to a turbo-reactor. Int. J. Fuzzy Syst. 2017, 19, 1768–1781. [Google Scholar] [CrossRef]
- Zhao, T.; Zou, X.; Dian, S. Fixed-time observer-based adaptive fuzzy tracking control for Mecanum-wheel mobile robots with guaranteed transient performance. Nonlinear Dyn. 2022, 107, 921–937. [Google Scholar] [CrossRef]
- Zhao, T.; Tong, W.; Mao, Y. Hybrid Non-singleton Fuzzy Strong Tracking Kalman Filtering for High Precision Photoelectric Tracking System. IEEE Trans. Ind. Inf. 2023, 19, 2395–2408. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, M. Fuzzy control systems: Past, present and future. IEEE Comput. Intell. Mag. 2019, 14, 56–68. [Google Scholar] [CrossRef]
- Yan, W.; Zhao, T.; Gong, X. An Explicit-Time and Explicit-Accuracy Control for A State-constrained Nonstrict-feedback Uncertain System Based on Adaptive Fuzzy Dynamic-approximation. J. Frankl. Inst. 2023. [Google Scholar] [CrossRef]
- Zhao, T.; Cao, H.; Dian, S. A Self-Organized Method for a Hierarchical Fuzzy Logic System based on a Fuzzy Autoencoder. IEEE Trans. Fuzzy Syst. 2022, 30, 5104–5115. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, C.; Cao, H. Evolutionary self-organizing fuzzy system using fuzzy-classification-based social learning particle swarm optimization. Inf. Sci. 2022, 606, 92–111. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhao, S.; Li, H.; Lu, R.; Wu, C. Adaptive neural network tracking control for robotic manipulators with dead zone. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3611–3620. [Google Scholar] [CrossRef] [PubMed]
- Baek, J.; Kwon, W.; Kim, B.; Han, S. A widely adaptive time-delayed control and its application to robot manipulators. IEEE Trans. Ind. Electron. 2018, 66, 5332–5342. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Sekiguchi, H.; Nozaki, T.; Ugurlu, B.; Ohnishi, K. A stability analysis for the acceleration-based robust position control of robot manipulators via disturbance observer. IEEE/ASME Trans. Mech. 2018, 23, 2369–2378. [Google Scholar] [CrossRef]
- Xie, L.; Si, J.; Hu, Y.; Wang, Z. Overview of 2-degree-of-freedom rotary-linear motors focusing on coupling effect. IEEE Trans. Magn. 2019, 55, 1–11. [Google Scholar] [CrossRef]
- Song, Z.; Li, J.; Li, G.; He, Y.; Zou, F. Flutter Analysis and Modal Test of A Six-degree-of-freedom Industrial Manipulator. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 487–491. [Google Scholar]
- Xie, K.; Chen, C.; Lewis, F.L.; Xie, S. Adaptive asymptotic neural network control of nonlinear systems with unknown actuator quantization. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6303–6312. [Google Scholar] [CrossRef]
- Huang, D.; Yang, C.; Pan, Y.; Cheng, L. Composite learning enhanced neural control for robot manipulator with output error constraints. IEEE Trans. Ind. Inf. 2019, 17, 209–218. [Google Scholar] [CrossRef]
- Tafti, B.E.F.; Teshnehlab, M.; Khanesar, M.A. Recurrent interval type-2 fuzzy wavelet neural network with stable learning algorithm: Application to model-based predictive control. Int. J. Fuzzy Syst. 2020, 22, 351–367. [Google Scholar] [CrossRef]
- Nguyen, H.B.; Lin, C.M.; Huynh, T.T.; Cho, H.Y.; Pham, D.H.; Chao, F.; Thanh, H.L.N.N. Fuzzy Hybrid Neural Network Control for Uncertainty Nonlinear Systems Based on Enhancement Search Algorithm. Int. J. Fuzzy Syst. 2022, 24, 3384–3402. [Google Scholar] [CrossRef]
- Ma, Z.; Xu, X.; Xie, J.; Jiang, X.; Wang, F. Negative Stiffness Control of Quasi-Zero Stiffness Air Suspension via Data-Driven Approach with Adaptive Fuzzy Neural Network Method. Int. J. Fuzzy Syst. 2022, 24, 3715–3730. [Google Scholar] [CrossRef]
- Doan, Q.V.; Le, T.D.; Le, Q.D.; Kang, H.J. A neural network–based synchronized computed torque controller for three degree-of-freedom planar parallel manipulators with uncertainties compensation. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418767307. [Google Scholar] [CrossRef]
- Moldovan, L.; Gligor, A.; Grif, H.S.; Moldovan, F. Dynamic numerical simulation of the 6-PGK parallel robot manipulator. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2019, 20, 67–75. [Google Scholar]
- Poignet, P.; Gautier, M. Nonlinear model predictive control of a robot manipulator. In Proceedings of the 6th International Workshop on Advanced Motion Control, Proceedings (Cat. No. 00TH8494), Nagoya, Japan, 30 March–1 April 2000; pp. 401–406. [Google Scholar]
- Kovecses, J.; Piedboeuf, J.C.; Lange, C. Dynamics modeling and simulation of constrained robotic systems. IEEE/ASME Trans. Mech. 2003, 8, 165–177. [Google Scholar] [CrossRef]
- Hu, B.; Guan, Z.H.; Lewis, F.L.; Chen, C.P. Adaptive tracking control of cooperative robot manipulators with markovian switched couplings. IEEE Trans. Ind. Electron. 2020, 68, 2427–2436. [Google Scholar] [CrossRef]
- Han, H.; Wu, X.; Qiao, J. Design of robust sliding mode control with adaptive reaching law. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 4415–4424. [Google Scholar] [CrossRef]
- Han, H.G.; Li, J.M.; Wu, X.L.; Qiao, J.F. Cooperative strategy for constructing interval type-2 fuzzy neural network. Neurocomputing 2019, 365, 249–260. [Google Scholar] [CrossRef]
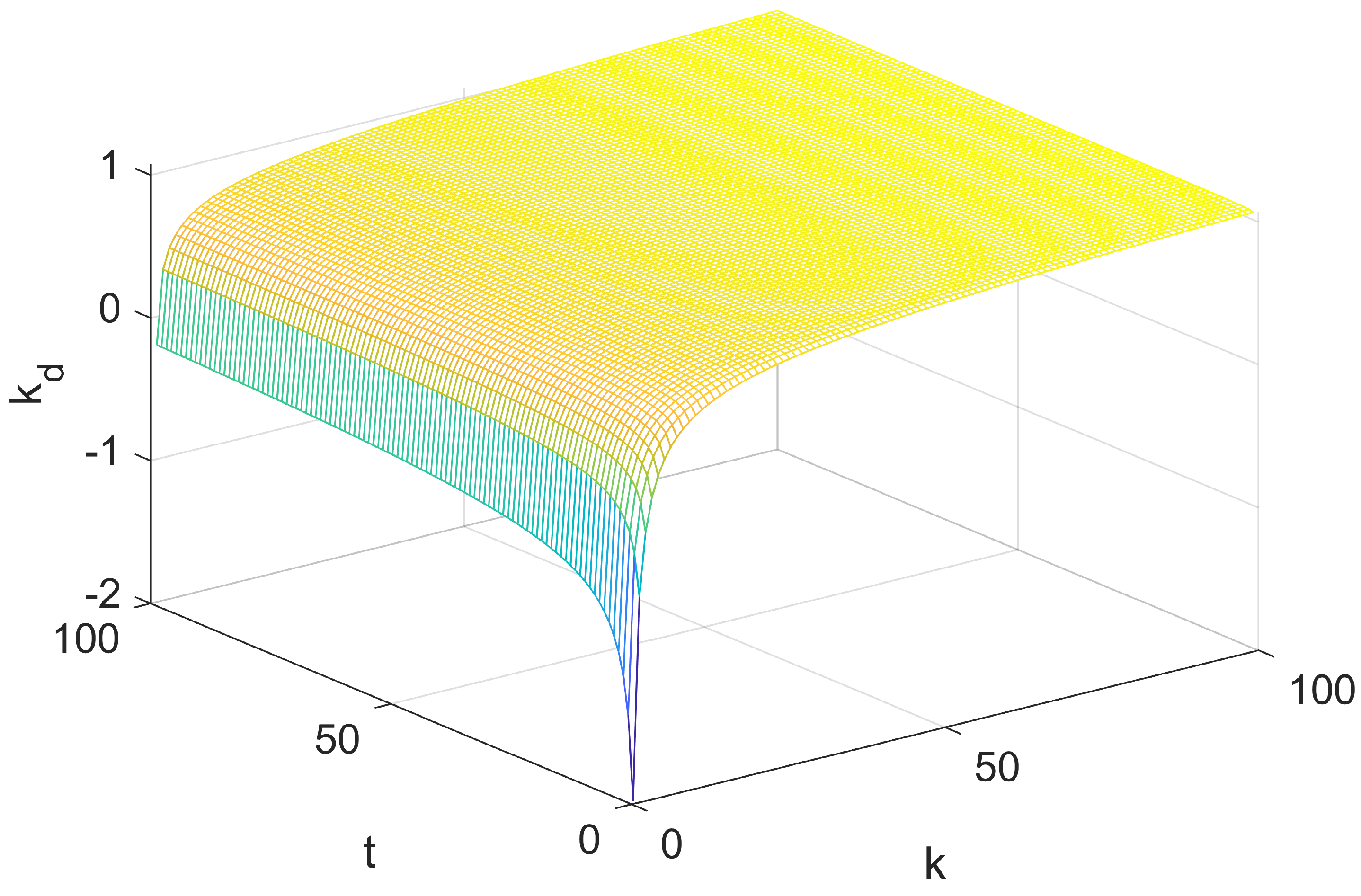
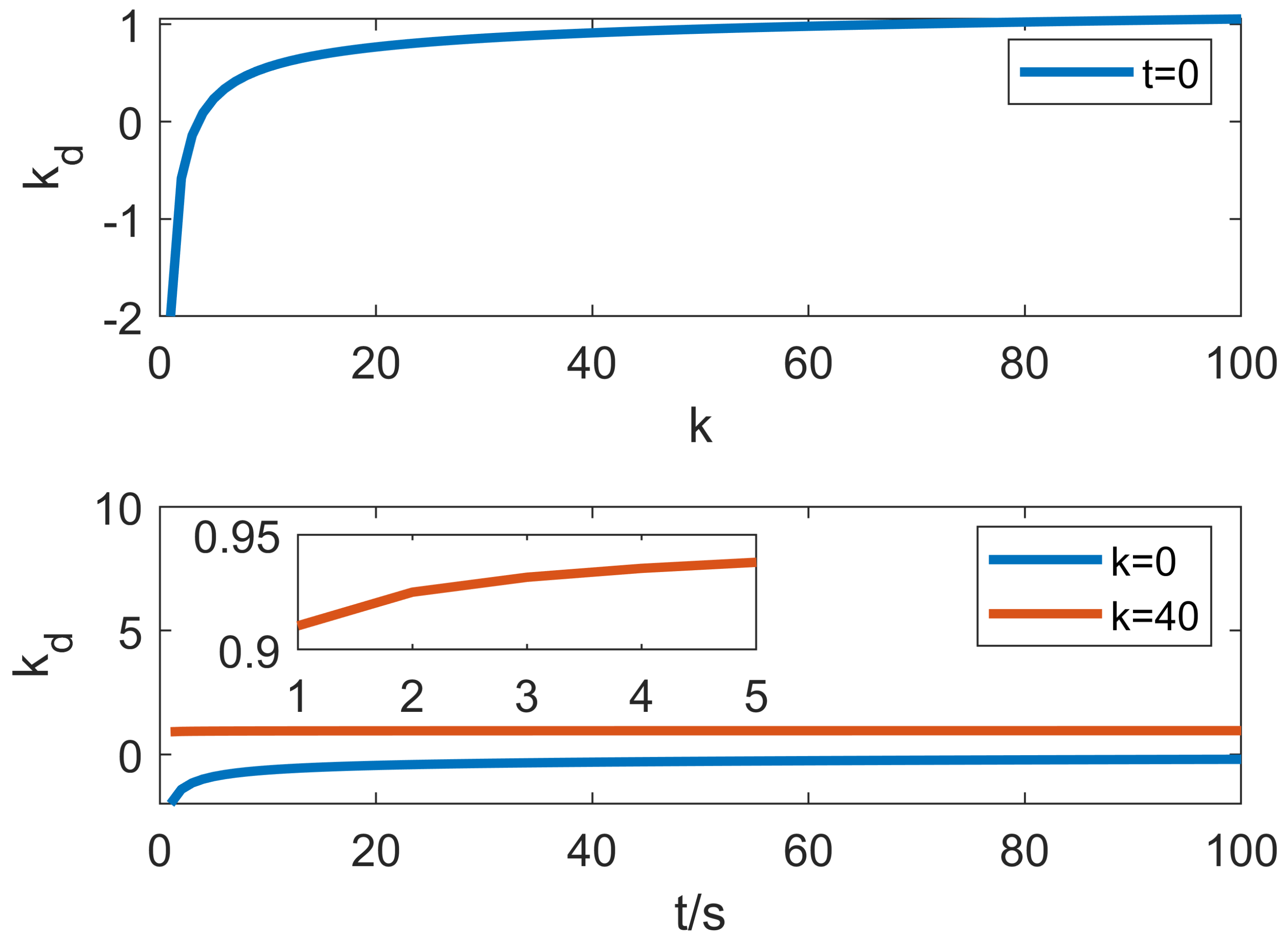


| DOF | Link Mass (kg) | Link Length//(m) | Link Centroid//(m) |
|---|---|---|---|
| 1 | 34 | 0 | 0 |
| 2 | 30 | 1 | 0.6 |
| 3 | 26 | 1 | 0.5 |
| DOF | Link’s Moment of Inertia about Its Axis of Rotation (kg·m) | Coulomb Friction Coefficient | Gravitational Acceleration (m/s) |
| 1 | 3.62 | 5 | 9.8 |
| 2 | 2.35 | 5 | 9.8 |
| 3 | 1.95 | 5 | 9.8 |
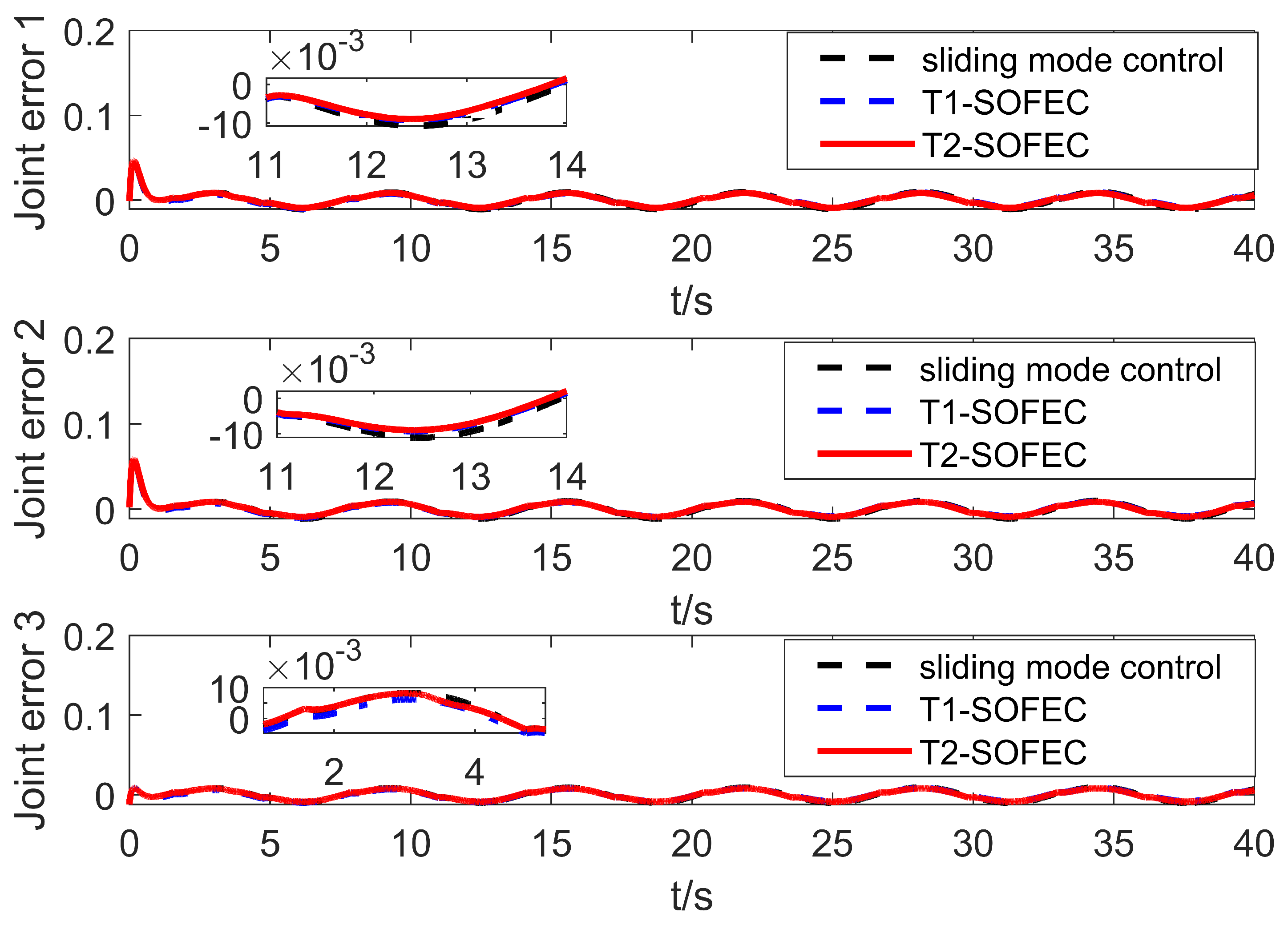
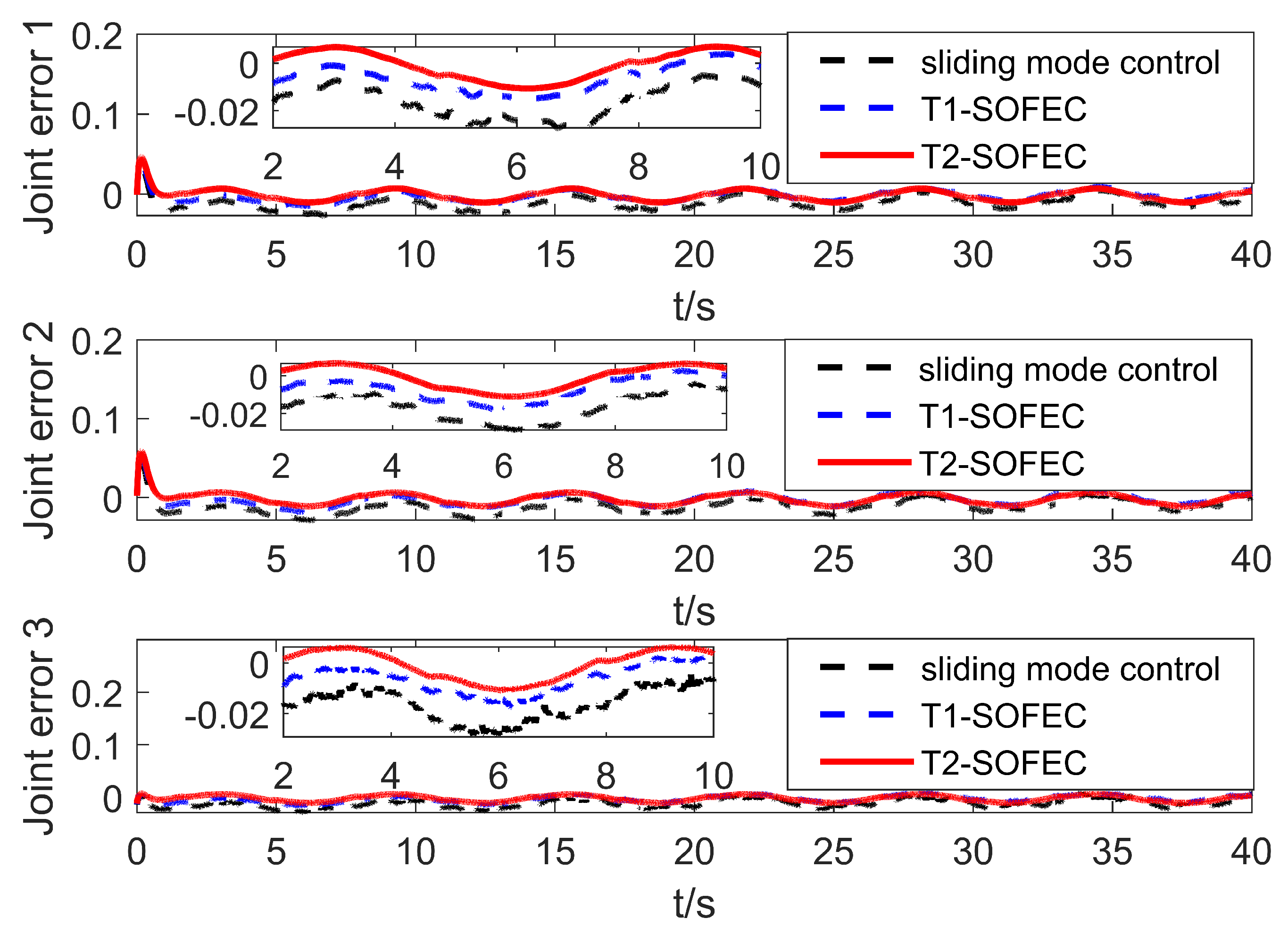
| Joint | SMC | T1-SOFNNEC | T2-SOFNNEC |
|---|---|---|---|
| 1 | 0.026075 | 0.021213 | 0.004734 |
| 2 | 0.029306 | 0.024071 | 0.004022 |
| 3 | 0.024777 | 0.020316 | 0.003727 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhao, T.; Liu, N. Self-Organizing Interval Type-2 Fuzzy Neural Network Compensation Control Based on Real-Time Data Information Entropy and Its Application in n-DOF Manipulator. Entropy 2023, 25, 789. https://doi.org/10.3390/e25050789
Sun Y, Zhao T, Liu N. Self-Organizing Interval Type-2 Fuzzy Neural Network Compensation Control Based on Real-Time Data Information Entropy and Its Application in n-DOF Manipulator. Entropy. 2023; 25(5):789. https://doi.org/10.3390/e25050789
Chicago/Turabian StyleSun, Youbo, Tao Zhao, and Nian Liu. 2023. "Self-Organizing Interval Type-2 Fuzzy Neural Network Compensation Control Based on Real-Time Data Information Entropy and Its Application in n-DOF Manipulator" Entropy 25, no. 5: 789. https://doi.org/10.3390/e25050789
APA StyleSun, Y., Zhao, T., & Liu, N. (2023). Self-Organizing Interval Type-2 Fuzzy Neural Network Compensation Control Based on Real-Time Data Information Entropy and Its Application in n-DOF Manipulator. Entropy, 25(5), 789. https://doi.org/10.3390/e25050789






