Optimal Pulse Design for Dissipative-Stimulated Raman Exact Passage
Abstract
1. Introduction
2. Definition of the Lossy-Driven Raman System
3. Energy-Optimal Dissipative STIREP
3.1. Construction of the Pseudo-Hamiltonian and Derivation of the Equations of Motion from PMP
3.2. Construction of the Optimal Trajectories
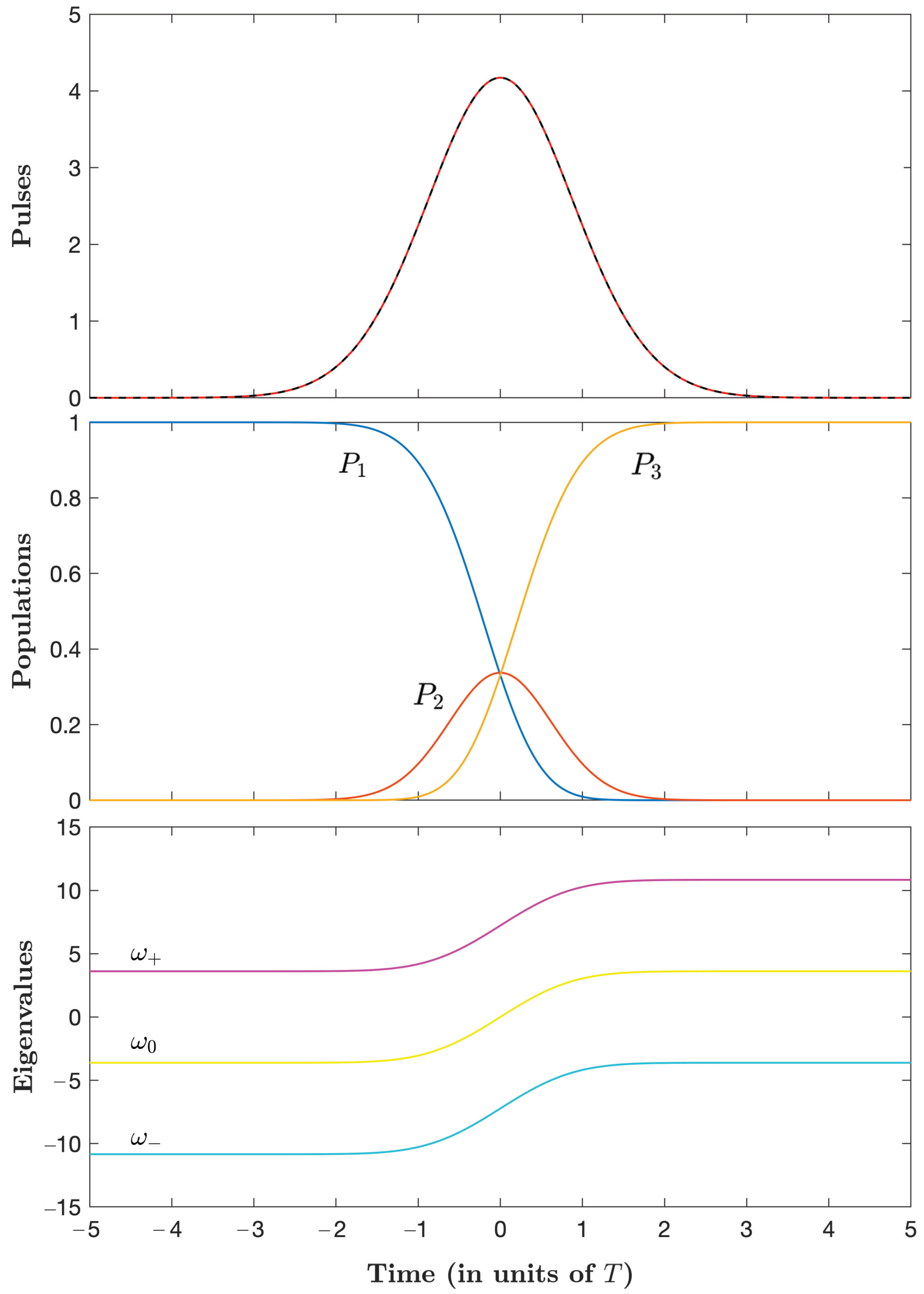
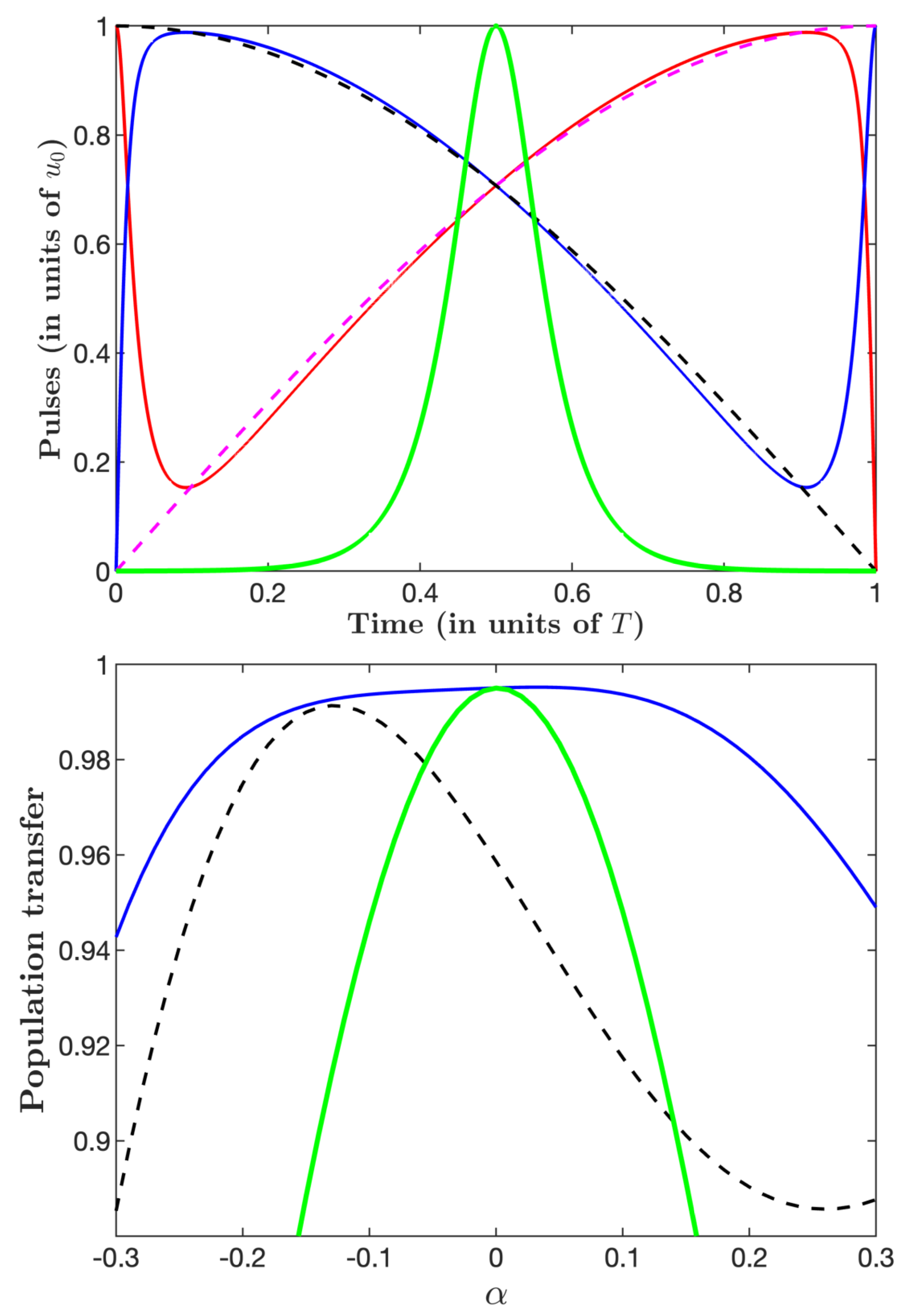
3.3. Derivation of the Pulses and the Dynamics
3.4. Comparison with Standard STIRAP and Parallel STIRAP
3.5. Analogy with a Planar Pendulum
4. Time-Optimal Dissipative STIREP
4.1. Construction of the Pseudo-Hamiltonian
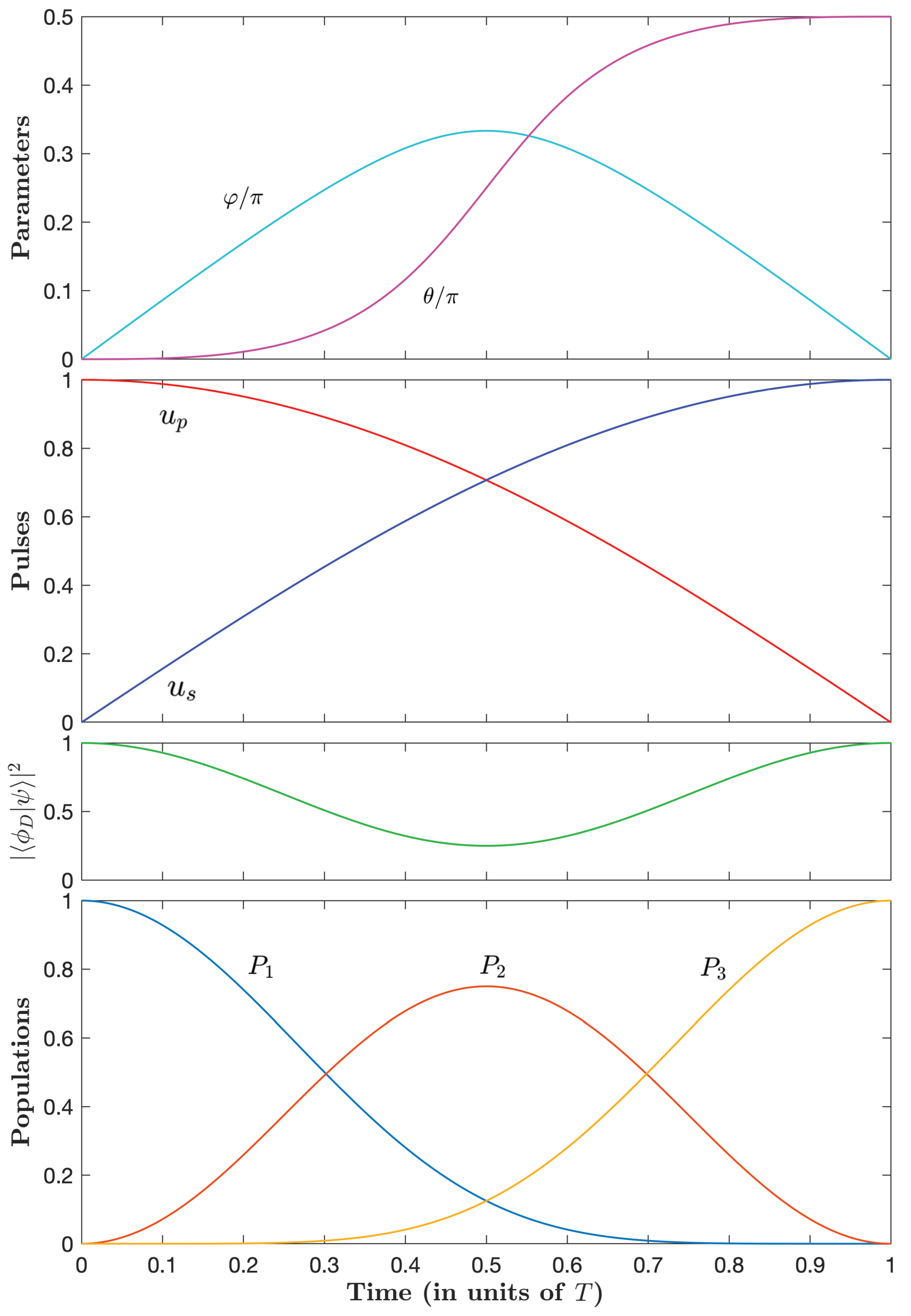
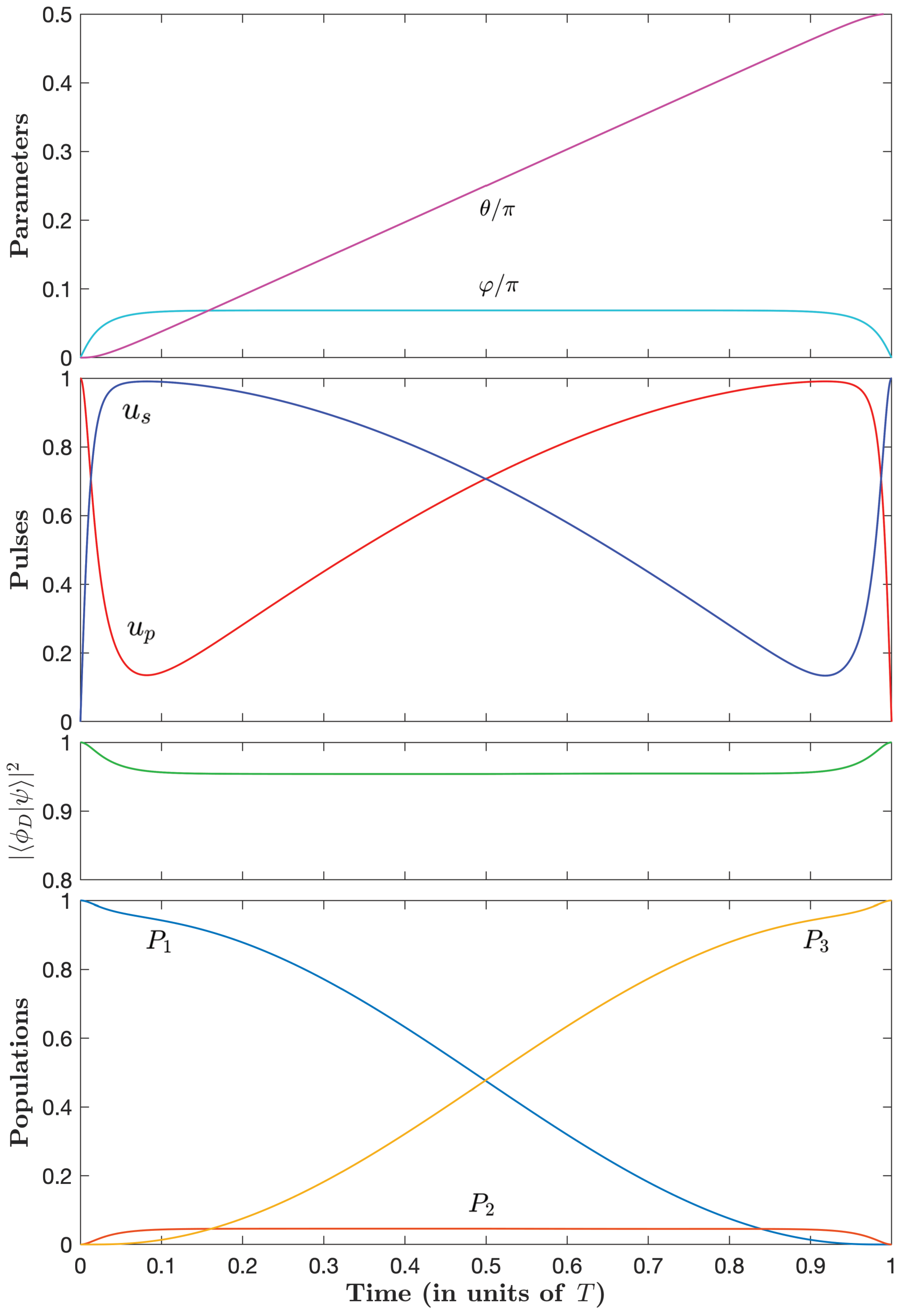
4.2. Construction of the Optimal Trajectories from the PMP
4.3. Derivation of the Pulses and the Dynamics
5. Conclusions and Discussion
- The energy optimization with the (low) given admissible loss with the time of the process, referred to as EO, yields with the peak of the pulse, , the energy , and the pulse area ;
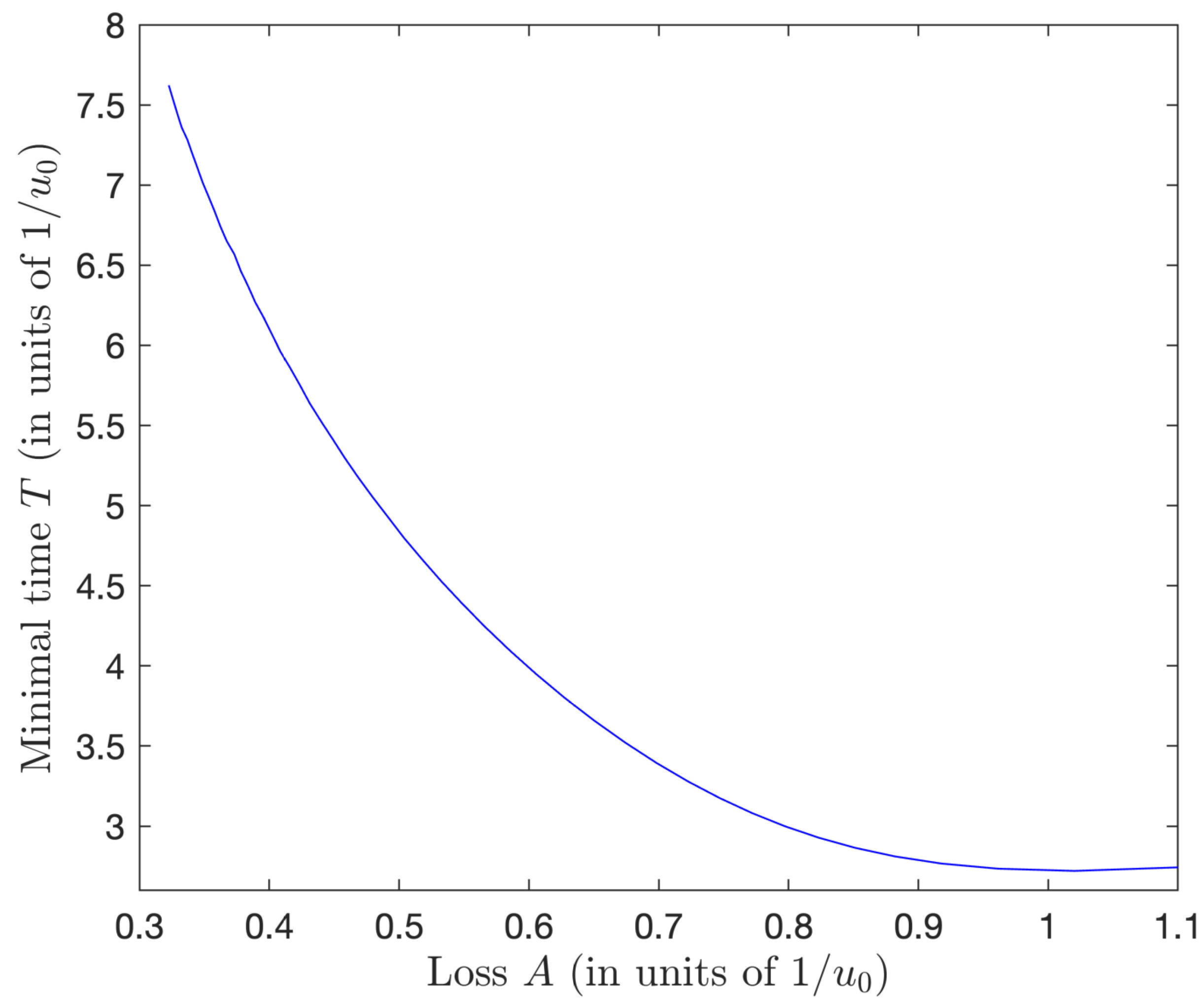
- The time-optimization with the same loss and the same peak amplitude , referred to as TO1, is roughly obtained for : , , and ; it shows a much smaller (roughly four times smaller) time of processing, but slightly larger pulse area and energy;
- The time-optimization with the same loss and the same duration as the energy optimization: , referred to as TO2, is roughly obtained for : this leads to a significant larger energy and a twice larger pulse area , but to a (twice) smaller peak pulse amplitude .We show the dependence of the pulse amplitude on the duration corresponding to these three examples in Figure 7. The energy-minimization strategy can, thus, achieve the transfer for a given loss in a relatively small pulse area, but with a relatively large pulse peak amplitude due to its sharp shape. On the other hand, the time-minimization strategy can achieve it with a weaker pulse amplitude, but for a larger pulse area (and energy).
Author Contributions
Funding
Conflicts of Interest
Appendix A. Pontryagin’s Maximum Principle
Appendix B. Integration of Equation (26)
Appendix C. Integration of Equation (27)
Appendix D. Stimulated Raman Parallel Adiabatic Passage
Appendix E. Optimal Control with Constrained Controls
Appendix F. Roots of Equation (91)
- •
- When , according to (91),-one root, when :-no root, when ;
- •
- When :-for :-for :
- In the range , the root given by (A74), where, for :gives:which is compatible with going to for going to 0.

Appendix G. Lindblad Equation
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Koch, C.P.; Boscain, U.; Calarco, T.; Dirr, G.; Filipp, S.; Glaser, S.J.; Kosloff, R.; Montangero, S.; Schulte-Herbrüggen, T.; Sugny, D.; et al. Quantum optimal control in quantum technologies. Strategic report on current status, visions and goals for research in Europe. EPJ Quantum Technol. 2022, 9, 19. [Google Scholar] [CrossRef]
- Guéry-Odelin, D.; Ruschhaupt, A.; Kiely, A.; Torrontegui, E.; Martínez-Garaot, S.; Muga, J.G. Shortcuts to adiabaticity: Concepts, methods, and applications. Rev. Mod. Phys. 2019, 91, 045001. [Google Scholar] [CrossRef]
- Bergmann, K.; Vitanov, N.V.; Shore, B.W. Perspective: Stimulated Raman adiabatic passage: The status after 25 years. J. Chem. Phys. 2015, 142, 170901. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.V.; Rangelov, A.A.; Shore, B.W.; Bergmann, K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev. Mod. Phys. 2017, 89, 015006. [Google Scholar] [CrossRef]
- Shore, B.W. Picturing stimulated raman adiabatic passage: A STIRAP tutorial. Adv. Opt. Photonics 2017, 9, 563. [Google Scholar] [CrossRef]
- Bergmann, K.; Nägerl, H.-C.; Panda, C.; Gabrielse, G.; Miloglyadov, E.; Quack, M.; Seyfang, G.; Wichmann, G.; Ospelkaus, S.; Kuhn, A.; et al. Roadmap on STIRAP applications. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 202001. [Google Scholar] [CrossRef]
- Boscain, U.; Charlot, G.; Gauthier, J.-P.; Guérin, S.; Jauslin, H.R. Optimal control in laser-induced population transfer for two- and three-level quantum systems. J. Math. Phys. 2002, 43, 5. [Google Scholar] [CrossRef]
- Daems, D.; Ruschhaupt, A.; Sugny, D.; Guérin, S. Robust Quantum Control by a Single-Shot Shaped Pulse. Phys. Rev. Lett. 2013, 111, 050404. [Google Scholar] [CrossRef] [PubMed]
- Van-Damme, L.; Schraft, D.; Genov, G.T.; Sugny, D.; Halfmann, T.; Guérin, S. Robust NOT gate by single-shotshaped pulses: Demonstration of the efficiency of the pulses in rephasing atomic coherences. Phys. Rev. A 2017, 96, 022309. [Google Scholar] [CrossRef]
- Laforgue, X.; Chen, X.; Guérin, S. Robust stimulated Raman exact passage using shaped pulses. Phys. Rev. A. 2019, 100, 023415. [Google Scholar] [CrossRef]
- Zeng, J.; Barnes, E. Fastest pulses that implement dynamically corrected single-qubit phase gates. Phys. Rev. A 2018, 98, 012301. [Google Scholar] [CrossRef]
- Dridi, G.; Liu, K.; Guérin, S. Optimal robust quantum control by inverse geometric optimization. Phys. Rev. Lett. 2020, 125, 250403. [Google Scholar] [CrossRef] [PubMed]
- Laforgue, X.; Dridi, G.; Guérin, S. Optimal robust quantum control against pulse inhonomogeneities: Analytic solutions. Phys. Rev. A 2022, 106, 052608. [Google Scholar] [CrossRef]
- Laforgue, X.; Dridi, G.; Guérin, S. Optimal robust stimulated Raman exact passage by inverse optimization. Phys. Rev. A 2022, 105, 032807. [Google Scholar] [CrossRef]
- Hegerfeldt, G.C. Driving at the Quantum Speed Limit: Optimal Control of a Two-Level System. Phys. Rev. Lett. 2013, 111, 260501. [Google Scholar] [CrossRef] [PubMed]
- Khaneja, N.; Reiss, T.; Kehlet, C.; Schulte-Herbrueggen, T.; Glaser, S.J. Optimal control of coupled spin dynamics: Design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson. 2005, 172, 296. [Google Scholar] [CrossRef] [PubMed]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mischenko, E.F. The Mathematical Theory of Optimal Processes; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Damme, L.V.; Ansel, Q.; Glaser, S.J.; Sugny, D. Robust optimal control of two-level quantum systems. Phys. Rev. A 2017, 95, 063403. [Google Scholar] [CrossRef]
- Boscain, U.; Sigalotti, M.; Sugny, D. Introduction to the Pontryagin Maximum Principle for Quantum Optimal Control. PRX Quantum 2021, 2, 030203. [Google Scholar] [CrossRef]
- Dorier, V.; Gevorgyan, M.; Ishkhanyan, A.; Leroy, C.; Jauslin, H.R.; Guérin, S. Nonlinear Stimulated Raman Exact Passage by Resonance-Locked Inverse Engineering. Phys. Rev. Lett. 2017, 119, 243902. [Google Scholar] [CrossRef]
- Assémat, E.; Sugny, D. Connection between optimal control theory and adiabatic-passage techniques in quantum systems. Phys. Rev. A 2012, 86, 023406. [Google Scholar] [CrossRef]
- Stefanatos, D.; Paspalakis, E. Optimal shape of STIRAP pulses for large dissipation at the intermediate level. Quantum Inf. Process. 2021, 20, 1. [Google Scholar] [CrossRef]
- Stefanatos, D.; Paspalakis, E. Optimal shortcuts of Stimulated Raman Adiabatic Passage in the presence of dissipation. Philos. Trans. R. Soc. 2022, 380, 20210283. [Google Scholar] [CrossRef] [PubMed]
- Guérin, S.; Yatsenko, L.P.; Halfmann, T.; Shore, B.W.; Bergmann, K. Stimulated hyper-Raman adiabatic passage. II. Static compensation of dynamic Stark shifts. Phys. Rev. A 1998, 58, 4691. [Google Scholar] [CrossRef]
- D’Alessandro, D. Introduction to Quantum Control and Dynamics; Chapman and Hall: Boca Raton, FL, USA, 2008. [Google Scholar]
- Bonnard, B.; Sugny, D. Optimal Control with Applications in Space and Quantum Dynamics, AIMS on Applied Mathematics; American Institute of Mathematical Sciences: Springfield, MA, USA, 2012; Volume 5. [Google Scholar]
- Dridi, G.; Guérin, S.; Hakobyan, V.; Jauslin, H.R.; Eleuch, H. Ultrafast stimulated Raman parallel adiabatic passage by shaped pulses. Phys. Rev. A 2009, 80, 043408. [Google Scholar] [CrossRef]
- Guérin, S.; Thomas, S.; Jauslin, H.R. Optimization of population transfer by adiabatic passage. Phys. Rev. A 2002, 65, 023409. [Google Scholar] [CrossRef]
- Schraft, D.; Halfmann, T.; Genov, G.T.; Vitanov, N.V. Experimental demonstration of composite adiabatic passage. Phys. Rev. A 2013, 88, 063406. [Google Scholar] [CrossRef]
- Bruns, A.; Genov, G.T.; Hain, M.; Vitanov, N.V.; Halfmann, T. Experimental demonstration of composite stimulated Raman adiabatic passage. Phys. Rev. A 2018, 98, 053413. [Google Scholar] [CrossRef]
- Sugny, D.; Kontz, C. Optimal control of a three-level quantum system by laser fields plus von Neumann measurements. Phys. Rev. A 2008, 77, 063420. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2007. [Google Scholar]



| A (in units of T) | 3/8 | 0.35 | 0.3 | 0.2 | 0.15 |
|---|---|---|---|---|---|
| m | 0 | ||||
| 1.0140 | 0.9502 | 0.8364 | 0.7995 | ||
| (in units of ) | 7.40 | 7.44 | 7.79 | 10.28 | 13.40 |
| (in units of ) | 2.72 | 2.51 | 2.54 | 3.60 | 4.73 |
| 2.72 | 2.72 | 2.75 | 2.91 | 3.03 | |
| A (in units of T) | 0.1 | 0.08 | 0.05 | 0.04 | 0.03 |
| m | |||||
| 0.7862 | 0.7855 | 0.7854 | 0.7854 | 0.7854 | |
| (in units of ) | 20.00 | 25.00 | 40.00 | 50.00 | 66.66 |
| (in units of ) | 7.07 | 8.84 | 14.14 | 17.68 | 23.57 |
| 3.12 | 3.14 | 3.14 | 3.14 | 3.14 |
| A () | T () | () | |||||
|---|---|---|---|---|---|---|---|
| 0.5 | 0.25879 | 1.1527 | 1.1177 | 2.7477 | 0.407 | 2.75 | 7.54 |
| 0 | 0.57735 | 1.0472 | 1.0203 | 2.7207 | 0.375 | 2.72 | 7.40 |
| −0.5 | 0.90476 | 0.9783 | 0.9612 | 2.7346 | 0.352 | 2.73 | 7.48 |
| −1 | 1.23456 | 0.9248 | 0.9176 | 2.7668 | 0.332 | 2.77 | 7.65 |
| −1.5 | 1.56434 | 0.8795 | 0.8821 | 2.8109 | 0.314 | 2.81 | 7.90 |
| −2 | 1.89263 | 0.8389 | 0.8513 | 2.8647 | 0.297 | 2.86 | 8.21 |
| −2.5 | 2.21825 | 0.8012 | 0.8234 | 2.9275 | 0.281 | 2.93 | 8.57 |
| −3 | 2.53997 | 0.7652 | 0.7972 | 2.9994 | 0.266 | 3.00 | 9.00 |
| −3.5 | 2.85642 | 0.7301 | 0.7720 | 3.0812 | 0.251 | 3.08 | 9.49 |
| −4 | 3.16595 | 0.6955 | 0.7473 | 3.1739 | 0.236 | 3.17 | 10.07 |
| −4.5 | 3.46665 | 0.6609 | 0.7228 | 3.2779 | 0.221 | 3.28 | 10.74 |
| −5 | 3.75639 | 0.6266 | 0.6984 | 3.3938 | 0.206 | 3.39 | 11.52 |
| −5.5 | 4.03322 | 0.5926 | 0.6742 | 3.5211 | 0.192 | 3.52 | 12.40 |
| −6 | 4.29565 | 0.5597 | 0.6504 | 3.6580 | 0.178 | 3.66 | 13.38 |
| −6.5 | 4.54311 | 0.5283 | 0.6273 | 3.8018 | 0.165 | 3.80 | 14.45 |
| −7 | 4.77607 | 0.4992 | 0.6055 | 3.9494 | 0.153 | 3.95 | 15.60 |
| −7.5 | 4.99577 | 0.4727 | 0.5850 | 4.0979 | 0.143 | 4.10 | 16.79 |
| −8 | 5.20381 | 0.4489 | 0.5660 | 4.2449 | 0.133 | 4.24 | 18.02 |
| −8.5 | 5.40180 | 0.4277 | 0.5485 | 4.3893 | 0.125 | 4.39 | 19.27 |
| −9 | 5.59116 | 0.4088 | 0.5323 | 4.5296 | 0.118 | 4.53 | 20.52 |
| −9.5 | 5.77306 | 0.3920 | 0.5175 | 4.6666 | 0.111 | 4.67 | 21.78 |
| −10 | 5.94845 | 0.3770 | 0.5037 | 4.7988 | 0.105 | 4.80 | 23.03 |
| −10.5 | 6.11800 | 0.3635 | 0.4913 | 4.9299 | 0.100 | 4.93 | 24.30 |
| −11 | 6.28261 | 0.3514 | 0.4794 | 5.0551 | 0.095 | 5.06 | 25.55 |
| −11.5 | 6.44250 | 0.3405 | 0.4684 | 5.1768 | 0.091 | 5.18 | 26.80 |
| −12 | 6.59818 | 0.3305 | 0.4582 | 5.2963 | 0.087 | 5.30 | 28.05 |
| −12.5 | 6.75000 | 0.3214 | 0.4488 | 5.4148 | 0.083 | 5.41 | 29.32 |
| −13 | 6.89827 | 0.3130 | 0.4397 | 5.5278 | 0.080 | 5.53 | 30.56 |
| −13.5 | 7.04324 | 0.3053 | 0.4311 | 5.6386 | 0.077 | 5.64 | 31.79 |
| −14 | 7.18513 | 0.2981 | 0.4235 | 5.7525 | 0.074 | 5.75 | 33.09 |
| −14.5 | 7.32416 | 0.2915 | 0.4160 | 5.8600 | 0.071 | 5.86 | 34.34 |
| −15 | 7.46049 | 0.2853 | 0.4085 | 5.9613 | 0.069 | 5.96 | 35.54 |
| −15.5 | 7.59429 | 0.2795 | 0.4020 | 6.0690 | 0.066 | 6.07 | 36.83 |
| −16 | 7.72569 | 0.2740 | 0.3957 | 6.1722 | 0.064 | 6.17 | 38.10 |
| −16.5 | 7.85483 | 0.2689 | 0.3892 | 6.2680 | 0.062 | 6.27 | 39.29 |
| −17 | 7.98182 | 0.2640 | 0.3836 | 6.3699 | 0.060 | 6.37 | 40.58 |
| −17.5 | 8.10678 | 0.2594 | 0.3779 | 6.4657 | 0.058 | 6.47 | 41.80 |
| −18 | 8.22979 | 0.2551 | 0.3730 | 6.5687 | 0.057 | 6.57 | 43.15 |
| −18.5 | 8.35096 | 0.2509 | 0.3671 | 6.6517 | 0.055 | 6.65 | 44.25 |
| −19 | 8.47035 | 0.2470 | 0.3622 | 6.7434 | 0.054 | 6.74 | 45.47 |
| −19.5 | 8.58806 | 0.2432 | 0.3577 | 6.8391 | 0.052 | 6.84 | 46.77 |
| −20 | 8.70414 | 0.2397 | 0.3531 | 6.9296 | 0.051 | 6.93 | 48.02 |
| −20.5 | 8.81868 | 0.2362 | 0.3486 | 7.0162 | 0.050 | 7.02 | 49.23 |
| −21 | 8.93172 | 0.2330 | 0.3446 | 7.1074 | 0.049 | 7.11 | 50.51 |
| −21.5 | 9.04333 | 0.2298 | 0.3406 | 7.1965 | 0.047 | 7.20 | 51.79 |
| −22 | 9.15356 | 0.2268 | 0.3368 | 7.2843 | 0.046 | 7.28 | 53.06 |
| −22.5 | 9.26246 | 0.2239 | 0.3325 | 7.3588 | 0.045 | 7.36 | 54.15 |
| −23 | 9.37008 | 0.2211 | 0.3290 | 7.4475 | 0.044 | 7.45 | 55.47 |
| −23.5 | 9.47647 | 0.2184 | 0.3234 | 7.4864 | 0.043 | 7.49 | 56.05 |
| −24 | 9.58166 | 0.2159 | 0.3225 | 7.6230 | 0.042 | 7.62 | 58.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Sugny, D.; Chen, X.; Guérin, S. Optimal Pulse Design for Dissipative-Stimulated Raman Exact Passage. Entropy 2023, 25, 790. https://doi.org/10.3390/e25050790
Liu K, Sugny D, Chen X, Guérin S. Optimal Pulse Design for Dissipative-Stimulated Raman Exact Passage. Entropy. 2023; 25(5):790. https://doi.org/10.3390/e25050790
Chicago/Turabian StyleLiu, Kaipeng, Dominique Sugny, Xi Chen, and Stéphane Guérin. 2023. "Optimal Pulse Design for Dissipative-Stimulated Raman Exact Passage" Entropy 25, no. 5: 790. https://doi.org/10.3390/e25050790
APA StyleLiu, K., Sugny, D., Chen, X., & Guérin, S. (2023). Optimal Pulse Design for Dissipative-Stimulated Raman Exact Passage. Entropy, 25(5), 790. https://doi.org/10.3390/e25050790







