An Entropy Generation Rate Model for Tropospheric Behavior That Includes Cloud Evolution
Abstract
:1. Introduction
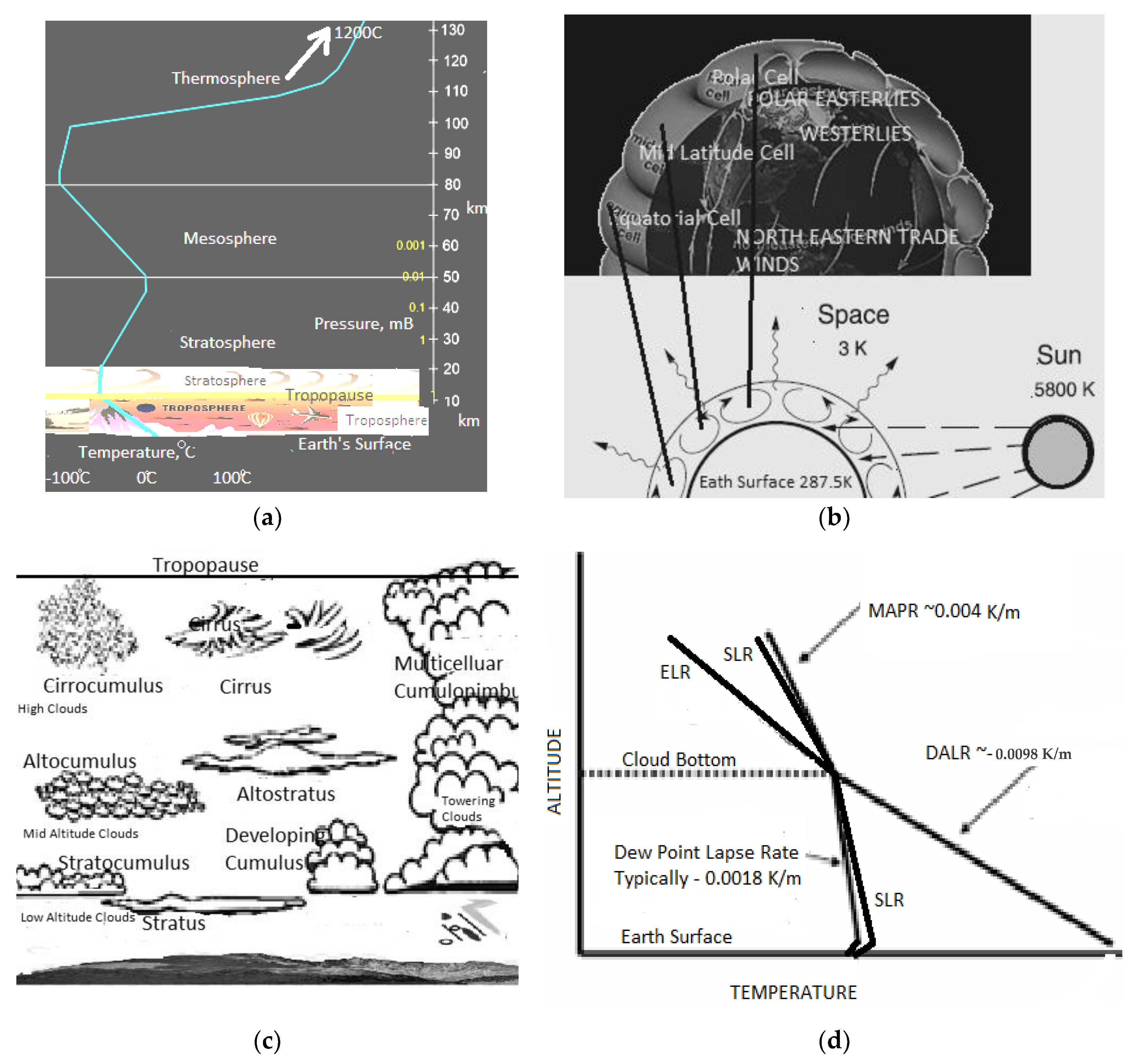
1.1. The Earth’s Atmosphere
1.2. Entropy Creation and Exchange
1.3. Atmospheric Stability
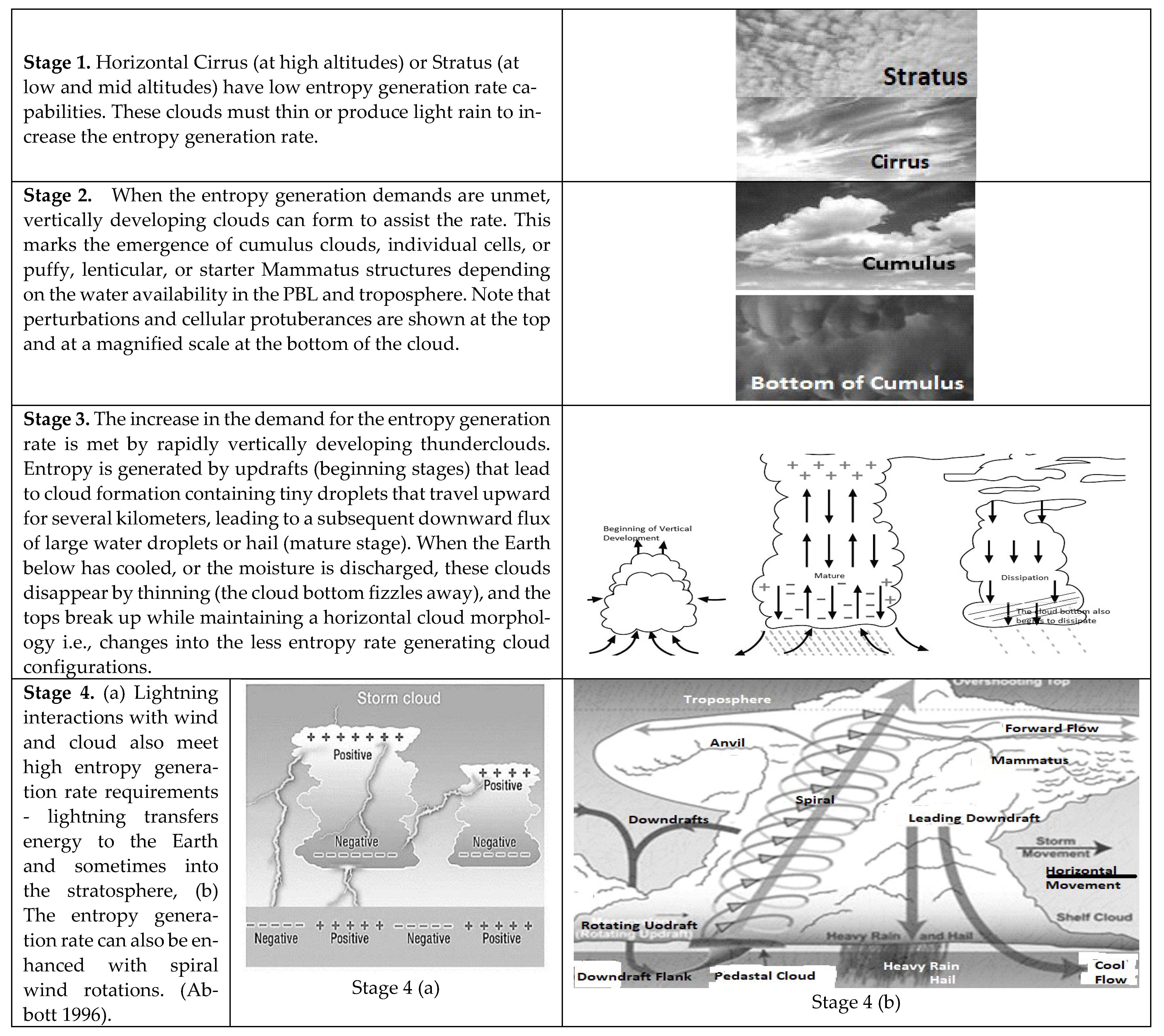
1.4. Cloud Evolution and Intense Weather
1.5. Lapse Rates
1.6. PBL
2. Tropospheric Entropy Generation Rate

3. Discussions
3.1. Entropy Generation in a Cloud without Significant Vertical Development

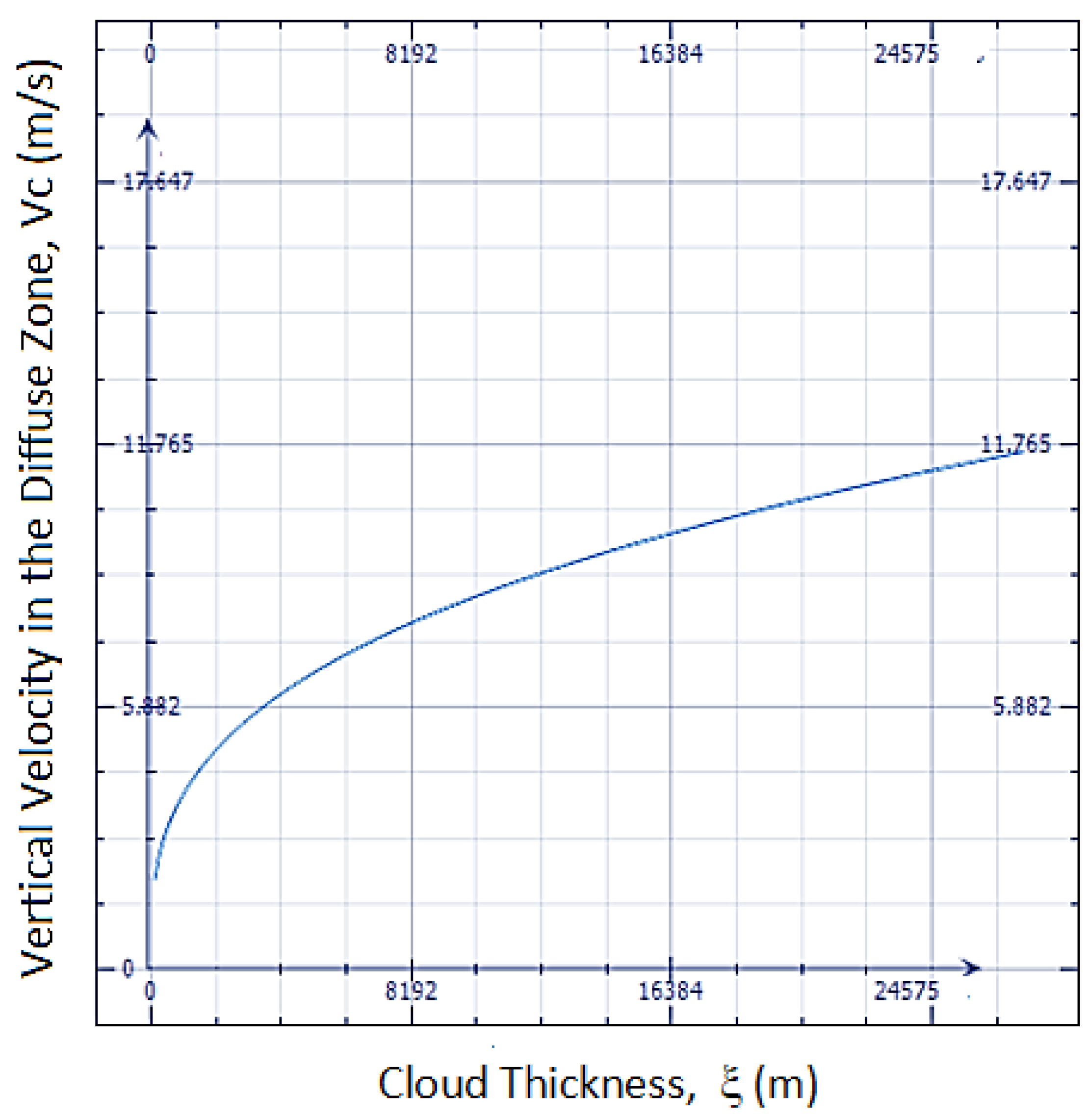
3.2. Entropy Generation in a Cloud with Vertical Development

3.3. Intense Weather and Entropy Generation in Complex Systems
3.4. Analogy with Solidification Patterns (Microstructures)

4. Summary, Comments, and Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Description Scheme of Various Phenomena in the Key Equations for Tropospheric and Cloud Entropy Balance
| Relevant Equation | Expression | Type | Units |
| Equation (5b) | (4AEarthΦεχ σTc3/3)Δt | Entropy lost from the troposphere from radiation with the average cloud temperature | J/m3.K |
| Equation (5b) | (4σAEarth(1 − Φ)εα TE3/3)Δt | Entropy lost from the troposphere from the Earth’s surface that do not see cloud cover | J/m3.K |
| Equation (5b) | (4σTsun3/3)κ1ψΔt | Entropy lost from the troposphere from radiation from the Earth that is mitigated by clouds | J/m3.K |
| Equation (6) | hρCp(ln(T)) = | Entropy changes per unit area of the tropospheric slice | J/m2.K |
| Equation (6) | (4σψTsun3/3)Δt | Entropy changes per unit area of the tropospheric slice | J/m2.K |
| Equation (6) | (4σTsun3/3)κψΔt | Entropy exchange not captured in the other terms that arise from reflections | J/m2.K |
| Equation (6) | hdsgen/dtΔt | Entropy generation term in the troposphere | J/m2.K |
| Equation (6) | dΔδ/dt.Δt | Entropy exchange from evaporation and condensation that crosses the control volume boundary located at the Earth’s surface | J/m2.K |
| Equation (6) | ΛΔt | Tηε entropy-loss term associated with the catch-all electron jet (like lightning) that crosses the boundaries of the tropospheric control volume | J/m2.K |
| Equation (15c) | Near-saturation and saturation lapse rate | K/m | |
| Equation (16) | 2εχκ1Tc(av)3/εα.λTE3 > 1 | Bifurcation condition | Dimensionless |
| Equation (17) | [ξ dΔ(fv(svpi)/dt)]SLR/ΔT | Rate of entropy generation per unit volume with moisture exchange processes | J/m3.K.s |
| Equation (17) | [Cpln(Tc(av))Vc]SLR/ΔT | Rate of entropy generation with tropospheric warming processes in the vertically expanding cloud | J/m3.K.s |
References
- Gibbins, G.; Haigh, J.D. Entropy Production Rates of the Climate. J. Atmos. Sci. 2022, 77, 3551–3566. [Google Scholar] [CrossRef]
- The Original Figure Is attributed to Dian Gaffen. 1995. Available online: https://www.eso.org/gen-fac/pubs/astclim/espas/pwv/mockler.html (accessed on 10 October 2023).
- Jeevanjee, N.; Romps, D.M. Mean precipitation change from a deepening troposphere. Proc. Natl. Acad. Sci. USA 2018, 115, 11465–11470. [Google Scholar] [CrossRef]
- Meng, L.; Liu, J.; Tarasick, D.W.; Randel, W.J.; Steiner, A.K.; Wilhelmsen, H.; Wang, L.; Haimberger, L. The continuous rise of the tropopause in the Northern Hemisphere over 1980–2020. Sci. Adv. 2021, 7, 45. [Google Scholar] [CrossRef]
- Santer, B.D.; Mears, C.; Wentz, F.J.; Taylor, K.E.; Gleckler, P.J.; Wigley, T.M.L.; Barnett, T.P.; Boyle, J.S.; Brüggemann, W.; Gillett, N.P.; et al. Identification of human-induced changes in atmospheric moisture content. Proc. Natl. Acad. Sci. USA 2007, 104, 15248–15253. [Google Scholar] [CrossRef] [PubMed]
- Marvel, K.; Bonfils, C. Identifying external influences on global precipitation. Proc. Natl. Acad. Sci. USA 2013, 110, 19301–19306. [Google Scholar] [CrossRef]
- Available online: https://ec.europa.eu/research-and-innovation/en/horizon-magazine/qa-why-clouds-are-still-one-biggest-uncertainties-climate-change (accessed on 10 October 2023).
- Allen, J.R. Measurements of Cloud Emissivity in the 8–13 μ Waveband. J. Appl. Meteorol. Climatol. 1971, 10, 260–265. [Google Scholar] [CrossRef]
- Stubenrauch, C.J.; Rossow, W.B.; Kinne, S.; Ackerman, S.; Cesana, G.; Chepfer, H.; Di Girolamo, L.; Getzewich, B.; Guignard, A.; Heidinger, A.; et al. Assessment of global cloud datasets from satellites: Project and Database initiated by GEWEX Radiation Panel. Bull. Am. Meteorol. Soc. 2013, 94, 1031–1049. [Google Scholar] [CrossRef]
- Martyushev, L.M. Maximum entropy production principle: History and status. Phys. Usp. 2021, 191, 64. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes, 3rd ed.; Interscience Publishers: New York, NY, USA, 1967. [Google Scholar]
- Ziegler, H. An Introduction to Thermomechanics; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Sekhar, J.A. The description of morphologically stable regimes for steady-state solidification based on the maximum entropy production rate postulate. J. Mater. Sci. 2011, 46, 6172–6190. [Google Scholar] [CrossRef]
- Nive, R.K. Simultaneous Extrema in the Entropy Production for Steady-State Fluid Flow in Parallel Pipes. arXiv 2009, arXiv:0911.5014. [Google Scholar] [CrossRef]
- Matyushev, L.M.; Selzenev, V.D. Maximum entropy production principle in physics, chemistry, and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Endres, R.G. Entropy production selects non-equilibrium states in multistable systems. Sci. Rep. 2017, 7, 14437. [Google Scholar] [CrossRef]
- Bensah, Y.D.; Sekhar, J.A. Solidification Morphology and Bifurcation Predictions with the Maximum Entropy Production Rate Model. Entropy 2020, 22, 40. [Google Scholar] [CrossRef]
- Vita, A. Beyond Linear Non-Equilibrium Thermodynamics. In Non-Equilibrium Thermodynamics; Lecture Notes in Physics; Springer: Cham, Switzerland, 2022; Volume 1007. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Nazarova, A.S.; Seleznev, V.D. On the problem of the minimum entropy production in the nonequilibrium stationary state. J. Phys. A 2007, 40, 371. [Google Scholar] [CrossRef]
- Klaidon, A. Nonequilibrium thermodynamics and maximum entropy production in the Earth system. Naturwissenschaften 2009, 96, 653. [Google Scholar] [CrossRef]
- Reis, A.H. Use and validity of principles of extremum of entropy production in the study of complex systems. Ann. Phys. 2014, 346, 22–27. [Google Scholar] [CrossRef]
- Sekhar, J.A. Self-Organization, Entropy Generation Rate, and Boundary Defects: A Control Volume Approach. Entropy 2021, 23, 1092. [Google Scholar] [CrossRef]
- Veveakis, E.; Regenauer-Lieb, K. Review of extremum postulates. Curr. Opin. Chem. Eng. 2015, 7, 40–46. [Google Scholar] [CrossRef]
- Pascale, S.; Gregory, J.M.; Ambaum, M.H.P.; Tailleux, R.; Lucarini, V. Vertical and horizontal processes in the global atmosphere and the maximum entropy production conjecture. Earth Syst. Dynam. 2012, 3, 19–32. [Google Scholar] [CrossRef]
- Sekhar, J.A. An Entropic Model for Assessing Avian Flight Formations. arXiv 2022, arXiv:2204.03102. [Google Scholar] [CrossRef]
- Available online: https://media.bom.gov.au/social/blog/1750/explainer-what-is-thunder/ (accessed on 10 October 2023).
- Alkama, R.; Taylor, P.C.; Martin, L.G.-S.; Douville, H.; Duveiller, G.; Forzieri, G.; Swingedouw, D.; Cescatti, A. Clouds damp the radiative impacts of polar sea ice loss. Cryosphere 2020, 14, 2673–2686. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Non-Equilibrium Systems: From Dissipative Structures to Order through Fluctuations; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Heylighen, F. Complexity and Self-organization. In Encyclopedia of Library and Information Sciences; Bates, M.J., Maack, M.N., Eds.; Taylor and Francis: Oxfordshire, UK, 2008. [Google Scholar]
- Cavagna, A.; Cimarelli, A.; Giardina, I.; Parisi, G.; Santagati, R.; Stefanini, F.; Viale, M. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 2010, 107, 11865–11870. [Google Scholar] [CrossRef] [PubMed]
- Raymond, D.J. Sources and sinks of entropy in the atmosphere. J. Adv. Model. Earth Syst. 2013, 5, 755–763. [Google Scholar] [CrossRef]
- Paltridge, G.W. The steady-state format of global climate. Quart. J. Roy. Meteor. Soc. 1978, 104, 927–945. [Google Scholar]
- Wu, W.; Liu, Y. Radiation entropy flux and entropy production of the earth system. Rev. Geophys. 2010, 48, 2008RG000275. [Google Scholar] [CrossRef]
- Pitt, M.A. Increased Temperature and Entropy Production in the Earth’s Atmosphere: Effect on Wind, Precipitation, Chemical Reactions, Freezing and Melting of Ice and Electrical Activity. J. Mod. Phys. 2019, 10, 966–973. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Coriell, S.R.; Greer, A.L.; Karma, A.; Kurz, W.; Rappaz, M.; Trivedi, R. Solidification microstructures: Recent developments, future directions. Acta Mater. 2000, 48, 43. [Google Scholar] [CrossRef]
- Flemings, M.C. Solidification Processing; McGraw Hill: New York, NY, USA, 1974. [Google Scholar]
- Trivedi, R.K.; Sekhar, J.A.; Seetharaman, V. Solidification microstructures near the limit of absolute stability. Metall. Trans. 1989, 20A, 769. [Google Scholar] [CrossRef]
- Sullivan, S.C.; Lee, D.; Oreopoulos, L.; Nenes, A. Role of updraft velocity in temporal variability of global cloud hydrometeor number. Proc. Natl. Acad. Sci. USA 2016, 113, 5791–5796. [Google Scholar] [CrossRef]
- Amann-Winkel, K.; Kim, K.H.; Giovambattista, N.; Ladd-Parada, M.; Späh, A.; Perakis, F.; Pathak, H.; Yang, C.; Eklund, T.; Lane, T.J.; et al. Liquid-liquid phase separation in supercooled water from ultrafast heating of low-density amorphous ice. Nat. Commun. 2023, 14, 442. [Google Scholar] [CrossRef]
- Fabietti, L.M.; Sekhar, J.A. Quantitative microstructure maps for restrained directional growth. J. Mater. Sci. 1994, 29, 473. [Google Scholar] [CrossRef]
- Fabietti, L.M.; Sekhar, J.A. Growth of noncrystallographic dendrites. J. Mater. Res. 1992, 7, 1987. [Google Scholar] [CrossRef]
- Cotton, W.R.; Anthes, R.A. Storm and Cloud Dynamics; Academic Press, Inc.: San Diego, CA, USA, 1989; Volume 44, 883p. [Google Scholar]
- Sherwood, S.C.; Webb, M.J.; Annan, J.D.; Armour, K.C.; Forster, P.M.; Hargreaves, J.C.; Hegerl, G.; Klein, S.A.; Marvel, K.D.; Rohling, E.J.; et al. An assessment of Earth’s climate sensitivity using multiple lines of evidence. Rev. Geophys. 2020, 58, e2019RG000678. [Google Scholar] [CrossRef] [PubMed]
- Villalba-Pradas, A.; Tapiador, F.J. Empirical values and assumptions in the convection schemes of numerical models. Geosci. Model. Dev. 2022, 15, 3447–3518. [Google Scholar] [CrossRef]
- Bensah, Y.D.; Sekhar, J.A. Interfacial instability of a planar interface and diffuseness at the solid-liquid interface for pure and binary materials. arXiv 2016, arXiv:1605.05005. [Google Scholar]
- Available online: https://en.wikipedia.org/w/index.php?title=Liquid_water_content&oldid=1104792635 (accessed on 10 October 2023).
- Available online: https://isccp.giss.nasa.gov/role.htm (accessed on 10 October 2023).
- Available online: https://climatekids.nasa.gov/cloud-climate (accessed on 10 October 2023).
- Mendoza, V.; Pazos, M.; Garduño, R.; Mendoza, B. Thermodynamics of climate change between cloud cover, atmospheric temperature, and humidity. Nat. Sci. Rep. 2021, 1112122444. [Google Scholar] [CrossRef]
- Fischer, E.M.; Sedláček, J.; Hawkins, E.; Knutti, R. Models agree on forced response pattern of precipitation and temperature extremes. Geophys. Res. Lett. 2014, 41, 8554–8562. [Google Scholar] [CrossRef]
- Pérez-Invernón, F.J.; Gordillo-Vázquez, F.J.; Huntrieser, H.; Jöckel, P. Variation of lightning-ignited wildfire patterns under climate change. Nat. Commun. 2023, 14, 1–11. [Google Scholar] [CrossRef]
- Available online: https://www.sciencedirect.com/topics/Earth-and-planetary-sciences/adiabatic-lapse-rate (accessed on 10 October 2023).
- Sekhar, J.A.; Mohan, M.; Divakar, C.; Singh, A.K. Rapid solidification by high-pressure application. Scr. Metall. 1984, 18, 1327–1330. [Google Scholar] [CrossRef]
- Levi, C.G.; Mehrabian, R. Heat flow during rapid solidification of undercooled metal droplets. Metall. Trans. A 1982, 13A, 221–234. [Google Scholar] [CrossRef]
- Sekhar, J.A. Rapid solidification and surface topography for additive manufacturing with beam surface heating. Curr. Opin. Chem. Eng. 2020, 28, 10–20. [Google Scholar] [CrossRef]
- Available online: https://www.climate-policy-watcher.org/global-climate-2/clouds-cumulus.html (accessed on 10 October 2023).
- Available online: https://phys.org/news/2023-03-global-hot-lightning-wildfires.html (accessed on 10 October 2023).
- Available online: https://www.jpl.nasa.gov/images/pia18833-nasa-spacecraft-maps-Earths-global-emissivity (accessed on 10 October 2023).
- Diamond, M.S. Detection of large-scale cloud microphysical changes within a major shipping corridor after implementation of the International Maritime Organization 2020 fuel sulfur regulations. Atmos. Chem. Phys. 2023, 23, 8259–8269. [Google Scholar] [CrossRef]
- Available online: https://glossary.ametsoc.org/wiki/Adiabatic_lapse_rate (accessed on 10 October 2023).
- Available online: https://uw.pressbooks.pub/fundamentalsofclimatechange/chapter/going-up/ (accessed on 10 October 2023).
- Zhu, Z.; Lamer, K.; Kollias, P.; Clothiaux, E.E. The vertical structure of liquid water content in shallow clouds as retrieved from dual-wavelength radar observations. J. Geophys. Res. Atmos. 2019, 124, 14184–14197. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Cumulus_cloud (accessed on 15 October 2023).
- Available online: https://agu.confex.com/agu/fm22/meetingapp.cgi/Paper/1195179 (accessed on 10 October 2023).
- Rantanen, M.; Karpechko, A.Y.; Lipponen, A.; Nordling, K.; Hyvärinen, O.; Ruosteenoja, K.; Vihma, T.; Laaksonen, A. The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ. 2022, 3, 168. [Google Scholar] [CrossRef]
- Available online: https://learnweather.com/basic-weather/atmosphere-where-do-thunderstorms-live-mk/ (accessed on 10 October 2023).
- Petela, R. Exergy of undiluted thermal radiation. Sol. Energy 2003, 74, 469–488. [Google Scholar] [CrossRef]
- Rostami, M.; Severino, L.; Petri, S.; Hariri, S. Dynamics of localized extreme heatwaves in the mid-latitude atmosphere: A conceptual examination. Atmos. Sci. Lett. 2023, e1188. [Google Scholar] [CrossRef]
- Epstein, I.R.; Pojman, J.A. An Introduction to Nonlinear Chemical Dynamics; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Sekhar, J.A.; Li, H.P.; Dey, G.K. Decay-dissipative Belousov–Zhabotinsky nanobands and nanoparticles in NiAl. Acta Mater. 2010, 58, 1056–1073. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. 1952, 237, 37. [Google Scholar]
- Available online: https://climate.nasa.gov/news/2585/is-climate-changing-cloud-heights-too-soon-to-say/ (accessed on 10 October 2023).
- Available online: https://www.britannica.com/science/planetary-boundary-layer (accessed on 10 October 2023).
- Bensah, Y.D.; Sekhar, J. Morphological assessment with the maximum entropy production rate (MEPR) postulate. Curr. Opin. Chem. Eng. 2014, 3, 91–98. [Google Scholar] [CrossRef]
- Available online: https://www.feynmanlectures.caltech.edu/II_09.html# (accessed on 10 October 2023).
- Available online: https://www.groundzeroshelters.com/the-science-of-tornados? (accessed on 27 November 2023).
- Pascalea, S.; Ragone, F.; Lucarini, V.; Wang, Y.; Boschi, R. Nonequilibrium thermodynamics of circulation regimes in optically-thin, dry atmospheres. arXiv 2012, arXiv:1208.2678. [Google Scholar] [CrossRef]
- Arakawa, A. The Cumulus Parameterization Problem: Past, Present, and Future. J. Clim. 2017, 17, 1–41. [Google Scholar] [CrossRef]
- Available online: https://www.brockmann-consult.de/CloudStructures/convection-cells-streets-description.htm (accessed on 10 October 2023).
- Deser, C.; Phillips, A.; Alexander, M.; Smoliak, B. Projecting North American climate over the next 50 years: Uncertainty due to internal variability. J. Clim. 2014, 27, 2271–2296. [Google Scholar] [CrossRef]
- Available online: https://www.zmescience.com/feature-post/natural-sciences/climate-and-weather/weather-and-atmosphere/types-of-clouds/ (accessed on 10 October 2023).
- Available online: https://owlcation.com/stem/Cloud-Types-with-Pictures (accessed on 10 October 2023).
- Available online: https://www.crh.noaa.gov (accessed on 27 November 2023).
- Available online: https://www.eurekalert.org/multimedia/814541 (accessed on 10 October 2023).
- Available online: https://sciencequery.com/cumulus-cloud-definition-and-description/ (accessed on 10 October 2023).
- Wei, Y.; Shen, P.; Wang, Z.; Liang, H.; Qian, Y. Time Evolution Features of Entropy Generation Rate in Turbulent Rayleigh-Bernard Convection with Mixed Insulating and Conducting Boundary Conditions. Entropy 2020, 22, 672. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 4. [Google Scholar] [CrossRef]
- Abbott, P.L. Natural Disasters; Wm. C. Brown Publishing Co.: Dubuque, IA, USA, 1996; p. 438. [Google Scholar]
- Alkama, R.; Koffi, E.N.; Vavrus, S.J.; Diehl, T.; Francis, J.A.; Stroeve, J.; Forzieri, G.; Vihma, T.; Cescatti, A. Wind amplifies the polar sea ice retreat. Environ. Res. Lett. 2020, 15, 124022. [Google Scholar] [CrossRef]
| Cloud Type | Liquid Water Content (g/m3) | Measured Vertical Updraft/Velocity (m/s) | Volume Fraction of Water, fv in Clouds |
|---|---|---|---|
| cirrus | 0.03 | Small | 3 × 10−8 |
| fog | 0.05 | 0.25 | 5 × 10−8 |
| stratus | 0.25–0.30 | Small | (2.5–3) × 10−7 |
| cumulus | 0.25–0.30 | 1 | (2.5–3) × 10−7 |
| stratocumulus | 0.45 | 0.5 | 4.5 × 10−7 |
| cumulonimbus | 1.0–3.0 | 10 | (1–3) × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekhar, J.A. An Entropy Generation Rate Model for Tropospheric Behavior That Includes Cloud Evolution. Entropy 2023, 25, 1625. https://doi.org/10.3390/e25121625
Sekhar JA. An Entropy Generation Rate Model for Tropospheric Behavior That Includes Cloud Evolution. Entropy. 2023; 25(12):1625. https://doi.org/10.3390/e25121625
Chicago/Turabian StyleSekhar, Jainagesh A. 2023. "An Entropy Generation Rate Model for Tropospheric Behavior That Includes Cloud Evolution" Entropy 25, no. 12: 1625. https://doi.org/10.3390/e25121625