Theoretical Improvements in Enzyme Efficiency Associated with Noisy Rate Constants and Increased Dissipation
Abstract
1. Introduction
2. Methods
2.1. Selected Enzymes for the Computational Modeling
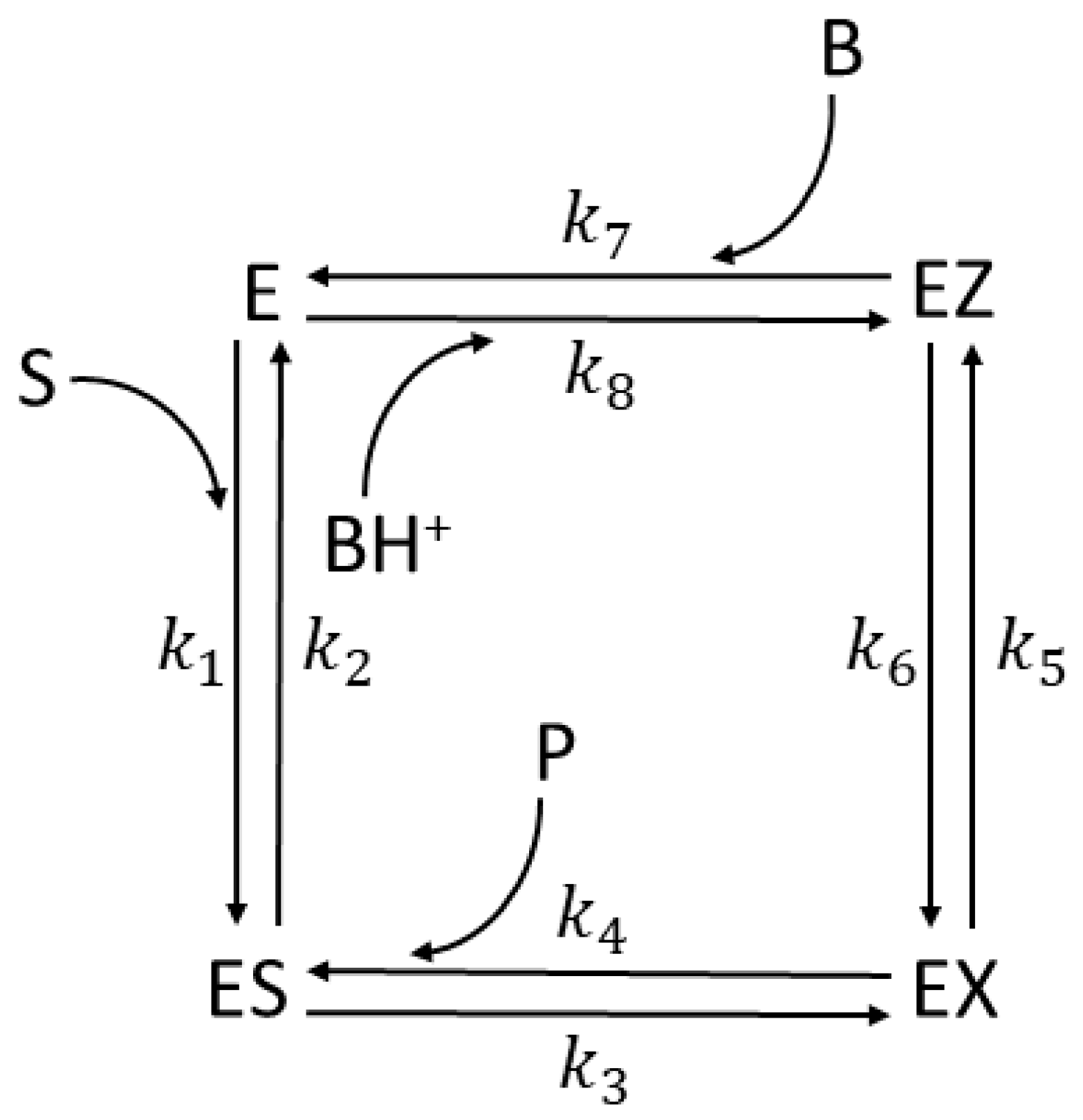
2.2. Description of Enzyme Kinetics in Terms of Nonequilibrium Thermodynamics
3. Software and Programs Used in This Paper
4. Triosephosphate Isomerase (TPI): The Favorite Enzyme for Computational Optimization of Michaelis–Menten-Type Kinetics
4.1. Stepwise Changes in Rate Constants
4.2. Computational Optimizations of TPI Catalytic Activity When Noise Is Included
4.3. Simulating Dynamics Using an Agent-Based Modeling Approach
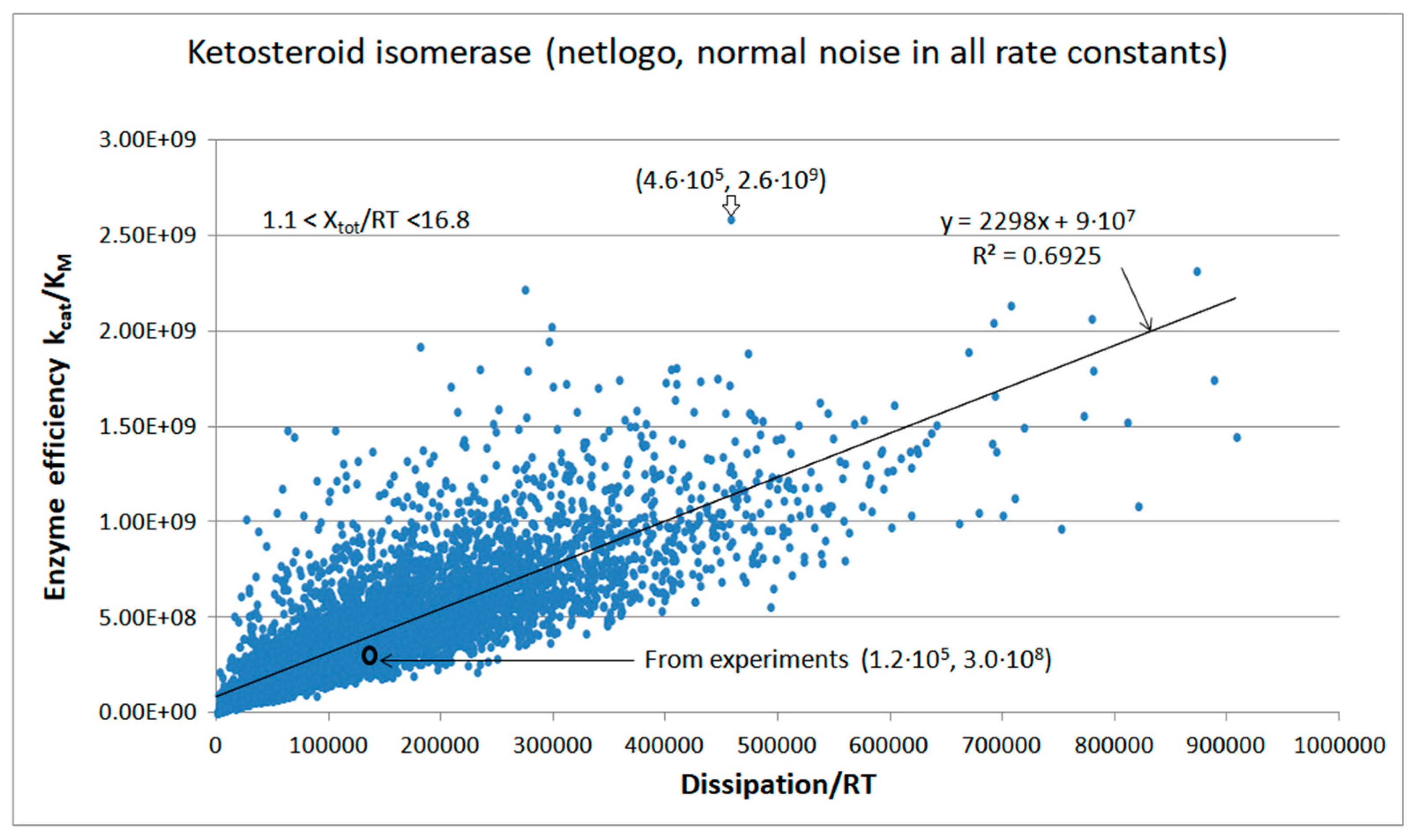
5. Ketosteroid Isomerase (KSI) Case: What Is Different When the Operating Range Is Farther from Equilibrium?
6. CA I, CA II, and CA II-T200H (Also Four-State Enzymes)
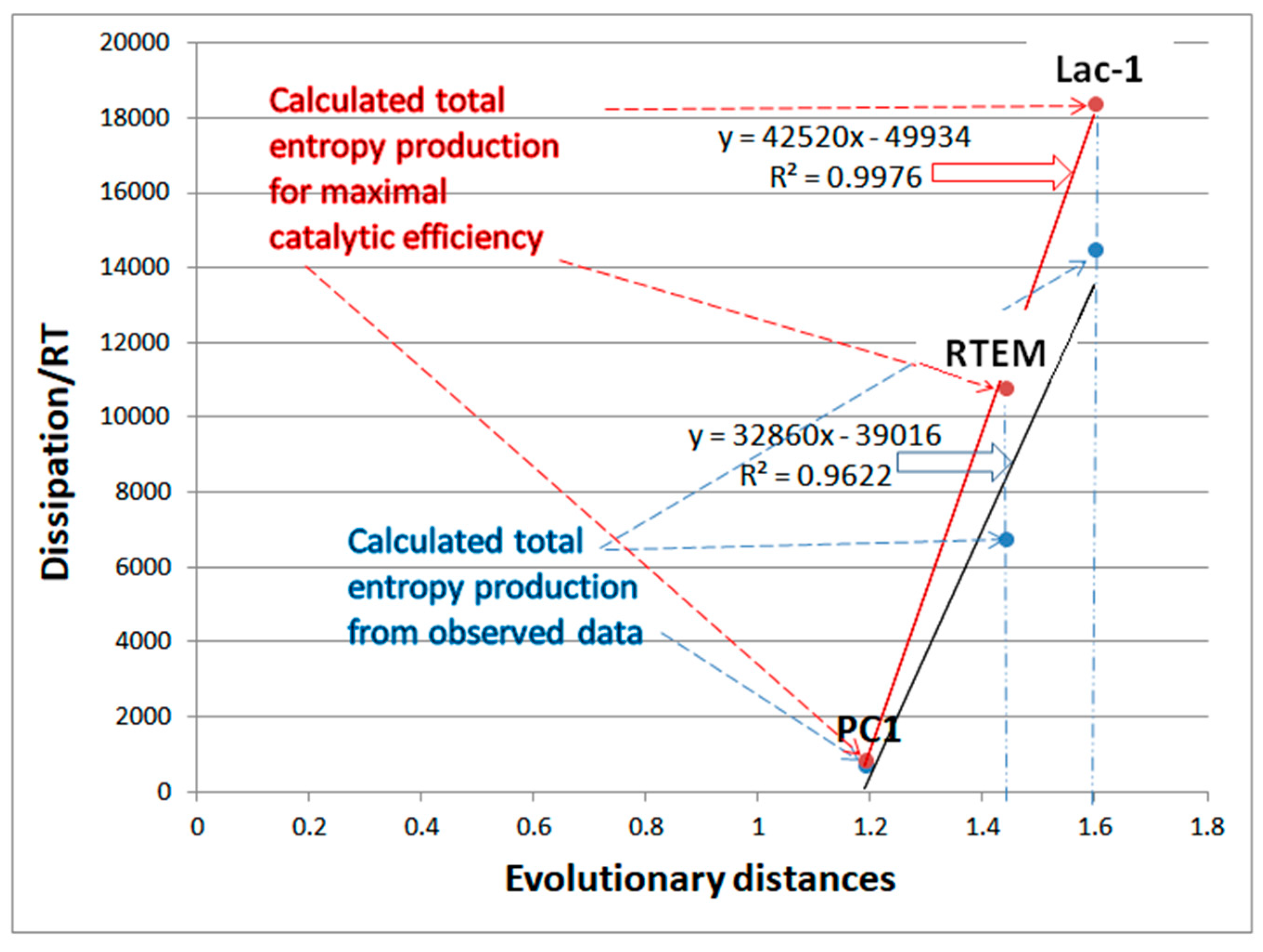
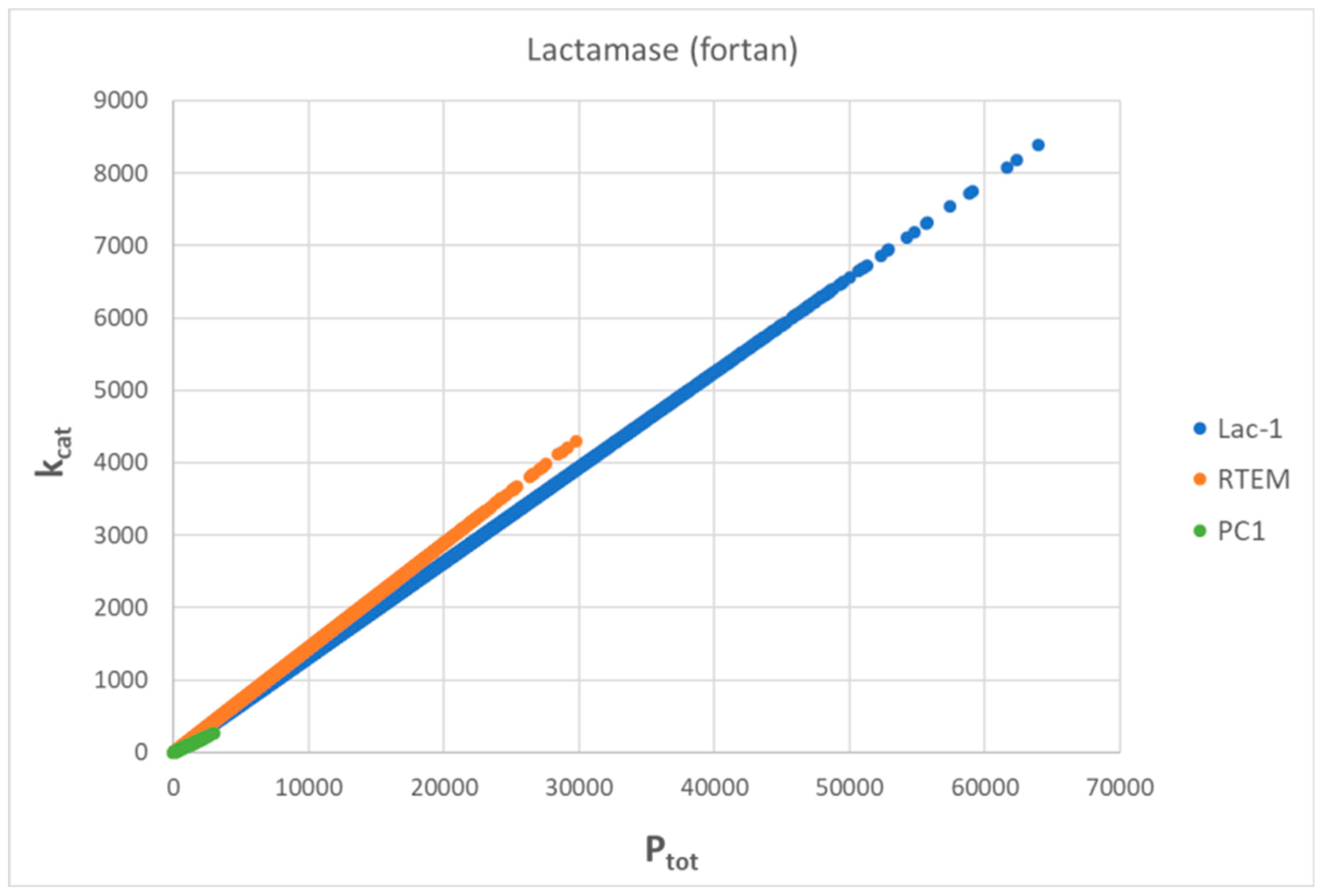
7. Evolutionary Related β-Lactamases
7.1. PC1 β-Lactamase
7.2. RTEM β-Lactamase
7.3. Lac-1 β-Lactamase
7.4. Summary for β-Lactamases
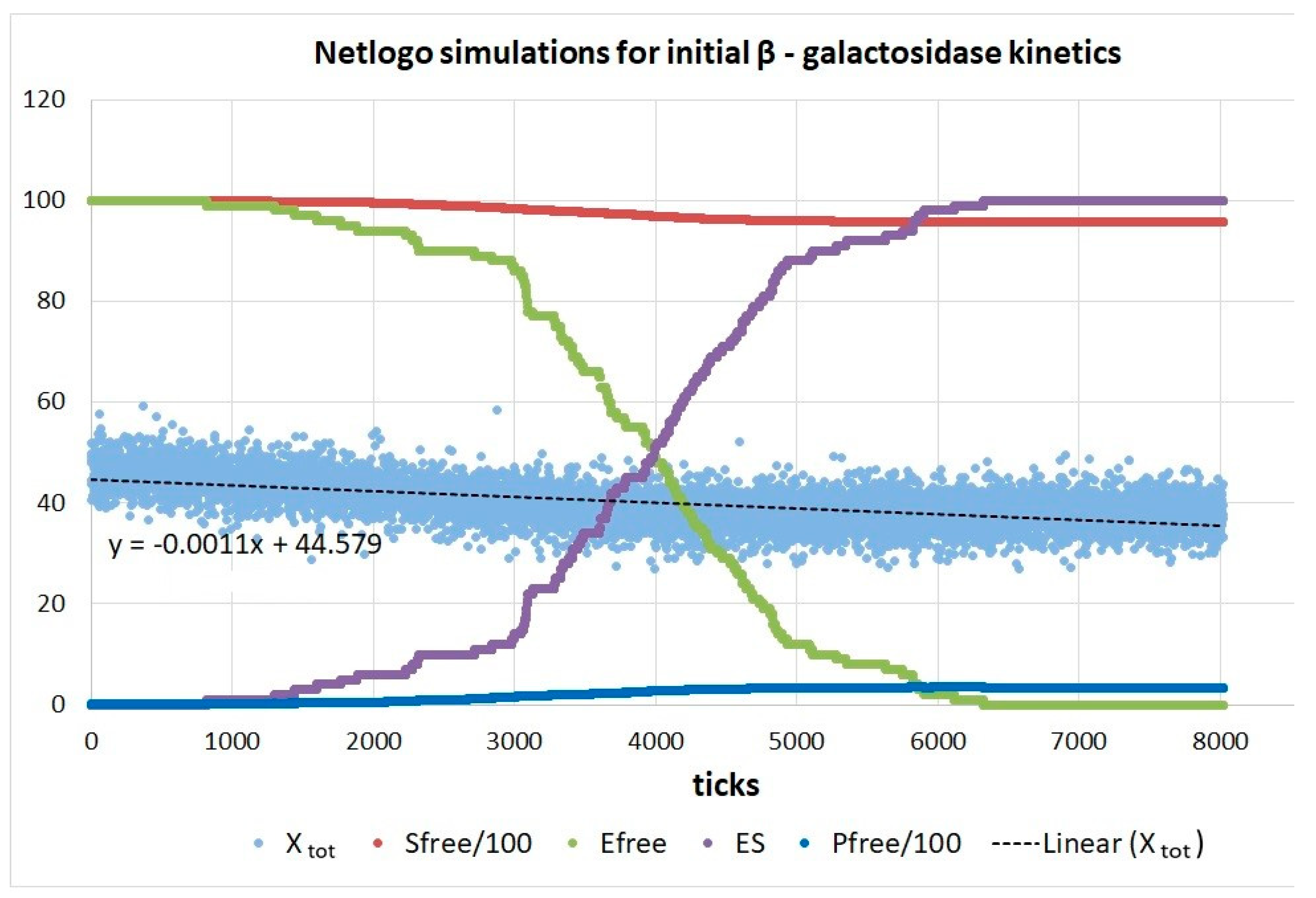
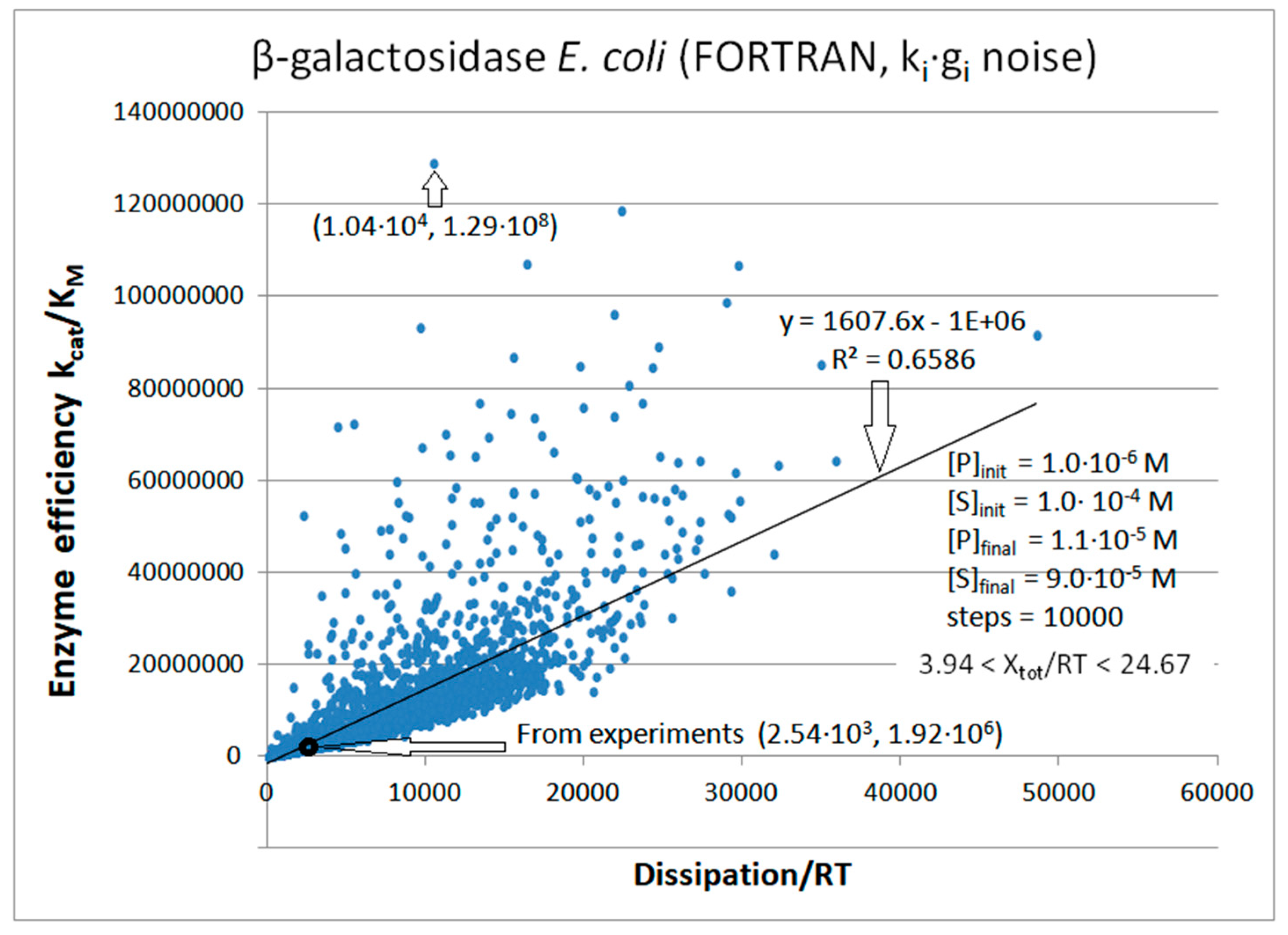
8. β-Galactosidase
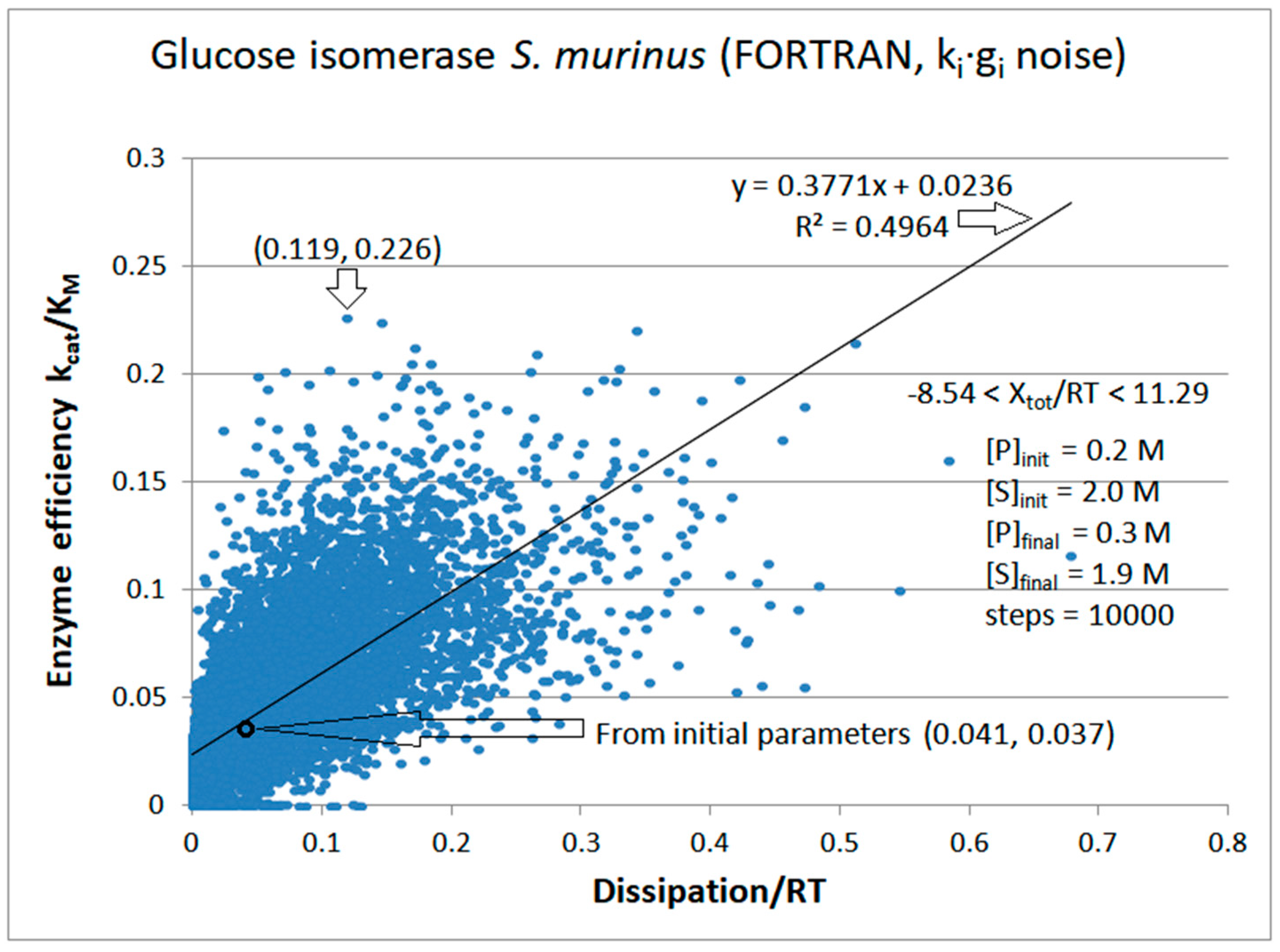
9. Glucose Isomerase
10. An Overall Summary of All Results
| Enzyme (# Functional States, Figure #) | Simulation Software Abbreviation (Noisy ki) | Efficiency Fold-Improv. | Dissipation Fold Increase | Eff/Disssip. (Fold Factor) * | Best Eff. (M−1s−1) |
|---|---|---|---|---|---|
| Glucose isomerase (2, 21) | S32-fortran (all ki noisy) | 6.1 | 2.9 | 1.9 (2.1) | 0.226 |
| Glucose isomerase (2, S19) | S30-netlogo (all ki noisy) | 5.8 | 5.2 | 1.0 (1.1) | 0.213 |
| β-galactosidase (2, 18) | S27-netlogo (all ki noisy) | 44.8 | 6.7 | 5.1 × 103 (6.7) | 8.59 × 107 |
| β-galactosidase (2, 20) | S29-fortran (all ki noisy) | 67.2 | 4.1 | 1.2 × 104 (16.4) | 1.29 × 108 |
| Lac-1 β-lactamase (3, S15) | S24-netlogo (noisy k1,k2) | 4.8 | 1.3 | 6.4 × 103 (3.6) | 1.3 × 108 |
| RTEM β-lactamase (3, 16) | S21-netlogo (noisy k1,k2) | 9.6 | 1.6 | 2.1 × 104 (6.0) | 2.3 × 108 |
| PC1 β-lactamase (3, S11) | S19-netlogo (noisy k1,k2) | 6.5 | 1.2 | 7.6 × 104 (5.2) | 6.5 × 107 |
| Carbonic anhyd. I (4, S7) | S14-fortran (all ki noisy) | 4.5 | 18.1 | 218 (0.25) | 1.1 × 108 |
| Carbonic anhyd. I (4, S8) | S15-netlogo (all ki noisy) | 5.9 | 22.4 | 231 (0.26) | 1.47 × 108 |
| Carbonic anhyd. II (4, 14) | S16-netlogo (all ki noisy) | 5.1 | 13.4 | 254 (0.38) | 4.25 × 108 |
| Carbonic anhyd. T200H (4, S9) | S17-netlogo (all ki noisy) | 5.5 | 14.0 | 421 (0.39) | 3.71 × 108 |
| Ketosteroid isomerase (4, 10) | S10-fortran (all ki noisy) | 6.2 | 4.6 | 3.5 × 103 (1.34) | 1.88 × 109 |
| Ketosteroid isomerase (4, 12) | S13-netlogo (all ki noisy) | 8.6 | 3.8 | 5.7 × 103 (2.26) | 2.59 × 109 |
| Triophosphate isomerase (4, 7) | S7-fortran (all ki noisy) | 29.9 | 160.6 | 1.5 × 104 (0.19) | 2.4 × 107 |
| Triophosphate isomerase (4, 9) | S9-netlogo (all ki noisy) | 28.1 | 198.4 | 1.1 × 104 (0.14) | 2.2 × 107 |
11. Discussion
11.1. Dissipation, Evolution, and the Catalytic Power of Enzymes
11.2. Computational Improvements of the Catalytic Power for Specific Enzymes
11.3. Possible Benefits of Considering Unanswered Questions
| Figure | Enzyme | Software | k1 (s−1) | k2 (s−1) | P1 (s−1) (%P) | P (s−1) | k3 (s−1) | k4 (s−1) | k5 (s−1) | k6 (s−1) | k7 (s−1) | k8 (s−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TPI | Exper&calc. | 400 | 7.0 × 103 | 0.573 (6) | 9.883 | 2.0 × 103 | 6.0 × 103 | 6.0 × 104 | 9.0 × 104 | 4 × 103 | 25.60 | |
| Figure 9 | NetLogo | 1.05 × 103 | 303 | 833 (42) | 1.96 × 103 | 5.4 × 103 | 12.6 × 103 | 9.4 × 104 | 9.97 × 104 | 6.5 × 103 | 128 | |
| Figure 7 | FORTRAN | 1.14 × 103 | 126 | 435 (27) | 1.59 × 103 | 1.05 × 103 | 6.0 × 103 | 6.0 × 104 | 6.15 × 103 | 937 | 25.60 | |
| KSI | Exper&calc. | 8.3 × 104 | 8.6 × 104 | 6.22 × 103 (5) (5) | 1.16 × 105 | 1.8 × 105 | 1.7 × 106 | 6.4 × 105 | 43 | 1.5 × 105 | 5.0 × 104 | |
| Figure 12 | NetLogo | 2.77 × 105 | 3.7 × 104 | 7.9 × 104 (18) | 4.50 × 105 | 4.95 × 105 | 7.1 × 105 | 1.02 × 106 | 16 | 6.9 × 104 | 7.7 × 104 | |
| Figure 10 | FORTRAN | 2.30 × 105 | 2.5 × 104 | 7.17 × 104 (13) | 5.39 × 105 | 1.8 × 105 | 3.97 × 105 | 6.4 × 105 | 43 | 1.5 × 105 | 2.9 × 104 | |
| CA I | Exper&calc. | 4.08 × 104 | 3.8 × 104 | 1.48 × 104 (52) | 2.84 × 104 | 2.9 × 105 | 6.24 × 105 | 9.0 × 105 | 9.0 × 106 | 5.5 × 106 | 4.5 × 104 | |
| Figure S8 | NetLogo | 2.0 × 105 | 2.3 × 104 | 2.51 × 105(40) | 6.36 × 105 | 4.7 × 105 | 6.55 × 105 | 2.0 × 106 | 9.3 × 106 | 8.8 × 106 | 1.8 × 104 | |
| Figure S7 | FORTRAN | 1.53 × 105 | 1.5 × 104 | 2.13 × 105 (41) | 5.14 × 105 | 1.95 × 106 | 7.71 × 105 | 2.3 × 106 | 8.5 × 106 | 6.6 × 106 | 3.1 × 104 | |
| CA II | Exper&calc. | 1.56 × 105 | 1.8 × 106 | 5.33 × 104 (43) | 1.25 × 105 | 1.7 × 107 | 4.80 × 106 | 1.2 × 106 | 1.2 × 106 | 2.0 × 107 | 1.0 × 106 | |
| Figure 14 | NetLogo | 6.38 × 105 | 2.5 × 106 | 5.61 × 105 (34) | 1.67 × 106 | 3.7 × 107 | 3.93 × 106 | 1.5 × 106 | 1.5 × 106 | 3.0 × 107 | 6.6 × 105 | |
| CA II T200H | Exper&calc. | 9.84 × 104 | 5.4 × 104 | 4.03 × 104 (64) | 6.3 × 104 | 3.0 × 105 | 2.16 × 105 | 2.7 × 106 | 2.1 × 107 | 1.8 × 107 | 9.0 × 105 | |
| Figure S9 | NetLogo | 6.49 × 105 | 6.7 × 104 | 4.05 × 105(46) | 8.82 × 105 | 7.98 × 105 | 7.4 × 104 | 3.2 × 106 | 2.9 × 107 | 7.4 × 106 | 4.6 × 105 | |
| PC1 | Exper&calc. | 3.28 × 104 | 196 | 37 (5) | 689 | 173 | 4.0 | 96 | 8.0 | |||
| Figure S11 | NetLogo | 1.15 × 105 | 32 | 111 (13) | 858 | 173 | 4 | 96 | 11 | |||
| RTEM | Exper&calc. | 1.71 × 105 | 1.18 × 104 | 185 (3) | 6.76 × 103 | 2.8 × 103 | 6.0 | 1.5 × 103 | 4.4 × 103 | |||
| Figure 16 | NetLogo | 4.07 × 105 | 851 | 1.4 × 103 (13) | 1.08 × 104 | 2.8 × 103 | 6 | 1.5 × 103 | 4.7 × 103 | |||
| Lac-1 | Exper&calc. | 5.27 × 104 | 2.32 × 103 | 1.8 × 103 (12) | 1.45 × 104 | 4.09 × 103 | 50 | 3.61 × 103 | 1.72 × 103 | |||
| Figure S15 | NetLogo | 1.98 × 105 | 976 | 3.1 × 103 (16) | 1.95 × 104 | 4.09 × 103 | 50 | 3.61 × 103 | 1.76 × 103 | |||
| β-galacto- sidas | Exper&calc. | 5.0 × 103 | 1.83 × 104 | 5.84 (0.2) | 2.55 × 103 | 730 | 1.0 × 10−5 | |||||
| Figure 18 | NetLogo | 1.4 × 104 | 467 | 628 (4) | 1.70 × 104 | 726 | 2.25 × 10−7 | |||||
| Figure 20 | FORTRAN | 1.3 × 104 | 61 | 1.12 × 103 (11) | 1.04 × 104 | 520 | 0.0001 | |||||
| Glucose isomerase | Exper&calc. | 0.126 | 0.021 | 0.0126 (31) | 0.0392 | 0.029 | 0.016 | |||||
| Figure S19 | NetLogo | 0.320 | 0.002 | 0.143 (68) | 0.211749 | 0.068 | 0.088 | |||||
| Figure 21 | FORTRAN | 0.499 | 0.004 | 0.057 (48) | 0.119 | 0.031 | 0.045 |
12. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Michaelis, L.; Menten, M.L. Kinetics of invertase action. Biochem. Z 1913, 49, 333–369. [Google Scholar]
- Michaelis, L.; Menten, M.L.; Johnson, K.A.; Goody, R.S. The original Michaelis constant: Translation of the 1913 Michaelis-Menten paper. Biochemistry 2011, 50, 8264–8269. [Google Scholar] [CrossRef]
- Juretić, D.; Simunić, J.; Bonačić Lošić, Ž. Maximum entropy production theorem for transitions between enzyme functional states and its application. Entropy 2019, 21, 743. [Google Scholar] [CrossRef] [PubMed]
- Juretić, D. Bioenergetics: A Bridge Across Life and Universe; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2021. [Google Scholar]
- Hill, T.L. Free Energy Transduction in Biology: The Steady State Kinetic and Thermodynamic Formalism; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Hill, T.L. Free Energy Transduction and Biochemical Cycle Kinetics; Dover Publications, Inc.: Mineola, NY, USA, 2005. [Google Scholar]
- Sica, L.; Gilli, R.; Briand, C.; Sari, J.C. A flow microcalorimetric method for enzyme activity measurements: Application to dihydrofolate reductase. Anal. Biochem. 1987, 165, 341–348. [Google Scholar] [CrossRef]
- Todd, M.J.; Gomez, J. Enzyme kinetics determined using calorimetry: A general assay for enzyme activity? Anal. Biochem. 2001, 296, 179–187. [Google Scholar] [CrossRef]
- Riedel, C.; Gabizon, R.; Wilson, C.A.M.; Hamadani, K.; Tsekouras, K.; Marqusee, S.; Pressé, S.; Bustamante, C. The heat released during catalytic turnover enhances the diffusion of an enzyme. Nature 2015, 517, 227–230. [Google Scholar] [CrossRef]
- Abramov, O.; Mojzsis, S.J. Microbial habitability of the Hadean Earth during the late heavy bombardment. Nature 2009, 459, 419–422. [Google Scholar] [CrossRef]
- Wolfenden, R. Benchmark reaction rates, the stability of biological molecules in water, and the evolution of catalytic power in enzymes. Annu. Rev. Biochem. 2011, 80, 645–667. [Google Scholar] [CrossRef]
- Goldman, A.D.; Kacar, B. Cofactors are Remnants of Life’s Origin and Early Evolution. J. Mol. Evol. 2021, 89, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Radzicka, A.; Wolfenden, R. A proficient enzyme. Science 1995, 267, 90–93. [Google Scholar] [CrossRef] [PubMed]
- Wolfenden, R. Thermodynamic and extrathermodynamic requirements of enzyme catalysis. Biophys. Chem. 2003, 105, 559–572. [Google Scholar] [CrossRef] [PubMed]
- Snider, M.G.; Temple, B.S.; Wolfenden, R. The path to the transition state in enzyme reactions: A survey of catalytic efficiencies. J. Phys. Org. Chem. 2004, 17, 586–591. [Google Scholar] [CrossRef]
- Stockbridge, R.B.; Lewis, C.A., Jr.; Yuan, Y.; Wolfenden, R. Impact of temperature on the time required for the establishment of primordial biochemistry, and for the evolution of enzymes. Proc. Natl. Acad. Sci. USA 2010, 107, 22102–22105. [Google Scholar] [CrossRef] [PubMed]
- Edwards, D.R.; Lohman, D.C.; Wolfenden, R. Catalytic proficiency: The extreme case of S-O cleaving sulfatases. J. Am. Chem. Soc. 2012, 134, 525–531. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, K.; Bhattacharyya, K. States with identical steady dissipation rate in reaction networks: A non-equilibrium thermodynamic insight in enzyme efficiency. Chem. Phys. 2014, 438, 1–6. [Google Scholar] [CrossRef]
- Davidi, D.; Longo, L.M.; Jabłońska, J.; Milo, R.; Tawfik, D.S. A Bird’s-Eye View of Enzyme Evolution: Chemical, Physicochemical, and Physiological Considerations. Chem. Rev. 2018, 118, 8786–8797. [Google Scholar] [CrossRef] [PubMed]
- Gusev, O.A.; Martyushev, L.M. An Evolution Based on Various Energy Strategies. Entropy 2021, 23, 317. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Johnson, K.A. A century of enzyme kinetic analysis, 1913 to 2013. FEBS Lett. 2013, 587, 2753–2766. [Google Scholar] [CrossRef]
- Cornish-Bowden, A. One hundred years of Michaelis–Menten kinetics. Perspect. Sci. 2015, 4, 3–9. [Google Scholar] [CrossRef]
- Voorsluijs, V.; Avanzini, F.; Esposito, M. Thermodynamic validity criterion for the irreversible Michaelis-Menten equation. arxiv 2020, arXiv:2006.06476v1. [Google Scholar] [CrossRef]
- Williams, D.L.; Sikora, V.M.; Hammer, M.A.; Amin, S.; Brinjikji, T.; Brumley, E.K.; Burrows, C.J.; Carrillo, P.M.; Cromer, K.; Edwards, S.J.; et al. May the Odds Be Ever in Your Favor: Non-deterministic Mechanisms Diversifying Cell Surface Molecule Expression. Front. Cell Dev. Biol. 2022, 9, 720798. [Google Scholar] [CrossRef]
- Das, B.; Banerjee, K.; Gangopadhyay, G. Propensity approach to nonequilibrium thermodynamics of a chemical reaction network: Controlling single E-coli β-galactosidase enzyme catalysis through the elementary reaction steps. J. Chem. Phys. 2013, 139, 244104. [Google Scholar] [CrossRef]
- Converti, A.; Borghi, M.D. Kinetics of glucose isomerization to fructose by immobilized glucose isomerase in the presence of substrate protection. Bioprocess Eng. 1998, 18, 27–33. [Google Scholar] [CrossRef]
- Dobovišek, A.; Vitas, M.; Brumen, M.; Fajmut, A. Energy conservation and maximal entropy production in enzyme reactions. Biosystems 2017, 158, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Christensen, H.; Martin, M.T.; Waley, G. β-lactamases as fully efficient enzymes. Determination of all the rate constants in the acyl-enzyme mechanism. Biochem. J. 1990, 266, 853–861. [Google Scholar] [PubMed]
- Juretić, D.; Bonačić Lošić, Ž.; Domagoj Kuić, D.; Juraj Simunić, J.; Dobovišek, A. The maximum entropy production requirement for proton transfers enhances catalytic efficiency for β-lactamases. Biophys. Chem. 2019, 244, 11–21. [Google Scholar] [CrossRef]
- Toney, M.D. Carbon Acidity in Enzyme Active Sites. Front. Bioeng. Biotechnol. 2019, 7, 25. [Google Scholar] [CrossRef] [PubMed]
- Knowles, J.R.; Albery, W.J. Perfection in enzyme catalysis: The energetics of triosephosphate isomerase. Acc. Chem. Res. 1977, 10, 105–111. [Google Scholar] [CrossRef]
- Behravan, G.; Jonsson, B.H.; Lindskog, S. Fine tuning of the catalytic properties of carbonic anhydrase. Studies of a Thr200→His variant of human isoenzyme II. Eur. J. Biochem. 1990, 190, 351–357. [Google Scholar] [CrossRef]
- Martyushev, L.M. Entropy and Entropy Production: Old Misconceptions and New Breakthroughs. Entropy 2013, 15, 1152–1170. [Google Scholar] [CrossRef]
- Zhang, D.; Ouyang, Q. Nonequilibrium Thermodynamics in Biochemical Systems and Its Application. Entropy 2021, 23, 271. [Google Scholar] [CrossRef]
- Ge, H. Multivariable fluctuation theorems in the steady-state cycle kinetics of single enzyme with competing substrates. J. Phys. Math. Theor. 2012, 45, 215002. [Google Scholar] [CrossRef]
- Ge, H.; Qian, M. Steady-state cycle kinetics of single enzymes: Competing substrates and multi-conformations. J. Theor. Comput. Chem. 2008, 7, 1001–1027. [Google Scholar] [CrossRef]
- Juretić, D.; Županović, P. Photosynthetic models with maximum entropy production in irreversible charge transfer steps. J. Comp. Biol. Chem. 2003, 27, 541–553. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, T.; Hoffmann-Klipp, E.; Heinrich, R. An evolutionary approach to enzyme kinetics: Optimization of ordered mechanisms. Bull. Math. Biol. 1994, 56, 65–106. [Google Scholar] [CrossRef]
- Toney, M.D. Common Enzymological Experiments Allow Free Energy Profile Determination. Biochemistry 2013, 52, 5952–5965. [Google Scholar] [CrossRef] [PubMed]
- Heinrich, R.; Schuster, S.; Holzhütter, H.-G. Mathematical analysis of enzymic reaction systems using optimmization principles. Eur. J. Biochem. 1991, 201, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.A. 1 Transient-State Kinetic Analysis of Enzyme Reaction Pathways. In The Enzymes; Sigman, D.S., Ed.; Academic Press: Cambridge, MA, USA, 1992; Volume 20, pp. 1–61. [Google Scholar] [CrossRef]
- Box, G.E.P.; Muller, M.E. A note on the generation of random normal derivatives. Ann. Math. Stat. 1958, 29, 610–611. [Google Scholar] [CrossRef]
- Wilensky, U.; Reisman, K. Thinking Like a Wolf, a Sheep, or a Firefly: Learning Biology Through Constructing and Testing Computational Theories—An Embodied Modeling Approach. Cogn. Instr. 2006, 24, 171–2009. [Google Scholar] [CrossRef]
- Apte, A. Computational Modeling of Biochemical Systems Using Cellular Automata. Ph.D. Thesis, Virginia Commonwealth University, Richmond, VA, USA, 2009. [Google Scholar] [CrossRef]
- Ishida, T. Possibility of Controlling Self-Organized Patterns with Totalistic Cellular Automata Consisting of Both Rules like Game of Life and Rules Producing Turing Patterns. Micromachines 2018, 9, 339. [Google Scholar] [CrossRef]
- Koopmans, L.; Youk, H. Predictive landscapes hidden beneath biological cellular automata. J. Biol. Phys. 2021, 47, 355–369. [Google Scholar] [CrossRef]
- Sklar, E. NetLogo, a multi-agent simulation environment. Artif. Life 2007, 13, 303–311. [Google Scholar] [CrossRef]
- Dong, X.; Foteinou, P.T.; Calvano, S.E.; Lowry, S.F.; Androulakis, I.P. Agent-Based Modeling of Endotoxin-Induced Acute Inflammatory Response in Human Blood Leukocytes. PLoS ONE 2010, 5, e9249. [Google Scholar] [CrossRef] [PubMed]
- Bravo, R.; Axelrod, D.E. A calibrated agent-based computer model of stochastic cell dynamics in normal human colon crypts useful for in silico experiments. Theor. Biol. Med. Model 2013, 10, 66. [Google Scholar] [CrossRef] [PubMed]
- Dutot, A.; Olivier, D. Swarm Problem-Solving. In Agent-Based Spatial Simulation with NetLogo; Banos, A., Lang, C., Marilleau, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; Volume 2, pp. 117–172. [Google Scholar] [CrossRef]
- Stieff, M.; Wilensky, U. NetLogo Enzyme Kinetics Model; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 2001; Available online: http://ccl.northwestern.edu/netlogo/models/EnzymeKinetics (accessed on 26 January 2024).
- Chapleau, R.R.; Robinson, P.J.; Schlager, J.J.; Gearhart, J.M. Potential new therapeutic modality revealed through agent-based modeling of the neuromuscular junction and acetylcholinesterase inhibition. Theor. Biol. Med. Model. 2014, 11, 42. [Google Scholar] [CrossRef] [PubMed]
- Wilensky, U. NetLogo; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 1999; Available online: http://ccl.northwestern.edu/netlogo/ (accessed on 26 January 2024).
- Wierenga, R.K.; Kapetaniou, E.G.; Venkatesan, R. Triosephosphate isomerase: A highly evolved biocatalyst. Cell. Mol. Life Sci. 2010, 67, 3961–3982. [Google Scholar] [CrossRef] [PubMed]
- Olivares-Illana, V.; Riveros-Rosas, H.; Nallely Cabrera, N.; de Gómez-Puyou, M.T.; Ruy Pérez-Montfort, R.; Costas, M.; Gómez-Puyou, A. A guide to the effects of a large portion of the residues of triosephosphate isomerase on catalysis, stability, druggability, and human disease. Proteins 2017, 85, 1190–1211. [Google Scholar] [CrossRef] [PubMed]
- Gerlt, J.A. Evolution of Enzyme Function and the Development of Catalytic Efficiency: Triosephosphate Isomerase, Jeremy, R. Knowles, and W. John Albery. Biochemistry 2021, 60, 3529–3538. [Google Scholar] [CrossRef] [PubMed]
- Albery, W.J.; Knowles, J.R. Evolution of enzyme function and the development of catalytic efficiency. Biochemistry 1976, 15, 5631–5640. [Google Scholar] [CrossRef]
- Richard, J.P. Acid-Base Catalysis of the Elimination and Isomerization Reactions of Triose Phosphates. J. Am. Chem. Soc. 1984, 106, 4926–4936. [Google Scholar] [CrossRef]
- Bar-Even, A.; Noor, E.; Savir, Y.; Liebermeister, W.; Davidi, D.; Tawfik, D.S.; Milo, R. The moderately efficient enzyme: Evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 2011, 50, 4402–4410. [Google Scholar] [CrossRef] [PubMed]
- Webster, K.A. Evolution of the coordinate regulation of glycolytic enzyme genes by hypoxia. J. Exp. Biol. 2003, 206, 2911–2922. [Google Scholar] [CrossRef] [PubMed]
- Orozco, J.M.; Krawczyk, P.A.; Scaria, S.M.; Cangelosi, A.L.; Chan, S.H.; Kunchok, T.; Lewis, C.A.; Sabatini, D.M. Dihydroxyacetone phosphate signals glucose availability to mTORC1. Nat. Metab. 2020, 2, 893–901. [Google Scholar] [CrossRef] [PubMed]
- Myers, T.D.; Palladino, M.J. Newly discovered roles of triosephosphate isomerase including functions within the nucleus. Mol. Med. 2023, 29, 18. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Jiménez, L.K.; Moreno-Herrera, A.; Juárez-Saldivar, A.; González-González, A.; Ortiz-Pérez, E.; Paz-González, A.D.; Palos, I.; Ramírez-Moreno, E.; Rivera, G. Recent Advances in the Development of Triose Phosphate Isomerase Inhibitors as Antiprotozoal Agents. Curr. Med. Chem. 2022, 29, 2504–2529. [Google Scholar] [CrossRef] [PubMed]
- Lincet, H.; Icard, P. How do glycolytic enzymes favour cancer cell proliferation by nonmetabolic functions? Oncogene 2014, 34, 3751–3759. [Google Scholar] [CrossRef]
- Ationu, A.; Humphries, A. The feasibility of replacement therapy for inherited disorder of glycolysis: Triosephosphate isomerase deficiency (review). Int. J. Mol. Med. 1998, 6, 701–704. [Google Scholar] [CrossRef]
- Blacklow, S.C.; Raines, R.T.; Lim, W.A.; Zamore, P.D.; Knowles, J.R. Triosephosphate isomerase catalysis is diffusion controlled. Biochemistry 1988, 27, 1158–1165. [Google Scholar] [CrossRef]
- Wade, R.C.; Davis, M.E.; Luty, B.A.; Madura, J.D.; McCammon, J.A. Gating of the active site of triose phosphate isomerase: Brownian dynamics simulations of flexible peptide loops in the enzyme. Biophys. J. 1993, 64, 9–15. [Google Scholar] [CrossRef]
- Wade, R.C.; Gabdoulline, R.R.; Lüdemann, S.K.; Lounnas, V. Electrostatic steering and ionic tethering in enzyme-ligand binding: Insights from simulations. Proc. Natl. Acad. Sci. USA 1998, 95, 5942–5949. [Google Scholar] [CrossRef]
- Katebi, A.R.; Jernigan, R.L. The critical role of the loops of triosephosphate isomerase for its oligomerization, dynamics, and functionality. Protein Sci. 2014, 23, 213–228. [Google Scholar] [CrossRef]
- Sharma, P.; Guptasarma, P. ‘Super-perfect’ enzymes: Structural stabilities and activities of recombinant triose phosphate isomerases from Pyrococcus furiosus and Thermococcus onnurineus produced in Escherichia coli. Biochem. Biophys. Res. Commun. 2015, 460, 753–758. [Google Scholar] [CrossRef] [PubMed]
- Schachner, L.F.; Soye, B.D.; Ro, S.; Kenney, G.E.; Ives, A.N.; Su, T.; Goo, Y.A.; Jewett, M.C.; Rosenzweig, A.C.; Kelleher, N.L. Revving an Engine of Human Metabolism: Activity Enhancement of Triosephosphate Isomerase via Hemi-Phosphorylation. ACS Chem. Biol. 2022, 17, 2769–2780. [Google Scholar] [CrossRef] [PubMed]
- Tajes, M.; Guivernau, B.; Ramos-Fernández, E.; Bosch-Morató, M.; Palomer, E.; Guix, F.X.; Muñoz, F.J. The pathophysiology of triose phosphate isomerase dysfunction in Alzheimer’s disease. Histol. Histopathol. 2013, 28, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Bonačić Lošić, Ž.; Donđivić, T.; Juretić, D. Is the catalytic activity of triosephosphate isomerase fully optimized? An investigation based on maximization of entropy production. J. Biol. Phys. 2017, 43, 69–86. [Google Scholar] [CrossRef] [PubMed]
- Juretić, D.; Bonačić Lošić, Ž. Comments on ‘Flexibility of enzymatic transitions as a hallmark of optimized enzyme steady-state kinetics and thermodynamics’. Comput. Biol. Chem. 2021, 95, 107571. [Google Scholar] [CrossRef]
- Šterk, M.; Markovič, R.; Marhl, M.; Fajmut, A.; Dobovišek, A. Flexibility of enzymatic transitions as a hallmark of optimized enzyme steady-state kinetics and thermodynamics. Comput. Biol. Chem. 2021, 91, 107449. [Google Scholar] [CrossRef]
- Klipp, E.; Heinrich, R. Evolutionary optimization of enzyme kinetic parameters; effect of constraints. J. Theor. Biol. 1994, 171, 309–323. [Google Scholar] [CrossRef]
- Bish, D.R.; Mavrovouniotis, M.L. Enzymatic reaction rate limits with constraints on equilibrium constants and experimental parameters. Biosystems 1998, 47, 37–60. [Google Scholar] [CrossRef]
- Talalay, P. A fascination with enzymes: The journey not the arrival matters. J. Biol. Chem. 2005, 280, 28829–28847. [Google Scholar] [CrossRef] [PubMed]
- Pollack, R.M. Enzymatic mechanisms for catalysis of enolization: Ketosteroid isomerase. Bioorg. Chem. 2004, 32, 341–353. [Google Scholar] [CrossRef]
- Fried, S.D.; Boxer, S.G.; Fayer, M.D.; Solomon, E.I. On the Origins of Catalysis by Ketosteroid Isomerase. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2014. Available online: http://purl.stanford.edu/bf687qj8918 (accessed on 26 January 2024).
- Pollack, R.M.; Zeng, B.; Mack, J.P.G.; Eldin, S. Determination of the microscopic rate constants for the base catalyzed conjugation of 5-androstene-3,17-dione. J. Am. Chem. Soc. 1989, 111, 6419–6423. [Google Scholar] [CrossRef]
- Pollack, R.M.; Thornburg, L.D.; Wu, Z.R.; Summers, M.F. Mechanistic insights from the three-dimensional structure of 3-oxo-Delta(5)-steroid isomerase. Arch. Biochem. Biophys. 1999, 370, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Fried, S.D.; Bagchi, S.; Boxer, S.G. Extreme electric fields power catalysis in the active site of ketosteroid isomerase. Science 2014, 346, 1510–1514. [Google Scholar] [CrossRef]
- Wu, Y.; Boxer, S.G. A Critical Test of the Electrostatic Contribution to Catalysis with Noncanonical Amino Acids in Ketosteroid Isomerase. J. Am. Chem. Soc. 2016, 138, 11890–11895. [Google Scholar] [CrossRef]
- Wu, Y.; Fried, S.D.; Boxer, S.G. A Preorganized Electric Field Leads to Minimal Geometrical Reorientation in the Catalytic Reaction of Ketosteroid Isomerase. J. Am. Chem. Soc. 2020, 142, 9993–9998. [Google Scholar] [CrossRef]
- Ito, M.; Brinck, T. Novel Approach for Identifying Key Residues in Enzymatic Reactions: Proton Abstraction in Ketosteroid Isomerase. J. Phys. Chem. B 2014, 118, 13050–13058. [Google Scholar] [CrossRef]
- Thomas, J.L.; Evans, B.W.; Blanco, G.; Mason, J.I.; Strickler, R.C. Creation of a fully active, cytosolic form of human type I 3β-hydroxysteroid dehydrogenase/isomerase by the deletion of a membrane-spanning domain. J. Mol. Endocrinol. 1999, 23, 231–239. [Google Scholar] [CrossRef]
- Hawkinson, D.C.; Eames, T.C.; Pollack, R.M. Energetics of 3-oxo-Δ5-steroid isomerase: Source of the catalytic power of the enzyme. Biochemistry 1991, 30, 10849–10858. [Google Scholar] [CrossRef]
- Kupriyanova, E.; Pronina, N.; Los, D. Carbonic anhydrase—A universal enzyme of the carbon-based life. Photosynthetica 2017, 55, 3–19. [Google Scholar] [CrossRef]
- Hirakawa, Y.; Senda, M.; Fukuda, K.; Yu, H.Y.; Ishida, M.; Taira, M.; Kinbara, K.; Senda, T. Characterization of a novel type of carbonic anhydrase that acts without metal cofactors. BMC Biol. 2021, 19, 105. [Google Scholar] [CrossRef] [PubMed]
- Lomelino, C.L.; Andring, J.T.; McKenna, R. Crystallography and Its Impact on Carbonic Anhydrase Research. Int. J. Med. Chem. 2018, 2018, 9419521. [Google Scholar] [CrossRef]
- Sanyal, G.; Maren, T.H. Thermodynamics of carbonic anhydrase catalysis. A comparison between human isoenzymes B and C. J. Biol. Chem. 1981, 256, 608–612. [Google Scholar] [CrossRef]
- Krishnamurthy, V.M.; Kaufman, G.K.; Urbach, A.R.; Gitlin, I.; Gudiksen, K.L.; Weibel, D.B.; Whitesides, G.M. Carbonic Anhydrase as a Model for Biophysical and Physical-Organic Studies of Proteins and Protein–Ligand Binding. Chem. Rev. 2008, 108, 946–1051. [Google Scholar] [CrossRef]
- McDevitt, M.E.; Lambert, L.A. Molecular evolution and selection pressure in alpha-class carbonic anhydrase family members. Biochim. Biophys. Acta 2011, 1814, 1854–18561. [Google Scholar] [CrossRef]
- Fisher, S.Z.; Tu, C.; Bhatt, D.; Govindasamy, L.; Agbandje-McKenna, M.; McKenna, R.; Silverman, D.N. Speeding up proton transfer in a fast enzyme: Kinetic and crystallographic studies on the effect of hydrophobic amino acid substitutions in the active site of human carbonic anhydrase II. Biochemistry 2007, 46, 3803–3813. [Google Scholar] [CrossRef] [PubMed]
- Lindskog, S. Structure and mechanism of carbonic anhydrase. Pharmacol. Ther. 1997, 74, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Hewett-Emmett, D.; Hopkins, P.J.; Tashian, R.E.; Czelusniak, J. Origins and molecular evolution of the carbonic anhydrase isozymes. Ann. N. Y. Acad. Sci. 1984, 429, 338–358. [Google Scholar] [CrossRef]
- Liljas, A.; Laurberg, M. A wheel invented three times. The molecular structures of the three carbonic anhydrases. EMBO Repb. 2000, 1, 16–17. [Google Scholar] [CrossRef]
- Supuran, C.T. Carbonic anhydrase activators. Future Med. Chem. 2018, 10, 561–573. [Google Scholar] [CrossRef] [PubMed]
- Supuran, C.T. Carbonic anhydrase inhibitors. Bioorg. Med. Chem. Lett. 2010, 20, 3467–3474. [Google Scholar] [CrossRef] [PubMed]
- Cabaleiro-Lago, C.; Lundqvist, M. The Effect of Nanoparticles on the Structure and Enzymatic Activity of Human Carbonic Anhydrase I and II. Molecules 2020, 25, 4405. [Google Scholar] [CrossRef] [PubMed]
- Diez-Fernandez, C.; Rüfenacht, V.; Santra, S.; Lund, A.M.; Santer, R.; Lindner, M.; Tangeraas, T.; Unsinn, C.; de Lonlay, P.; Burlina, A.; et al. Defective hepatic bicarbonate production due to carbonic anhydrase VA deficiency leads to early-onset life-threatening metabolic crisis. Genet. Med. 2016, 18, 991–1000. [Google Scholar] [CrossRef] [PubMed]
- De Souza, L.C.; Provensi, G.; Vullo, D.; Carta, F.; Scozzafava, A.; Costa, A.; Schmidt, S.D.; Passani, M.B.; Supuran, C.T.; Blandina, P. Carbonic anhydrase activation enhances object recognition memory in mice through phosphorylation of the extracellular signal-regulated kinase in the cortex and the hippocampus. Neuropharmacology 2017, 118, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, S.D.; Nachtigall, E.G.; Marcondes, L.A.; Zanluchi, A.; Furini, C.R.G.; Passani, M.B.; Supuran, C.T.; Blandina, P.; Izquierdo, I.; Provensi, G.; et al. Modulation of Carbonic Anhydrases Activity in the Hippocampus or Prefrontal Cortex Differentially Affects Social Recognition Memory in Rats. Neuroscience 2022, 497, 184–195. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Zhang, S.; Fang, X.; Salmon, S. Carbonic Anhydrase Enhanced UV-Crosslinked PEG-DA/PEO Extruded Hydrogel Flexible Filaments and Durable Grids for CO2 Capture. Gels 2023, 9, 341. [Google Scholar] [CrossRef]
- Perez, F.; Endimiani, A.; Hujer, K.M.; Bonomo, R.A. The continuing challenge of ESBLs. Curr. Opin. Pharmacol. 2007, 7, 459–469. [Google Scholar] [CrossRef]
- Fair, R.J.; Tor, Y. Antibiotics and Bacterial Resistance in the 21st Century. Perspect. Medicin. Chem. 2014, 6, 25–64. [Google Scholar] [CrossRef]
- Bush, K. Past and Present Perspectives on β-Lactamases. Antimicrob. Agents Chemother. 2018, 62, e01076-18. [Google Scholar] [CrossRef]
- Liras, P.; Martin, J.F. Gene clusters for beta-lactam antibiotics and control of their expression: Why have clusters evolved, and from where did they originate? Int. Microbiol. 2006, 9, 9–19. [Google Scholar]
- Ambler, R.P. The structure of β-lactamases. Philos. Trans. R Soc. Lond. B Biol. Sci. 1980, 289, 321–331. [Google Scholar]
- Burbaum, J.J.; Raines, R.T.; Albery, W.J.; Knowles, J.R. Evolutionary optimization of the catalytic effectiveness of an enzyme. Biochemistry 1989, 28, 9293–9305. [Google Scholar] [CrossRef]
- Brocklehurst, K.; Topham, C.M. Kinetic parameters of the acyl-enzyme mechanism and conditions for quasi-equilibrium and for optimal catalytic characteristics. Biochem. J. 1990, 270, 561–563. [Google Scholar] [CrossRef]
- Matagne, A.; Dubus, A.; Galleni, M.; Frère, J.M. The beta-lactamase cycle: A tale of selective pressure and bacterial ingenuity. Nat. Prod. Rep. 1999, 16, 1–19. [Google Scholar] [CrossRef]
- Haldane, J.B.S. Enzymes; Longmans: London, UK, 1930. [Google Scholar]
- Brocklehurst, K. Evolution of enzyme catalytic power. Characteristics of optimal catalysis evaluated for the simplest plausible kinetic model. Biochem. J. 1977, 163, 111–116. [Google Scholar] [CrossRef]
- Jacob, F.; Monod, J. Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 1961, 3, 318–356. [Google Scholar] [CrossRef]
- Walter, N. Michaelis-Menten is dead, long live Michaelis-Menten! Nat. Chem. Biol. 2006, 2, 66–67. [Google Scholar] [CrossRef] [PubMed]
- English, B.P.; Min, W.; van Oijen, A.M.; Lee, K.T.; Luo, G.; Sun, H.; Cherayil, B.J.; Kou, S.C.; Xie, X.S. Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited. Nat. Chem. Biol. 2006, 2, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Juers, D.H.; Matthews, B.W.; Huber, R.E. LacZ β-galactosidase: Structure and function of an enzyme of historical and molecular biological importance. Protein Sci. 2012, 21, 1792–1807. [Google Scholar] [CrossRef] [PubMed]
- Vera, C.; Guerrero, C.; Aburto, C.; Cordova, A.; Illanes, A. Conventional and non-conventional applications of β-galactosidases. Biochim. Biophys. Acta Proteins Proteom. 2020, 1868, 140271. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Labrador, A.; Lebron-Aguilar, R.; Quintanilla-Lopez, J.E.; Galindo-Iranzo, P.M.; Azcarate, S.A.; Kolida, S.; Kachrimanidou, V.; Garcia-Cañas, V.; Methven, L.; Rastall, R.A.; et al. Prebiotic Potential of a New Sweetener Based on Galactooligosaccharides and Modified Mogrosides. J. Agric. Food Chem. 2022, 70, 9048–9056. [Google Scholar] [CrossRef] [PubMed]
- Das, B.; Gangopadhyay, G. Large deviation theory for the kinetics and energetics of turnover of enzyme catalysis in a chemiostatic flow. J. Chem. Phys. 2018, 148, 174104. [Google Scholar] [CrossRef] [PubMed]
- Bhosale, S.H.; Rao, M.B.; Deshpande, V.V. Molecular and Industrial Aspects of Glucose Isomerase. Microbiol. Rev. 1996, 60, 280–300. [Google Scholar] [CrossRef] [PubMed]
- Nam, K.H. Glucose Isomerase: Functions, Structures, and Applications. Appl. Sci. 2022, 12, 428. [Google Scholar] [CrossRef]
- Seike, T.; Kobayashi, Y.; Sahara, T.; Ohgiya, S.; Kamagata, Y.; Fujimori, K.E. Molecular evolutionary engineering of xylose isomerase to improve its catalytic activity and performance of micro-aerobic glucose/xylose co-fermentation in Saccharomyces cerevisiae. Biotechnol. Biofuels 2019, 12, 139. [Google Scholar] [CrossRef] [PubMed]
- DiCosimo, R.; McAuliffe, J.; Ayrookaran, J.P.; Bohlmann, G. Industrial use of immobilized enzymes. Chem. Soc. Rev. 2013, 42, 6437–6474. [Google Scholar] [CrossRef]
- Meng, M.; Bagdasarian, M.; Zeikus, J.G. The role of active-site aromatic and polar residues in catalysis and substrate discrimination by xylose isomerase. Proc. Natl. Acad. Sci. USA 1993, 90, 8459–8463. [Google Scholar] [CrossRef]
- Hartley, B.S.; Hanlon, N.; Jackson, R.J.; Rangarajan, M. Glucose isomerase: Insights into protein engineering for increased thermostability. Biochim. Biophys. Acta 2000, 1543, 294–335. [Google Scholar] [CrossRef]
- Harris, J.M.; Epting, K.L.; Kelly, R.M. N-terminal fusion of a hyperthermophilic chitin-binding domain to xylose isomerase from Thermotoga neapolitana enhances kinetics and thermostability of both free and immobilized enzymes. Biotechnol. Prog. 2010, 26, 993–1000. [Google Scholar] [CrossRef]
- Boersma, J.G.; Vellenga, K.; De Wilt, H.G.J.; Joosten, G.E.H. Mass transfer effects on the rate of isomerization of D-glucose into D-fructose, catalyzed by whole-cell immobilized glucose isomerase. Biotechnol. Bioeng. 1979, 21, 1711–1724. [Google Scholar] [CrossRef] [PubMed]
- Kikkert, A.; Vellenga, K.; De Wilt, H.G.J.; Joosten, G.E.H. The isomerization of D-glucose into D-fructose catalyzed by whole-cell immobilized glucose isomerase. The dependence of the intrinsic rate of reaction on substrate concentration, pH, and temperature. Biotechnol. Bioeng. 1981, 23, 1087–1101. [Google Scholar] [CrossRef]
- Chen, K.-C.; Wu, J.-Y. Substrate protection of immobilized glucose isomerase. Biotechnol. Bioeng. 1987, 30, 817–824. [Google Scholar] [CrossRef] [PubMed]
- Carrazco-Escalante, M.; Caro-Corrales, J.; Iribe-Salazar, R.; Ríos-Iribe, E.; Vázquez-López, Y.; Gutiérrez-Dorado, R.; Hernández-Calderón, O. A new approach for describing and solving the reversible Briggs-Haldane mechanism using immobilized enzyme. Can. J. Chem. Eng. 2020, 98, 316–329. [Google Scholar] [CrossRef]
- Smolin, L. The Life of the Cosmos; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Metzner, H. Bioelectrochemistry of photosynthesis: A theoretical approach. Bioelectrochem. Bioenerg. 1984, 13, 183–190. [Google Scholar] [CrossRef]
- Martyushev, L.M. Life Defined in Terms of Entropy Production: 20th Century Physics Meets 21st Century Biology. Bioessays 2020, 42, e2000101. [Google Scholar] [CrossRef] [PubMed]
- Hystad, G.; Downs, R.T.; Grew, E.S.; Hazen, R.M. Statistical analysis of mineral diversity and distribution: Earth’s mineralogy is unique. Earth Planet. Sci. Lett. 2015, 426, 154–157. [Google Scholar] [CrossRef]
- Laland, K.; Uller, T.; Feldman, M.; Sterelny, K.; Müller, G.B.; Moczek, A.; Jablonka, E.; Odling-Smee, J.; Wray, G.A.; Hoekstra, H.E.; et al. Does evolutionary theory need a rethink? Nature 2014, 514, 161–164. [Google Scholar] [CrossRef] [PubMed]
- Auboeuf, D. Physicochemical Foundations of Life that Direct Evolution: Chance and Natural Selection are not Evolutionary Driving Forces. Life 2020, 10, 7. [Google Scholar] [CrossRef]
- Bermudez, J.; Wagensberg, J. On the entropy production in microbiological stationary states. J. Theor. Biol. 1986, 122, 347–358. [Google Scholar] [CrossRef]
- Von Stockar, U. Biothermodynamics of live cells: A tool for biotechnology and biochemical engineering. J. Non-Equilib. Thermodyn. 2010, 35, 415–475. [Google Scholar] [CrossRef]
- England, J.L. Statistical physics of self-replication. J. Chem. Phys. 2013, 139, 121923. [Google Scholar] [CrossRef] [PubMed]
- Saadat, N.P.; Nies, T.; Rousset, Y.; Ebenhöh, O. Thermodynamic Limits and Optimality of Microbial Growth. Entropy 2020, 22, 277. [Google Scholar] [CrossRef] [PubMed]
- Aoki, I. Entropy principle for human development, growth and aging. J. Theor. Biol. 1991, 150, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Harms, M.J.; Thornton, J.W. Evolutionary biochemistry: Revealing the historical and physical causes of protein properties. Nat. Rev. Genet. 2013, 14, 559–571. [Google Scholar] [CrossRef]
- Keleti, T. Two rules of enzyme kinetics for reversible Michaelis-Menten mechanisms. FEBS Lett. 1986, 208, 109–112. [Google Scholar] [CrossRef]
- Brooks, S.P.; Storey, K.B. A kinetic description of sequential, reversible, Michaelis-Menten reactions: Practical application of theory to metabolic pathways. Mol. Cell. Biochem. 1992, 115, 43–48. [Google Scholar] [CrossRef]
- Pettersson, G. Evolutionary optimization of the catalytic efficiency of enzymes. Eur. J. Biochem. 1992, 206, 289–295. [Google Scholar] [CrossRef]
- Lee, J.K.; Houk, K.N. A proficient enzyme revisited: The predicted mechanism for orotidine monophosphate decarboxylase. Science 1997, 276, 942–945. [Google Scholar] [CrossRef]
- Hammes-Schiffer, S. Catalytic Efficiency of Enzymes: A Theoretical Analysis. Biochemistry 2013, 52, 2012–2020. [Google Scholar] [CrossRef]
- Richard, J.P.; Amyes, T.L.; Goryanova, B.; Zhai, X. Enzyme Architecture: On the Importance of Being in a Protein Cage. Curr. Opin. Chem. Biol. 2014, 21, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Weinert, T.; Skopintsev, P.; James, D.; Dworkowski, F.; Panepucci, E.; Kekilli, D.; Furrer, A.; Brünle, S.; Mous, S.; Ozerov, D.; et al. Proton uptake mechanism in bacteriorhodopsin captured by serial synchrotron crystallography. Science 2019, 365, 61–65. [Google Scholar] [CrossRef] [PubMed]
- Blow, D. So do we understand how enzymes work? Structure 2000, 8, R77–R81. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Viloca, M.; Gao, J.; Karplus, M.; Truhlar, D.G. How enzymes work: Analysis by modern rate theory and computer simulations. Science 2004, 303, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production: Application to crystal growth and chemical kinetics. Curr. Opin. Chem. Eng. 2015, 7, 23–31. [Google Scholar] [CrossRef]
- Grima, R.; Walter, N.G.; Schnell, S. Single-molecule enzymology à la Michaelis-Menten. FEBS J. 2014, 281, 518–530. [Google Scholar] [CrossRef]
- Dóka, É.; Lente, G. Stochastic mapping of the Michaelis-Menten mechanism. J. Chem. Phys. 2012, 136, 054111. [Google Scholar] [CrossRef]
- Zwanzig, R. Rate processes with dynamical disorder. Acc. Chem. Res. 1990, 23, 148–152. [Google Scholar] [CrossRef]
- Kou, S.C.; Cherayil, B.J.; Min, K.; English, B.P.; Xie, X.S. Single-Molecule Michaelis−Menten Equations. J. Phys. Chem. B 2005, 109, 19068–19081. [Google Scholar] [CrossRef] [PubMed]
- Astumian, R.D.; Chock, P.B.; Tsong, T.Y.; Chen, Y.D.; Westerhoff, H.V. Can free energy be transduced from electric noise? Proc. Natl. Acad. Sci. USA 1987, 84, 434–438. [Google Scholar] [CrossRef] [PubMed]
- Qian, H. Cooperativity in Cellular Biochemical Processes: Noise-Enhanced Sensitivity, Fluctuating Enzyme, Bistability with Nonlinear Feedback, and Other Mechanisms for Sigmoidal Responses. Annu. Rev. Biophys. 2012, 41, 179–204. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Milias-Argeitis, A.; Khammash, M. Dynamic disorder in simple enzymatic reactions induces stochastic amplification of substrate. J. R. Soc. Interface 2017, 14, 20170311. [Google Scholar] [CrossRef]
- Ariga, T.; Tateishi, K.; Tomishige, M.; Mizuno, D. Noise-Induced Acceleration of Single Molecule Kinesin-1. Phys. Rev. Lett. 2021, 127, 178101. [Google Scholar] [CrossRef]
- Eisenthal, R.; Danson, M.J.; Hough, D.W. Catalytic efficiency and kcat/KM: A useful comparator? Trends Biotechnol. 2007, 25, 247–249. [Google Scholar] [CrossRef]
- Benner, S.A. Enzyme kinetics and moleculer evolution. Chem. Rev. 1989, 89, 789–806. [Google Scholar] [CrossRef]
- Cornish-Bowden, A.; Cárdenas, M.L. Specificity of Non-Michaelis-Menten Enzymes: Necessary Information for Analyzing Metabolic Pathways. J. Phys. Chem. B 2010, 114, 16209–16213. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bar-Even, A.; Milo, R.; Noor, E.; Tawfik, D.S. The Moderately Efficient Enzyme: Futile Encounters and Enzyme Floppiness. Biochemistry 2015, 54, 4969–4977. [Google Scholar] [CrossRef]
- Kraut, D.A.; Sigala, P.A.; Pybus, B.; Liu, C.W.; Ringe, D.; Petsko, G.A.; Herschlag, D. Testing electrostatic complementarity in enzyme catalysis: Hydrogen bonding in the ketosteroid isomerase oxyanion hole. PLoS Biol. 2006, 4, e99. [Google Scholar] [CrossRef]
- Chakravorty, D.K.; Hammes-Schiffer, S. Impact of Mutation on Proton Transfer Reactions in Ketosteroid Isomerase: Insights from Molecular Dynamics Simulations. J. Am. Chem. Soc. 2010, 132, 7549–7555. [Google Scholar] [CrossRef][Green Version]
- Kemp, M.T.; Lewandowski, E.M.; Chen, Y. Low barrier hydrogen bonds in protein structure and function. Biochim. Biophys. Acta Proteins Proteom. 2021, 1869, 140557. [Google Scholar] [CrossRef]
- Fried, S.D.; Boxer, S.G. Electric Fields and Enzyme Catalysis. Annu. Rev. Biochem. 2017, 86, 387–415. [Google Scholar] [CrossRef]
- Asbóth, B.; Náray-Szabó, G. Mechanism of action of D-xylose isomerase. Curr. Protein Pept. Sci. 2000, 1, 237–254. [Google Scholar] [CrossRef]
- Goldsmith, M.; Tawfik, D.S. Enzyme engineering: Reaching the maximal catalytic efficiency peak. Curr. Opin. Struct. Biol. 2017, 47, 140–150. [Google Scholar] [CrossRef]
- Branscomb, E.; Russell, M.J. Frankenstein or a Submarine Alkaline Vent: Who Is Responsible for Abiogenesis?: Part 1: What is life-that it might create itself? Bioessays 2018, 40, 1700179. [Google Scholar] [CrossRef]
- Branscomb, E.; Russell, M.J. Frankenstein or a submarine alkaline vent: Who is responsible for abiogenesis? Part 2: As life is now, so it must have been in the beginning. BioEssays 2018, 40, 1700182. [Google Scholar] [CrossRef] [PubMed]
- Peretó, J. Prebiotic chemistry that led to life. In Handbook of Astrobiology; Kolb, V.M., Ed.; CRC Press: Boca Raton, FL, USA, 2019; pp. 219–233. [Google Scholar]
- Wang, Q.A. Maximum entropy change and least action principle for nonequilibrium systems. Astrophys. Space Sci. 2006, 305, 273–281. [Google Scholar] [CrossRef]
- Annila, A.; Baverstock, K. Genes without prominence: A reappraisal of the foundations of biology. J. R. Soc. Interface 2014, 11, 20131017. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Wu, H.; Zhang, A.; Tian, L.; Liu, L.; Wang, C.; Fang, X. Microwave irradiation-assisted isomerization of glucose to fructose by immobilized glucose isomerase. Process Biochem. 2011, 46, 599–603. [Google Scholar] [CrossRef]
- Britton, J.; Meneghini, L.M.; Raston, C.L.; Weiss, G.A. Accelerating Enzymatic Catalysis Using Vortex Fluidics. Angew. Chem. Int. Ed. Engl. 2016, 55, 11387–11391. [Google Scholar] [CrossRef] [PubMed]
- Jee, A.-Y.; Tlusty, T.; Granick, S. Master curve of boosted diffusion for 10 catalytic enzymes. Proc. Natl. Acad. Sci. USA 2020, 117, 29435–29441. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Tharp, S.; Selzer, T.; Benkovic, S.J.; Kohen, A. Effects of a distal mutation on active site chemistry. Biochemistry 2006, 45, 1383–1392. [Google Scholar] [CrossRef]
- Losa, J.; Leupold, S.; Alonso-Martinez, D.; Vainikka, P.; Thallmair, S.; Tych, K.M.; Marrink, S.J.; Heinemann, M. Perspective: A stirring role for metabolism in cells. Mol. Syst. Biol. 2022, 18, e10822. [Google Scholar] [CrossRef]
- Khersonsky, O.; Röthlisberger, D.; Wollacott, A.M.; Murphy, P.; Dym, O.; Albeck, S.; Kiss, G.; Houk, K.N.; Baker, D.; Tawfik, D.S. Optimization of the in silico designed Kemp eliminase KE70 by computational design and directed evolution. J. Mol. Biol. 2011, 407, 391–412. [Google Scholar] [CrossRef]
- Labas, A.; Szabo, E.; Mones, L.; Fuxreiter, M. Optimization of reorganization energy drives evolution of the designed Kemp eliminase KE07. Biochim. Biophys. Acta 2013, 1834, 908–917. [Google Scholar] [CrossRef]
- Fuxreiter, M.; Mones, L. The role of reorganization energy in rational enzyme design. Curr. Opin. Chem. Biol. 2014, 21, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Frushicheva, M.P.; Mills, M.J.L.; Schopf, P.; Singh, M.K.; Warshel, A. Computer Aided Enzyme Design and Catalytic Concepts. Curr. Opin. Chem. Biol. 2014, 21, 56–62. [Google Scholar] [CrossRef]
- Crean, R.M.; Gardner, J.M.; Kamerlin, S.C.L. Harnessing Conformational Plasticity to Generate Designer Enzymes. J. Am. Chem. Soc. 2020, 142, 11324–11342. [Google Scholar] [CrossRef] [PubMed]
- Mondal, D.; Kolev, V.; Warshel, A. Combinatorial Approach for Exploring Conformational Space and Activation Barriers in Computer-Aided Enzyme Design. ACS Catal. 2020, 10, 6002–6012. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.K.; Wu, Z.; Arnold, F.H. Machine-learning-guided directed evolution for protein engineering. Nat. Methods 2019, 16, 687–694. [Google Scholar] [CrossRef] [PubMed]
- Jacob, F. The Logic of Life; Pantheon Books: New York, NY, USA, 1973. [Google Scholar]
- Agarwal, P.K. A Biophysical Perspective on Enzyme Catalysis. Biochemistry 2019, 58, 438–449. [Google Scholar] [CrossRef] [PubMed]

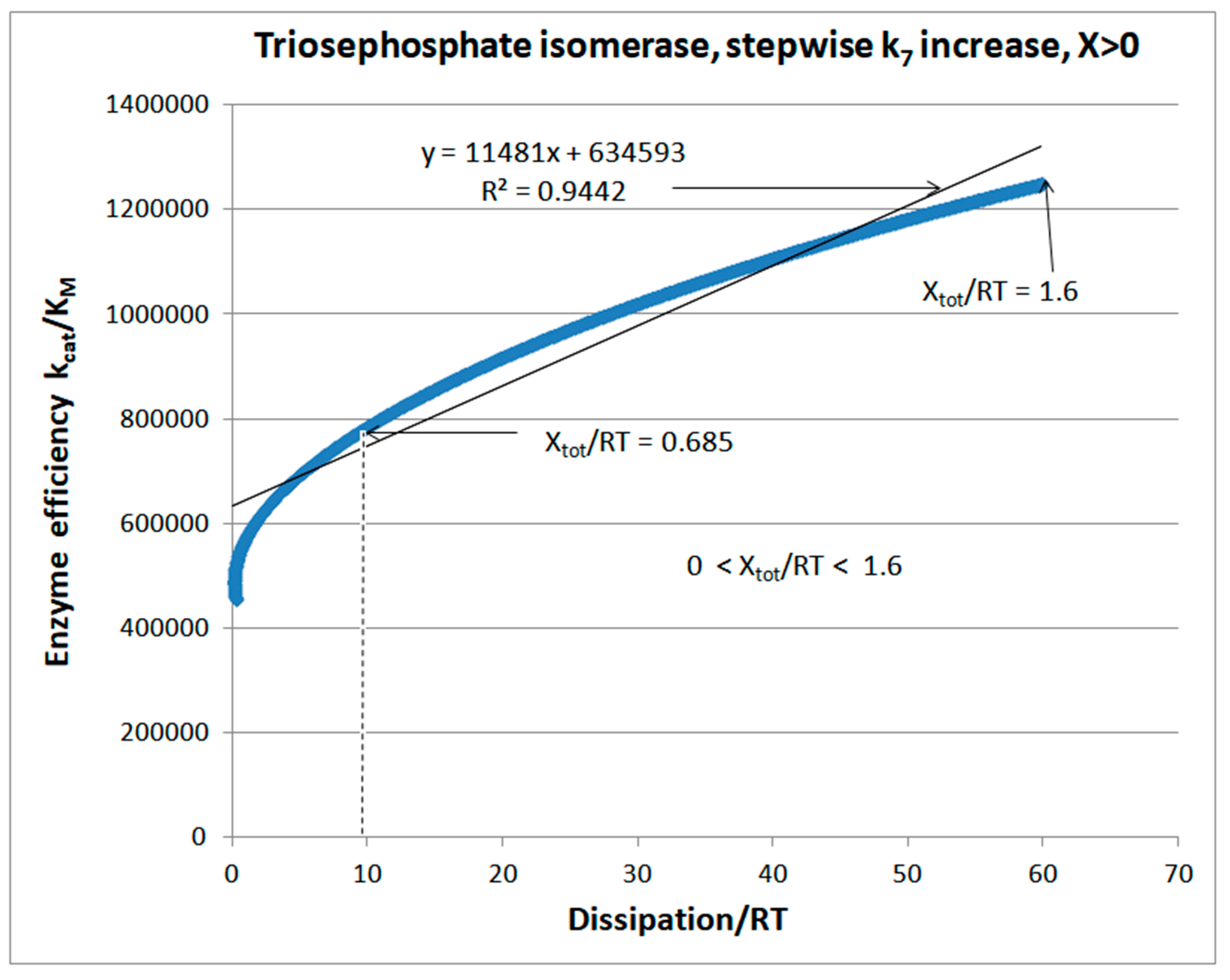
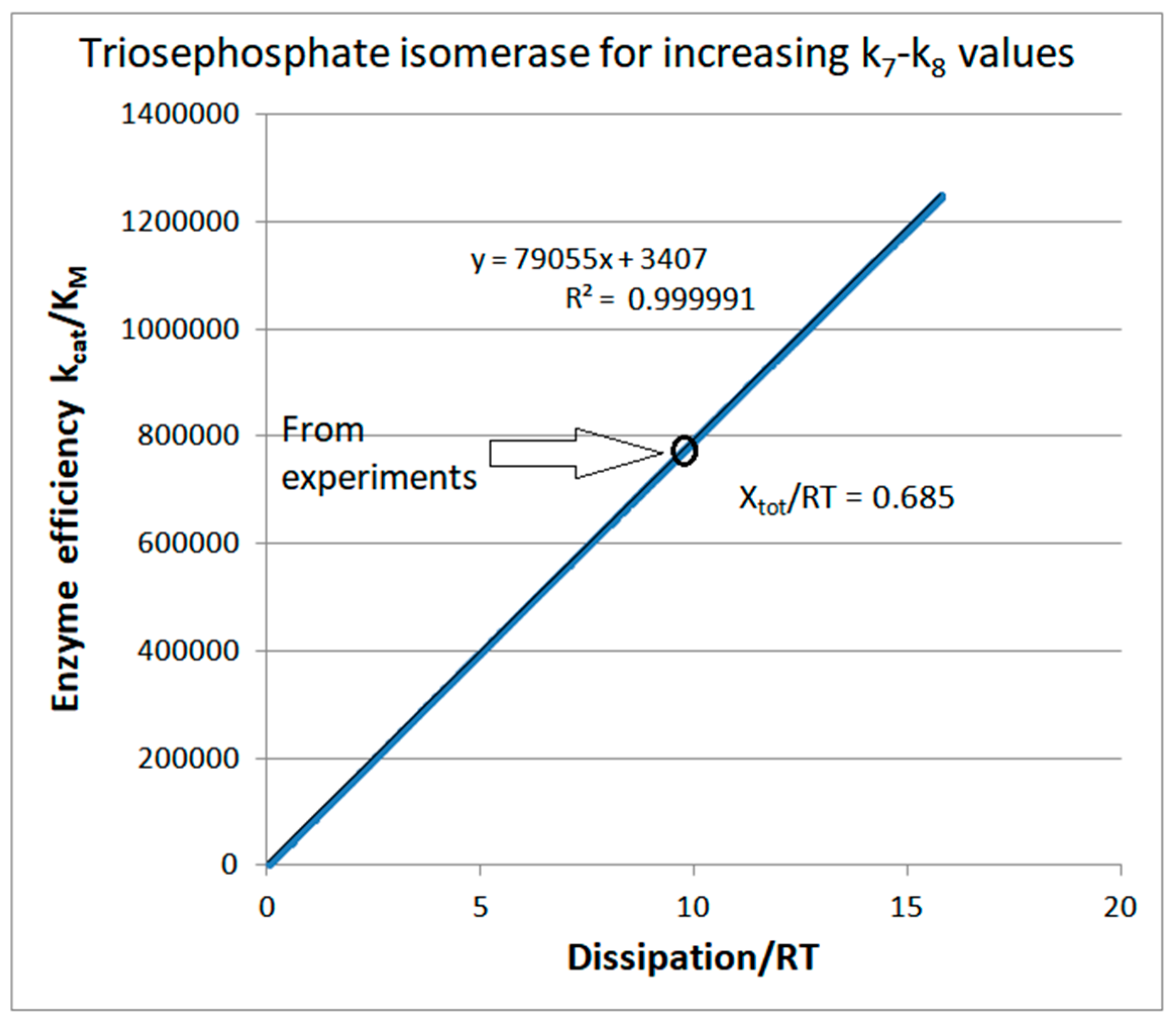
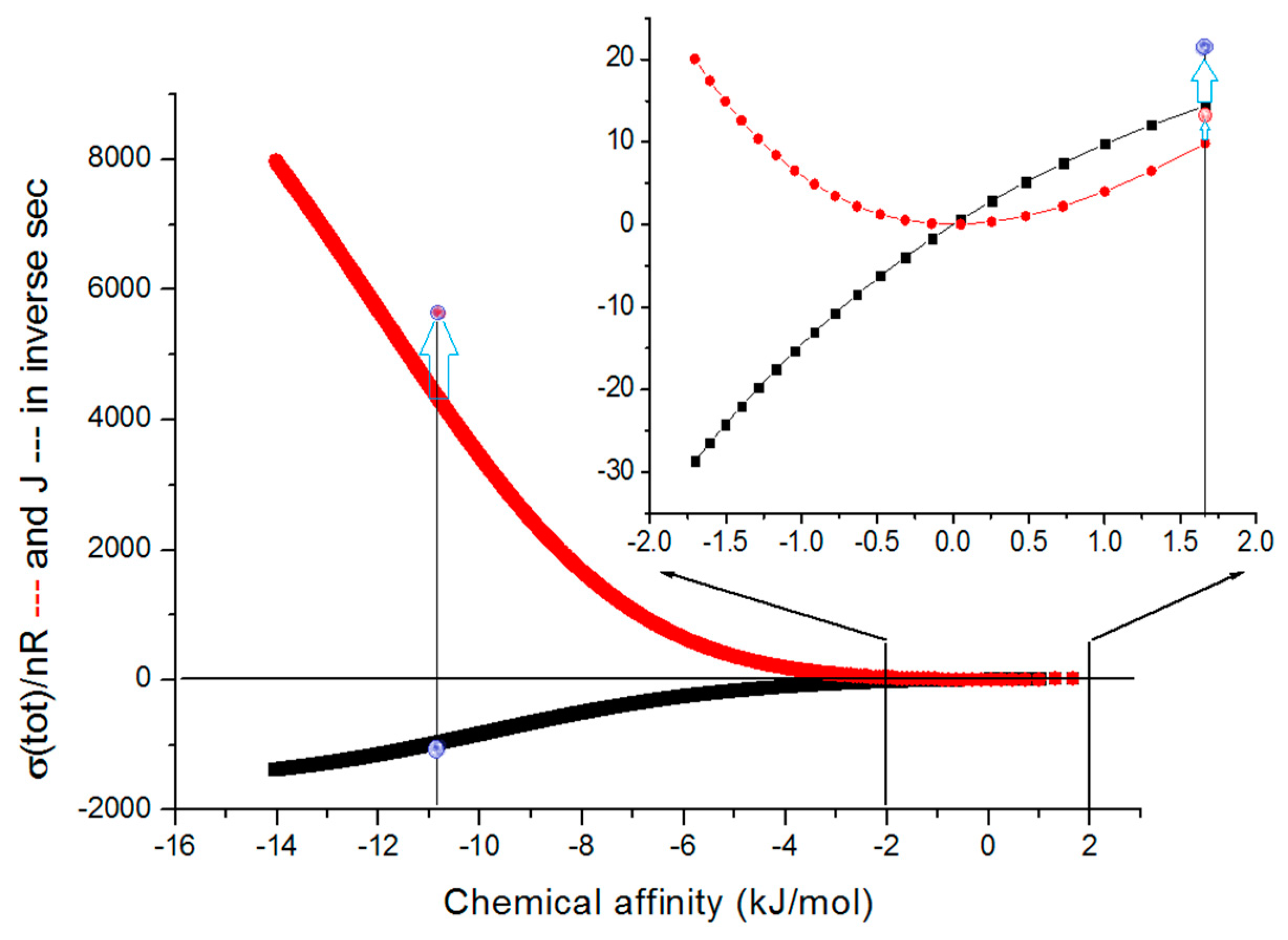
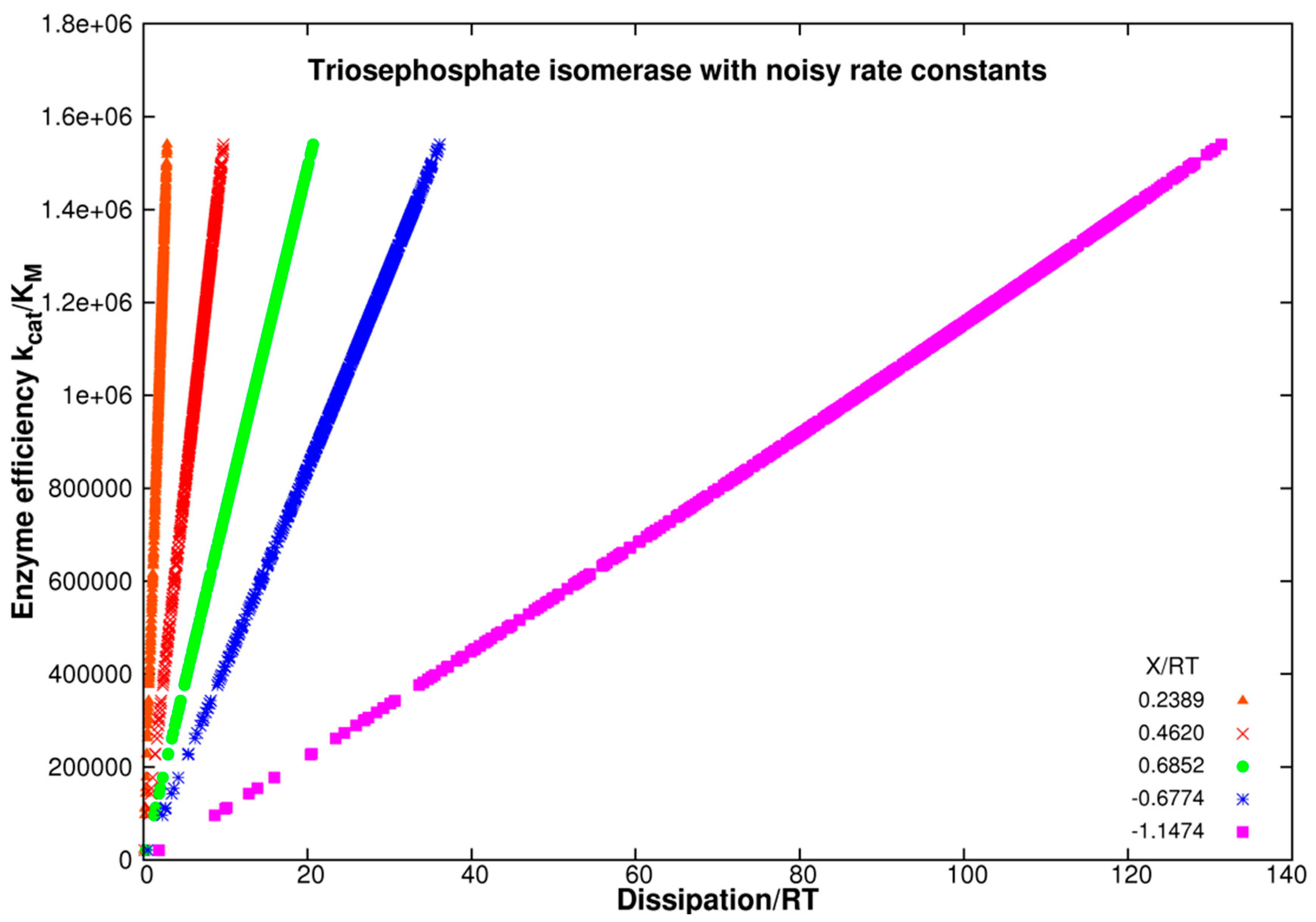

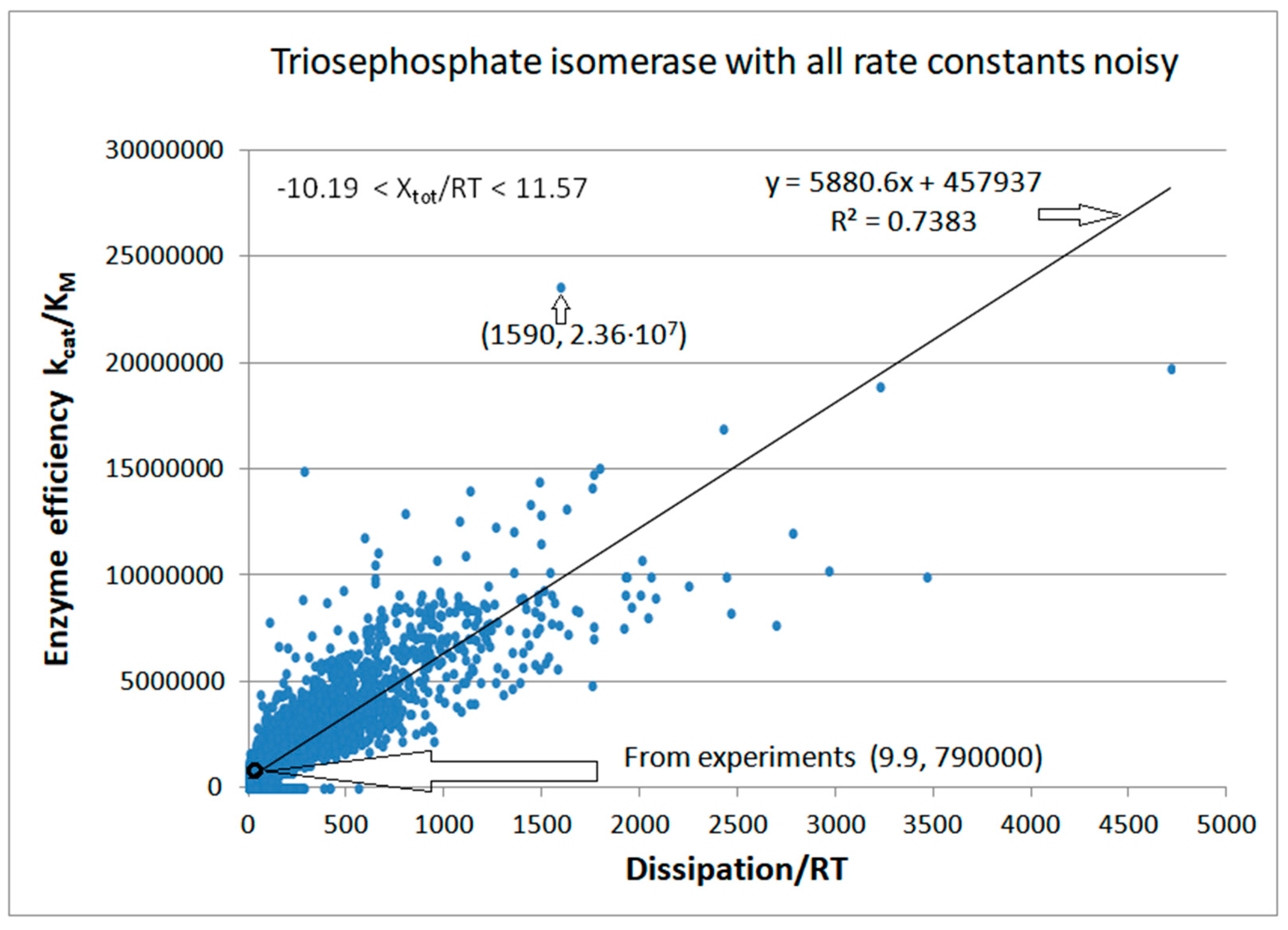
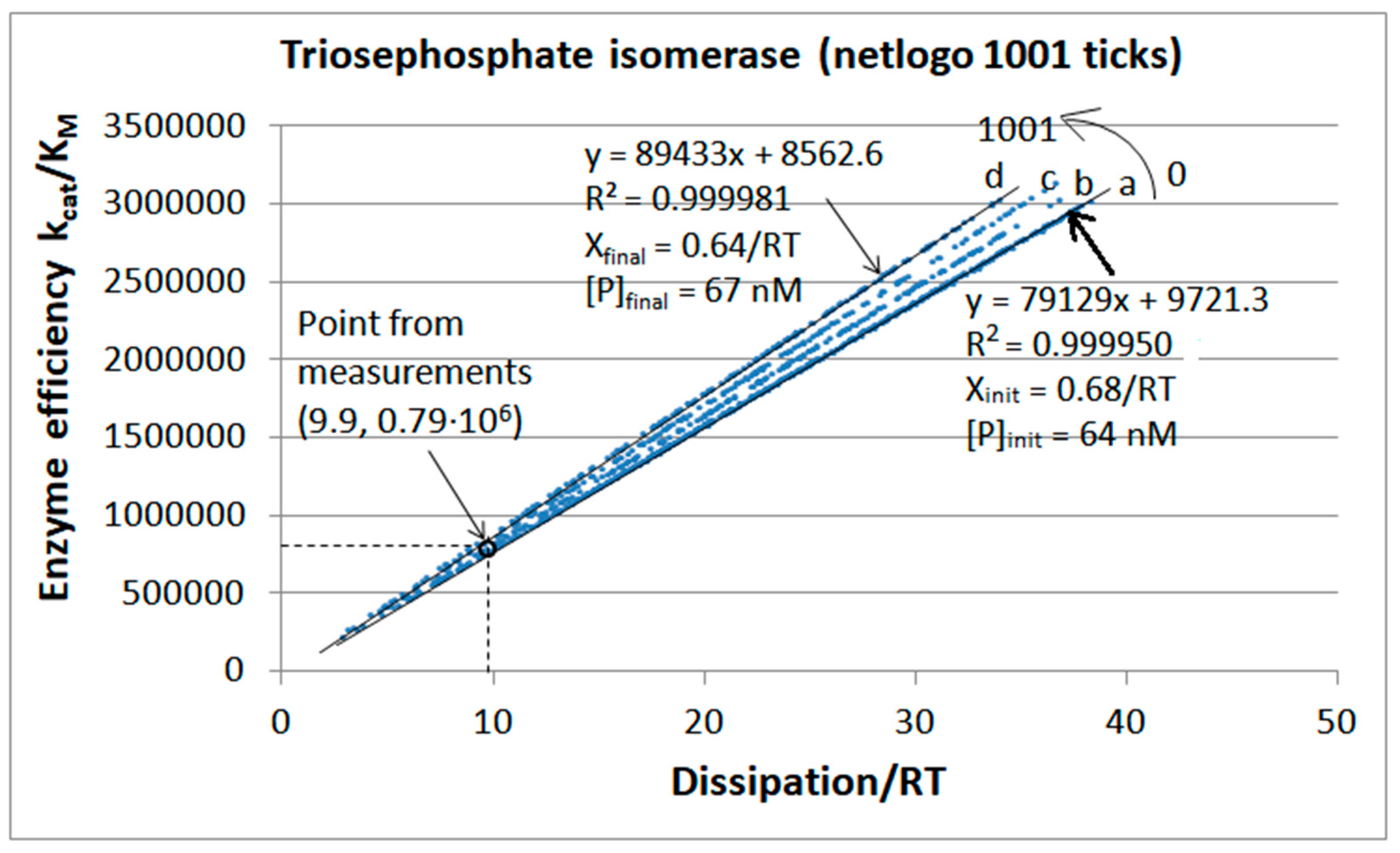

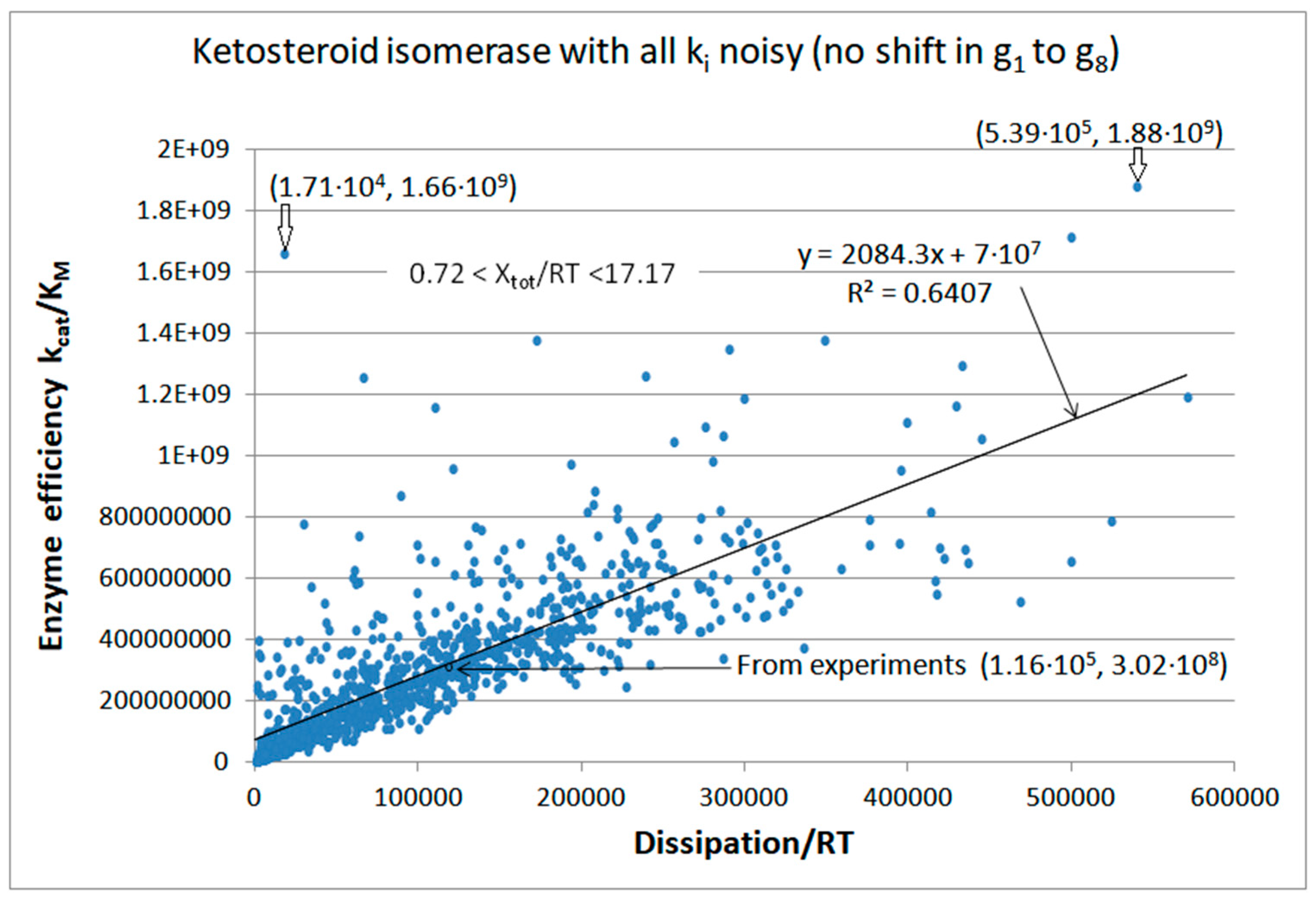
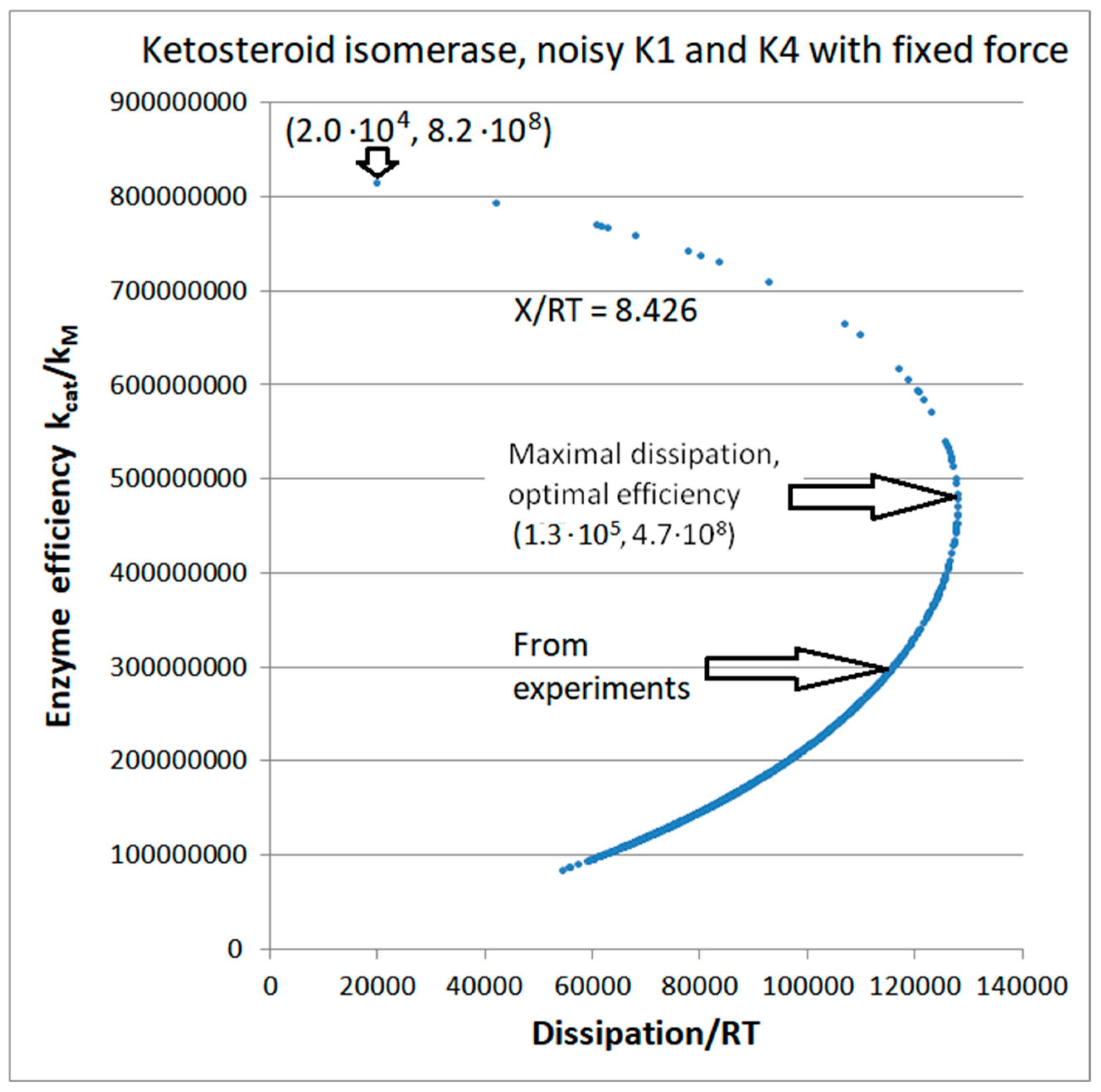




| Rate Constants | Observed Values [32,74] | Kinetic and Thermod. Parameters | Calculated Initial Values [74] |
|---|---|---|---|
| k1* | 107 M−1s−1 | [S] | 4 × 10−5 M |
| k2 | 7000 s−1 | [P] | 6.4 × 10−8 M |
| k3 | 2000 s−1 | [E] | 5 × 10−8 M |
| k4 | 6000 s−1 | kcat | 432 s−1 |
| k5 | 60,000 s−1 | KM | 5.5 × 10−4 M |
| k6 | 90,000 s−1 | kcat/KM | 7.86 × 105 M−1s−1 |
| k7 | 4000 s−1 | Keqtot | 3.2 × 10−3 |
| k8* | 4 × 108 M−1s−1 | Xtot/RT | 0.685 |
| k1 = k1* · [S] | 400 s−1 | P () | 9.9 s−1 |
| k8 = k8* · [P] | 25.60 s−1 |
| Rate Constants | Calculated Values [89] | Calculated Values [31] | Kinetic and Thermod. Parameters [31] | Initial Values ([31] and This Work) |
|---|---|---|---|---|
| k1* | 8.6 × 108 M−1s−1 | 8.3 × 108 M−1s−1 | [S] | 10−4 M |
| k2 | 8.6 × 104 s−1 | 8.6 × 104 s−1 | [P] | 5 × 10−5 M |
| k3 | 1.7 × 105 s−1 | 1.8 × 105 s−1 | [E] | 5 × 10−6 M |
| k4 | >3 × 105 s−1 | 1.7 × 106 s−1 | kcat | 3.5 × 104 s−1 |
| k5 | >1 × 105 s−1 | 6.4 × 105 s−1 | KM | 1.16 × 10−4 M |
| k6 | 40 s−1 | 43 s−1 | kcat/KM | 3 × 108 M−1s−1 |
| k7 | 1.3 × 105 s−1 | 1.5 × 105 s−1 | Keqtot | 2281 |
| k8* | 8.6 × 108 M−1s−1 | 1 × 109 M−1s−1 | Xtot/RT | 8.426 |
| k1 | 8.3 × 104 s−1 | Initial value (this paper) | ||
| k8 | 5 × 104 s−1 | P | 1.16 × 105 s−1 |
| Rate Constants [33] | Initial Values CA I | Initial Values CA II | Initial Values CA II T200H |
|---|---|---|---|
| k1* | 3.4 × 107 M−1s−1 | 1.3 × 108 M−1s−1 | 8.2 × 107 M−1s−1 |
| k2 | 3.8 × 104 s−1 | 1.8 × 106 s−1 | 5.4 × 104 s−1 |
| k3 | 2.9 × 105 s−1 | 1.7 × 107 s−1 | 3.0 × 105 s−1 |
| k4* | 2.6 × 107 M−1s−1 | 2.0 × 108 M−1s−1 | 9.0 × 106 M−1s−1 |
| k5 | 9.0 × 105 s−1 | 1.2 × 106 s−1 | 2.7 × 106 s−1 |
| k6 | 9.0 × 106 s−1 | 1.2 × 106 s−1 | 2.1 × 107 s−1 |
| k7* | 1.1 × 108 M−1s−1 | 4.0 × 108 M−1s−1 | 3.6 × 108 M−1s−1 |
| k8* | 9.0 × 105 M−1s−1 | 2.0 × 107 M−1s−1 | 1.8 × 107 M−1s−1 |
| k1 | 4.08 × 104 s−1 | 1.56 × 105 s−1 | 9.84 × 104 s−1 |
| k4 | 6.24 × 105 s−1 | 4.80 × 106 s−1 | 2.16 × 105 s−1 |
| k7 | 5.50 × 106 s−1 | 2.00 × 107 s−1 | 1.80 × 107 s−1 |
| k8 | 4.50 × 104 s−1 | 1.00 × 106 s−1 | 9.00 × 105 s−1 |
| Kinetic parameters | Our initial and calculated values (CA I) | Our initial and calculated values (CA II) | Our initial and calculated values (CA II T200H) |
| [S] | 1.2 × 10−3 M | 1.2 × 10−3 M | 1.2 × 10−3 M |
| [P] | 2.4 × 10−2 M | 2.4 × 10−2 M | 2.4 × 10−2 M |
| [B] | 5.0 × 10−2 M | 5.0 × 10−2 M | 5.0 × 10−2 M |
| [E] | 1.0 × 10−4 M | 1.0 × 10−4 M | 1.0 × 10−4 M |
| kcat | 7.77 × 104 s−1 | 8.05 × 105 s−1 | 2.10 × 105 s−1 |
| KM | 3.13 × 10−3 M | 9.63 × 10−3 M | 3.10 × 10−3 M |
| kcat/KM | 2.48 × 107 M−1s−1 | 8.36 × 107 M−1s−1 | 6.77 × 107 M−1s−1 |
| Keqtot | 6.10 | 6.14 | 6.51 |
| Xtot/RT | 1.81 | 1.81 | 1.87 |
| CA I (this paper) | CA II (this paper) | CA II T200H (this paper) | |
| Pinitial | 2.84 × 104 s−1 | 1.25 × 105 s−1 | 6.29 × 104 s−1 |
| Rate Constants [3] | Observed Values, PC1 | Observed Values, RTEM | Observed Values, Lac-1 |
|---|---|---|---|
| k1* | 2.2 × 107 M−1s−1 | 1.23 × 108 M−1s−1 | 4.1 × 107 M−1s−1 |
| k2 | 196 s−1 | 1.18 × 104 s−1 | 2.32 × 103 s−1 |
| k3 | 173 s−1 | 2.8 × 103 s−1 | 4.09 × 103 s−1 |
| k4 | 4.0 s−1 | 6.0 s−1 | 50 s−1 |
| k5 | 96 s−1 | 1.5 × 103 s−1 | 3.61 × 103 s−1 |
| k6* | 1.0 × 106 M−1s−1 | 4.0 × 107 M−1s−1 | 8.0 × 106 M−1s−1 |
| k1 | 3.28 × 104 s−1 | 1.71 × 105 s−1 | 5.27 × 104 s−1 |
| k6 | 8.0 s−1 | 4.4 × 103 s−1 | 1.72 × 103 s−1 |
| Kinetic parameters | Initial values PC1 (this paper) | Initial values RTEM (this paper) | Initial values Lac-1 (this paper) |
| [S] | 1.492 × 10−3 M | 1.390 × 10−3 M | 1.285 × 10−3 M |
| [P] | 8.0 × 10−6 M | 1.1 × 10−4 M | 2.15 × 10−4 M |
| [E] | 10−5 M | 10−5 M | 10−5 M |
| kcat | 61 s−1 | 9.75 × 102 s−1 | 1.91 × 103 s−1 |
| KM | 6.0 × 10−6 M | 4.15 × 10−5 M | 7.32 × 10−5 M |
| kcat/KM | 1.01 × 107 M−1s−1 | 2.35 × 107 M−1s−1 | 2.60 × 107 M−1s−1 |
| Keqtot | 8.69 × 104 | 2.3 × 103 | 3.9 × 103 |
| Xtot/RT | 11.4 | 7.74 | 8.3 |
| Initial value PC1 [3] | Initial value RTEM [3] | Initial value Lac-1 [3] | |
| P | 689 s−1 | 6757 s−1 | 14,526 s−1 |
| Rate Constants | Initial Values (This Work and [26]) | Initial Kinetic Parameters | This Work |
|---|---|---|---|
| k1* | 5.0 × 107 M−1s−1 | [S] | 10−4 M |
| k2 | 1.83 × 104 s−1 | [P] | 10−7 M |
| k3 | 7.3 × 102 s−1 | [E] | 10−6 M |
| k4* | 10 M−1s−1 | kcat | 730 s−1 |
| k1 | 5.0 × 103 s−1 | KM | 3.81 × 10−4 M |
| k4 | 10−5 s−1 | kcat/KM | 1.92 × 106 M−1s−1 |
| Initial thermodynamic parameters | |||
| Keqtot | 2.0 × 107 | ||
| Xtot/RT | 16.81 | ||
| Initial value (this paper) | |||
| P | 2.55 × 103 s−1 |
| Rate Constants | Observed Values [27] | Calculated Values [28] | Other Relevant Parameters | Initial Values ([28] and This Paper) |
|---|---|---|---|---|
| k1* | 3.8 M−1min−1 | 0.063 M−1s−1 | [S] | 2.0 M |
| k2 | 1.23 min−1 | 0.021 s−1 | [P] | 0.2 M |
| k3 | 1.75 min−1 | 0.029 s−1 | [E] | 0.01 M |
| k4* | 4.9 M−1min−1 | 0.082 M−1s−1 | kcat | 0.029 s−1 |
| k1 = k1* · [S] | 0.126 s−1 | KM | 0.794 M | |
| k4 = k4* · [P] | 0.0164 s−1 | kcat/KM | 0.0365 M−1s−1 | |
| Keqtot | 10.61 | |||
| Xtot/RT | 2.36 | |||
| Initial value (this paper) | ||||
| P | 0.0406 s−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juretić, D.; Bonačić Lošić, Ž. Theoretical Improvements in Enzyme Efficiency Associated with Noisy Rate Constants and Increased Dissipation. Entropy 2024, 26, 151. https://doi.org/10.3390/e26020151
Juretić D, Bonačić Lošić Ž. Theoretical Improvements in Enzyme Efficiency Associated with Noisy Rate Constants and Increased Dissipation. Entropy. 2024; 26(2):151. https://doi.org/10.3390/e26020151
Chicago/Turabian StyleJuretić, Davor, and Željana Bonačić Lošić. 2024. "Theoretical Improvements in Enzyme Efficiency Associated with Noisy Rate Constants and Increased Dissipation" Entropy 26, no. 2: 151. https://doi.org/10.3390/e26020151
APA StyleJuretić, D., & Bonačić Lošić, Ž. (2024). Theoretical Improvements in Enzyme Efficiency Associated with Noisy Rate Constants and Increased Dissipation. Entropy, 26(2), 151. https://doi.org/10.3390/e26020151






