Observations of Bell Inequality Violations with Causal Isolation between Source and Detectors
Abstract
:1. Motivation and Hypothesis
1.1. On Bell Inequality Violations and Local Realism
1.2. On Experimental Locality: Observer-to-Observer vs. Observer-to-Emitting Atoms
1.3. Hypothesis: On a Background Influence between Emitting Atoms and Polarizer Atoms
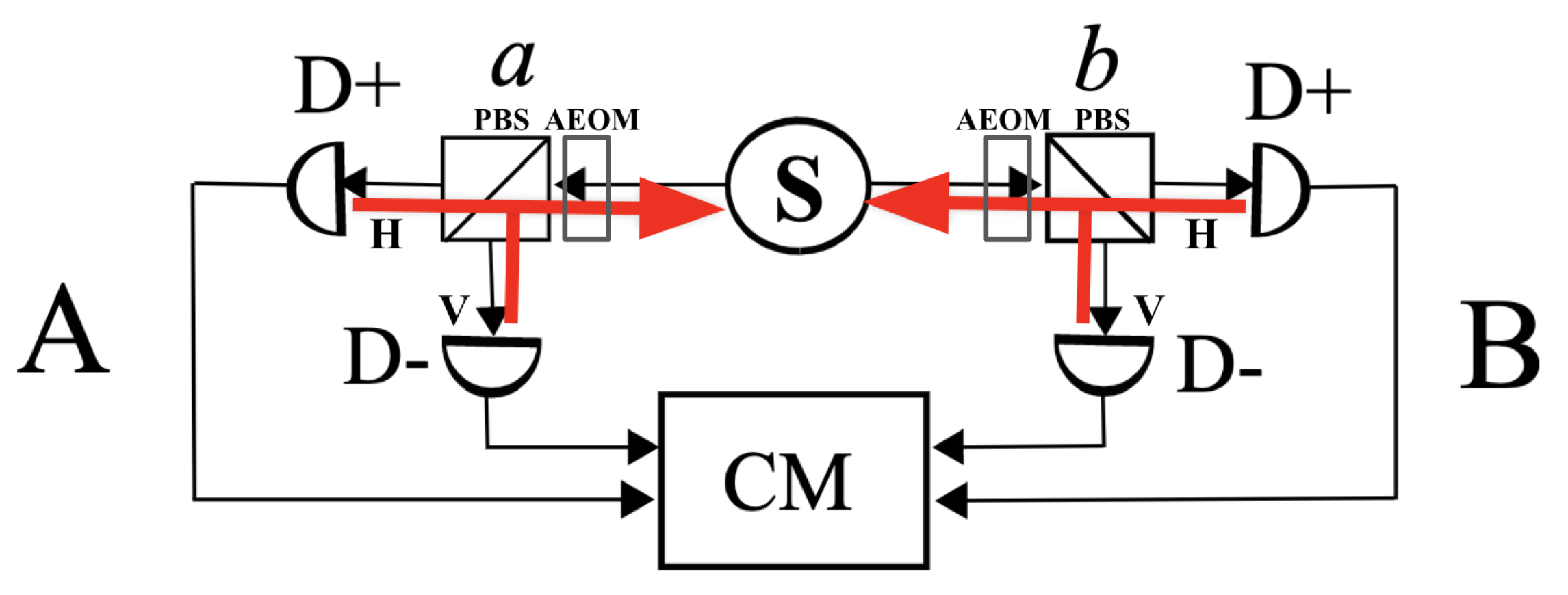
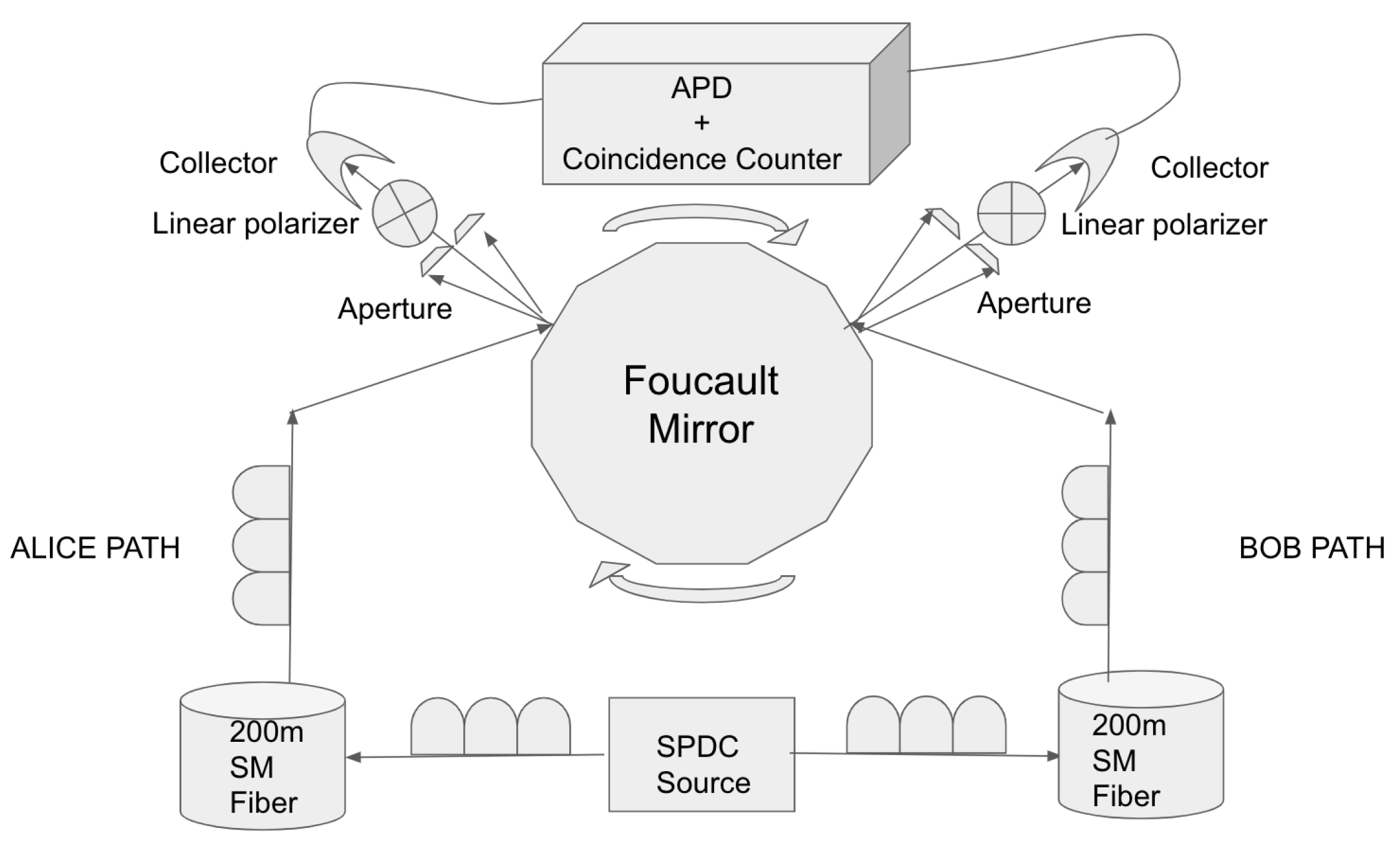
2. Experimental Setup
A 2-Channel Photon Entanglement Measure Using a Rotating Mirror
3. Results
4. Conclusions
5. Discussion
- 1/ There is no background influence, or;
- 2/ There is a background influence, and either:
- –
- 2a/ It is a traveling local wave, or;
- –
- 2b/ It is not (standing wave or deBroglie hypothesis).
6. Outlook and Prospects
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 1982, 49, 1804. [Google Scholar] [CrossRef]
- Weihs, G.; Jennewein, T.; Simon, C.; Weinfurter, H.; Zeilinger, A. Violation of bell’s inequality under strict einstein locality conditions. Phys. Rev. Lett. 1998, 81, 5039–5043. [Google Scholar] [CrossRef]
- Wengerowsky, S.; Joshi, S.K.; Steinlechner, F.; Zichi, J.R.; Dobrovolskiy, S.M.; van der Molen, R.; Los, J.W.N.; Zwiller, V.; Versteegh, M.A.M.; Mura, A.; et al. Entanglement distribution over a 96-km-long submarine optical fiber. Proc. Natl. Acad. Sci. USA 2019, 116, 6684–6688. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.-H.; Liao, S.-K.; Zhang, L.; Ren, J.-G.; Cai, W.-Q.; Liu, W.-Y.; Li, B.; Dai, H.; et al. Satellite-based entanglement distribution over 1200 km. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef] [PubMed]
- Rauch, D.; Handsteiner, J.; Hochrainer, A.; Gallicchio, J.; Friedman, A.S.; Leung, C.; Liu, B.; Bulla, L.; Ecker, S.; Steinlechner, F.; et al. Cosmic bell test using random measurement settings from high-redshift quasars. Phys. Rev. Lett. 2018, 121, 080403. [Google Scholar] [CrossRef] [PubMed]
- Weihs, G. Ein Experiment zum Test der Bellschen Ungleichung unter Einsteinscher Lokalit. Ph.D. Thesis, Universitat Wien, Wien, Austria, 1999. Available online: www.uibk.ac.at/exphys/photonik/people/gwdiss.pdf (accessed on 4 July 2022). (In Germany).
- Giustina, M.; Versteegh, M.A.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.-Å.; Abellán, C.; et al. Significant-loophole-free test of bell’s theorem with entangled photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
- Vervoort, L. Are Hidden-Variable Theories for Pilot-Wave Systems Possible? Found. Phys. 2018, 48, 803–826. [Google Scholar] [CrossRef]
- Cour, B.R.L.; Yudichak, T.W. Classical model of a delayed-choice quantum eraser. Phys. Rev. A 2021, 103, 062213. [Google Scholar] [CrossRef]
- Casado, A.; Marshall, T.W.; Santos, E. Type ii parametric downconversion in the wigner-function formalism: Entanglement and bell’s inequalities. J. Opt. Soc. Am. B 1998, 15, 1572. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T. Is the contextuality loophole fatal for the derivation of bell inequalities? Found. Phys. 2011, 41, 580–591. [Google Scholar] [CrossRef] [Green Version]
- Nieuwenhuizen, T.M.; Kupczynski, M. The contextuality loophole is fatal for derivation of Bell inequalities: Reply to a Comment by I. Schmelzer. Found. Phys. 2017, 47, 316–319. [Google Scholar] [CrossRef]
- Muchowski, E. On a contextual model refuting bell’s theorem. EPL (Europhys. Lett.) 2021, 134, 10004. [Google Scholar] [CrossRef]
- Fine, A. Hidden variables, joint probability and the Bell inequalities. Phys. Rev. Lett. 1982, 48, 291. [Google Scholar] [CrossRef]
- Kupczynski, M. Contextuality-by-Default Description of Bell Tests: Contextuality as the Rule and Not as an Exception. Entropy 2021, 23, 1104. [Google Scholar] [CrossRef]
- Ham, B. The origin of anticorrelation for photon bunching on a beam splitter. Sci. Rep. 2020, 10, 7309. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.H.; Twiss, R.Q. Correlation between Photons in two Coherent Beams of Light. Nature 1956, 177, 27–29. [Google Scholar] [CrossRef]
- Jung, K. Polarization correlation of entangled photons derived without using non-local interactions. Front. Phys. 2020, 8, 170. [Google Scholar] [CrossRef]
- Bell, J.S.; Aspect, A. The Theory of Local Beables, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 52–62. [Google Scholar]
- Iannuzzi, M.; Francini, R.; Messi, R.; Moricciani, D. Bell-type polarization experiment with pairs of uncorrelated optical photons. Phys. Lett. A 2020, 384, 126200. [Google Scholar] [CrossRef]
- Couder, Y.; Protiere, S.; Fort, E.; Boudaoud, A. Walking and orbiting droplets. Nature 2005, 437, 7056. [Google Scholar] [CrossRef]
- Budanur, N.B.; Fleury, M. State Space Geometry of the Chaotic Pilot-Wave Hydrodynamics. Chaos 2019, 29, 013122. [Google Scholar] [CrossRef] [Green Version]
- Bush, J.W.M.; Durey, M. Hydrodynamic quantum field theory: The onset of particle motion and the form of the pilot wave. Front. Phys. 2020, 8, 300. [Google Scholar]
- Papatryfonos, K.; Ruelle, M.; Bourdiol, C.; Nachbin, A.; Bush, J.W.M.; Labousse, M. Hydrodynamic superradiance in wave-mediated cooperative tunneling. Commun. Phys. 2022, 5, 142. [Google Scholar]
| Singles A (/s) | Singles B (/s) | Coincidences (/s) | |
|---|---|---|---|
| Dark Counts | 1300 | 600 | 0.08 |
| No rotation | 33,894 | 20,329 | 389 |
| With rotation | 2301 | 1098 | 7 |
| Degradation |
| Angle in | 0 | 45 | 90 | 135 |
|---|---|---|---|---|
| 22.5 | 226-5 | 85-4 | 42-4 | 184-4 |
| 67.5 | 70-5 | 34-4 | 182-4 | 239-5 |
| 112.5 | 46-5 | 187-5 | 227-4 | 70-4 |
| 157.5 | 198-5 | 217-5 | 88-4 | 34-4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fleury, M.J.J. Observations of Bell Inequality Violations with Causal Isolation between Source and Detectors. Entropy 2022, 24, 1230. https://doi.org/10.3390/e24091230
Fleury MJJ. Observations of Bell Inequality Violations with Causal Isolation between Source and Detectors. Entropy. 2022; 24(9):1230. https://doi.org/10.3390/e24091230
Chicago/Turabian StyleFleury, Marc Jean Jose. 2022. "Observations of Bell Inequality Violations with Causal Isolation between Source and Detectors" Entropy 24, no. 9: 1230. https://doi.org/10.3390/e24091230
APA StyleFleury, M. J. J. (2022). Observations of Bell Inequality Violations with Causal Isolation between Source and Detectors. Entropy, 24(9), 1230. https://doi.org/10.3390/e24091230






