Abstract
Detecting many-body localization (MBL) typically requires the calculation of high-energy eigenstates using numerical approaches. This study investigates methods that assume the use of a quantum device to detect disorder-induced localization. Numerical simulations for small systems demonstrate how the magnetization and twist overlap, which can be easily obtained from the measurement of qubits in a quantum device, changing from the thermal phase to the localized phase. The twist overlap evaluated using the wave function at the end of the time evolution behaves similarly to the one evaluated with eigenstates in the middle of the energy spectrum under a specific condition. The twist overlap evaluated using the wave function after time evolution for many disorder realizations is a promising probe for detecting MBL in quantum computing approaches.
1. Introduction
Many-body localization (MBL) has recently attracted significant interest [1,2,3,4,5]. MBL is a generalization of Anderson localization for disordered quantum many-body systems with interactions. When the disorder is strong enough, MBL prevents the system from thermalizing. The transition from the thermal to localized phase, i.e., MBL transition, is recognized as an eigenstate phase transition from the ergodic phase to non-ergodic phase [6,7,8]. The MBL transition is typically detected by quantities evaluated using eigenstates, such as entanglement, inverse participation ratio, one-particle density matrix [9,10,11,12,13,14,15,16,17,18,19,20,21,22], and spectral properties, such as level statistics [6,15,16,17,18,19,23] as well as local observables [6,14,15,16]. The random matrix theory and quantum chaos conjecture support the relationship between spectral properties and quantum chaos [24,25] as well as provide a framework for characterizing the MBL transition [26,27]. Experimental studies have also captured the signature of the MBL transition in disordered quantum systems with different architectures [28,29,30,31,32,33,34,35,36,37,38,39,40,41]. In experiments, MBL is often explored by the investigation of quantum dynamics. For example, the imbalance between the populations of even and odd sites in an atomic system is a measurable quantity for localization detection. The initial state has populations only on even sites, while odd sites are empty. Then, the imbalance is close to 1 initially and relaxes to zero as the system thermalizes. However, the imbalance maintains a finite value in the localized phase due to the initial state memory.
Recently, new approaches using quantum annealers were studied to simulate the properties of disordered quantum systems [42,43,44,45,46,47,48,49]. Probing MBL is also within the scope of quantum annealers and quantum computers. Although current quantum devices are still noisy and cannot compute exact eigenstates, some dynamical characteristics of MBL are robust against noise. In the localized phase, local quantities are conserved to some extent. For example, if the initial state is the all-spin-up state, then the magnetization maintains a large value because of the initial state memory. The magnetization, in this case, is similar to the imbalance in an atomic system in the sense that the memory effect characterizes localization. A recent experiment using a quantum annealer detected by the localization transition through magnetization measurements at the end of the time evolution [49].
This study investigated the localization detection based on quantum dynamics in a disordered quantum spin chain. Magnetization is a simple quantity that can be easily measured in quantum devices. We also employed another measurable quantity, the twist overlap. The twist overlap is a quantity proposed to detect the MBL transition and measure the extent to which an eigenstate overlaps with its twisted state [50]. A twisted state is obtained by applying a twist operator that rotates spins over the chain at gradually increasing angles. The twist overlap almost vanishes for thermal eigenstates, whereas it has a finite value for localized ones [50]. The twist overlap can also be evaluated using the state after time evolution. Using the twist overlap is convenient for localization detection in quantum devices because it can be easily obtained from the measurement of each spin.
The numerical simulations of small system sizes in this study demonstrate how the magnetization and twist overlap change from the thermal phase to the localized phase. These quantities were obtained at the end of the time evolution and averaged over different disorder realizations. They often oscillate at different frequencies for each disorder realization. Thus, we also examined the time dependence of these quantities to understand their dynamics. The time dependence, whose observation in experiments may require enormous time and effort, is also helpful in understanding the characteristics of these quantities. Although the difference between the thermal and localized phases in those quantities is evident, we cannot decide the existence of a phase transition from the limited numerical simulations. This work aims to demonstrate the effectiveness of experimentally measurable quantities, specifically twist overlap, as a localization probe.
2. Model and Methods
2.1. Model
The model used in this study is a one-dimensional transverse Ising model with local random fields, which is applied to a quantum annealer. The Hamiltonian is given by
where L is the system size and and are the Pauli operators of components x and z, respectively, at site j. The local field consists of random numbers with a uniform distribution in the interval , wherein w denotes the disorder strength. The interactions and transverse fields are given by , where is a uniform random number in the interval . Here, we refer to weak disorders in and as static noises. They are introduced to mimic the static noises of couplings between qubits and local fields in a quantum device.
2.2. Entanglement Entropy and Twist Overlap
The MBL transition is typically detected using quantities calculated using eigenstates. Moreover, the quantum dynamics reflects the properties of eigenstates. Before examining the quantum dynamics, we examine several quantities calculated using eigenstates. Here, we employ the half-chain entanglement entropy and twist overlap evaluated with eigenstates in the middle of the energy spectrum.
The half-chain entanglement entropy is defined by
where is the reduced density matrix for subsystem A. Subsystem A corresponds to the first half of the spin chain. Eigenstates obey the volume and area laws of entanglement in the thermal and localized phases, respectively. In other words, decreases when the thermal-to-MBL transition occurs. The transition point is characterized by the variance peak of the half-chain entanglement entropy [14,18].
The twist operator is defined by
It generates a spin-wave-like excitation by rotating the spins around the z axis at angles [50,51]. The factor originates from spin . The overlap between a state and its twisted state is the twist overlap, which is represented as
where denotes the eigenstate of the Hamiltonian in the original definition [50]. In the thermal phase, the twist overlap is expected to vanish because the twisted state with a spin-wave-like excitation is orthogonal to the original state. In contrast, the long-wavelength perturbation given by the twist operator has little effect on the eigenstates in the localized phase, which implies a finite twist overlap.
In quantum devices, the twist overlap is easily obtained by measuring each qubit. Writing as a linear combination of the computational basis yields
where . Since each measurement provides the configuration of () with probability , many measurements provide the expected value of the twist overlap.
2.3. Time Evolution
The solution of the Schrödinger equation,
is represented as
where denotes the initial state. In the numerical simulations below, the initial state is the all-spin-up state. The exact diagonalization of the Hamiltonian provides the time dependence of . We observe the magnetization and twist overlap at the end of the time evolution, which is at the final time .
When the initial state is expressed as with eigenstates of the Hamiltonian, Equation (7) becomes
where denotes the eigenenergy corresponding to . The z component of the magnetization defined by evolves as
Similarly, the twist overlap evolves as
Equations (9) and (10) suggest the oscillatory behavior of and . Therefore, the observed quantities depend on both the eigenstates and the final time. Since the frequency and amplitude of the oscillation differ from sample to sample, the average over disorder realizations characterizes the observed quantities if the final time is sufficiently large.
3. Results
3.1. Quantities Calculated from Eigenstates
Before investigating quantum dynamics, we confirm the localization properties characterized by eigenstates of the Hamiltonian. They help understand the quantities obtained from quantum dynamics. The exact diagonalization of the Hamiltonian without noise () was performed for each pair of the system size L and disorder strength w. The number of disorder realizations was for and for and 12. For each realization, the half-chain entanglement entropy and twist overlap were calculated and averaged over 20 eigenstates around the center of the energy spectrum.
Figure 1 shows the dependence on the disorder strength w of the half-chain entanglement entropy and the absolute square of the twist overlap averaged over the disorder realizations. The averages of and are plotted with error bars in Figure 1a and Figure 1c, respectively, where the error bar represents the standard deviation. Figure 1b and Figure 1d show the standard deviations of and , respectively.
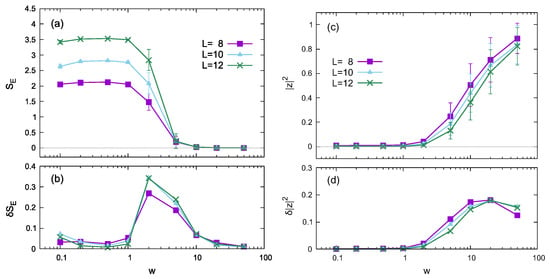
Figure 1.
Disorder strength dependence of the entanglement entropy (a,b) and the twist overlap (c,d), calculated using eigenstates for different system sizes in the noiseless case (). (a,b) plot the half-chain entanglement entropy and its standard deviation as functions of disorder strength w, respectively. Similarly, (c,d) plot the absolute square of the twist overlap and its standard deviation , respectively. The error bars in (a,c) represent standard deviation.
The disorder strength dependence of the half-chain entanglement entropy shown in Figure 1a,b shows a behavior similar to that of Ref. [49], although the values were different because of the differences in the models. For each L, the variance (standard deviation) peaks around –5, where the transition or crossover between the thermal and localized phases occurs.
As expected, the twist overlap, whose absolute square is shown in Figure 1c, increases with the disorder strength. The variance is almost zero in the weak-disorder region and becomes finite in the strong-disorder region. These results indicate that both the average and variance of the twist overlap are almost zero in the thermal phase, but large in the localized phase. The disorder-strength dependence of the variance was not observed in Ref. [50], which used the random-field Heisenberg chain. The difference in the variance behavior is likely due to differences in the models.
Whereas the peaks of appear in the middle of changes in , those of occur as is large enough. The peaks of appear probably due to the saturation of . Thus, the peak position of is not related to the transition or crossover between the thermal and localized phases.
3.2. Properties Based on Quantum Dynamics
In this subsection, we investigate the magnetization and twist overlap evaluated using the wave function at the end of time evolution. The wave function at the final time was calculated from the exact diagonalization of the Hamiltonian. The final time was , which is sufficient to capture the difference between the thermal and localized phases, as shown in the following subsection. The initial state is taken as the all-spin-up state. and were calculated for each disorder realization. The number of disorder realizations was the same as that in the previous subsection: for and for and 12.
Figure 2 shows the dependence on the disorder strength w of the z component of the magnetization and the absolute square of the twist overlap averaged over the disorder realizations. Here, the noise strength is . The averages of and are plotted with error bars in Figure 2a and Figure 2c, respectively, where the error bar represents standard deviation. Figure 2b and Figure 2d show the standard deviations of and , respectively.
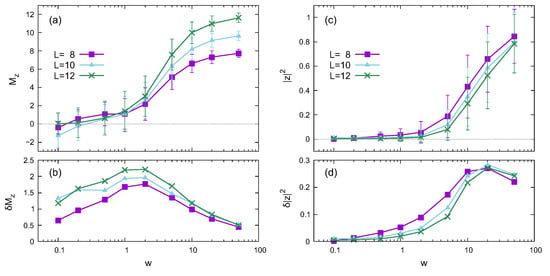
Figure 2.
Disorder strength dependence based on quantum dynamics for different system sizes in the noiseless case (). (a,b) plot the z component of the magnetization and its standard deviation as functions of disorder strength w, respectively. (c,d) plot the absolute square of the twist overlap and its standard deviation , respectively. The error bars in (a,c) represent standard deviation.
The average magnetization is in the weak-disorder region, indicating thermalization. When the disorder is strong enough, , which is a signature of the memory effect because in the initial state. The memory effect is characteristic of the localized phase, which was also observed in Ref. [49]. The variance (standard deviation) of the magnetization peaks at a disorder strength slightly weaker than that of the entanglement entropy. Since magnetization fluctuates with time and can have negative values, is relatively large in the weak-disorder region. Thus, the variance peak of the magnetization in this situation cannot apply to determining the transition or overlap point.
The twist overlap also increases with the disorder strength. However, the memory effect is not the leading cause for the large value of in the strong disorder region. If the memory effect dominates the twist overlap behavior, should be close to 1, and its variance should be small. Considering the fact that the twist overlap shown in Figure 2c is similar to that in Figure 1c, we expect that the behavior of the twist overlap reflects the properties of eigenstates. The variance (standard deviation) in Figure 2d is relatively large compared with that in Figure 1d. The large variance in Figure 2d is due to the difference in the eigenstates of different disorder realizations and the oscillatory behavior of .
Similar results to the noiseless case () also appear in the presence of static noise. While several types of noises exist in quantum devices, we here consider static noises in the interaction between spins and the transverse field. As shown in Figure 3, the disorder strength of and has little dependence on noise strength . However, the time evolution is affected by the static noises, as shown in the following subsection. The details of the time evolution are averaged out in the results in Figure 3, making the noise dependence negligible.
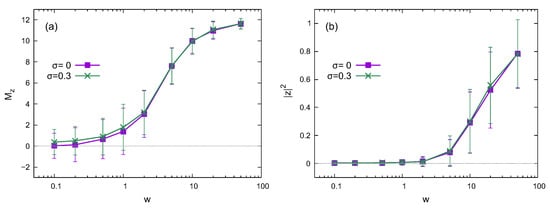
Figure 3.
Disorder strength dependence of (a) the z component of the magnetization and (b) the absolute square of the twist overlap for different noise strengths. The error bars represent the standard deviation. The system size is .
3.3. Time Dependence
The time dependence of the magnetization and twist overlap helps us understand the characteristics of quantum dynamics in the system. Figure 4 illustrates (in the upper row) and (in the lower row) for several combinations of disorder strength w and noise strength . Each graph plots ten samples of the time series calculated at different disorder realizations. The graphs in the same column, for example, (a) and (e), share the same wave-function samples. That is, the curves of and with the same color in the same column are evaluated using the same wave functions.
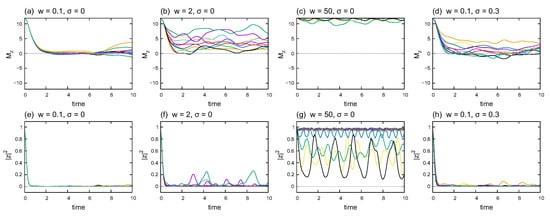
Figure 4.
Time dependence of (a–d) the magnetization and (e–h) the absolute square of the twist overlap. Each graph plots ten different samples of the time series. (a,e) share the same wave-function samples, and the same applies to (b,f), (c,g), and (d,h). The system size is .
Figure 4a–c and Figure 4e–g demonstrate how the behaviors of and change with disorder strength w, respectively, in the noiseless case (). Initially, , which then decreases to when the disorder is weak. As the disorder strengthens, fluctuates around positive values. Finally, fluctuates around the initial value in the localized phase. However, at the initial time decreases rapidly to when the disorder is weak. As the disorder strengthens, the fluctuations in become noticeable. In contrast to , some samples of oscillate with large amplitudes around relatively low values.
Figure 4d,h show the time dependence of and , respectively, for the noisy () and weak-disorder () cases. A comparison with Figure 4a,d suggests that the time average of is larger in the noisy case than that in the noiseless case in general. The difference in time dependence indicates that the static noise in the interaction strength and transverse field affects the quantum dynamics, which is not reflected in Figure 3.
4. Discussion
The absolute square of the twist overlap exhibits a slight variance in the weak-disorder region, as shown in Figure 2 and Figure 3. However, the z component of the magnetization has a relatively large variance in the same region. The time dependences of and also support this behavior, which seems curious. Figure 1c,d illustrates that in the small-disorder region, implying that in Equation (10) nearly vanishes in the middle of the energy spectrum. Since the eigenstates in the high and low regions of the energy spectrum also contribute to the time-dependent , the variance of has a small finite value in Figure 2 and Figure 3. However, fluctuates around zero because of thermalization, which causes a relatively large variance.
As shown in Figure 4, oscillates with a large amplitude in some strong-disorder cases, even though remains around the initial value. Large-amplitude oscillations arise from the combination of with different eigenstates and . As shown in Figure 1c,d, the average and variance of are significant in the strong-disorder region, which supports the variation in the combination of .
5. Conclusions
We investigated a method that assumes the use of a quantum device to detect disorder-induced localization. Localization in a disordered spin chain is detected by evaluating the magnetization and twist overlap at the end of the time evolution for many disorder realizations. Numerical simulations demonstrated how the magnetization and twist overlap characteristics change between the thermal and localized phases. We found evident differences between them, although the existence of a phase transition was not decided. The disorder-strength dependence of the magnetization and twist overlap is robust against static noises in the interaction between spins and the local field.
Under the condition in this work, the twist overlap evaluated using the wave function at the end of the time evolution behaved similarly to that calculated using eigenstates in the middle of the energy spectrum. In other words, the twist overlap after time evolution can provide information on the properties of eigenstates beyond the memory effect. The twist overlap is easily obtained from the measurement of qubits in a quantum device. Although this work assumes an ideal quantum device, the results suggest that the twist overlap is a promising probe for detecting MBL in quantum computing approaches.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviation
The following abbreviation is used in this manuscript:
| MBL | Many-body localization |
References
- Alet, F.; Laflorencie, N. Many-body localization: An introduction and selected topics. Comptes Rendus Phys. 2018, 19, 498–525. [Google Scholar] [CrossRef]
- Parameswaran, S.A.; Vasseur, R. Many-body localization, symmetry and topology. Rep. Prog. Phys. 2018, 81, 082501. [Google Scholar] [CrossRef] [PubMed]
- Abanin, D.A.; Altman, E.; Bloch, I.; Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 2019, 91, 021001. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Parameswaran, S.A. Dynamics and transport at the threshold of many-body localization. Phys. Rep. 2020, 862, 1–62. [Google Scholar] [CrossRef]
- Tikhonov, K.S.; Mirlin, A.D. From Anderson localization on random regular graphs to many-body localization. Ann. Phys. 2021, 435, 168525. [Google Scholar] [CrossRef]
- Pal, A.; Huse, D.A. Many-body localization phase transition. Phys. Rev. B 2010, 82, 174411. [Google Scholar] [CrossRef]
- Huse, D.A.; Nandkishore, R.; Oganesyan, V. Phenomenology of fully many-body-localized systems. Phys. Rev. B 2014, 90, 174202. [Google Scholar] [CrossRef]
- Pekker, D.; Clark, B.K.; Oganesyan, V.; Refael, G. Fixed Points of Wegner-Wilson Flows and Many-Body Localization. Phys. Rev. Lett. 2017, 119, 075701. [Google Scholar] [CrossRef]
- Bardarson, J.H.; Pollmann, F.; Moore, J.E. Unbounded Growth of Entanglement in Models of Many-Body Localization. Phys. Rev. Lett. 2012, 109, 017202. [Google Scholar] [CrossRef]
- Serbyn, M.; Papić, Z.; Abanin, D.A. Universal Slow Growth of Entanglement in Interacting Strongly Disordered Systems. Phys. Rev. Lett. 2013, 110, 260601. [Google Scholar] [CrossRef]
- Serbyn, M.; Papić, Z.; Abanin, D.A. Local Conservation Laws and the Structure of the Many-Body Localized States. Phys. Rev. Lett. 2013, 111, 127201. [Google Scholar] [CrossRef] [PubMed]
- Bera, S.; Schomerus, H.; Heidrich-Meisner, F.; Bardarson, J.H. Many-Body Localization Characterized from a One-Particle Perspective. Phys. Rev. Lett. 2015, 115, 046603. [Google Scholar] [CrossRef] [PubMed]
- Bera, S.; Lakshminarayan, A. Local entanglement structure across a many-body localization transition. Phys. Rev. B 2016, 93, 134204. [Google Scholar] [CrossRef]
- Kjäll, J.A.; Bardarson, J.H.; Pollmann, F. Many-Body Localization in a Disordered Quantum Ising Chain. Phys. Rev. Lett. 2014, 113, 107204. [Google Scholar] [CrossRef] [PubMed]
- Enss, T.; Andraschko, F.; Sirker, J. Many-body localization in infinite chains. Phys. Rev. B 2017, 95, 045121. [Google Scholar] [CrossRef]
- Orell, T.; Michailidis, A.A.; Serbyn, M.; Silveri, M. Probing the many-body localization phase transition with superconducting circuits. Phys. Rev. B 2019, 100, 134504. [Google Scholar] [CrossRef]
- Luitz, D.J.; Laflorencie, N.; Alet, F. Many-body localization edge in the random-field Heisenberg chain. Phys. Rev. B 2015, 91, 081103. [Google Scholar] [CrossRef]
- Khemani, V.; Lim, S.; Sheng, D.; Huse, D.A. Critical Properties of the Many-Body Localization Transition. Phys. Rev. X 2017, 7, 021013. [Google Scholar] [CrossRef]
- Khemani, V.; Sheng, D.; Huse, D.A. Two Universality Classes for the Many-Body Localization Transition. Phys. Rev. Lett. 2017, 119, 075702. [Google Scholar] [CrossRef]
- Hopjan, M.; Heidrich-Meisner, F. Many-body localization from a one-particle perspective in the disordered one-dimensional Bose-Hubbard model. Phys. Rev. A 2020, 101, 063617. [Google Scholar] [CrossRef]
- Zhang, S.X.; Yao, H. Universal Properties of Many-Body Localization Transitions in Quasiperiodic Systems. Phys. Rev. Lett. 2018, 121, 206601. [Google Scholar] [CrossRef] [PubMed]
- Gray, J.; Bose, S.; Bayat, A. Many-body localization transition: Schmidt gap, entanglement length, and scaling. Phys. Rev. B 2018, 97, 201105. [Google Scholar] [CrossRef]
- Kudo, K.; Deguchi, T. Finite-size scaling with respect to interaction and disorder strength at the many-body localization transition. Phys. Rev. B 2018, 97, 220201. [Google Scholar] [CrossRef]
- Casati, G.; Valz-Gris, F.; Guarnieri, I. On the connection between quantization of nonintegrable systems and statistical theory of spectra. Lett. Nuovo Cimento 1980, 28, 279–282. [Google Scholar] [CrossRef]
- Bohigas, O.; Giannoni, M.J.; Schmit, C. Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuation Laws. Phys. Rev. Lett. 1984, 52, 1. [Google Scholar] [CrossRef]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef]
- Šuntajs, J.; Bonča, J.; Prosen, T.; Vidmar, L. Quantum chaos challenges many-body localization. Phys. Rev. E 2020, 102, 062144. [Google Scholar] [CrossRef]
- Schreiber, M.; Hodgman, S.S.; Bordia, P.; Lüschen, H.P.; Fischer, M.H.; Vosk, R.; Altman, E.; Schneider, U.; Bloch, I. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 2015, 349, 842–845. [Google Scholar] [CrossRef]
- Kondov, S.; McGehee, W.; Xu, W.; DeMarco, B. Disorder-Induced Localization in a Strongly Correlated Atomic Hubbard Gas. Phys. Rev. Lett. 2015, 114, 083002. [Google Scholar] [CrossRef]
- Smith, J.; Lee, A.; Richerme, P.; Neyenhuis, B.; Hess, P.W.; Hauke, P.; Heyl, M.; Huse, D.A.; Monroe, C. Many-body localization in a quantum simulator with programmable random disorder. Nat. Phys. 2016, 12, 907–911. [Google Scholar] [CrossRef]
- Bordia, P.; Lüschen, H.P.; Hodgman, S.S.; Schreiber, M.; Bloch, I.; Schneider, U. Coupling Identical one-dimensional Many-Body Localized Systems. Phys. Rev. Lett. 2016, 116, 140401. [Google Scholar] [CrossRef] [PubMed]
- Bordia, P.; Lüschen, H.; Scherg, S.; Gopalakrishnan, S.; Knap, M.; Schneider, U.; Bloch, I. Probing Slow Relaxation and Many-Body Localization in Two-Dimensional Quasiperiodic Systems. Phys. Rev. X 2017, 7, 041047. [Google Scholar] [CrossRef]
- Lüschen, H.P.; Bordia, P.; Hodgman, S.S.; Schreiber, M.; Sarkar, S.; Daley, A.J.; Fischer, M.H.; Altman, E.; Bloch, I.; Schneider, U. Signatures of Many-Body Localization in a Controlled Open Quantum System. Phys. Rev. X 2017, 7, 011034. [Google Scholar] [CrossRef]
- Lüschen, H.P.; Bordia, P.; Scherg, S.; Alet, F.; Altman, E.; Schneider, U.; Bloch, I. Observation of Slow Dynamics near the Many-Body Localization Transition in One-Dimensional Quasiperiodic Systems. Phys. Rev. Lett. 2017, 119, 260401. [Google Scholar] [CrossRef]
- Wei, K.X.; Ramanathan, C.; Cappellaro, P. Exploring Localization in Nuclear Spin Chains. Phys. Rev. Lett. 2018, 120, 070501. [Google Scholar] [CrossRef]
- Xu, K.; Chen, J.J.; Zeng, Y.; Zhang, Y.R.; Song, C.; Liu, W.; Guo, Q.; Zhang, P.; Xu, D.; Deng, H.; et al. Emulating Many-Body Localization with a Superconducting Quantum Processor. Phys. Rev. Lett. 2018, 120, 050507. [Google Scholar] [CrossRef]
- Kohlert, T.; Scherg, S.; Li, X.; Lüschen, H.P.; Das Sarma, S.; Bloch, I.; Aidelsburger, M. Observation of Many-Body Localization in a One-Dimensional System with a Single-Particle Mobility Edge. Phys. Rev. Lett. 2019, 122, 170403. [Google Scholar] [CrossRef]
- Rispoli, M.; Lukin, A.; Schittko, R.; Kim, S.; Tai, M.E.; Léonard, J.; Greiner, M. Quantum critical behaviour at the many-body localization transition. Nature 2019, 573, 385–389. [Google Scholar] [CrossRef]
- Rubio-Abadal, A.; Choi, J.Y.; Zeiher, J.; Hollerith, S.; Rui, J.; Bloch, I.; Gross, C. Many-Body Delocalization in the Presence of a Quantum Bath. Phys. Rev. X 2019, 9, 041014. [Google Scholar] [CrossRef]
- Zhu, D.; Johri, S.; Nguyen, N.H.; Alderete, C.H.; Landsman, K.A.; Linke, N.M.; Monroe, C.; Matsuura, A.Y. Probing many-body localization on a noisy quantum computer. Phys. Rev. A 2021, 103, 032606. [Google Scholar] [CrossRef]
- Gong, M.; de Moraes Neto, G.D.; Zha, C.; Wu, Y.; Rong, H.; Ye, Y.; Li, S.; Zhu, Q.; Wang, S.; Zhao, Y.; et al. Experimental characterization of the quantum many-body localization transition. Phys. Rev. Res. 2021, 3, 033043. [Google Scholar] [CrossRef]
- King, A.D.; Carrasquilla, J.; Raymond, J.; Ozfidan, I.; Andriyash, E.; Berkley, A.; Reis, M.; Lanting, T.; Harris, R.; Altomare, F.; et al. Observation of topological phenomena in a programmable lattice of 1800 qubits. Nature 2018, 560, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Harris, R.; Sato, Y.; Berkley, A.J.; Reis, M.; Altomare, F.; Amin, M.H.; Boothby, K.; Bunyk, P.; Deng, C.; Enderud, C.; et al. Phase transitions in a programmable quantum spin glass simulator. Science 2018, 361, 162–165. [Google Scholar] [CrossRef]
- Kairys, P.; King, A.D.; Ozfidan, I.; Boothby, K.; Raymond, J.; Banerjee, A.; Humble, T.S. Simulating the Shastry-Sutherland Ising Model Using Quantum Annealing. PRX Quantum 2020, 1, 020320. [Google Scholar] [CrossRef]
- Bando, Y.; Susa, Y.; Oshiyama, H.; Shibata, N.; Ohzeki, M.; Gómez-Ruiz, F.J.; Lidar, D.A.; Suzuki, S.; del Campo, A.; Nishimori, H. Probing the universality of topological defect formation in a quantum annealer: Kibble-Zurek mechanism and beyond. Phys. Rev. Research 2020, 2, 033369. [Google Scholar] [CrossRef]
- Bando, Y.; Nishimori, H. Simulated quantum annealing as a simulator of nonequilibrium quantum dynamics. Phys. Rev. A 2021, 104, 022607. [Google Scholar] [CrossRef]
- King, A.D.; Raymond, J.; Lanting, T.; Isakov, S.V.; Mohseni, M.; Poulin-Lamarre, G.; Ejtemaee, S.; Bernoudy, W.; Ozfidan, I.; Smirnov, A.Y.; et al. Scaling advantage over path-integral Monte Carlo in quantum simulation of geometrically frustrated magnets. Nat. Comm. 2021, 12, 1113. [Google Scholar] [CrossRef]
- King, A.D.; Nisoli, C.; Dahl, E.D.; Poulin-Lamarre, G.; Lopez-Bezanilla, A. Qubit spin ice. Science 2021, 373, 576–580. [Google Scholar] [CrossRef]
- Filho, J.L.C.d.C.; Izquierdo, Z.G.; Saguia, A.; Albash, T.; Hen, I.; Sarandy, M.S. Localization transition induced by programmable disorder. Phys. Rev. B 2022, 105, 134201. [Google Scholar] [CrossRef]
- Kutsuzawa, T.; Todo, S. Nested Iterative Shift-invert Diagonalization for Many-body Localization in the Random-field Heisenberg Chain. arXiv 2022, arXiv:2203.09732. [Google Scholar] [CrossRef]
- Nakamura, M.; Todo, S. Order Parameter to Characterize Valence-Bond-Solid States in Quantum Spin Chains. Phys. Rev. Lett. 2002, 89, 077204. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).