Abstract
By utilizing the non-maximally entangled four-qubit cluster states as the quantum channel, we first propose a hierarchical quantum information splitting scheme of arbitrary three-qubit states among three agents with a certain probability. Then we generalize the scheme to arbitrary multi-qubit states. Hierarchy is reflected on the different abilities of agents to restore the target state. The high-grade agent only needs the help of one low-grade agent, while the low-grade agent requires all the other agents’ assistance. The designated receiver performs positive operator-valued measurement (POVM) which is elaborately constructed with the aid of Hadamard matrix. It is worth mentioning that a general expression of recovery operation is derived to disclose the relationship with measurement outcomes. Moreover, the scheme is extended to multiple agents by means of the symmetry of cluster states.
1. Introduction
With the rapid development of computer networks, the demand for information security is sharply increasing. Quantum cryptography has unconditional security, which depends on the internal physical characteristics of quantum mechanics, such as the Heisenberg uncertainty principle and non-cloning theorem [1]. As the counterpart of classical secret sharing [2], quantum secret sharing (QSS) was first introduced by Hillery et al. [3] and has been one of the most significant branches of quantum cryptography. In QSS, the secret is divided into multiple pieces (called shares) and it can be constructed only through the cooperation of the shares. When the shared secret is a quantum state, QSS is termed quantum state sharing (QSTS) or quantum information splitting (QIS). The other agents can be regarded as the controlling party if one agent is identified as the receiver. From this point of view, QIS can be used to complete the task of controlled quantum teleportation (CQT) [4] in which an unknown state is teleported from a sender to a spatially separated receiver under the supervision of one or more controllers. Owing to its potential applications, e.g., creating joint accounts containing quantum money [5] and secure distributed quantum computation [6], QIS has been intensively studied [7,8,9,10,11,12,13,14,15] in the past two decades. For example, Luo et al. [11] investigated the application of state for QIS of an arbitrary three-qubit state. Li et al. [12] proposed a novel class of universal and flexible QIS schemes of arbitrary qubit and qudit states using quantum walks with multiple coins. In the meantime, experimental implementation of QIS has been reported [16,17,18].
The QIS schemes mentioned above mainly focus on the situation in which the authorities of the agents are identical. Considering the actual communication circumstance, Wang et al. [19] first proposed a hierarchical quantum information splitting (HQIS) scheme in the case where the agents are graded according to their abilities to restore the secret state. The high-grade agent requires some of the other agents’ help to complete the task, while the low-grade agent can do it only if all the other agents supply the assistance. Since then, much attention [20,21,22,23,24,25] has been paid to HQIS due to its useful applications in practice. Like many other quantum communication schemes [26,27,28], HQIS prefers using maximal entanglement to achieve perfect transmission. Nevertheless, the maximally entangled states are hard to maintain owing to the decoherence induced by the surrounding environment [29]. Thus, it is of great importance to investigate quantum communication via non-maximally entangled (NME) states [30,31,32,33,34,35,36]. Recently, based on NME four-particle cluster states, Xu et al. [35] and Guo et al. [36] respectively sketched new HQIS protocols to probabilistically realize the QSS of arbitrary unknown single-qubit state and two-qubit state via POVM. To our knowledge, there are no universal HQIS schemes of arbitrary multi-qubit states via POVM.
In this paper, we intend to devise a universal scheme to achieve the HQIS of arbitrary multi-qubit states with three agents via the NME resource. The agents lie in two disparate grades of which one agent lies in the high grade and two agents lie in the low grade. With the aid of the Hadamard matrix, we construct the general POVM operators. The recovery operation is derived from a general expression which distinctly discloses the relationship with measurement results. Based on the assistance of one inferior agent, the high-grade agent as the designated receiver can recover the target state with a certain probability by performing POVM rather than the usual projective measurement. While the low-grade agent requires all agents’ help. Then, we generalize the scheme from three agents to multiple agents by means of the symmetry of cluster states.
The outline of this paper is organized as follows. In Section 2, we first put forward a probabilistic HQIS scheme of arbitrary three-qubit states with three agents by utilizing the NME four-qubit cluster states as the entangled resource. The above scheme is extended to arbitrary n-qubit states in Section 3. In Section 4, we generalize the universal scheme of multi-qubit states from three agents to multiple agents. Section 5 is the security analysis. Some discussions and conclusions are given in the last section.
2. Probabilistic HQIS of Arbitrary Three-Qubit States with Three Agents
There are four participants, Alice, Bob, Charlie1 and Charlie2. Alice is the sender who wishes to teleport an unknown state to three agents in an asymmetric way such that any one of them can restore the secret state under the cooperation of other agents. The three agents are divided into two grades according to their abilities to recover the target state. High-grade agent Bob can restore the secret state only with the help of one low-grade agent while low-grade agent Charlie1 or Charlie2 needs the assistance of all the other agents.
Alice possesses a secret three-qubit state:
She knows nothing about the state except that the complex parameters satisfy the normalization condition .
Three NME four-qubit cluster states,
are selected as entangled resource, where
are nonzero real numbers satisfying and . The qubit is held by Alice, qubits , and are distributed to the agents Bob, Charlie1 and Charlie2, respectively.
The initial whole system can be expressed as:
For convenience, we denote , where p is the decimal form of the binary string . In other words, .
To complete the task, the participants need to perform the following operations.
Step 1 The sender Alice performs two-qubit projective measurements on her qubits , , under Bell basis,
After the measurements, she broadcasts 6 bit classical information corresponding to her measurement outcome , .
As a result, the remaining state collapses with equal probability into one of the 64 states :
Here and hereafter ⊕ means modulo 2 addition.
In order to clearly explain how our protocol implements, suppose Alice’s measurement result is . The three agents’ qubits become
At this time, none of the agents can recover the target state privately since their qubits are entangled with each other. Other agents’ cooperation is indispensable for the designated agent to complete his recovery task.
Step 2 According to Alice’s classical message, the agents apply the appropriate operations to achieve the goal that any one of agents recovers the secret state.
It will be discussed in two cases as far as the agents’ different authorities are concerned.
Case 1 The high-grade agent is designated as the receiver.
It is clear that Charlie1’s and Charlie2’s qubits are identical. From Equation (8), if one of them carries out single-qubit projective measurements under Z-basis , the qubits of Bob and the other low-grade agent will collapse into a product state. That means only one of the low-grade agents is sufficient to supply assistance. Suppose Charlie1 performs projective measurements and gets result , which is sent to Bob in the form of classical message 010. Then Bob’s qubits collapse into:
One can see that Bob’s state mix the information of the secret state and the entangled channel. To reconstruct the secret state, Bob introduces three auxiliary qubits with initial states and executes Controlled-NOT (CNOT) operations with the qubit as the controlled qubit and as the target one, . Thus, Bob’s state transforms into:
Denote
and
where H is the Hadamard matrix . Then Equation (11) can be rephrased as:
It shows that can be obtained if performing appropriate measurements on the auxiliary qubits and obtains the measurement result . Unfortunately, are not mutually orthogonal such that they cannot be distinguished deterministically by the usual projective measurement. To differentiate non-orthogonal states, Bob needs to execute POVM on his auxiliary qubits under measurement operators :
where is a coefficient related with and
Here, . In order to ensure operator is positive, should satisfy .
If Bob obtains the measurement result with the probability , he can restore the target state by performing appropriate Pauli operations. For clarity, assume his measurement result is . Then Bob performs operation on his collapsed state
and recovers the target state. Bob’s recovery operations conditioned on Charlie1’s (or Charlie2’s) measurement result and his own POVM outcome are summarized in Table 1, where I, X, Y, Z are the Pauli operations. However, Bob may also get with the probability . In this case, he cannot infer the secret state of his qubits. Therefore, the total success probability is:

Table 1.
Bob’s recovery operations (BRO) depending on one low-grade agent’s measurement outcome (LAMO) and his own POVM outcome .
Case 2 The low-grade agent is designated as the receiver.
Suppose Charlie1 is appointed as the receiver since Charlie1 and Charlie2 have the same authority.
To achieve the goal, both Bob and Charlie2 carry out projective measurements under X-basis and inform Charlie1 of the measurement outcomes in forms of classical message. Corresponding to Charlie2’s measurement outcome, Charlie1 first performs the unitary operation listed in Table 2.

Table 2.
Charlie1’s operations depending on Charlie2’s measurement outcome (MO).
To be explicit, assume Bob and Charlie2’s measurement outcomes are and , then the remaining qubits collapse into:
Charlie1 performs the operation and gets:
In the following, Charlie1 employs similar operations to those of the assigned receiver Bob in Case 1. Charlie1 introduces three qubits with initial states and obtains
after performing the CNOT operations , . Then he performs POVM defined in Equation (15). If Charlie1 obtains with equal probability , he can execute appropriate Pauli operations listed in Table 3 to recover the secret state. Otherwise, he fails.

Table 3.
Charlie1’s recovery operation (CRO) depending on his own POVM measurement outcome when Bob and Charlie2’s outcomes are and .
Similar discussions can be made for other measurement results of Alice, Bob and Charlie2. Take all the possible measurement results into account, one can find that the success probability of Charlie1 is identical to that in Equation (18).
3. Probabilistic HQIS of Arbitrary -Qubit States with Three Agents
The above scheme for an arbitrary three-qubit state can be generalized to an arbitrary n-qubit state,
where the subscript a represents the decimal form of binary string , is a complex number satisfying .
n NME four-qubit cluster states defined in Equation (2) are shared as the quantum channel, where the particle is in Alice’s possession, while the agents Bob, Charlie1 and Charlie2 possess particles , , , .
The combined state of the total system is:
The detailed process is described as follows.
Step 1 Alice initially executes joint projective measurements on her qubits under the Bell basis. Then, she broadcasts cbits to announce her measurement result .
Since
the state collapses into
Step 2 According to Alice’s measurement result, the agents perform the appropriate operations to realize that any one of agents recovers the secret state.
Due to the different grades of agents, we still discuss it in two cases.
Case 1 The high-grade agent is designated as the receiver.
The high-grade agent Bob only requires the help of one low-grade agent as Charlie1 and Charlie2 have exactly the same qubits. If one of the low-grade agents performs n single-qubit projective measurements under the Z-basis and obtains the measurement result which is sent to Bob in the form of classical bits , Bob’s qubits collapse into
Bob introduces n auxiliary qubits and performs CNOT operations . Thus, he gets
The state in the above equation can be decomposed into:
where
and
Since are not mutually orthogonal in general, Bob had better perform POVM which plays an important role in state discrimination. The measurement operators are:
where is related to the coefficient of the quantum channel and
Here, and satisfies which is to meet the condition that the elements of POVM must be positive operators. If Bob obtains measurement result with equal probability , his qubits collapse to . Then, Bob performs
and recovers the target state. If his measurement outcome is , he fails.
Case 2 The low-grade agent is designated as the receiver.
Suppose Charlie1 is assigned as the receiver. Bob and Charlie2 need to perform projective measurements under the X-basis and inform him of the measurement outcomes. Since
Charlie1’s qubits collapse into:
If Bob’s and Charlie2’s measurement outcomes are and , , . Charlie1 performs and gets:
Similar to Case 1, Charlie1 carries out POVM in Equation (35) after introducing auxiliary qubits and performing CNOT operations. If his measurement outcome is , Charlie1 can reconstruct the secret state by performing recovery operation
While measurement result indicates the task is failed.
Regardless of the grade of agents, the total success probability is:
Since , the total success probability is
4. Probabilistic HQIS of Arbitrary -Qubit States with Agents
It is necessary to investigate the situation of multiple agents as there are many users in a practical communication network. The hierarchy of agents may be diverse. Here, we consider one simple case in which the N agents are divided into two grades: u agents (Bob1, ⋯, Bobu) lie in high grade and v agents (Charlie1, ⋯, Charliev) lie in low grade.
The main aim is teleporting an arbitrary n-qubit state shown in Equation (26) from the sender to any one of the N agents in an asymmetrical way.
Before the scheme officially begins, Alice prepares n NME four-qubit cluster states , and introduces some qubits . Then she carries out a series of CNOT operations as shown in Figure 1 and gets
where
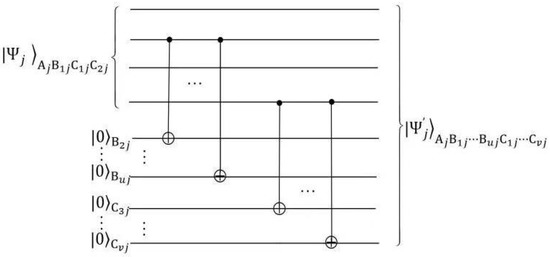
Figure 1.
The generation circuit of the state .
Next, Alice distributes the qubits , to Bob1, ⋯, Bobu, Charlie1, ⋯, and Charliev, respectively. The distribution of qubits among N agents is shown in Figure 2.
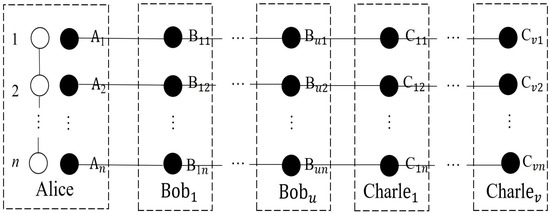
Figure 2.
The qubit shared by the sender and N agents. White points represent Alice’s secret particles, black points represent particles in the NME cluster states. The solid lines stand for entanglements.
The initial whole system is:
The scheme can be illustrated as follows.
Step 1 The sender Alice carries out Bell-basis measurements on her qubits . If the measurement result is , she broadcasts classical bits , , .
Step 2 According to Alice’s classical message, the agents apply the appropriate operations to achieve the goal that any one of agents recovers the secret state.
Since the same-grade agents have the same authority, we assume that the high-grade agent Bob1 or the low-grade agent Charlie1 recovers the secret state.
Case 1 The high-grade agent Bob1 is designated as the receiver.
The state in Equation (48) can be rewritten as:
up to the global phase.
Only if the other high-grade agent and one low-grade agent respectively perform projective measurements under the X-basis and Z-basis, can Bob1 restore the target state with a certain probability. Assume the measurement results of Bob2, ⋯, Bobu are and the measurement outcomes of Charlie1 are , where , , . At the moment, Bob1’s qubits collapse into:
up to the global phase.
Bob1 introduces auxiliary qubits and performs CNOT operations . Thus, he gets:
Then he performs POVM in Equation (35) on the auxiliary qubits. Analogously, if his POVM outcome is , Bob1 carries out unitary operation
and restores the secret state on his own qubits. If he obtains measurement result , the goal cannot be achieved.
Case 2 The low-grade agent Charlie1 is designated as the receiver.
To assist Charlie1 in recovering the target state, all the other agents perform projective measurements under the X-basis and inform him of the measurement outcomes. Assume the measurement outcomes of Bob1, ⋯, Bobu, Charlie2, ⋯ Charliev are , , . Then Charlie1’s qubits collapse into:
up to a global phase.
Charlie1 performs and gets
Similar to Case 1, Charlie1 performs POVM in Equation (35) after introducing auxiliary qubits and executing CNOT operations. If the measurement outcome is , his recovery operation can be summarized as:
While measurement result indicates task is failed.
The total success probability is the same as the case of three agents.
5. Security Analysis
For simplicity, take the case of three agents as an example. In order to ensure the security, Alice adopts the following strategies to detect eavesdropping. Besides n NME four-qubit cluster states , , Alice generates an ordered sequence using all the first qubits in her possession. Similarly, she forms another three ordered sequences , and . Then she prepares decoy photons chosen from and randomly insert them into the three sequence to yield the larger sequences , , . It should be emphasized that the final order of all sequences is only known by Alice.
There are two kinds of eavesdropping. One is that an illegal external eavesdropper Eve manages to steal secret information, the other is that there is a dishonest internal eavesdropper.
(I) Outsider attack.
It is not determined which agent is the receiver until the entangled channel particles are distributed. In order to obtain the secret state, Eve intercepts all particles distributed from Alice to the three agents and resends the forged one to them. In this case, once Alice conducts eavesdropping inspection, she tells the three agents about the location, state and measurement basis (Z-basis or X-basis). Then she asks each agent to measure the decoy photons under the measurement basis and publish the measurement results. Only if the agents’ measurement results are consistent with Alice’s predicted results, does the protocol continue. In addition, since Eve has no access to the coefficients of the NME channel, he can not carry out correct POVM to restore the secret state even if he intercepts the agents’ particles.
(II) Insider attack.
The influence of dishonest agents is destructive. Without loss of generality, assume that high-grade agent Bob is the internal eavesdropper. If everyone completely ignores his identity and consents to him as the receiver, he can easily acquire the secret state. In this case, our agreement cannot resist internal attacks. If the low-grade agent is designated as the receiver and Bob wants to steal the confidential state, one way is to intercept the channel particles of the low-grade agents and resend them false particles. However, because the decoy photons of different agents are different, eavesdropping will be found by the eavesdropping inspection. Another way is an entanglement measurement attack. Bob performs the unitary operation to act on Charlie1’s or Charlie2’s particles he has intercepted and the auxiliary particles he has prepared, so that he can measure the auxiliary particles to obtain information about the secret state. This attack will also be detected because of errors caused by decoy particles. The specific process is similar to that in Ref. [37].
6. Discussions and Conclusions
In fact, besides POVM, the designated receiver can adopt the collective unitary operation to restore the secret state. Taking the high-grade agent Bob as the receiver, based on one of the low-grade agent’s help, Bob’s qubits collapse into the state in Equation (30). Similar to Ref. [34], Bob first introduces an auxiliary qubit and performs a collective unitary transformation on his qubits . Then Bob measures the auxiliary qubit under the Z-basis. If the measurement result is , he performs appropriate operations on the collapsed state and recovers the target state. If the measurement result is , the protocol fails.
In conclusion, we devise a universal scheme to probabilistically realize the HQIS of arbitrary multi-qubit states among multiple agents by using NME four-qubit cluster states as the quantum resource. Comparing with the HQIS scheme for arbitrary single- and two-qubit states [22,23], our work has the following advantages: (1) Our schemes are applicable for arbitrary multi-qubit states with the aid of elaborately constructed multi-qubit POVM; (2) We derive the general expression of a recovery operation which clearly discloses the relationship with the measurement results; (3) We describe the specific process of HQIS with multiple agents. Our schemes are practical as NME states are easier to generate and maintain than the maximally entangled resources and agents’ unequal authorities are in line with the actual communication. Moreover, the preparation of the NME four-qubit cluster states, Bell-basis measurement, local CNOT and Pauli operations and POVM are required in our schemes. Besides POVM, other operations are easily implemented. Fortunately, POVM can be realized by using measurement assisted programmable quantum processors [38] and the ensemble approach to polarization optics [39]. It means our schemes are achievable since these necessary operations are feasible under the current experimental technologies.
Author Contributions
Writing—original draft, J.T.; writing—review and editing, S.-Y.M. and Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos. 62172341, 62172196, 61572246, 61201253), the Open Foundation of State Key Laboratory of Networking and Switching Technology (Beijing University of Posts and Telecommunications) (Grant No. SKLNST-2020-2-02), the Open Foundation of Guangxi Key Laboratory of Trusted Software (Grant No. KX202040).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wotters, W.K.; Zurek, W.H. A single quantum cannot be clone. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Ahlswede, R.; Csiszar, I. Common randomness in information theory and cryptography. IEEE Trans. Inf. Theor. 1993, 39, 1121–1132. [Google Scholar] [CrossRef]
- Hillery, M.; Buzek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar] [CrossRef] [Green Version]
- He, M.Y.; Ma, S.Y.; Kang, K.P. A universal protocol for bidirectional controlled teleportation with network coding. Commun. Theor. Phys. 2021, 73, 105104. [Google Scholar] [CrossRef]
- Wiesner, S. Conjugate coding. ACM Sigact News 1983, 15, 78–88. [Google Scholar] [CrossRef]
- Humphreys, P.C.; Kalb, N.; Morits, J.P.J.; Schouten, R.N.; Vermenulen, R.F.L.; Twitchen, D.J.; Markham, M.; Hanson, R. Deterministic delivery of remote entanglement on a quantum network. Nature 2018, 558, 268–273. [Google Scholar] [CrossRef] [Green Version]
- Gottesman, D. Theory of quantum secret sharing. Phys. Rev. A 2000, 61, 042311. [Google Scholar] [CrossRef] [Green Version]
- Wen, Z.; Liu, Y.M.; Zhang, Z.J. Splitting a qudit state via Greenberger-Horne-Zeilinger states of qubits. Opt. Commun. 2010, 28, 628–632. [Google Scholar]
- Hou, K.; Liu, G.H.; Zhang, X.Y.; Sheng, S.Q. An efficient scheme for five-party quantum state sharing of an arbitrary m-qubit state using multiqubit cluster states. Quantum Inf. Process. 2011, 10, 463–473. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, M.; Chen, X.P.; Li, H. Quantum state sharing of an arbitrary three-qubit state by using three sets of W-class states. Quantum Inf. Process. 2013, 12, 2405–2416. [Google Scholar] [CrossRef]
- Luo, M.X.; Deng, Y. Quantum splitting an arbitrary three-qubit state with χ-state. Quantum Inf. Process. 2013, 12, 773–784. [Google Scholar] [CrossRef]
- Li, H.J.; Li, J.; Xiang, N.; Zheng, Y.; Yang, Y.G.; Naseri, M. A new kind of universal and flexible quantum information splitting scheme with multi-coin quantum walks. Quantum Inf. Process. 2019, 18, 316. [Google Scholar] [CrossRef]
- Ma, L.Y. Two-qubit quantum state sharing protocol based on Bell state. Int. J. Theor. Phys. 2020, 59, 1844. [Google Scholar] [CrossRef]
- Xu, G.; Zhou, T.A.; Chen, X.B.; Wang, X.J. Splitting an arbitrary three-qubit state via a five-qubit cluster state and a Bell state. Entropy 2022, 24, 381. [Google Scholar] [CrossRef]
- Ma, X.J.; Zhou, R.G.; Hu, W.W. Improved two-qubit quantum state sharing protocol based on entanglement swapping of bell states. Quantum Inf. Process. 2022, 21, 100. [Google Scholar] [CrossRef]
- Xia, Y.; Jie, S.; Song, H.S. Quantum state sharing using linear optical elements. Opt. Commun. 2008, 281, 4946–4950. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, Z.; Chen, L.K.; Li, Z.D.; Liu, C.; Li, L.; Liu, N.L.; Ma, X.F.; Chen, Y.A.; Pan, J.W. Secret sharing of a quantum state. Phys. Rev. Lett. 2016, 117, 030501. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.M.; Lee, S.W.; Jeong, H.; Park, H.S. Quantum teleportation of shared quantum secret. Phys. Rev. Lett. 2020, 124, 060501. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.W.; Xia, L.X.; Wang, Z.Y.; Zhang, D.Y. Hierarchical quantum information splitting. Opt. Commun. 2010, 283, 1196–1199. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.W.; Zhang, D.Y.; Tang, S.Q. Hierarchical quantum information splitting with six-photon cluster states. Int. J. Theor. Phys. 2010, 48, 2691–2697. [Google Scholar] [CrossRef]
- Wang, X.W.; Zhang, D.Y.; Tang, S.Q. Multiparty hierarchical quantum-information splitting. J. Phys. B-At. Mol. Opt. 2011, 44, 035505. [Google Scholar] [CrossRef] [Green Version]
- Li, D.F.; Zheng, Y.D.; Liu, X.F. Hierarchical quantum teleportation of arbitrary single-qubit state by using four-qubit cluster state. Int. J. Theor. Phys. 2021, 60, 1911–1919. [Google Scholar] [CrossRef]
- Xu, G.; Wang, C.; Yang, Y.X. Hierarchical quantum information splitting of an arbitrary two-qubit state via the cluster state. Quantum Inf. Process. 2014, 13, 43–57. [Google Scholar] [CrossRef]
- Zha, X.W.; Miao, N.; Wang, H.F. Hierarchical quantum information splitting of an arbitrary two-qubit using a single quantum resource. Int. J. Theor. Phys. 2019, 58, 2428–2434. [Google Scholar] [CrossRef]
- Wang, N.N.; Ma, S.Y.; Li, X. Hierarchical controlled quantum communication via the χ-state under noisy environment. Mod. Phys. Lett. A 2020, 35, 2050306. [Google Scholar] [CrossRef]
- Zhou, N.R.; Zhu, K.N.; Zou, X.F. Multi-party semi-quantum key distribution protocol with four-particle cluster states. Ann. Phys. 2019, 531, 1800520. [Google Scholar] [CrossRef]
- Wang, N.N.; Ma, S.Y. Hierarchical controlled remote preparation via Brown state under noisy environment. Int. J. Theor. Phys. 2020, 59, 2816–2829. [Google Scholar] [CrossRef]
- Ma, S.Y.; Wang, N.N. Hierarchical remote preparation of an arbitrary two-qubit state with multiparty. Quantum Inf. Process. 2021, 20, 276. [Google Scholar] [CrossRef]
- Shor, P.W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 1995, 52, R2493–R2496. [Google Scholar] [CrossRef]
- Javed, S.; Prakash, R.; Prakash, H. High success perfect transmission of 1-qubit information using purposefully delayed sharing of non-maximally entangled 2-qubit resource and repeated generalized Bell-state measurements. Int. J. Quantum Inf. 2021, 19, 2150015. [Google Scholar] [CrossRef]
- Chen, W.L.; Ma, S.Y.; Qu, Z.G. Controlled remote preparation of an arbitrary four-qubit cluster-type state. Chin. Phys. B. 2016, 25, 100304. [Google Scholar] [CrossRef]
- Ma, S.Y.; Chen, X.B.; Luo, M.X. Probabilistic quantum network coding of M-qudit states over the butterfly network. Opt. Commun. 2010, 283, 497–501. [Google Scholar] [CrossRef]
- Pan, X.B.; Chen, X.B.; Xu, G.; Ahmad, H.; Shang, T.; Li, Z.P.; Yang, Y.X. Quantum network coding without loss of information. Quantum Inf. Process. 2021, 20, 65. [Google Scholar] [CrossRef]
- Feng, K.H.; Lu, X.Q.; Ping, Z. Probabilistic hierarchically controlled teleportation of an arbitrary m-qudit state with a pure entangled quantum channel. Sci. Sin.-Phys. Mech. Astron. 2022, 52, 230311. (In Chinese) [Google Scholar] [CrossRef]
- Xu, G.; Shan, R.T.; Chen, X.B. Probabilistic and hierarchical quantum information splitting based on the non-maximally entangled cluster state. CMC-Comput. Mater. Con. 2021, 69, 339–349. [Google Scholar] [CrossRef]
- Guo, W.M.; Qin, L.R. Hierarchical and probabilistic quantum information splitting of an arbitrary two-qubit state via two cluster states. Chin. Phys. B 2018, 27, 110302. [Google Scholar] [CrossRef]
- Li, F.; Yan, J.; Zhu, S. General quantum secret sharing scheme based on two qudit. Quantum Inf. Process. 2021, 20, 328. [Google Scholar] [CrossRef]
- Ziman, M.; Bužek, V. Realization of positive-operator-valued measures using measurement-assisted programmable quantum processors. Phys. Rev. A 2005, 72, 022343. [Google Scholar] [CrossRef] [Green Version]
- Rao, A.V.G.; Devi, A.R.U.; Rajagopal, A.K. Positive-operator-valued-measure view of the ensemble approach to polarization optics. J. Opt. Soc. Am. A 2008, 25, 874–880. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).