Abstract
We investigate quantum information by a theoretical measurement approach of an Aharanov–Bohm (AB) ring with Yukawa interaction in curved space with disclination. We obtained the so-called Shannon entropy through the eigenfunctions of the system. The quantum states considered come from Schrödinger theory with the AB field in the background of curved space. With this entropy, we can explore the quantum information at the position space and reciprocal space. Furthermore, we discussed how the magnetic field, the AB flux, and the topological defect influence the quantum states and the information entropy.
1. Introduction
Structures with the profile of quantum rings have attracted the attention of several researchers [1,2,3,4] due to their various technological applications, e.g., nano-flash memories [5,6], photonic detectors [5,7], and spintronics [5]. Generally, this type of system is classified into two classes, i.e., one-dimensional rings (configurations with a constant radius) [8,9,10,11,12] and two-dimensional rings (with a variable radius) [13,14,15,16]. A particular category of these structures is the Aharanov–Bohm (AB) rings. Indeed, many works study AB rings [17,18,19]. In summary, we can understand the AB ring as structures produced by particles in a circular motion and subjected to the AB field. Actually, there are works in the literature discussing these structures with mesoscopic decoherence [20], electromagnetic resonator [21], and spin–orbit interaction [22,23].
A physical model of great interest is a system composed of particles of spin-zero [24,25,26]. In these systems, there is a screened Coulomb potential known as the Yukawa potential (YP) [27,28]. This potential has the profile
where the parameter is a coupling constant that regulates the magnitude of the effective force and the parameter is a parameter that makes the exponential argument dimensionless. Naturally, this potential is central and attractive. These characteristics of this potential make the interest in this topic growing [29,30,31,32,33]. In his seminal work, H. Yukawa shows that this potential results in the interaction of a massive scalar field with a massive bosonic field [34]. The fact is that today’s theories with Yukawa’s interaction have several applications [35,36,37]. For example, Carvalho et al. [35] consider a classical system of two-dimensionally charged particles interacting with a Yukawa potential. As a result, the ground state of the particle ensemble configuration is adjustable, and the system has multiple phase transitions. Furthermore, in investigations of the resonance energy of particles, Yukawa’s potential has been used [36]. Moreover, using the shifted expansion approach, it is possible to predict an appropriate value for of the interaction [37]. In particular, a stimulating application is an interaction between two nuclei. In this case, this application is interesting because two cores can experience attractive interaction due to the interaction of charged pions [34]. In other words, pions are similar to two particles interacting electromagnetically through the exchange of photons.
The growing interest in Yukawa-type theories nowadays is notorious. For example, in the study of spin-0 particles, a modified scalar-vector potential of type Yukawa was used [38]. Furthermore, to investigate the approximate analytical solutions of hydrogen and neutral atoms, Yukawa interactions were considered [39]. Yukawa’s interactions were also used in the bound state study of fermionic particles considering spin symmetry and pseudospin symmetry [40]. Moreover, another interesting application is the theoretical measurements of quantum information in Aharanov–Bohm theories with Yukawa interaction, which was recently studied [41].
Not far from quantum theory, information theory has been a practical tool to investigate uncertainty measurements related to quantum-mechanical systems [42,43,44,45,46]. Information theory emerged with Shannon’s seminal paper A Mathematical Theory of Communication in 1948 [47]. Shannon sought to understand the propagation of information in a noisy channel. Consequently, he sought to explain the possible savings due to the statistical structure of the original message and due to the nature of the final destination of the message [47]. Analyzing the likely interference events in the information, Shannon proposes the entropic quantity
where is the probability density associated with the event. Shannon’s theory has also provided support for cryptography [48] and for noise theory [49].
We seek in this study to answer the issue of how the magnetic field, the AB flux, and the topological defect (i.e., the disclination defect) will influence a particle restricted to a Yukawa-like potential. To reach our purpose, we numerically investigate Shannon entropy. This study is influential because it allows us to predict how the measurement uncertainties will change as the magnetic field, AB flux, or topological defect varies.
The paper is organized as follows. In Section 2, we build the model considering a particle confined by a Yukawa interaction. Furthermore, the model was structured considering a disclination defect. In Section 2, we exposed the analytical solutions of the quantum eigenstates. Posteriorly, in Section 3, the numerical result of Shannon entropy is discussed. Finally, we close by announcing our findings in Section 4.
2. Theory and Solutions
Let us consider that the particle is confined by a Yukawa potential (YP), under the complete effect of the AB and magnetic fields. Let us assume that there exists a disclination or topological defect in this region. The disclination is described by the line element [50]
where is the parameter associated with the deficit of angle. The parameter is related to the linear mass density of the string via [51]. Notice that the azimuthal angle is defined in the range [52].
The Hamiltonian operator of a particle that is charged and confined to move in the region of YP under the collective impact of AB flux and an external magnetic fields with topological defect can be written in cylindrical coordinates. Thus, the Schrödinger equation for this consideration is written as follows [53];
where denotes the energy level, is the effective mass of the system, and the vector potential which is denoted by “” can be written as a superposition of two terms having the azimuthal components [53] and external magnetic field with , , where is the magnetic field. and represents the additional magnetic flux created by a solenoid with . The Del and Laplacian operator are used as in Ref. [53].
The vector potential in full is written in a simple form as
Let us take a wave function in the cylindrical coordinates as
where m denotes the magnetic quantum number. Inserting this wave function and the vector potential into Equation (5) we arrive at the following radial second-order differential equation:
where is the effective potential defined as
where is an integer with the flux quantum and denotes the cyclotron frequency. Figure 1 displays the behavior of the effective potential when the magnetic field, the topological defect, and the AB flux undergo changes. Equation (7) is a complicated differential equation that cannot be solvable easily due to the presence of centrifugal term. Therefore, we employ the Greene and Aldrich approximation scheme [54] to bypass the centrifugal term. This approximation is given
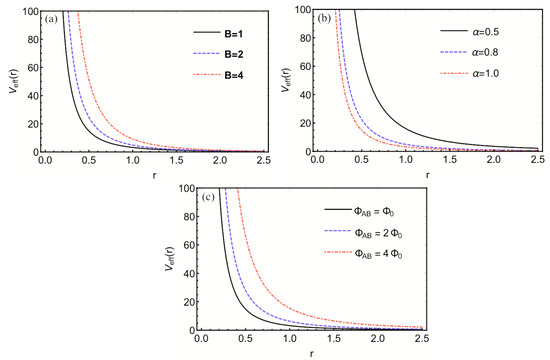
Figure 1.
(a) Effective potential when the magnetic field changes. (b) Effective potential when the parameter (topological defect) varies. (c) Effective potential when flux AB varies.
We point out here that this approximation is only valid for small values of the screening parameter . It is interesting to mention that Greene and Aldrich’s approach [54] has been widely used in recent years. For example, an approach similar was used in the study of the analytical approximations for the solutions of the Manning–Rosen potential with centrifugal term [55]. Moreover, the investigation of the analytical approximations for the l-wave solutions of the Schrödinger equation with the Eckart potential considered a similar approach [56]. Inserting Equation (9) into Equation (8) and introducing a new variable allows us to obtain
For mathematical simplicity, let us introduce the following dimensionless notations:
In order to solve Equation (10), we have transform the differential Equation (8) into a form solvable by any of the existing standard mathematical technique. Hence, we take the radial wave function of the form
where , and . On substitution of Equation (12) into Equation (10), we obtain the following hypergeometric equation:
By considering the finiteness of the solutions, the quantum condition is given by
which in turn transforms into the energy eigenvalue equation, as follows:
Substituting Equation (11) into Equation (15) and carrying some simple manipulative algebra, we arrive at the energy eigenvalue equation of the Yukawa potential in the presence of magnetic and AB fields with a topological defect in the form
Furthermore, the wave eigenfunction is
where , , and .
Figure 2 displays the plots of the probability density of the particle confined to the Yukawa interaction (Equation (8)) in the presence of a disclination defect. Note that the wave function profile changes when the magnetic field, the AB flux, and the topological defect change in the theory. Furthermore, when the declination defect (i.e., when ) is changed, the probability density of the wave function translates in its profile so that the highest probability is close to the atomic core. Here it is interesting to mention that the excited eigenstates of the model will have a profile similar to that shown in Figure 2. However, a change in the height of the solitonic wave function can be verified in excited states.
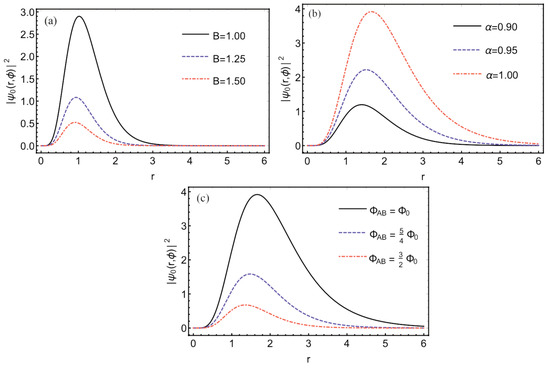
Figure 2.
Probability density in position space r when magnetic field changes (a), the parameter (topological defect) varies (b) and AB flux varies (c).
Although we have considered the asymptotic condition to obtain a quantized system, notice that this condition produces a two-dimensional AB ring. As shown in Figure 2, the probability densities will only be non-zero at the ring. Therefore, the probability density is null at the origin and after the value (ring boundary). It is crucial to mention that maximal radius is obtained numerically. Furthermore, it is possible to observe that the AB ring will have a maximum radius depending on the magnetic field, the AB flux, and the disclination.
3. Shannon’s Entropy
Quantum information entropy has helped to understand the physics of several systems [57,58,59]. Moreover, quantum information entropy appears in several studies due to the essential information about the physical system it provides. Some applications of quantum entropy are studies of a symmetrically (and asymmetrically) trigonometric Rosen–Morse potential [60,61], a solitonic mass profile [62], and a hyperbolic-single potential well [63].
One of the quantum entropies used to study the information of quantum systems is Shannon entropy. Shannon’s entropy emerged within the scope of information theory seeking to describe the best way to propagate information between a source and a receiver [47]. Along with the development of the Shannon entropy concept in physics, studies on the thermodynamics of an ensemble of particles led to mathematical expressions with a similar profile. This similarity of Shannon information and Boltzmann entropy allowed Shannon information to be called Shannon entropy [64]. Some conceptual applications of Shannon’s entropy help us understand the information and uncertainty measurement of quantum systems, e.g., Shannon entropy gives us the uncertainty of non-Hermitian particle systems [65]. Furthermore, Shannon formalism allowed the study of fermionic particles [66], problems with effective mass distribution [67,68], and mechanical-quantum models with double-well potential [69].
An interpretation of the Shannon entropy of a quantum-mechanical system tells us the measure of uncertainties of a probability distribution associated with a source of information [70,71]. The Born interpretation of the quantum mechanics [72] takes us to the statistical perception of the stationary quantum system, i.e.,
In this case, is the probability of finding the particle in the state between and [72]. Furthermore, is the probability density of the quantum-mechanical system. Let us now study Shannon’s entropy in the context of quantum mechanics. Remembering that the probability density has the form of Equation (17), we define Shannon’s entropy as
so that for a probability density of a continuous system in position space, Shannon entropy takes the form
On the other hand, Shannon’s entropy in reciprocal space (or momentum space) is
Perceive that the expressions (19) and (20) have only two independent variables. Our model is two-dimensional, i.e., a model of (2+1)D with spatial coordinates r and . However, is a cyclic coordinate. In this way, only the r coordinate contributes to Shannon information. The wave function in reciprocal space is given by Fourier transform, namely,
The entropic quantities of Equations (19) and (20) play a role analogous to the Heisenberg uncertainty measures [65,66]. An entropic uncertainty relation that relates to the entropic uncertainties was obtained by Beckner [71] and Bialynicki–Birula and Mycielski (BBM) [73]. The BBM relation of uncertainties is
where D is the dimension of effective spatial coordinates, i.e., the number of spatial coordinates that contribute to the information propagation. In our case, the results must respect the relation
To investigate the quantum information of the model presented in Section 2, we consider the wave function (16) and numerically normalize it through the expression
Here, we have that and . Furthermore, we use Equation (19) to calculate Shannon entropy in position space. Using the Fourier transform (21), it comes to eigenfunctions at the reciprocal space. With the eigenfunctions normalized in the momentum space, we use Equation (20) to obtain Shannon’s entropy in this space. The numerical results of Shannon’s entropy for the first energy levels are shown in Table 1 and Table 2. Although the definition of Shannon’s entropy is all space, quantum information will only have a non-zero contribution up to (maximum radius of the ring). After the ring boundary, the quantum information will be null. We presented the physical discussion of the results found in the next section.

Table 1.
Numerical result of Shannon’s entropy for several values of the magnetic field and flux AB.

Table 2.
Numerical result of Shannon’s entropy when the disclination varies.
4. Final Remarks
Throughout the paper, we studied the influences of the external magnetic field, the AB flux, and the disclination defect on the AB quantum ring. The wave function that describes the system is the confluent hypergeometric function. Furthermore, the complete solution set, i.e., the wave eigenfunctions, reproduces a null probability at the spatial infinity. This condition leads us to a discretized energy spectrum indicating the existence of bound states.
We measure the Shannon entropy to analyze the quantum information. It was possible to notice that the disclination, the external magnetic field, and AB flux directly influence the quantum information of the system. Considering the numerical results displayed in Table 1 and Table 2, it is notorious that the informational content decreases in the position space when the contribution of the AB flux to the magnetic field increases. This is because the contribution of the magnetic field and the AB field, when increasing their intensity, make the quantum rings more localized, so the informational content decreases. Indeed, this indicates a decrease in the uncertainties related to the measurements of the position of the AB ring. In counterpoint, it is prominent that if the disclination increases, quantum information increases (in position space). Therefore, the increases in information (or uncertainties) in the position space grow. Thereby, this is a consequence of the type of defect. In the absence of disclination (i.e., ), position uncertainty is greater. However, occurring during the rotational symmetry breaking, the position measurement uncertainties begin to decrease. In this case, this is because the ring becomes thinner and thinner.
On the other hand, quantum information (and consequently, measurement uncertainty) increases in the momentum space. The measurement uncertainties increase as the magnetic field and AB flux increase. However, when the topological defect increase, the information decrease in reciprocal space. The increment (or reduction) of the information at the momentum space is a consequence of the Heisenberg uncertainty principle (HUP). Moreover, in the communication theory, the BBM relation plays the role of the HUP. Here is essential to mention that BBM relation is valid in our model.
A direct perspective of this work is the study of the quantum information measurement of a quantum ring in the presence of other topological defects. Another possibility is to study the relativistic version of this theory. Furthermore, an immediate generalization is the analysis of Fisher’s information. We know that the quantum information entropy used in this work tells us how good the information is. Fisher’s information may inform us of loss of system-related information [74]. Therefore, Fisher’s information is a complementary quantity to Shannon’s entropy [74]. We found some studies on applications of Fisher’s entropy in quantum-mechanical systems. An application of Fisher’s information is performed in Ref. [75] to study a position-dependent mass. We hope to produce these studies in the future.
Author Contributions
Conceptualization, C.O.E. and F.C.E.L.; validation, F.C.E.L. and C.O.E.; writing—original draft preparation, C.O.E., F.C.E.L., C.A.S.A., N.A. and M.A.; writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been carried out under LRGS Grant LRGS/1/2020/UM/01/5/2 (9012-00009) Fault-tolerant Photonic Quantum States for Quantum Key Distribution provided by Ministry of Higher Education of Malaysia (MOHE).
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
F.C.E. Lima is grateful to the Coordenação de Aperfeiçoamento do Pessoal de Nível Superior (CAPES), for financial support. C.A.S. Almeida thanks the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for the financial support in the project no. 309553/2021-0. M.A. thanks Khalifa University for financial support in the project no. 8474000358 (FSU-2021-018).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kuroda, T.; Mano, T.; Ochiai, T.; Sanguinetti, S.; Kido, K.S.G.; Koguchi, N. Optical transitions in quantum ring complexes. Phys. Rev. B 2005, 72, 205301. [Google Scholar] [CrossRef]
- Chakraborty, T.; Pietiläinen, P. Electron-electron interaction and the persistent current in a quantum ring. Phys. Rev. B 1994, 50, 8460. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.C.; Kwak, K.S.; Park, B.H.; Kang, H.Y.; Kim, J.Y.; Kwon, O. Photonic quantum ring. Phys. Rev. Lett. 1999, 82, 536. [Google Scholar] [CrossRef]
- Netto, A.S.; Chesman, C.; Furtado, C. Influence of topology in a quantum ring. Phys. Lett. A 2008, 372, 3894. [Google Scholar] [CrossRef]
- Fomin, V.M. (Ed.) Physics of Quantum Rings, in NanoScience and Technology; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Nowozin, T. Self-Organized Quantum Dots for Memories: Electronic Properties and Carrier Dynamics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Michler, P. Single Quantum Dots: Fundamentals, Applications, and New Concepts; Springer: Berlin, Germany, 2003; Volume 90. [Google Scholar]
- Cheung, H.F.; Gefen, Y.; Riedel, E.K.; Shih, W.H. Persistent currents in small one-dimensional metal rings. Phys. Rev. B 1988, 37, 6050. [Google Scholar] [CrossRef] [PubMed]
- Meijer, F.E.; Morpurgo, A.F.; Klapwijk, T.M. One-dimensional ring in the presence of Rashba spin-orbit interaction: Derivation of the correct Hamiltonian. Phys. Rev. B 2002, 66, 033107. [Google Scholar] [CrossRef]
- Frustaglia, D.; Richter, K. Spin interference effects in ring conductors subject to Rashba coupling. Phys. Rev. B 2004, 69, 235310. [Google Scholar] [CrossRef]
- Lorke, A.; Luyken, R.J.; Govorov, A.O.; Kotthaus, J.P.; Garcia, J.M.; Petroff, P.M. Spectroscopy of nanoscopic semiconductor rings. Phys. Rev. Lett. 2000, 84, 2223. [Google Scholar] [CrossRef]
- Kettemann, S.; Fulde, P.; Strehlow, P. Correlated persistent tunneling currents in glasses. Phys. Rev. Lett. 1999, 83, 4325. [Google Scholar] [CrossRef]
- Tan, W.C.; Inkson, J.C. Magnetization, persistent currents, and their relation in quantum rings and dots. Phys. Rev. B 1999, 60, 5626. [Google Scholar] [CrossRef]
- Bulaev, D.V.; Geyler, V.A.; Margulis, V.A. Effect of surface curvature on magnetic moment and persistent currents in two-dimensional quantum rings and dots. Phys. Rev. B 2004, 69, 195313. [Google Scholar] [CrossRef]
- Duque, C.M.; Morales, A.L.; Mora-Ramos, M.E.; Duque, C.A. Optical nonlinearities associated to applied electric fields in parabolic two-dimensional quantum rings. J. Lumin. 2013, 143, 81. [Google Scholar] [CrossRef]
- Nowak, M.P.; Szafran, B. Spin-orbit coupling effects in two-dimensional circular quantum rings: Elliptical deformation of confined electron density. Phys. Rev. B 2009, 80, 195319. [Google Scholar] [CrossRef]
- Oliveira, R.R.S.; Filho, A.A.A.; Lima, F.C.E.; Maluf, R.V.; Almeida, C.A.S. Thermodynamic properties of an Aharonov-Bohm quantum ring. Eur. Phys. J. Plus 2019, 134, 495. [Google Scholar] [CrossRef]
- Russo, S.; Oostinga, J.B.; Wehenkel, D.; Heersche, H.B.; Sobhani, S.S.; Vandersypen, L.M.K.; Morpurgo, A.F. Observation of Aharonov-Bohm conductance oscillations in a graphene ring. Phys. Rev. B 2008, 77, 085413. [Google Scholar] [CrossRef]
- Yeyati, A.L.; Büttiker, M. Aharonov-Bohm oscillations in a mesoscopic ring with a quantum dot. Phys. Rev. B 1995, 52, R14360(R). [Google Scholar] [CrossRef]
- Hansen, A.E.; Kristensen, A.; Pedersen, S.; Sorensen, C.B.; Lindelof, P.E. Mesoscopic decoherence in Aharonov-Bohm rings. Phys. Rev. B 2001, 64, 045327. [Google Scholar] [CrossRef]
- Reulet, B.; Ramin, M.; Bouchiat, H.; Mailly, D. Dynamic response of isolated aharonov-bohm rings coupled to an electromagnetic resonator. Phys. Rev. Lett. 1995, 75, 124. [Google Scholar] [CrossRef]
- Aeberhard, U.; Wakabayashi, K.; Sigrist, M. Effect of spin-orbit coupling on zero-conductance resonances in asymmetrically coupled one-dimensional rings. Phys. Rev. B 2005, 72, 075328. [Google Scholar] [CrossRef]
- Shelykh, I.A.; Bagraev, N.T.; Galkin, N.G.; Klyachkin, L.E. Interplay of h/e and h/2e oscillations in gate-controlled Aharonov-Bohm rings. Phys. Rev. B 2005, 71, 113311. [Google Scholar] [CrossRef]
- Ahmed, F. Relativistic motions of spin-zero quantum oscillator field in a global monopole space-time with external potential and AB-effect. Sci. Rep. 2022, 12, 8794. [Google Scholar] [CrossRef] [PubMed]
- Zare, S.; Hassanabadi, H.; Guvendi, A.; Chung, W.S. On the interaction of a Cornell-type nonminimal coupling with the scalar field under the background of topological defects. Int. J. Mod. Phys. A 2022, 37, 2250033. [Google Scholar] [CrossRef]
- Shikakhwa, M.S.; Chair, N. Constructing Hermitian Hamiltonians for spin zero neutral and charged particles on a curved surface: Physical approach. Eur. Phys. J. Plus 2022, 137, 560. [Google Scholar] [CrossRef]
- Yukawa, H. On the interaction of elementary particles. I. Proc. Phys. Math. Soc. Jpn. 1935, 17, 48. [Google Scholar]
- Rowlinson, J.S. The Yukawa potential. Phys. Stat. Mech. Its Appl. 1989, 156, 15. [Google Scholar] [CrossRef]
- Okorie, U.S.; Ibekwe, E.E.; Ikot, A.N.; Onyeaju, M.C.; Chukwuocha, E.O. Thermodynamic properties of the modified Yukawa potential. J. Kor. Phys. Soc. 2018, 73, 1211. [Google Scholar] [CrossRef]
- Edet, C.O.; Okoi, P.O.; Chima, S.O. Persistent Current, Magnetic Susceptibility, and Thermal Properties for a Class of Yukawa Potential in the Presence of External Magnetic and Aharanov–Bohm Fields. Int. J. Thermophys. 2020, 42, e20190083. [Google Scholar] [CrossRef]
- Khrapak, S.A.; Ivlev, A.V.; Morfill, G.E.; Zhdanov, S.K. Scattering in the Attractive Yukawa Potential in the Limit of Strong Interaction. Phys. Rev. Lett. 2020, 90, 225002. [Google Scholar] [CrossRef]
- Loeb, A.; Weiner, N. Cores in dwarf galaxies from dark matter with a Yukawa potential. Phys. Rev. Lett. 2011, 106, 171302. [Google Scholar] [CrossRef]
- Hamzavi, M.; Movahedi, M.; Thylwe, K.-E.; Rajabi, A.A. Approximate analytical solution of the Yukawa potential with arbitrary angular momenta. Chin. Phys. Lett. 2012, 29, 080302. [Google Scholar] [CrossRef]
- Martin, B.R.; Shaw, G. Particle Physics, 3rd ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Carvalho, J.C.N.; Ferreira, W.P.; Farias, G.A.; Peeters, F.M. Yukawa particles confined in a channel and subject to a periodic potential: Ground state and normal modes. Phys. Rev. B 2011, 83, 094109. [Google Scholar] [CrossRef]
- Bahlouli, H.; Abdelmonem, M.S.; Nasser, I.M. Analytical treatment of the Yukawa potential. Phys. Scr. 2010, 82, 065005. [Google Scholar] [CrossRef]
- Imbo, T.; Pagnamenta, A.; Sukhatme, U. Bound states of the Yukawa potential via the shifted 1/N expansion technique. Phys. Lett. A 1984, 105, 183. [Google Scholar] [CrossRef]
- Maireche, A. A model of modified Klein-Gordon equation with modified scalar-vector Yukawa potential. Afr. Rev. Phys. 2020, 15, 0001. [Google Scholar]
- Maireche, A. Nonrelativistic treatment of Hydrogen-like and neutral atoms subjected to the generalized perturbed Yukawa potential with centrifugal barrier in the symmetries of noncommutative Quantum mechanics. Int. J. Geo. Met. Mod. Phys. 2020, 17, 2050067. [Google Scholar] [CrossRef]
- Maireche, A. Approximate Arbitrary k State Solutions of Dirac Equation with Improved Inversely Quadratic Yukawa Potential within Improved Coulomb-like Tensor Interaction in Deformation Quantum Mechanics Symmetries. Few-Body Syst. 2022, 63, 54. [Google Scholar] [CrossRef]
- Edet, C.O.; Ettah, E.B.; Aljunid, S.A.; Endut, R.; Ali, N.; Ikot, A.N.; Asjad, M. Global Quantum Information-Theoretic Measures in the Presence of Magnetic and Aharanov-Bohm (AB) Fields. Symmetry 2022, 14, 976. [Google Scholar] [CrossRef]
- Jiao, L.G.; Zan, L.R.; Zhang, Y.Z.; Ho, Y.K. Benchmark values of S hannon entropy for spherically confined hydrogen atom. Int. J. Quantum Chem. 2017, 117, e25375. [Google Scholar] [CrossRef]
- Amadi, P.O.; Ikot, A.N.; Ngiangia, A.T.; Okorie, U.S.; Rampho, G.J.; Abdullah, H.Y. Shannon entropy and Fisher information for screened Kratzer potential. Int. J. Quantum Chem. 2020, 120, e26246. [Google Scholar] [CrossRef]
- Dehesa, J.G.; Belega, E.D.; Toranzo, I.V.; Aptekarev, A.I. The Shannon entropy of high-dimensional hydrogenic and harmonic systems. Int. J. Quantum Chem. 2019, 119, e25977. [Google Scholar] [CrossRef]
- Martínez-Flores, C. Shannon entropy and Fisher information for endohedral confined one- and two-electron atoms. Phys. Lett. A 2021, 386, 126988. [Google Scholar] [CrossRef]
- Sekh, G.A.; Saha, A.; Talukdar, B. Shannon entropies and Fisher information of K-shell electrons of neutral atoms. Phys. Lett. A 2018, 382, 315. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tecn. J. 1948, 27, 379. [Google Scholar] [CrossRef]
- Grasselli, F. Quantum Cryptography; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Amigó, J.M.; Dale, R.; Tempesta, P. A generalized permutation entropy for noisy dynamics and random processes. Chaos 2021, 31, 013115. [Google Scholar] [CrossRef] [PubMed]
- Hassanabadi, H.; Hosseinpour, M. Thermodynamic properties of neutral particle in the presence of topological defects in magnetic cosmic string background. Eur. Phys. J. C 2016, 76, 553. [Google Scholar] [CrossRef]
- Bakke, K.; Ribeiro, L.R.; Furtado, C.; Nascimento, J.R. Landau quantization for a neutral particle in the presence of topological defects. Phys. Rev. D 2009, 79, 024008. [Google Scholar] [CrossRef]
- Nwabuzor, P.; Edet, C.; Ikot, A.N.; Okorie, U.; Ramantswana, M.; Horchani, R. Analyzing the Effects of Topological Defect (TD) on the Energy Spectra and Thermal Properties of LiH, TiC and I2 Diatomic Molecules. Entropy 2021, 198, 1060. [Google Scholar] [CrossRef] [PubMed]
- Edet, C.O.; Ikot, A.N. Effects of Topological Defect on the Energy Spectra and Thermo-magnetic Properties of CO Diatomic Molecule. J. Low Temp. Phys. 2021, 203, 84. [Google Scholar] [CrossRef]
- Greene, R.L.; Aldrich, C. Variational wave functions for a screened Coulomb potential. Phys. Rev. A 1976, 14, 2363. [Google Scholar] [CrossRef]
- Qiang, W.-C.; Dong, S.-H. Analytical approximations to the solutions of the Manning–Rosen potential with centrifugal term. Phys. Lett. A 2007, 368, 13. [Google Scholar] [CrossRef]
- Dong, S.; García-Ravelo, J.; Dong, S.-H. Analytical approximations to the l-wave solutions of the Schrödinger equation with an exponential-type potential. Phys. Scr. 2007, 76, 393. [Google Scholar] [CrossRef]
- Dong, S.; Sun, G.-H.; Dong, S.-H.; Draayer, J.P. Quantum information entropies for a squared tangent potential well. Phys. Lett. A 2014, 378, 124. [Google Scholar] [CrossRef]
- Sun, G.-H.; Aoki, M.A.; Dong, S.-H. Quantum information entropies of the eigenstates for the Pöschl—Teller-like potential. Chin. Phys. B 2013, 22, 050302. [Google Scholar] [CrossRef]
- Song, X.-D.; Sun, G.-H.; Dong, S.-H. Shannon information entropy for an infinite circular well. Phys. Lett. A 2015, 379, 1402. [Google Scholar] [CrossRef]
- Sun, G.-H.; Dong, S.-H. Quantum information entropies of the eigenstates for a symmetrically trigonometric Rosen–Morse potential. Phys. Scr. 2013, 87, 045003. [Google Scholar] [CrossRef]
- Sun, G.-H.; Dong, S.-H.; Saad, N. Quantum information entropies for an asymmetric trigonometric Rosen-Morse potential. Ann. Phys. 2013, 525, 943. [Google Scholar] [CrossRef]
- Serrano, F.A.; Falaye, B.J.; Dong, S.-H. Information-theoretic measures for a solitonic profile mass Schrödinger equation with a squared hyperbolic cosecant potential. Physica A 2016, 446, 152. [Google Scholar] [CrossRef]
- Gil-Barrera, C.A.; Carrillo, R.S.; Sun, G.-H.; Dong, S.-H. Quantum Information Entropies on Hyperbolic Single Potential Wells. Entropy 2022, 24, 604. [Google Scholar] [CrossRef]
- Pathria, R.K. Statistical Mechanics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1996. [Google Scholar]
- Lima, F.C.E.; Moreira, A.R.P.; Machado, L.E.S.; Almeida, C.A.S. Statistical properties of linear Majorana fermions. Int. J. Quantum Chem. 2021, 121, e26749. [Google Scholar] [CrossRef]
- Lima, F.C.E.; Moreira, A.R.P.; Almeida, C.A.S. Information and thermodynamic properties of a non-Hermitian particle ensemble. Int. J. Quantum Chem. 2021, 121, e26645. [Google Scholar] [CrossRef]
- Yanez-Navarro, G.; Sun, G.-H.; Dytrych, T.; Launey, K.D.; Dong, S.-H.; Draayer, J.P. Quantum information entropies for position-dependent mass Schrödinger problem. Ann. Phys. 2014, 348, 153. [Google Scholar] [CrossRef]
- Lima, F.C.E. Quantum information entropies for a soliton at hyperbolic well. Ann. Phys. 2022, 442, 168906. [Google Scholar] [CrossRef]
- Sun, G.-H.; Dong, S.-H.; Launey, K.D.; Dytrych, T.; Draayer, J.P. Shannon information entropy for a hyperbolic double-well potential. Int. J. Quantum Chem. 2015, 115, 891. [Google Scholar] [CrossRef]
- Hirschmann, I.I., Jr. American Journal of Mathematics; The Johns Hopkins University Press: Baltimore, MD, USA, 1957; Volume 79, p. 152. [Google Scholar]
- Beckner, W. Inequalities in Fourier analysis. Ann. Math. 1975, 102, 159. [Google Scholar] [CrossRef]
- Born, M. Statistical interpretation of quantum mechanics. Science 1955, 122, 675. [Google Scholar] [CrossRef] [PubMed]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Comm. Math. Phys. 1975, 44, 129. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of statistical estimation. Math. Proc. Cambridge Philos. Soc. 1925, 22, 700. [Google Scholar] [CrossRef]
- Falaye, B.J.; Serrano, F.A.; Dong, S.-H. Fisher information for the position-dependent mass Schrödinger system. Phys. Lett. A 2016, 380, 267. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).