Multiband Spectrum Sensing Based on the Sample Entropy
Abstract
:1. Introduction
2. Sample Entropy
- Build a vector with m consecutive data points taken from X; i.e.,where P varies in the interval , and m is the length of sequences to be compared, also called the embedding dimension.
- For each P, definewhere is the tolerance for accepting matches, and it is usually selected as a factor of the standard deviation of vector , . is the Heaviside functionand is the Chebyshev distance, defined aswhere represents the proportion of , P ≠ h whose distances to are less than r.
- Now, for each P, definewhere represents the proportion corresponding to the dimension of m + 1. and have the same mold, but embedding vectors in both cases are defined in different spaces.
- Average across all embedding vectors to obtainand
- The SampEn is computed as
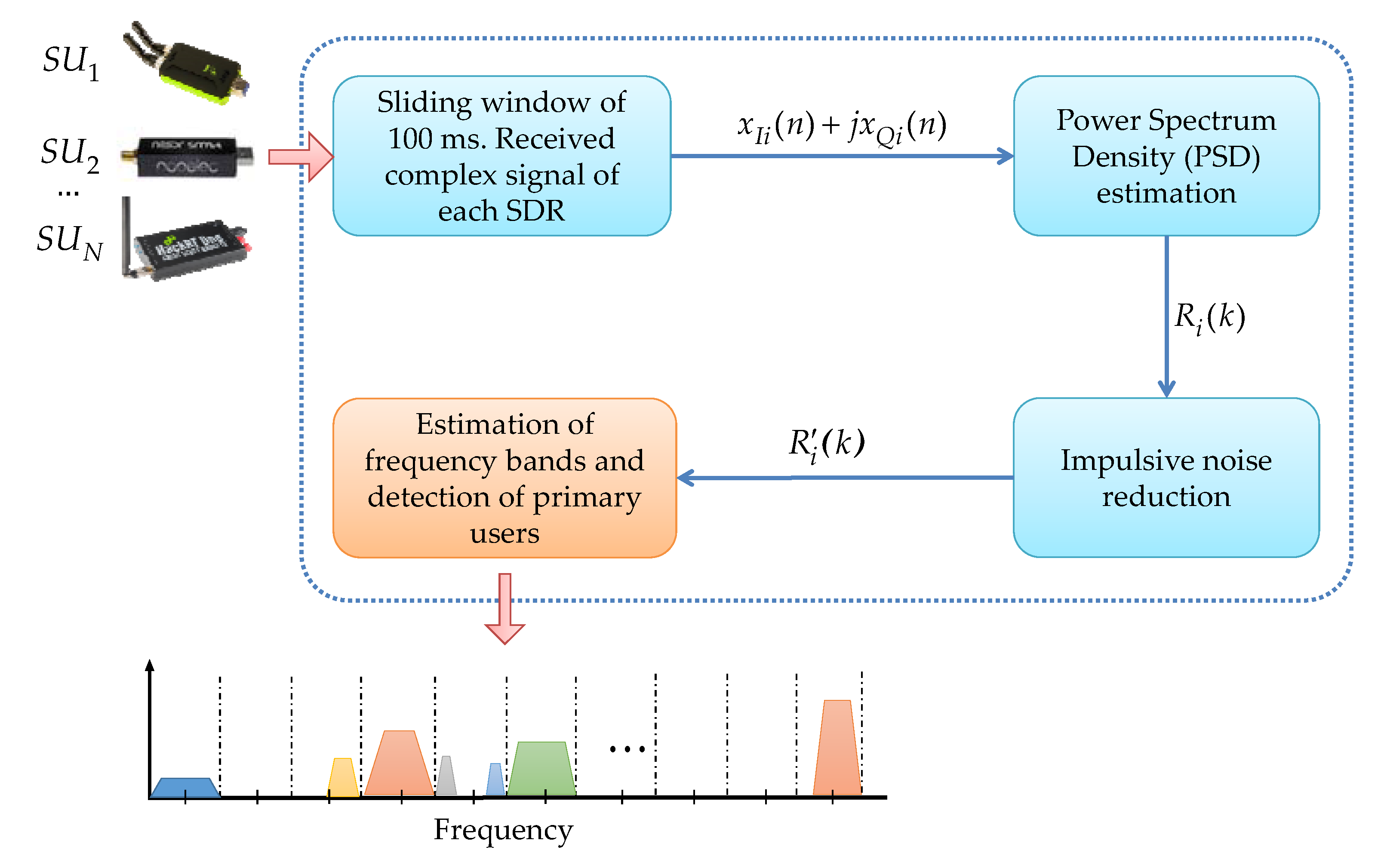
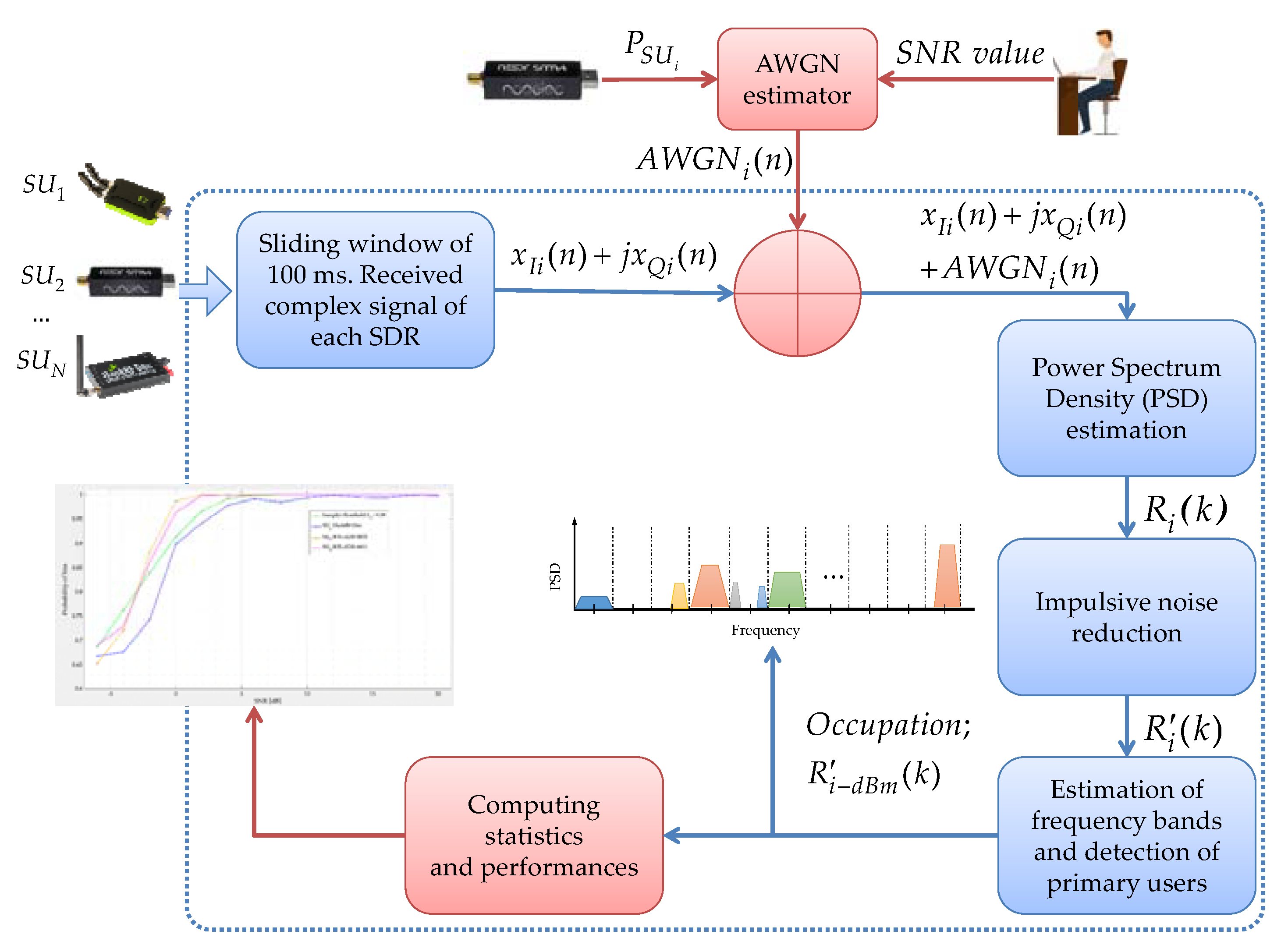
3. Methodology
- Sliding time window. This block receives the complex signal from each connected device , refreshed every 100 ms. In this block, it is possible to manipulate the parameters of the sampling rate , center frequency , and gain of each device i.
- Estimation of the power spectral density. In this block, from the signal , the PSD is computed directly in a linear scale for every frame of 100 ms. For this, a Welch estimator [17] is used, resulting in the signal . The number of samples for each frame, used to estimate PSD, is a value chosen by the user and depends on the type of used device: 512, 1024, 2048, or 4096 for the RTL-SDR devices, and 1024, 2048, 4096, or 8192 for HackRf One and LimeSDR mini devices.
- Impulsive noise inhibition. Impulsive noise and high-frequency noise are greatly reduced in this module. Here, the processing is done through the detail coefficients and the approximation coefficients resulting from having applied the MRA to the PSD estimate [18]. This noise reduction proposal is a novel technique introduced by the authors, giving excellent results. The result of this block is the modified PSD .
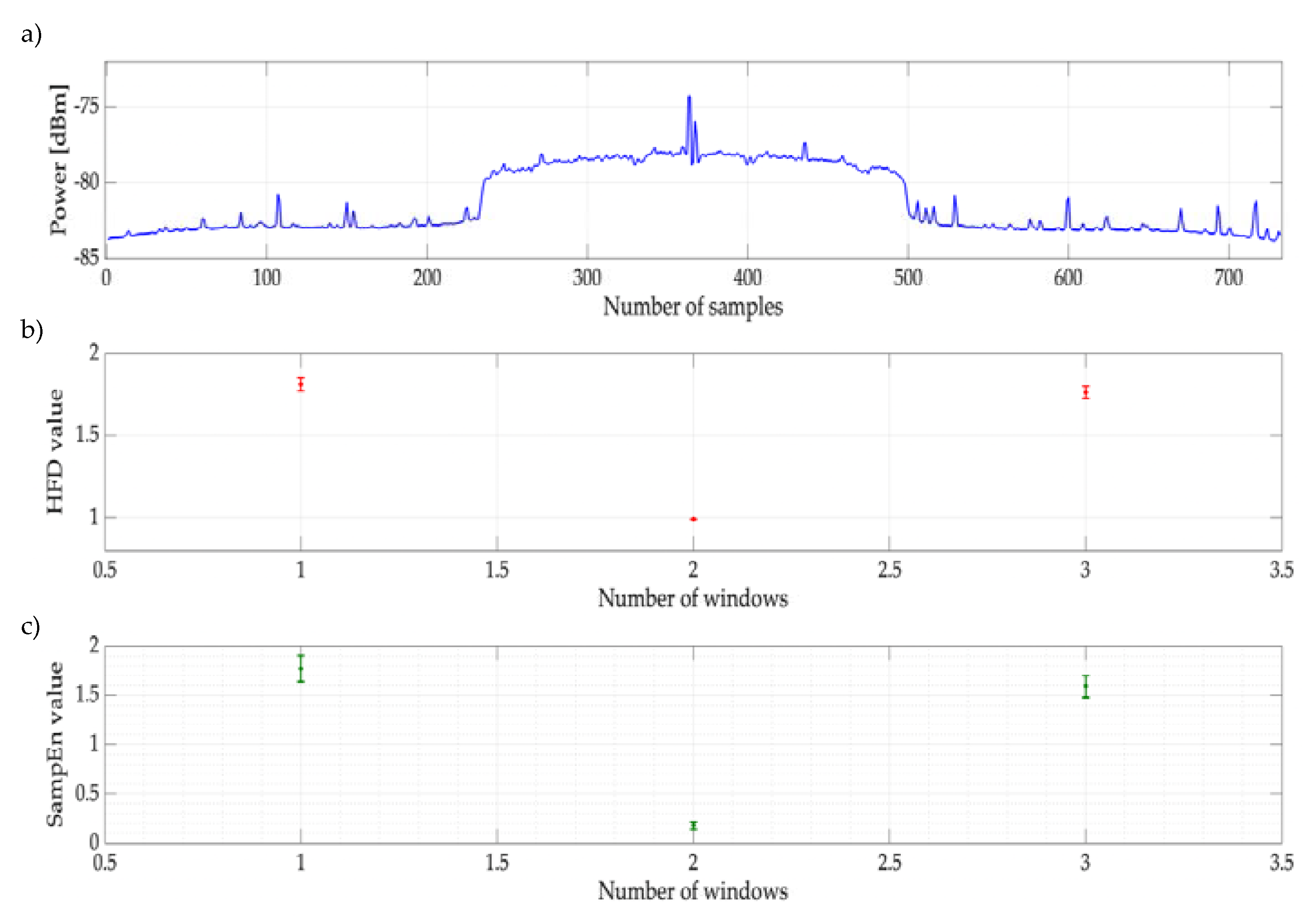
- PU detection. This module detects spectral gaps and possible PU transmissions in a wide frequency range. As can be seen in [6], MRA and K-means [19] algorithms are used to detect the start and end edges of a PU transmission, and HFD [20] is used as the decision rule to distinguish what is noise from a possible transmission.
- PSD perceived by each connected SDR device is evaluated in dBm to obtain the signal. MRA is applied to this signal, resulting in the approximation and detail coefficients at different levels of decomposition.
- The analysis of the reconstructed signal of the approximation coefficients allows us to know the number of clusters in which the normalized and rescaled approximation coefficients will be classified by the K-means algorithm to build the test signal.
- Processing the changes of state of this signal, it is possible to detect the start and end edges of the transmissions in the analyzed frame. With this information, it is possible to build windows of dynamic size.
- Each dynamic window (test window) represents a section of the spectrum that corresponds directly to a section of the test signal; i.e., to a section of the reconstructed signal from the coefficients. Each test window is compared with a threshold equal to 1. If the test window comparison matches the threshold, the SampEn will be directly applied to the original spectrum window. Otherwise, the SampEn will be applied to the reconstructed spectrum window.
- If the value of the SampEn is greater than 0.38, it means only noise is present in the analyzed window. If the value of the SampEn is lower, it is highly probable that there is a PU in the analyzed window. Finally, processing each frame of each connected SDR device, the occupation is obtained; i.e., the spectral location of the PU and the possible spectral gaps in which the SU could be placed. In Section 5.1, the choice of the decision threshold is justified.
4. Simulations and Real-Time Controlled Scenario
4.1. Simulation
4.2. Implementation of the Controlled Scenario
5. Results
5.1. Threshold Selection in the Decision Rule
5.2. Simulation Results
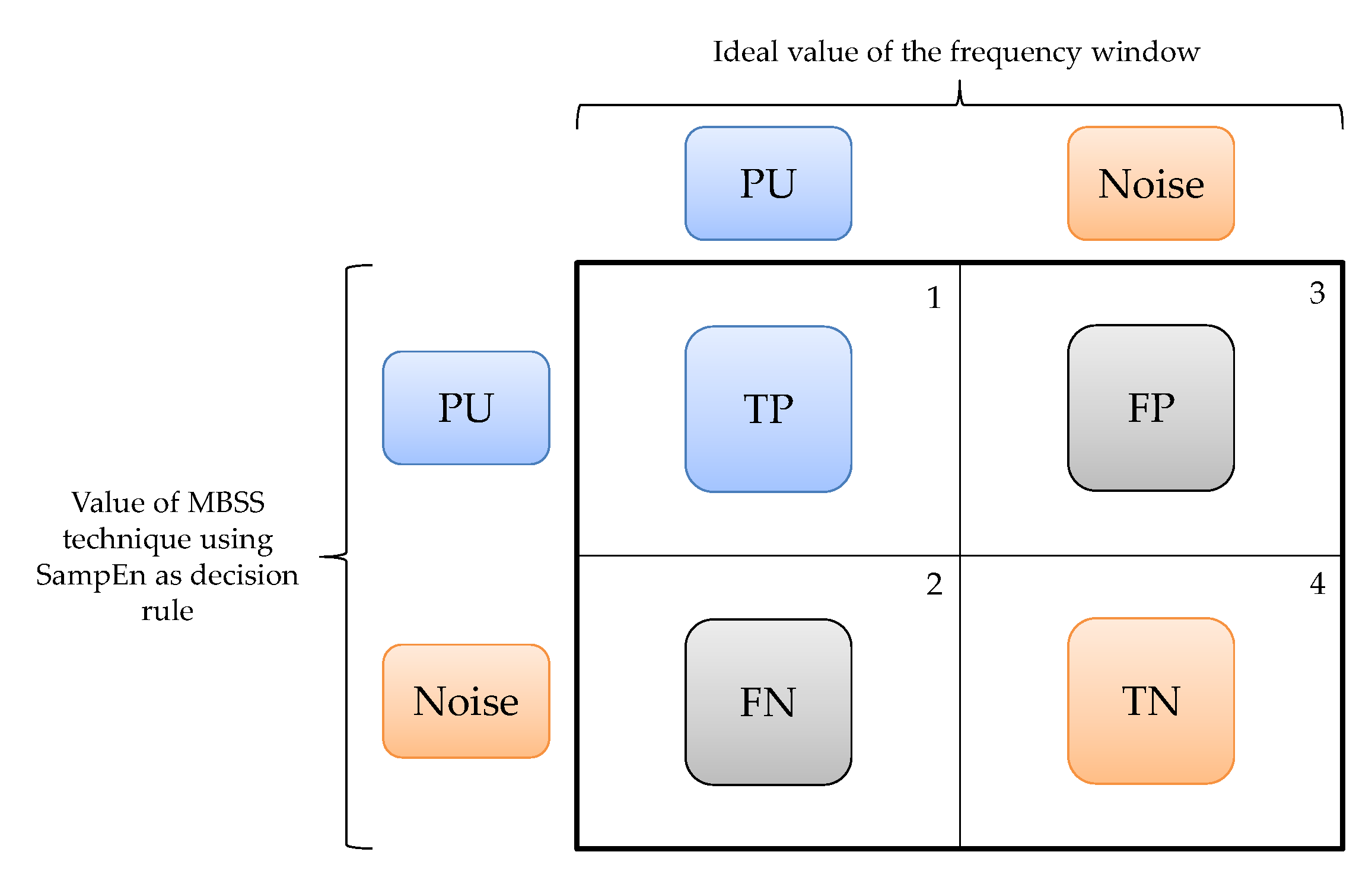
- A window that corresponds to a PU transmission and that SU classifies as a PU transmission is a true positive (TP) value.
- A frequency window that corresponds to a transmission of the PU and that SU classifies as noise is a false negative (FN) value.
- A window that corresponds to noise and that SU classifies as a PU transmission is a false positive (FP) value.
- A frequency window that corresponds to noise and that SU classifies as noise is a true negative (TN) value.
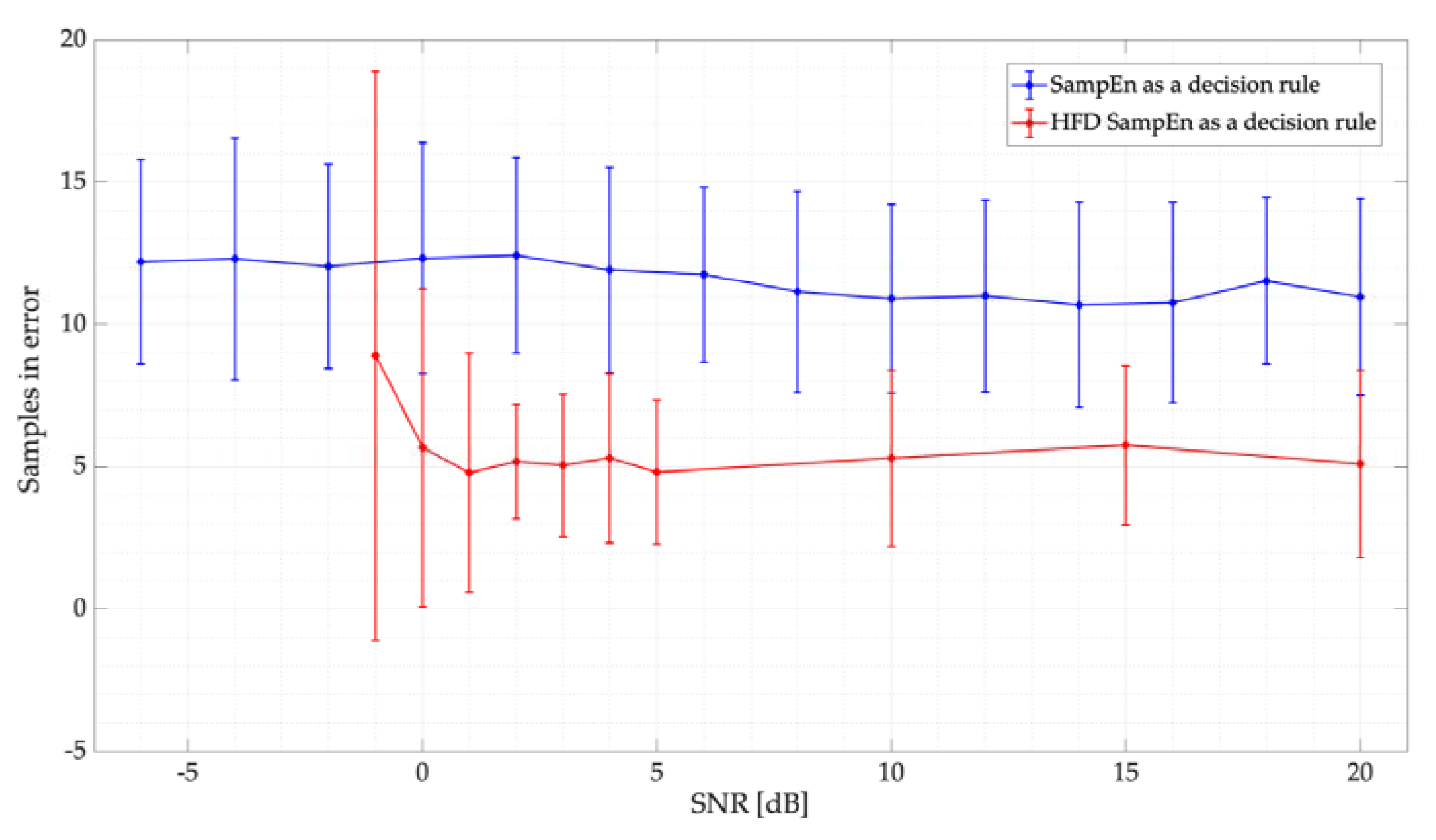
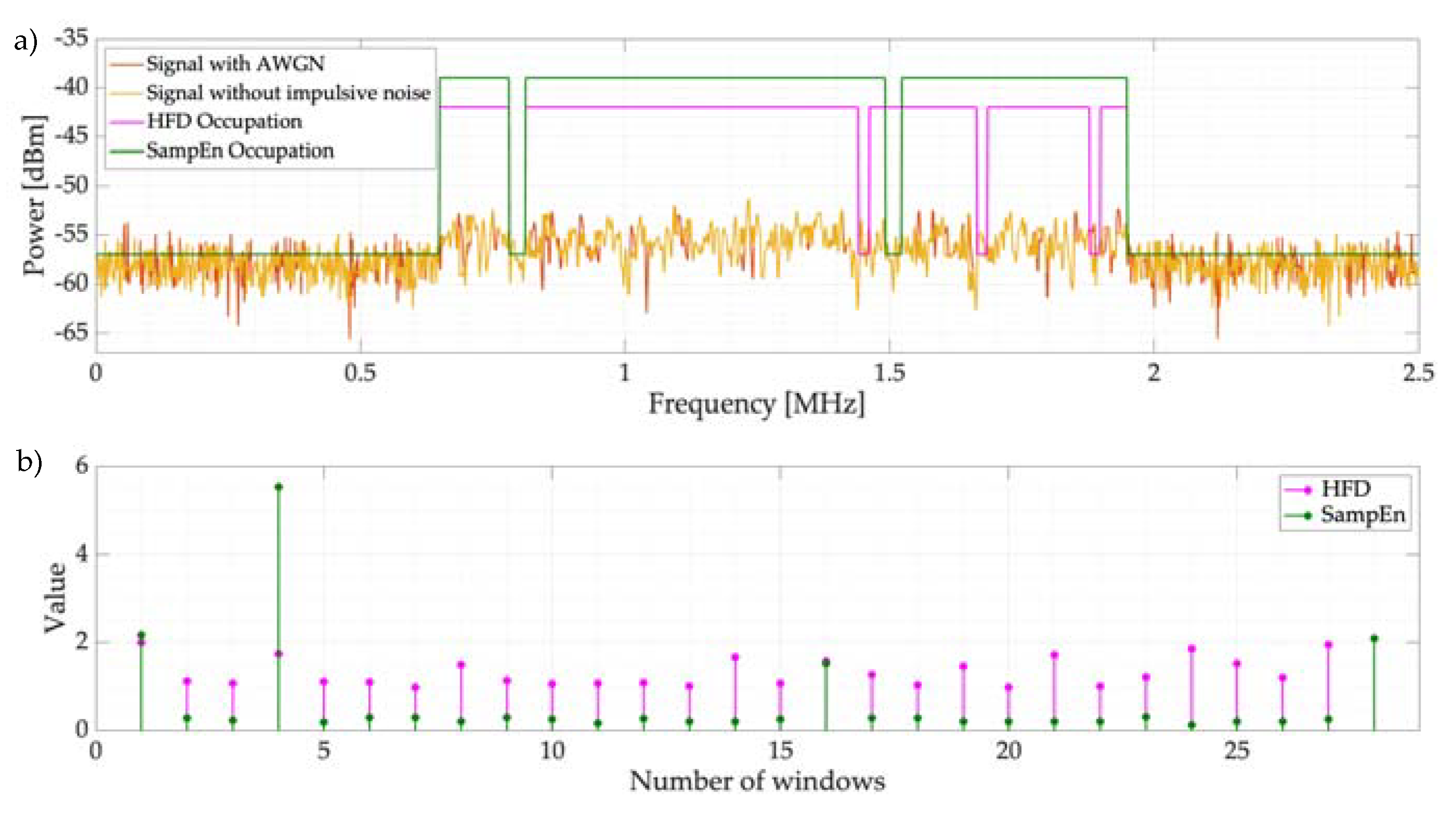
5.3. Results of the Controlled Scenario
6. Conclusions
- Experimental results for the detection of the primary users are consistent with the results of the simulated calculation, indicating that the proposed MBSS technique is correct and feasible to be considered for a real wireless communication environment. Power levels of the proposal are like those where spectrum sensing can be considered; for example, the case of coexistence between LTE-U and Wi-Fi [32].
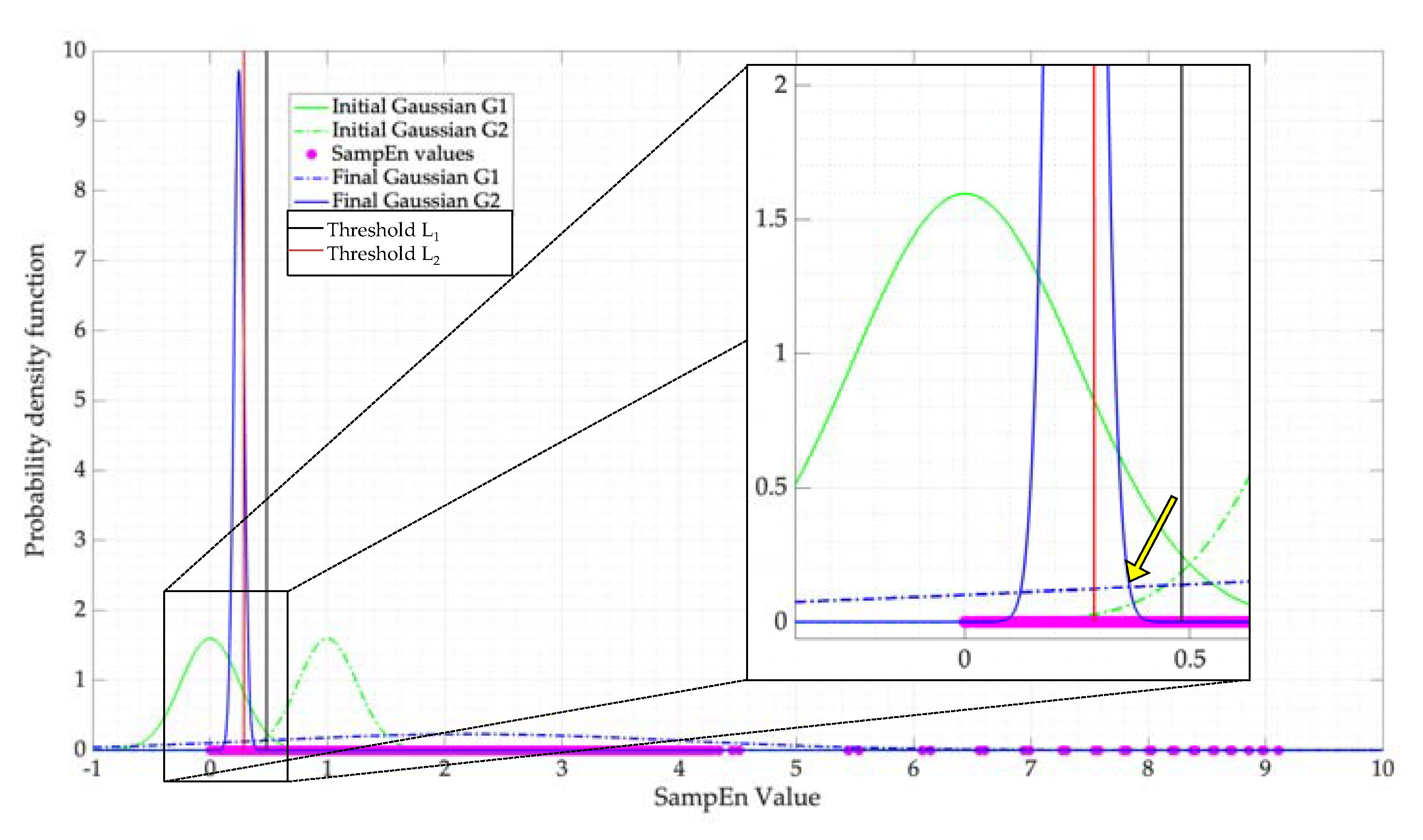
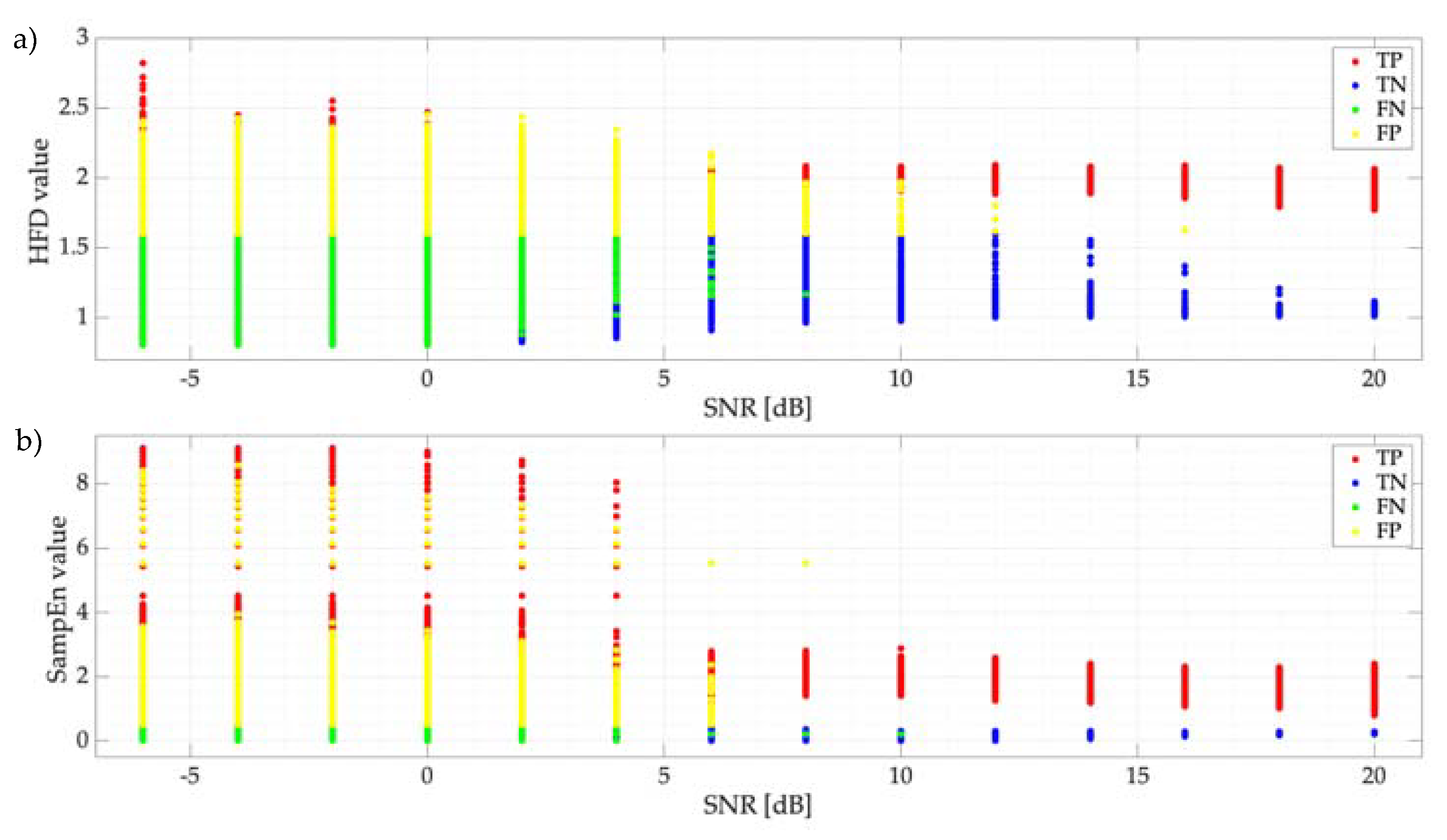
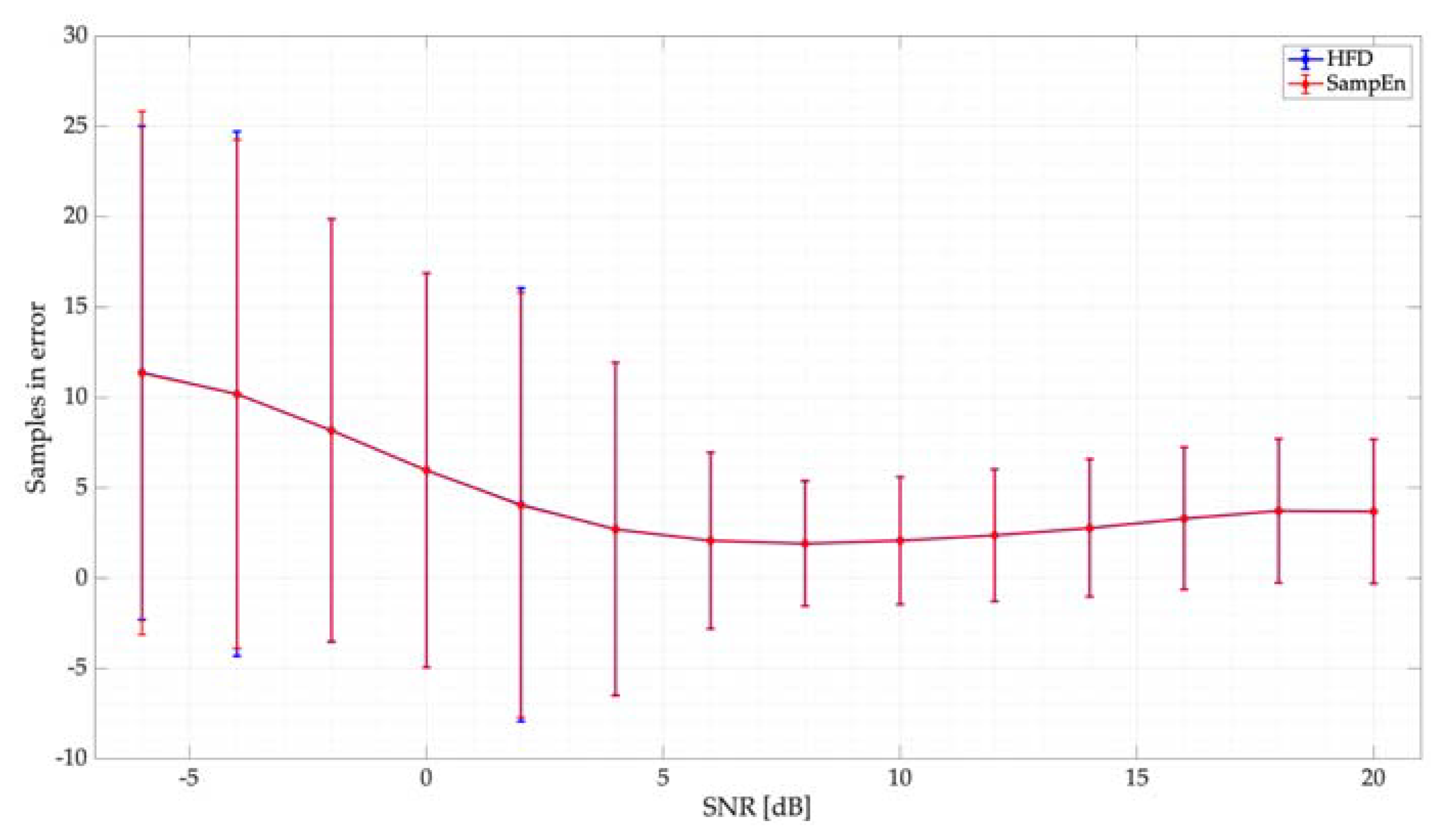
- It is difficult to give an interval in which the SampEn is located—this is because, in this investigation, the frames analyzed by the proposed technique are variable, and these can change depending on the SNR or the number of samples that the PSD contains. However, it is possible to observe (see Figure 9) that the SampEn value is between 0 and 9. These limits can be obtained with Equations (9) and (10). Nevertheless, the value obtained for these edges is not exact in a real environment since the number of samples of each analyzed window is variable. On the other hand, for an ideal environment in which the frame analyzed for both noise and a PU transmission is 512 samples, the lower limit is and the upper limit is . Besides, it is possible to observe from this same figure that the entropy always increases as the SNR decreases.
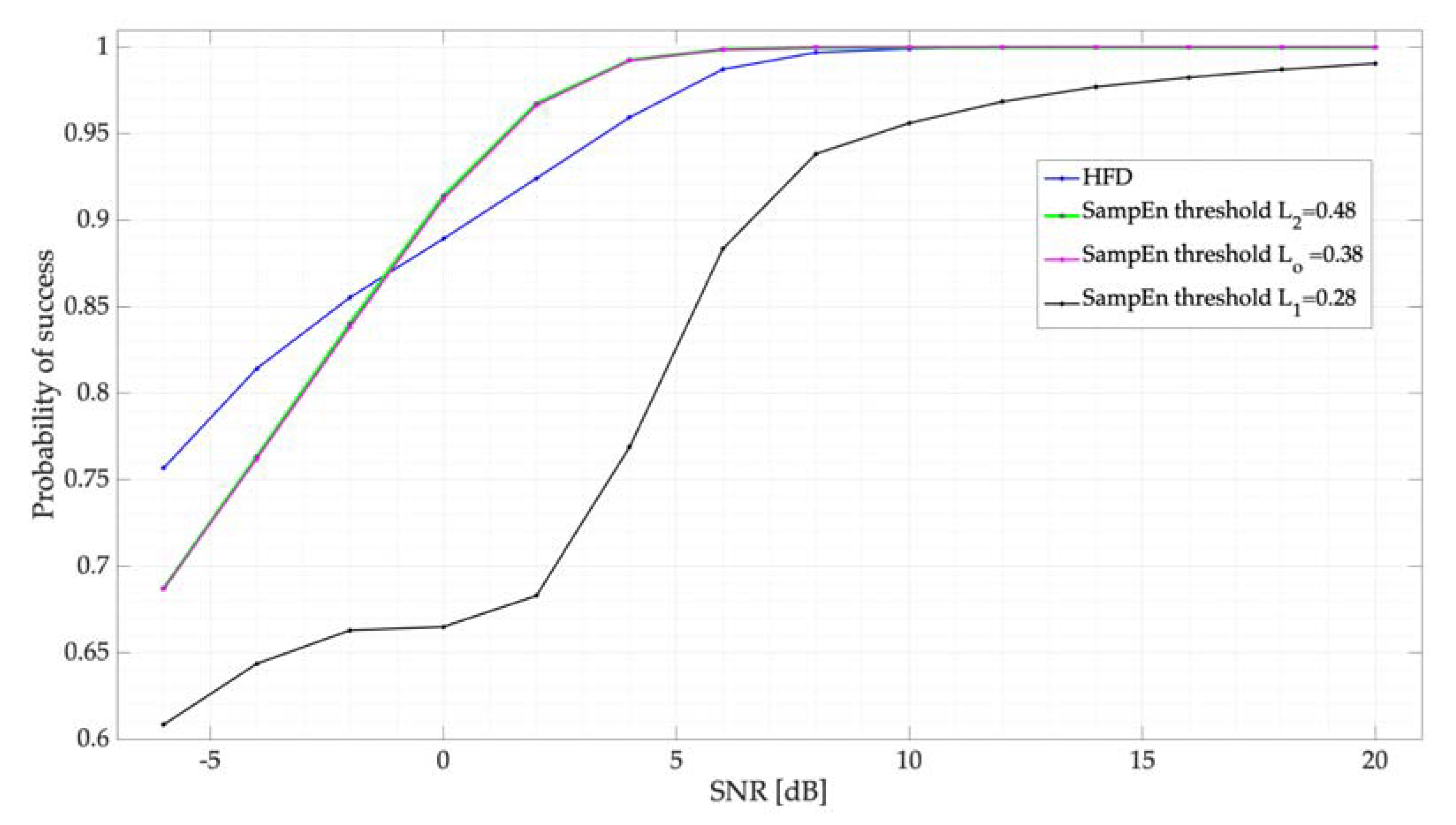
- Results of applying or as the threshold for the SampEn are practically the same. Hence, the question arises: what is the maximum value that the SampEn could take while permitting good performance to be obtained in terms of classifying the two possible states? It is possible to consider this topic as a future research perspective.
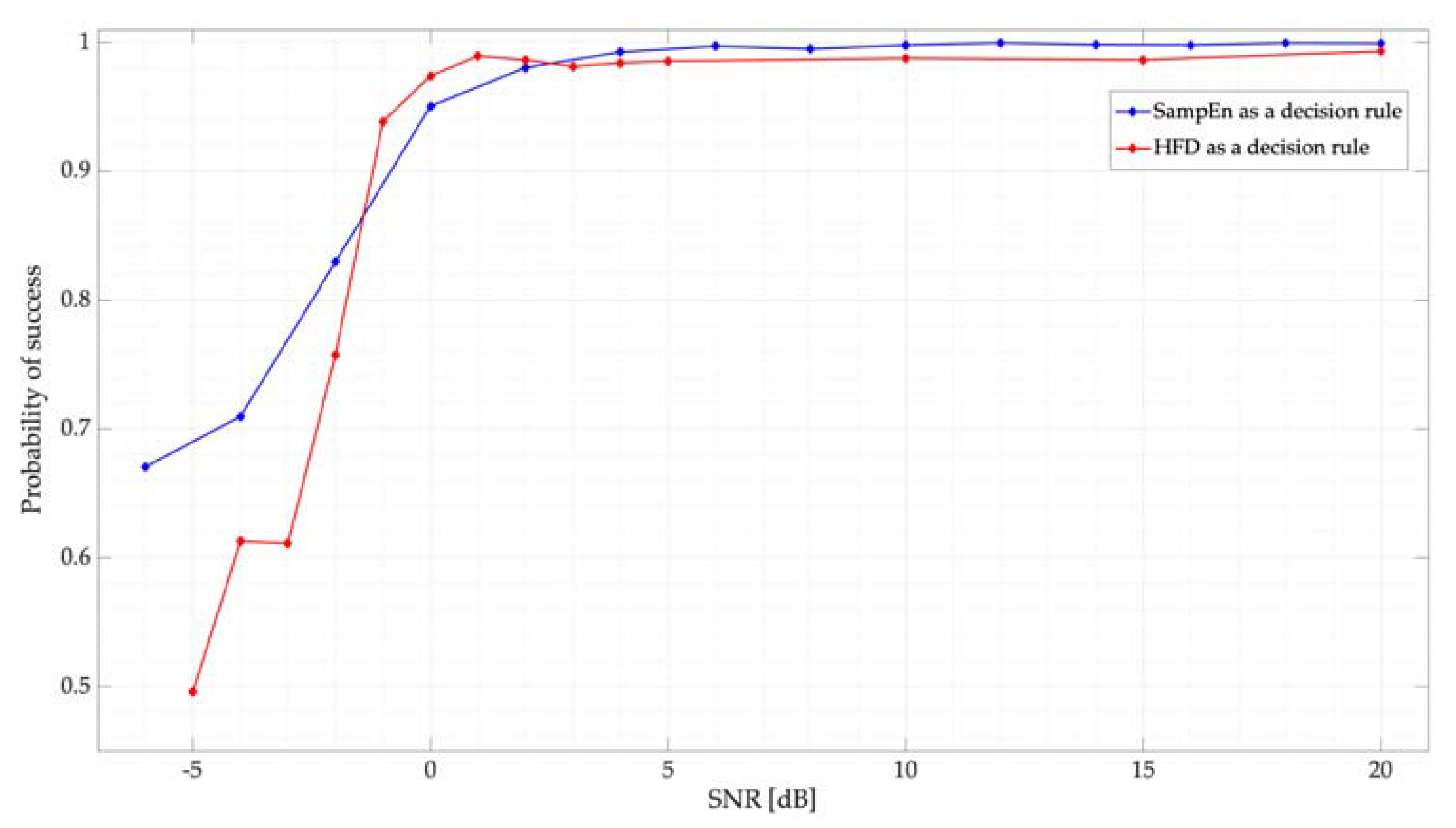
- Both decision rules, HFD and SampEn, are fast and feasible techniques to detect the presence of a PU in the spectrum. From Figure 12, it is possible to see that both techniques have excellent performance in scenarios with SNR values greater than 0 dB; however, for values less than 0 dB, SampEn has better performance. With this analysis, it is possible to affirm that both techniques, which measure the complexity of a signal, are accurate in detecting PUs in a multiband environment.
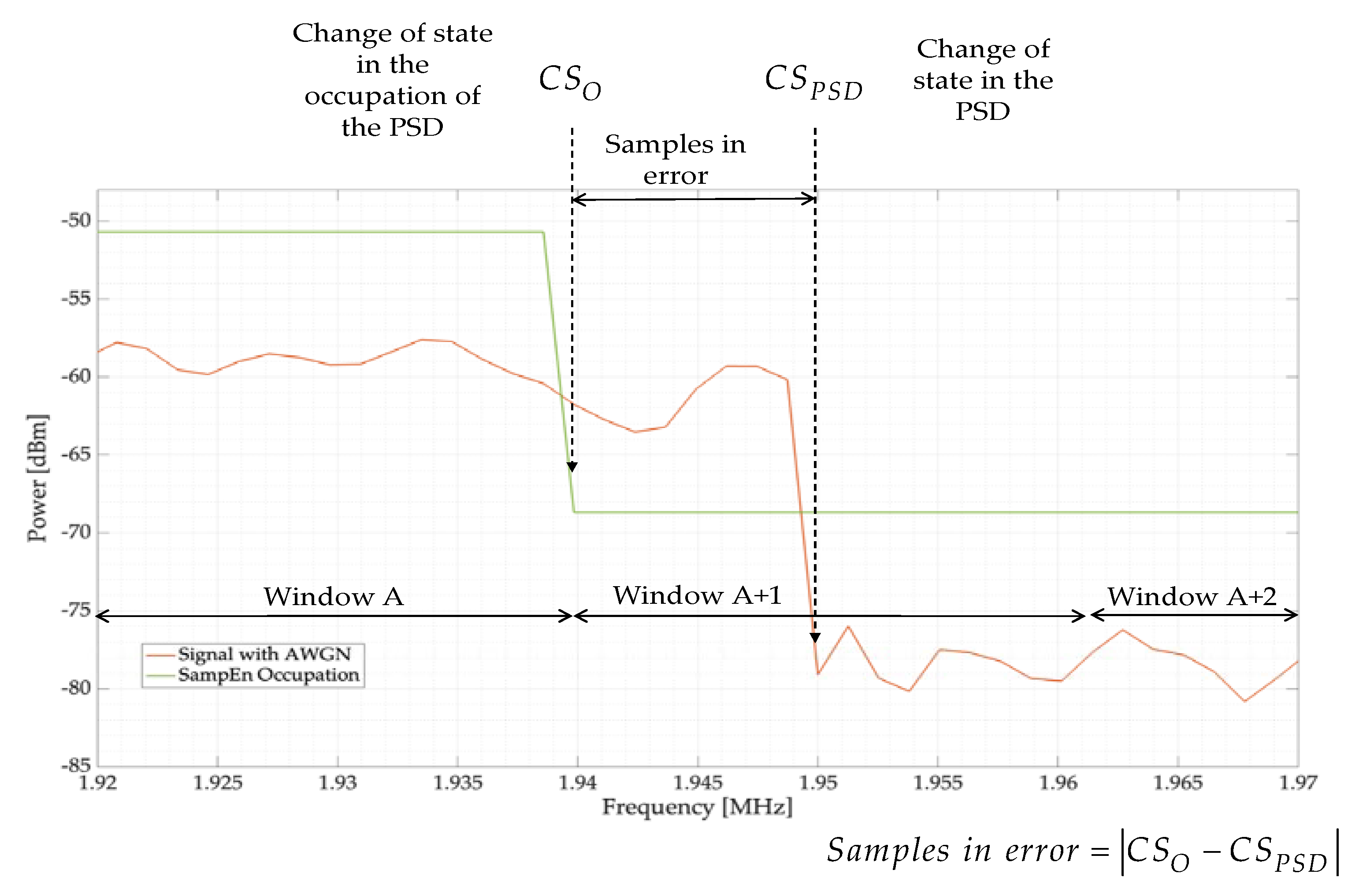
- Finally, with an average of 99% precision at detecting the PU, and with 12 samples (mean) showing errors in locating the start and end edges of a transmission, we can conclude that SampEn is a viable technique for the precision detection of PUs in a wide spectrum.
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CR | Cognitive radio |
| PU | Primary user |
| SU | Secondary user |
| SS | Spectrum sensing |
| MBSS | Multi-band spectrum sensing |
| SampEn | Sample entropy |
| MRA | Multiresolution analysis |
| HFD | Higuchi fractal dimension |
| SNR | Signal-to-noise ratio |
| ApEn | Approximate entropy |
| BispEn | Bispectral entropy |
| RenyiEn | Rényi entropy |
| PSD | Power spectral density |
| EM | Expectation maximization |
| Tx | Transmitters |
| Rx | Receivers |
| MSPS | Mega samples per second |
| TP | True positive |
| FN | False negative |
| FP | False positive |
| TN | True negative |
| OFDM | Orthogonal frequency division multiplexing |
| AWGN | Additive white Gaussian noise |
| PS | Probability of success |
References
- Mitola, J.; Maguire, G.Q. Cognitive radio: Making software radios more personal. IEEE Pers. Commun. 1999, 6, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Akyildiz, I.F.; Lee, W.-Y.; Vuran, M.C.; Mohanty, S. NeXt generation/dynamic spectrum access/cognitive radio wireless networks: A survey. Comput. Netw. 2006, 50, 2127–2159. [Google Scholar] [CrossRef]
- Masonta, M.T.; Mzyece, M.; Ntlatlapa, N. Spectrum Decision in Cognitive Radio Networks: A Survey. IEEE Commun. Surv. Tutor. 2013, 15, 1088–1107. [Google Scholar] [CrossRef] [Green Version]
- Hattab, G.; Ibnkahla, M. Multiband Spectrum Sensing: Challenges and Limitations. arXiv 2014, arXiv:1409.6394. [Google Scholar]
- Arjoune, Y.; Kaabouch, N. A Comprehensive Survey on Spectrum Sensing in Cognitive Radio Networks: Recent Advances, New Challenges, and Future Research Directions. Sensors 2019, 19, 126. [Google Scholar] [CrossRef] [Green Version]
- Molina-Tenorio, Y.; Prieto-Guerrero, A.; Aguilar-Gonzalez, R.; Ruiz-Boqué, S. Machine Learning Techniques Applied to Multiband Spectrum Sensing in Cognitive Radios. Sensors 2019, 19, 4715. [Google Scholar] [CrossRef] [Green Version]
- Molina-Tenorio, Y.; Prieto-Guerrero, A.; Aguilar-Gonzalez, R. Real-Time Implementation of Multiband Spectrum Sensing Using SDR Technology. Sensors 2021, 21, 3506. [Google Scholar] [CrossRef]
- Welvaert, M.; Rosseel, Y. On the Definition of Signal-To-Noise Ratio and Contrast-To-Noise Ratio for fMRI Data. PLoS ONE 2013, 8, e77089. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Ma, J.; Faust, O. A Comparative Study of Different Entropies for Spectrum Sensing Techniques. Wirel. Pers. Commun. 2013, 69, 1719–1733. [Google Scholar] [CrossRef]
- Chen, X.; Nagaraj, S. Entropy based spectrum sensing in cognitive radio. In Proceedings of the 2008 Wireless Telecomunications Symposium, Pomona, CA, USA, 24–26 April 2008; pp. 57–61. [Google Scholar]
- Nagaraj, S.V. Entropy-based spectrum sensing in cognitive radio. Signal Process. 2009, 89, 174–180. [Google Scholar] [CrossRef]
- Li, H.; Hu, Y.; Wang, S. A Novel Blind Signal Detector Based on the Entropy of the Power Spectrum Subband Energy Ratio. Entropy 2021, 23, 448. [Google Scholar] [CrossRef] [PubMed]
- Cadena Muñoz, E.; Pedraza Martínez, L.F.; Hernandez, C.A. Rényi Entropy-Based Spectrum Sensing in Mobile Cognitive Radio Networks Using Software Defined Radio. Entropy 2020, 22, 626. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chon, K.H.; Scully, C.G.; Lu, S. Approximate entropy for all signals. IEEE Eng. Med. Biol. Mag. 2009, 28, 18–23. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [Green Version]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Selva, A.F.B.; Reis, A.L.G.; Lenzi, K.G.; Meloni, L.G.P.; Barbin, S.E. Introduction to the Software-defined Radio Approach. IEEE Lat. Am. Trans. 2012, 10, 6. [Google Scholar]
- Daneshgaran, F.; Laddomada, M. Transceiver front-end technology for software radio implementation of wideband satellite communication systems. Wirel. Pers. Commun. 2003, 24, 99–121. [Google Scholar] [CrossRef]
- Ulversoy, T. Software Defined Radio: Challenges and Opportunities. IEEE Commun. Surv. Tutor. 2010, 12, 531–550. [Google Scholar] [CrossRef] [Green Version]
- Nastase, C.-V.; Martian, A.; Vladeanu, C.; Marghescu, I. Spectrum Sensing Based on Energy Detection Algorithms Using GNU Radio and USRP for Cognitive Radio. In Proceedings of the 2018 International Conference on Communications (COMM), Bucharest, Romania, 14–16 June 2018; pp. 381–384. [Google Scholar]
- Chamran, M.K.; Yau, K.-L.A.; Noor, R.M.D.; Wong, R. A Distributed Testbed for 5G Scenarios: An Experimental Study. Sensors 2019, 20, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LimeSDR Mini Is a $135 Open Source Hardware, Full Duplex USB SDR Board (Crowdfunding). Available online: https://www.cnx-software.com/2017/09/18/limesdr-mini-is-a-135-open-source-hardware-full-duplex-usb-sdr-board-crowdfunding/ (accessed on 12 March 2022).
- HackRF One—Great Scott Gadgets. Available online: https://greatscottgadgets.com/hackrf/one/ (accessed on 12 March 2022).
- Nooelec—Nooelec NESDR SMArt v4 SDR—Premium RTL-SDR w/Aluminum Enclosure, 0.5PPM TCXO, SMA Input. RTL2832U & R820T2-Based—Software Defined Radio. Available online: https://www.nooelec.com/store/sdr/nesdr-smart-sdr.html (accessed on 12 March 2022).
- LimeSDR Mini. Available online: https://limemicro.com/products/boards/limesdr-mini/ (accessed on 12 March 2022).
- Cuadro Nacional de Atribución de Frecuencias (CNAF)|Cuadro Nacional de Atribución de Frecuencias (CNAF)—IFT. Available online: http://cnaf.ift.org.mx/ (accessed on 12 March 2022).
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Sathya, V.; Mehrnoush, M.; Roy, S. Wi-Fi/LTE-U Coexistence: Real-Tome Issues and Solutions. IEEE Access 2020, 8, 9221–9234. [Google Scholar] [CrossRef]


| Software | MATLAB 2019 |
|---|---|
| SNR values | −6 to 20 dB spaced by 2 dB |
| Number of frames per each SNR value | 10,000 |
| Samples per frame | 743 |
| Number of symbols per frame | One symbol, OFDM |
| Device | HackRF One [27] | RTL-SDR [28] | LimeSDR Mini [29] |
|---|---|---|---|
| Frequency range | [1 MHz–6 GHz] | [22 MHz–2.2 GHz] | [10 MHz–3.5 GHz] |
| RF bandwidth | 20 MHz | 3.2 MHz | 30.72 MHz |
| Sample depth | 8 bit | 8 bit | 12 bit |
| Sample rate | 20 MSPS | 3.2 MSPS | 30.72 MSPS |
| Tx channels | 1 | 0 | 1 |
| Rx channels | 1 | 1 | 1 |
| Duplex | Half | - | Full |
| Transmit power | −10 dBm + (15 dBm @ 2.4 GHz) | - | Max 10 dBm (depending on frequency) |
| Tx/Rx | SU1 | SU2 | SU3 | PU1 | PU2 |
|---|---|---|---|---|---|
| Device | HackRF One | RTL-SDR 0005 | RTL-SDR 0002 | LimeSDR Mini | Cell phone call |
| Tx Frequency (MHz) | - | - | - | 847.8 | 842.5 |
| Type of transmission | - | - | - | OFDM | CDMA [30] |
| Tx Bandwidth (MHz) | - | - | - | 1 | 5 |
| Rx Frequency (MHz) | 835 | 846.2 | 848.6 | - | - |
| Rx Bandwidth (MHz) | 20 | 2.4 | 2.4 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina-Tenorio, Y.; Prieto-Guerrero, A.; Aguilar-Gonzalez, R. Multiband Spectrum Sensing Based on the Sample Entropy. Entropy 2022, 24, 411. https://doi.org/10.3390/e24030411
Molina-Tenorio Y, Prieto-Guerrero A, Aguilar-Gonzalez R. Multiband Spectrum Sensing Based on the Sample Entropy. Entropy. 2022; 24(3):411. https://doi.org/10.3390/e24030411
Chicago/Turabian StyleMolina-Tenorio, Yanqueleth, Alfonso Prieto-Guerrero, and Rafael Aguilar-Gonzalez. 2022. "Multiband Spectrum Sensing Based on the Sample Entropy" Entropy 24, no. 3: 411. https://doi.org/10.3390/e24030411
APA StyleMolina-Tenorio, Y., Prieto-Guerrero, A., & Aguilar-Gonzalez, R. (2022). Multiband Spectrum Sensing Based on the Sample Entropy. Entropy, 24(3), 411. https://doi.org/10.3390/e24030411






