Equilibration and “Thermalization” in the Adapted Caldeira–Leggett Model
Abstract
:1. Introduction
2. ACL Model
3. Basic Equilibration and Dephasing
4. Equilibration without “Thermalization”
5. Varying the Coupling Strength
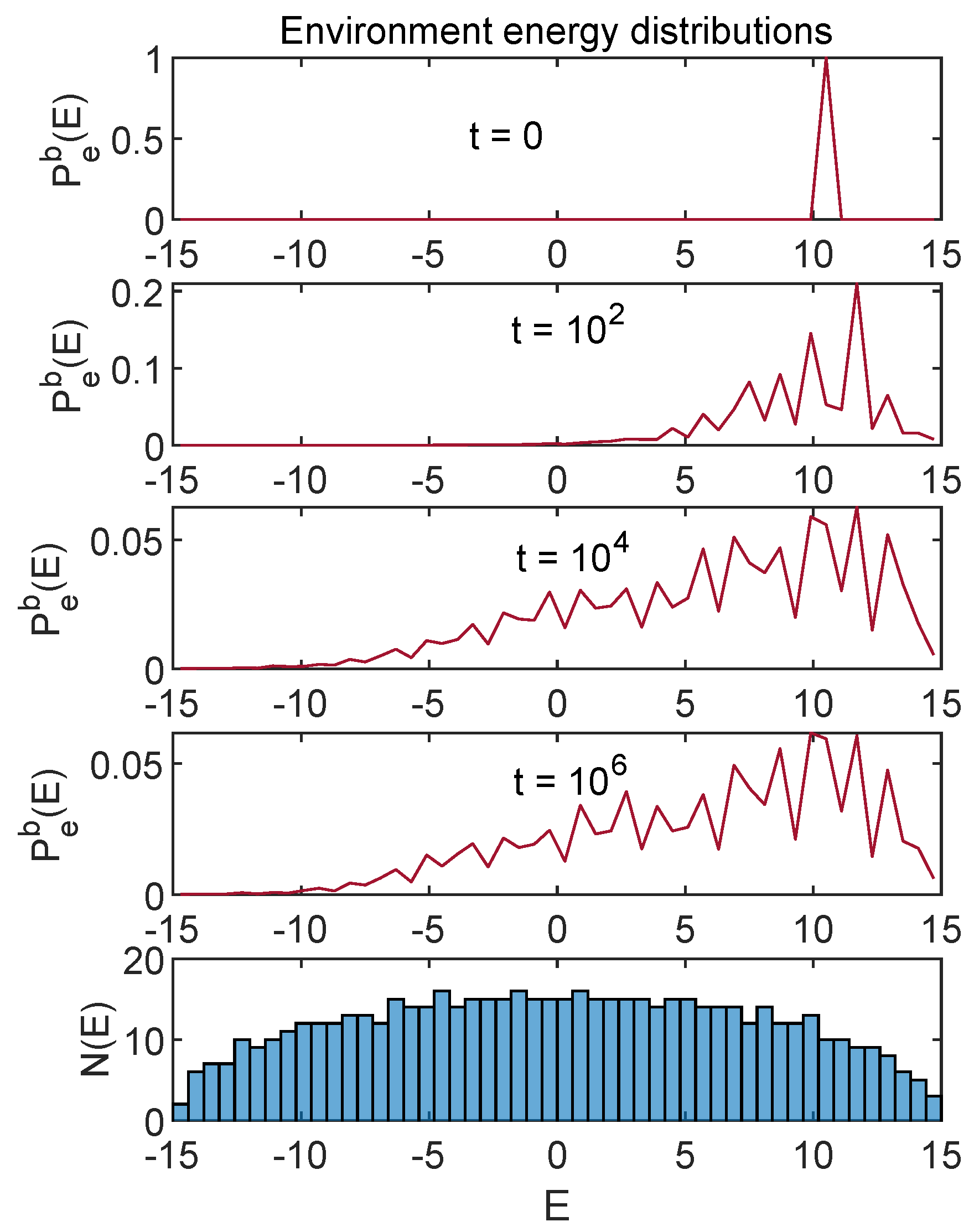
6. Energy Distributions
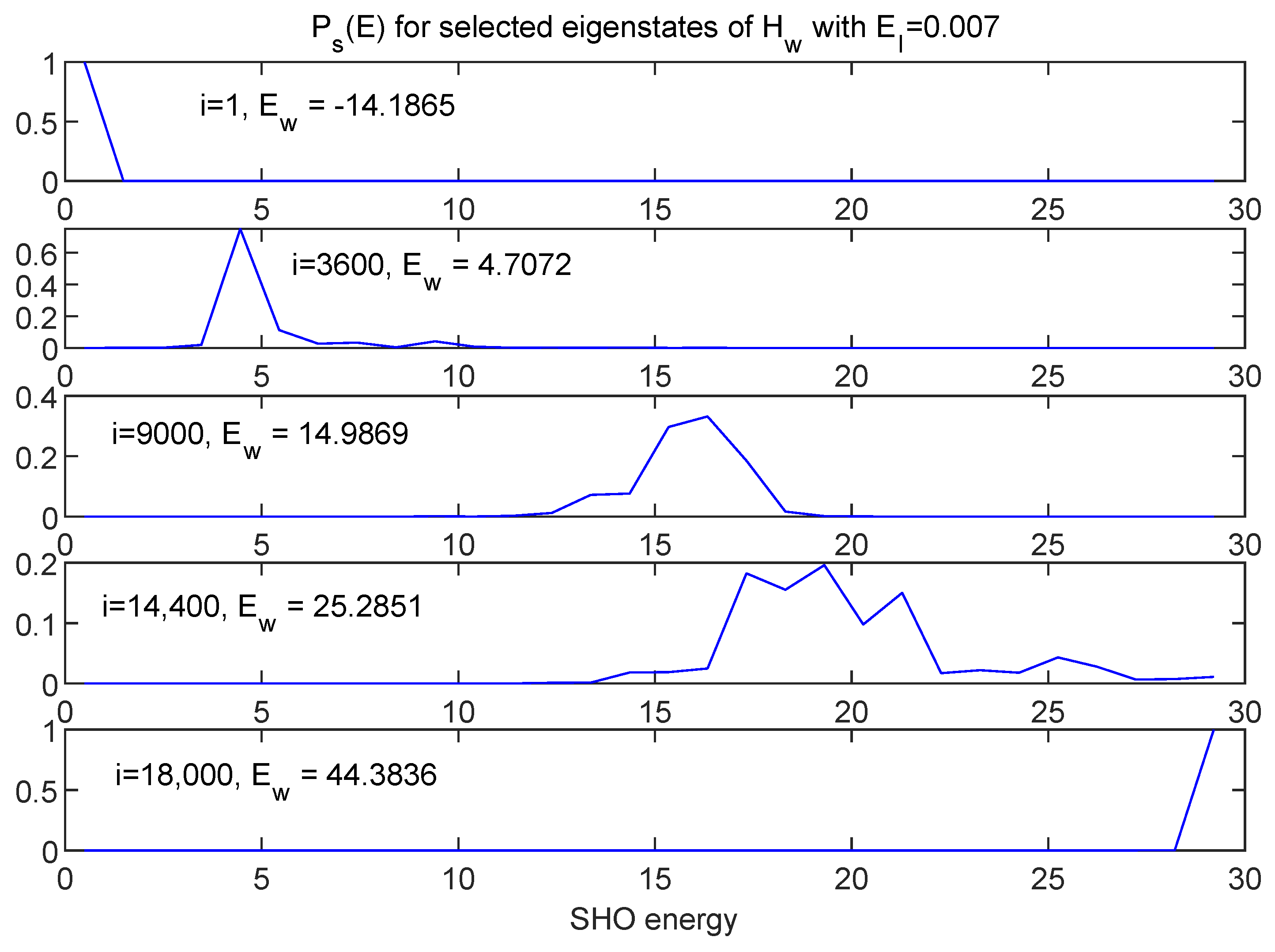
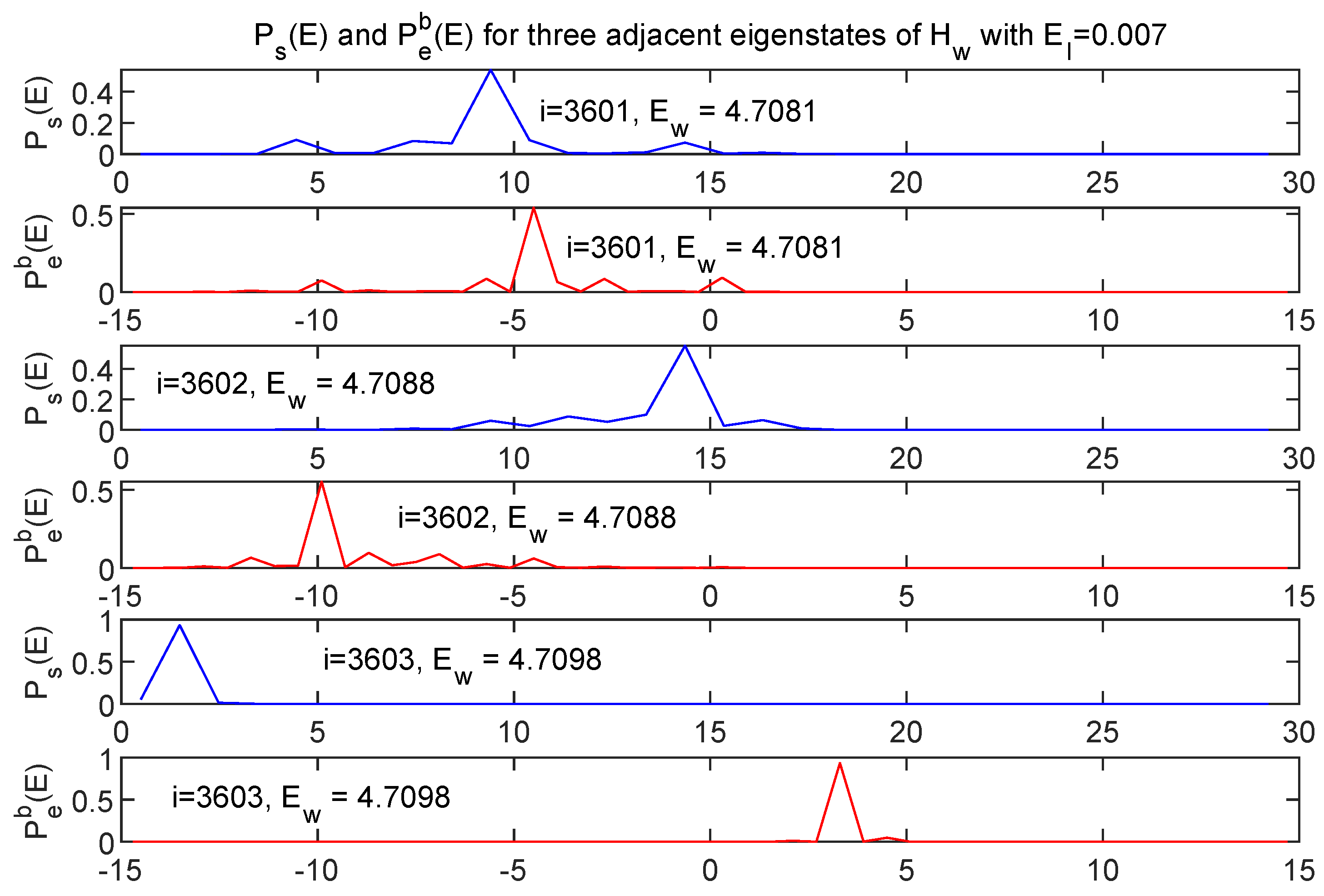
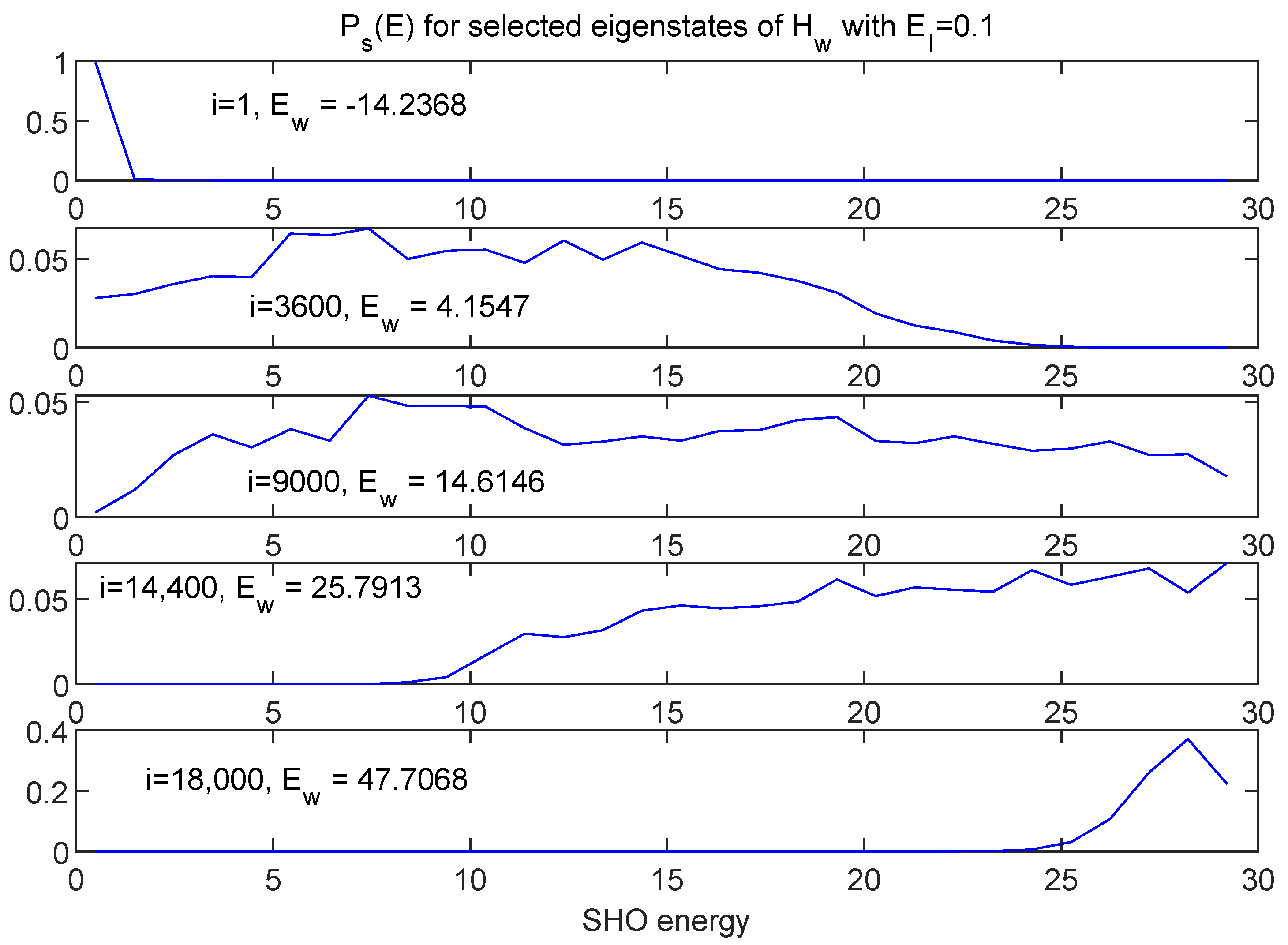
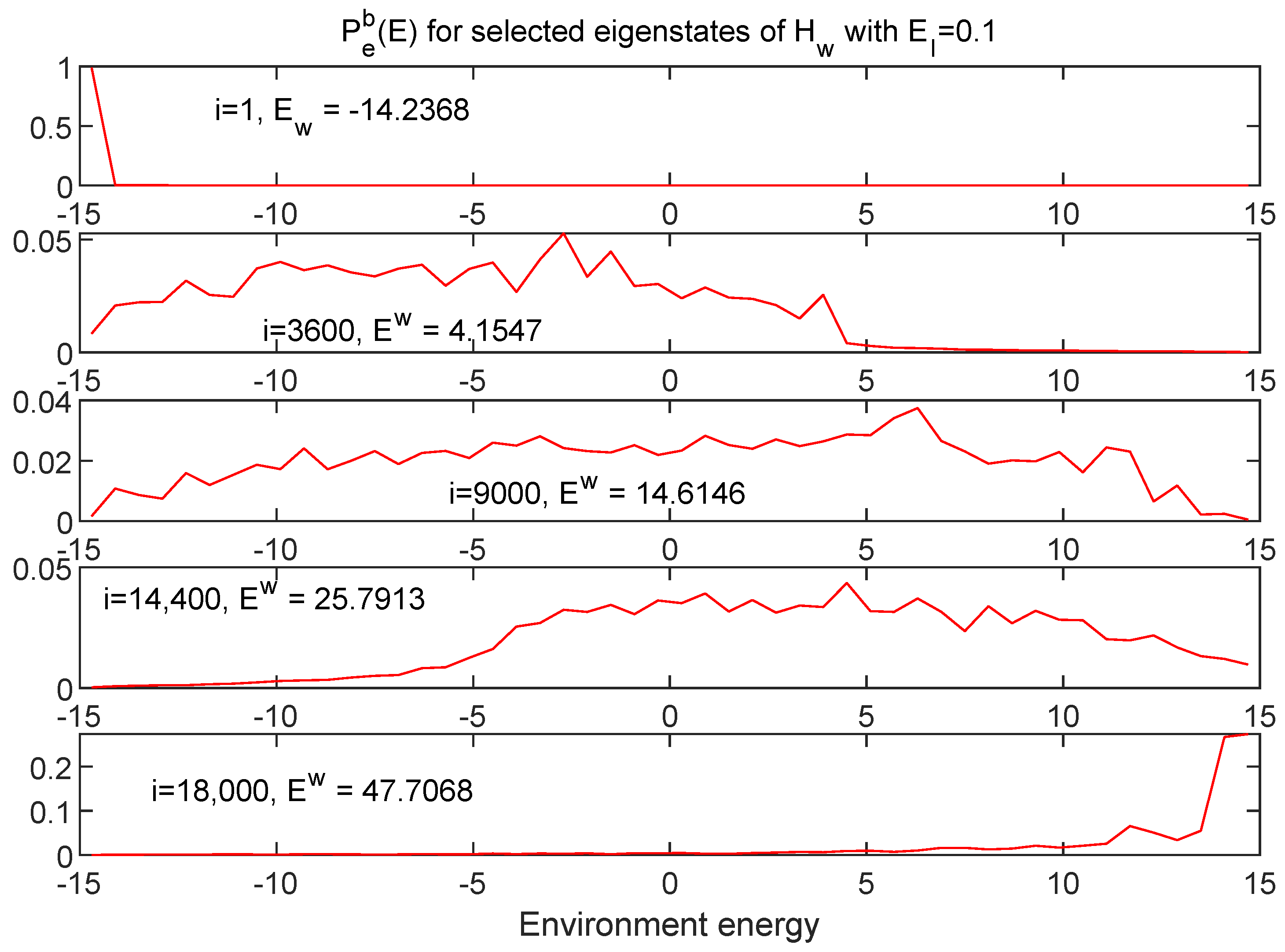
7. The Eigenstates
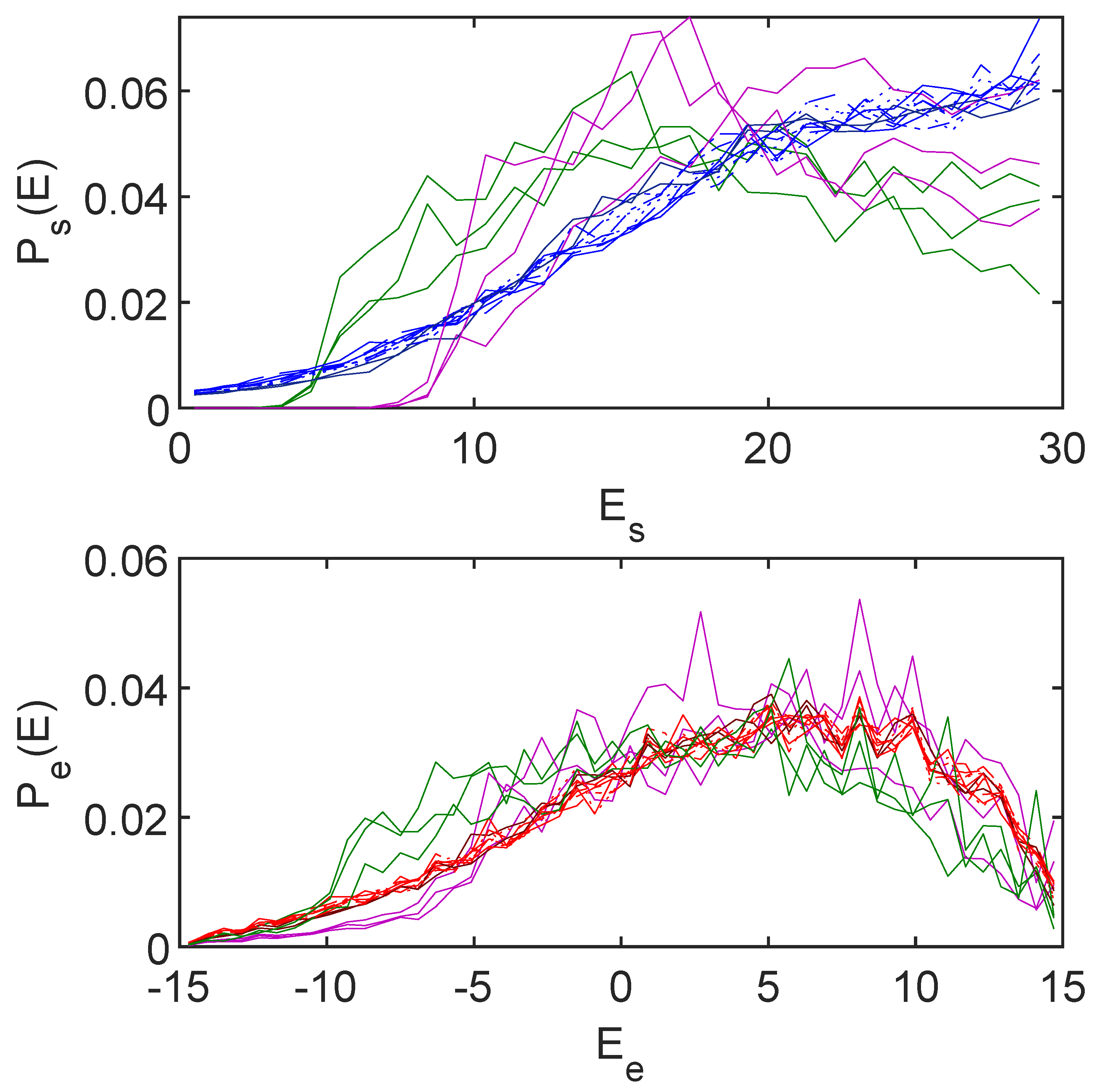
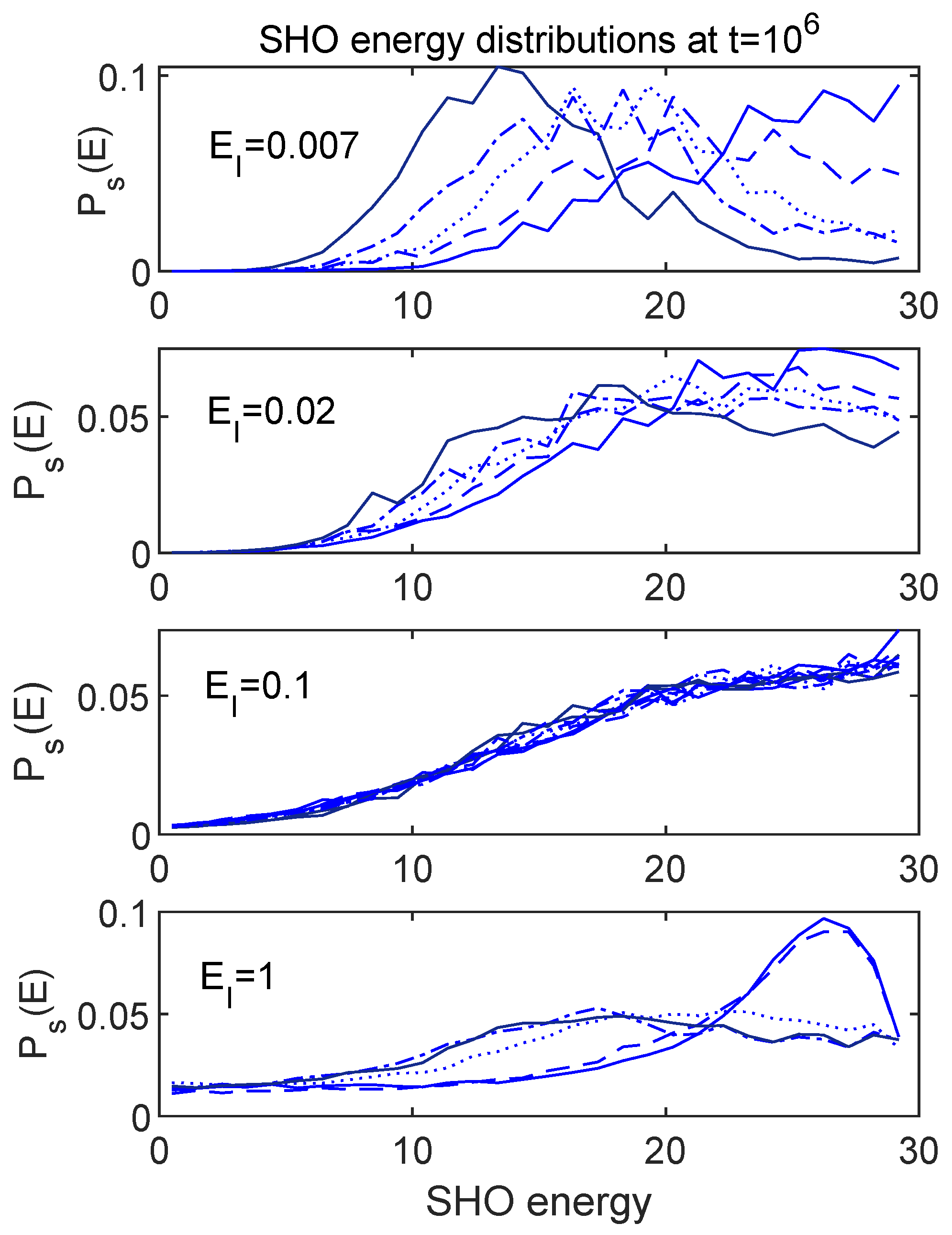
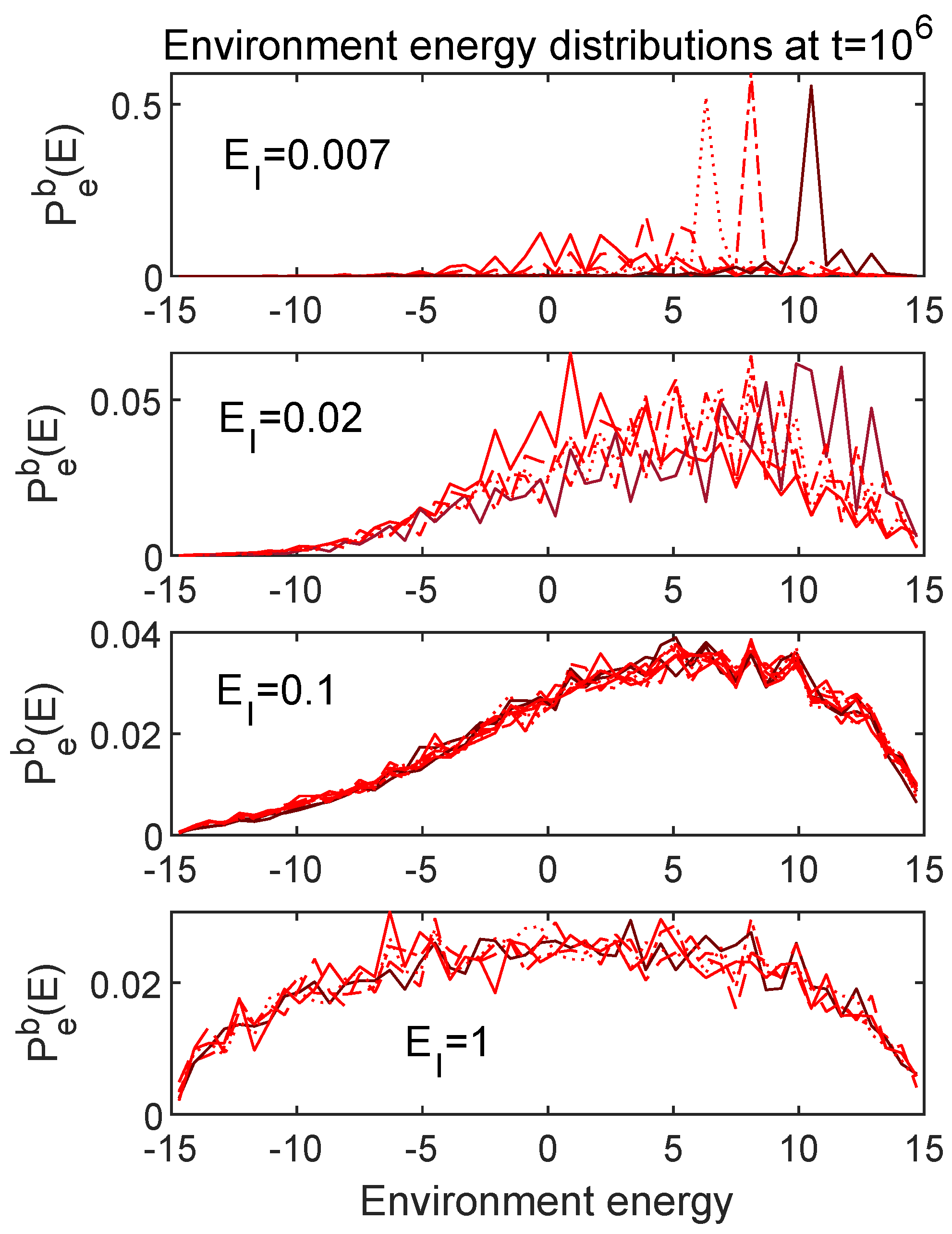
7.1. Energy Distributions in the Subspaces
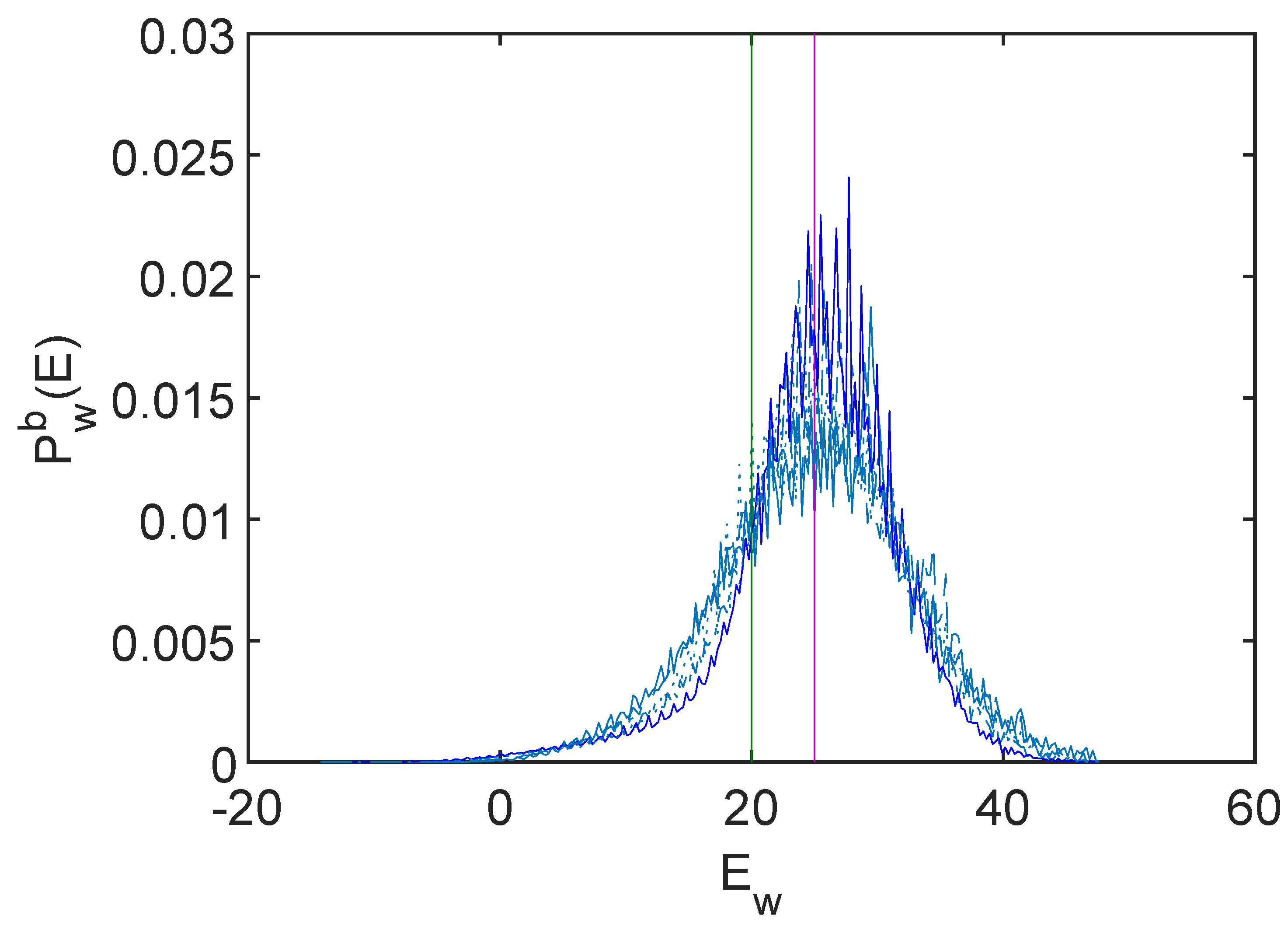
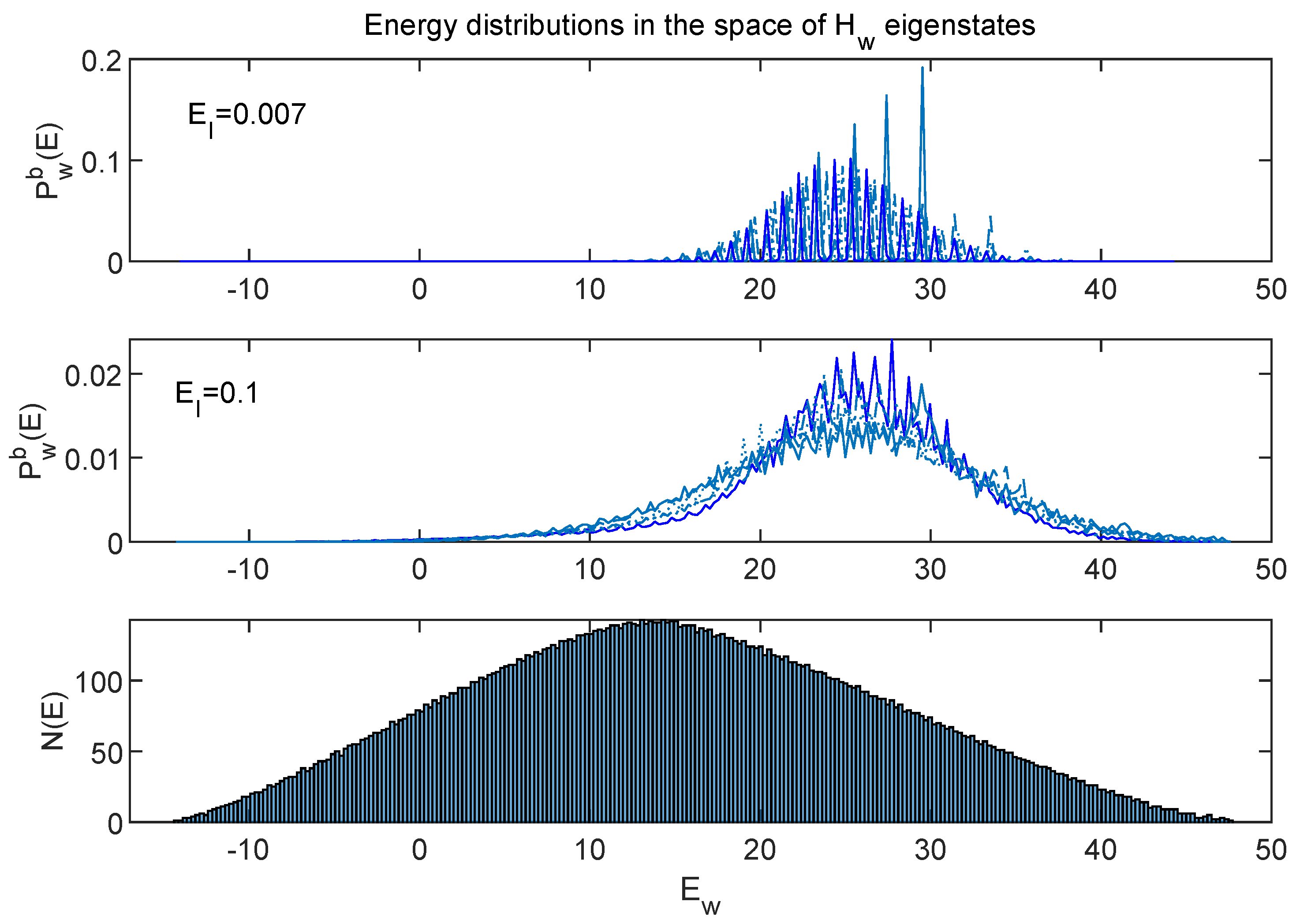
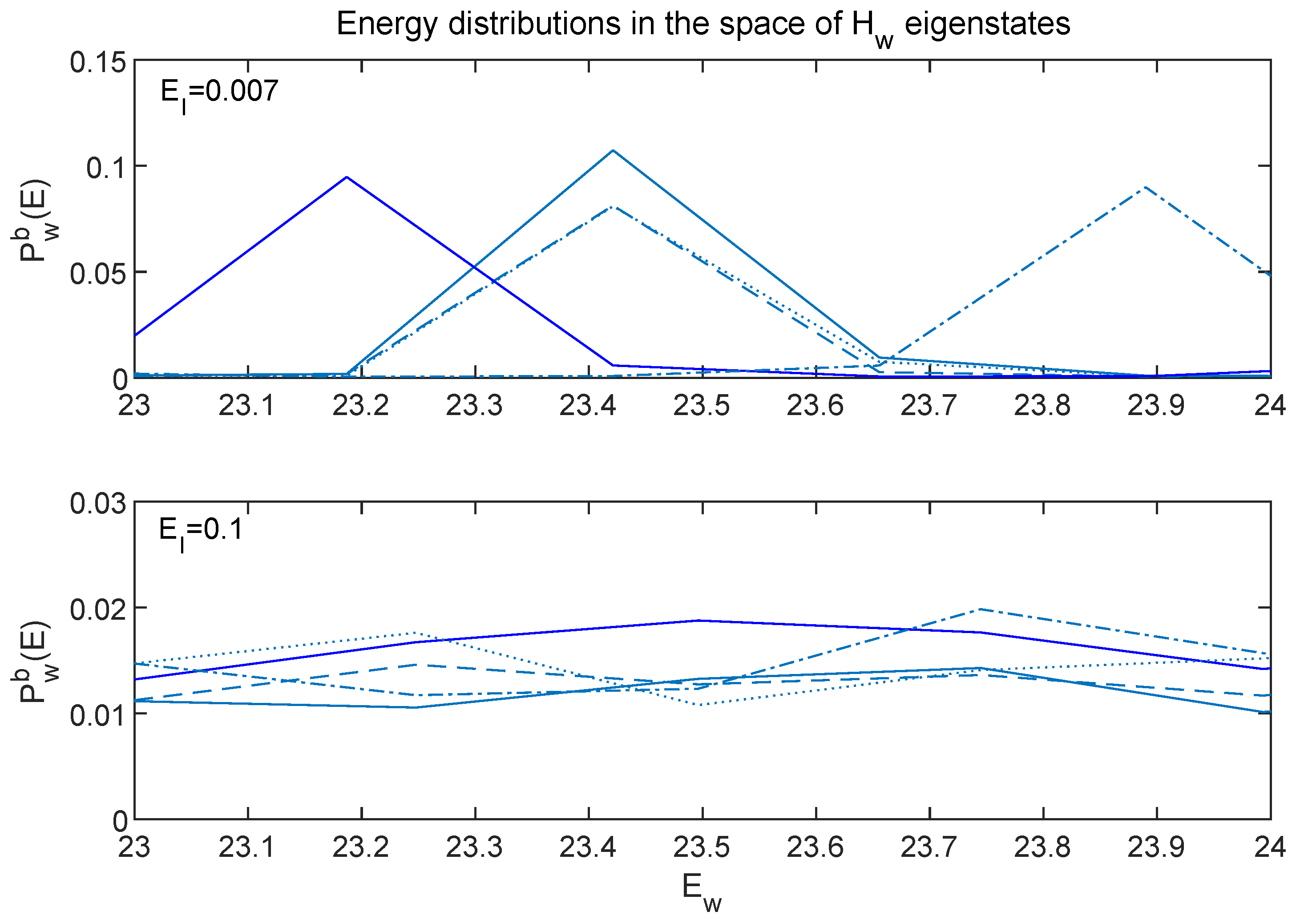
7.2. Energy Distributions in the Global Space w
7.3. Interpretation
7.4. The Effective Dimension as a Diagnostic
8. Tuning of States and Parameters
9. Discussion and Conclusions
10. Reflections
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Initial Conditions
Appendix B. Dephasing, Decoherence and Dissipation
Appendix C. Eigenstate Thermalization Hypothesis
References
- Albrecht, A.; Baunach, R.; Arrasmith, A. Adapted Caldeira–Leggett Model. arXiv 2021, arXiv:2105.14040. [Google Scholar]
- Albrecht, A.; Baunach, R.; Arrasmith, A. Einselection, Equilibrium and Cosmology. arXiv 2021, arXiv:2105.14017. [Google Scholar]
- Zurek, W.H.; Habib, S.; Paz, J.P. Coherent states via decoherence. Phys. Rev. Lett. 1993, 70, 1187–1190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baunach, R.; Albrecht, A.; Arrasmith, A. Copycat process in the early stages of einselection. arXiv 2021, arXiv:2105.14032. [Google Scholar]
- Albrecht, A.; Iglesias, A. The Clock ambiguity and the emergence of physical laws. Phys. Rev. D 2008, 77, 063506. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, A.; Iglesias, A. Lorentz symmetric dispersion relation from a random Hamiltonian. Phys. Rev. D 2015, 91, 043529. [Google Scholar] [CrossRef] [Green Version]
- Binder, F.; Correa, L.; Gogolin, C.; Anders, J.; Adesso, G. Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Fundamental Theories of Physics; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Lloyd, S. Excuse our ignorance. Nat. Phys. 2006, 2, 727–728. [Google Scholar] [CrossRef]
- Cucchietti, F.M.; Paz, J.P.; Zurek, W.H. Decoherence from spin environments. Phys. Rev. A 2005, 72, 052113. [Google Scholar] [CrossRef] [Green Version]
- Zurek, W.H.; Cucchietti, F.M.; Paz, J.P. Gaussian Decoherence and Gaussian Echo from Spin Environments. arXiv 2006, arXiv:quant-ph/quant-ph/0611200. [Google Scholar]
- Nandkishore, R.; Huse, D.A. Many-Body Localization and Thermalization in Quantum Statistical Mechanics. Annu. Rev. Condens. Matter Phys. 2015, 6, 15–38. [Google Scholar] [CrossRef] [Green Version]
- Popescu, S.; Short, A.J.; Winter, A. Entanglement and the foundations of statistical mechanics. Nat. Phys. 2006, 2, 754–758. [Google Scholar] [CrossRef] [Green Version]
- Rigol, M.; Dunjko, V.; Yurovsky, V.; Olshanii, M. Relaxation in a Completely Integrable Many-Body Quantum System: An Ab Initio Study of the Dynamics of the Highly Excited States of 1D Lattice Hard-Core Bosons. Phys. Rev. Lett. 2007, 98, 050405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lenard, A. Thermodynamical proof of the Gibbs formula for elementary quantum systems. J. Stat. Phys. 1978, 19, 575–586. [Google Scholar] [CrossRef]
- Ikeda, T.N.; Watanabe, Y.; Ueda, M. Eigenstate randomization hypothesis: Why does the long-time average equal the microcanonical average? Phys. Rev. E 2011, 84, 021130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paz, J.P.; Zurek, W.H. Quantum limit of decoherence: Environment induced superselection of energy eigenstates. Phys. Rev. Lett. 1999, 82, 5181–5185. [Google Scholar] [CrossRef] [Green Version]
- Serbyn, M.; Papić, Z.; Abanin, D.A. Local Conservation Laws and the Structure of the Many-Body Localized States. Phys. Rev. Lett. 2013, 111, 127201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Penrose, R. Singularities and time-asymmetry. In General Relativity; An Einstein Centenary Survey; University of Oxford: Oxford, UK, 1979. [Google Scholar]
- Rauch, H.; Suda, M.; Pascazio, S. Decoherence, dephasing and depolarization. Phys. Condens. Matter 1999, 267–268, 277–284. [Google Scholar] [CrossRef]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef] [Green Version]




| % of | |||
|---|---|---|---|
| 1 | 0.087 | 30% | 27% |
| 0.1 | 0.24 | 8% | 100% |
| 0.02 | 0.06 | 33% | 25% |
| 0.007 | 0.004 | 70% | 1.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albrecht, A. Equilibration and “Thermalization” in the Adapted Caldeira–Leggett Model. Entropy 2022, 24, 316. https://doi.org/10.3390/e24030316
Albrecht A. Equilibration and “Thermalization” in the Adapted Caldeira–Leggett Model. Entropy. 2022; 24(3):316. https://doi.org/10.3390/e24030316
Chicago/Turabian StyleAlbrecht, Andreas. 2022. "Equilibration and “Thermalization” in the Adapted Caldeira–Leggett Model" Entropy 24, no. 3: 316. https://doi.org/10.3390/e24030316
APA StyleAlbrecht, A. (2022). Equilibration and “Thermalization” in the Adapted Caldeira–Leggett Model. Entropy, 24(3), 316. https://doi.org/10.3390/e24030316






