1. Introduction
The van der Waals (vdW) fluid is the simplest instance of a system endowed with interacting particles. It is well known that it exhibits a gas–liquid phase transition (GLPT) [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10]. We wish to point out here that there exists a second vdW instability, at low temperatures
T, that could be interpreted as pre-announcing the classical quantum passage (CQP) [
11] (see also Ref. [
12]).
An important proviso: we definitely not studying quantum phase transitions such as those found in the excellent book [
13] or the interesting papers [
14,
15,
16]. We are dealing only with a classical equation and investigating its low
T validity limits. At low temperatures, we find indeed one such limitation that is interpreted as stated above.
More precisely, we ask how the GLPT and the putative CQP are related. Is there an interplay between them? This effort is devoted to answer these questions, using the noble gases as the target-system and rather novel thermal statistical quantifiers as the appropriate mathematical tools. We will try to set the ensuing discussion into an order–disorder disjunction framework, using the thermal quantifiers referred to above. They are the thermal efficiency
, the statistical complexity
C, and the disequilibrium
D. Further,
C is intimately associated to
D via the entropy
S [
17]
We point out that it is well known that
C and
D are useful quantities for detecting phase transitions [
17].
1.1. Special Thermal Quantifiers Used Here
Consider some particular probability distributions (PDs). Maximum statistical disorder is associated to a uniform probability distribution (UF) [
18]. The more dissimilar the extant PD is from the UF, the more statistically “ordered” this PD is [
18]. The dissimilarity we are speaking about is linked to a distance in probability space between our actual PD and UF called the disequilibrium
D [
18]. Note that [
18]
As stated above, the quantifier called statistical complexity
C is given by [
18]
Such
form is today routinely employed in dozens of papers [
19,
20,
21,
22,
23,
24,
25,
26,
27]. In addition, we use the standard forms for the Helmholtz’ free energy
F [
1]. With it, we introduce a further thermal quantifier called the thermal efficiency
[
17,
28] of an arbitrary control parameter
X of our system
that represents the work needed to change from
X to
[
28].
1.2. Goal
In this work, we use the thermal quantifiers D, C, and to scrutinize the relations that may exist between the vdW’s (1) liquid–gas transition (GLPT) and (2) putative quantum–classic frontier (CQ). Some rewarding insights will be obtained.
1.3. Organization
This paper has the following organization. In
Section 2, we introduce preliminary concepts. In
Section 3, we present our results and exhaustively discuss the relation between our GLPT and the CQP for five noble gases. Finally, we draw some conclusions in
Section 4.
2. Basic Relations for Ideal and van der Waals Gases
To undertake the present endeavor, we collect in this section some basic gas relations, as recounted in Refs. [
11,
12]. We will need expressions for the partition function, the mean energy
U, the free energy
F, etc.
The ideal gas is a collection of
N identical particles contained in a volume
V. One assumes thermal equilibrium at temperature
T. The Hamiltonian reads
.
m is the mass and
the momenta,
. One deals with a canonical partition function [
1]
where
.
is the average thermal wavelength
The free energy becomes [
1]
with
the specific volume. [
1]. Having
F, one also has all the important thermodynamic quantities, that we enumerate below, and one also deals with the chemical potential [
1]
The classical entropy (Sackur–Tetrode equation) is
One has
for
[
12], which is already telling us just where the classical regime is tenable.
indicates that the classical description is failing [
12].
Next, the internal energy reads
Amongst the main thermal statistical quantifiers, we have the disequilibrium
D [
12]
D can also be obtained from the free energy as shown in Ref. [
20].
One obtains
and, for the statistical complexity one has [
12],
The complexity and
D vanish for
and
[
12,
29]. It is useful to have a disequilibrium and complexity per particle:
2.1. Van der Waals Scenario
Now we add to our former picture inter-particle interactions and face the Hamiltonian [
1]
with
representing the interaction energy between molecules
i and
j, that depends only on the distance
. One sums
over the
possible pairs [
1].
Now, the associated canonical partition function (CPF) reads [
1]
where
is given by Equation (
4).
is an integral, denominated the configuration one (CI) [
1,
2]
For
the CI becomes [
2]
Here
is called the second virial coefficient [
2]. One usually approximates the interaction in the form of a particular
-form to be explained below (see Equation (
22)) [
2]. Then
The grand partition function is of the form [
1]
with
called the fugacity.
is the chemical potential [
1]. Via Equation (
16), we analytically obtain
The essential van der Waals step is to take the particle–particle interaction as [
12]
where
is the minimum possible distance between molecules [
2]. One is led then, via Equation (
19), to write
with
, with an average potential
a 2.2. The van der Waals (vdW) Thermal Quantifiers
Noting that
one has [
11]
where
is that of Equation (
6) [
1]. Now, following usual text book-recipes [
1], from the relation
we easily are led to a chemical potential of the form
The entropy
S is given by
that using Equation (
25) becomes
where
is gained from by Equation (
8) [
1]. The internal energy
reads then
where
is given by Equation (
9).
For the pressure
one has
so that using Equation (
25) we encounter
For a dilute gas with
(low density) one specializes this, in the case of the van der Waals gas, to [
1]
For the vdW distribution [
11]
the disequilibrium
D becomes
that, per particle, reads
where
is found in (
13). Thus,
C per particle becomes
2.3. The vdW QC Passage and the Temperature Benchmark
This is a central topic. One looks for it by following the prescriptions of Ref. [
12]. We take (1)
equal to the energy per particle of the vdW gas and (2)
as the chemical potential. Accordingly, the vdW classical regime is characterized by [
12]
Furthermore (see again Ref. [
12]), the classical regime is characterized by [
11]
and thus
so that, calling
an indicator of the CQ passage temperature, the classical vdW regime is found at
T’s such that [
11]
Note that the QC-passage’s indicative temperature
is merely a theoretical benchmark, not an experimental quantity.
2.4. The Thermal Efficiency
According to Ref. [
28], if we regard the vdW constant
b as a control parameter then
Via Equations (
25) and (
29), we come up with
For the classical–quantum passage’s indicative temperature
, Equation (
43) yields
In addition, we calculate, for the gas–liquid transition temperature
with
[
11].
2.5. Boyle Temperature
The Boyle temperature can be defined as the point in the temperature range at which a real gas starts to behave like an ideal one. Define the reduced variables
with
and
the well-known critical points of the van dew Waals equation [
6]. The so called Boyle temperature is the
value [
6]
The thermal efficiency here is
and diverges for
, i.e., when
(close-packing). When
tends to infinity, one has
, with
being the limit of the Boyle temperature for large volumes (
) [
6]. According to Ref. [
6], the minimum value of
. Thus, our
always (see
Figure 1). We have now collected all the necessary weaponry in order to tackle our job. We illustrate the usefulness of this quantifier in
Figure 1. The thermal efficiency displays a singularity at close packing.
3. The Relation between our Two vdW-Significant Points for Five Noble Gases
We have two kinds of vdW-significant points:
That which signals the gas–liquid phase transition. For this, we use the sub-index “c”, e.g., .
That which preannounces the classical–quantum passage. For this, we use the sub-index “2”, e.g., .
We deal with Helium, Neon, Argon, Krypton, and Xenon, vdW-parametrized by Johnston in Ref. [
6]. The
b parameter fitted for each gas is called
, with
the Avogadro constant [
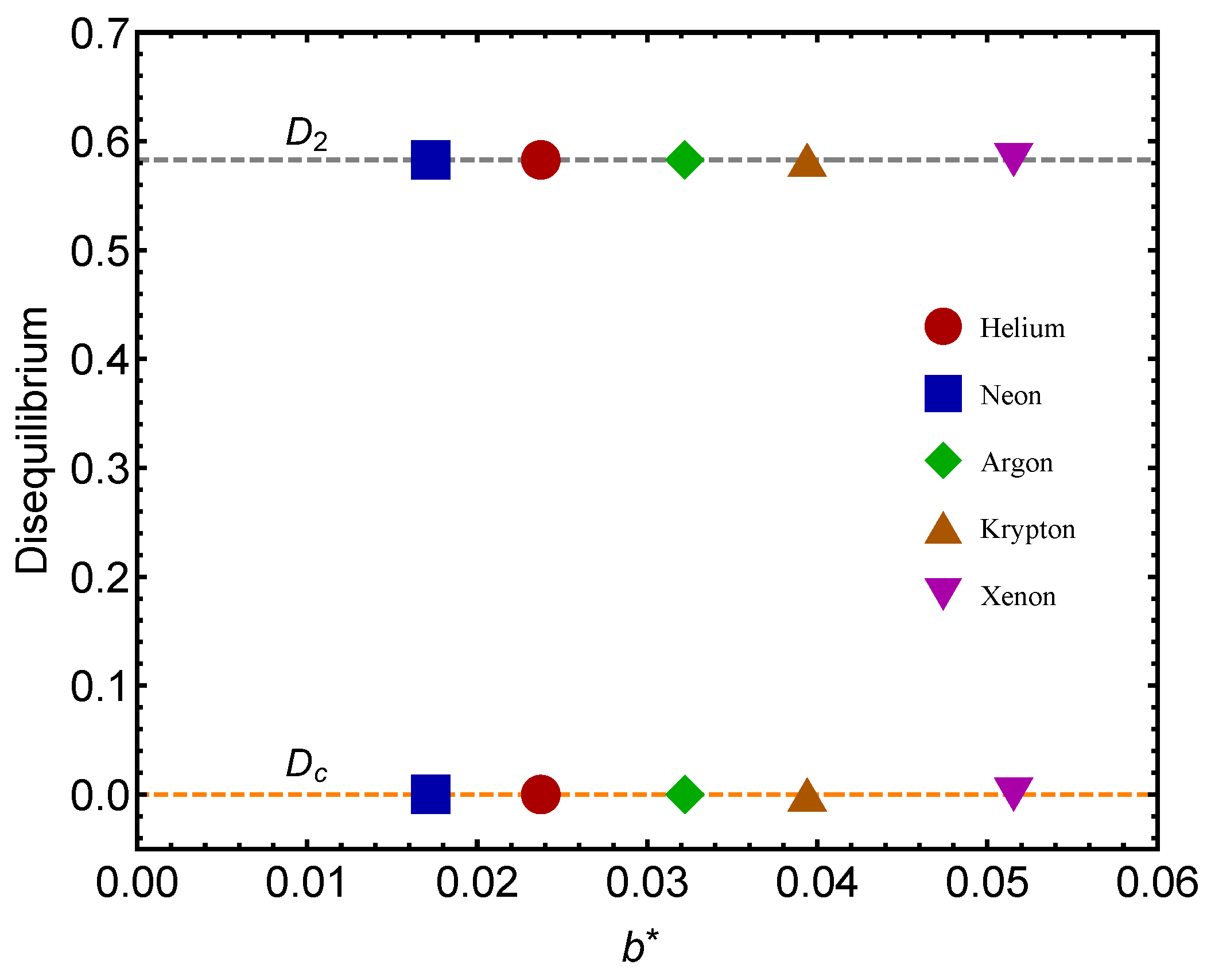
6]. We concoct a special icon for each of our noble gases (see
Figure 2). In each of the following figures, gas-icons appearing in the upper portion of the graph correspond to the QC-values, while those depicted in the lower portion correspond to the GL-value. Additionally, the lines depicted in the graphs are visual aids.
Remember that the disequilibrium
D signals statistical order. The larger
D, the larger the order-degree of the concomitant system. In
Figure 2, we consider the disequilibrium
D for each of the two significant points: (1) gas–liquid (GL)
and (2) quantum–classical (QC)
. We see that the
D-values are different for the two benchmarks. The lower values in our graphs always correspond to
(the GL phase). What is this fact telling us? That there is a larger ordering degree in the classical–quantum (CQ) passage than in the GL one, a novel fact discovered here. The ensuing differences for a given gas are much smaller for
than for the other gases. Let us emphasize that
represents a high degree of statistical order, as
.
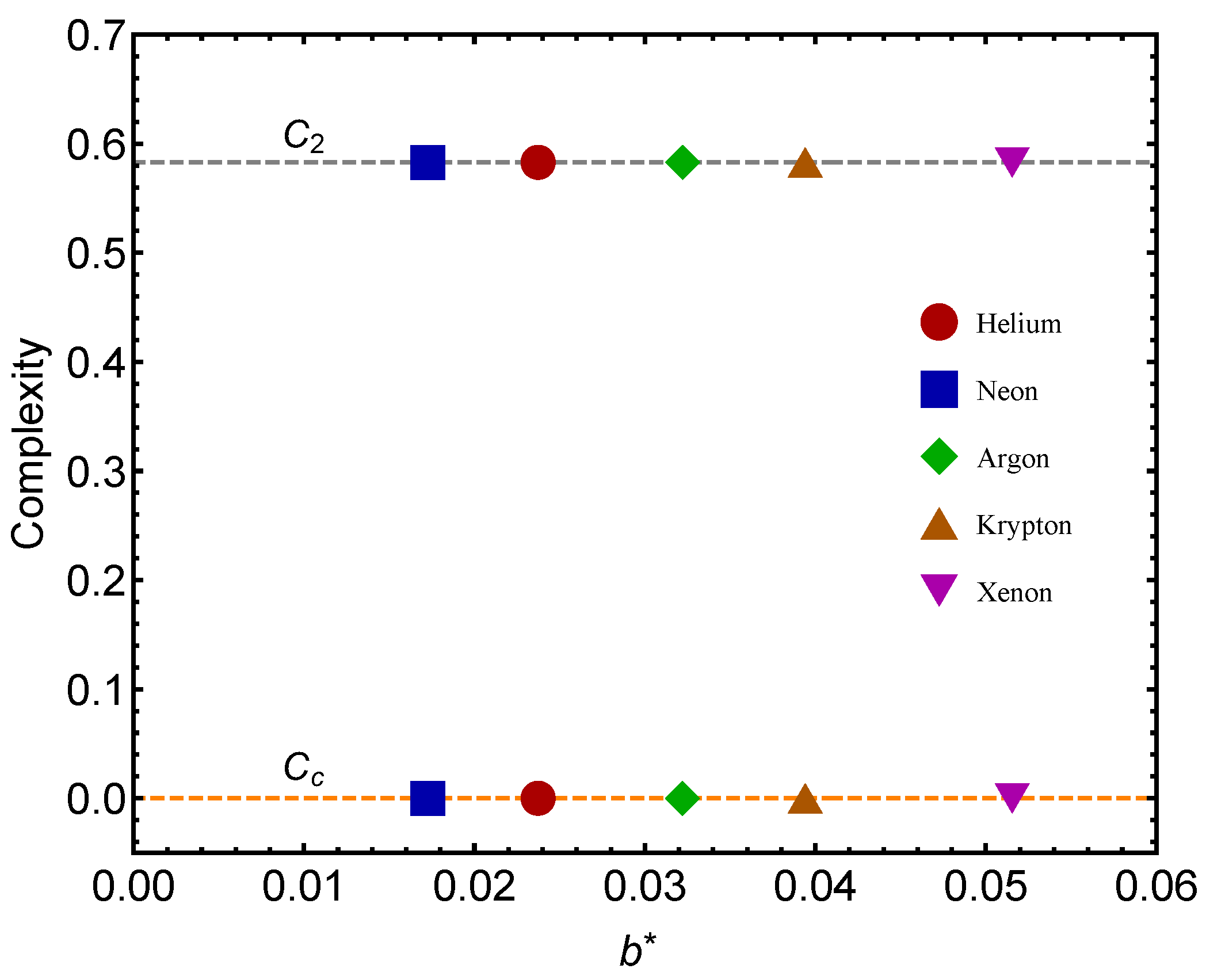
Figure 3 is the counterpart of
Figure 2 but for the complexity quantifier. The same rather surprising finding is here re-encountered. The vicinity of a quantum regime generates more statistical complexity than passing from the gas to the liquid phase, a novel fact discovered here. Note that the complexity-difference QC–GL is much smaller for
than for the remaining gases.
In
Figure 4, we deal with the vdW entropy
S for the noble gases.
S tends to grow with the molecule’s mass. Helium is a special case, as explained in the caption.
In
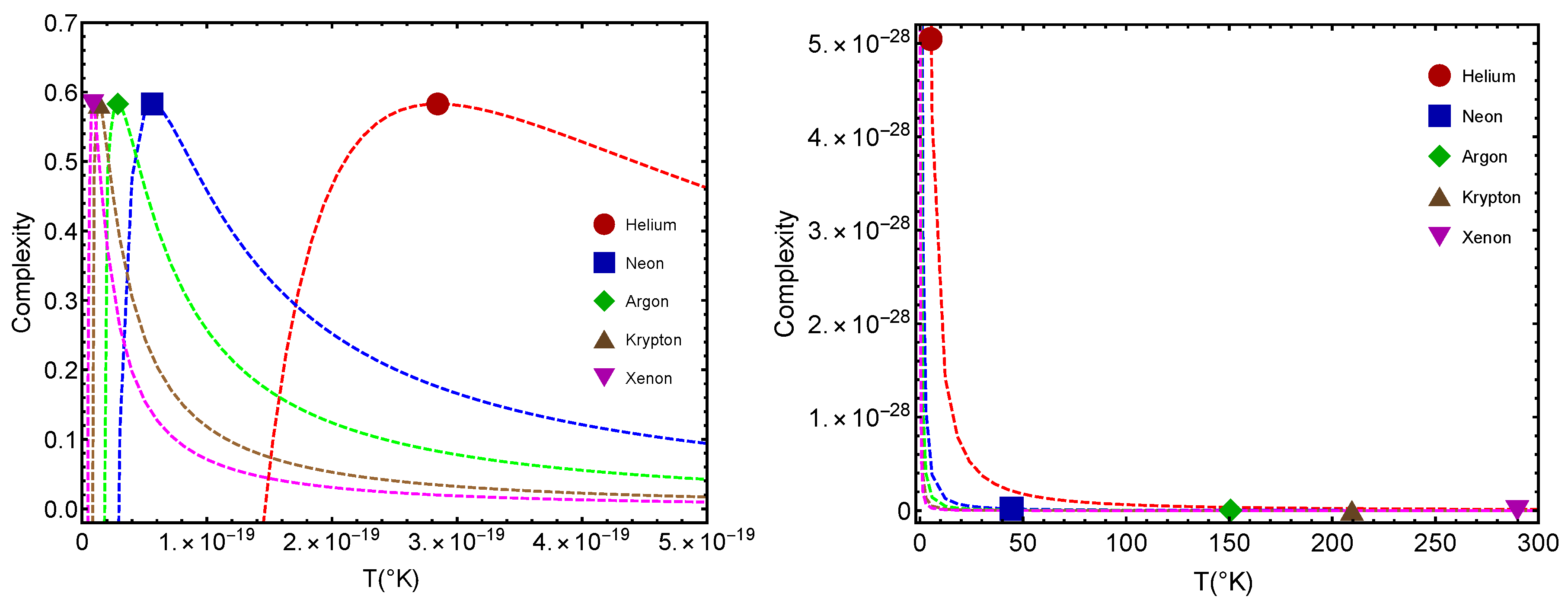
Figure 5 we inspect the complexities
(larger values) and
(smaller values) versus the temperature
T for
L.
is the critical temperature for the QC passage, while
is that for the GL one. Notably enough, for most of them, this difference between
and
is constant. Note that, consistently,
. This entails that complexity at the putative classical–quantum stage is larger than that at the gas–liquid one. Furthermore, the complexity is maximal at the benchmark
.
Figure 6 displays the disequilibrium-difference
for
L.
is the indicative temperature for the QC passage, while
is that for the GL one. We consider the noble gases and find always
. Notably enough, for most of them (save for
), this difference
is constant.
is the “degree of statistical order-difference”, a constant here. The order–disorder disjunction is seen to display a characteristic vdW behavior.
entails, let us insist, that the statistical order generated at the putative classical–quantum passage is larger than that at the gas–liquid one.
We consider the thermal efficiency
in
Figure 7. This quantity measures the work involved in changing the
-value. The larger the atom’s mass, the more work is performed by the atom in modifying its
-value.
In
Figure 7, we encounter a major difference between (1) the GL and (2) the (putative) QC passages. This difference is related to the
-value. In the GL transition, the system needs to release energy to change its
-value. One might be reminded of the fact that when vapor condenses to a liquid, the vapor’s latent energy is released.
In the second passage (CQ) one must work on the atom to change that -value. This is a typical quantum effect in the sense that the observer somehow becomes involved in dealing with quantum matters.
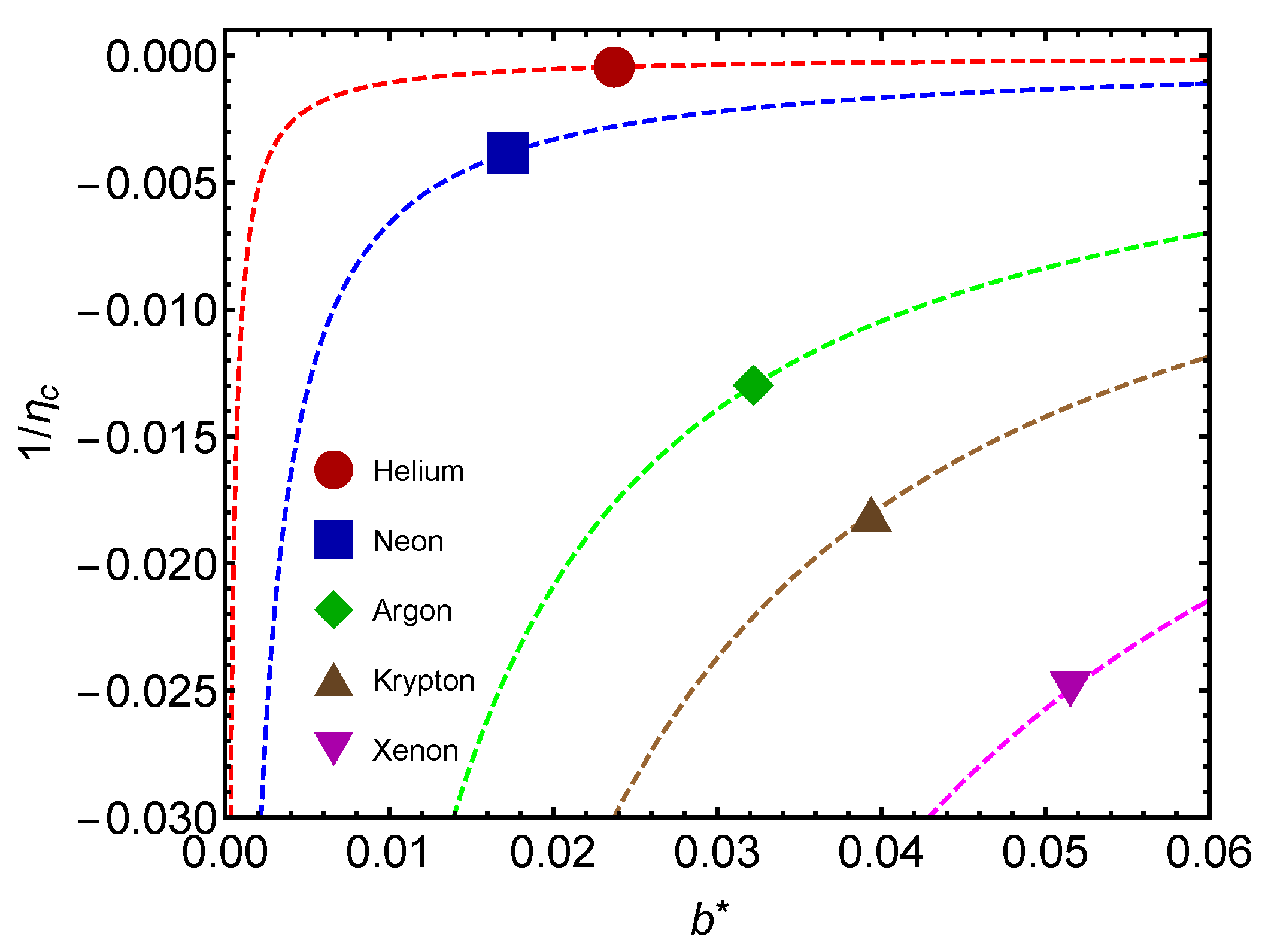
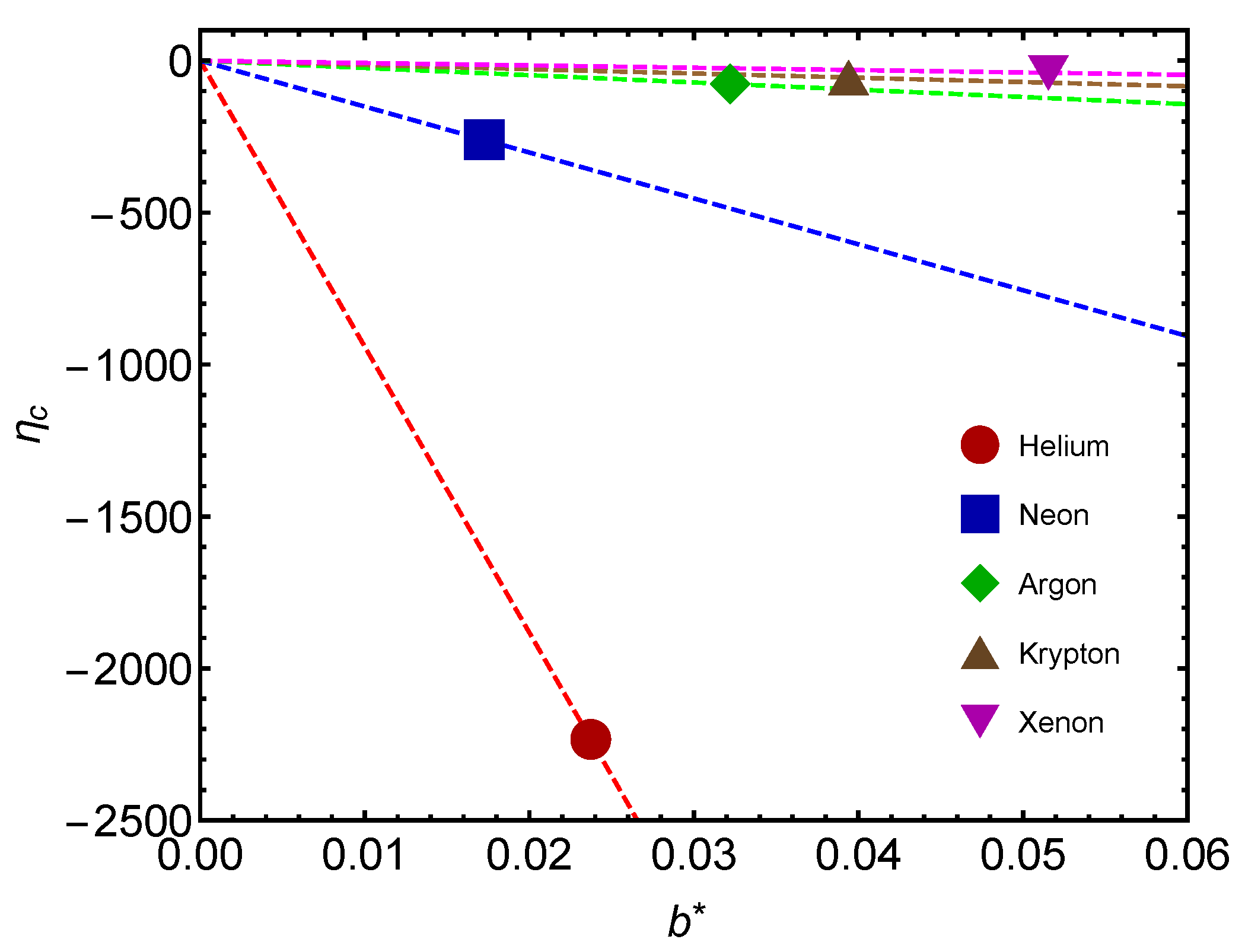
Another interesting plot is that of
Figure 8. We depict
versus
for several gases. Values are negative, as expected from previous considerations. As mass augments, less work is involved in changing
.
4. Conclusions
In this work, we have performed a thermal statistical study of the (putative) classical–quantum frontier in a van der Waals scenario, with emphasis on the noble gases. For the purpose, we used rather novel thermal statistical quantifiers such as the disequilibrium, the statistical complexity, and the thermal efficiency. Fruitful insights have been thereby gained. The two benchmark temperatures are (GL) and (QC).
We discovered that there is a larger (statistical) ordering degree in the classical–quantum (CQ) passage than in the GL one. This a novel fact discovered here. The need to effect a “CQ change of appropriate describing-formalism” carries more order than the entirely classic vdW GL description. The same kind of comparison applies also to the statistical complexity. Furthermore, the differences and tend to be constant for most noble gases ( excluded).
In the GL transition, the system needs to release energy to change its -value, while in the putative CQ passage we must do work on the atom to change that value, a notable difference between the two kinds of transformation. One might perhaps dare to interpret this work that we must do as that of Schrödinger–Heisenberg in creating quantum mechanics.
We emphasize the fact that the classical vdW-structure somehow anticipates, at low enough T, a jump in the statistical order-degree that we a posteriori associate with the quantum–classical frontier.
Our present classical van der Waals treatment is not capable to allow us to discuss out of equilibrium systems such as Josephson junction systems and many body systems [
30,
31,
32].