Kibble–Zurek Scaling from Linear Response Theory
Abstract
:1. Introduction
2. Preliminaries
2.1. Kibble–Zurek Mechanism
2.2. Excess work in Linear Response Theory
2.3. Excess Work from Kibble–Zurek Arguments
3. The Relaxation Function
3.1. Large N Limit
Ferromagnetic and Paramagnetic Phases
Divergence at the Critical Point
Variance of the Magnetic Moment Per Spin
3.2. Relaxation Time
4. Kibble–Zurek Scaling of the Excess Work
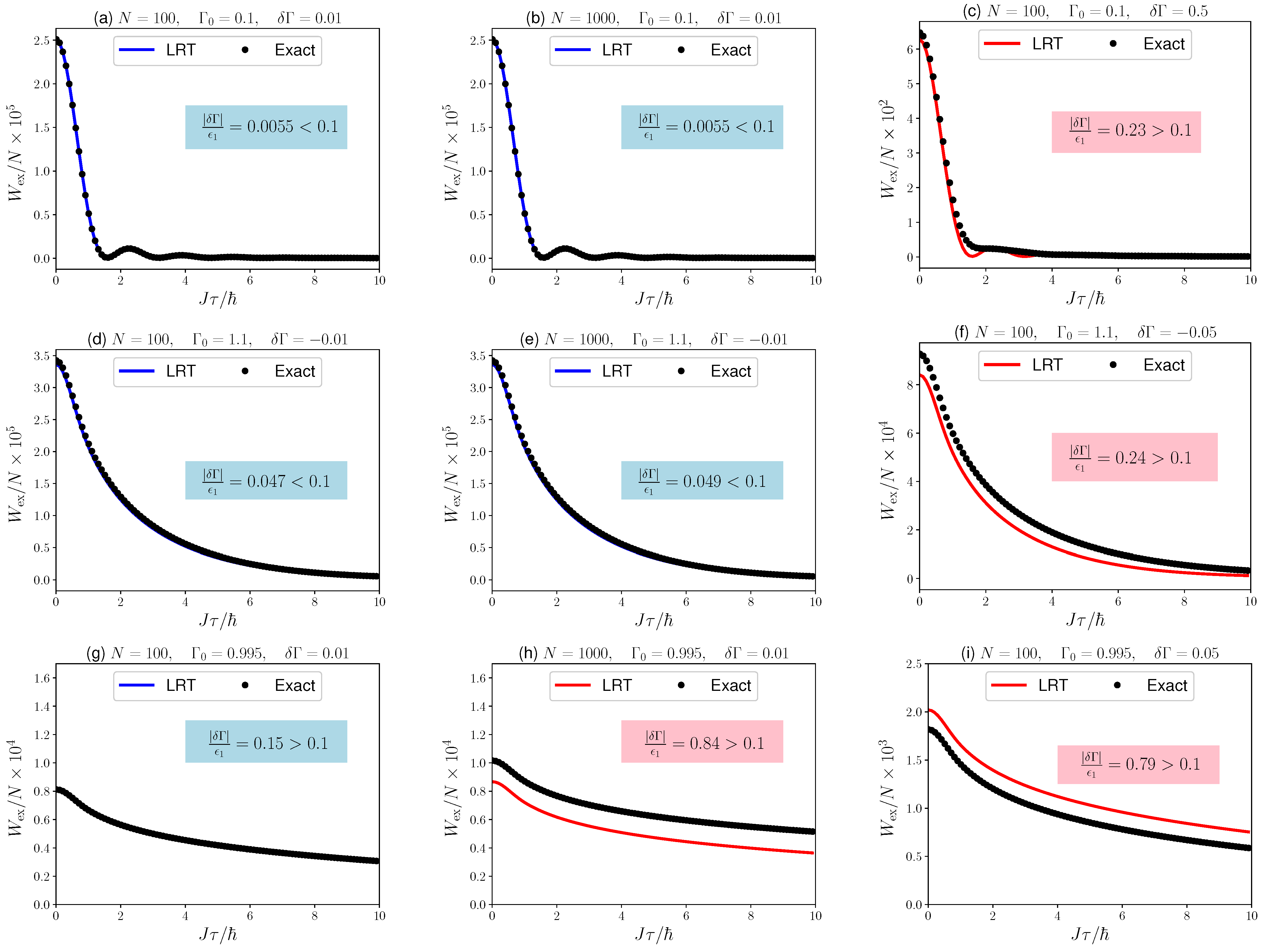
4.1. Range of Validity
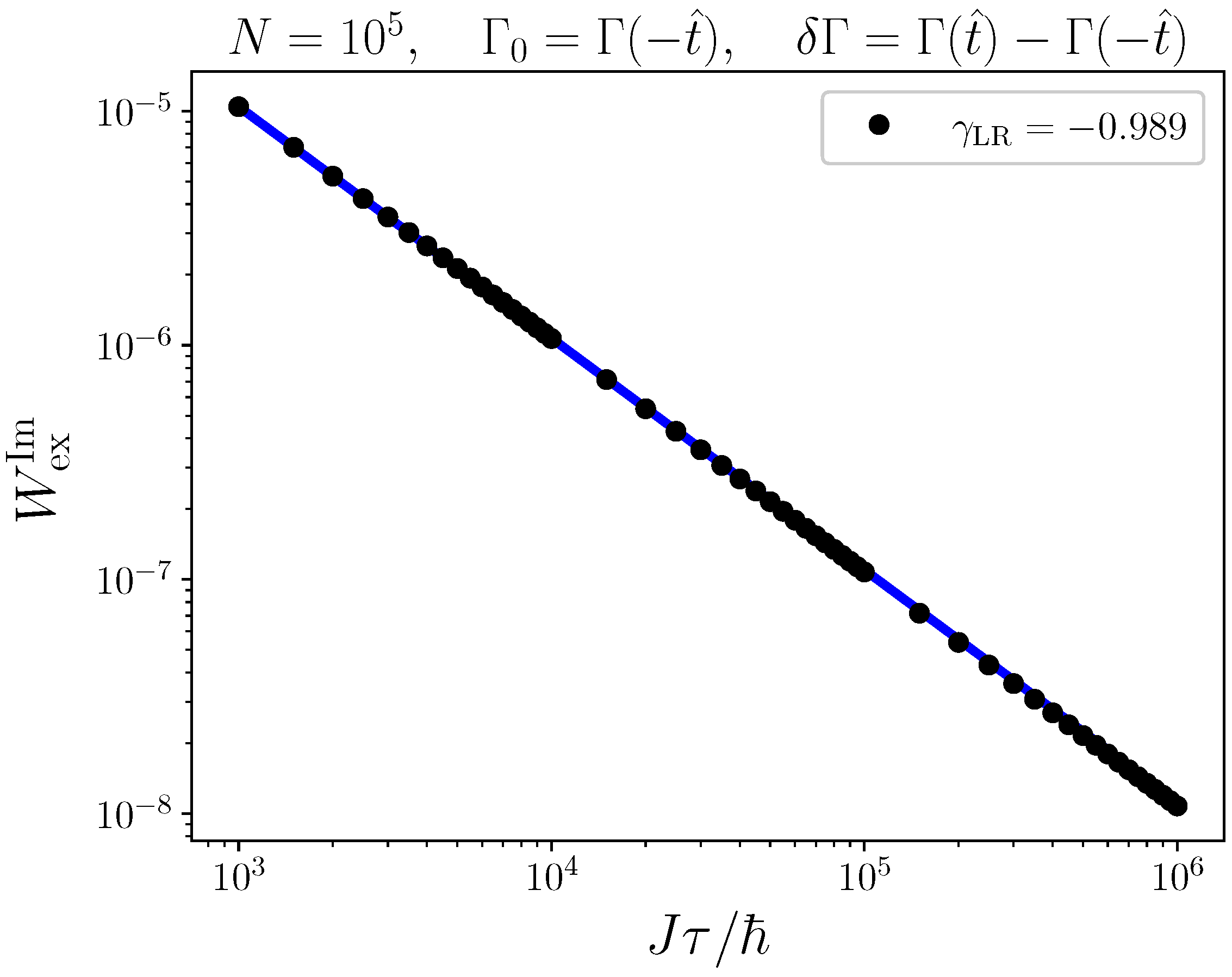
4.2. Kibble–Zurek Scaling from Linear Response Theory
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Relaxation Function for the Quantum Ising Model
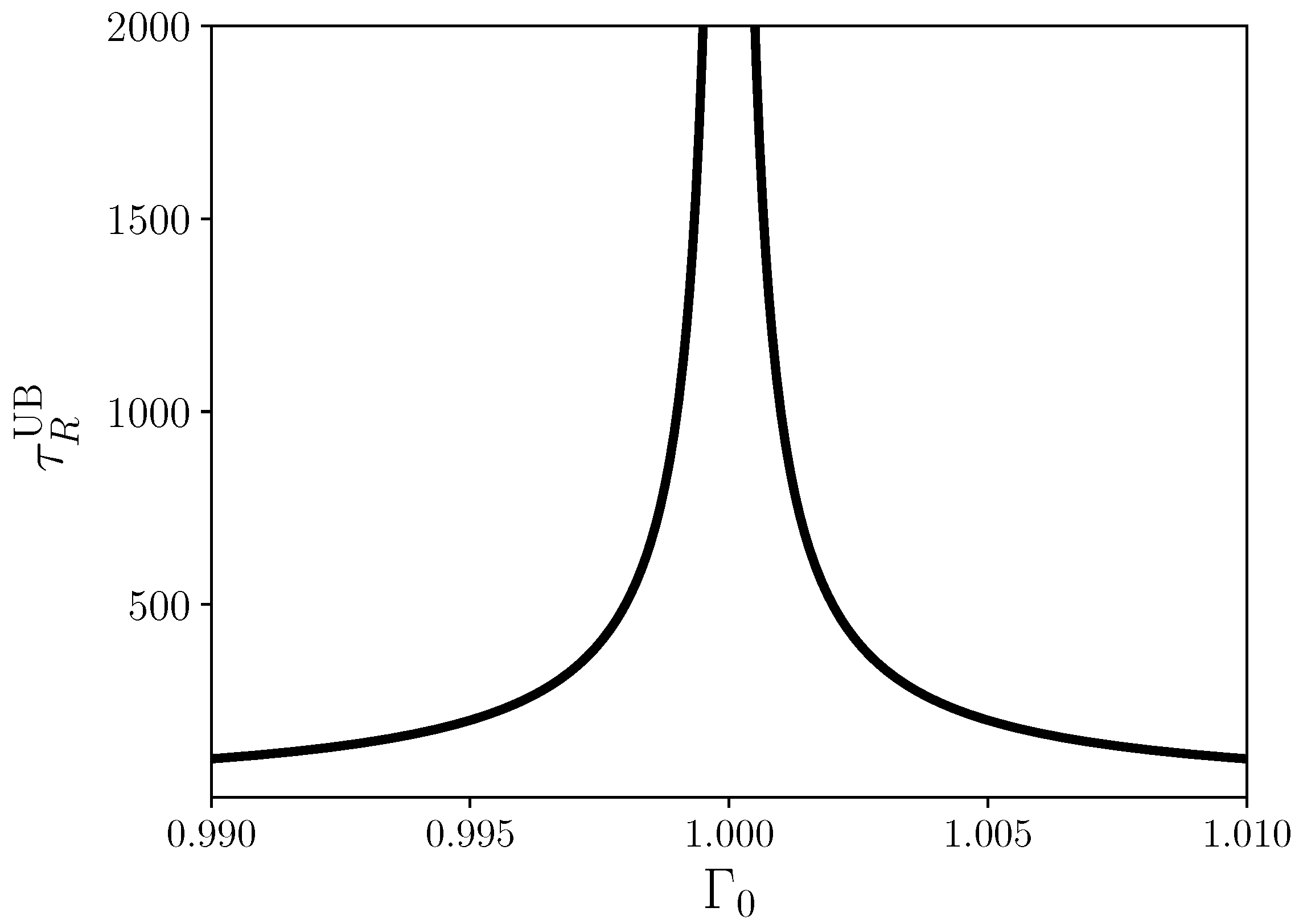
Appendix B. The Upper Envelop for the Relaxation Time
References
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1985. [Google Scholar]
- Fisher, M.E. The renormalization group theory of critical behavior. Rev. Mod. Phys. 1974, 46, 597. [Google Scholar] [CrossRef]
- Kibble, T.W. Topology of cosmic domains and strings. J. Phys. A Math. Gen. 1976, 9, 1387. [Google Scholar] [CrossRef]
- Zurek, W.H. Cosmological experiments in superfluid helium? Nature 1985, 317, 505–508. [Google Scholar] [CrossRef] [Green Version]
- Zurek, W.H. Cosmological experiments in condensed matter systems. Phys. Rep. 1996, 276, 177. [Google Scholar] [CrossRef] [Green Version]
- Laguna, P.; Zurek, W.H. Density of Kinks after a Quench: When Symmetry Breaks, How Big are the Pieces? Phys. Rev. Lett. 1997, 78, 2519. [Google Scholar] [CrossRef] [Green Version]
- Biroli, G.; Cugliandolo, L.F.; Sicilia, A. Kibble-Zurek mechanism and infinitely slow annealing through critical points. Phys. Rev. E 2010, 81, 050101. [Google Scholar] [CrossRef] [Green Version]
- Chandran, A.; Erez, A.; Gubser, S.S.; Sondhi, S.L. Kibble-Zurek problem: Universality and the scaling limit. Phys. Rev. B 2012, 86, 064304. [Google Scholar] [CrossRef] [Green Version]
- Chandran, A.; Burnell, F.J.; Khemani, V.; Sondhi, S.L. Kibble-Zurek scaling and string-net coarsening in topologically ordered systems. J. Phys. Condens. Matt. 2013, 25, 404214. [Google Scholar] [CrossRef] [Green Version]
- Ulm, S.; Roßnagel, J.; Jacob, G.; Degünther, C.; Dawkins, S.T.; Poschinger, U.G.; Nigmatullin, R.; Retzker, A.; Plenio, M.B.; Schmidt-Kaler, F.; et al. Observation of the Kibble-Zurek scaling law for defect formation in ion crystals. Nat. Commun. 2013, 4, 2290. [Google Scholar] [CrossRef]
- Del Campo, A.; Kibble, T.W.B.; Zurek, W.H. Causality and non-equilibrium second-order phase transitions in inhomogeneous systems. J. Phys. Condens. Matter 2013, 25, 404210. [Google Scholar] [CrossRef] [Green Version]
- Partner, H.L.; Nigmatullin, R.; Burgermeister, T.; Pyka, K.; Keller, J.; Retzker, A.; Plenio, M.B.; Mehlstäubler, T.E. Dynamics of topological defects in ion Coulomb crystals. New J. Phys. 2013, 15, 102013. [Google Scholar] [CrossRef]
- del Campo, A.; Zurek, W.H. Universality of phase transitions: Toplological defects from symmetry breaking. Int. J. Mod. Phys. A 2014, 29, 1430018. [Google Scholar] [CrossRef] [Green Version]
- Deutschländer, S.; Dillmann, P.; Maret, G.; Keim, P. Kibble-Zurek mechanism in colloidal monolayers. Proc. Natl. Acad. Sci. USA 2015, 112, 6925–6930. [Google Scholar] [CrossRef] [Green Version]
- Keesling, A.; Omran, A.; Levine, H.; Bernien, H.; Pichler, H.; Choi, S.; Samajdar, R.; Schwartz, S.; Silvi, P.; Sachdev, S.; et al. Quantum Kibble–Zurek mechanism and critical dynamics on a programmable Rydberg simulator. Nature 2019, 568, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Zamora, A.; Dagvadorj, G.; Comaron, P.; Carusotto, I.; Proukakis, N.P.; Szymańska, M.H. Kibble-Zurek Mechanism in Driven Dissipative Systems Crossing a Nonequilibrium Phase Transition. Phys. Rev. Lett. 2020, 125, 095301. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.M.; Gómez-Ruiz, F.J.; Huang, Y.F.; Li, C.F.; Guo, G.C.; del Campo, A. Experimentally testing quantum critical dynamics beyond the Kibble–Zurek mechanism. Commun. Phys. 2020, 3, 44. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum phase transitions. In Handbook of Magnetism and Advanced Magnetic Materials; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Zurek, W.H.; Dorner, U.; Zoller, P. Dynamics of a Quantum Phase Transition. Phys. Rev. Lett. 2005, 95, 105701. [Google Scholar] [CrossRef] [Green Version]
- Scherer, D.R.; Weiler, C.N.; Neely, T.W.; Anderson, B.P. Vortex formation by merging of multiple trapped Bose-Einstein condensates. Phys. Rev. Lett. 2007, 98, 110402. [Google Scholar] [CrossRef] [Green Version]
- Weiler, C.N.; Neely, T.W.; Scherer, D.R.; Bradley, A.S.; Davis, M.J.; Anderson, B.P. Spontaneous vortices in the formation of Bose-Einstein condensates. Nature 2008, 455, 14. [Google Scholar] [CrossRef] [Green Version]
- Gardas, B.; Dziarmaga, J.; Zurek, W.H. Dynamics of the quantum phase transition in the one-dimensional Bose-Hubbard model: Excitations and correlations induced by a quench. Phys. Rev. B 2017, 95, 104306. [Google Scholar] [CrossRef] [Green Version]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Kubo, R.; Toda, M.; Hashitsume, N. Statistical Physics II: Nonequilibrium Statistical Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Soriani, A.; Nazé, P.; Bonança, M.V.S.; Gardas, B.; Deffner, S. Three phases of quantum annealing: Fast, slow, and very slow. Phys. Rev. A 2022, 105, 042423. [Google Scholar] [CrossRef]
- Soriani, A.; Nazé, P.; Bonança, M.V.; Gardas, B.; Deffner, S. Assessing performance of quantum annealing with non-linear driving. arXiv 2022, arXiv:2203.17009. [Google Scholar]
- Deffner, S. Kibble-Zurek scaling of the irreversible entropy production. Phys. Rev. E 2017, 96, 052125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfeuty, P. The one-dimensional Ising model with a transverse field. Ann. Phys. 1970, 57, 79–90. [Google Scholar] [CrossRef]
- Dziarmaga, J. Dynamics of a Quantum Phase Transition: Exact Solution of the Quantum Ising Model. Phys. Rev. Lett. 2005, 95, 245701. [Google Scholar] [CrossRef] [Green Version]
- Mbeng, G.B.; Russomanno, A.; Santoro, G.E. The quantum Ising chain for beginners. arXiv 2020, arXiv:2009.09208. [Google Scholar]
- Fusco, L.; Pigeon, S.; Apollaro, T.J.G.; Xuereb, A.; Mazzola, L.; Campisi, M.; Ferraro, A.; Paternostro, M.; De Chiara, G. Assessing the Nonequilibrium Thermodynamics in a Quenched Quantum Many-Body System via Single Projective Measurements. Phys. Rev. X 2014, 4, 031029. [Google Scholar] [CrossRef] [Green Version]
- Francuz, A.; Dziarmaga, J.; Gardas, B.; Zurek, W.H. Space and time renormalization in phase transition dynamics. Phys. Rev. B 2016, 93, 075134. [Google Scholar] [CrossRef] [Green Version]
- Gardas, B.; Dziarmaga, J.; Zurek, W.H.; Zwolak, M. Defects in Quantum Computers. Sci. Rep. 2018, 8, 4539. [Google Scholar] [CrossRef] [Green Version]
- Piccitto, G.; Silva, A. Dynamical phase transition in the transverse field Ising chain characterized by the transverse magnetization spectral function. Phys. Rev. B 2019, 100, 134311. [Google Scholar] [CrossRef] [Green Version]
- Puebla, R.; Deffner, S.; Campbell, S. Kibble-Zurek scaling in quantum speed limits for shortcuts to adiabaticity. Phys. Rev. Res. 2020, 2, 032020. [Google Scholar] [CrossRef]
- Carolan, E.; Kiely, A.; Campbell, S. Counterdiabatic control in the impulse regime. Phys. Rev. A 2022, 105, 012605. [Google Scholar] [CrossRef]
- Sivak, D.A.; Crooks, G.E. Thermodynamic Metrics and Optimal Paths. Phys. Rev. Lett. 2012, 108, 190602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zulkowski, P.; Sivak, D.A.; Crooks, G.E.; DeWeese, M.E. Geometry of thermodynamic control. Phys. Rev. E 2012, 86, 041108. [Google Scholar] [CrossRef] [Green Version]
- Bonança, M.V.S.; Deffner, S. Optimal driving of isothermal processes close to equilibrium. J. Chem. Phys. 2014, 140, 244119. [Google Scholar] [CrossRef]
- Acconcia, T.V.; Bonança, M.V.S. Degenerate optimal paths in thermally isolated systems. Phys. Rev. E 2015, 91, 042141. [Google Scholar] [CrossRef] [Green Version]
- Acconcia, T.V.; Bonança, M.V.; Deffner, S. Shortcuts to adiabaticity from linear response theory. Phys. Rev. E 2015, 92, 042148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonança, M.V.S.; Deffner, S. Minimal dissipation in processes far from equilibrium. Phys. Rev. E 2018, 98, 042103. [Google Scholar] [CrossRef] [Green Version]
- Nazé, P.; Bonança, M.V. Compatibility of linear-response theory with the second law of thermodynamics and the emergence of negative entropy production rates. J. Stat. Mech. Theo. Exp. 2020, 2020, 013206. [Google Scholar] [CrossRef] [Green Version]
- Deffner, S.; Bonança, M.V.S. Thermodynamic control—An old paradigm with new applications. EPL (Europhys. Lett.) 2020, 131, 20001. [Google Scholar] [CrossRef]
- Bonança, M.V.S.; Nazé, P.; Deffner, S. Negative entropy production rates in Drude-Sommerfeld metals. Phys. Rev. E 2021, 103, 012109. [Google Scholar] [CrossRef] [PubMed]
- Bonança, M.V.S.; Deffner, S. Fluctuation theorem for irreversible entropy production in electrical conduction. Phys. Rev. E 2022, 105, L012105. [Google Scholar] [CrossRef] [PubMed]
- Polkovnikov, A. Universal adiabatic dynamics in the vicinity of a quantum critical point. Phys. Rev. B 2005, 72, 161201. [Google Scholar] [CrossRef] [Green Version]
- Mandal, D.; Jarzynski, C. Analysis of slow transitions between nonequilibrium steady states. J. Stat. Mech. 2016, 2016, 063204. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964.
- Deffner, S.; Campbell, S. Quantum Thermodynamics: An Introduction to the Thermodynamics of Quantum Information; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019. [Google Scholar]
- Katsura, S. Statistical Mechanics of the Anisotropic Linear Heisenberg Model. Phys. Rev. 1962, 127, 1508–1518. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazé, P.; Bonança, M.V.S.; Deffner, S. Kibble–Zurek Scaling from Linear Response Theory. Entropy 2022, 24, 666. https://doi.org/10.3390/e24050666
Nazé P, Bonança MVS, Deffner S. Kibble–Zurek Scaling from Linear Response Theory. Entropy. 2022; 24(5):666. https://doi.org/10.3390/e24050666
Chicago/Turabian StyleNazé, Pierre, Marcus V. S. Bonança, and Sebastian Deffner. 2022. "Kibble–Zurek Scaling from Linear Response Theory" Entropy 24, no. 5: 666. https://doi.org/10.3390/e24050666
APA StyleNazé, P., Bonança, M. V. S., & Deffner, S. (2022). Kibble–Zurek Scaling from Linear Response Theory. Entropy, 24(5), 666. https://doi.org/10.3390/e24050666






