Solving the Incompressible Surface Stokes Equation by Standard Velocity-Correction Projection Methods
Abstract
1. Introduction
2. Surface Differential Operator
3. Finite Element Approximation of Surface
4. Standard Velocity Correction Method
4.1. First-Order Velocity Correction Method
- Implementation of the standard form
4.2. Second-Order Velocity Correction Method
- Implementation of the standard form
4.3. Stability Analysis
4.3.1. First-Order Scheme Stability Analysis
4.3.2. Stability Analysis of Second-Order Schemes
4.4. Fully Discrete Scheme
4.4.1. First-Order Fully Discrete Velocity Correction Method
4.4.2. Second-Order Fully Discrete Velocity Correction Method
5. Numerical Experiments
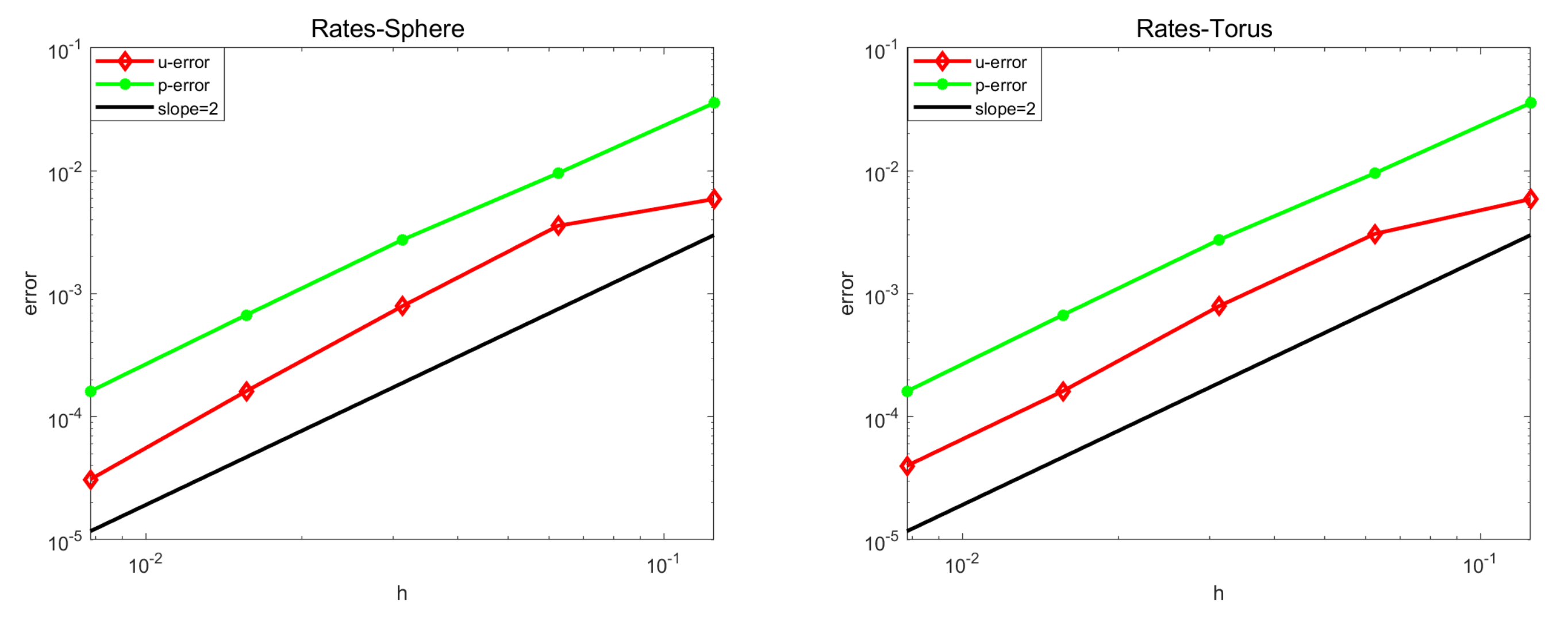
5.1. Convergence Test
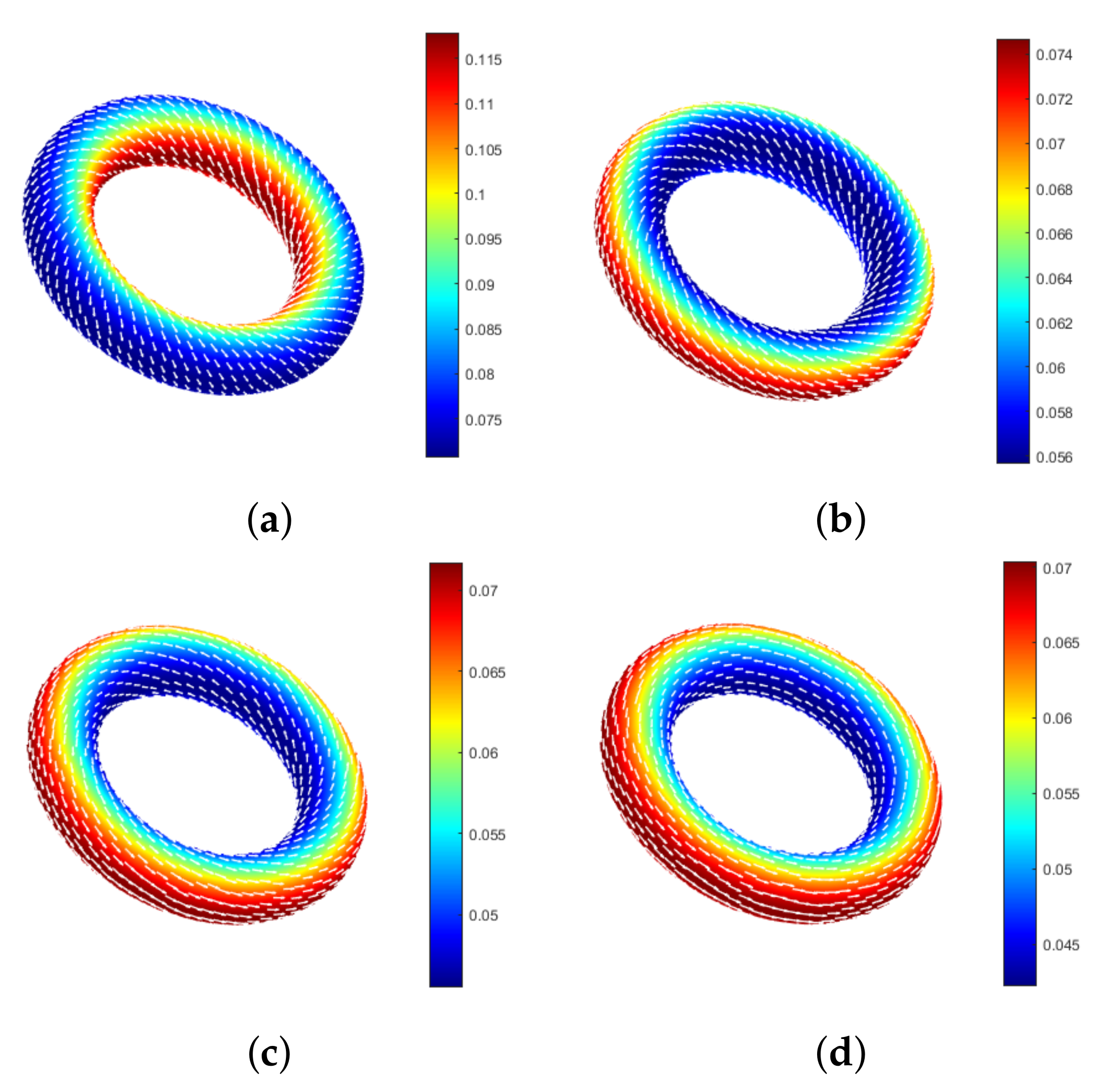
5.2. A Circular Flow on a Ring
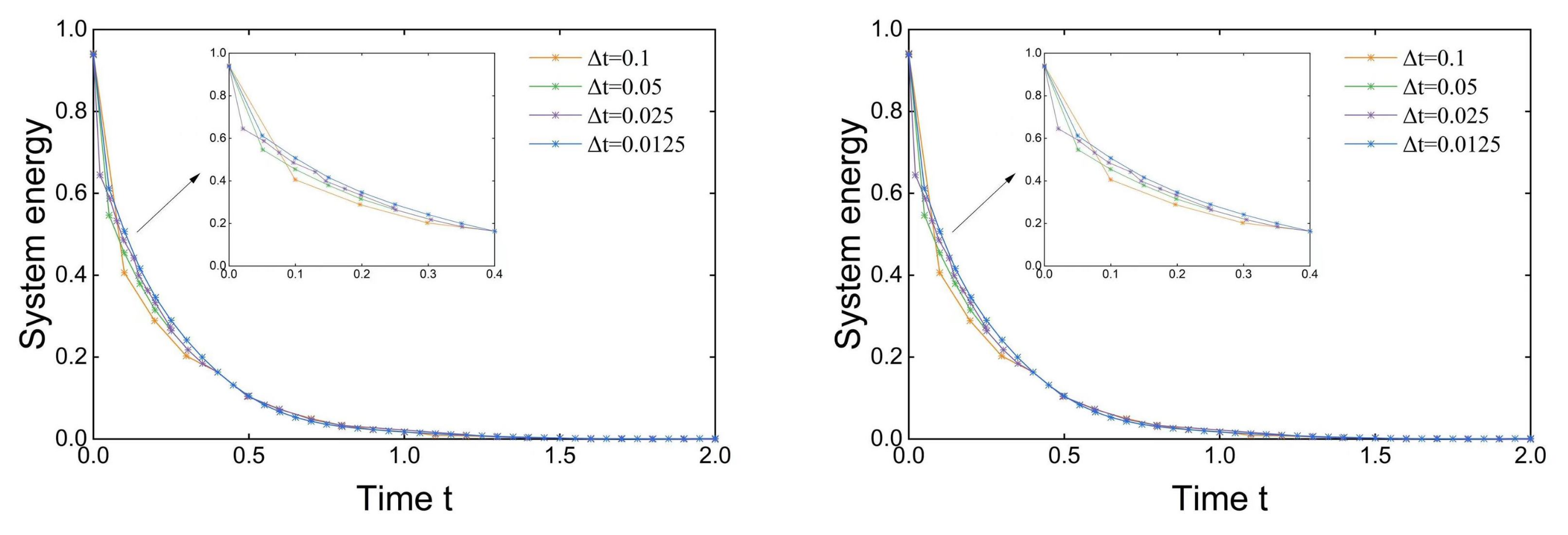
5.3. Stability Test
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scriven, L.E. Dynamics of a fluid interface equation of motion for Newtonian surface fluids. Chem. Eng. Sci. 1960, 12, 98–108. [Google Scholar] [CrossRef]
- Slattery, J.C.; Sagis, L.M.C.; Oh, E.S. Interfacial Transport Phenomena; Springer: New York, NY, USA, 2007. [Google Scholar]
- Arroyo, M.; DeSimone, A. Relaxation dynamics of fluid membranes. Phys. Rev. E 2009, 79, 031915. [Google Scholar] [CrossRef]
- Rahimi, M.; DeSimone, A.; Arroyo, M. Curved fluid membranes behave laterally as effective viscoelastic media. Soft Matter 2013, 9, 11033–11045. [Google Scholar] [CrossRef]
- Dziuk, G.; Elliott, C.M. Finite element methods for surface PDEs. Acta Numer. 2013, 22, 289–396. [Google Scholar] [CrossRef]
- Olshanskii, M.A.; Reusken, A. Trace finite element methods for PDEs on surfaces. In Geometrically Unfitted Finite Element Methods and Applications; Springer: Cham, Switzerland, 2017; pp. 211–258. [Google Scholar]
- Nitschke, I.; Voigt, A.; Wensch, J. A finite element approach to incompressible two-phase flow on manifolds. J. Fluid Mech. 2012, 708, 418–438. [Google Scholar] [CrossRef]
- Reuther, S.; Voigt, A. The interplay of curvature and vortices in flow on curved surfaces. Multiscale Model. Simul. 2015, 13, 632–643. [Google Scholar] [CrossRef]
- Reuther, S.; Voigt, A. Solving the incompressible surface Navier–Stokes equation by surface finite elements. Phys. Fluids 2018, 30, 012107. [Google Scholar] [CrossRef]
- Fries, T.P. Higher-order surface FEM for incompressible Navier-Stokes flows on manifolds. Int. J. Numer. Methods Fluids 2018, 88, 55–78. [Google Scholar] [CrossRef]
- Gross, S.; Jankuhn, T.; Olshanskii, M.A.; Reusken, A. A trace finite element method for vector-Laplacians on surfaces. SIAM J. Numer. Anal. 2018, 56, 2406–2429. [Google Scholar] [CrossRef]
- Hansbo, P.; Larson, M.G.; Larsson, K. Analysis of finite element methods for vector Laplacians on surfaces. IMA J. Numer. Anal. 2020, 40, 1652–1701. [Google Scholar] [CrossRef]
- Lederer, P.L.; Lehrenfeld, C.; Schöberl, J. Divergence-free tangential finite element methods for incompressible flows on surfaces. Int. J. Numer. Methods Eng. 2020, 121, 2503–2533. [Google Scholar] [CrossRef] [PubMed]
- Reusken, A. Stream function formulation of surface Stokes equations. IMA J. Numer. Anal. 2020, 40, 109–139. [Google Scholar] [CrossRef]
- Jankuhn, T.; Olshanskii, M.A.; Reusken, A. Incompressible fluid problems on embedded surfaces: Modeling and variational formulations. Interfaces Free Boundaries 2018, 20, 353–377. [Google Scholar] [CrossRef]
- Vu-Huu, T.; Le-Thanh, C.; Nguyen-Xuan, H.; Abdel-Wahab, M. An equal-order mixed polygonal finite element for two-dimensional incompressible Stokes flows. Eur. J.-Mech.-B/Fluids 2020, 79, 92–108. [Google Scholar] [CrossRef]
- Qu, W.; Chen, W. Solution of two-dimensional stokes flow problems using improved singular boundary method. Adv. Appl. Math. Mech. 2015, 7, 13–30. [Google Scholar] [CrossRef]
- Jiao, S.; Yao, G.; Wang, L.V. Depth-resolved two-dimensional Stokes vectors of backscattered light and Mueller matrices of biological tissue measured with optical coherence tomography. Appl. Opt. 2000, 39, 6318–6324. [Google Scholar] [CrossRef]
- Li, J.; Gao, Z.; Dai, Z.; Feng, X. Divergence-free radial kernel for surface Stokes equations based on the surface Helmholtz decomposition. Comput. Phys. Commun. 2020, 256, 107408. [Google Scholar] [CrossRef]
- Jankuhn, T.; Reusken, A. Higher order trace finite element methods for the surface Stokes equation. arXiv 2019, arXiv:1909.08327. [Google Scholar]
- Olshanskii, M.A.; Quaini, A.; Reusken, A.; Yushutin, V. A finite element method for the surface Stokes problem. SIAM J. Sci. Comput. 2018, 40, A2492–A2518. [Google Scholar] [CrossRef]
- Guermond, J.; Shen, J. On the error estimates for the rotational pressure-correction projection methods. Math. Comput. 2004, 73, 1719–1737. [Google Scholar] [CrossRef]
- Huang, X.; Xiao, X.; Zhao, J.; Feng, X. An efficient operator-splitting FEM-FCT algorithm for 3D chemotaxis models. Eng. Comput. 2020, 36, 1393–1404. [Google Scholar] [CrossRef]
- Guermond, J.L.; Shen, J. Velocity-correction projection methods for incompressible flows. SIAM J. Numer. Anal. 2003, 41, 112–134. [Google Scholar] [CrossRef]
- Reuter, M.; Biasotti, S.; Giorgi, D.; Patanè, G.; Spagnuolo, M. Discrete Laplace–Beltrami operators for shape analysis and segmentation. Comput. Graph. 2009, 33, 381–390. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Feng, X. Solving the Incompressible Surface Stokes Equation by Standard Velocity-Correction Projection Methods. Entropy 2022, 24, 1338. https://doi.org/10.3390/e24101338
Zhao Y, Feng X. Solving the Incompressible Surface Stokes Equation by Standard Velocity-Correction Projection Methods. Entropy. 2022; 24(10):1338. https://doi.org/10.3390/e24101338
Chicago/Turabian StyleZhao, Yanzi, and Xinlong Feng. 2022. "Solving the Incompressible Surface Stokes Equation by Standard Velocity-Correction Projection Methods" Entropy 24, no. 10: 1338. https://doi.org/10.3390/e24101338
APA StyleZhao, Y., & Feng, X. (2022). Solving the Incompressible Surface Stokes Equation by Standard Velocity-Correction Projection Methods. Entropy, 24(10), 1338. https://doi.org/10.3390/e24101338





