Security Analysis of Sending or Not-Sending Twin-Field Quantum Key Distribution with Weak Randomness
Abstract
1. Introduction
2. Protocol Description
- Preparation. At any times window i, Alice (Bob) independently determines whether it is a decoy window or a signal window with probabilities and . If it is a decoy window, Alice (Bob) sends out to Charlie a decoy pulse in a phase-randomized coherent state , or (, or ) with probabilities of , , . We suppose . If it is a signal window, Alice (Bob) decides to send out to Charlie a signal pulse in phase-randomized coherent states or a vacuum state ( or ) with probabilities of and , where is random in . Here, we assume that consecutive photons are well-separated in the decoy and the signal time windows. Note that a coherent state of intensity and global phase is a linear superposition of photon-number states . Whenever Alice or Bob sends a coherent state of intensity , it can be equivalently regarded as a probabilistic mixture of different photon-number states .
- Measurement. Alice and Bob send the chosen states to Charlie. Charlie then performs interferometric measurements on the incoming quantum signals after taking phase compensation and announces the measurement results of which detector clicks to Alice and Bob. An effective event is defined as follows: (1) if only one detector clicks corresponding to a time window i when both Alice and Bob have determined the signal window, it is defined as an effective event. (2) If only one detector clicks corresponding to a time window i when both Alice and Bob have determined a decoy window and sent the coherent states with the same intensity, and in that time window, the pre-chosen values and satisfy post-selection criterion, which is:where and are the random phases of coherent states prepared by Alice and Bob, respectively. could take an arbitrary value and it is set properly to acquire a satisfactory key rate, which will be different from time to time due to phase drift. The value of is determined by the size of the phase slice , which is chosen by Alice and Bob. In fact, Equation (1) is equivalent to:where represents the minor angle enclosed by two rays, which enclose the rotational angle.
- Sifting. Alice and Bob announce decoy windows and signal windows of each other. If both Alice and Bob choose the decoy window, it is defined to be an window. If both Alice and Bob choose the signal window, it is defined to be a Z window. In an window, it is an window, which is a subset of windows, when they choose the same intensity . Additionally, it is an window when Alice (Bob) determines a signal window, while Bob (Alice) determines a decoy window, or when both Alice and Bob determine the decoy window, but choose different intensities. According to the effective events criterion introduced above, Alice and Bob decide whether one-detector clicks event is an effective event. We define three kinds of sets: , and , which include all effective events in Z, and windows.
- Parameter estimation. For the events in the set of the Z window, if Alice decides to send out a phased-randomized weak coherent state, she (he) denotes a bit 1 and if she (he) decides to send a vacuum state, she (he) denotes a bit 0. If Bob decides to send out a phased-randomized weak coherent state, she (he) denotes a bit 0 and if she (he) decides not to send a vacuum state, she (he) denotes a bit 0. We notice that it is the decision that determines the bit value rather than what they send. Then, Alice and Bob could obtain the bit strings, and they will get an error bit if an effective event happens when both Alice and Bob decide to send or not send. Finally, adopting the decoy-state method, Alice and Bob could estimate the number of the single-photon states and phase-flip error rate according to the events in windows. They could estimate the lower bound of and upper bound of according to the events in and windows.
- Error correction. Alice and Bob perform an error correction scheme to correct bit strings obtained in the last step. To achieve this goal, it consumes at most bits of error correction data. Then, Alice and Bob exploit a random two-universal hash function to carry out an error verification operation, which Alice sends a hash of length to make sure that the key bits of Alice are the same as Bob.
- Private amplification. In order to reduce Eve’s information of final keys, Alice and Bob exploit the random two-universal hash function to extract two shorter strings of length l. Finally, Alice and Bob obtain the secret key strings and .
3. Security Analysis
3.1. Parameter Estimation in the Asymptotic Case
3.2. Parameter Estimation with the Finite-Key Size
- Correctness. A protocol is -correct if and of Alice and Bob are not identical with the maximal probability of :
- Secrecy. The final key strings S ( or ) are said to be -secret with respect to the Eve holding a quantum system E if:where denotes the probability of protocol failure aborted, denotes the classical-quantum states of the system for Alice (Bob) and system E, and denotes the fully mixed states on or .
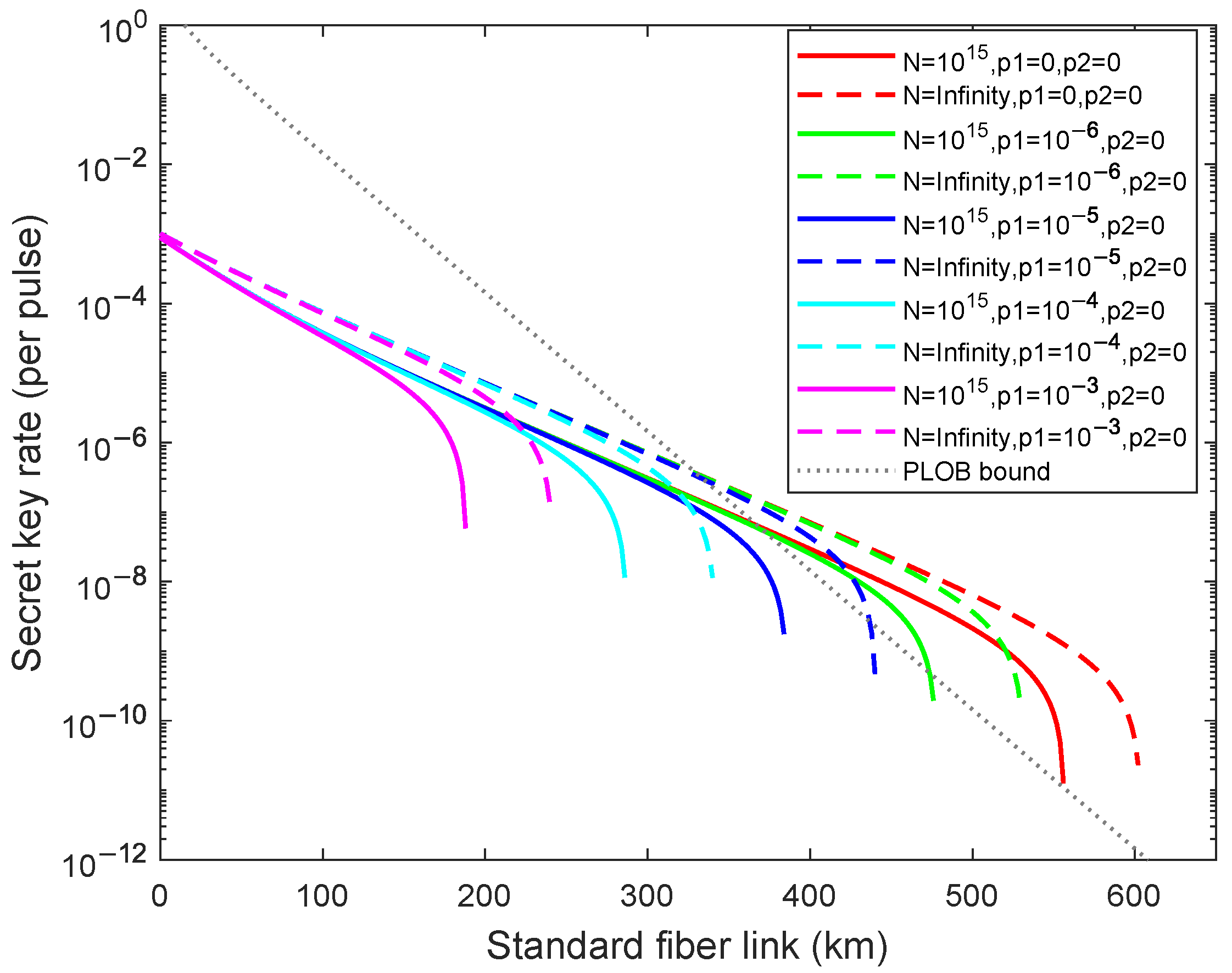
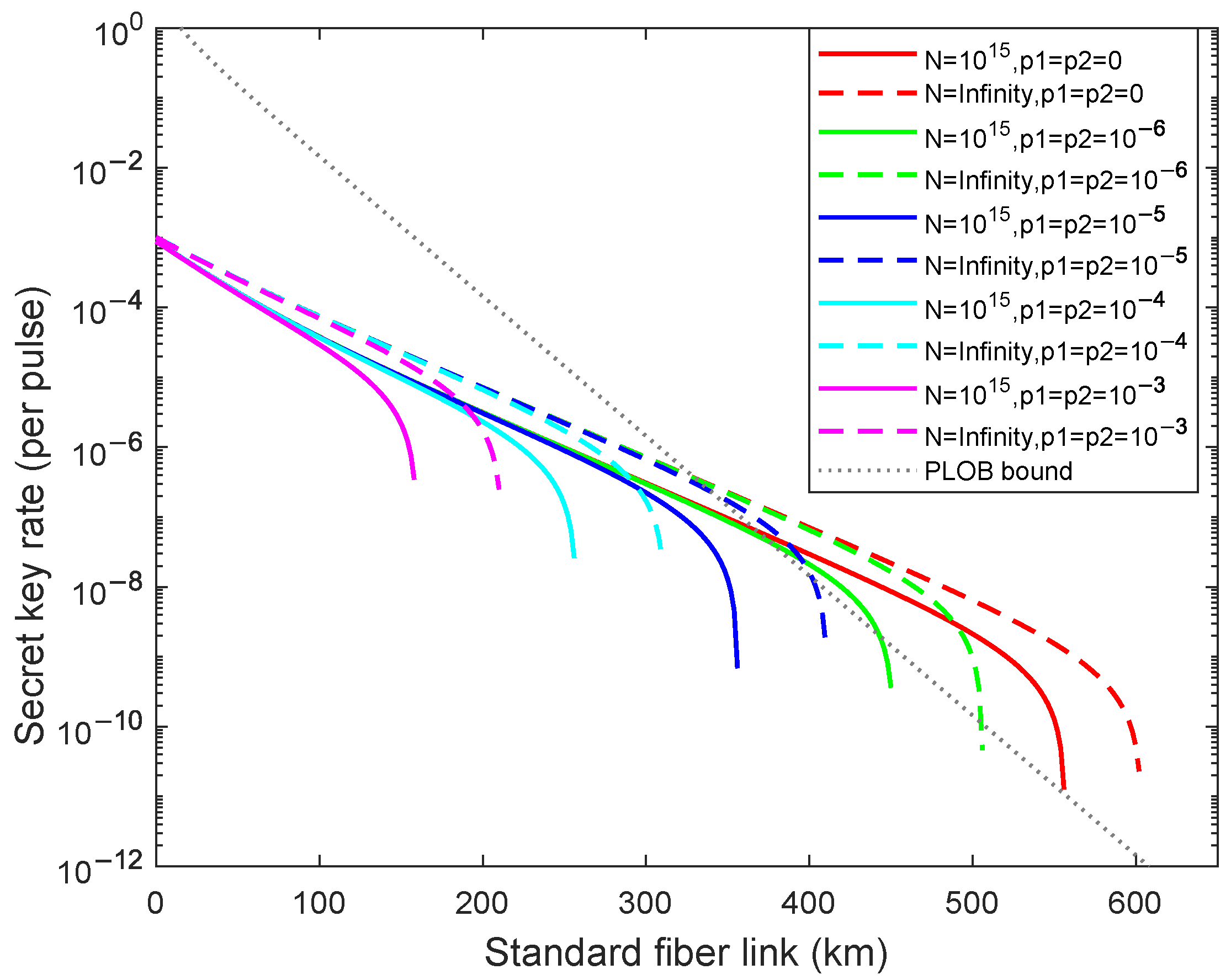
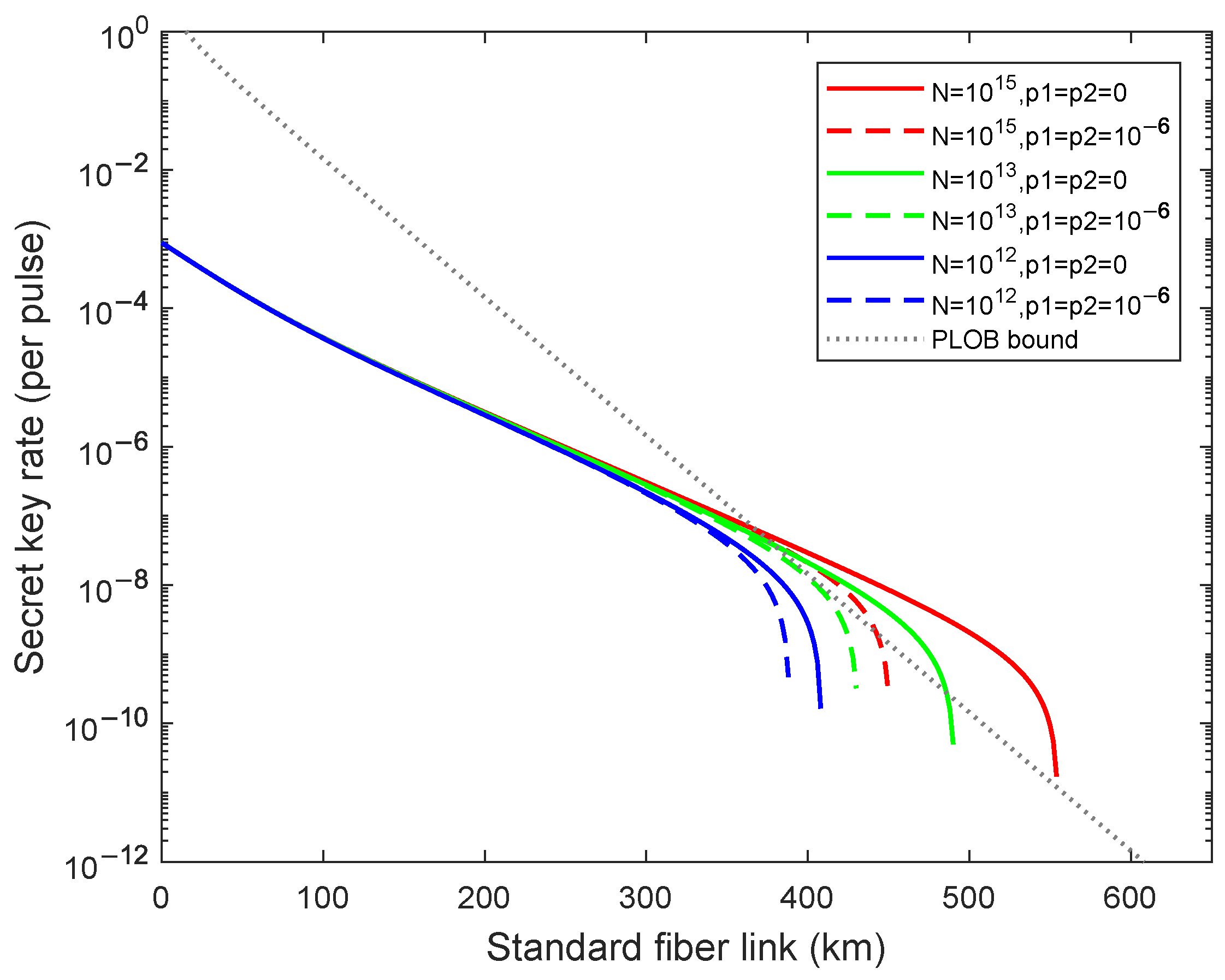
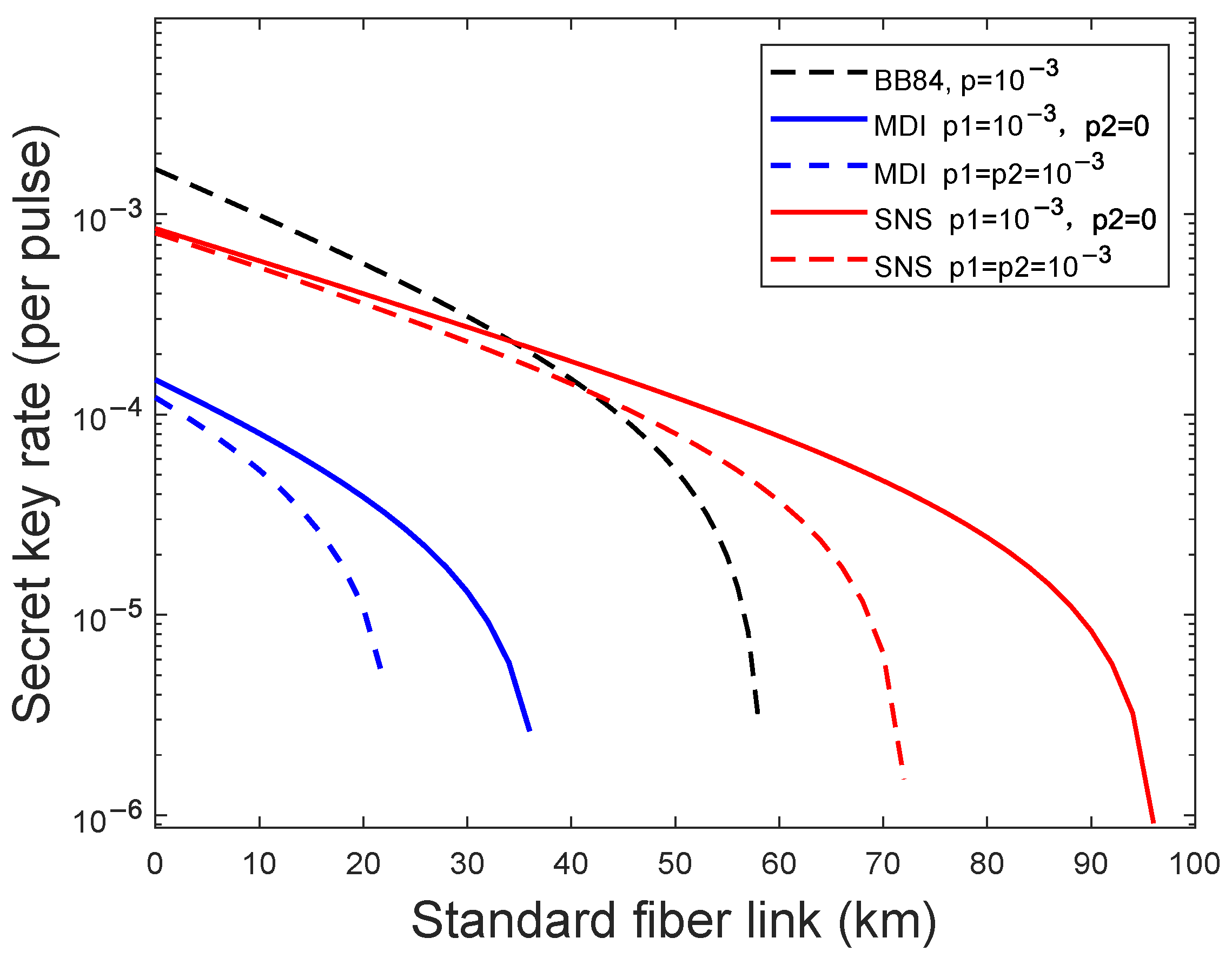
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Li, H.W.; Wang, S.; Huang, J.Z.; Chen, W.; Yin, Z.Q.; Li, F.Y.; Zhou, Z.; Liu, D.; Zhang, Y.; Guo, G.C.; et al. Attacking a practical quantum-key-distribution system with wavelength-dependent beam-splitter and multiwavelength sources. Phys. Rev. A 2011, 84, 062308. [Google Scholar] [CrossRef]
- Lydersen, L.; Wiechers, C.; Wittmann, C.; Elser, D.; Skaar, J.; Makarov, V. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photonics 2010, 4, 686–689. [Google Scholar] [CrossRef]
- Qian, Y.J.; He, D.Y.; Wang, S.; Chen, W.; Yin, Z.Q.; Guo, G.C.; Han, Z.F. Robust countermeasure against detector control attack in a practical quantum key distribution system. Optica 2019, 6, 1178–1184. [Google Scholar] [CrossRef]
- Jain, N.; Anisimova, E.; Khan, I.; Makarov, V.; Marquardt, C.; Leuchs, G. Trojan-horse attacks threaten the security of practical quantum cryptography. New J. Phys. 2014, 16, 123030. [Google Scholar] [CrossRef]
- Lucamarini, M.; Choi, I.; Ward, M.B.; Dynes, J.F.; Yuan, Z.; Shields, A.J. Practical security bounds against the trojan-horse attack in quantum key distribution. Phys. Rev. X 2015, 5, 031030. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef]
- Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef]
- Xie, Y.M.; Lu, Y.S.; Weng, C.X.; Cao, X.Y.; Jia, Z.Y.; Bao, Y.; Wang, Y.; Fu, Y.; Yin, H.L.; Chen, Z.B. Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quantum 2022, 3, 020315. [Google Scholar] [CrossRef]
- Pirandola, S.; Laurenza, R.; Ottaviani, C.; Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 2017, 8, 1–15. [Google Scholar] [CrossRef]
- Wang, X.B.; Yu, Z.W.; Hu, X.L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 2018, 98, 062323. [Google Scholar] [CrossRef]
- Ma, X.; Zeng, P.; Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 2018, 8, 031043. [Google Scholar] [CrossRef]
- Cui, C.; Yin, Z.Q.; Wang, R.; Chen, W.; Wang, S.; Guo, G.C.; Han, Z.F. Twin-field quantum key distribution without phase postselection. Phys. Rev. Appl. 2019, 11, 034053. [Google Scholar] [CrossRef]
- Curty, M.; Azuma, K.; Lo, H.K. Simple security proof of twin-field type quantum key distribution protocol. npj Quantum Inf. 2019, 5, 1–6. [Google Scholar] [CrossRef]
- Jiang, C.; Yu, Z.W.; Hu, X.L.; Wang, X.B. Unconditional security of sending or not sending twin-field quantum key distribution with finite pulses. Phys. Rev. Appl. 2019, 12, 024061. [Google Scholar] [CrossRef]
- Yu, Z.W.; Hu, X.L.; Jiang, C.; Xu, H.; Wang, X.B. Sending-or-not-sending twin-field quantum key distribution in practice. Sci. Rep. 2019, 9, 1–8. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Zhang, C.H.; Zhang, C.M.; Wang, Q. Asymmetric sending or not sending twin-field quantum key distribution in practice. Phys. Rev. A 2019, 99, 062316. [Google Scholar] [CrossRef]
- Hu, X.L.; Jiang, C.; Yu, Z.W.; Wang, X.B. Sending-or-not-sending twin-field protocol for quantum key distribution with asymmetric source parameters. Phys. Rev. A 2019, 100, 062337. [Google Scholar] [CrossRef]
- Xu, H.; Yu, Z.W.; Jiang, C.; Hu, X.L.; Wang, X.B. Sending-or-not-sending twin-field quantum key distribution: Breaking the direct transmission key rate. Phys. Rev. A 2020, 101, 042330. [Google Scholar] [CrossRef]
- Lu, Y.F.; Wang, Y.; Jiang, M.S.; Zhang, X.X.; Liu, F.; Li, H.W.; Zhou, C.; Tang, S.B.; Wang, J.Y.; Bao, W.S. Sending or Not-Sending Twin-Field Quantum Key Distribution with Flawed and Leaky Sources. Entropy 2021, 23, 1103. [Google Scholar] [CrossRef]
- Lu, Y.F.; Wang, Y.; Jiang, M.S.; Liu, F.; Zhang, X.X.; Bao, W.S. Finite-key analysis of sending-or-not-sending twin-field quantum key distribution with intensity fluctuations. Quantum Inf. Process. 2021, 20, 1–15. [Google Scholar] [CrossRef]
- Jiang, C.; Yu, Z.W.; Hu, X.L.; Wang, X.B. Robust twin-field quantum key distribution through sending-or-not-sending. Natl. Sci. Rev. 2022. [Google Scholar] [CrossRef]
- Jiang, C.; Hu, X.L.; Yu, Z.W.; Wang, X.B. Composable security for practical quantum key distribution with two way classical communication. New J. Phys. 2021, 23, 063038. [Google Scholar] [CrossRef]
- Jiang, C.; Hu, X.L.; Xu, H.; Yu, Z.W.; Wang, X.B. Zigzag approach to higher key rate of sending-or-not-sending twin field quantum key distribution with finite-key effects. New J. Phys. 2020, 22, 053048. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.W.; Zhang, W.; Guan, J.Y.; Chen, J.P.; Zhang, C.; Hu, X.L.; Li, H.; Jiang, C.; Lin, J.; et al. Experimental twin-field quantum key distribution through sending or not sending. Phys. Rev. Lett. 2019, 123, 100505. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.; Chen, Z.; Zhang, Y.; Xu, B.; Guo, H. Sending-or-not-sending twin-field quantum key distribution with light source monitoring. Entropy 2019, 22, 36. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.; Hu, X.L.; Guan, J.Y.; Yu, Z.W.; Xu, H.; Lin, J.; et al. Sending-or-not-sending with independent lasers: Secure twin-field quantum key distribution over 509 km. Phys. Rev. Lett. 2020, 124, 070501. [Google Scholar] [CrossRef] [PubMed]
- Pittaluga, M.; Minder, M.; Lucamarini, M.; Sanzaro, M.; Woodward, R.I.; Li, M.J.; Yuan, Z.; Shields, A.J. 600-km repeater-like quantum communications with dual-band stabilization. Nat. Photonics 2021, 15, 530–535. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, C.; Zhu, H.T.; Zou, M.; Yu, Z.W.; Hu, X.L.; Xu, H.; Ma, S.; Han, Z.; Chen, J.P.; et al. Field test of twin-field quantum key distribution through sending-or-not-sending over 428 km. Phys. Rev. Lett. 2021, 126, 250502. [Google Scholar] [CrossRef]
- Chen, J.P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.J.; Han, Z.Y.; Ma, S.Z.; Hu, X.L.; Li, Y.H.; Liu, H.; et al. Twin-field quantum key distribution over a 511 km optical fibre linking two distant metropolitan areas. Nat. Photonics 2021, 15, 570–575. [Google Scholar] [CrossRef]
- Li, H.W.; Yin, Z.Q.; Wang, S.; Qian, Y.J.; Chen, W.; Guo, G.C.; Han, Z.F. Randomness determines practical security of BB84 quantum key distribution. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Li, H.W.; Xu, Z.M.; Cai, Q.Y. Small imperfect randomness restricts security of quantum key distribution. Phys. Rev. A 2018, 98, 062325. [Google Scholar] [CrossRef]
- Sun, S.H.; Tian, Z.Y.; Zhao, M.S.; Ma, Y. Security evaluation of quantum key distribution with weak basis-choice flaws. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.M.; Wang, W.B.; Li, H.W.; Wang, Q. Weak randomness impacts the security of reference-frame-independent quantum key distribution. Opt. Lett. 2019, 44, 1226–1229. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.L.; Deng, X.Q.; Wang, Y.; Lu, Y.F.; Li, J.J.; Zhou, C.; Bao, W.S. Weak Randomness Analysis of Measurement-Device-Independent Quantum Key Distribution with Finite Resources. Photonics 2022, 9, 356. [Google Scholar] [CrossRef]
- Hwang, W.Y. Quantum key distribution with high loss: Toward global secure communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef]
- Wang, X.B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef]
- Lo, H.K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef]
- Müller-Quade, J.; Renner, R. Composability in quantum cryptography. New J. Phys. 2009, 11, 085006. [Google Scholar] [CrossRef]
- Chernoff, H. A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Ann. Math. Stat. 1952, 23, 493–507. [Google Scholar] [CrossRef]
- Curty, M.; Xu, F.; Cui, W.; Lim, C.C.W.; Tamaki, K.; Lo, H.K. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhao, Q.; Razavi, M.; Ma, X. Improved key-rate bounds for practical decoy-state quantum-key-distribution systems. Phys. Rev. A 2017, 95, 012333. [Google Scholar] [CrossRef]
- Tomamichel, M.; Lim, C.C.W.; Gisin, N.; Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 2012, 3, 1–6. [Google Scholar] [CrossRef] [PubMed]

| f | |||||
|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.-L.; Wang, Y.; Lu, Y.-F.; Li, J.-J.; Zhou, C.; Bao, W.-S. Security Analysis of Sending or Not-Sending Twin-Field Quantum Key Distribution with Weak Randomness. Entropy 2022, 24, 1339. https://doi.org/10.3390/e24101339
Jiang X-L, Wang Y, Lu Y-F, Li J-J, Zhou C, Bao W-S. Security Analysis of Sending or Not-Sending Twin-Field Quantum Key Distribution with Weak Randomness. Entropy. 2022; 24(10):1339. https://doi.org/10.3390/e24101339
Chicago/Turabian StyleJiang, Xiao-Lei, Yang Wang, Yi-Fei Lu, Jia-Ji Li, Chun Zhou, and Wan-Su Bao. 2022. "Security Analysis of Sending or Not-Sending Twin-Field Quantum Key Distribution with Weak Randomness" Entropy 24, no. 10: 1339. https://doi.org/10.3390/e24101339
APA StyleJiang, X.-L., Wang, Y., Lu, Y.-F., Li, J.-J., Zhou, C., & Bao, W.-S. (2022). Security Analysis of Sending or Not-Sending Twin-Field Quantum Key Distribution with Weak Randomness. Entropy, 24(10), 1339. https://doi.org/10.3390/e24101339






