Error Analysis of a PFEM Based on the Euler Semi-Implicit Scheme for the Unsteady MHD Equations
Abstract
1. Introduction
2. Functional Setting of the Unsteady MHD Equation
3. The Euler Semi-Implicit Scheme and Its Error Estimates: Time Discretization
4. PFEM for the MHD Equations
5. Error Analysis for the Fully Discrete Euler Semi-Implicit Scheme
6. Error Estimates
7. Numerical Example
7.1. Convergence Tests
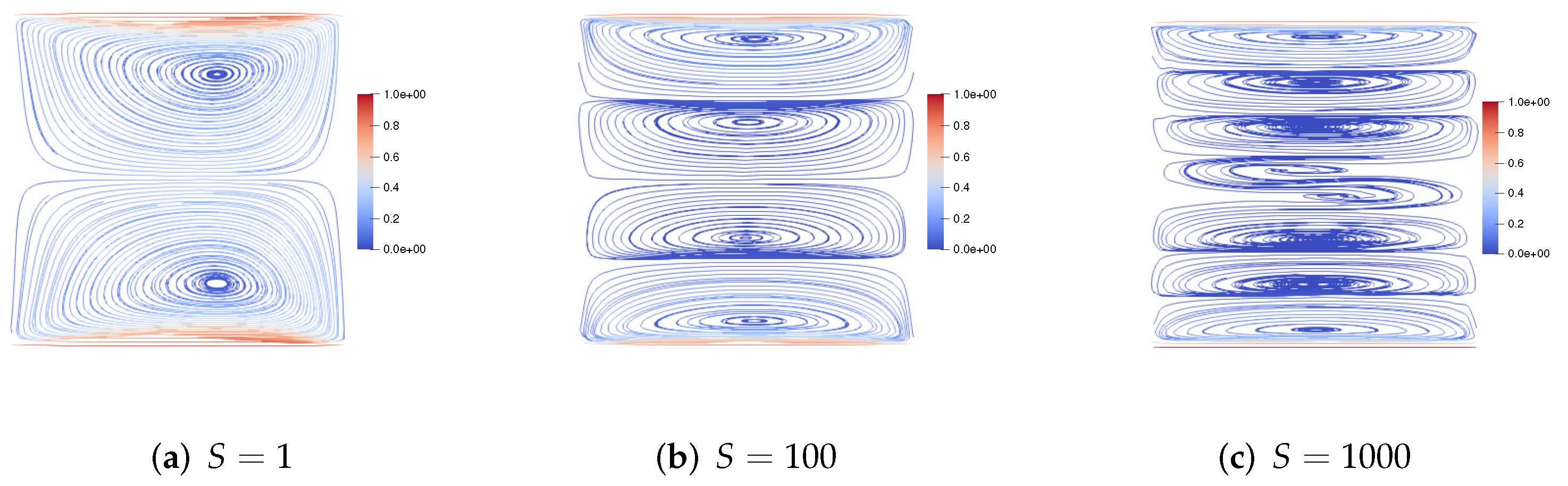
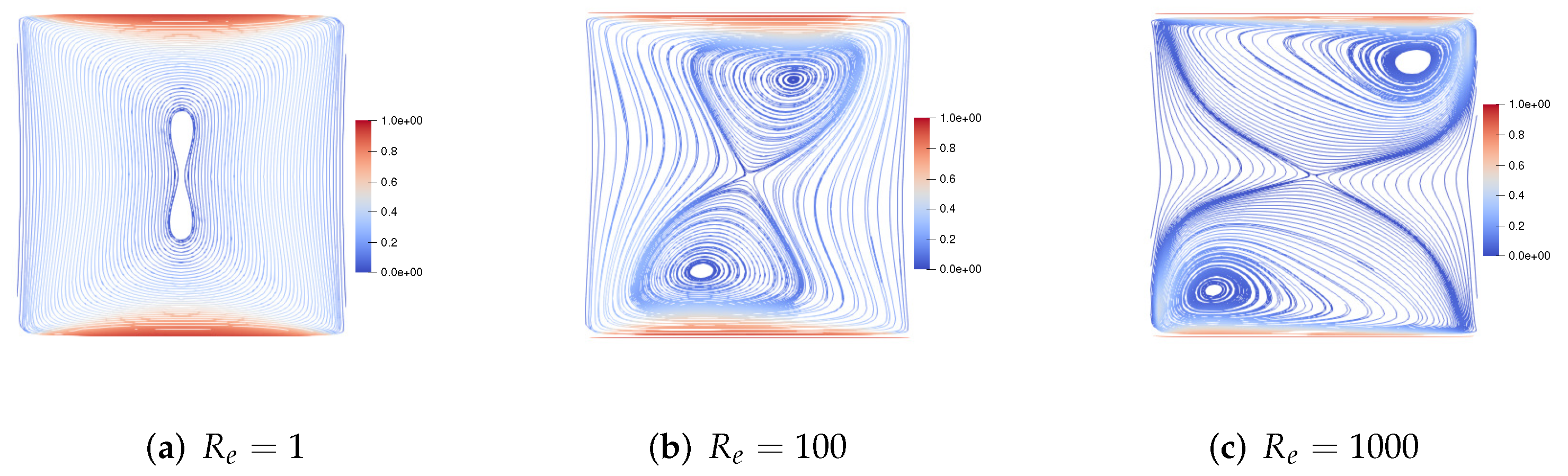
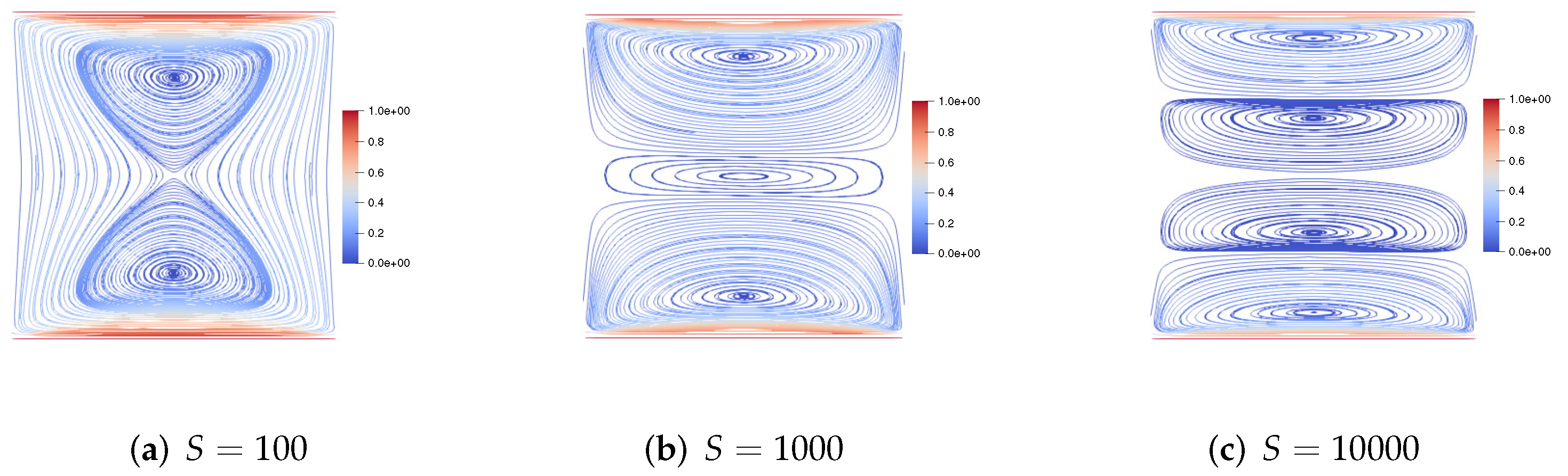
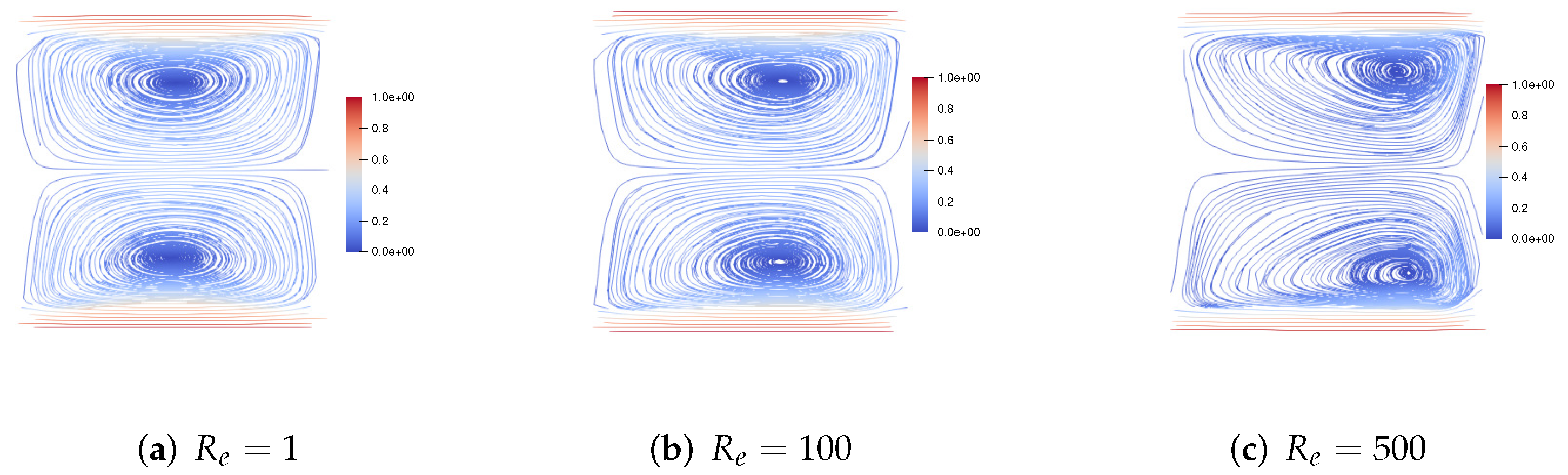
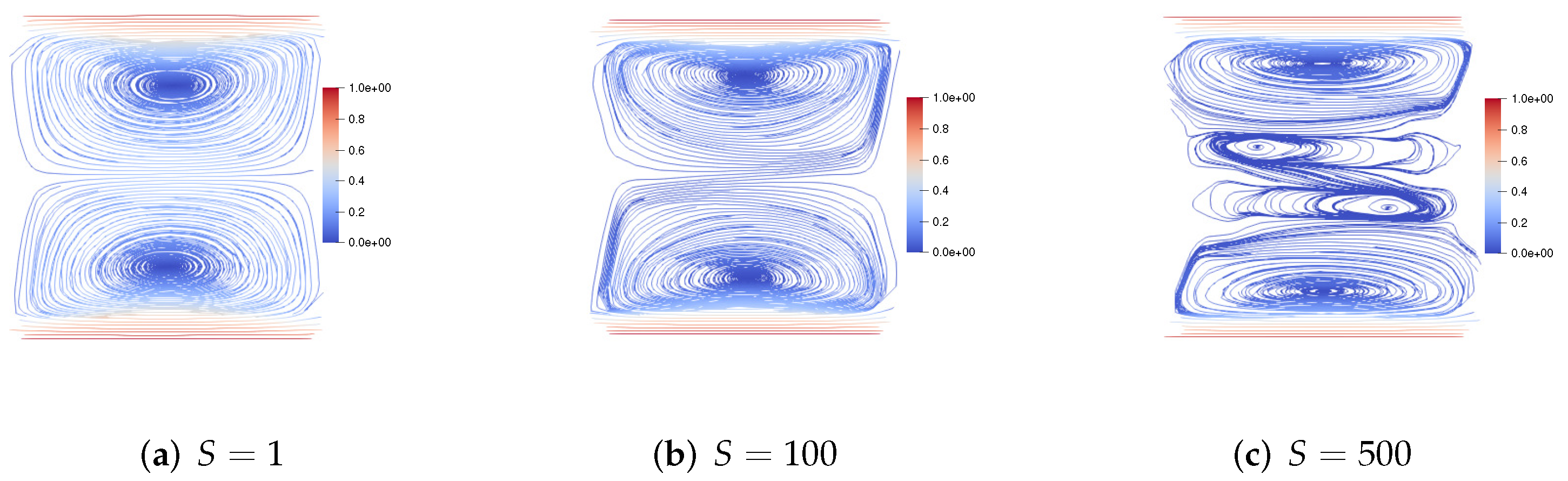
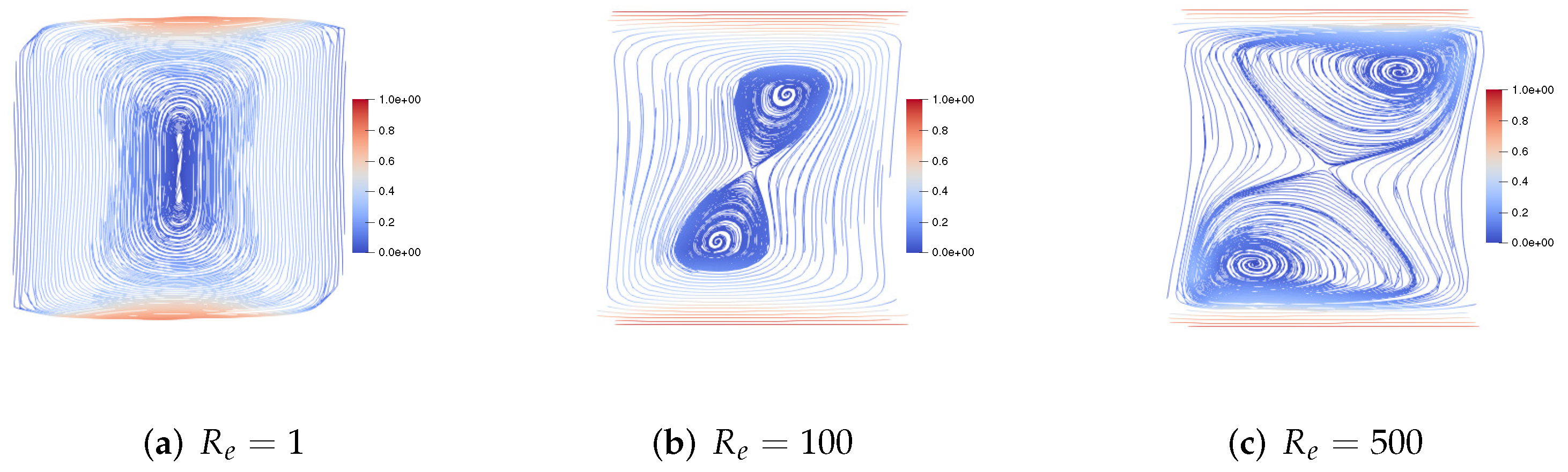
7.2. Two-Sided Lid-Driven Square Cavity Flow
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, G.; He, Y. Decoupled schemes for unsteady MHD equations. I. Time discretization. Numer. Methods Partial Differ. Equ. 2017, 33, 956–973. [Google Scholar] [CrossRef]
- Zhang, G.; He, X.; Yang, X. Fully decoupled, linear and unconditionally energy stable time discretization scheme for solving the magneto-hydrodynamic equations. J. Comput. Appl. Math. 2020, 369, 112636. [Google Scholar] [CrossRef]
- Zhang, G.; He, Y. Decoupled schemes for unsteady MHD equations II: Finite element spatial discretization and numerical implementation. Comput. Math. Appl. 2015, 69, 1390–1406. [Google Scholar] [CrossRef]
- He, Y. Unconditional convergence of the Euler semi-implicit scheme for the three-dimensional incompressible MHD equations. IMA J. Numer. Anal. 2015, 35, 767–801. [Google Scholar] [CrossRef]
- Sermange, M.; Temam, R. Some mathematical questions related to the MHD equations. Commun. Pure Appl. Math. 1983, 36, 635–664. [Google Scholar] [CrossRef]
- Dong, X.; He, Y.; Zhang, Y. Convergence analysis of three finite element iterative methods for the 2D/3D stationary incompressible magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 2014, 276, 287–311. [Google Scholar] [CrossRef]
- Yang, J.; He, Y. Stability and error analysis for the first-order Euler implicit/explicit scheme for the 3D MHD equations. Int. J. Comput. Methods 2018, 15, 1750077. [Google Scholar] [CrossRef]
- Wiedmer, M. Finite element approximation for equations of magnetohydrodynamics. Math. Comput. 2000, 69, 83–101. [Google Scholar] [CrossRef]
- Gerbeau, J. A stabilized finite element method for the incompressible magnetohydrodynamic equations. Numer. Math. 2000, 87, 83–111. [Google Scholar] [CrossRef]
- Schötzau, D. Mixed finite element methods for stationary incompressible magneto-hydrodynamics. Numer. Math. 2004, 96, 771–800. [Google Scholar] [CrossRef]
- Schmidt, P. A Galerkin method for time-dependent MHD flow with nonideal boundaries. Commun. Appl. Anal. 1999, 3, 383–398. [Google Scholar]
- Schonbek, M.; Schonbek, T.; Süli, E. Large-time behaviour of solutions to the magneto-hydrodynamics equations. Math. Ann. 1996, 304, 717–756. [Google Scholar] [CrossRef]
- Gerbeau, J.; Le Bris, C.; Lelièvre, T. Mathematical Methods for the Magnetohydrodynamics of Liquid Metals; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Prohl, A. Convergent finite element discretizations of the nonstationary incompressible magnetohydrodynamics system. ESAIM Math. Model. Numer. Anal. 2008, 42, 1065–1087. [Google Scholar] [CrossRef]
- Brezzi, F.; Pitkäranta, J. On the Stabilization of Finite Element Approximations of the Stokes Equations; Springer Fachmedien Wiesbaden: Wiesbaden, Geymany, 1984. [Google Scholar]
- Chorin, A. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Chorin, A. On the convergence of discrete approximations to the Navier-Stokes equations. Math. Comput. 1969, 23, 341–353. [Google Scholar] [CrossRef]
- Deng, J.; Si, Z. A decoupling penalty finite element method for the stationary incompressible MagnetoHydroDynamics equation. Int. J. Heat Mass Transf. 2019, 128, 601–612. [Google Scholar] [CrossRef]
- Témam, R. Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (I). Arch. Ration. Mech. Anal. 1969, 32, 135–153. [Google Scholar] [CrossRef]
- Témam, R. Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Arch. Ration. Mech. Anal. 1969, 33, 377–385. [Google Scholar] [CrossRef]
- Courant, R. Variational methods for the solution of problems of equilibrium and vibrations. Bull. Am. Math. Soc. 1943, 49, 1–23. [Google Scholar] [CrossRef]
- He, Y. Optimal error estimate of the penalty finite element method for the time-dependent Navier–Stokes equations. Math. Comput. 2005, 74, 1201–1216. [Google Scholar] [CrossRef]
- He, Y.; Li, J. A penalty finite element method based on the Euler implicit/explicit scheme for the time-dependent Navier–Stokes equations. J. Comput. Appl. Math. 2010, 235, 708–725. [Google Scholar] [CrossRef]
- Lu, X.; Lin, P. Error estimate of the P1 nonconforming finite element method for the penalized unsteady Navier–Stokes equations. Numer. Math. 2010, 115, 261–287. [Google Scholar] [CrossRef]
- Su, H.; Feng, X.; Huang, P. Iterative methods in penalty finite element discretization for the steady MHD equations. Comput. Methods Appl. Mech. Eng. 2016, 304, 521–545. [Google Scholar] [CrossRef]
- Shen, J. On error estimates of the penalty method for unsteady Navier–Stokes equations. SIAM J. Numer. Anal. 1995, 32, 386–403. [Google Scholar] [CrossRef]
- He, Y.; Zou, J. A priori estimates and optimal finite element approximation of the MHD flow in smooth domains. ESAIM Math. Model. Numer. Anal. 2018, 52, 181–206. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.; Zhang, G. On an efficient second order backward difference Newton scheme for MHD system. J. Math. Anal. Appl. 2018, 458, 676–714. [Google Scholar] [CrossRef]
- Shi, K.; Feng, X.; Su, H. Optimal Error Estimate of the Penalty Method for the 2D/3D Time-Dependent MHD Equations; College of Mathematics and System Sciences, Xinjiang University: Urumqi, China, 2022; In Preparation. [Google Scholar]
- He, Y. A fully discrete stabilized finite-element method for the time-dependent Navier–Stokes problem. IMA J. Numer. Anal. 2003, 23, 665–691. [Google Scholar] [CrossRef]
- Shen, J. Long time stability and convergence for fully discrete nonlinear Galerkin methods. Appl. Anal. 1990, 38, 201–229. [Google Scholar] [CrossRef]
- Shi, K.; Su, H.; Feng, X. Optimal Error Estimate of the PFEM for the 2D/3D Unsteady MHD Equations; College of Mathematics and System Sciences, Xinjiang University: Urumqi, China, 2022; In Preparation. [Google Scholar]
- Perumal, D.; Dass, A. Simulation of Incompressible Flows in Two-Sided Lid-Driven Square Cavities: Part I-FDM. CFD Lett. 2010, 2, 13–24. [Google Scholar]


| h | Ratio | Ratio | Ratio | Ratio | Ratio | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1/8 | 2.46 × 10 | 5.34 × 10 | 5.01 × 10 | 1.39 × 10 | 3.30 × 10 | |||||
| 1/16 | 6.18 × 10 | 2.00 | 2.59 × 10 | 1.04 | 1.43 × 10 | 1.81 | 3.55 × 10 | 1.97 | 1.66 × 10 | 0.99 |
| 1/32 | 1.53 × 10 | 2.01 | 1.28 × 10 | 1.02 | 4.29 × 10 | 1.74 | 8.92 × 10 | 1.99 | 8.33 × 10 | 1.00 |
| 1/64 | 3.80 × 10 | 2.01 | 6.34 × 10 | 1.01 | 1.37 × 10 | 1.65 | 2.23 × 10 | 2.00 | 4.17 × 10 | 1.00 |
| 1/128 | 9.45 × 10 | 2.01 | 3.16 × 10 | 1.00 | 4.56 × 10 | 1.58 | 5.59 × 10 | 2.00 | 2.08 × 10 | 1.00 |
| h | Ratio | Ratio | Ratio | Ratio | Ratio | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1/4 | 2.41 × 10 | 2.49 × 10 | 9.05 × 10 | 1.53 × 10 | 2.44 × 10 | |||||
| 1/8 | 6.11 × 10 | 1.98 | 1.26 × 10 | 0.99 | 2.95 × 10 | 1.61 | 3.60 × 10 | 2.08 | 1.21 × 10 | 1.01 |
| 1/12 | 2.72 × 10 | 2.00 | 8.38 × 10 | 1.00 | 1.46 × 10 | 1.73 | 1.58 × 10 | 2.03 | 8.02 × 10 | 1.01 |
| 1/16 | 1.53 × 10 | 2.00 | 6.29 × 10 | 1.00 | 8.84 × 10 | 1.75 | 8.83 × 10 | 2.02 | 6.01 × 10 | 1.00 |
| 1/20 | 9.80 × 10 | 2.00 | 5.03 × 10 | 1.00 | 6.00 × 10 | 1.74 | 5.64 × 10 | 2.01 | 4.81 × 10 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Su, H.; Feng, X. Error Analysis of a PFEM Based on the Euler Semi-Implicit Scheme for the Unsteady MHD Equations. Entropy 2022, 24, 1395. https://doi.org/10.3390/e24101395
Shi K, Su H, Feng X. Error Analysis of a PFEM Based on the Euler Semi-Implicit Scheme for the Unsteady MHD Equations. Entropy. 2022; 24(10):1395. https://doi.org/10.3390/e24101395
Chicago/Turabian StyleShi, Kaiwen, Haiyan Su, and Xinlong Feng. 2022. "Error Analysis of a PFEM Based on the Euler Semi-Implicit Scheme for the Unsteady MHD Equations" Entropy 24, no. 10: 1395. https://doi.org/10.3390/e24101395
APA StyleShi, K., Su, H., & Feng, X. (2022). Error Analysis of a PFEM Based on the Euler Semi-Implicit Scheme for the Unsteady MHD Equations. Entropy, 24(10), 1395. https://doi.org/10.3390/e24101395





