Flexible and Efficient Inference with Particles for the Variational Gaussian Approximation
Abstract
:1. Introduction
2. Related Work
2.1. The Variational Gaussian Approximation
2.2. Natural Gradients
2.3. Particle-Based VI
2.4. GVA in Bayesian Neural Networks
2.5. Related Approaches
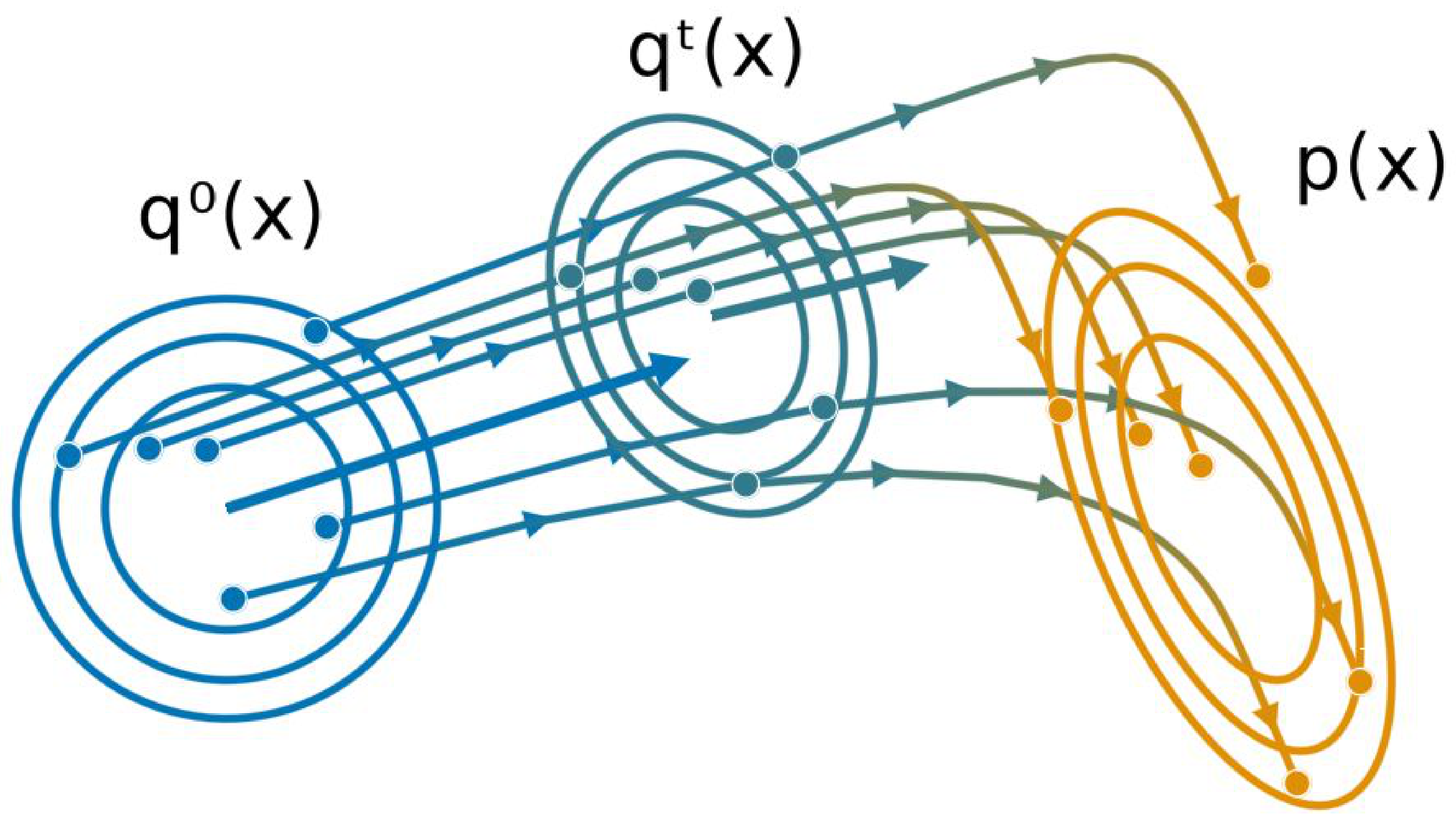
3. Gaussian (Particle) Flow
3.1. Gaussian Variable Flows
3.2. From Variable Flows to Parameter Flows
3.3. Particle Dynamics
Relaxation of Empirical Free Energy and Convergence
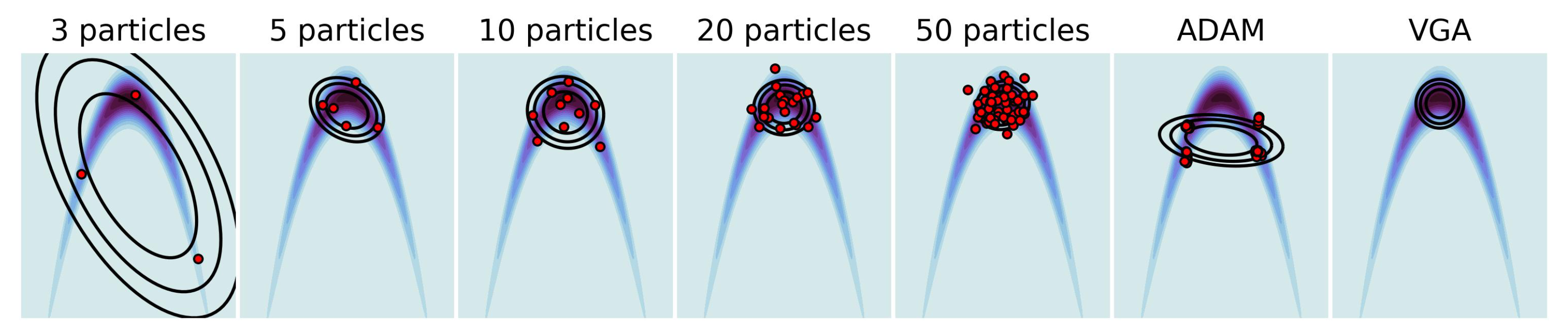
3.4. Algorithm and Properties
- Gradients of expectations have zero variance, at the cost of a bias decreasing with the number of particles and equal to zero for Gaussian target (see Theorem 1);
- It works with noisy gradients (when using subsampling data, for example);
- The rank of the approximated covariance C is . When , the algorithm can be used to obtain a low-rank approximation.
- The complexity of our algorithm is and storing complexity is . By adjusting the number of particles used, we can control the performance trade-off;
- GPF (and GF) are also compatible with any kind of structured MF (see Section 3.5);
- Despite working with an empirical distribution, we can compute a surrogate of the free energy to optimize hyper-parameters, compute the lower bound of the log-evidence, or simply monitor convergence.
| Algorithm 1: Gaussian Flow (GF) |
 |
| Algorithm 2: Gaussian Particle Flow (GPF) |
 |
3.4.1. Relaxation of Empirical Free Energy
3.4.2. Dynamics and Fixed Points for Gaussian Targets
3.5. Structured Mean-Field
3.6. Comparison with SVGD
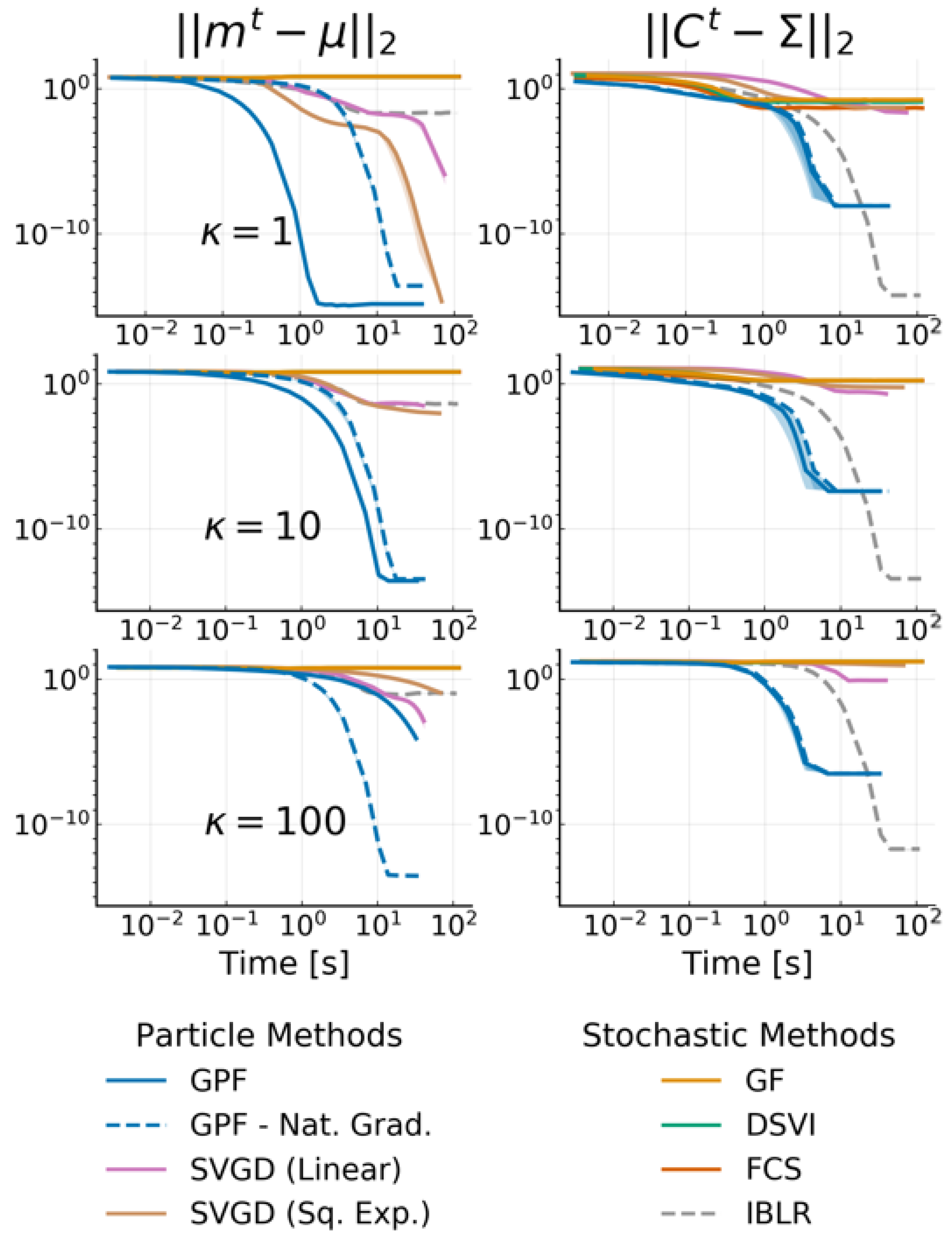
4. Experiments
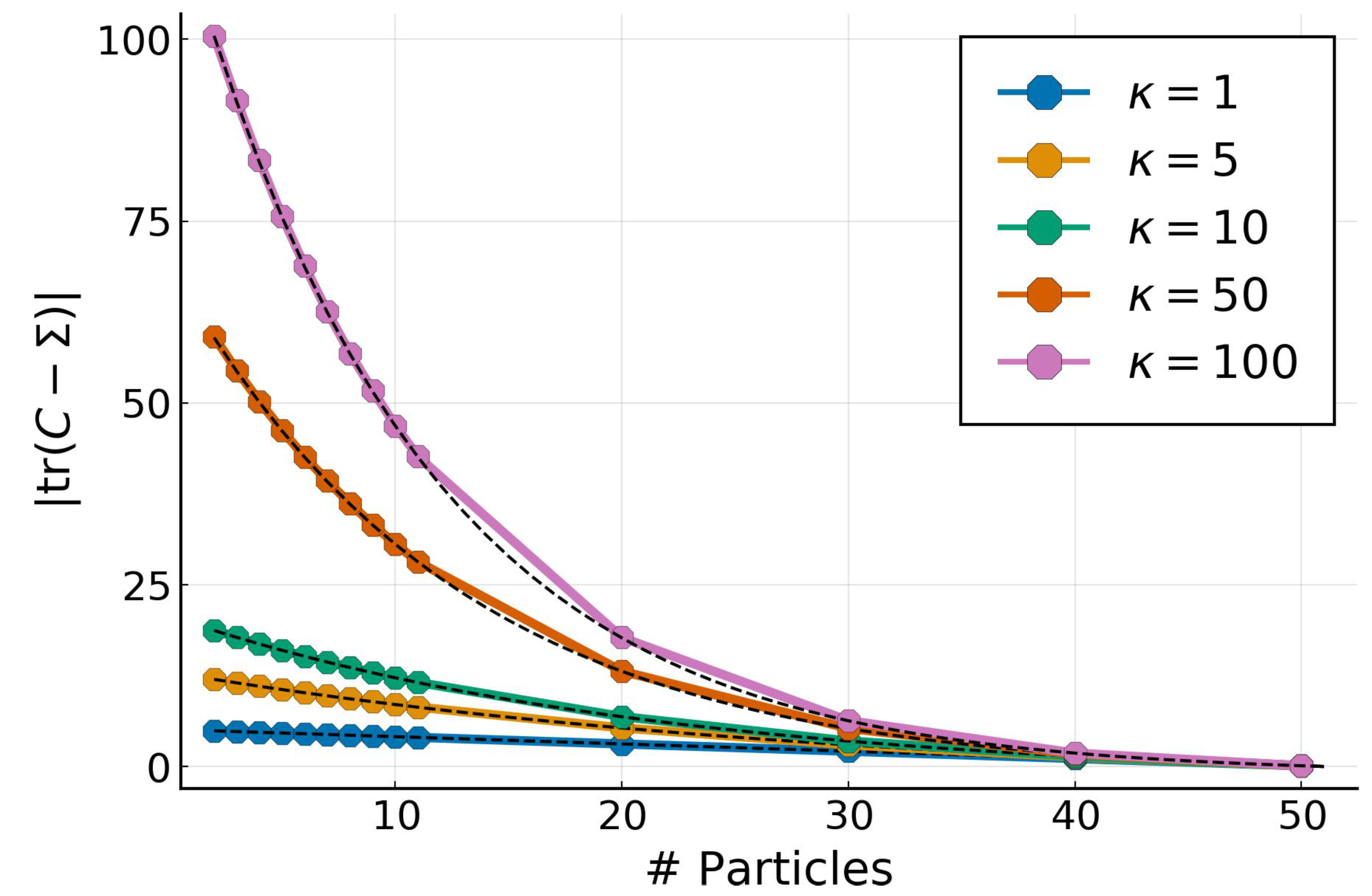
4.1. Multivariate Gaussian Targets
4.2. Low-Rank Approximation for Full Gaussian Targets
4.3. High-Dimensional Low-Rank Gaussian Targets
4.4. Non-Gaussian Target
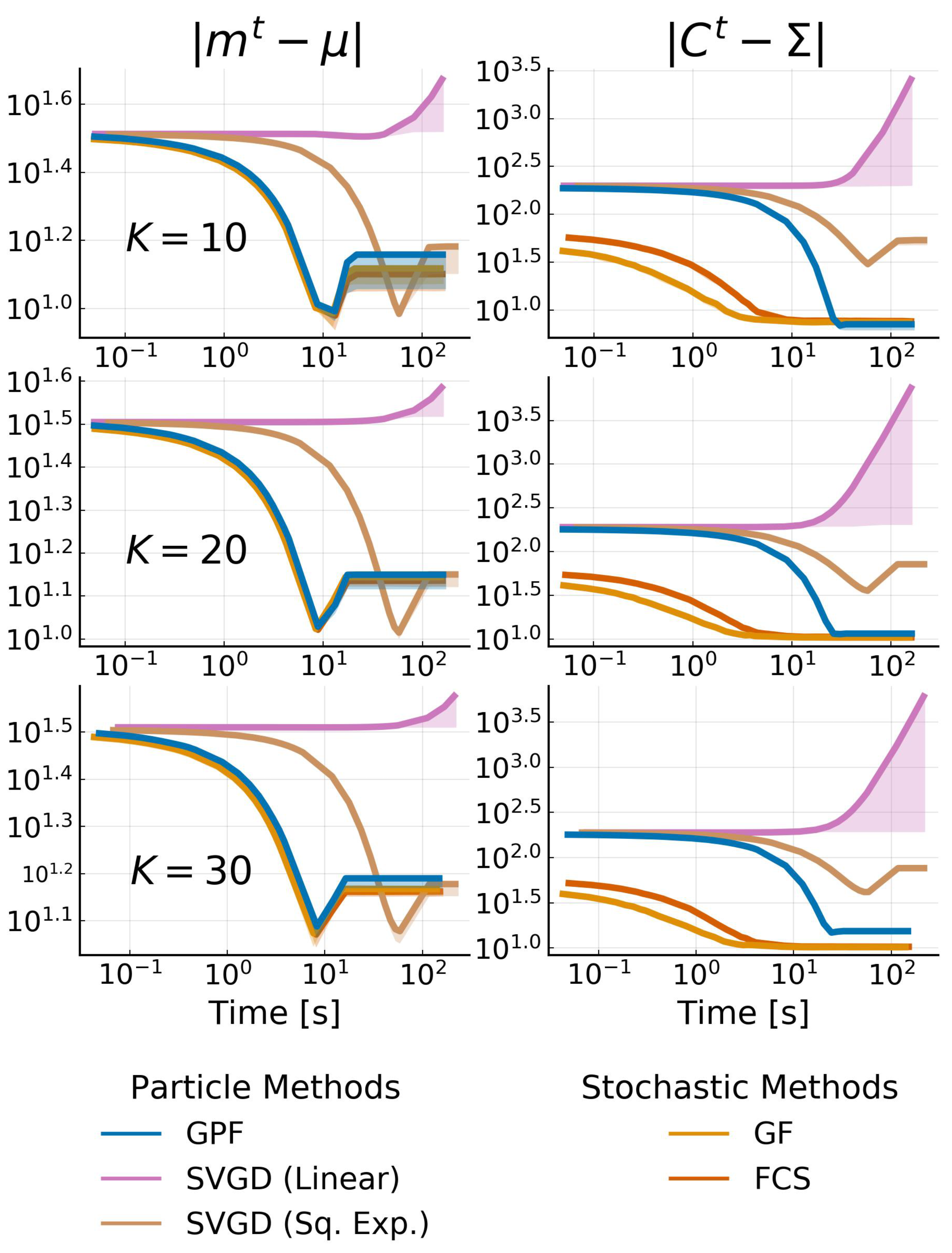
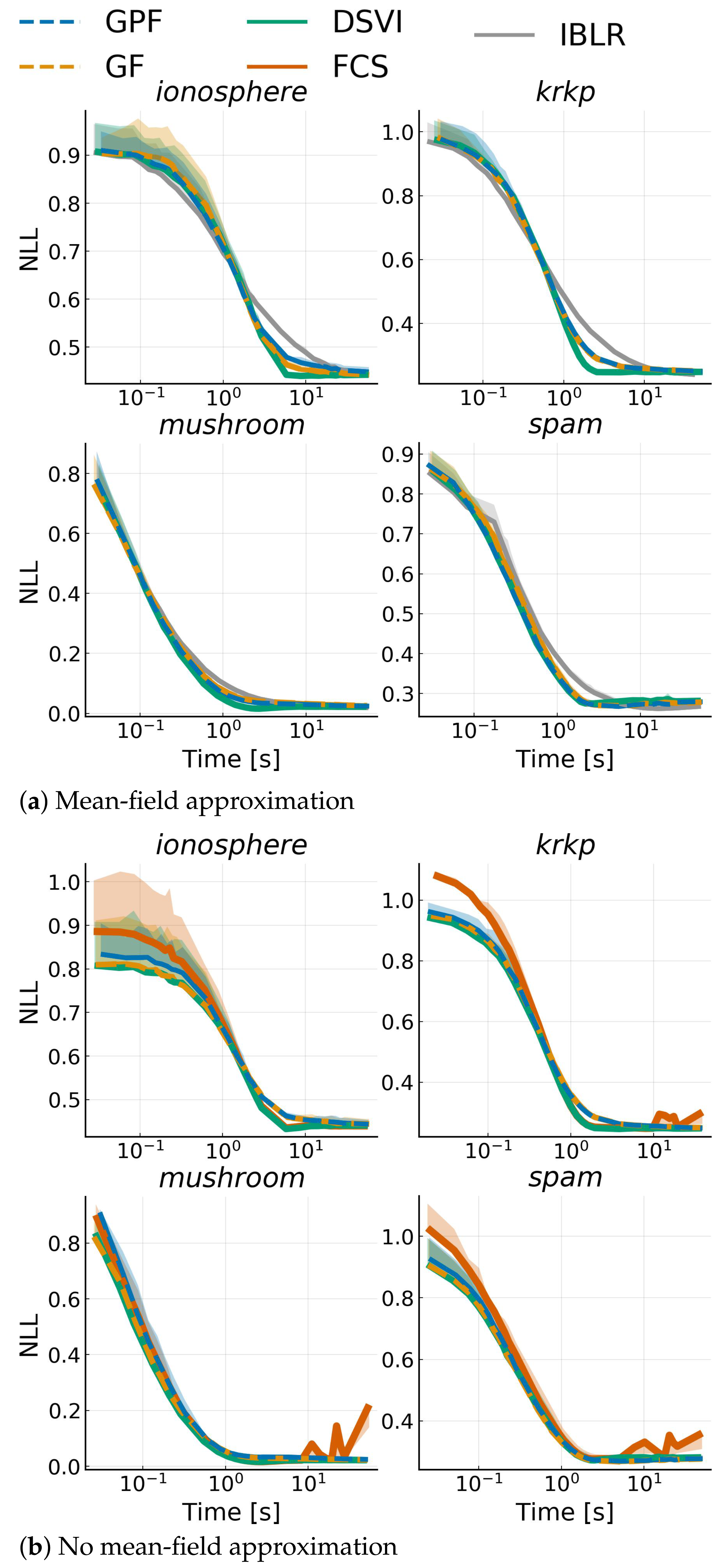
4.5. Bayesian Logistic Regression
4.6. Bayesian Neural Network
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Optimal Parameters
Appendix B. Relaxation of the Empirical Free Energy
Appendix C. Riemannian Gradient for Matrix Parameter Γ
Appendix D. Regularised Free Energy for N ≤ D
Efficient Computation of
Appendix E. Proof of Theorem 1: Fixed Points for a Gaussian Model (N > d)
Appendix F. Proof of Theorem 2: Rates of Convergence for Gaussian Targets
Appendix F.1. Convergence of the Mean
Appendix F.2. Convergence of the Covariance Matrix
Appendix F.3. Convergence of the Trace of the Covariance
Appendix F.4. Decay of Fluctuation Part of the Free Energy
Appendix F.5. Asymptotic Decay of the Free Energy:
Appendix G. Proof of Theorem 3: Fixed-Points for Gaussian Model (N ≤ D)
Appendix H. Dimension-Wise Optimizers
Appendix H.1. ADAM
| Algorithm A1: ADAM |
| Input: Output: |
| Algorithm A2: Dimension-wise ADAM |
| Input: Output: ; ; |
Appendix H.2. AdaGrad
| Algorithm A3: AdaGrad |
| Input: Output: |
| Algorithm A4: Dimension-wise AdaGrad |
| Input: Output: ; |
Appendix H.3. RMSProp
| Algorithm A5: RMSProp |
| Input: Output: |
| Algorithm A6: Dimension-wise RMSProp |
| Input: Output: |
Appendix I. Additional Figures
Appendix I.1. Bayesian Logistic Regression
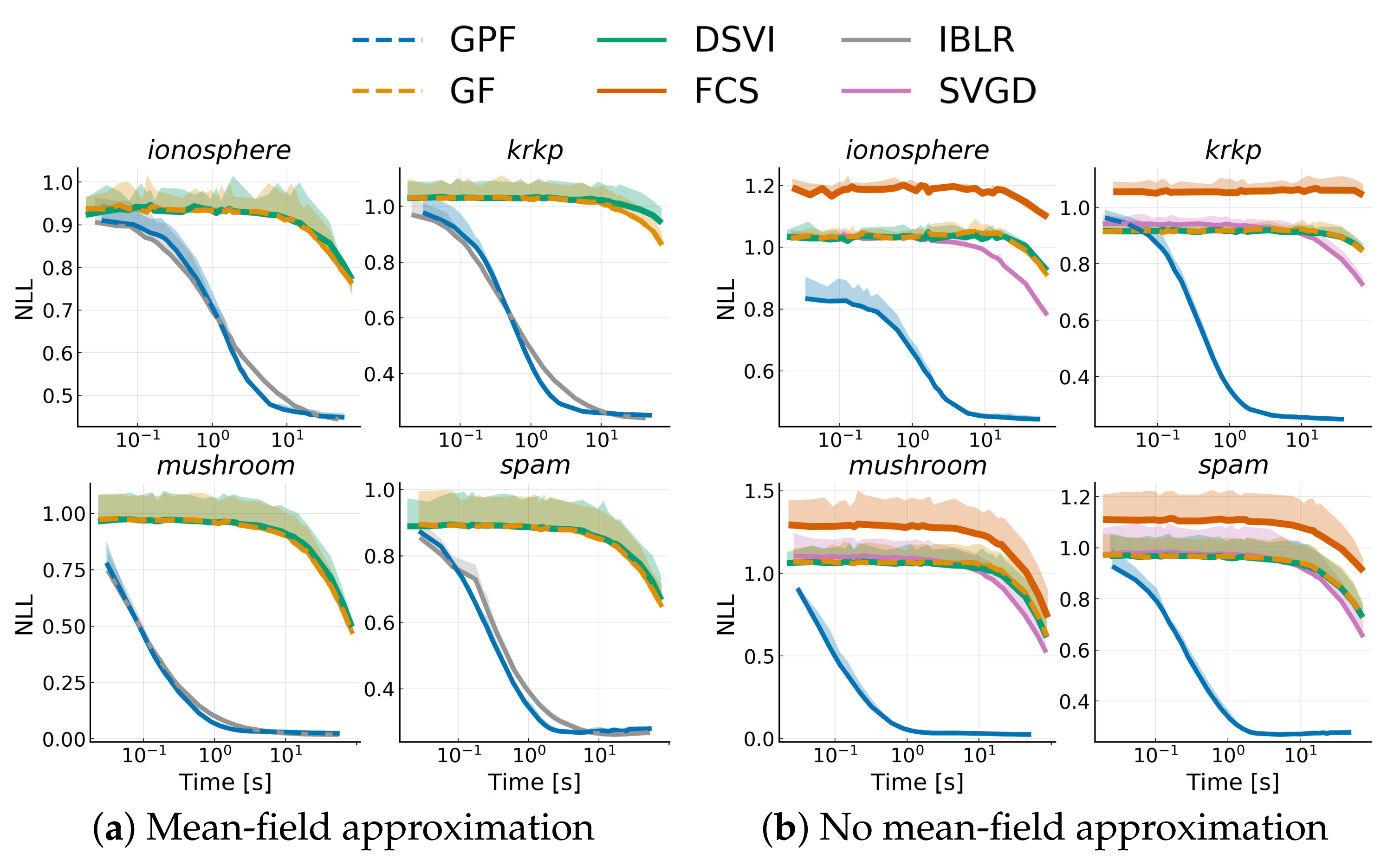
Appendix I.2. Bayesian Neural Network
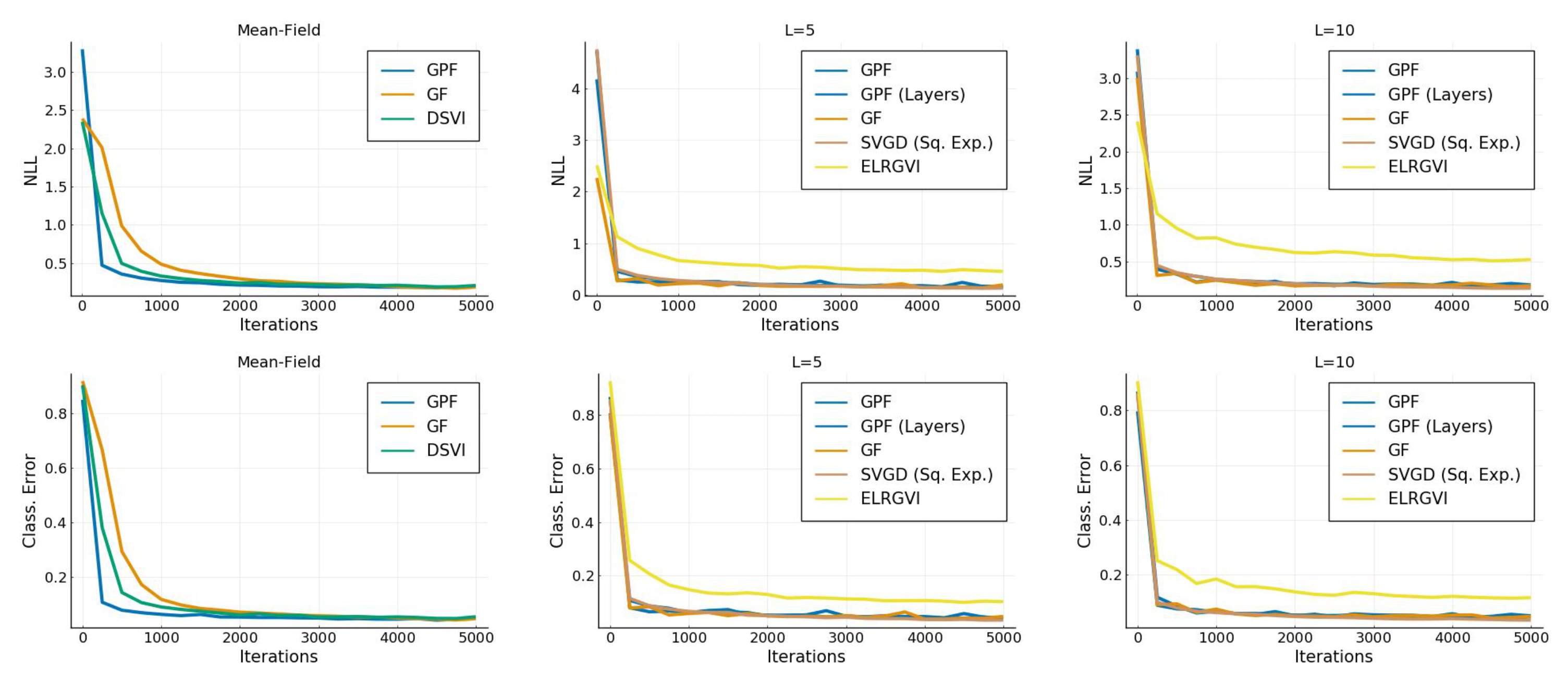
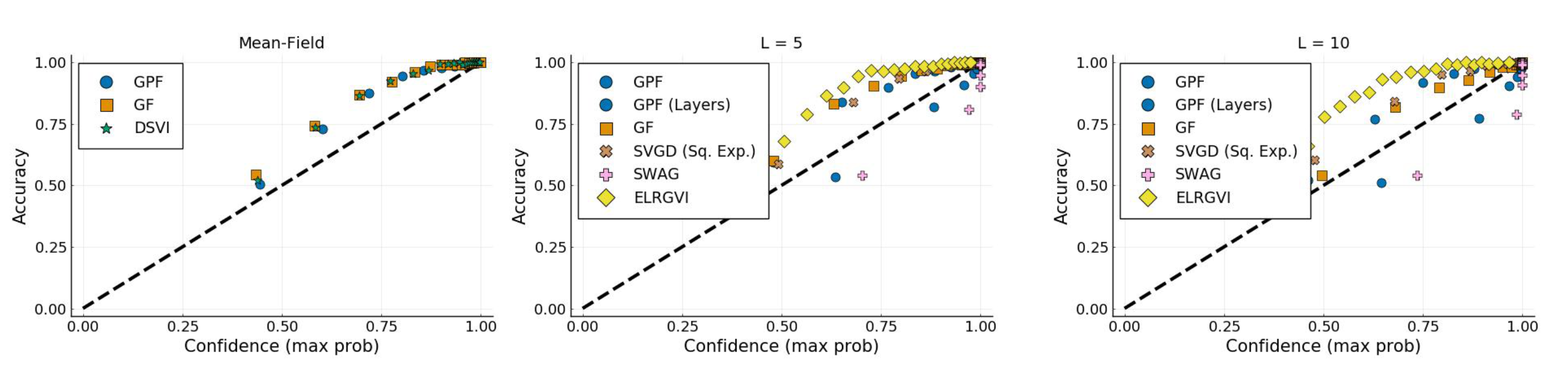
References
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- Settles, B. Active Learning Literature Survey; Computer Sciences Technical Report 1648; University of Wisconsin–Madison: Madison, WI, USA, 2009. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Bardenet, R.; Doucet, A.; Holmes, C. On Markov chain Monte Carlo methods for tall data. J. Mach. Learn. Res. 2017, 18, 1515–1557. [Google Scholar]
- Cowles, M.K.; Carlin, B.P. Markov chain Monte Carlo convergence diagnostics: A comparative review. J. Am. Stat. Assoc. 1996, 91, 883–904. [Google Scholar] [CrossRef]
- Barber, D.; Bishop, C.M. Ensemble learning for multi-layer networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1998; pp. 395–401. [Google Scholar]
- Graves, A. Practical Variational Inference for Neural Networks. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Volume 24, pp. 2348–2356. [Google Scholar]
- Ranganath, R.; Gerrish, S.; Blei, D. Black box variational inference. In Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; pp. 814–822. [Google Scholar]
- Liu, Q.; Lee, J.; Jordan, M. A kernelized Stein discrepancy for goodness-of-fit tests. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 276–284. [Google Scholar]
- Liu, Q.; Wang, D. Stein variational gradient descent as moment matching. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 32, pp. 8868–8877. [Google Scholar]
- Zhuo, J.; Liu, C.; Shi, J.; Zhu, J.; Chen, N.; Zhang, B. Message Passing Stein Variational Gradient Descent. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 6018–6027. [Google Scholar]
- Opper, M.; Archambeau, C. The variational Gaussian approximation revisited. Neural Comput. 2009, 21, 786–792. [Google Scholar] [CrossRef] [PubMed]
- Challis, E.; Barber, D. Gaussian kullback-leibler approximate inference. J. Mach. Learn. Res. 2013, 14, 2239–2286. [Google Scholar]
- Titsias, M.; Lázaro-Gredilla, M. Doubly stochastic variational Bayes for non-conjugate inference. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1971–1979. [Google Scholar]
- Ong, V.M.H.; Nott, D.J.; Smith, M.S. Gaussian variational approximation with a factor covariance structure. J. Comput. Graph. Stat. 2018, 27, 465–478. [Google Scholar] [CrossRef] [Green Version]
- Tan, L.S.; Nott, D.J. Gaussian variational approximation with sparse precision matrices. Stat. Comput. 2018, 28, 259–275. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.; Schmidt, M.; Khan, M.E. Handling the Positive-Definite Constraint in the Bayesian Learning Rule. In Proceedings of the 37th International Conference on Machine Learning, Virtual. 13–18 July 2020; Volume 119, pp. 6116–6126. [Google Scholar]
- Hinton, G.E.; van Camp, D. Keeping the Neural Networks Simple by Minimizing the Description Length of the Weights. In Proceedings of the Sixth Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 26–28 July 1993; COLT ’93;. Association for Computing Machinery: New York, NY, USA, 1993; pp. 5–13. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef] [Green Version]
- Amari, S.I. Natural Gradient Works Efficiently in Learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Khan, M.E.; Nielsen, D. Fast yet simple natural-gradient descent for variational inference in complex models. In Proceedings of the International Symposium on Information Theory and Its Applications (ISITA), Singapore, 28–31 October 2018; pp. 31–35. [Google Scholar]
- Lin, W.; Khan, M.E.; Schmidt, M. Fast and simple natural-gradient variational inference with mixture of exponential-family approximations. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 3992–4002. [Google Scholar]
- Salimbeni, H.; Eleftheriadis, S.; Hensman, J. Natural Gradients in Practice: Non-Conjugate Variational Inference in Gaussian Process Models. In Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, Lanzarote, Canary Islands, 9–11 April 2018; pp. 689–697. [Google Scholar]
- Liu, Q.; Wang, D. Stein variational gradient descent: A general purpose bayesian inference algorithm. arXiv 2016, arXiv:1608.04471. [Google Scholar]
- Ba, J.; Erdogdu, M.A.; Ghassemi, M.; Suzuki, T.; Sun, S.; Wu, D.; Zhang, T. Towards Characterizing the High-dimensional Bias of Kernel-based Particle Inference Algorithms. In Proceedings of the 2nd Symposium on Advances in Approximate Bayesian Inference, Vancouver, BC, Canada, 8 December 2019. [Google Scholar]
- Tomczak, M.; Swaroop, S.; Turner, R. Efficient Low Rank Gaussian Variational Inference for Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Virtual. 6–12 December 2020; Volume 33. [Google Scholar]
- Maddox, W.J.; Izmailov, P.; Garipov, T.; Vetrov, D.P.; Wilson, A.G. A simple baseline for bayesian uncertainty in deep learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 13153–13164. [Google Scholar]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Rezende, D.; Mohamed, S. Variational inference with normalizing flows. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1530–1538. [Google Scholar]
- Chen, R.T.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural ordinary differential equations. In Proceedings of the 32nd International Conference on Neural Information Processing, Montréal, QC, Canada, 3–8 December 2018; pp. 6572–6583. [Google Scholar]
- Ingersoll, J.E. Theory of Financial Decision Making; Rowman & Littlefield: Lanham, MD, USA, 1987; Volume 3. [Google Scholar]
- Barfoot, T.D.; Forbes, J.R.; Yoon, D.J. Exactly sparse gaussian variational inference with application to derivative-free batch nonlinear state estimation. Int. J. Robot. Res. 2020, 39, 1473–1502. [Google Scholar] [CrossRef]
- Korba, A.; Salim, A.; Arbel, M.; Luise, G.; Gretton, A. A Non-Asymptotic Analysis for Stein Variational Gradient Descent. In Proceedings of the 32nd International Conference on Neural Information Processing, Virtual, 6–12 December 2020; Volume 33. pp. 4672–4682.
- Berlinet, A.; Thomas-Agnan, C. Reproducing Kernel Hilbert Spaces in Probability and Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zaki, N.; Galy-Fajou, T.; Opper, M. Evidence Estimation by Kullback-Leibler Integration for Flow-Based Methods. In Proceedings of the Third Symposium on Advances in Approximate Bayesian Inference, Virtual Event. January–February 2021. [Google Scholar]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef] [Green Version]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop, Coursera: Neural Networks for Machine Learning; Technical Report; University of Toronto: Toronto, ON, USA, 2012. [Google Scholar]
- Zhang, G.; Li, L.; Nado, Z.; Martens, J.; Sachdeva, S.; Dahl, G.; Shallue, C.; Grosse, R.B. Which Algorithmic Choices Matter at Which Batch Sizes? Insights From a Noisy Quadratic Model. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32, pp. 8196–8207. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: https://archive.ics.uci.edu/ml/datasets.php (accessed on 28 July 2021).
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- LeCun, Y. The MNIST Database of Handwritten Digits. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 20 July 2021).
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Liu, C.; Zhuo, J.; Cheng, P.; Zhang, R.; Zhu, J. Understanding and accelerating particle-based variational inference. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 4082–4092. [Google Scholar]
- Zhu, M.H.; Liu, C.; Zhu, J. Variance Reduction and Quasi-Newton for Particle-Based Variational Inference. In Proceedings of the 37th International Conference on Machine Learning, Virtual. 13–18 July 2020. [Google Scholar]
- Gronwall, T.H. Note on the derivatives with respect to a parameter of the solutions of a system of differential equations. Ann. Math. 1919, 20, 292–296. [Google Scholar] [CrossRef]
- Zhang, F. Matrix Theory: Basic Results and Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
| Alg. | Mean-Field | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| NLL | Acc | ECE | NLL | Acc | ECE | NLL | Acc | ECE | |
| GPF | 0.96 | ||||||||
| GPF (Layers) | - | - | - | 0.147 | 0.0181 | ||||
| GF | |||||||||
| DSVI | - | - | - | - | - | - | |||
| SVGD (Sq. Exp) | - | - | - | 0.133 | 0.967 | ||||
| SWAG | - | - | - | ||||||
| ELRGVI | - | - | - | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galy-Fajou, T.; Perrone, V.; Opper, M. Flexible and Efficient Inference with Particles for the Variational Gaussian Approximation. Entropy 2021, 23, 990. https://doi.org/10.3390/e23080990
Galy-Fajou T, Perrone V, Opper M. Flexible and Efficient Inference with Particles for the Variational Gaussian Approximation. Entropy. 2021; 23(8):990. https://doi.org/10.3390/e23080990
Chicago/Turabian StyleGaly-Fajou, Théo, Valerio Perrone, and Manfred Opper. 2021. "Flexible and Efficient Inference with Particles for the Variational Gaussian Approximation" Entropy 23, no. 8: 990. https://doi.org/10.3390/e23080990
APA StyleGaly-Fajou, T., Perrone, V., & Opper, M. (2021). Flexible and Efficient Inference with Particles for the Variational Gaussian Approximation. Entropy, 23(8), 990. https://doi.org/10.3390/e23080990






