Accelerated Diffusion-Based Sampling by the Non-Reversible Dynamics with Skew-Symmetric Matrices
Abstract
:1. Introduction
2. Preliminaries
2.1. LD and Stochastic Gradient LD
2.2. Poincaré Inequality and Convergence Speed
2.3. Non-Reversible Dynamics
3. Theoretical Analysis of Skew Acceleration
3.1. Acceleration Characterization by the Poincaré Constant
3.2. Skew Acceleration from the Hessian Matrix
3.2.1. Strongly Convex Potential Function
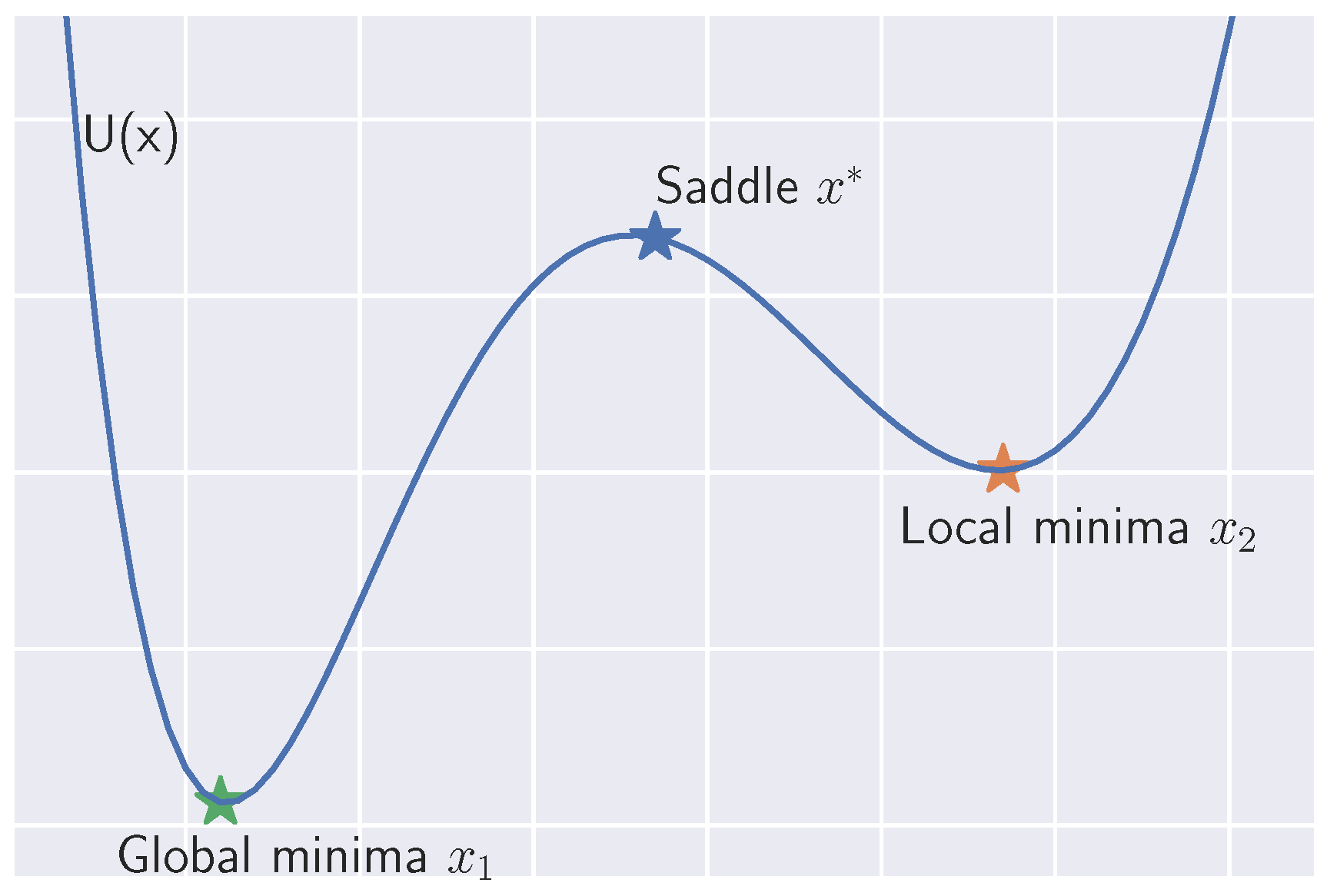
3.2.2. Non-Convex Potential Function
3.3. Choosing J
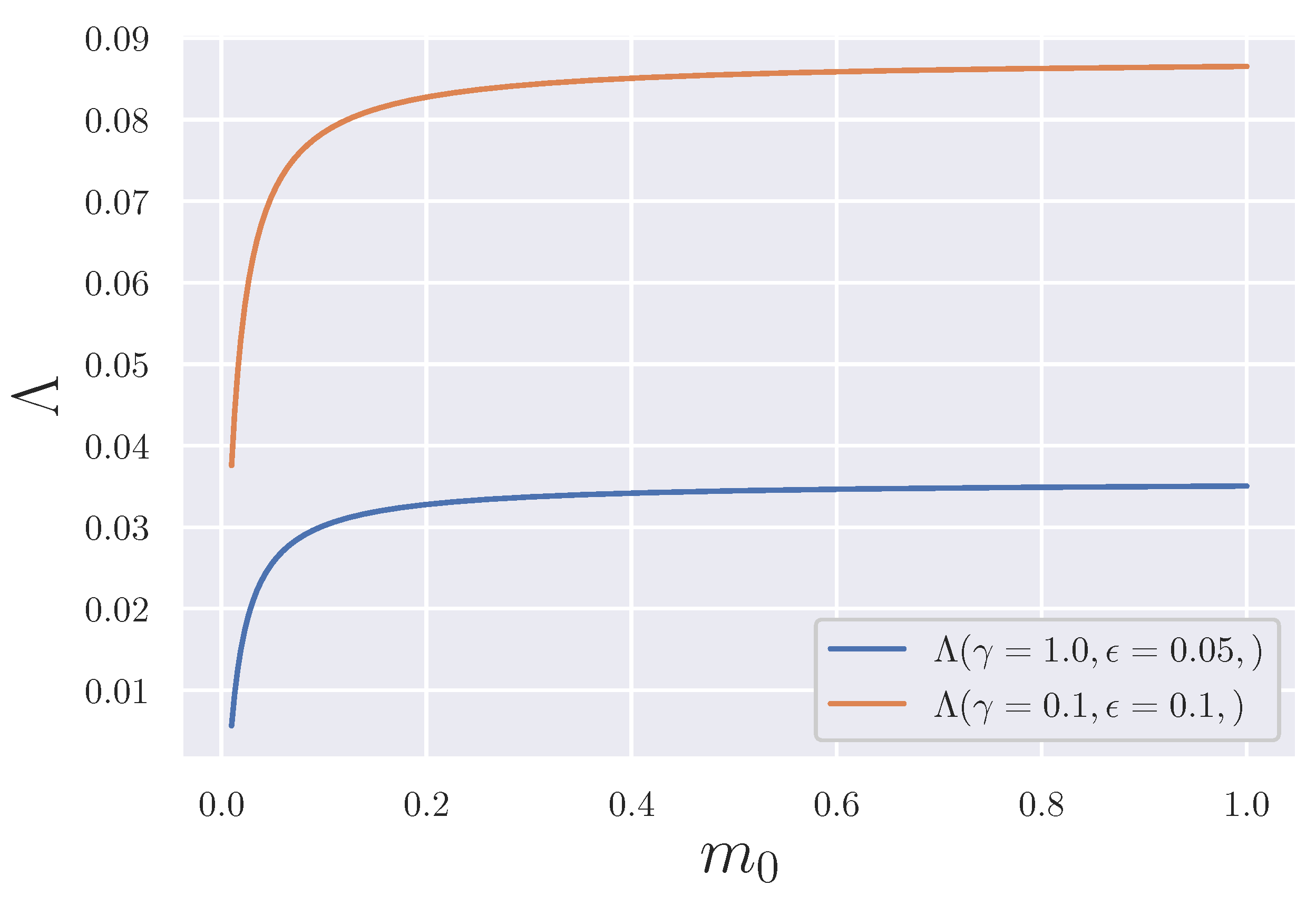
3.4. Qualitative Evaluation of The Acceleration
4. Practical Algorithm for Skew Acceleration
4.1. Memory Issue of Skew Acceleration and Ensemble Sampling
4.2. Discussion of the Discretization of SDE and Stochastic Gradient and Practical Algorithm
4.2.1. Trade-off Caused by Discretization and Stochastic Gradient
4.2.2. Practical Algorithm Controlling the Trade-off
| Algorithm 1 Tuning |
| Input: Output:
|
| Algorithm 2 Proposed algorithm |
| Input: Output: |
4.3. Refined Analysis for the Bias of Skew-SGLD
5. Related Work
5.1. Relation to Non-Reversible Methods
5.2. Relation to Ensemble Methods
6. Numerical Experiments
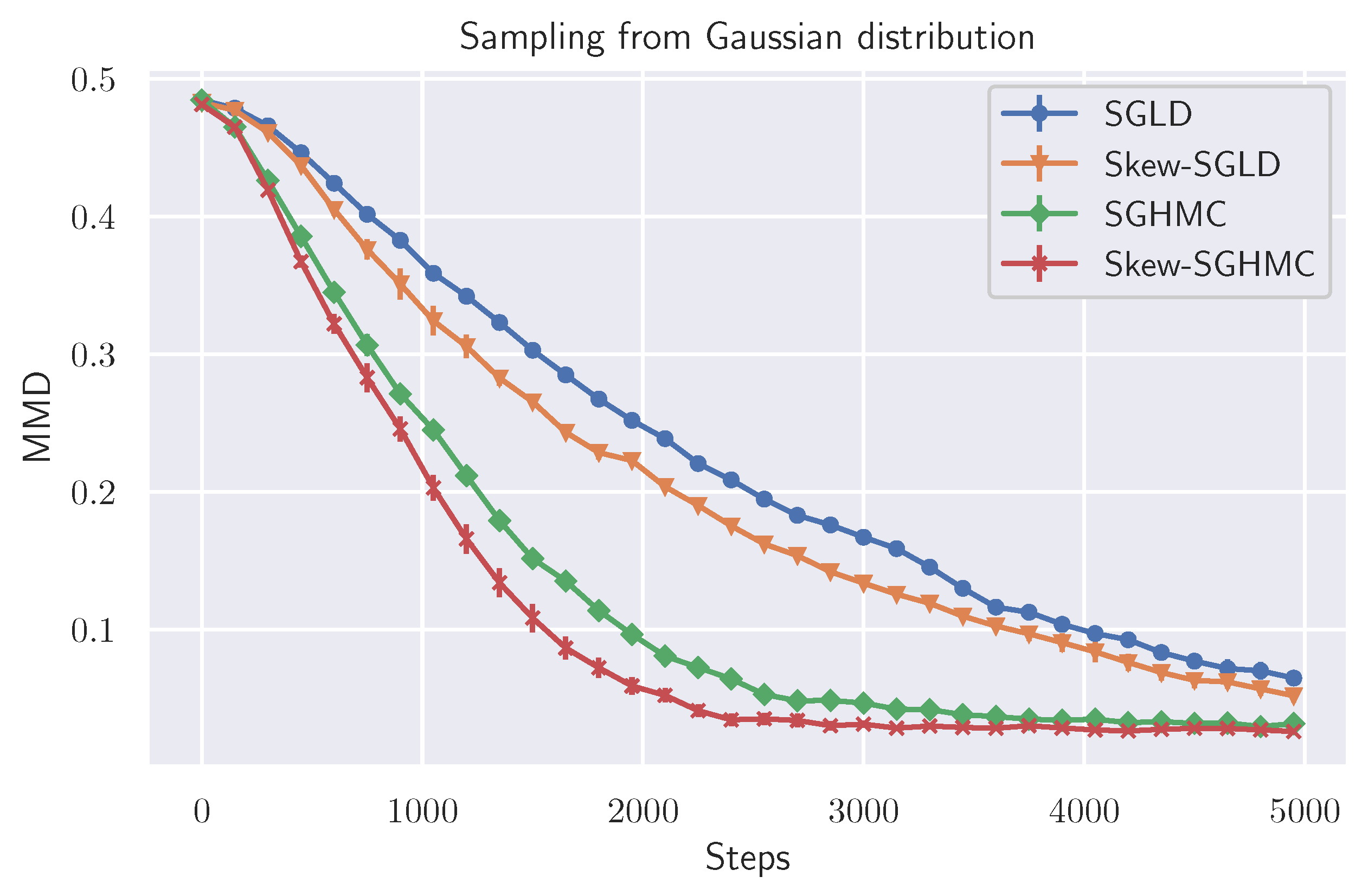
6.1. Toy Data Experiment
6.2. LDA Experiment
6.3. BNN Regression and Classification
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LD | Langevin Dynamics |
| MCMC | Markov Chain Monte Carlo |
| ULD | Underdamped Langevin Dynamics |
| SGLD | Stochastic Gradient Langevin Dynamics |
| SGHMC | Stochastic Gradient Hamilton Monte Carlo |
| PLD | Parallel Langevin Dynamics |
| PULD | Parallel Underdamped Langevin Dynamics |
| SLD | Skew Langevin Dynamics |
| S-ULD | Skew Underdamped Langevin Dynamics |
| S-PLD | Skew Parallel Langevin Dynamics |
| S-PULD | Skew Parallel Underdamped Langevin Dynamics |
| KSD | Kernelized Stein Discrepancy |
Appendix A. Additional Backgrounds
Appendix A.1. Wasserstein Distance and Kullback–Leibler Divergence
Appendix A.2. Markov Diffusion and Generator
Appendix A.3. Poincaré Inequality
Appendix B. Generator of the Underdamped Langevin Dynamics (ULD)
Appendix C. Proof of Theorem 1
Appendix C.1. Proof for S-LD
Appendix C.2. Proof of Theorem 2 (S-ULD)
Appendix D. Eigenvalue and Poincaré Constant
Appendix D.1. Strongly Convex Potential Function
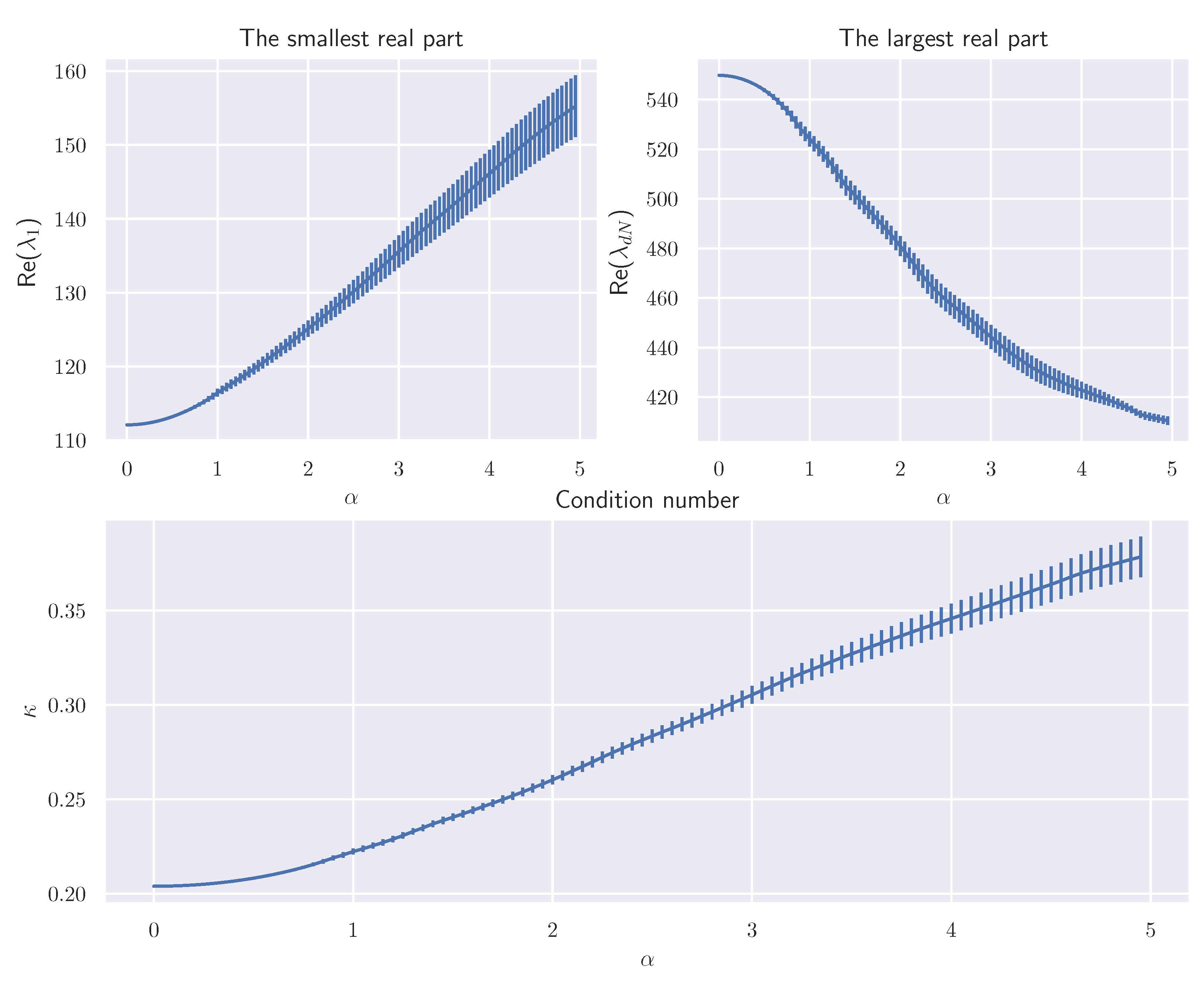
Appendix D.2. Non-Convex Potential Function
Appendix E. Properties of a Skew-Symmetric Matrix
Appendix F. Proof of Theorem 3
Appendix G. Proofs of Random Matrices
Appendix G.1. Proof of Theorem 5
Appendix G.2. Proof of Lemma 1
Appendix G.3. Extending the Theorem to the Path
Appendix H. Proof of Theorem 6
Appendix H.1. Asymptotic Expansion When the Smallest Eigenvalue of H(x) Is Positive
Appendix H.2. Expansion of the Eigenvalue at the Saddle Point
Appendix I. Convergence Rate of Parallel Sampling Schemes
Appendix I.1. Proof of Lemma 2
Appendix I.2. Proof for S-ULD
Appendix J. Proof of Theorem 7
Appendix J.1. Proof of Lemma A1
Appendix K. Order Expansion
Bias Expansion for S-PLD
Appendix L. Hyperparameters of the Proposed Algorithm
Appendix M. Proof of Theorem 8
Appendix M.1. Estimation of the Logarithmic Sobolev Constant
Appendix M.2. Computational Complexity
References
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Raginsky, M.; Rakhlin, A.; Telgarsky, M. Non-convex learning via Stochastic Gradient Langevin Dynamics: A nonasymptotic analysis. In Proceedings of the Conference on Learning Theory, Amsterdam, The Netherlands, 7–10 July 2017; pp. 1674–1703. [Google Scholar]
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the International Conference on Machine Learning, Washington, DC, USA, 28 June–2 July 2011; pp. 681–688. [Google Scholar]
- Livingstone, S.; Girolami, M. Information-Geometric Markov Chain Monte Carlo Methods Using Diffusions. Entropy 2014, 16, 3074–3102. [Google Scholar] [CrossRef]
- Hartmann, C.; Richter, L.; Schütte, C.; Zhang, W. Variational Characterization of Free Energy: Theory and Algorithms. Entropy 2017, 19, 626. [Google Scholar] [CrossRef] [Green Version]
- Neal, R.M. Improving asymptotic variance of MCMC estimators: Non-reversible chains are better. arXiv 2004, arXiv:math/0407281. [Google Scholar]
- Neklyudov, K.; Welling, M.; Egorov, E.; Vetrov, D. Involutive mcmc: A unifying framework. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 13–18 July 2020; pp. 7273–7282. [Google Scholar]
- Gao, X.; Gurbuzbalaban, M.; Zhu, L. Breaking Reversibility Accelerates Langevin Dynamics for Non-Convex Optimization. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; pp. 17850–17862. [Google Scholar]
- Eberle, A.; Guillin, A.; Zimmer, R. Couplings and quantitative contraction rates for Langevin dynamics. Ann. Probab. 2019, 47, 1982–2010. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Gürbüzbalaban, M.; Zhu, L. Global convergence of stochastic gradient Hamiltonian Monte Carlo for non-convex stochastic optimization: Non-asymptotic performance bounds and momentum-based acceleration. arXiv 2018, arXiv:1809.04618. [Google Scholar]
- Cheng, X.; Chatterji, N.S.; Abbasi-Yadkori, Y.; Bartlett, P.L.; Jordan, M.I. Sharp convergence rates for Langevin dynamics in the nonconvex setting. arXiv 2018, arXiv:1805.01648. [Google Scholar]
- Chen, T.; Fox, E.; Guestrin, C. Stochastic gradient hamiltonian monte carlo. In Proceedings of the International conference on machine learning, Beijing, China, 21–26 June 2014; pp. 1683–1691. [Google Scholar]
- Hwang, C.R.; Hwang-Ma, S.Y.; Sheu, S.J. Accelerating gaussian diffusions. Ann. Appl. Probab. 1993, 3, 897–913. [Google Scholar] [CrossRef]
- Hwang, C.R.; Hwang-Ma, S.Y.; Sheu, S.J. Accelerating diffusions. Ann. Appl. Probab. 2005, 15, 1433–1444. [Google Scholar] [CrossRef] [Green Version]
- Hwang, C.R.; Normand, R.; Wu, S.J. Variance reduction for diffusions. Stoch. Process. Their Appl. 2015, 125, 3522–3540. [Google Scholar] [CrossRef]
- Duncan, A.B.; Lelièvre, T.; Pavliotis, G.A. Variance Reduction Using Nonreversible Langevin Samplers. J. Stat. Phys. 2016, 163, 457–491. [Google Scholar] [CrossRef] [Green Version]
- Duncan, A.B.; Nüsken, N.; Pavliotis, G.A. Using Perturbed Underdamped Langevin Dynamics to Efficiently Sample from Probability Distributions. J. Stat. Phys. 2017, 169, 1098–1131. [Google Scholar] [CrossRef] [Green Version]
- Futami, F.; Sato, I.; Sugiyama, M. Accelerating the diffusion-based ensemble sampling by non-reversible dynamics. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 13–18 July 2020; pp. 3337–3347. [Google Scholar]
- Bakry, D.; Gentil, I.; Ledoux, M. Analysis and Geometry of Markov Diffusion Operators; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 348. [Google Scholar]
- Roussel, J.; Stoltz, G. Spectral methods for Langevin dynamics and associated error estimates. ESAIM Math. Model. Numer. Anal. 2018, 52, 1051–1083. [Google Scholar] [CrossRef] [Green Version]
- Menz, G.; Schlichting, A. Poincaré and logarithmic Sobolev inequalities by decomposition of the energy landscape. Ann. Probab. 2014, 42, 1809–1884. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Lee, J.; Jordan, M. A kernelized Stein discrepancy for goodness-of-fit tests. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 24–26 June 2016; pp. 276–284. [Google Scholar]
- Vempala, S.; Wibisono, A. Rapid convergence of the unadjusted langevin algorithm: Isoperimetry suffices. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 8094–8106. [Google Scholar]
- Lelièvre, T.; Nier, F.; Pavliotis, G.A. Optimal non-reversible linear drift for the convergence to equilibrium of a diffusion. J. Stat. Phys. 2013, 152, 237–274. [Google Scholar] [CrossRef] [Green Version]
- Tripuraneni, N.; Rowland, M.; Ghahramani, Z.; Turner, R. Magnetic Hamiltonian Monte Carlo. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3453–3461. [Google Scholar]
- Nusken, N.; Pavliotis, G. Constructing sampling schemes via coupling: Markov semigroups and optimal transport. SIAM/ASA J. Uncertain. Quantif. 2019, 7, 324–382. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, D. Stein variational gradient descent: A general purpose bayesian inference algorithm. In Proceedings of the Advances In Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2378–2386. [Google Scholar]
- Zhang, J.; Zhang, R.; Chen, C. Stochastic particle-optimization sampling and the non-asymptotic convergence theory. arXiv 2018, arXiv:1809.01293. [Google Scholar]
- Wang, Y.; Li, W. Information Newton’s flow: Second-order optimization method in probability space. arXiv 2020, arXiv:2001.04341. [Google Scholar]
- Wibisono, A. Sampling as optimization in the space of measures: The Langevin dynamics as a composite optimization problem. In Proceedings of the Conference On Learning Theory, Stockholm, Sweden, 6–9 July 2018; pp. 2093–3027. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Ding, N.; Fang, Y.; Babbush, R.; Chen, C.; Skeel, R.D.; Neven, H. Bayesian sampling using stochastic gradient thermostats. In Proceedings of the Advances in neural information processing systems, Montreal, QC, Canada, 8–11 December 2014; pp. 3203–3211. [Google Scholar]
- Patterson, S.; Teh, Y.W. Stochastic gradient Riemannian Langevin dynamics on the probability simplex. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 3102–3110. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 21 July 2021).
- Villani, C. Optimal transportation, dissipative PDE’s and functional inequalities. In Optimal Transportation and Applications; Springer: Berlin/Heidelberg, Germany, 2003; pp. 53–89. [Google Scholar]
- Bakry, D.; Barthe, F.; Cattiaux, P.; Guillin, A. A simple proof of the Poincaré inequality for a large class of probability measures including the log-concave case. Electron. Commun. Probab 2008, 13, 21. [Google Scholar] [CrossRef]
- Nelson, E. Dynamical Theories of Brownian Motion; Princeton University Press: Princeton, NJ, USA, 1967; Volume 3. [Google Scholar]
- Pavliotis, G.A. Stochastic Processes and Applications: Diffusion Processes, the Fokker-Planck and Langevin Equations; Springer: Berlin/Heidelberg, Germany, 2014; Volume 60. [Google Scholar]
- Franke, B.; Hwang, C.R.; Pai, H.M.; Sheu, S.J. The behavior of the spectral gap under growing drift. Trans. Am. Math. Soc. 2010, 362, 1325–1350. [Google Scholar] [CrossRef] [Green Version]
- Landim, C.; Seo, I. Metastability of Nonreversible Random Walks in a Potential Field and the Eyring-Kramers Transition Rate Formula. Commun. Pure Appl. Math. 2018, 71, 203–266. [Google Scholar] [CrossRef]
- Landim, C.; Mariani, M.; Seo, I. Dirichlet’s and Thomson’s principles for non-selfadjoint elliptic operators with application to non-reversible metastable diffusion processes. Arch. Ration. Mech. Anal. 2019, 231, 887–938. [Google Scholar] [CrossRef] [Green Version]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2012; Volume 3. [Google Scholar]
- Okamoto, M. Distinctness of the Eigenvalues of a Quadratic form in a Multivariate Sample. Ann. Statist. 1973, 1, 763–765. [Google Scholar] [CrossRef]
- Petersen, K.B.; Pedersen, M.S. The Matrix Cookbook; Technical University of Denmark: Lynby, Denmark, 2012; Available online: http://www2.compute.dtu.dk/pubdb/pubs/3274-full.html (accessed on 21 July 2021).
- Van Erven, T.; Harremos, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef] [Green Version]
- Chewi, S.; Le Gouic, T.; Lu, C.; Maunu, T.; Rigollet, P.; Stromme, A. Exponential ergodicity of mirror-Langevin diffusions. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; pp. 19573–19585. [Google Scholar]
- Bolley, F.; Villani, C. Weighted Csiszár-Kullback-Pinsker inequalities and applications to transportation inequalities. In Annales de la Faculté des Sciences de Toulouse: Mathématiques; Université Paul Sabatier: Toulouse, France, 2005; Volume 14, pp. 331–352. [Google Scholar]
- Donsker, M.D.; Varadhan, S.S. Asymptotic evaluation of certain Markov process expectations for large time. IV. Commun. Pure Appl. Math. 1983, 36, 183–212. [Google Scholar] [CrossRef]
- Carlen, E.; Loss, M. Logarithmic Sobolev inequalities and spectral gaps. Contemp. Math. 2004, 353, 53–60. [Google Scholar]
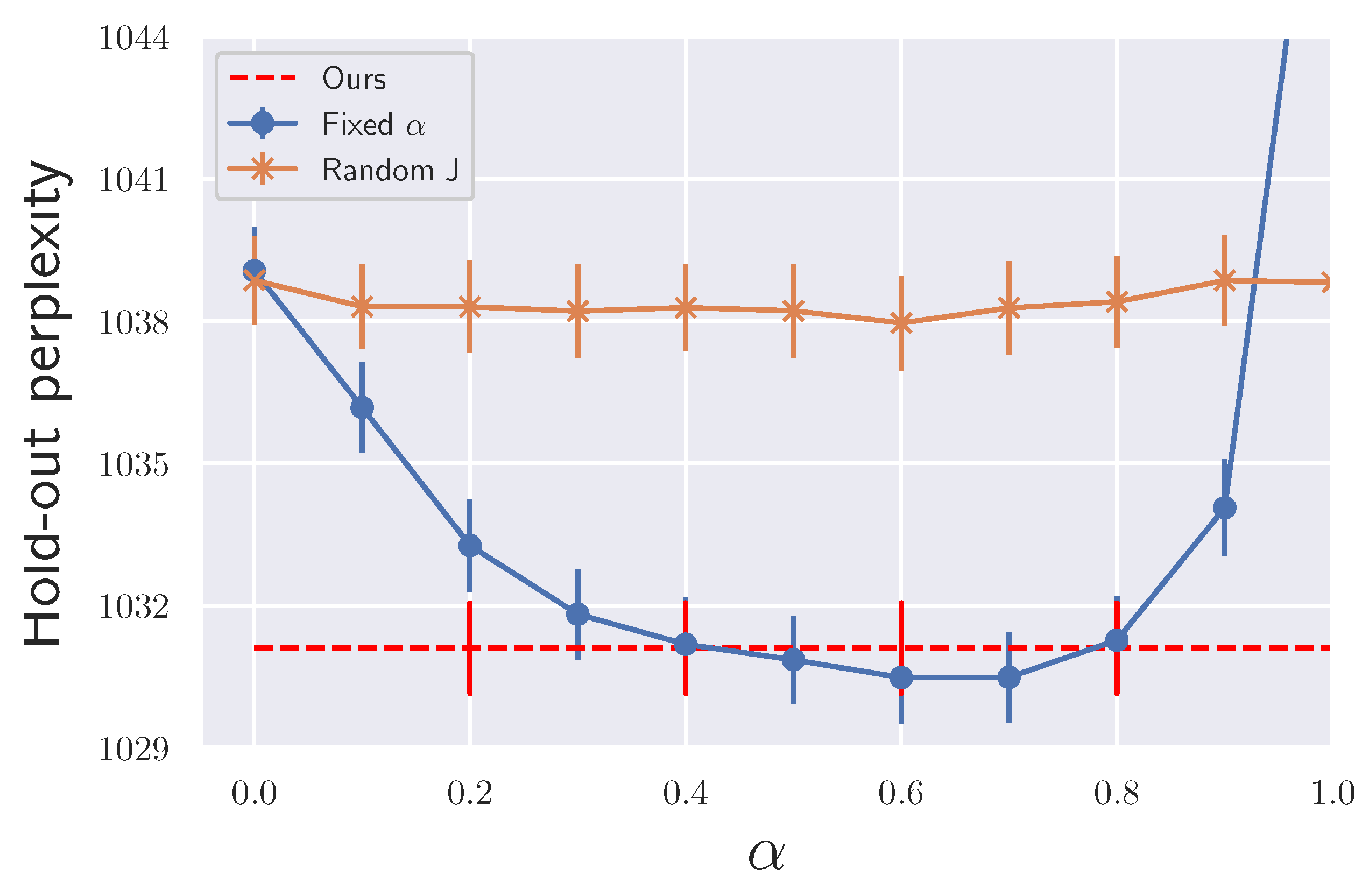
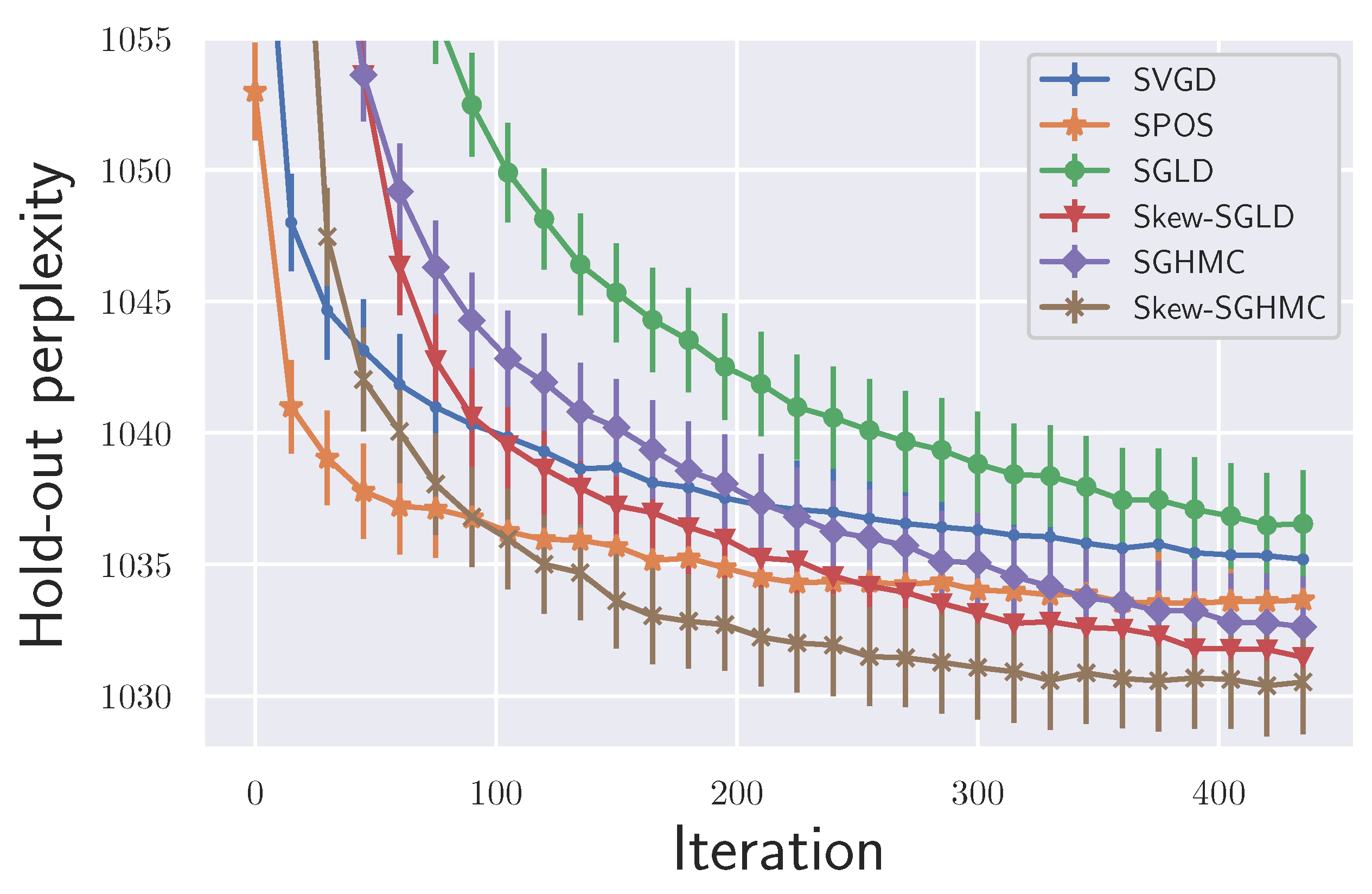
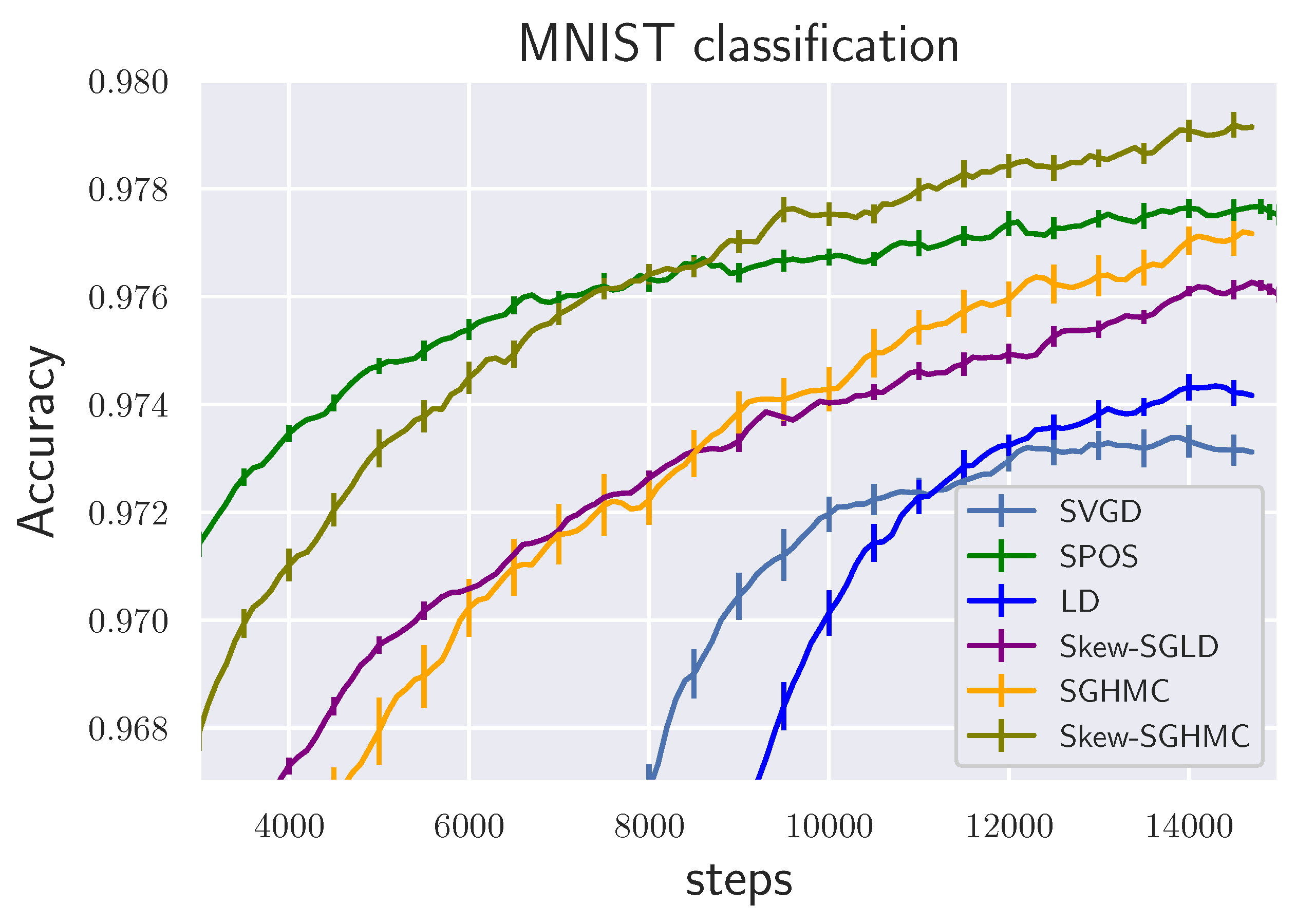
| Dataset | Avg. Test RMSE | |||||
|---|---|---|---|---|---|---|
| SVGD | SPOS | SGLD | Skew-SGLD | SGHMC | Skew-SGHMC | |
| Concrete | 5.709 ± 0.040 | 5.239 ± 0.199 | 5.009 ± 0.091 | 4.973 ± 0.057 | 4.949 ± 0.144 | 4.790 ± 0.081 |
| Kin8nm | 0.0731 ± 0.0006 | 0.0688 ± 0.0003 | 0.0693 ± 0.0006 | 0.0689 ± 0.0005 | 0.0687 ± 0.0001 | 0.0683 ± 0.0003 |
| Energy | 0.520 ± 0.060 | 0.456 ± 0.030 | 0.428 ± 0.045 | 0.412 ± 0.045 | 0.406 ± 0.019 | 0.403 ± 0.008 |
| Bostonhousing | 3.306 ± 0.005 | 3.107 ± 0.173 | 2.948 ± 0.084 | 2.930 ± 0.095 | 3.053 ± 0.093 | 2.986 ± 0.143 |
| Winequality | 0.619 ± 0.001 | 0.618 ± 0.007 | 0.641 ± 0.003 | 0.634 ± 0.004 | 0.614 ± 0.004 | 0.613 ± 0.004 |
| PowerPlant | 4.219 ± 0.012 | 4.160 ± 0.009 | 4.129 ± 0.002 | 4.118 ± 0.006 | 4.112 ± 0.009 | 4.105 ± 0.008 |
| Yacht | 0.475 ± 0.049 | 0.467 ± 0.110 | 0.464 ± 0.058 | 0.442 ± 0.046 | 0.464 ± 0.078 | 0.432 ± 0.051 |
| Dataset | Avg. Test Negative Log Likelihood | |||||
|---|---|---|---|---|---|---|
| SVGD | SPOS | SGLD | Skew-SGLD | SGHMC | Skew-SGHMC | |
| Concrete | −3.157 ± 0.008 | −3.124 ± 0.025 | −3.052 ± 0.009 | −3.049 ± 0.012 | −3.046 ± 0.025 | −3.033 ± 0.021 |
| Kin8nm | 1.153 ± 0.0084 | 1.212 ± 0.008 | 1.223 ± 0.002 | 1.223 ± 0.005 | 1.230 ± 0.0015 | 1.235 ± 0.0025 |
| Energy | −0.816 ± 0.102 | −0.976 ± 0.079 | −0.867 ± 0.056 | −0.845 ± 0.021 | −0.843 ± 0.045 | −0.844 ± 0.041 |
| Bostonhousing | −2.98 ± 0.000 | −2.644 ± 0.027 | −2.548 ± 0.016 | −2.539 ± 0.002 | −2.574 ± 0.019 | −2.561 ± 0.017 |
| Winequality | −1.012 ± 0.000 | −0.959 ± 0.007 | −0.976 ± 0.006 | −0.968 ± 0.005 | −0.941 ± 0.007 | −0.938 ± 0.005 |
| PowerPlant | −2.871 ± 0.004 | −2.850 ± 0.004 | −2.844 ± 0.002 | −2.842 ± 0.001 | −2.838 ± 0.004 | −2.835 ± 0.003 |
| Yacht | −1.184 ± 0.06 | −1.372 ± 0.07 | −1.077 ± 0.066 | −1.078 ± 0.030 | −1.083 ± 0.030 | −1.079 ± 0.051 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Futami, F.; Iwata, T.; Ueda, N.; Sato, I. Accelerated Diffusion-Based Sampling by the Non-Reversible Dynamics with Skew-Symmetric Matrices. Entropy 2021, 23, 993. https://doi.org/10.3390/e23080993
Futami F, Iwata T, Ueda N, Sato I. Accelerated Diffusion-Based Sampling by the Non-Reversible Dynamics with Skew-Symmetric Matrices. Entropy. 2021; 23(8):993. https://doi.org/10.3390/e23080993
Chicago/Turabian StyleFutami, Futoshi, Tomoharu Iwata, Naonori Ueda, and Issei Sato. 2021. "Accelerated Diffusion-Based Sampling by the Non-Reversible Dynamics with Skew-Symmetric Matrices" Entropy 23, no. 8: 993. https://doi.org/10.3390/e23080993
APA StyleFutami, F., Iwata, T., Ueda, N., & Sato, I. (2021). Accelerated Diffusion-Based Sampling by the Non-Reversible Dynamics with Skew-Symmetric Matrices. Entropy, 23(8), 993. https://doi.org/10.3390/e23080993








