Design of a 2-Bit Neural Network Quantizer for Laplacian Source
Abstract
:1. Introduction
2. A 2-Bit Uniform Scalar Quantizer of Laplacian Source
2.1. The Variance-Matched 2-Bit Uniform Quantizer
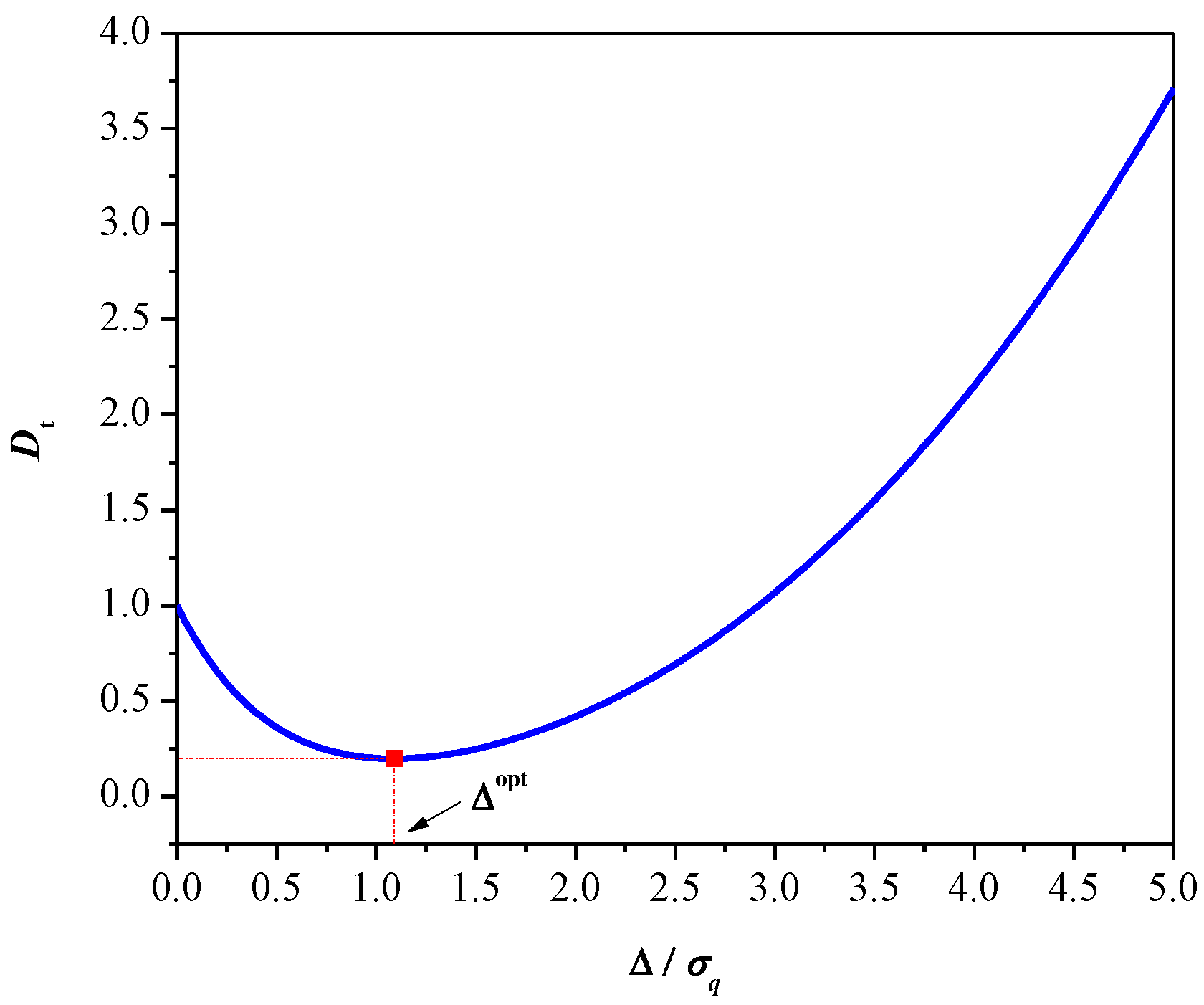
2.2. The Variance-Mismatched 2-Bit Uniform Quantizer
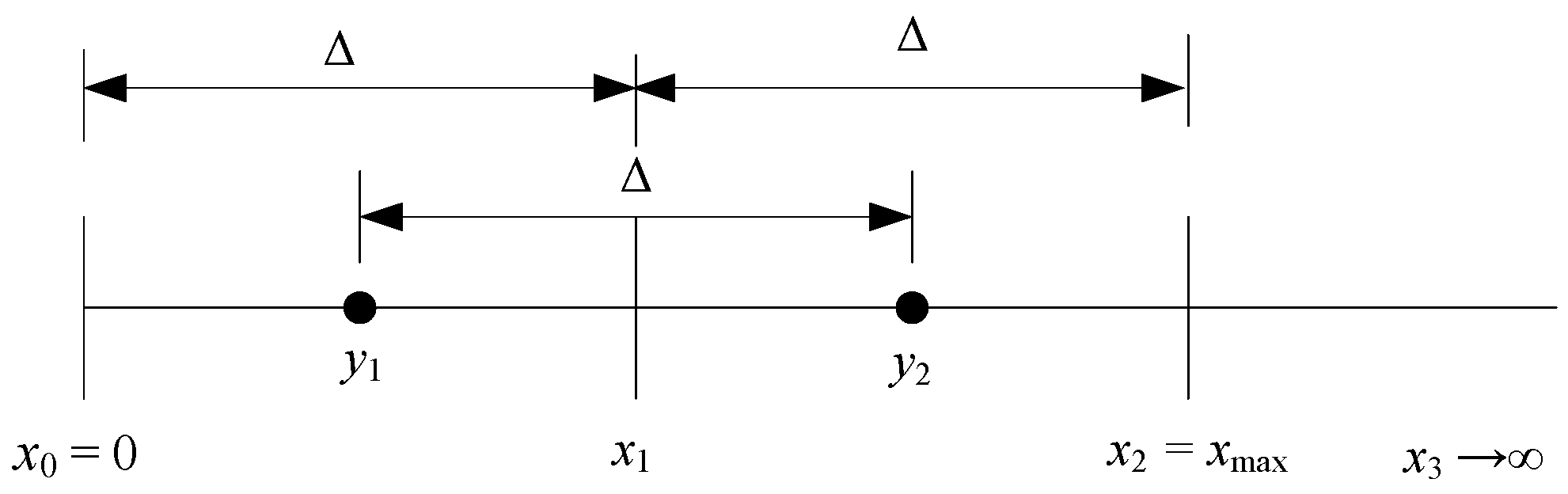
2.3. Adaptation of the 2-Bit Uniform Quantizer
- Step 1.
- Estimation of the mean value and quantization.
- Step 2.
- Estimation of the standard deviation (rms value) and quantization.
- Step 3.
- Normalization of the input data. Each element of the input source X is normalized according to:and the source T with transformed (normalized) coefficients is formed.
- Step 4.
- Quantization of the normalized data. To quantize normalized data (modeled as the PDF with zero mean and unit variance), the quantizer designed in Section 2.1 can be used, and quantized data tiq are obtained.
- Step 5.
- Denormalization of the data. Since the input data are appropriately transformed for the purpose of efficient quantization, an inverse process referred to as denormalization has to be performed to recover the original data:
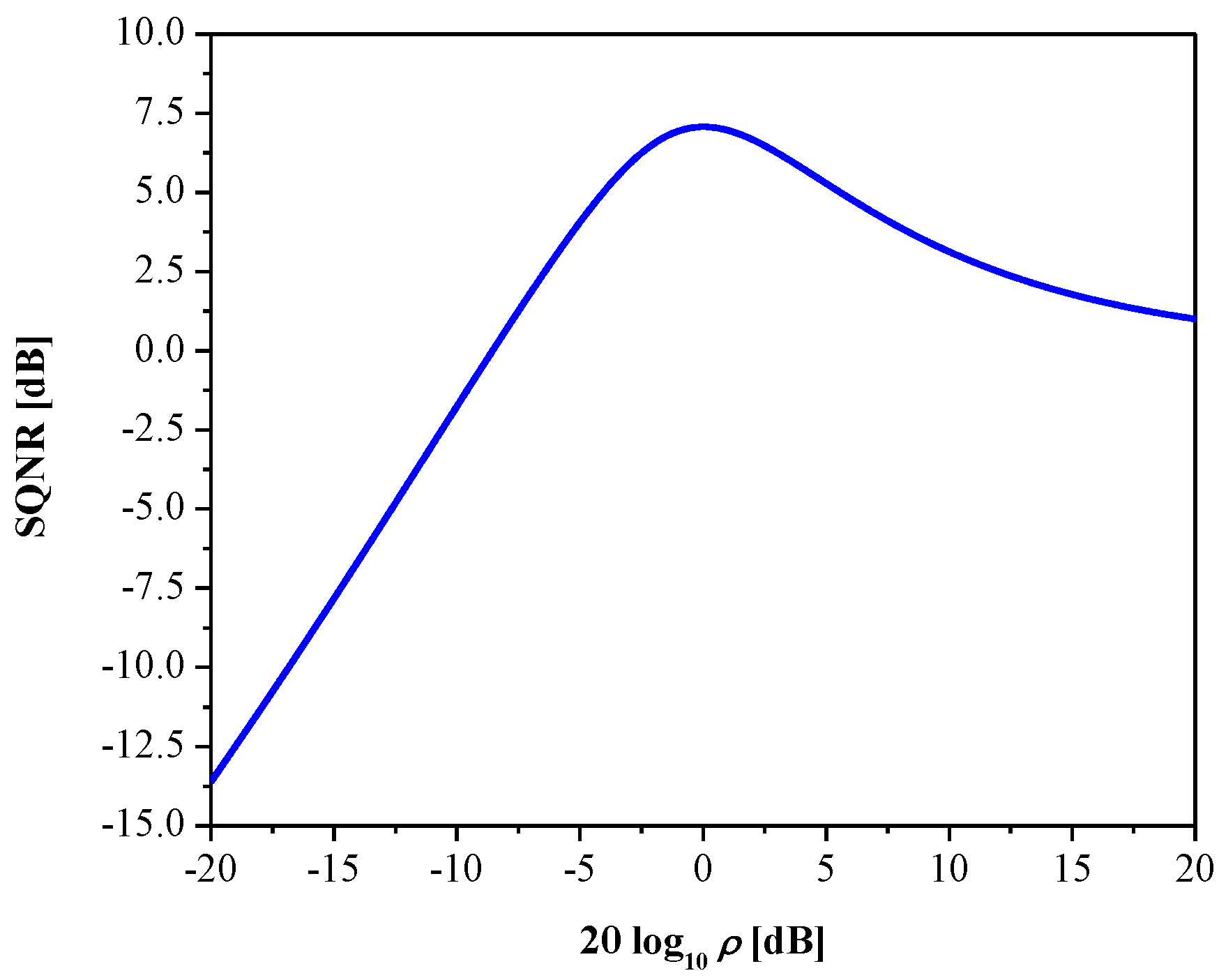
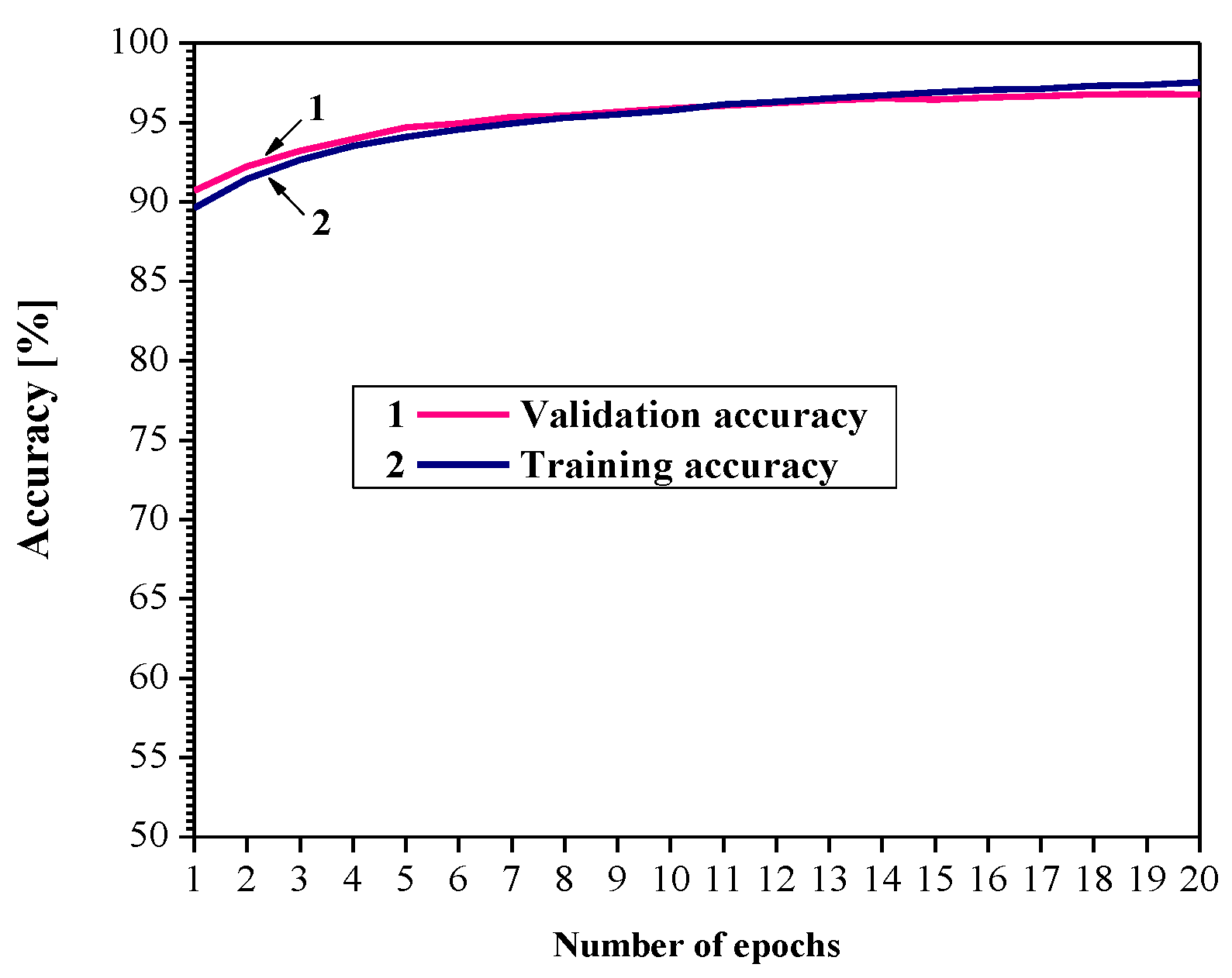
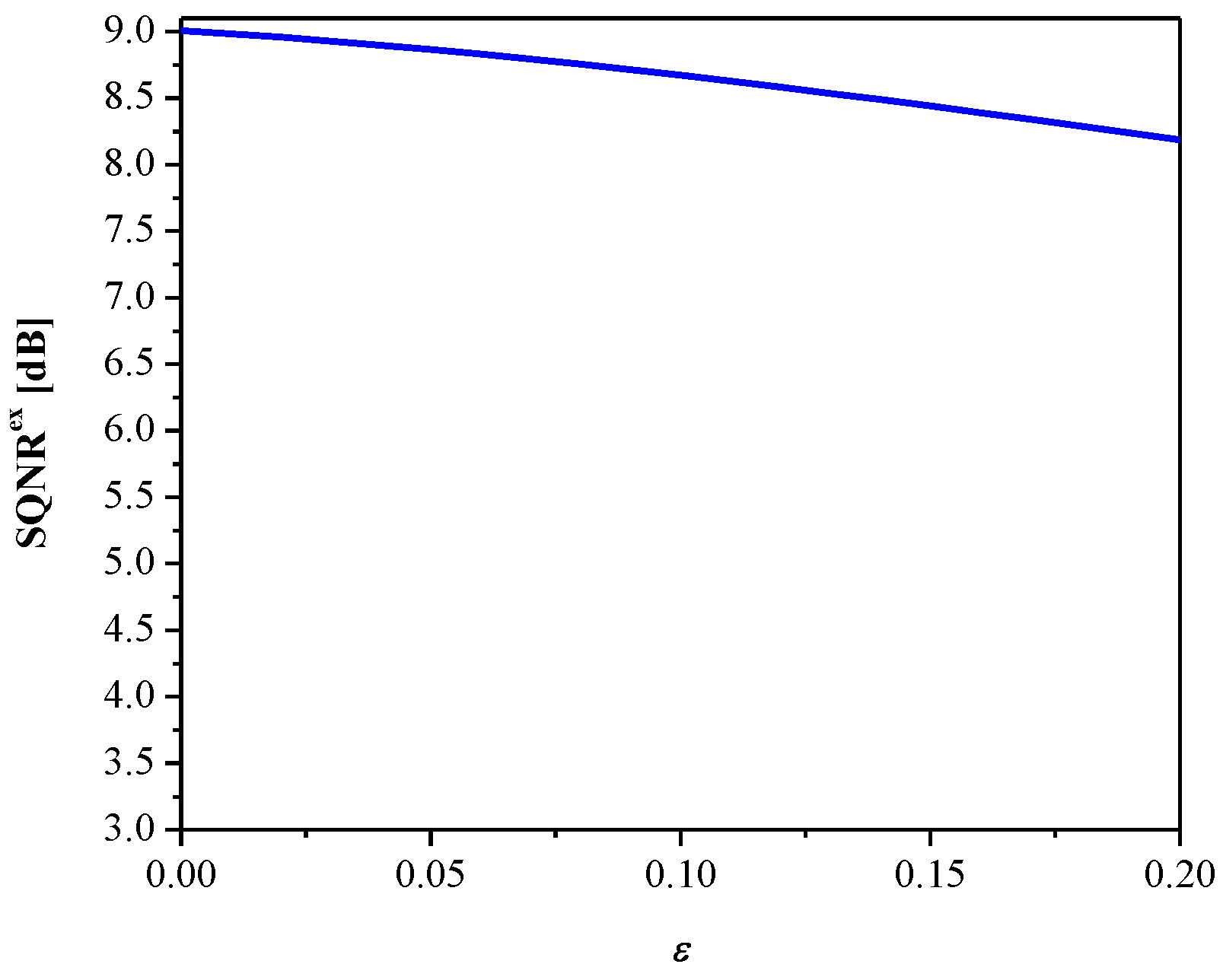
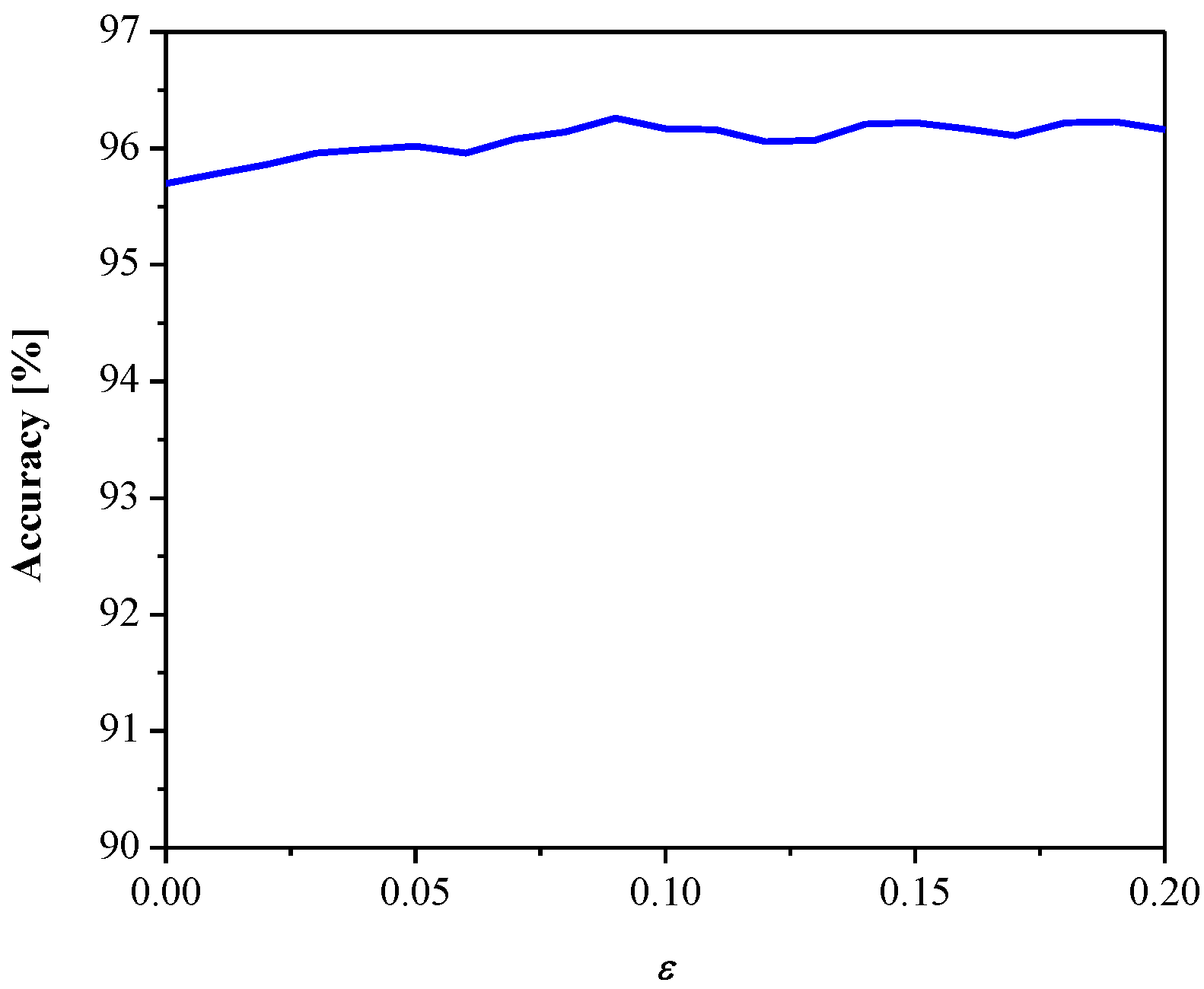
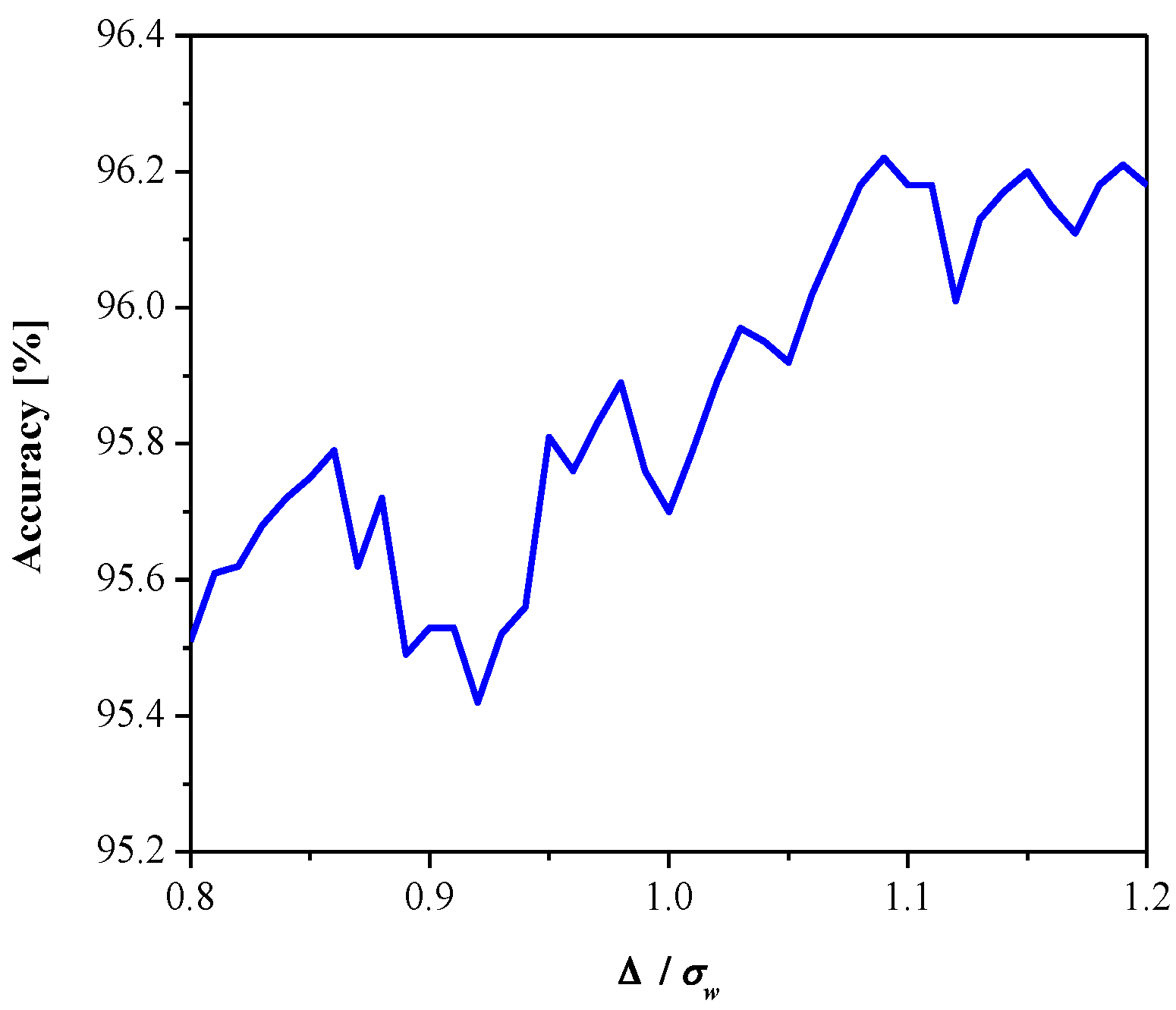
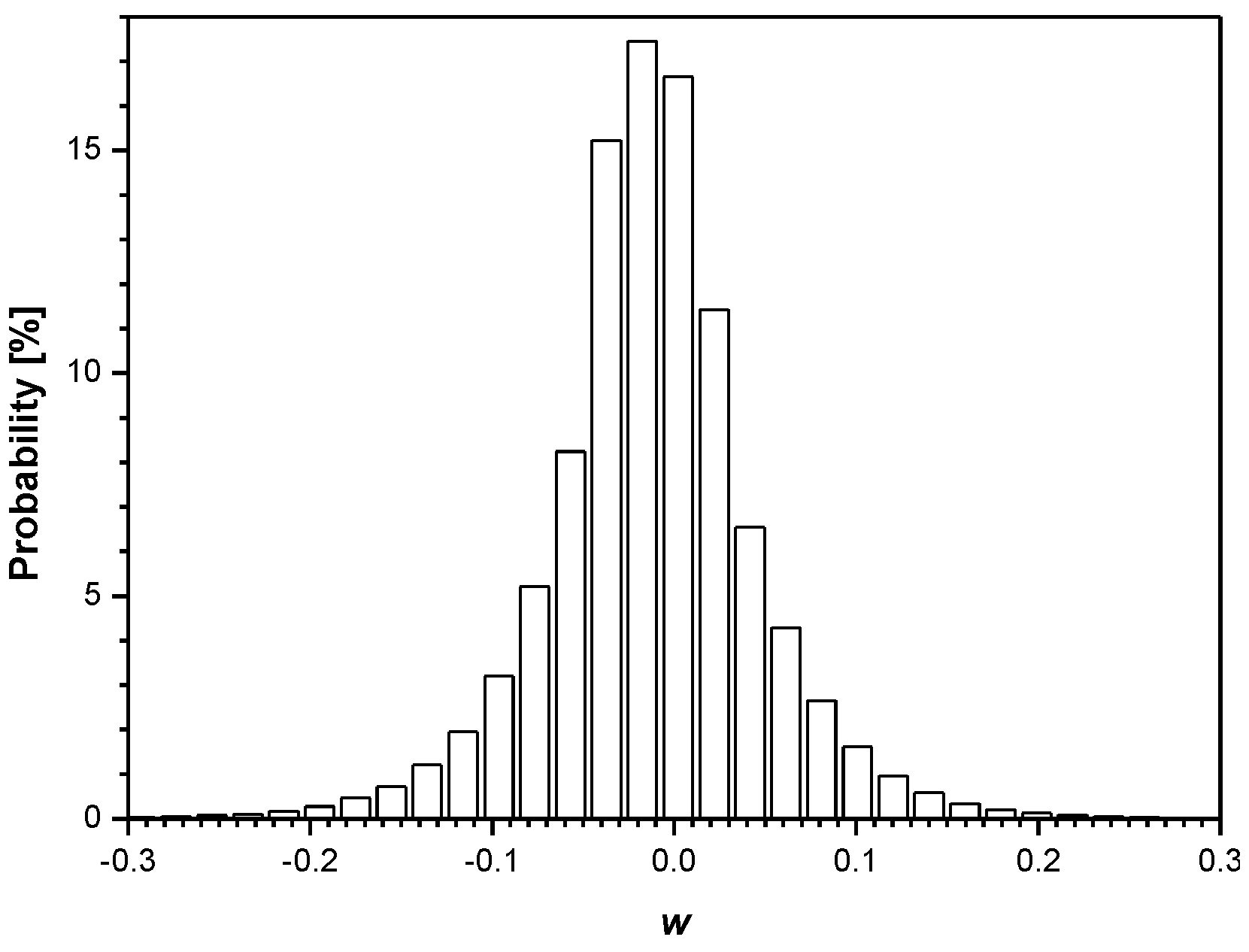
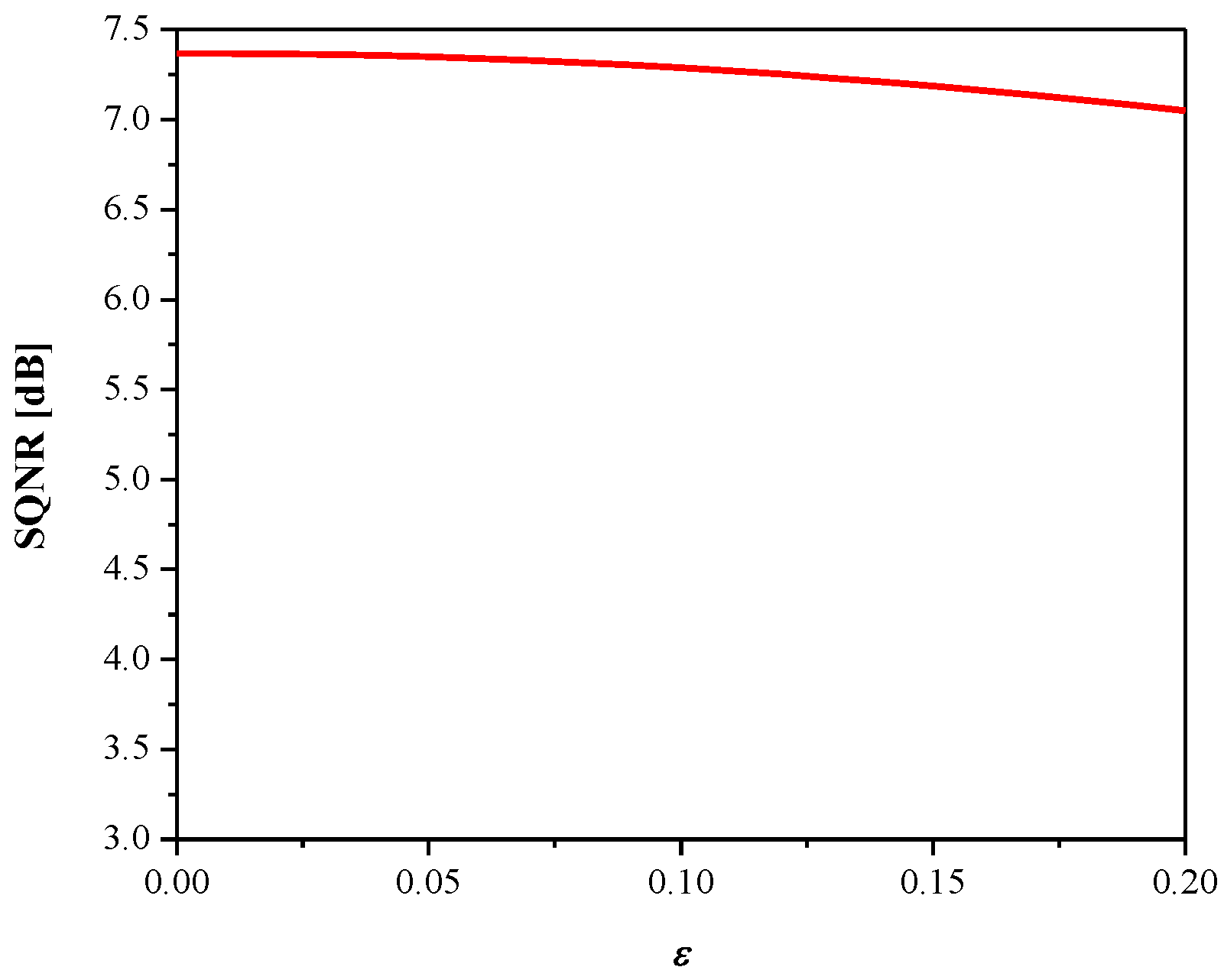
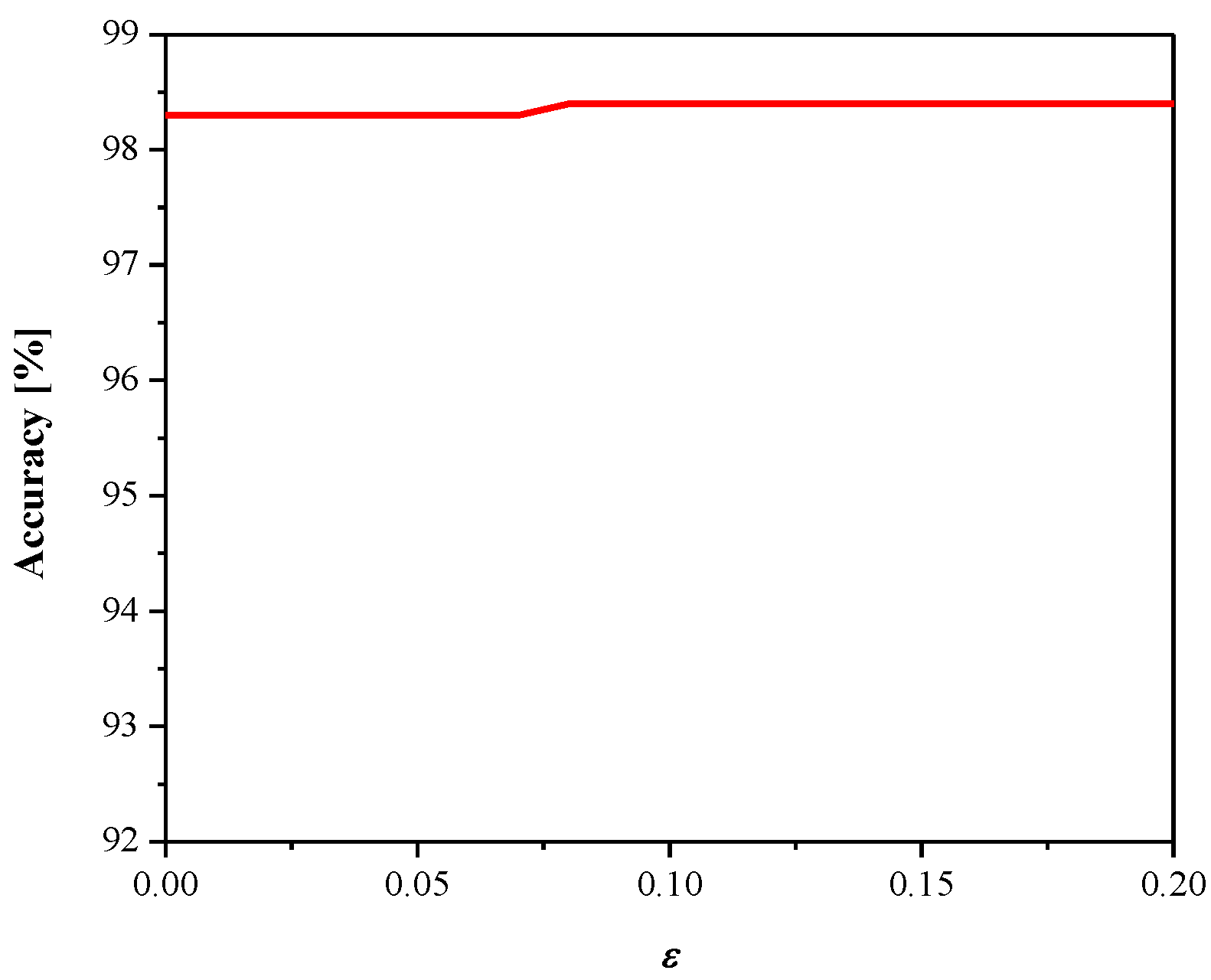
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Teerapittayanon, S.; McDanel, B.; Kung, H.T. Distributed Deep Neural Networks Over the Cloud, the Edge and End Devices. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 328–339. [Google Scholar]
- Gysel, P.; Pimentel, J.; Motamedi, M.; Ghiasi, S. Ristretto: A Framework for Empirical Study of Resource-Efficient Inference in Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5784–5789. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; CRC Press: Belmont, CA, USA, 1984. [Google Scholar]
- Langley, P.; Iba, W.; Thompson, K. An analysis of Bayesian classifiers. In Proceedings of the 10th National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; AAAI and MIT Press: Cambridge, MA, USA, 1992; pp. 223–228. [Google Scholar]
- Fu, L. Quantizability and learning complexity in multilayer neural networks. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 1998, 28, 295–299. [Google Scholar] [CrossRef]
- Sayood, K. Introduction to Data Compression, 5th ed.; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar]
- Jayant, N.S.; Noll, P. Digital Coding of Waveforms: Principles and Applications to Speech and Video; Prentice Hall: Hoboken, NJ, USA, 1984. [Google Scholar]
- Perić, Z.; Simić, N.; Nikolić, J. Design of single and dual-mode companding scalar quantizers based on piecewise linear approximation of the Gaussian PDF. J. Frankl. Inst. 2020, 357, 5663–5679. [Google Scholar] [CrossRef]
- Nikolic, J.; Peric, Z.; Jovanovic, A. Two forward adaptive dual-mode companding scalar quantizers for Gaussian source. Signal Process. 2016, 120, 129–140. [Google Scholar] [CrossRef]
- Na, S.; Neuhoff, D.L. Asymptotic MSE Distortion of Mismatched Uniform Scalar Quantization. IEEE Trans. Inf. Theory 2012, 58, 3169–3181. [Google Scholar] [CrossRef]
- Na, S.; Neuhoff, D.L. On the Convexity of the MSE Distortion of Symmetric Uniform Scalar Quantization. IEEE Trans. Inf. Theory 2017, 64, 2626–2638. [Google Scholar] [CrossRef]
- Na, S.; Neuhoff, D.L. Monotonicity of Step Sizes of MSE-Optimal Symmetric Uniform Scalar Quantizers. IEEE Trans. Inf. Theory 2018, 65, 1782–1792. [Google Scholar] [CrossRef]
- Banner, R.; Hubara, I.; Hoffer, E.; Soudry, D. Scalable Methods for 8-bit Training of Neural Networks. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Pham, P.; Abraham, J.; Chung, J. Training Multi-Bit Quantized and Binarized Networks with a Learnable Symmetric Quantizer. IEEE Access 2021, 9, 47194–47203. [Google Scholar] [CrossRef]
- Banner, R.; Nahshan, Y.; Soudry, D. Post Training 4-bit Quantization of Convolutional Networks for Rapid-Deployment. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–10 December 2019. [Google Scholar]
- Choi, J.; Venkataramani, S.; Srinivasan, V.; Gopalakrishnan, K.; Wang, Z.; Chuang, P. Accurate and Efficient 2-Bit Quantized Neural Networks. In Proceedings of the 2nd SysML Conference, Stanford, CA, USA, 31 March–2 April 2019. [Google Scholar]
- Bhalgat, Y.; Lee, J.; Nagel, M.; Blankevoort, T.; Kwak, N. LSQ+: Improving Low-Bit Quantization Through Learnable Offsets and Better Initialization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations. J. Mach. Learn. Res. 2018, 18, 1–30. [Google Scholar]
- Zamirai, P.; Zhang, J.; Aberger, C.R.; De Sa, C. Revisiting BFloat16 Training. arXiv 2020, arXiv:2010.06192v1. [Google Scholar]
- Li, Y.; Dong, X.; Wang, W. Additive Powers-of-Two Quantization: An Efficient Non-uniform Discretization for Neural Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Conference, Formerly Addis Ababa, Ethiopia, 26 April–1 May 2020. [Google Scholar]
- Baskin, C.; Liss, N.; Schwartz, E.; Zheltonozhskii, E.; Giryes, R.; Bronstein, M.; Mendelso, A. Uniq: Uniform Noise Injection for Non-Uniform Quantization of Neural Networks. ACM Trans. Comput. Syst. 2021, 37, 1–15. [Google Scholar] [CrossRef]
- Simons, T.; Lee, D.-J. A Review of Binarized Neural Networks. Electronics 2019, 8, 661. [Google Scholar] [CrossRef] [Green Version]
- Qin, H.; Gong, R.; Liu, X.; Bai, X.; Song, J.; Sebe, N. Binary Neural Networks: A Survey. Pattern Recognit. 2020, 105, 107281. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Bao, Y.; Chen, W. Fixed-Sign Binary Neural Network: An Efficient Design of Neural Network for Internet-of-Things Devices. IEEE Access 2018, 8, 164858–164863. [Google Scholar] [CrossRef]
- Zhao, W.; Teli, M.; Gong, X.; Zhang, B.; Doermann, D. A Review of Recent Advances of Binary Neural Networks for Edge Computing. IEEE J. Miniat. Air Space Syst. 2021, 2, 25–35. [Google Scholar] [CrossRef]
- Perić, Z.; Denić, B.; Savić, M.; Despotović, V. Design and Analysis of Binary Scalar Quantizer of Laplacian Source with Applications. Information 2020, 11, 501. [Google Scholar] [CrossRef]
- Gazor, S.; Zhang, W. Speech Probability Distribution. IEEE Signal Proc. Lett. 2003, 10, 204–207. [Google Scholar] [CrossRef]
- Simić, N.; Perić, Z.; Savić, M. Coding Algorithm for Grayscale Images—Design of Piecewise Uniform Quantizer with Golomb–Rice Code and Novel Analytical Model for Performance Analysis. Informatica 2017, 28, 703–724. [Google Scholar] [CrossRef]
- Banner, R.; Nahshan, Y.; Hoffer, E.; Soudry, D. ACIQ: Analytical Clipping for Integer Quantization of Neural Networks. arXiv 2018, arXiv:1810.05723. [Google Scholar]
- Zhang, A.; Lipton, Z.C.; Li, M.; Smola, A.J. Dive into Deep Learning. arXiv 2020, arXiv:2106.11342. [Google Scholar]
- Wiedemann, S.; Shivapakash, S.; Wiedemann, P.; Becking, D.; Samek, W.; Gerfers, F.; Wiegand, T. FantastIC4: A Hardware-Software Co-Design Approach for Efficiently Running 4Bit-Compact Multilayer Perceptrons. IEEE Open J. Circuits Syst. 2021, 2, 407–419. [Google Scholar] [CrossRef]
- Kim, D.; Kung, J.; Mukhopadhyay, S. A Power-Aware Digital Multilayer Perceptron Accelerator with On-Chip Training Based on Approximate Computing. IEEE Trans. Emerg. Top. Comput. 2017, 5, 164–178. [Google Scholar] [CrossRef]
- Savich, A.; Moussa, M.; Areibi, S. A Scalable Pipelined Architecture for Real-Time Computation of MLP-BP Neural Networks. Microprocess. Microsyst. 2012, 36, 138–150. [Google Scholar] [CrossRef]
- Wang, X.; Magno, M.; Cavigelli, L.; Benini, L. FANN-on-MCU: An Open-Source Toolkit for Energy-Efficient Neural Network Inference at the Edge of the Internet of Things. IEEE Internet Things J. 2020, 7, 4403–4417. [Google Scholar] [CrossRef]
- Hui, D.; Neuhoff, D.L. Asymptotic Analysis of Optimal Fixed-Rate Uniform Scalar Quantization. IEEE Trans. Inf. Theory 2001, 47, 957–977. [Google Scholar] [CrossRef] [Green Version]
- Na, S. Asymptotic Formulas for Mismatched Fixed-Rate Minimum MSE Laplacian Quantizers. IEEE Signal Process. Lett. 2008, 15, 13–16. [Google Scholar]
- Na, S. Asymptotic Formulas for Variance-Mismatched Fixed-Rate Scalar Quantization of a Gaussian source. IEEE Trans. Signal Process. 2011, 59, 2437–2441. [Google Scholar] [CrossRef]
- Peric, Z.; Denic, B.; Savić, M.; Dincic, M.; Mihajlov, D. Quantization of Weights of Neural Networks with Negligible Decreasing of Prediction Accuracy. Inf. Technol. Control 2012. Accept. [Google Scholar]
- Peric, Z.; Savic, M.; Dincic, M.; Vucic, N.; Djosic, D.; Milosavljevic, S. Floating Point and Fixed Point 32-bits Quantizers for Quantization of Weights of Neural Networks. In Proceedings of the 12th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 25–27 March 2021. [Google Scholar]
- Peric, Z.; Nikolic, Z. An Adaptive Waveform Coding Algorithm and its Application in Speech Coding. Digit. Signal Process. 2012, 22, 199–209. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortez, C.; Burges, C. The MNIST Handwritten Digit Database. Available online: yann.lecun.com/exdb/mnist/ (accessed on 15 May 2021).



| Quantizer | Full Precision | ||||||
|---|---|---|---|---|---|---|---|
| 1-Bit [26] | 2-Bit Uniform [17] | 2-Bit Uniform [18] | 2-Bit Non-Uniform [20] | 2-Bit Non-Uniform [21] | 2-Bit Uniform Proposed | ||
| Accuracy (%) | 91.12 | 94.70 | 94.49 | 92.38 | 92.73 | 96.26 | 96.86 |
| SQNR (dB) | 4.25 | 1.63 | 1.19 | −8.89 | −2.41 | 8.71 | - |
| Quantizer | Full Precision | ||||||
|---|---|---|---|---|---|---|---|
| 1-Bit [26] | 2-Bit Uniform [17] | 2-Bit Uniform [18] | 2-Bit Non-Uniform [20] | 2-Bit Non-Uniform [21] | 2-Bit Uniform Proposed | ||
| Accuracy (%) | 96.2 | 96.3 | 96.9 | 96.1 | 96.1 | 98.4 | 98.7 |
| SQNR (dB) | 3.21 | −7.08 | −4.01 | −14.85 | −9.07 | 7.32 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perić, Z.; Savić, M.; Simić, N.; Denić, B.; Despotović, V. Design of a 2-Bit Neural Network Quantizer for Laplacian Source. Entropy 2021, 23, 933. https://doi.org/10.3390/e23080933
Perić Z, Savić M, Simić N, Denić B, Despotović V. Design of a 2-Bit Neural Network Quantizer for Laplacian Source. Entropy. 2021; 23(8):933. https://doi.org/10.3390/e23080933
Chicago/Turabian StylePerić, Zoran, Milan Savić, Nikola Simić, Bojan Denić, and Vladimir Despotović. 2021. "Design of a 2-Bit Neural Network Quantizer for Laplacian Source" Entropy 23, no. 8: 933. https://doi.org/10.3390/e23080933
APA StylePerić, Z., Savić, M., Simić, N., Denić, B., & Despotović, V. (2021). Design of a 2-Bit Neural Network Quantizer for Laplacian Source. Entropy, 23(8), 933. https://doi.org/10.3390/e23080933








