Magnetic Resonance Imaging Segmentation via Weighted Level Set Model Based on Local Kernel Metric and Spatial Constraint
Abstract
:1. Introduction
2. Weighted Level Set Model
2.1. Weighted Neighborhood Information
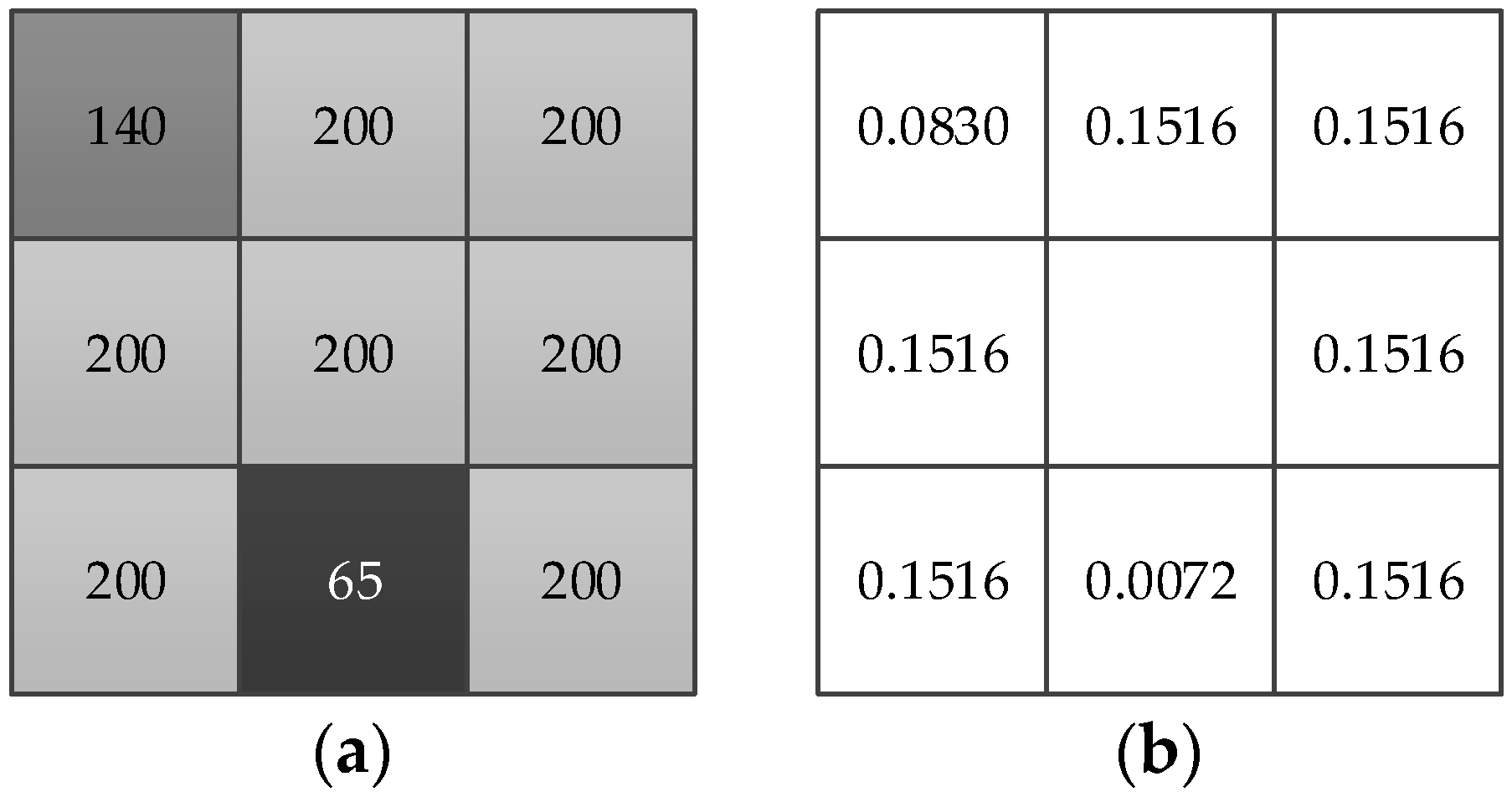
2.1.1. Local Variation Coefficient
2.1.2. Adaptive Spatial Measure
2.1.3. Synthetic Weight of Neighborhood Term
2.2. The Improved External Energy Function
2.3. Internal Energy Function
- (1)
- Two minimum points of double potential function p2(s) should be at s = 0 and s = 1, respectively;
- (2)
- p2(s) is second-order derivable in [0,∞);
- (3)
- Function dp(s) defined by p′(s)/s should satisfy |dp(s)| < 1, s∈(0,∞);
- (4)
2.4. Energy Formulation and Its Minimization
| Algorithm 1: WLSM. |
| Begin Input: original image; weighted coefficients ν and μ; Initialization: bias field b and clustering center c randomly Process: update the current central pixel xi for all pixels according to Equation (8); while |c(n) − c(n−1)| > 0.001 update level set function ϕ according to Equation (25); update bias field b according to Equation (32); update clustering center c according to Equation (33) Output: enhanced image; corrected image; segmentation result; estimated bias field End |
3. Experiments and Results
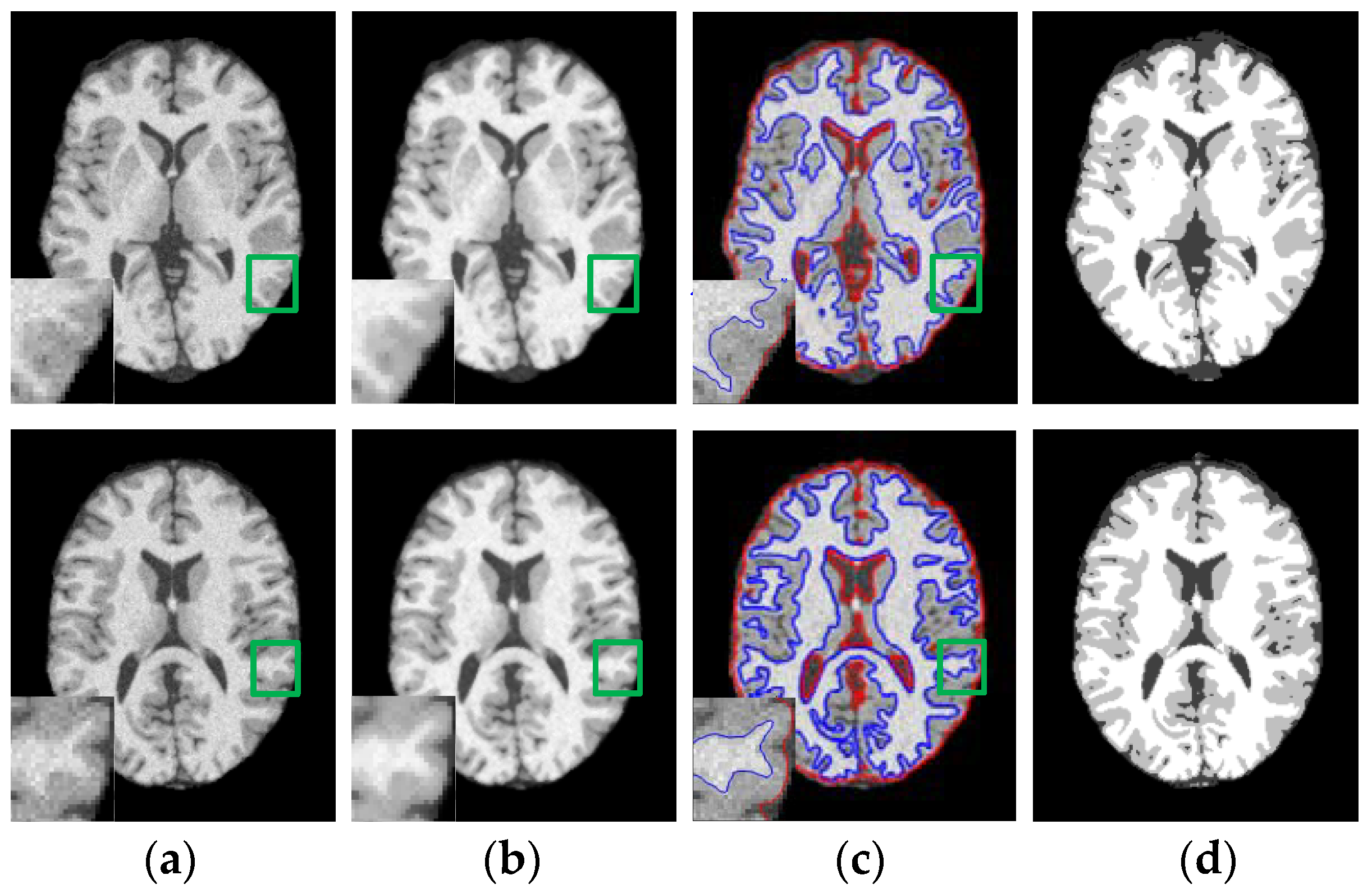
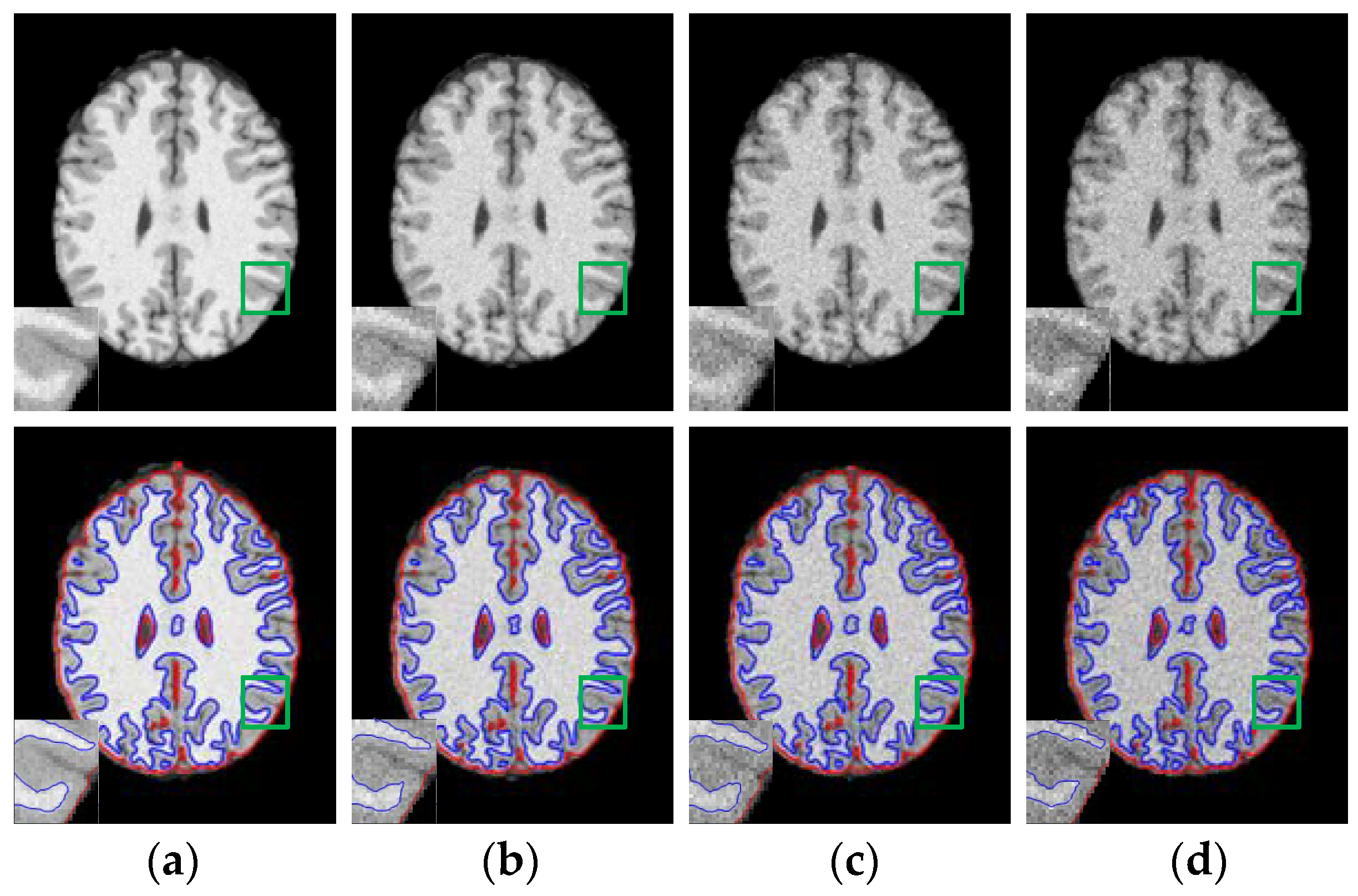
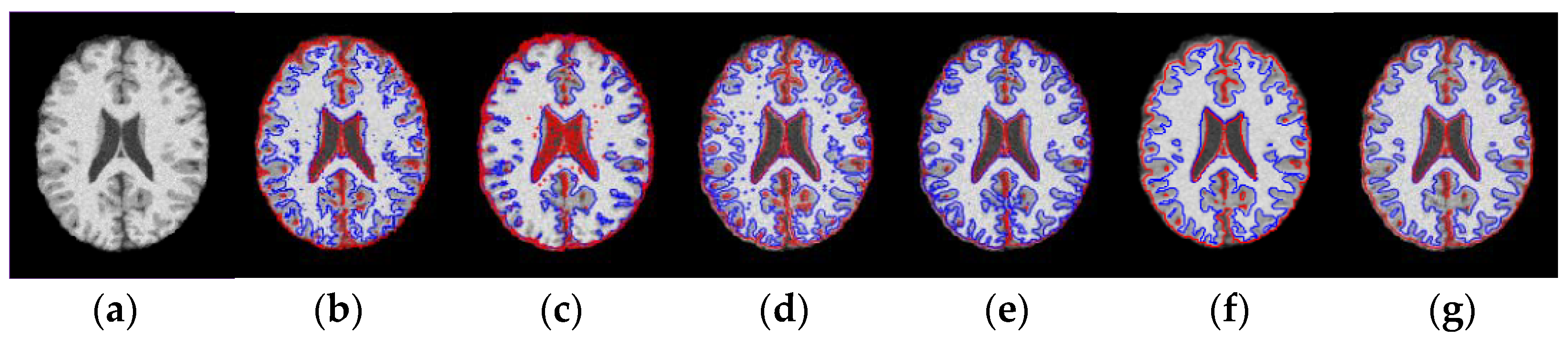
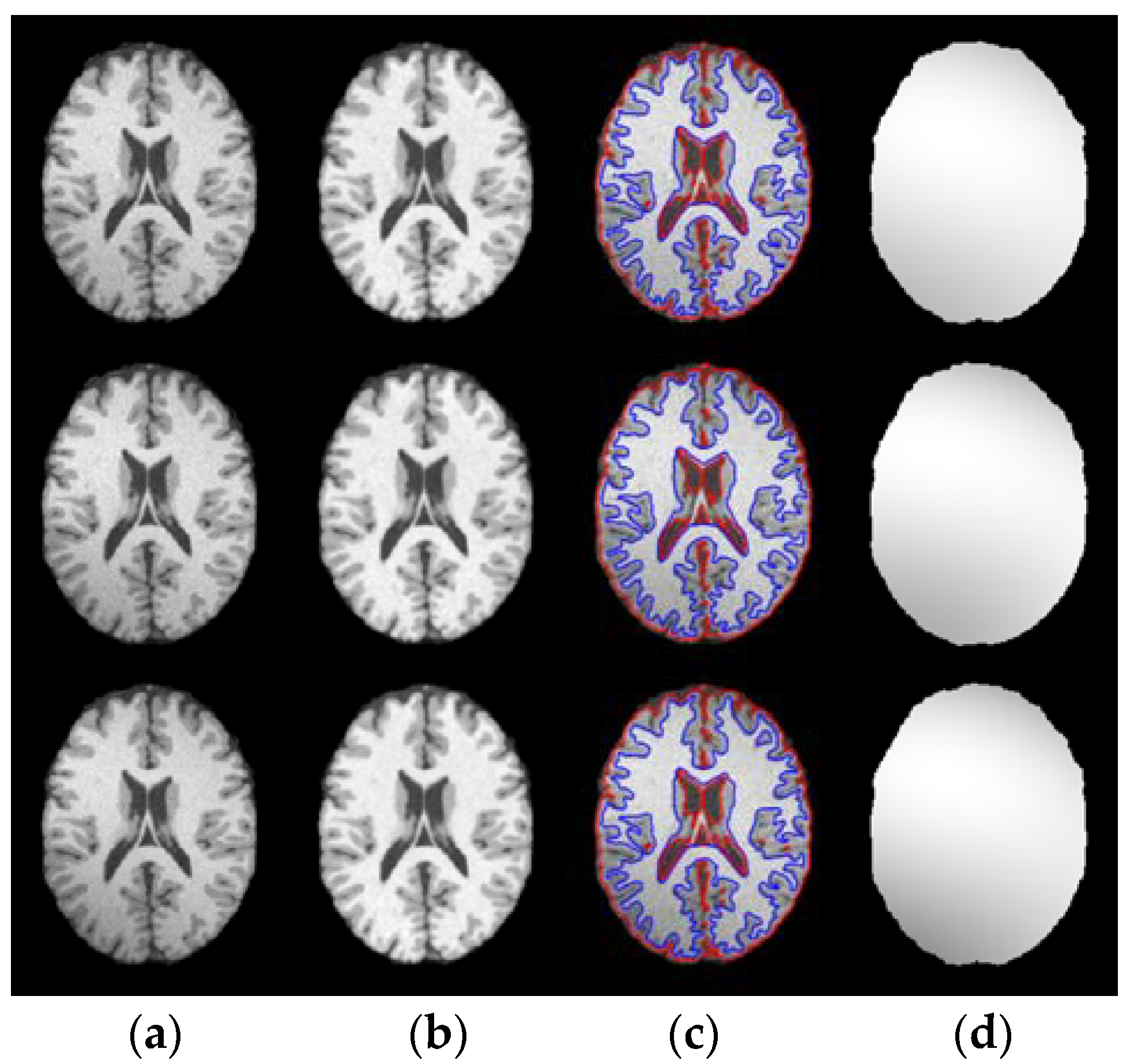
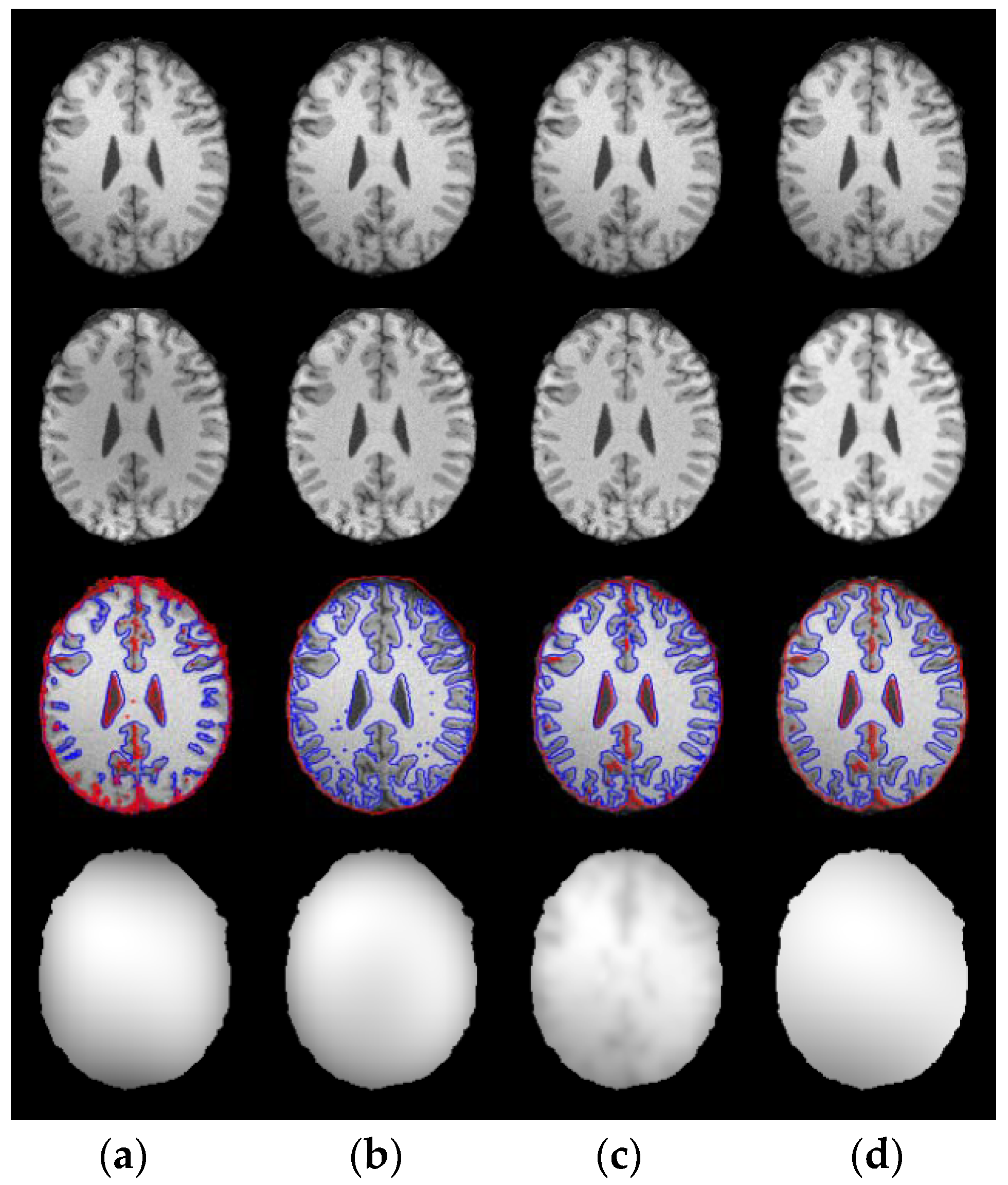
3.1. Results on Noisy Images
3.2. Results on Inhomogeneous Intensity Images
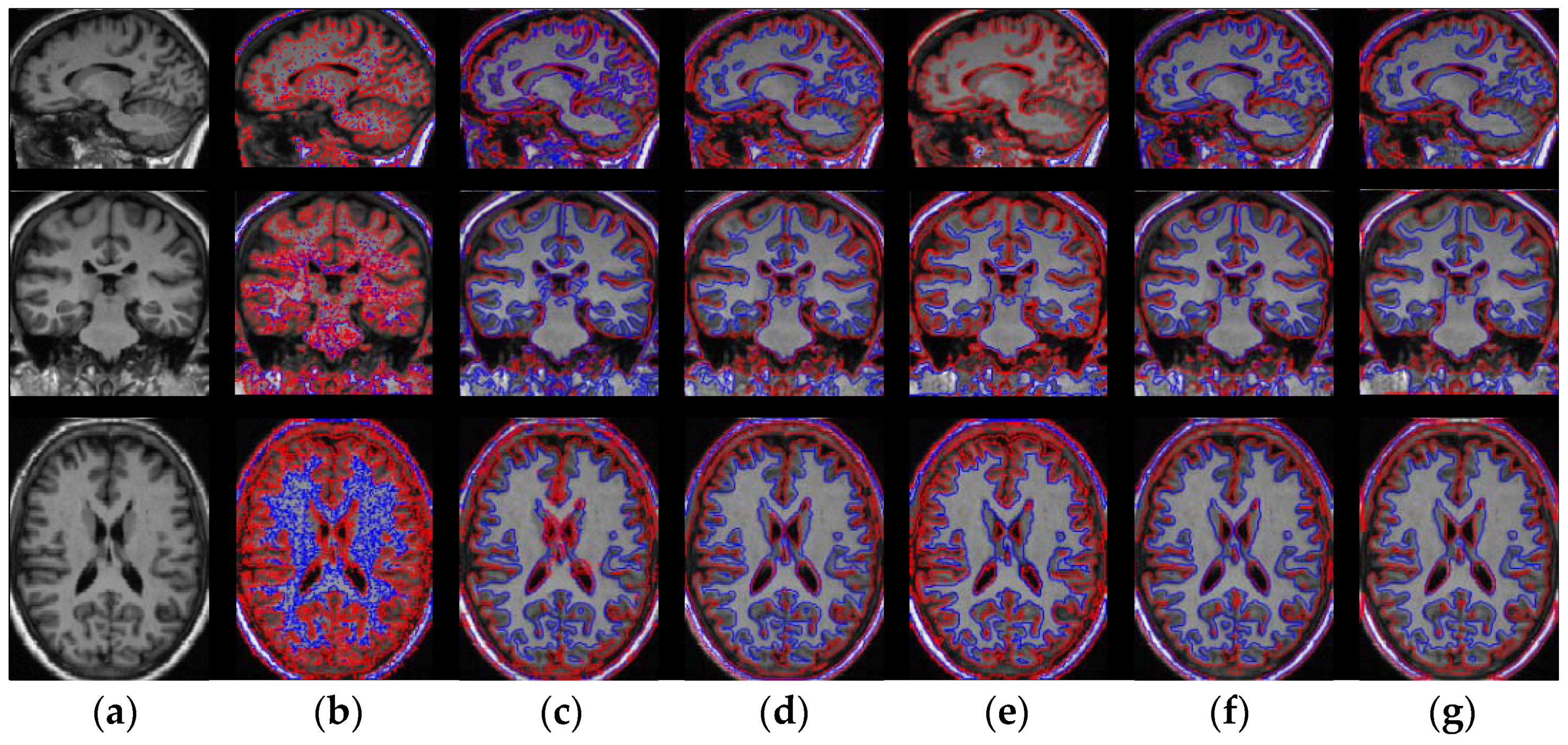
3.3. Results on Sagital, Coronal and Axial Slices of Images
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Despoina, V.; Michalis, M.; Gerukis, T.; Heva, A.; Birbilis, T.; Prassopoulos, P. Magnetic resonance imaging patterns in central nervous system lymphomas: A pictorial review. Clin. Imaging 2021, 78, 1–7. [Google Scholar]
- Colatutto, D.; Sonaglia, A.; Zabotti, A.; Cereser, L.; Girometti, R.; Quartuccio, L. Post-COVID-19 arthritis and sacroiliitis: Natural history with longitudinal magnetic resonance imaging study in two cases and review of the literature. Viruses 2021, 13, 1558. [Google Scholar] [CrossRef]
- Ren, J.; Zhu, M.; Dong, S. Three-dimensional volumetric magnetic resonance imaging detects early alterations of the brain growth in fetuses with congenital heart disease. J. Magn. Reson. Imaging 2021, 54, 263–272. [Google Scholar] [CrossRef]
- Tufail, A.; Ma, Y.; Zhang, Q. Binary classification of alzheimer’s disease using smri imaging modality and deep learning. J. Digit. Imaging 2020, 33, 1073–1090. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Zhang, Z. Brain tissue segmentation and bias field correction of mr image based on spatially coherent FCM with nonlocal constraints. Comput. Math. Method. Med. 2019, 2019, 4762490. [Google Scholar] [CrossRef]
- Chen, L.; Wu, Z.; Hu, D.; Wang, F.; Smith, J.; Lin, W.; Wang, L.; Shen, D.; Li, G. ABCnet: Adversarial bias correction network for infant brain MR images. Med. Image Anal. 2021, 72, 102133. [Google Scholar] [CrossRef]
- Mishro, P.K.; Agrawal, S.; Panda, R.; Abraham, A. A novel Type-2 fuzzy C-Means clustering for brain MR image segmentation. IEEE Trans. Cybern. 2020, 51, 3901–3912. [Google Scholar] [CrossRef] [PubMed]
- Rehman, Z.U.; Zia, M.S.; Bojja, G.R.; Yaqub, M.; Feng, J.; Arshid, K. Texture based Localization of a Brain tumor from MR-images by using a Machine learning Approach. Med. Hypotheses 2020, 141, 109705. [Google Scholar] [CrossRef]
- Govindaraj, V.; Thiyagarajan, A.; Rajasekaran, P.; Zhang, Y.; Krishnasamy, R. Automated unsupervised learning-based clustering approach for effective anomaly detection in brain magnetic resonance imaging (MRI). IET Image Process. 2020, 14, 3516–3526. [Google Scholar] [CrossRef]
- Bennai, M.T.; Guessoum, Z.; Mazouzi, S.; Cormier, S.; Mezghichea, M. A stochastic multi-agent approach for medical-image segmentation: Application to tumor segmentation in brain MR images. Artif. Intell. Med. 2020, 110, 101980. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Guo, S.; Luo, M.; Liu, Y.; Bilello, M.; Li, C. An energy minimization method for MS lesion segmentation from T1-w and FLAIR images. Magn. Reson. Imaging 2017, 39, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Khadidos, A.; Sanchez, V.; Li, C. Weighted level set evolution based on local edge features for medical image segmentation. IEEE Trans. Image Process. 2017, 26, 1979–1991. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, Q.; Gao, Y.; Zheng, Y.; Zhu, J.; Dai, Y.; Shi, Y. Crossover-net: Leveraging vertical-horizontal crossover relation for robust medical image segmentation. Pattern Recognit. 2021, 1131, 107756. [Google Scholar] [CrossRef]
- Khosravanian, A.; Rahmanimanesh, M.; Keshavarzi, P.; Mozaffari, S. Fuzzy local intensity clustering (FLIC) model for automatic medical image segmentation. Visual Comput. 2020, 37, 1185–1206. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, D.; Jia, W.; Shu, X.; Wu, B. Split bregman method based level set formulations for segmentation and correction with application to MR images and color images. Magn. Reson. Imaging 2019, 57, 50–67. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, B.; Zhu, Y. Review of level set in image segmentation. Arch Comput. Method Eng. 2021, 28, 2429–2446. [Google Scholar] [CrossRef]
- Shakir, H.; Khan, T.; Rasheed, H. 3-D segmentation of lung nodules using hybrid level sets. Comput. Biol. Med. 2018, 96, 214–226. [Google Scholar] [CrossRef] [PubMed]
- Ciecholewski, M.; Spodnik, J. Semi-automatic corpus callosum segmentation and 3d visualization using active contour methods. Symmetry 2018, 10, 589. [Google Scholar] [CrossRef] [Green Version]
- Zou, L.; Song, L.; Weise, T.; Wang, X.; Huang, Q.; Deng, R.; Wu, Z. A survey on regional level set image segmentation models based on the energy functional similarity measure. Neurocomputing 2020, 452, 606–622. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, E.; Zhu, Y. Image segmentation evaluation: A survey of methods. Artif. Intell. Rev. 2020, 53, 5637–5674. [Google Scholar] [CrossRef]
- Khorram, B.; Yazdi, M. A new optimized thresholding method using ant colony algorithm for MR brain image segmentation. J. Digit. Imaging 2019, 32, 162–174. [Google Scholar] [CrossRef] [PubMed]
- Tarkhaneh, O.; Shen, H. An adaptive differential evolution algorithm to optimal multi-level thresholding for MRI brain image segmentation. Expert Syst. Appl. 2019, 138, 112820. [Google Scholar] [CrossRef]
- Ji, Z.; Liu, J.; Cao, G.; Sun, Q.; Chen, Q. Robust spatially constrained fuzzy c-means algorithm for brain MR image segmentation. Pattern Recognit. 2014, 47, 2454–2466. [Google Scholar] [CrossRef]
- Feng, C.; Da Zhao, D.; Huang, M. Image segmentation using CUDA accelerated non-local means denoising and bias correction embedded fuzzy c-means (BCEFCM). Signal Process. 2016, 122, 164–189. [Google Scholar] [CrossRef] [Green Version]
- Xuan, T.P.; Siarry, P.; Oulhadj, H. Integrating fuzzy entropy clustering with an improved PSO for MRI brain image segmentation. Appl. Soft Comput. 2018, 65, 230–242. [Google Scholar]
- Huang, H.; Meng, F.; Zhou, S.; Jiang, F.; Manogaran, G. Brain image segmentation based on FCM clustering algorithm and rough set. IEEE Access 2019, 7, 12386–12396. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, J. A robust brain MRI segmentation and bias field correction method integrating local contextual information into a clustering model. Appl. Sci. 2019, 9, 1332. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Wu, J.; Ren, X.; Zhang, B.; Li, Y. The study and application of the improved region growing algorithm for liver segmentation. Optik 2014, 125, 2142–2147. [Google Scholar] [CrossRef]
- Dehdasht-Heydari, R.; Gholami, S. Automatic Seeded Region Growing (ASRG) using genetic algorithm for brain MRI segmentation. Wirel. Pers. Commun. 2019, 109, 897–908. [Google Scholar] [CrossRef]
- Ge, T.; Mu, N.; Li, L. A brain tumor segmentation method based on softmax regression and graph cut. Acta Electron. Sinica. 2017, 45, 644–649. [Google Scholar]
- Wang, C.; Oda, M.; Hayashi, Y.; Yoshino, Y.; Yamamoto, T.; Frangi, A.F.; Mori, K. Tensor-cut: A Tensor-based Graph-cut blood vessel segmentation method and its application to renal artery segmentation. Med. Image Anal. 2019, 60, 101623. [Google Scholar] [CrossRef]
- Kéchichian, R.; Valette, S.; Desvignes, M. Automatic multiorgan segmentation via multiscale registration and graph cut. IEEE Trans. Med. Imaging 2018, 37, 2739–2749. [Google Scholar] [CrossRef] [PubMed]
- Angulakshmi, M.; Deepa, M. A review on deep learning architecture and methods for MRI brain tumour segmentation. Curr. Med. Imaging Rev. 2021, 16, 695–706. [Google Scholar] [CrossRef]
- Di Ieva, A.; Russo, C.; Liu, S.; Jian, A.; Bai, M.Y.; Qian, Y.; Magnussen, J. Application of deep learning for automatic segmentation of brain tumors on magnetic resonance imaging: A heuristic approach in the clinical scenario. Neuroradiology 2021, 63, 1253–1262. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, J. An adaptive fuzzy level set model with local spatial information for medical image segmentation and bias correction. IEEE Access 2019, 7, 27322–27338. [Google Scholar] [CrossRef]
- Chen, Y. A novel approach to segmentation and measurement of medical image using level set methods. Magn. Reson. Imaging 2017, 39, 175–193. [Google Scholar] [CrossRef]
- Liu, L.; Fan, S.; Ning, X.; Liao, L. An efficient level set model with self-similarity for texture segmentation. Neurocomputing 2017, 266, 150–164. [Google Scholar] [CrossRef]
- Li, C.; Xu, C.; Gui, C.; Fox, M.D. Distance regularized level set evolution and its application to image segmentation. IEEE Trans. Image Process. 2010, 19, 3243–3254. [Google Scholar]
- Zhang, X.; Weng, G. Level set evolution driven by optimized area energy term for image segmentation. Optik 2018, 168, 517–532. [Google Scholar] [CrossRef]
- Gibou, F.; Fedkiw, R.; Osher, S. A review of level-set methods and some recent applications. J. Comput. Phys. 2017, 353, 82–109. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Huang, R.; Ding, Z.; Gatenby, J.C.; Metaxas, D.N.; Gore, J. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI. IEEE Trans. Image Process. 2011, 20, 2007–2016. [Google Scholar] [PubMed]
- Feng, C.; Zhao, D.; Huang, M. Image segmentation and bias correction using local inhomogeneous iNtensity clustering (LINC): A region-based level set method. Neurocomputing 2017, 219, 107–129. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Gore, J.; Davatzikos, C. Multiplicative intrinsic component optimization (MICO) for MRI bias field estimation and tissue segmentation. Magn. Reson. Imaging 2014, 32, 913–923. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Wang, J.; Zhang, M.; Cai, Q.; Gong, Y. Correntropy-based level set method for medical image segmentation and bias correction. Neurocomputing 2017, 234, 216–229. [Google Scholar] [CrossRef]
- Huang, G.; Ji, H.; Zhang, W. A fast level set method for inhomogeneous image segmentation with adaptive scale parameter. Magn. Reson. Imaging 2018, 52, 33–45. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, D. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 1907–1916. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Zhang, G.; Lu, J.; Ma, J. A kernel fuzzy C-means clustering-based fuzzy support vector machine algorithm for classification problems with outliers or noises. IEEE Trans. Fuzzy Syst. 2011, 19, 105–115. [Google Scholar] [CrossRef] [Green Version]
- BrainWeb: Simulated Brain Database. Available online: http://brainweb.bic.mni.mcgill.ca/brainweb/ (accessed on 6 April 2021).
- Li, C.; Kao, C.; Gore, J.; Ding, Z. Minimization of region-scalable fitting energy for image segmentation. IEEE Trans. Image Process. 2008, 17, 1940–1949. [Google Scholar]
- IBSR: The Internet Brain Segmentation Repository. Available online: http://www.nitrc.org/projects/ibsr (accessed on 8 April 2021).
- Elazab, A.; Wang, C.; Jia, F.; Wu, J.; Li, G.; Hu, Q. Segmentation of brain tissues from magnetic resonance images using adaptively regularized kernel-based fuzzy c-means clustering. Comput. Math. Methods Med. 2015, 2015, 485495. [Google Scholar] [CrossRef] [PubMed] [Green Version]



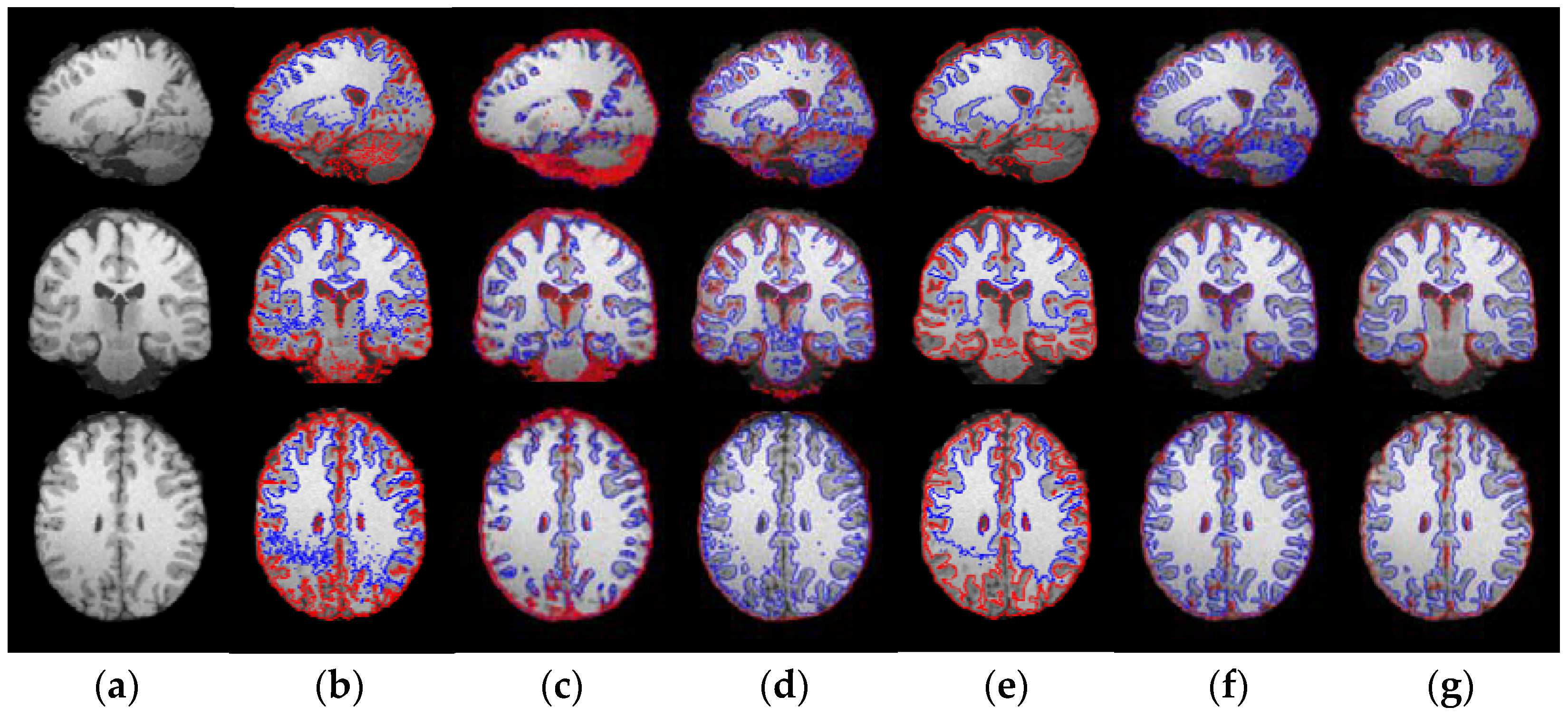
| Name of the Method | Advantages | Disadvantages |
|---|---|---|
| CV [41] | Able to detect interior contours and thus, could be used for medical images with weak boundaries. Piecewise smooth model could work for medical images with IIH. | Limited by images with complicated background and irregular intensity. Piecewise constant case only works with images having homogeneous regions. |
| LIC [42] | Able to estimate bias field and segment brain tissues simultaneously. | Bias field model is an idealized model without fully considering its own properties. |
| MICO [44] | The slowly and the smoothly varying property of the bias field is ensured by a linear combination of a given set of smooth basis functions. | The model is not a level set method and is sensitive to noise without considering local neighborhood information. |
| LINC [43] | A local clustering criterion function is defined to cluster intensities in the neighborhood for utilizing local neighborhood information. | All pixels including noise pixels are clustered into local clustering criterion, so LINC is sensitive to noise and weak boundaries. |
| CLSM [45] | Incorporate the correntropy criterion into the energy function of local bias-field-corrected fitting image. | Difficult to discriminate pixels having same or minor differences between foreground and background, program execution efficiency is low. |
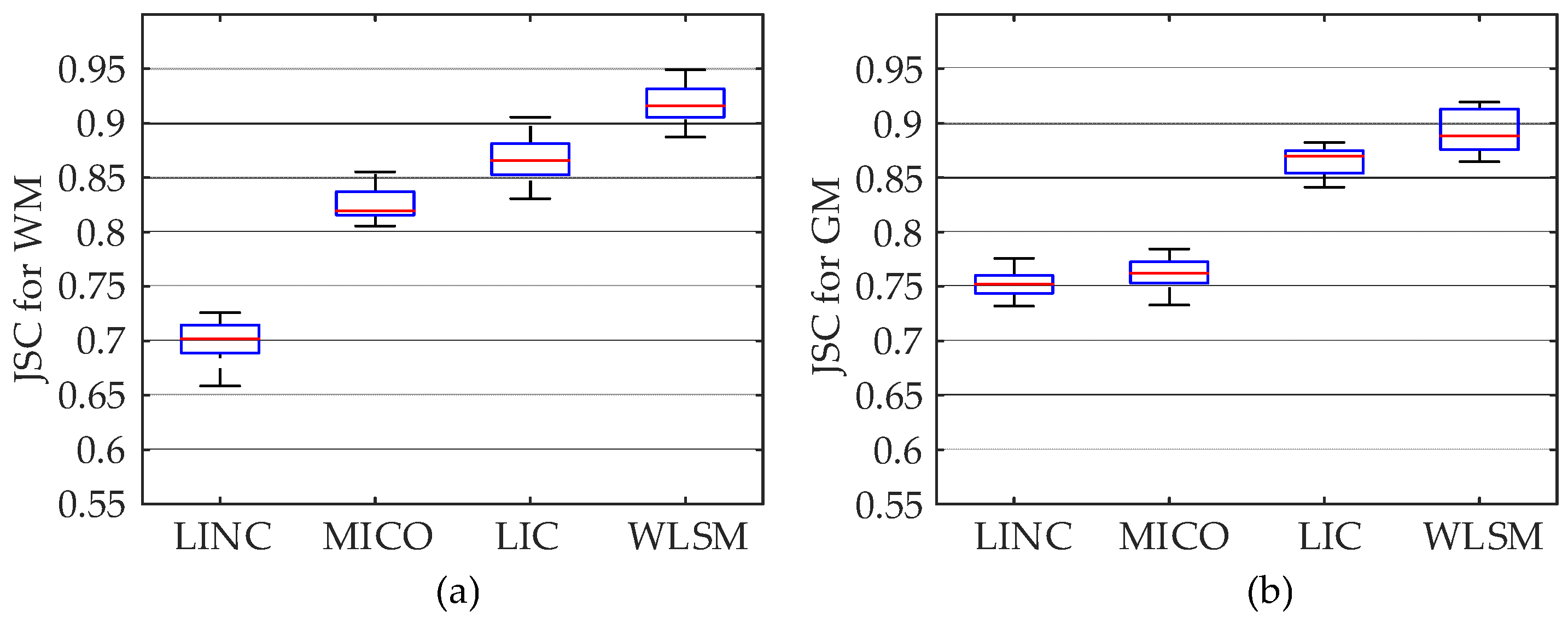
| FCM | LINC | MICO | ARKFCM | LIC | WLSM | |
|---|---|---|---|---|---|---|
| WM | 0.8135 | 0.8551 | 0.9175 | 0.9518 | 0.9633 | 0.9787 |
| GM | 0.7632 | 0.8810 | 0.8453 | 0.9027 | 0.9174 | 0.9470 |
| Average | 0.7883 | 0.8680 | 0.8814 | 0.9272 | 0.9404 | 0.9628 |
| LINC | MICO | LIC | WLSM | |
|---|---|---|---|---|
| Iterations | 983 | 54 | 405 | 651 |
| Time (s) | 42.14 | 31.65 | 29.82 | 27.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Zhang, Z. Magnetic Resonance Imaging Segmentation via Weighted Level Set Model Based on Local Kernel Metric and Spatial Constraint. Entropy 2021, 23, 1196. https://doi.org/10.3390/e23091196
Song J, Zhang Z. Magnetic Resonance Imaging Segmentation via Weighted Level Set Model Based on Local Kernel Metric and Spatial Constraint. Entropy. 2021; 23(9):1196. https://doi.org/10.3390/e23091196
Chicago/Turabian StyleSong, Jianhua, and Zhe Zhang. 2021. "Magnetic Resonance Imaging Segmentation via Weighted Level Set Model Based on Local Kernel Metric and Spatial Constraint" Entropy 23, no. 9: 1196. https://doi.org/10.3390/e23091196
APA StyleSong, J., & Zhang, Z. (2021). Magnetic Resonance Imaging Segmentation via Weighted Level Set Model Based on Local Kernel Metric and Spatial Constraint. Entropy, 23(9), 1196. https://doi.org/10.3390/e23091196






