1. Introduction
MCMC (Markov chain Monte Carlo) remains, to this day, the most popular approach to sampling from a target distribution
p, in particular in Bayesian computations [
1].
Standard practice is to run a single chain, according to a Markov kernel that leaves invariant p. It is also common to discard part of the simulated chain, either to reduce its memory footprint, or to reduce the CPU cost of later post-processing operations, or more generally for the user’s convenience. Historically, the two common recipes for compressing an MCMC output are:
burn-in, which allows discarding the b first states;
thinning, which allows retaining only one out of t (post burn-in) states.
The impact of either recipes on the statistical properties of the subsampled estimates are markedly different. Burn-in reduces the bias introduced by the discrepancy between
p and the distribution of the initial state
(since
for
b large enough). On the other hand, thinning always increases the (asymptotic) variance of MCMC estimators [
2].
Practitioners often choose
b (the burn-in period) and
t (the thinning frequency) separately, in a somewhat ad hoc fashion (i.e., through visual inspection of the initial chain), or using convergence diagnosis such as, e.g., those reviewed in [
3].
Two recent papers [
4,
5] cast a new light on the problem of compressing an MCMC chain by considering, more generally, the problem, for a given
M, of selecting the subsample of size
M that best represents (according to a certain criterion) the target distribution
p. We focus for now on [
5], for reasons we explain below.
Stein thinning, the method developed in [
5], chooses the subsample
of size
M which minimises the following criterion:
where
is a
p-dependent kernel function derived from another kernel function
k:
, as follows:
with
being the Euclidean inner product,
is the so-called score function (gradient of the log target density), and ∇ is the gradient operator.
The rationale behind criterion (
1) is that it may be interpreted as the KSD (kernel Stein discrepancy) between the true distribution
p and the empirical distribution of subsample
S. We refer to [
5] for more details on the theoretical background of the KSD, and its connection to Stein’s method.
Stein thinning is appealing, as it seems to offer a principled, quasi-automatic way to compress an MCMC output. However, closer inspection reveals the following three limitations.
First, it requires computing the gradient of the log-target density, . This restricts the method to problems where this gradient exists and is tractable (and, in particular, to ).
Second, its CPU cost is
. This makes it nearly impossible to use Stein thinning for
. This cost stems from the greedy algorithm proposed in [
5], see their Algorithm 1, which adds at iteration
t the state
which minimises
, where
is the sample obtained from the
previous iterations.
Third, its performance seems to depend in a non-trivial way on the original kernel function
k; the authors of [
5] propose several strategies for choosing and scaling
k, but none of them seem to perform uniformly well in their numerical experiments.
We propose a different approach in this paper, which we call cube thinning, and which addresses these shortcomings to some extent. Assuming the availability of
J control variates (that is, of functions
with known expectation under
p), we cast the problem of MCMC compression as that of resampling the initial chain under constraints based on these control variates. The main advantage of cube thinning is that its complexity is
; in particular, it does not depend on
M. That makes it possible to use it for much larger values of
M. We shall discuss the choice of
J, but, by and large,
J should be of the same order as
d, the dimension of the sampling space. The name stems from the cube method of [
6], which plays a central part in our approach, as we explain in the body of the paper.
The availability of control variates may seem like a strong requirement. However, if we assume we are able to compute
, then (for a large class of functions
, which we define later)
where
denotes the divergence of
. In other words, the availability of the score function implies, automatically, the availability of control variates. The converse is not true: there exists control variates, e.g., [
7], that are not gradient-based. One of the examples we consider in our numerical examples feature such non gradient-based control variates; as a result, we are able to apply cube thinning, although Stein thinning is not applicable.
The supporting methods of [
4] do not require control variates. It is thus more generally applicable than either cube thinning or Stein thinning. On the other hand, when gradients (and thus control variates) are available, the numerical experiments of [
5] suggest that Stein thinning outperforms support points. From now on, we focus on situations where control variates are available.
This paper is organised as follows.
Section 2 recalls the concept of control variates, and explains how control variates may be used to reweight an MCMC sample.
Section 3 describes the cube method of [
6].
Section 4 explains how to combine control variates and the cube method to perform cube thinning.
Section 5 assesses the statistical performance of cube thinning through two numerical experiments.
We use the following notations throughout: p denotes both the target distribution and its probability density; is a short-hand for the expectation of under p. The gradient of a function f is denoted by , or simply when there is no ambiguity. The -th component of a vector is denoted by , and it is transposed by . The vectors of the canonical basis of are denoted by , i.e., if , 0 otherwise. Matrices are written in upper-case; the kernel (null space) of matrix A is denoted by . The set of functions that are continuously differentiable is denoted by .
3. The Cube Method
We review in this section the cube method of [
6]. This method originated from survey sampling and is a way to sample from a finite population under constraints. The first subsection gives some definitions, the second one explains the flight phase of the cube method and the third subsection discusses the landing phase of the method.
3.1. Definitions
Suppose we have a finite population of N individuals and that to each individual is associated a variable of interest and J auxiliary variables, . Without loss of generality, suppose also that the J vectors are linearly independent. We are interested in estimating the quantity using a subsample of . Furthermore, we know the exact value of each sum , and we wish to use this auxiliary information to better estimate Y.
We assign, to each individual
n, a sampling probability
. We consider random variables
such that, marginally,
. We may then define the Horvitz–Thompson estimator of
Y as
which is unbiased, and which depends only on selected individuals (i.e.,
).
We define similarly the Horvitz–Thompson estimator of
as
Our objective is to construct a joint distribution
for the inclusion variables
such that
for all
, and
where
,
. Such a probability distribution is called a balanced sampling design.
3.2. Subsamples as Vertices
We can view all the possible samples from as the vertices of the hypercube in . A sampling design with inclusion probabilities is then a distribution over the set of these vertices such that , where , and is the vector of inclusion probabilities. Hence, is expressed as a convex combination of the vertices of the hypercube.
We can think of a sampling algorithm as finding a way to reach any vertex of the cube, starting at
, while satisfying the balancing Equation (
14). However, before we describe such a sampling algorithm, we may wonder if it is possible to find a vertex such that (
14) is satisfied.
3.3. Existence of a Solution
The balancing equation, Equation (
14), defines a linear system. Indeed, we can re-express (
14) as
S, as a solution to
, where
is of dimension
,
. This system defines a hyperplane
Q of dimension
in
.
What we want is to find vertices of the hypercube
that also belong to the hyperplane
Q. Unfortunately, it is not necessarily possible, as it depends on how the hyperplane
Q intersects cube
. In addition, there is no way to know beforehand if such a vertex exists. Since
, we know that
and is of dimension
. The only thing we can say is stated Proposition 1 in [
6]: if
r is a vertex of
, then in general
.
The next section describes the flight phase of the cube algorithm, which generates a vertex in
when such vertices exist, or which, alternatively, returns a point in
with most (but not all) components set to zero or one. In the latter case, one needs to implement a landing phase, which is discussed in
Section 3.5.
3.4. Flight Phase
The flight phases simulates a process which takes values in , and starts at . At every time t, one selects a unit vector , then one chooses randomly between one of the two points that are in the intersection of the hypercube and the line parallel to that passes through . The probability of selecting these two points are set to ensure that is a martingale; in that way, we have at every time step. The random direction must be generated to fulfil the following two requirements: (a) that the two points are in Q, i.e., , and (b) whenever reaches one of the faces of the hypercube, it must stay within that face; thus, if or 1.
Algorithm 1 describes one step of the flight phase.
| Algorithm 1: Flight phase iteration |
Input:
Output:
1 Sample in with if the k-th component of is an integer.
2 Compute and , the largest values of and such that: and .
3 With probability , set ; otherwise, set . |
The flight phase stops when Step 1 of Algorithm 1 cannot be performed (i.e., no vector fulfils these conditions). Until this happens, each iteration increases by at least one the number of components in that are either zero or one. Thus, the flight phases completes at most in N steps.
In practice, to generate , one may proceed as follows: first generate a random vector , then project it in the constraint hyperplane: , where is a diagonal matrix such that is 0 if is an integer and 1 otherwise, and denotes the pseudo-inverse of the matrix M.
The authors of [
14] propose a particular method to generate vector
, which ensures that the complexity of a single iteration of the flight phase is
. This leads to an overall complexity of
for the flight phase, since it terminates in at most
N iterations.
3.5. Landing Phase
Denote by the value of process when the flight phase terminates. If is a vertex of (i.e., all its components are either zero or one), one may stop and return as the output of the cube algorithm. If is not a vertex, this informs us that no vertex belongs to . One may implement a landing phase, which aims at choosing randomly a vertex which is close to , and such that the variance of the components of is small.
Appendix A gives more details on the landing phase. Note that its worst-case complexity is
. However, in practice, it is typically either much faster, or not required (i.e.,
is already a vertex) as soon as
.
5. Experiments
We consider two examples. The first example is taken from [
5], and is used to compare cube thinning with KSD thinning. The second example illustrates cube thinning when used in conjunction with control variates that are not gradient-based. We also include standard thinning in our comparisons.
Note that there is little point in comparing these methods in terms of CPU cost, as KSD thinning is considerably slower than cube thinning and standard thinning whenever . (In one of our experiments, for , KSD took close to 7 h to run, while cube thinning with all the covariates took about 30 s.) Thus, our comparison will be in terms of statistical error, or, more precisely, in terms of how representative of p is the selected subsample.
In the following (in particular in the plots), “cubeFull” (resp. “cubeDiagonal”) will refer to our approach based on the full (resp. diagonal) set of control variates, as discussed in
Section 2.3. “NoBurnin” means that burn-in has been discarded manually (hence, no burn-in in the inputs). Finally, “thinning” denotes the usual thinning approach, “SMPCOV”, “MED” and “SCLMED” are the same names used in [
5] for KSD thinning, based on three different kernels.
To implement the cube method, we used R package BalancedSampling.
5.1. Evaluation Criteria
We could compare the three different methods in terms of variance of the estimates of
for certain functions
f. However, it is easy to pick functions
f that are strongly correlated with the chosen control variates; this would bias the comparison in favour of our approach. In fact, as soon as the target is Gaussian-like, the control variates we chose in
Section 2.3 should be strongly correlated with the expectation of any polynomial function of order two, as we discussed in that section.
Rather, we consider criteria that are indicative of the performance of the methods for a general class of function. Specifically, we consider three such criteria. The first one is the kernel Stein discrepency (KSD) as defined in [
5] and recalled in the introduction—see (
1). Note that this criterion is particularly favourable for KSD thinning, since this approach specifically minimises this quantity. (We use the particular version based on the median kernel in Riabiz et al. [
5].)
The second criterion is the energy distance (ED) between
p and the empirical distribution defined by the thinning method, e.g., (
19) for cube thinning. Recall that the ED between two distributions
F and
G is:
where
and
, and that this quantity is actually a pseudo-distance:
,
,
, but ED does not fulfil the triangle inequality [
17,
18].
One technical difficulty is that (
19) is a signed measure, not a probability measure; see
Appendix B on how we dealt with this issue.
Our third criterion is inspired by the star discrepancy, a well-known measure of the uniformity of
N points
in the context of quasi-Monte Carlo sampling [
9] (Chapter 15). Specifically, we consider the quantity
where
,
and
are the push-forward measures associated to empirical distributions
, and
as defined in (
19), and
is the set of hyper-rectangles
. In practice, we defined function
as follows: we apply the linear transform that makes the considered sample to have zero mean and unit variance, and then we applied the inverse CDF (cumulative distribution function) of a unit Gaussian to each component.
Additionally, since the sup above is not tractable, we replace it by a maximum over a finite number of (simulated uniformly).
5.2. Lotka–Volterra Model
This example is taken from [
5]. The Lotka–Volterra model describes the evolution of a prey–predator system in a closed environment. We denote the number of prey by
and the number of predators by
. The growth rate of the prey is controlled by a parameter
and its death rate—due to the interactions with the predators—is controlled by a parameter
. In the same way, the predator population has a death rate of
and a growth rate of
. Given these parameters, the evolution of the system is described by a system of ODEs:
Ref. [
5] set
, the initial condition
, and simulate synthetic data. They assume they observe the populations of prey and predator at times
where the
are taken uniformly on
and that these observations are corrupted with a centered Gaussian noise with a covariance matrix
. Finally, the model is parametrised in terms of
and a standard normal distribution as a prior on
x is used.
The authors have provided their code as well as the sampled values they obtained by running different MCMC chains for a long time. We use the exact same experimental set-up, and we do not run any MCMC chain on our own, but use the ones they provide instead, specifically the simulated chain, of length , from preconditionned MALA.
We compress this chain into a subsample of size either
or
. For each value of
M, we run different variations of our cube method 50 times and make a comparison with the usual thinning method and with the KSD thinning method with different kernels, see [
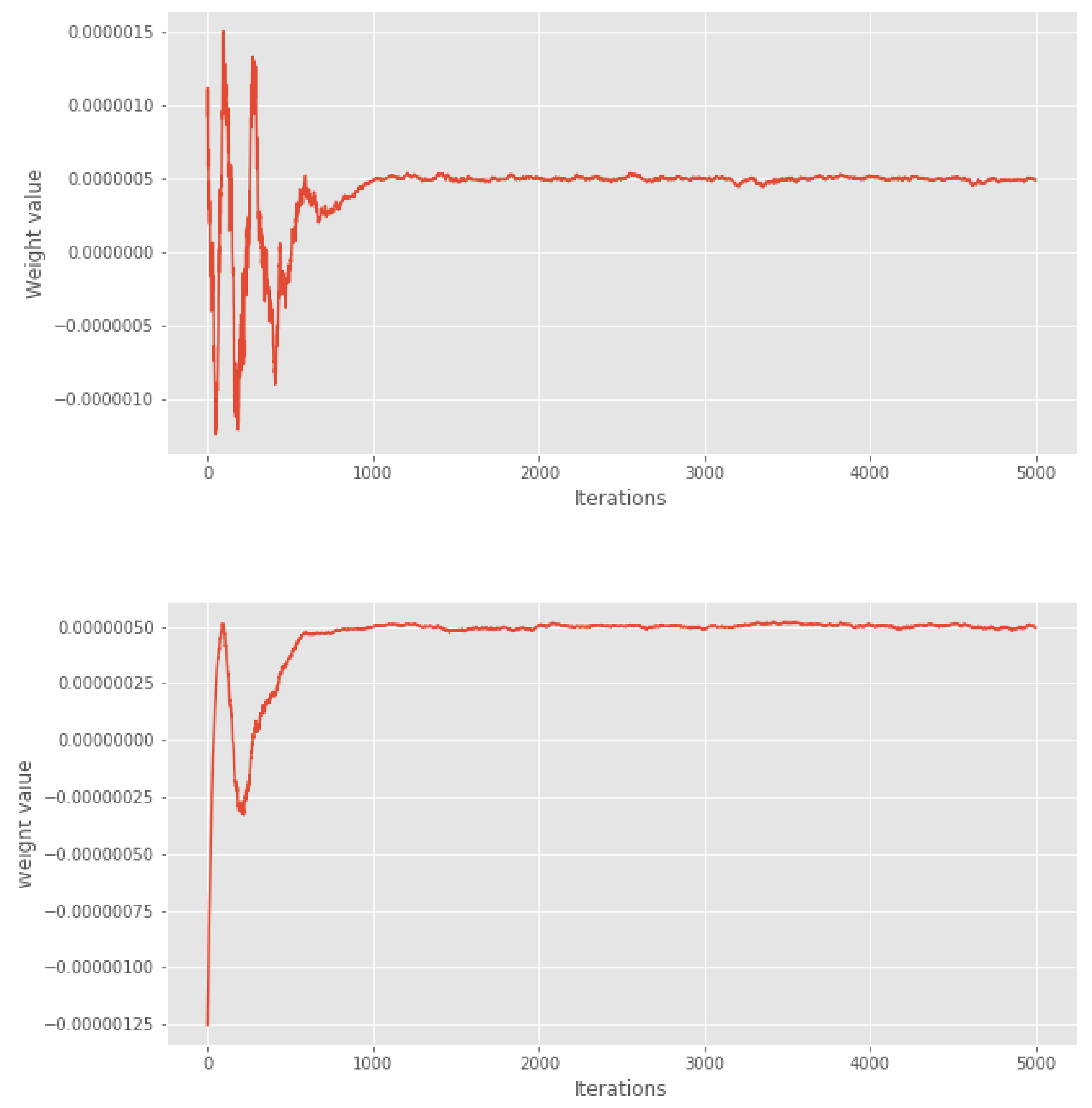
5]. In
Figure 1, we show the first 5000 weights of the cube method. We can see that after 1000 iterations, the weights seem to stabilise. Based on visual examination of these weights, we chose a conservative burn-in period of 2000 iterations for the variants where burn-in is removed manually.
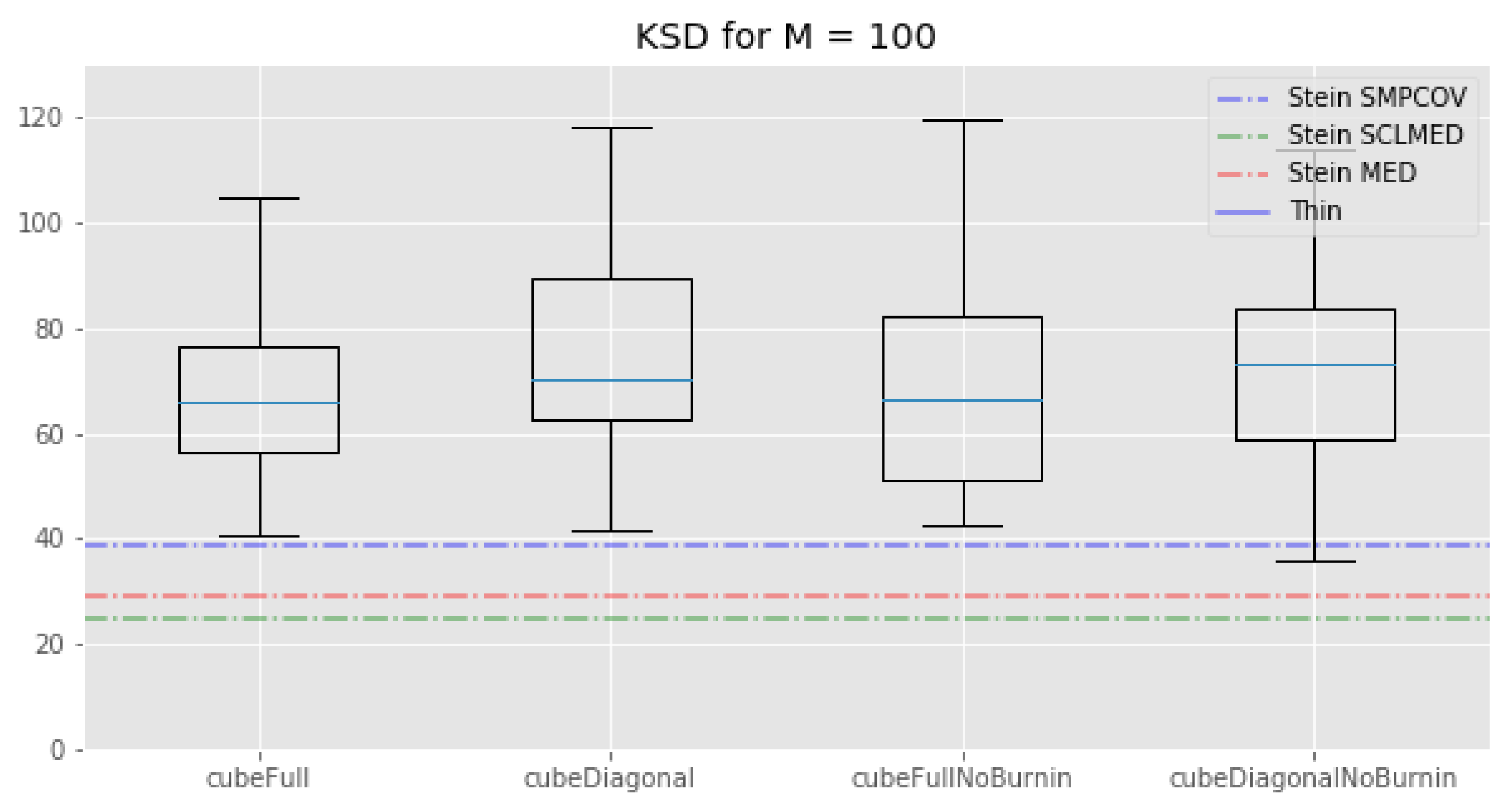
First, we see that regarding the kernel Stein discrepancy metric,
Figure 2, the KSD method performs better than the standard thinning procedure and the cube method. This is not surprising since, even if this method does not properly minimise the Kernel–Stein Discrepency, this is still its target. We also see that, for
, the KSD method performs a bit better than our cube method which in turn performs better than the standard thinning procedure. Note that the relative performance of the KSD method to our cube methods depends on the kernel that is being used and that there is no way to determine which kernel will perform best before running any experiment.
The picture is different for : KSD thinning outperforms standard thinning, which in turn outperforms all of our cube thinning variations. Once again, the fact that the KSD method performs better than any other method seems reasonable: since it regards minimizing the Kernel–Stein Discrepancy, the KSD method is “playing at home” on this metric.
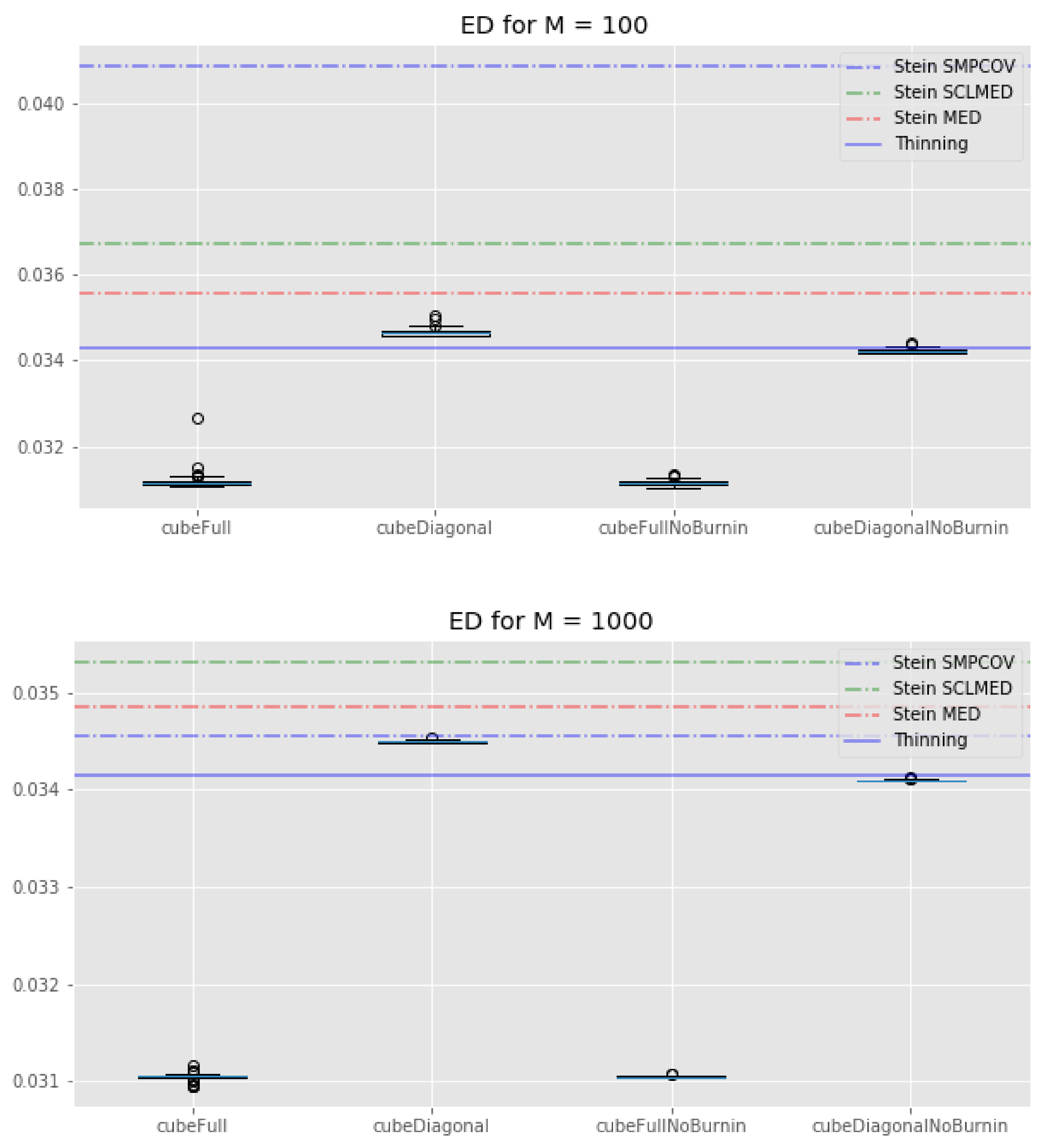
If we look at
Figure 4, we see that all of our cube methods outperform the KSD method with any kernel. Interestingly, the standard thinning methods has a similar energy distance as the cube methods with “diagonal” control variates. These observations are true for both
and
. We can also note that the cube method with the full set of control variates tends to perform much better than its “diagonal” counterpart, whatever the value of
M.
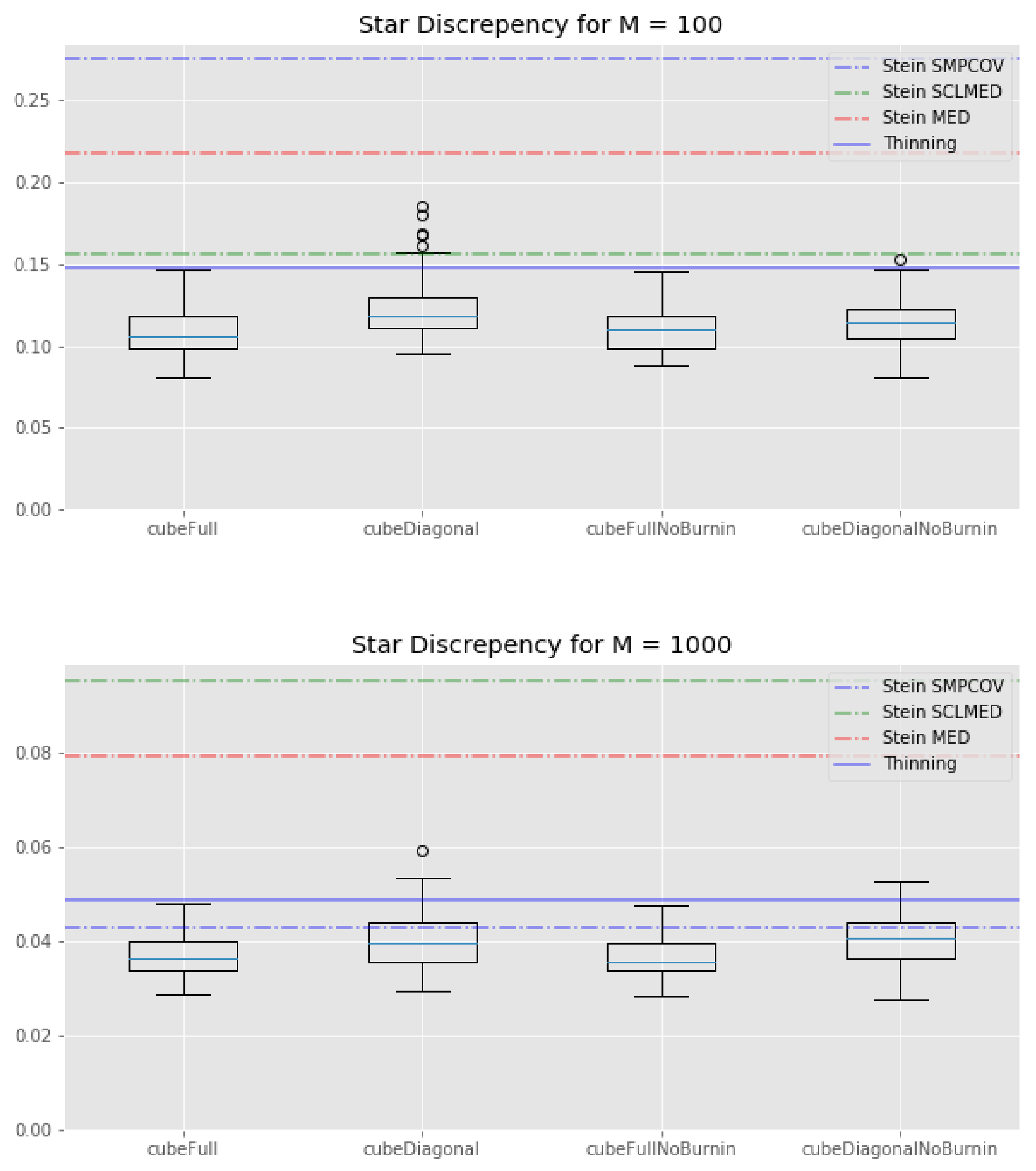
Finally, looking at
Figure 3, it is clear that the KSD method—with any kernel—performs worse than any cube method in terms of star discrepancy.
Overall, the relative performance of the cube methods and KSD methods can change a lot depending on the metric being used and the number of points we keep. In addition, while all the cube methods tend to perform roughly the same, this is not the case of the KSD method, whose performances depend on the kernel we use. Unfortunately, we have no way to determine beforehand which kernel will perform best. This is a problem since the KSD method is computationally expensive for subsamples of cardinality .
Thus, by and large, cube thinning seems much more convenient to use (both in terms of CPU time and sensitivity to tuning parameters) while offering, roughly, the same level of statistical performance.
5.3. Truncated Normal
In this example, we use the (random-scan version of) the Gibbs sampler of [
1] to sample from 10-dimensional multivariate normal truncated to
. We generated the parameters of this truncated normal as follows: the mean was set as the realisation of a 10-dimensional standard normal distribution, while for the covariance matrix
, we first generated a matrix
for which each entry was the realisation of a standard normal distribution. Then, we set
.
Since we used a Gibbs sampler, we have access to the Gibbs control variates of [
7], based on the expectation of each update (which amounts to simulating from a univariate Gaussian). Thus, we consider 10 control variates.
The Gibbs sampler was run for
iterations and no burn-in was performed. We compare the following estimators of the expectation of the target distribution the standard estimator, based on the whole chain ("usualEstim" in the plots), the estimator based on standard thinning ("thinEstim" in the plots), the control variate estimator based on the whole chain, i.e., (
7) ("regressionEstim" in the plots), and finally our cube estimator described in
Section 4 ("cubeEstim" in the plots). For standard thinning and cube thinning, the thinning sample size was set to
, which corresponds to a compression factor of
.
The results are shown in
Figure 5. First, we can see that the control variates we chose led to a substantial decrease in the variance of the estimates for regressionEstim compared to usualEstim. Second, the cube estimator performed worse than the regression estimator in terms of variance, but this was expected, as explained in
Section 4. More interestingly, if we cannot say that the cube estimator performs better than the usual MCMC estimator in general, we can see that for some components it performed as well or even better, even though the cube estimator used only
points while the usual estimator used
points. This is largely due to the good choice of the control variates. Finally, the cube estimator outperformed the regular thinning estimator for every component, sometimes significantly.