Bispectral Analysis of Heart Rate Variability to Characterize and Help Diagnose Pediatric Sleep Apnea
Abstract
1. Introduction
2. Subjects and Signals under Study
3. Methods
3.1. Bispectrum Estimation
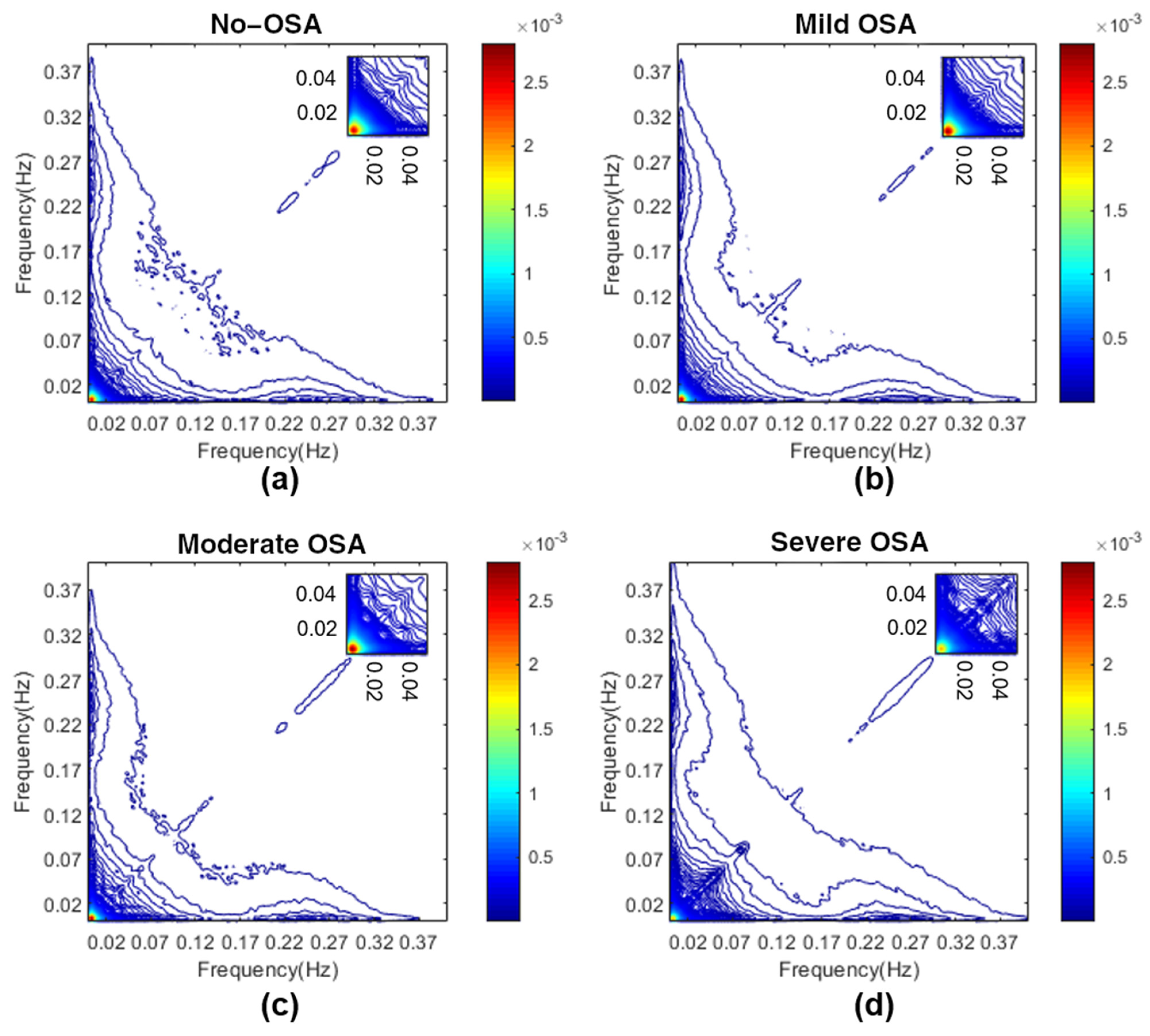
3.2. Determination of Bispectral Regions
3.3. Feature Extraction Stage
3.3.1. Bispectral Region Amplitude Features
- Maximum amplitude (Bmax), measured as the maximum magnitude value inside each of the regions considered [46]:where represents one of the six regions considered.
- Minimum amplitude (Bmin), measured as the minimum magnitude value inside each of the regions considered [46]:
- Total bispectral power (Btotal), measured as the sum of all magnitudes inside each of the regions considered [46]:
3.3.2. Bispectral Entropy Features
- Normalized bispectral entropy (BE1), normalized squared bispectral entropy (BE2) and normalized cubed bispectral entropy (BE3). These parameters, based on Shannon’s entropy, quantify the irregularity of the bispectral distribution in each region and are computed as [29,34]where p is the magnitude distribution of the region elements:
- Phase entropy (PE), which quantifies the phase regularity of the region [29]. PE, as with the bispectral entropies, is higher as the randomness of a process increases, meaning it would be zero for a harmonic, periodic and predictable process [34]. PE computation is performed applying Shannon’s entropy to the normalized distribution of the region phase angles [29,46]:wherewhere () is the indicator function (equal to 1 if φ is within the range of histogram bins ), φ is the phase angle of the region, and N is the bin number of the histogram.
3.3.3. Bispectral Region Moment Features
- The sum of the logarithmic magnitude values of the region (H1), sum of the logarithmic magnitude values of the diagonal of the region (H2) and first- and second-order spectral moments of the magnitude values of the diagonal elements of the region (H3 and H4, respectively). These features were included as they allow characterizing the nonlinearity of the regions and are computed as follows [46]:
3.3.4. Bispectral WCOB Features
- WCOB allows reflecting the interaction of different frequency components through the assignment of a weight to each bispectral point of the region [46]. The weighted center of each region is composed of two vectors, f1m and f2m, which indicate the coupling focus of the region as a summary of the frequency interaction [46]. Those components of WCOB are computed as [46]
3.3.5. Relative Power of the Diagonal, a Novel Bispectral Feature
- The relative power of the diagonal (RPDiag), computed as the sum of the bispectral amplitudes of the diagonal elements of the region, after a normalization applied over the whole diagonal. This novel parameter evaluates the relative bispectral magnitude value inside the diagonal of the region with respect to the complete bispectral diagonal magnitude:where represents the diagonal elements of one of the regions considered except BWRes, and is the normalized bispectral diagonal after the normalization performed such thatwhere Diag is the diagonal of the bispectral matrix, and DP is the diagonal power, measured as the sum of all amplitudes of the Diag elements.
3.4. Feature Selection Stage
3.5. Classification Stage
3.6. Statistical Analysis
4. Results
4.1. Feature Selection in the Training Set
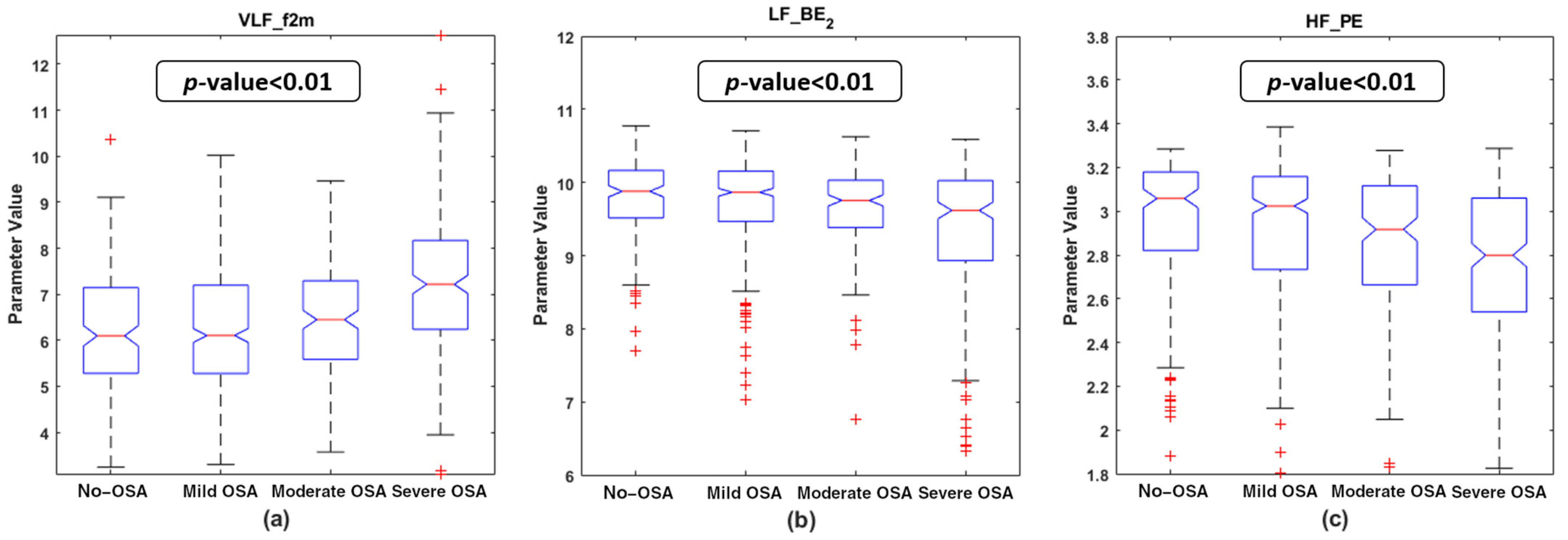
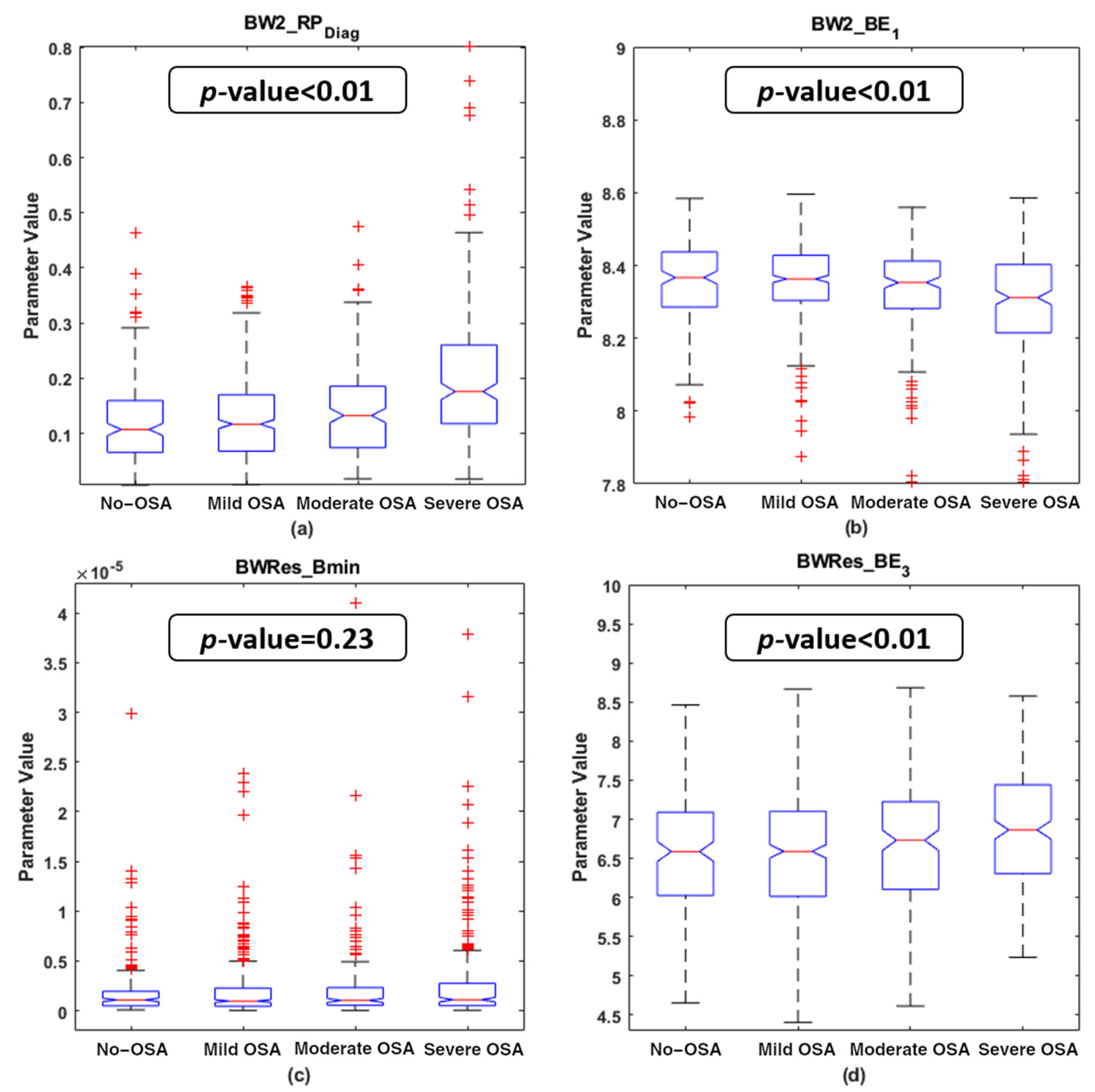
4.2. Descriptive Analysis of the Features Selected
4.3. MLP Network Optimization and Training
4.4. Correlation Analysis in the Test Set
4.5. Diagnostic Ability Assessments
5. Discussion
5.1. Physiological Interpretation of the Features Selected
5.2. Diagnostic Performance of the Bispectral Models
5.3. Comparison with Previous Work
5.4. Limitations and Outlook
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Determination of HRV OSA-Specific Frequency Ranges and Averaged Bispectral Regions in the Training Set

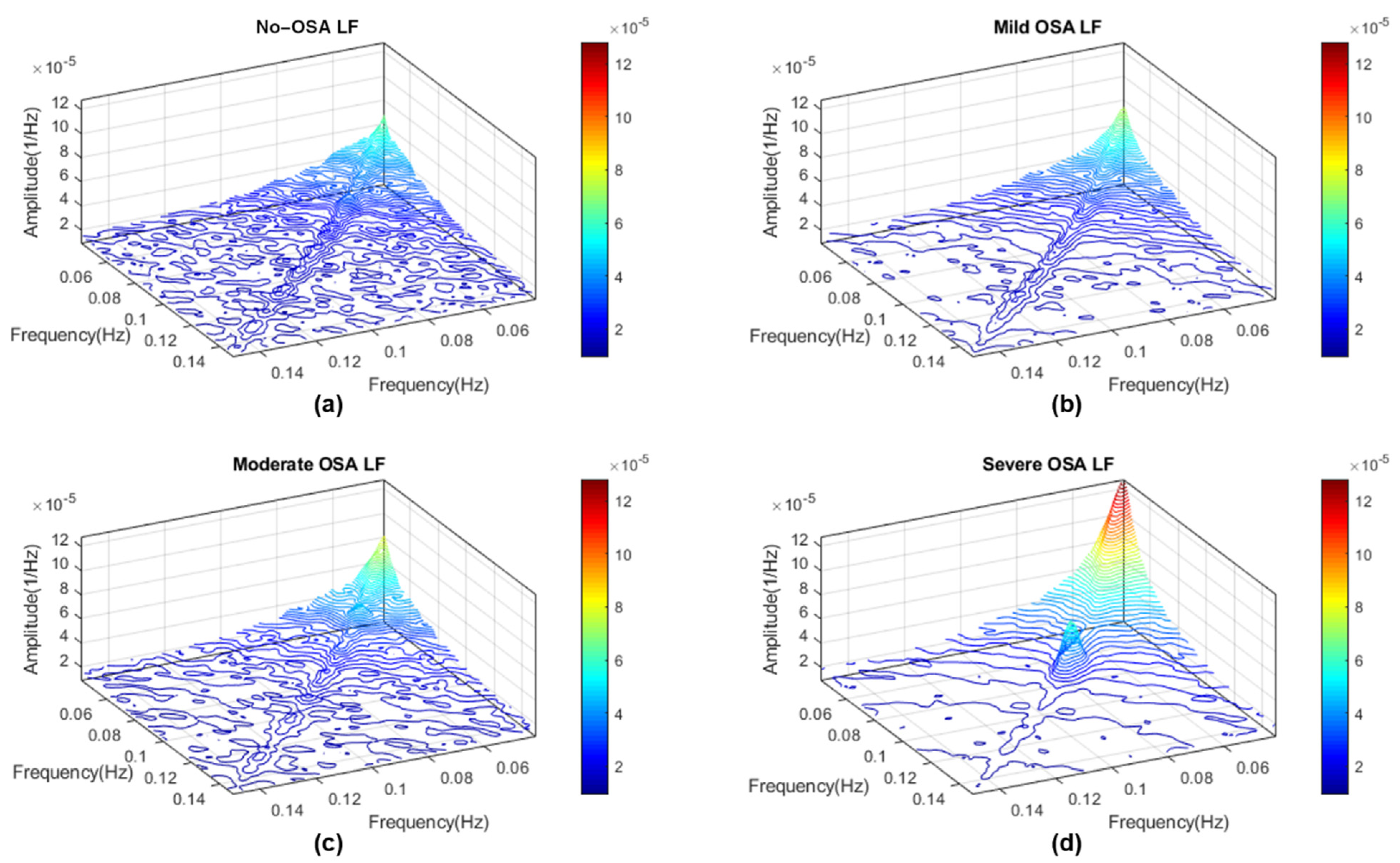



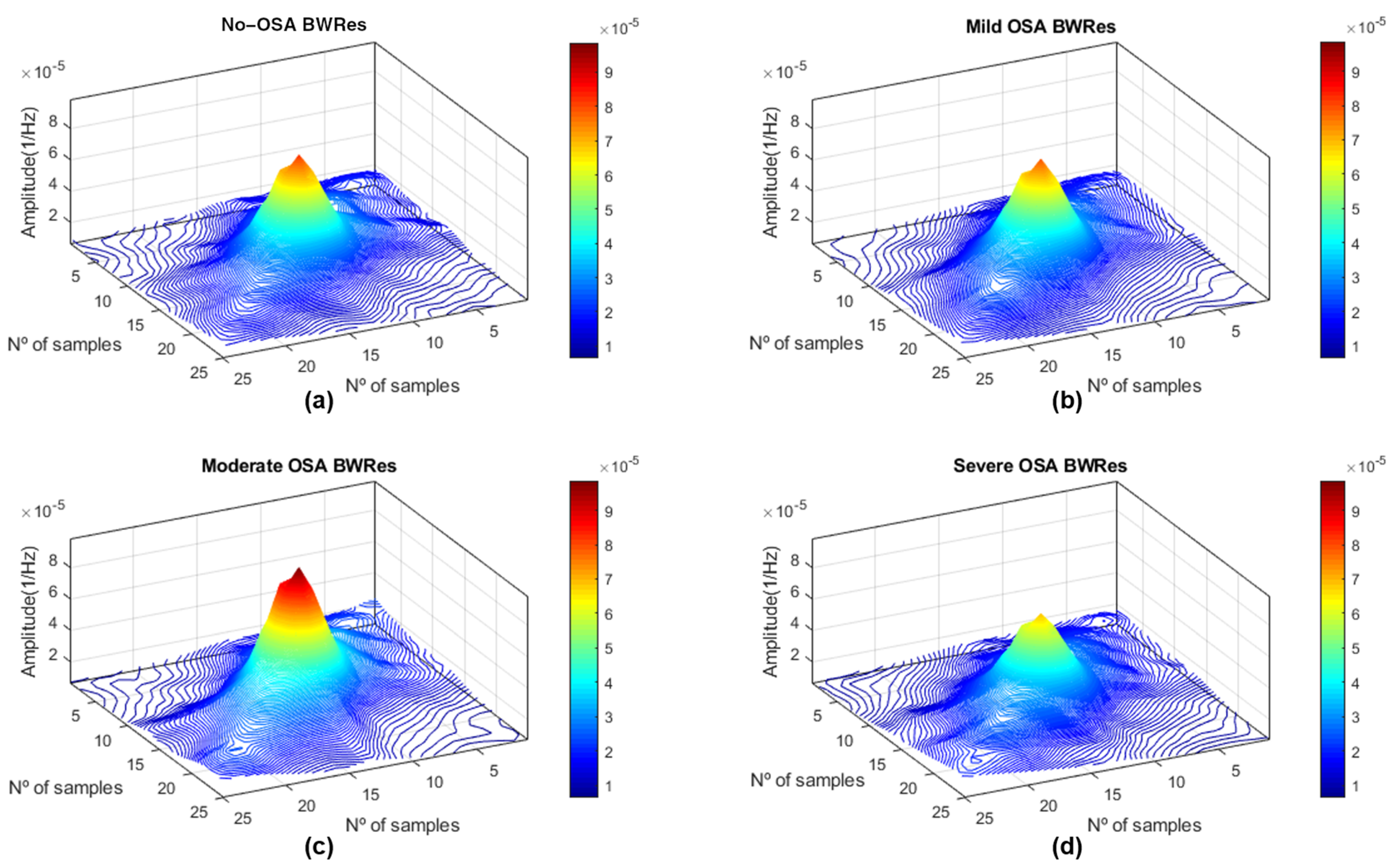
Appendix B. Diagnostic Performance of Bispectral Region Models with a Linear Discriminant Analysis Classifier
| Feature/Model | AHI Threshold = 1 e/h | AHI Threshold = 5 e/h | AHI Threshold = 10 e/h | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Se | Sp | Acc | AUC | Se | Sp | Acc | AUC | Se | Sp | Acc | AUC | ||
| RPVLF | 68.9 | 31.6 | 56.3 | 0.518 | 33.0 | 65.0 | 60.2 | 0.456 | 40.6 | 64.2 | 62.1 | 0.495 | |
| Previous work (frequency analysis approach) | RPLF | 43.5 | 62.9 | 50.1 | 0.557 | 52.7 | 58.4 | 57.6 | 0.590 | 59.4 | 58.4 | 58.5 | 0.666 |
| RPHF | 35.5 | 71.9 | 47.8 | 0.523 | 39.3 | 68.1 | 63.8 | 0.540 | 43.5 | 76.7 | 73.7 | 0.605 | |
| LF/HF | 37.7 | 70.3 | 48.7 | 0.540 | 45.5 | 66.8 | 63.7 | 0.567 | 49.3 | 70.8 | 68.8 | 0.643 | |
| RPBW1 | 66.3 | 45.3 | 59.2 | 0.559 | 65.2 | 54.0 | 55.6 | 0.621 | 69.6 | 52.3 | 53.9 | 0.624 | |
| RPBW2 | 32.7 | 78.1 | 48.1 | 0.591 | 45.5 | 82.0 | 76.6 | 0.670 | 58.0 | 78.2 | 76.4 | 0.751 | |
| RPBWRes | 45.5 | 56.6 | 49.3 | 0.532 | 44.6 | 64.0 | 61.2 | 0.571 | 49.3 | 64.0 | 62.6 | 0.628 | |
| LDA Classic Bands | 25.7 | 81.3 | 44.5 | 0.559 | 46.4 | 72.2 | 68.4 | 0.633 | 50.7 | 75.3 | 73.1 | 0.685 | |
| LDA Bands of Interest | 42.5 | 72.3 | 52.6 | 0.592 | 50.0 | 80.9 | 76.4 | 0.688 | 63.8 | 84.7 | 82.8 | 0.796 | |
| Present work (bispectral analysis approach) | LDAClassic | 30.1 | 81.3 | 47.4 | 0.601 | 53.6 | 85.3 | 80.6 | 0.779 | 66.7 | 89.7 | 87.6 | 0.847 |
| LDASpecific | 37.9 | 77.3 | 51.3 | 0.615 | 63.4 | 82.8 | 79.9 | 0.792 | 71.0 | 85.9 | 84.5 | 0.842 | |
Appendix C. Surrogate Data Approach
Appendix C.1. Testing for Nonlinearities
Appendix C.2. Bispectrum with Surrogate
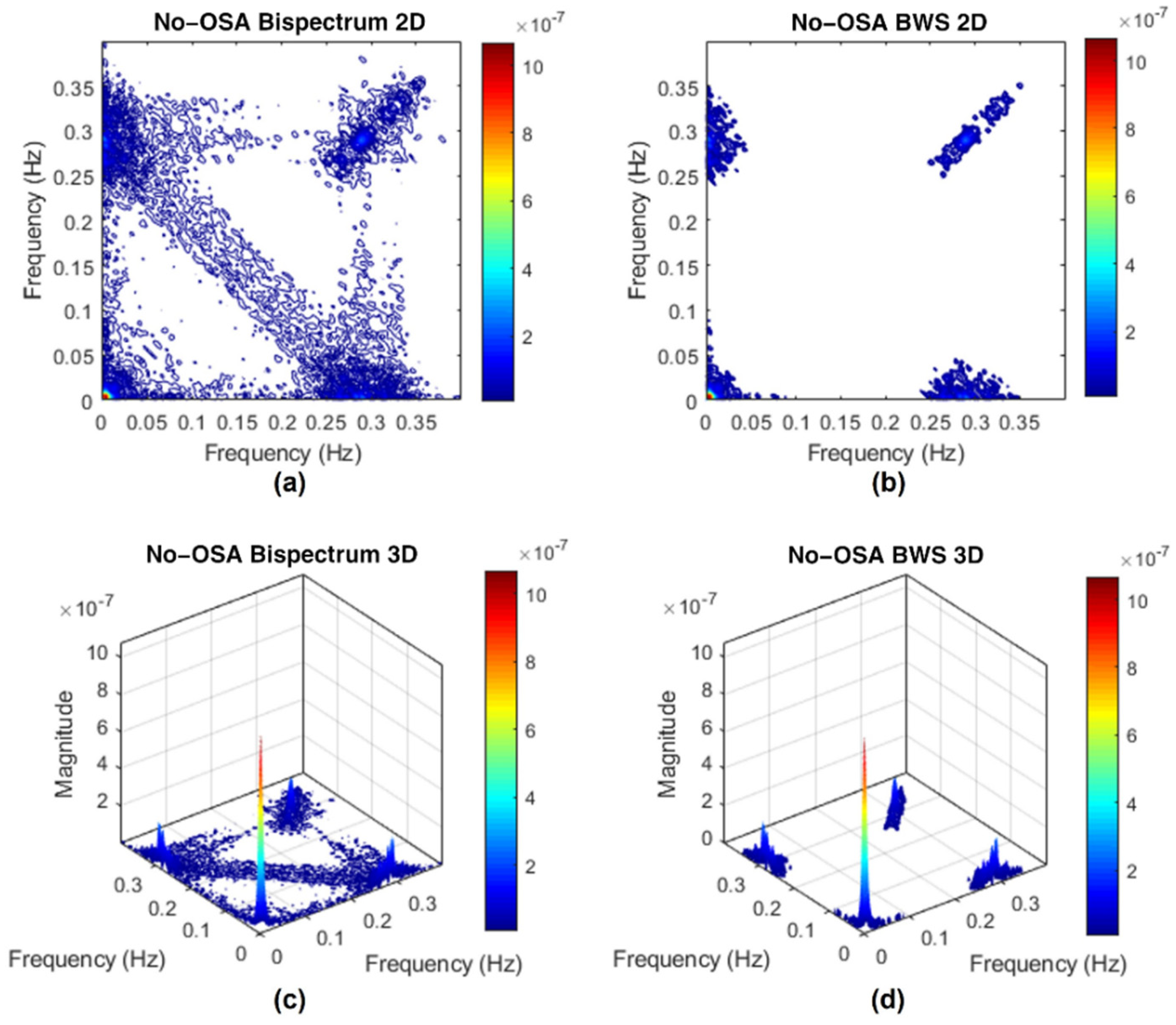


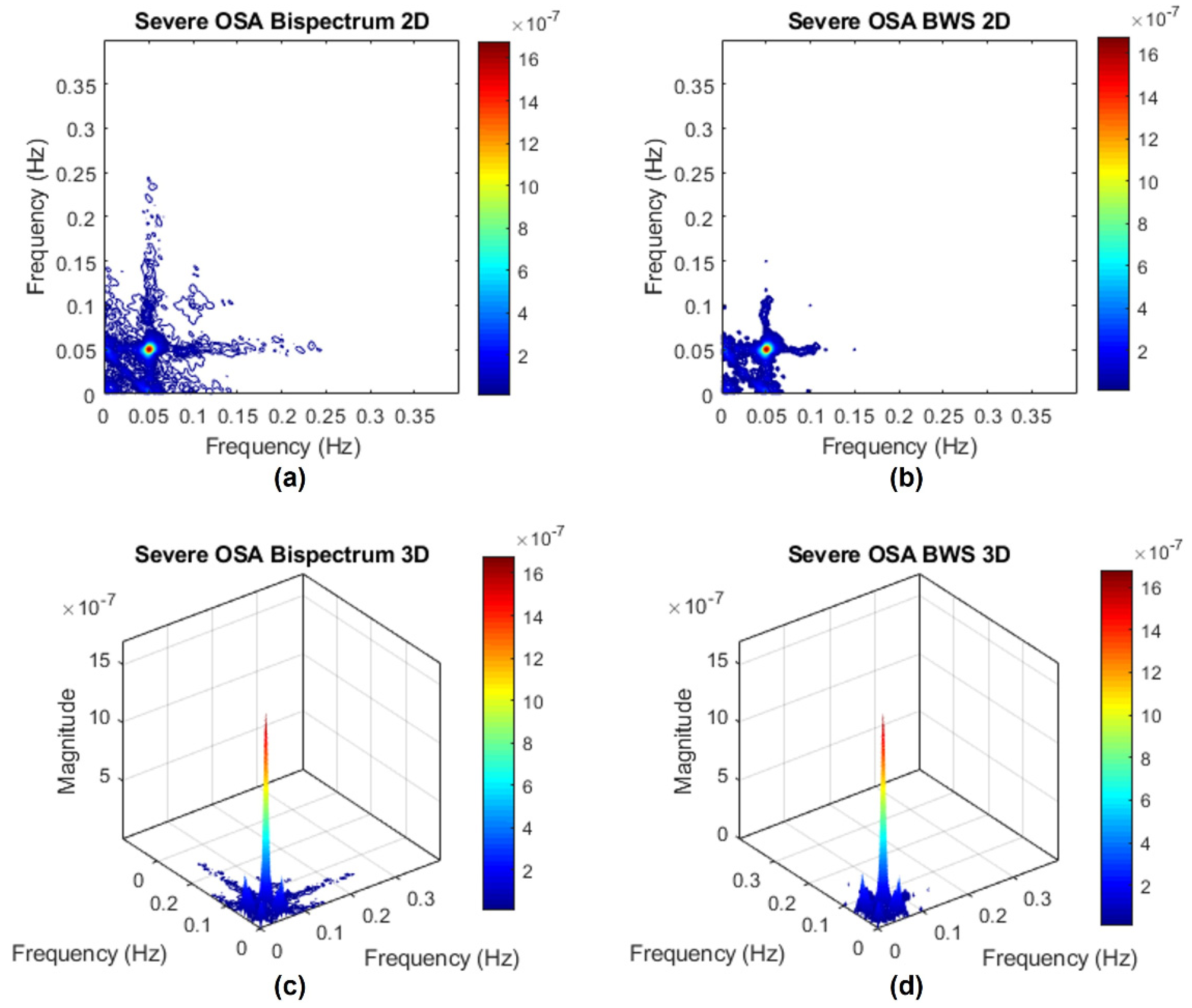
References
- Marcus, C.L.; Chapman, D.; Ward, S.D.; McColley, S.A.; Herrerias, C.T.; Stilwell, P.C.; Howenstine, M.; Light, M.J.; Schaeffer, D.A.; Wagener, J.S.; et al. Clinical practice guideline: Diagnosis and management of childhood. Pediatrics 2002, 109, 704–712. [Google Scholar]
- Society, A.T. Standards and indications for cardiopulmonary sleep studies in children. Am. J. Respir. Crit. Care Med. 1996, 153, 866–878. [Google Scholar] [CrossRef]
- Tauman, R.; Gozal, D. Obstructive sleep apnea syndrome in children. Expert Rev. Respir. Med. 2011, 5, 425–440. [Google Scholar] [CrossRef] [PubMed]
- Gozal, D. Sleep-Disordered Breathing and School Performance in Children. Pediatrics 1998, 102, 616–620. [Google Scholar] [CrossRef]
- Hunter, S.J.; Gozal, D.; Smith, D.L.; Philby, M.F.; Kaylegian, J.; Kheirandish-Gozal, L. Effect of sleep-disordered breathing severity on cognitive performance measures in a large community cohort of young school-aged children. Am. J. Respir. Crit. Care Med. 2016, 194, 739–747. [Google Scholar] [CrossRef] [PubMed]
- Kwok, K.L.; Ng, D.K.K.; Cheung, Y.F. BP and Arterial Distensibility in Children With Primary Snoring. Chest 2003, 123, 1561–1566. [Google Scholar] [CrossRef]
- Gozal, D.; Pope, D.W., Jr. Snoring During Early Childhood and Academic Performance at Ages Thirteen to Fourteen Years. Pediatrics 2001, 107, 1394–1399. [Google Scholar] [CrossRef]
- Iber, C.; Ancoli-Israel, S.; Chesson, A.L.; Quan, S.F. The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology and Technical Specifications, 1st ed.; American Academy Sleep Medicine: Westchester, IL, USA, 2007. [Google Scholar]
- Marcus, C.L.; Brooks, L.J.; Ward, S.D.; Draper, K.A.; Gozal, D.; Halbower, A.C.; Jones, J.; Lehmann, C.; Schechter, M.S.; Sheldon, S.; et al. Diagnosis and management of childhood obstructive sleep apnea syndrome. Pediatrics 2012, 130, e714–e755. [Google Scholar] [CrossRef] [PubMed]
- Berry, R.B.; Budhiraja, R.; Gottlieb, D.J.; Gozal, D.; Iber, C.; Kapur, V.K.; Marcus, C.L.; Mehra, R.; Parthasarathy, S.; Quan, S.F.; et al. Rules for Scoring Respiratory Events in Sleep: Update of the 2007 AASM Manual for the Scoring of Sleep and Associated Events. J. Clin. Sleep Med. 2012, 08, 597–619. [Google Scholar] [CrossRef]
- Tan, H.-L.; Gozal, D.; Ramirez, H.M.; Bandla, H.P.R.; Kheirandish-Gozal, L. Overnight polysomnography versus respiratory polygraphy in the diagnosis of pediatric obstructive sleep apnea. Sleep 2014, 37, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Álvarez, M.L.; Terán-Santos, J.; Ordax Carbajo, E.; Cordero-Guevara, J.A.; Navazo-Egüia, A.I.; Kheirandish-Gozal, L.; Gozal, D. Reliability of Home Respiratory Polygraphy for the Diagnosis of Sleep Apnea in Children. Chest 2015, 147, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Chiner, E.; Cánovas, C.; Molina, V.; Sancho-Chust, J.N.; Vañes, S.; Pastor, E.; Martinez-Garcia, M.A. Home Respiratory Polygraphy is Useful in the Diagnosis of Childhood Obstructive Sleep Apnea Syndrome. J. Clin. Med. 2020, 9, 2067. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Kheirandish-Gozal, L.; Campo, F.; Gozal, D.; Hornero, R. Reliability of machine learning to diagnose pediatric obstructive sleep apnea: Systematic review and meta-analysis. Pediatr. Pulmonol. 2021, 25423. [Google Scholar] [CrossRef]
- Vlahandonis, A.; Walter, L.M.; Horne, R.S.C. Does treatment of SDB in children improve cardiovascular outcome? Sleep Med. Rev. 2013, 17, 75–85. [Google Scholar] [CrossRef]
- Horne, R.S.C.; Shandler, G.; Tamanyan, K.; Weichard, A.; Odoi, A.; Biggs, S.N.; Davey, M.J.; Nixon, G.M.; Walter, L.M. The impact of sleep disordered breathing on cardiovascular health in overweight children. Sleep Med. 2018, 41, 58–68. [Google Scholar] [CrossRef]
- Vitelli, O.; Del Pozzo, M.; Baccari, G.; Rabasco, J.; Pietropaoli, N.; Barreto, M.; Villa, M.P. Autonomic imbalance during apneic episodes in pediatric obstructive sleep apnea. Clin. Neurophysiol. 2016, 127, 551–555. [Google Scholar] [CrossRef]
- Malik, M.; Bigger, J.T.; Camm, A.J.; Kleiger, R.E.; Malliani, A.; Moss, A.J.; Schwartz, P.J. Heart rate variability. Standards of measurement, physiological interpretation, and clinical use. Eur. Heart J. 1996, 17, 354–381. [Google Scholar] [CrossRef]
- Acharya, U.R.; Joseph, K.P.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med. Biol. Eng. Comput. 2006, 44, 1031–1051. [Google Scholar] [CrossRef]
- Guilleminault, C.; Winkle, R.; Connolly, S.; Melvin, K.; Tilkian, A. Cyclical Variation of the Heart Rate in Sleep Apnoea Syndrome. Lancet 1984, 323, 126–131. [Google Scholar] [CrossRef]
- Penzel, T.; Kantelhardt, J.W.; Grote, L.; Peter, J.H.; Bunde, A. Comparison of Detrended fluctuation Analysis and Spectral Analysis of Heart Rate Variability in Sleep and Sleep Apnea. IEEE Trans. Biomed. Eng. 2003, 50, 1143–1151. [Google Scholar] [CrossRef]
- Liao, D.; Li, X.; Vgontzas, A.N.; Liu, J.; Rodriguez-Colon, S.; Calhoun, S.; Bixler, E.O. Sleep-disordered breathing in children is associated with impairment of sleep stage-specific shift of cardiac autonomic modulation. J. Sleep Res. 2010, 19, 358–365. [Google Scholar] [CrossRef][Green Version]
- Walter, L.M.; Nixon, G.M.; Davey, M.J.; Anderson, V.; Walker, A.M.; Horne, R.S.C. Autonomic dysfunction in children with sleep disordered breathing. Sleep Breath. 2013, 17, 605–613. [Google Scholar] [CrossRef]
- Shouldice, R.B.; O’Brien, L.M.; O’Brien, C.; De Chazal, P.; Gozal, D.; Heneghan, C. Detection of Obstructive Sleep Apnea in Pediatric Subjects using Surface Lead Electrocardiogram Features. Sleep 2004, 27, 784–792. [Google Scholar] [CrossRef]
- Kwok, K.L.; Yung, T.C.; Ng, D.K.; Chan, C.H.; Lau, W.F.; Fu, Y.M. Heart Rate Variability in Childhood Obstructive Sleep Apnea. Pediatr. Pulmonol. 2011, 46, 205–210. [Google Scholar] [CrossRef]
- Gil, E.; Mendez, M.; Vergara, J.M.; Cerutti, S.; Bianchi, A.M.; Laguna, P. Discrimination of sleep-apnea-related decreases in the amplitude fluctuations of ppg signal in children by HRV analysis. IEEE Trans. Biomed. Eng. 2009, 56, 1005–1014. [Google Scholar] [CrossRef]
- Martín-Montero, A.; Gutiérrez-Tobal, G.C.; Kheirandish-Gozal, L.; Jiménez-García, J.; Álvarez, D.; del Campo, F.; Gozal, D.; Hornero, R. Heart rate variability spectrum characteristics in children with sleep apnea. Pediatr. Res. 2021, 89, 1771–1779. [Google Scholar] [CrossRef] [PubMed]
- Baharav, A.; Kotagal, S.; Rubin, B.K.; Pratt, J.; Akselrod, S. Autonomic cardiovascular control in children with obstructive sleep apnea. Clin. Auton. Res. 1999, 9, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Chua, K.C.; Chandran, V.; Acharya, U.R.; Lim, C.M. Application of higher order statistics/spectra in biomedical signals-A review. Med. Eng. Phys. 2010, 32, 679–689. [Google Scholar] [CrossRef] [PubMed]
- Atri, R.; Mohebbi, M. Obstructive sleep apnea detection using spectrum and bispectrum analysis of single-lead ECG signal. Physiol. Meas. 2015, 36, 1963–1980. [Google Scholar] [CrossRef]
- Porta, A.; Bari, V.; Marchi, A.; De Maria, B.; Cysarz, D.; Van Leeuwen, P.; Takahashi, A.C.M.; Catai, A.M.; Gnecchi-Ruscone, T. Complexity analyses show two distinct types of nonlinear dynamics in short heart period variability recordings. Front. Physiol. 2015, 6, 71. [Google Scholar] [CrossRef][Green Version]
- Martín-González, S.; Navarro-Mesa, J.L.; Juliá-Serdá, G.; Ramírez-Ávila, G.M.; Ravelo-García, A.G. Improving the understanding of sleep apnea characterization using Recurrence Quantification Analysis by defining overall acceptable values for the dimensionality of the system, the delay, and the distance threshold. PLoS ONE 2018, 13, e0194462. [Google Scholar] [CrossRef] [PubMed]
- Aljadeff, G.; Gozal, D.; Schechtman, V.L.; Burrell, B.; Harper, R.M.; Davidson Ward, S.L. Heart Rate Variability in Children With Obstructive Sleep Apnea. Sleep 1997, 20, 151–157. [Google Scholar] [CrossRef] [PubMed]
- Chua, K.C.; Chandran, V.; Acharya, U.R.; Lim, C.M. Cardiac state diagnosis using higher order spectra of heart rate variability. J. Med. Eng. Technol. 2008, 32, 145–155. [Google Scholar] [CrossRef]
- Chua, K.C. Cardiac Health Diagnosis Using Higher Order Spectra and Support Vector Machine. Open Med. Inform. J. 2009, 3, 1–8. [Google Scholar] [CrossRef]
- Saliu, S.; Birand, A.; Kudaiberdieva, G. Bispectral analysis of heart rate variability signal. In Proceedings of the 11th European Signal Processing Conference, Toulouse, France, 3–6 September 2002; IEEE: Piscataway, NJ, USA, 2015; Volume 2002. [Google Scholar]
- Yu, S.-N.; Lee, M.-Y. Bispectral analysis and genetic algorithm for congestive heart failure recognition based on heart rate variability. Comput. Biol. Med. 2012, 42, 816–825. [Google Scholar] [CrossRef] [PubMed]
- Garcia, R.G.; Valenza, G.; Tomaz, C.A.; Barbieri, R. Instantaneous bispectral analysis of heartbeat dynamics for the assessment of major depression. In Proceedings of the 2015 Computing in Cardiology Conference (CinC), Nice, France, 6–9 September 2015; IEEE: Piscataway, NJ, USA, 2016; Volume 42, pp. 781–784. [Google Scholar]
- Shao, S.; Wang, T.; Song, C.; Chen, X.; Cui, E.; Zhao, H. Obstructive Sleep Apnea Recognition Based on Multi-Bands Spectral Entropy Analysis of Short-Time Heart Rate Variability. Entropy 2019, 21, 812. [Google Scholar] [CrossRef]
- Zheng, L.; Pan, W.; Li, Y.; Luo, D.; Wang, Q.; Liu, G. Use of Mutual Information and Transfer Entropy to Assess Interaction between Parasympathetic and Sympathetic Activities of Nervous System from HRV. Entropy 2017, 19, 489. [Google Scholar] [CrossRef]
- Liu, D.; Yang, X.; Wang, G.; Ma, J.; Liu, Y.; Peng, C.-K.; Zhang, J.; Fang, J. HHT based cardiopulmonary coupling analysis for sleep apnea detection. Sleep Med. 2012, 13, 503–509. [Google Scholar] [CrossRef]
- Hornero, R.; Kheirandish-Gozal, L.; Gutiérrez-Tobal, G.C.; Philby, M.F.; Alonso-Álvarez, M.L.; Alvarez, D.; Dayyat, E.A.; Xu, Z.; Huang, Y.S.; Kakazu, M.T.; et al. Nocturnal oximetry-based evaluation of habitually snoring children. Am. J. Respir. Crit. Care Med. 2017, 196, 1591–1598. [Google Scholar] [CrossRef]
- Redline, S.; Amin, R.; Beebe, D.; Chervin, R.D.; Garetz, S.L.; Giordani, B.; Marcus, C.L.; Moore, R.H.; Rosen, C.L.; Arens, R.; et al. The Childhood Adenotonsillectomy Trial (CHAT): Rationale, Design, and Challenges of a Randomized Controlled Trial Evaluating a Standard Surgical Procedure in a Pediatric Population. Sleep 2011, 34, 1509–1517. [Google Scholar] [CrossRef]
- Marcus, C.L.; Moore, R.H.; Rosen, C.L.; Giordani, B.; Garetz, S.L.; Taylor, H.G.; Mitchell, R.B.; Amin, R.; Katz, E.S.; Arens, R.; et al. A randomized trial of adenotonsillectomy for childhood sleep apnea. N. Engl. J. Med. 2013, 368, 2366–2376. [Google Scholar] [CrossRef] [PubMed]
- Barroso-García, V.; Gutiérrez-Tobal, G.C.; Kheirandish-Gozal, L.; Álvarez, D.; Vaquerizo-Villar, F.; Núñez, P.; del Campo, F.; Gozal, D.; Hornero, R. Usefulness of recurrence plots from airflow recordings to aid in paediatric sleep apnoea diagnosis. Comput. Methods Programs Biomed. 2020, 183, 105083. [Google Scholar] [CrossRef]
- Barroso-García, V.; Gutiérrez-Tobal, G.C.; Kheirandish-Gozal, L.; Vaquerizo-Villar, F.; Álvarez, D.; del Campo, F.; Gozal, D.; Hornero, R. Bispectral analysis of overnight airflow to improve the pediatric sleep apnea diagnosis. Comput. Biol. Med. 2021, 129, 104167. [Google Scholar] [CrossRef] [PubMed]
- Barroso-García, V.; Gutiérrez-Tobal, G.C.; Kheirandish-Gozal, L.; Álvarez, D.; Vaquerizo-Villar, F.; Crespo, A.; del Campo, F.; Gozal, D.; Hornero, R. Irregularity and variability analysis of airflow recordings to facilitate the diagnosis of paediatric sleep apnoea-hypopnoea syndrome. Entropy 2017, 19, 447. [Google Scholar] [CrossRef]
- Benitez, D.; Gaydecki, P.A.; Zaidi, A.; Fitzpatrick, A.P. The use of the Hilbert transform in ECG signal analysis. Comput. Biol. Med. 2001, 31, 399–406. [Google Scholar] [CrossRef]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Gomez-Pilar, J.; Del Campo, F.; Hornero, R. Assessment of time and frequency domain entropies to detect sleep apnoea in heart rate variability recordings from men and women. Entropy 2015, 17, 123–141. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Efficient Feature Selection via Analysis of Relevance and Redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Vaquerizo-Villar, F.; Álvarez, D.; Kheirandish-Gozal, L.; Gutiérrez-Tobal, G.C.; Barroso-García, V.; Crespo, A.; del Campo, F.; Gozal, D.; Hornero, R. Utility of bispectrum in the screening of pediatric sleep apnea-hypopnea syndrome using oximetry recordings. Comput. Methods Programs Biomed. 2018, 156, 141–149. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A.; Kaelbling, L.P. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Wang, R.; Wang, J.; Li, S.; Yu, H.; Deng, B.; Wei, X. Multiple feature extraction and classification of electroencephalograph signal for Alzheimers’ with spectrum and bispectrum. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 013110. [Google Scholar] [CrossRef] [PubMed]
- Gil, E.; Bailón, R.; Vergara, J.M.; Laguna, P. PTT variability for discrimination of sleep apnea related decreases in the amplitude fluctuations of PPG signal in children. IEEE Trans. Biomed. Eng. 2010, 57, 1079–1088. [Google Scholar] [CrossRef]
- Lázaro, J.; Gil, E.; Vergara, J.M.; Laguna, P. Pulse rate variability analysis for discrimination of sleep-apnea-related decreases in the amplitude fluctuations of pulse photoplethysmographic signal in children. IEEE J. Biomed. Health Inform. 2014, 18, 240–246. [Google Scholar] [CrossRef] [PubMed]
- Cohen, G.; de Chazal, P. Automated detection of sleep apnea in infants: A multi-modal approach. Comput. Biol. Med. 2015, 63, 118–123. [Google Scholar] [CrossRef]
- Vaquerizo-Villar, F.; Alvarez, D.; Kheirandish-Gozal, L.; Gutierrez-Tobal, G.C.; Barroso-Garcia, V.; Santamaria-Vazquez, E.; Del Campo, F.; Gozal, D.; Hornero, R. A convolutional neural network architecture to enhance oximetry ability to diagnose pediatric obstructive sleep apnea. IEEE J. Biomed. Health Inform. 2021. Early Access. [Google Scholar] [CrossRef] [PubMed]
- Milagro, J.; Gracia, J.; Seppa, V.-P.; Karjalainen, J.; Paassilta, M.; Orini, M.; Bailon, R.; Gil, E.; Viik, J. Noninvasive Cardiorespiratory Signals Analysis for Asthma Evolution Monitoring in Preschool Children. IEEE Trans. Biomed. Eng. 2019, 67, 1863–1871. [Google Scholar] [CrossRef] [PubMed]
- Milagro, J.; Gil, E.; Lazaro, J.; Seppa, V.P.; Pekka Malmberg, L.; Pelkonen, A.S.; Kotaniemi-Syrjanen, A.; Makela, M.J.; Viik, J.; Bailon, R. Nocturnal Heart Rate Variability Spectrum Characterization in Preschool Children with Asthmatic Symptoms. IEEE J. Biomed. Heal. Inform. 2018, 22, 1332–1340. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Faes, L. Wiener–Granger Causality in Network Physiology With Applications to Cardiovascular Control and Neuroscience. Proc. IEEE 2016, 104, 282–309. [Google Scholar] [CrossRef]
- Siu, K.L.; Ahn, J.M.; Ju, K.; Lee, M.; Shin, K.; Chon, K.H. Statistical Approach to Quantify the Presence of Phase Coupling Using the Bispectrum. IEEE Trans. Biomed. Eng. 2008, 55, 1512–1520. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Doyne Farmer, J. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Maestri, R.; Pinna, G.D.; Porta, A.; Balocchi, R.; Sassi, R.; Signorini, M.G.; Dudziak, M.; Raczak, G. Assessing nonlinear properties of heart rate variability from short-term recordings: Are these measurements reliable? Physiol. Meas. 2007, 28, 1067–1077. [Google Scholar] [CrossRef]

| All | Training Set (UofC) | Test Set (CHAT) | |
|---|---|---|---|
| Subjects (n) | 1738 | 981 | 757 |
| Age (years) | 6.4 [3.3] | 6.0 [6.0] | 7.0 [2.4] |
| Males (n) | 962 (55.35%) | 602 (61.37%) | 360 (47.95%) |
| BMI (kg/m2) | 17.63 [5.37] | 18.02 [5.86] | 17.28 [4.64] |
| AHI (e/h) | 2.23 [5.27] | 3.8 [7.76] | 1.46 [2.07] |
| AHI ≥ 1 (e/h) | 1309 (75.31%) | 808 (82.36%) | 501 (66.18%) |
| AHI ≥ 5 (e/h) | 519 (29.86%) | 407 (41.49%) | 112 (14.80%) |
| AHI ≥ 10 (e/h) | 298 (17.15%) | 229 (23.34%) | 69 (9.11%) |
| Classic Region Feature Set | OSA-Specific Region Feature Set | |||||
|---|---|---|---|---|---|---|
| Features | VLF | LF | HF | BW1 | BW2 | BWRes |
| RPDiag | VLF_RPDiag | LF_RPDiag | HF_RPDiag | BW1_RPDiag | BW2_RPDiag | - |
| Bmax | VLF_Bmax | LF_Bmax | HF_Bmax | BW1_Bmax | BW2_Bmax | BWRes_Bmax |
| Bmin | VLF_Bmin | LF_Bmin | HF_Bmin | BW1_Bmin | BW2_Bmin | BWRes_Bmin |
| BTotal | VLF_BTotal | LF_BTotal | HF_BTotal | BW1_BTotal | BW2_BTotal | BWRes_BTotal |
| BE1 | VLF_BE1 | LF_BE1 | HF_BE1 | BW1_BE1 | BW2_BE1 | BWRes_BE1 |
| BE2 | VLF_BE2 | LF_BE2 | HF_BE2 | BW1_BE2 | BW2_BE2 | BWRes_BE2 |
| BE3 | VLF_BE3 | LF_BE3 | HF_BE3 | BW1_BE3 | BW2_BE3 | BWRes_BE3 |
| PE | VLF_PE | LF_PE | HF_PE | BW1_PE | BW2_PE | BWRes_PE |
| H1 | VLF_H1 | LF_H1 | HF_H1 | BW1_H1 | BW2_H1 | BWRes_H1 |
| H2 | VLF_H2 | LF_H2 | HF_H2 | BW1_H2 | BW2_H2 | - |
| H3 | VLF_H3 | LF_H3 | HF_H3 | BW1_H3 | BW2_H3 | - |
| H4 | VLF_H4 | LF_H4 | HF_H4 | BW1_H4 | BW2_H4 | - |
| f1m | VLF_f1m | LF_f1m | HF_f1m | BW1_f1m | BW2_f1m | BWRes_f1m |
| f2m | VLF_f2m | LF_f2m | HF_f2m | BW1_f2m | BW2_f2m | BWRes_f2m |
| BISPClassic Features | ||||||||
| PSG Index | VLF_f2m | LF_BE2 | HF_PE | |||||
| ρS | p-Value | ρS | p-Value | ρS | p-Value | |||
| AHI | 0.274 | <<0.01 | −0.185 | <<0.01 | −0.112 | 0.002 * | ||
| OAHI | 0.261 | <<0.01 | −0.149 | <<0.01 | −0.097 | 0.008 | ||
| OAI | 0.167 | <<0.01 | −0.105 | 0.004 * | −0.064 | 0.079 | ||
| ODI | 0.215 | <<0.01 | −0.123 | 0.001 * | −0.054 | 0.138 | ||
| #Awakenings | −0.075 | 0.039 | −0.027 | 0.461 | −0.020 | 0.586 | ||
| WASO | −0.003 | 0.929 | 0.065 | 0.076 | −0.022 | 0.538 | ||
| %N1 | 0.089 | 0.014 | −0.071 | 0.052 | −0.030 | 0.404 | ||
| %N2 | −0.034 | 0.357 | 0.099 | 0.007 * | 0.013 | 0.715 | ||
| %N3 | 0.034 | 0.355 | −0.025 | 0.497 | −0.044 | 0.23 | ||
| %REM | −0.125 | 0.001 | −0.052 | 0.154 | 0.059 | 0.108 | ||
| TAI | 0.213 | <<0.01 | −0.158 | <<0.01 | −0.115 | 0.002 * | ||
| BISPSpecific Features | ||||||||
| PSG Index | BW2_RPDiag | BW2_BE1 | BWRes_Bmin | BWRes_BE3 | ||||
| ρS | p-Value | ρS | p-Value | ρS | p-Value | ρS | p-Value | |
| AHI | 0.308 | <<0.01 | −0.180 | <<0.01 | 0.054 | 0.136 | 0.045 | 0.214 |
| OAHI | 0.261 | <<0.01 | −0.180 | <<0.01 | 0.098 | 0.007 * | 0.028 | 0.435 |
| OAI | 0.177 | <<0.01 | −0.173 | <<0.01 | 0.071 | 0.051 | 0.058 | 0.112 |
| ODI | 0.247 | <<0.01 | −0.139 | 0.001 | 0.019 | 0.61 | 0.072 | 0.047 |
| #Awakenings | −0.033 | 0.372 | −0.001 | 0.994 | −0.006 | 0.876 | 0.035 | 0.331 |
| WASO | 0.071 | 0.05 | 0.078 | 0.031 | −0.018 | 0.622 | 0.056 | 0.126 |
| %N1 | 0.107 | 0.003 * | −0.061 | 0.093 | 0.023 | 0.527 | 0.028 | 0.441 |
| %N2 | −0.061 | 0.091 | 0.008 | 0.837 | 0.048 | 0.184 | 0.059 | 0.104 |
| %N3 | 0.053 | 0.147 | 0.008 | 0.817 | −0.075 | 0.04 | −0.092 | 0.011 |
| %REM | −0.139 | 0.001 | 0.048 | 0.192 | −0.007 | 0.855 | 0.013 | 0.722 |
| TAI | 0.225 | <<0.01 | −0.144 | <<0.01 | 0.068 | 0.062 | 0.068 | 0.06 |
| Threshold: AHI = 1 e/h | ||||
| Feature/Model | Se | Sp | Acc | AUC |
| VLF_f2m | 44.5 | 72.3 | 53.9 | 0.605 |
| LF_BE2 | 42.1 | 72.7 | 52.4 | 0.581 |
| HF_PE | 42.9 | 63.3 | 49.8 | 0.550 |
| BW2_RPDiag | 50.9 | 64.8 | 55.6 | 0.629 |
| BW2_BE1 | 47.1 | 59.4 | 51.3 | 0.559 |
| BWRes_Bmin | 40.5 | 57.4 | 46.2 | 0.482 |
| BWRes_BE3 | 41.5 | 57.4 | 46.9 | 0.513 |
| MLP1Classic | 52.3 | 59.4 | 54.7 | 0.600 |
| MLP1Specific | 76.3 | 38.3 | 63.4 | 0.627 |
| Threshold: AHI = 5 e/h | ||||
| Feature/Model | Se | Sp | Acc | AUC |
| VLF_f2m | 62.5 | 72.2 | 70.8 | 0.749 |
| LF_BE2 | 56.3 | 74.4 | 71.7 | 0.670 |
| HF_PE | 45.5 | 72.1 | 68.2 | 0.628 |
| BW2_RPDiag | 60.7 | 77.7 | 75.2 | 0.747 |
| BW2_BE1 | 56.3 | 70.1 | 68.0 | 0.671 |
| BWRes_Bmin | 58.9 | 45.3 | 47.3 | 0.567 |
| BWRes_BE3 | 47.3 | 58.4 | 56.8 | 0.569 |
| MLP5Classic | 50.9 | 86.2 | 81.0 | 0.774 |
| MLP5Specific | 62.5 | 84.2 | 81.0 | 0.791 |
| Threshold: AHI = 10 e/h | ||||
| Feature/Model | Se | Sp | Acc | AUC |
| VLF_f2m | 63.8 | 76.7 | 75.6 | 0.784 |
| LF_BE2 | 58.0 | 81.5 | 79.4 | 0.740 |
| HF_PE | 53.6 | 72.1 | 70.4 | 0.663 |
| BW2_RPDiag | 68.1 | 76.0 | 75.3 | 0.789 |
| BW2_BE1 | 47.8 | 76.0 | 73.4 | 0.692 |
| BWRes_Bmin | 56.5 | 50.6 | 51.1 | 0.557 |
| BWRes_BE3 | 55.1 | 59.4 | 59.0 | 0.614 |
| MLP10Classic | 43.5 | 96.5 | 91.7 | 0.847 |
| MLP10Specific | 66.7 | 91.6 | 89.3 | 0.841 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Montero, A.; Gutiérrez-Tobal, G.C.; Gozal, D.; Barroso-García, V.; Álvarez, D.; del Campo, F.; Kheirandish-Gozal, L.; Hornero, R. Bispectral Analysis of Heart Rate Variability to Characterize and Help Diagnose Pediatric Sleep Apnea. Entropy 2021, 23, 1016. https://doi.org/10.3390/e23081016
Martín-Montero A, Gutiérrez-Tobal GC, Gozal D, Barroso-García V, Álvarez D, del Campo F, Kheirandish-Gozal L, Hornero R. Bispectral Analysis of Heart Rate Variability to Characterize and Help Diagnose Pediatric Sleep Apnea. Entropy. 2021; 23(8):1016. https://doi.org/10.3390/e23081016
Chicago/Turabian StyleMartín-Montero, Adrián, Gonzalo C. Gutiérrez-Tobal, David Gozal, Verónica Barroso-García, Daniel Álvarez, Félix del Campo, Leila Kheirandish-Gozal, and Roberto Hornero. 2021. "Bispectral Analysis of Heart Rate Variability to Characterize and Help Diagnose Pediatric Sleep Apnea" Entropy 23, no. 8: 1016. https://doi.org/10.3390/e23081016
APA StyleMartín-Montero, A., Gutiérrez-Tobal, G. C., Gozal, D., Barroso-García, V., Álvarez, D., del Campo, F., Kheirandish-Gozal, L., & Hornero, R. (2021). Bispectral Analysis of Heart Rate Variability to Characterize and Help Diagnose Pediatric Sleep Apnea. Entropy, 23(8), 1016. https://doi.org/10.3390/e23081016










