Global Sensitivity Analysis Based on Entropy: From Differential Entropy to Alternative Measures
Abstract
1. Introduction
2. Entropy of a Random Variable
3. Entropy-Based Sensitivity Analysis
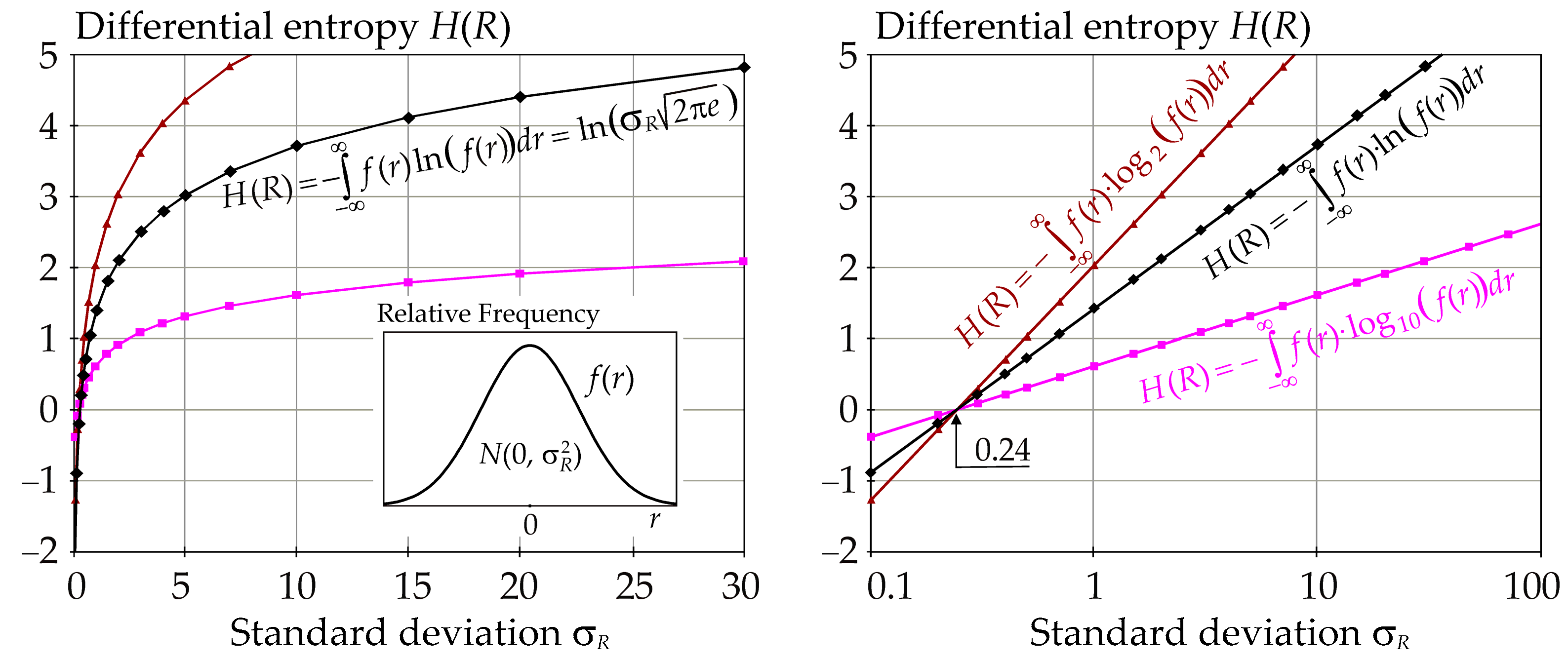
3.1. Sensitivity Indices based on Differential Entropy H(R)
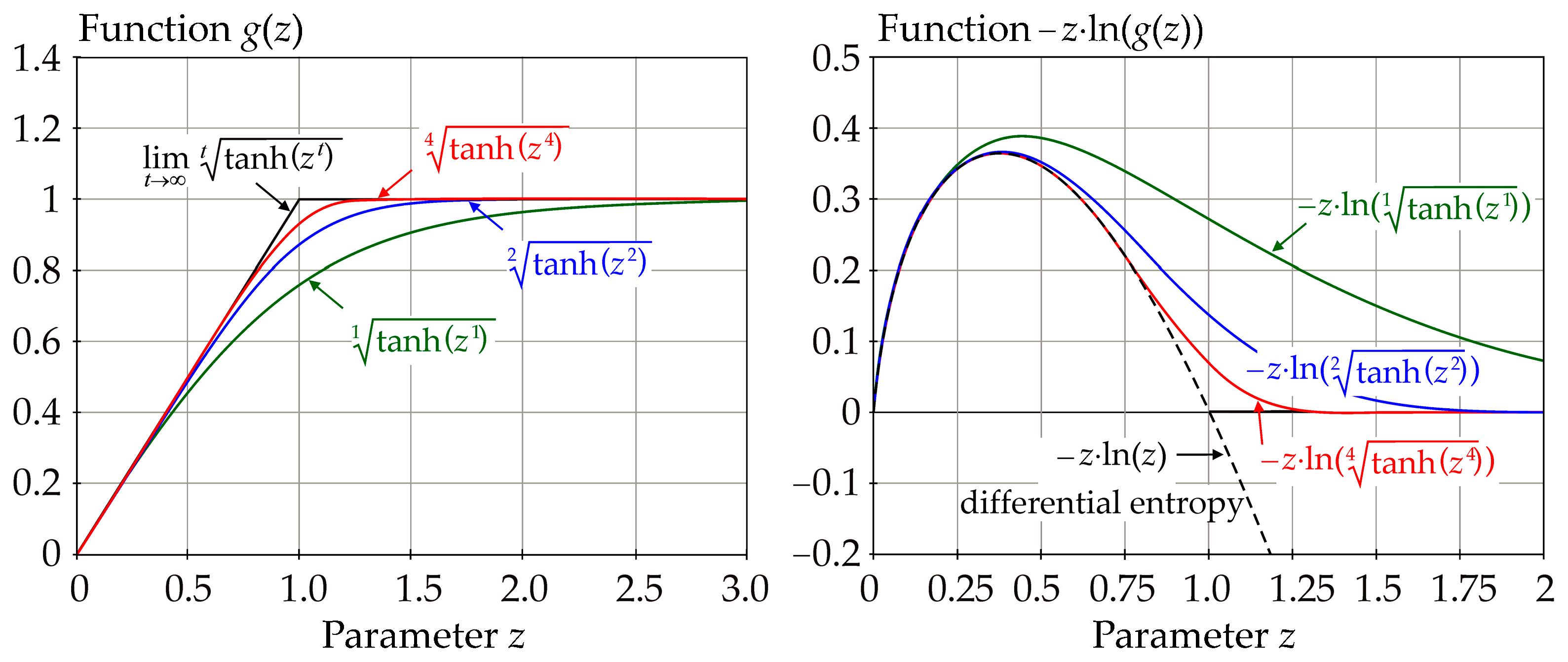
3.2. Approximation of Differential Entropy by Functional for Sensitivity Indices
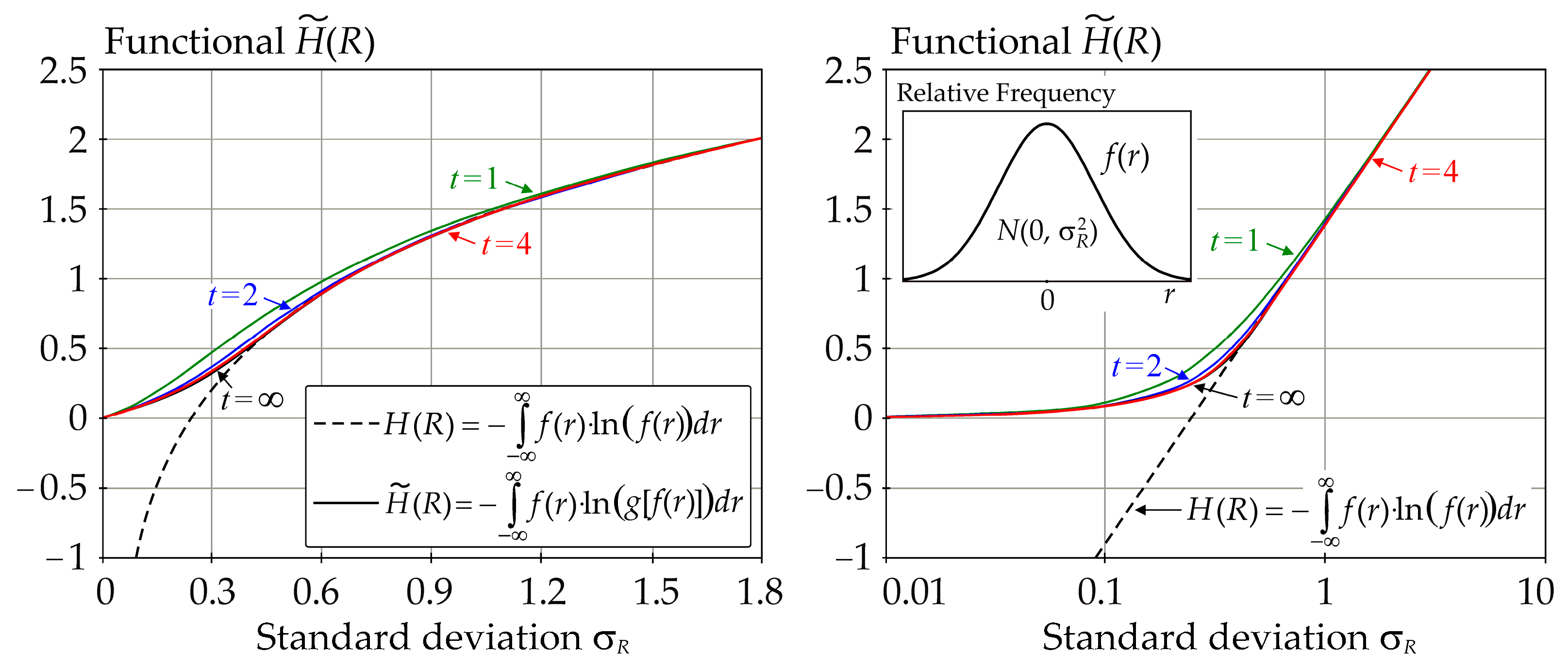
3.3. Approximation of Differential Entropy by Functional and Sensitivity Indices
4. Standard Distribution-Based Sensitivity Analyzes
4.1. Cramér-von Mises Sensitivity Indices
4.2. Borgonovo Moment-Independent Sensitivity Indices
5. Variance-Based Sensitivity Analysis
6. The Case Studies
6.1. Computational Model
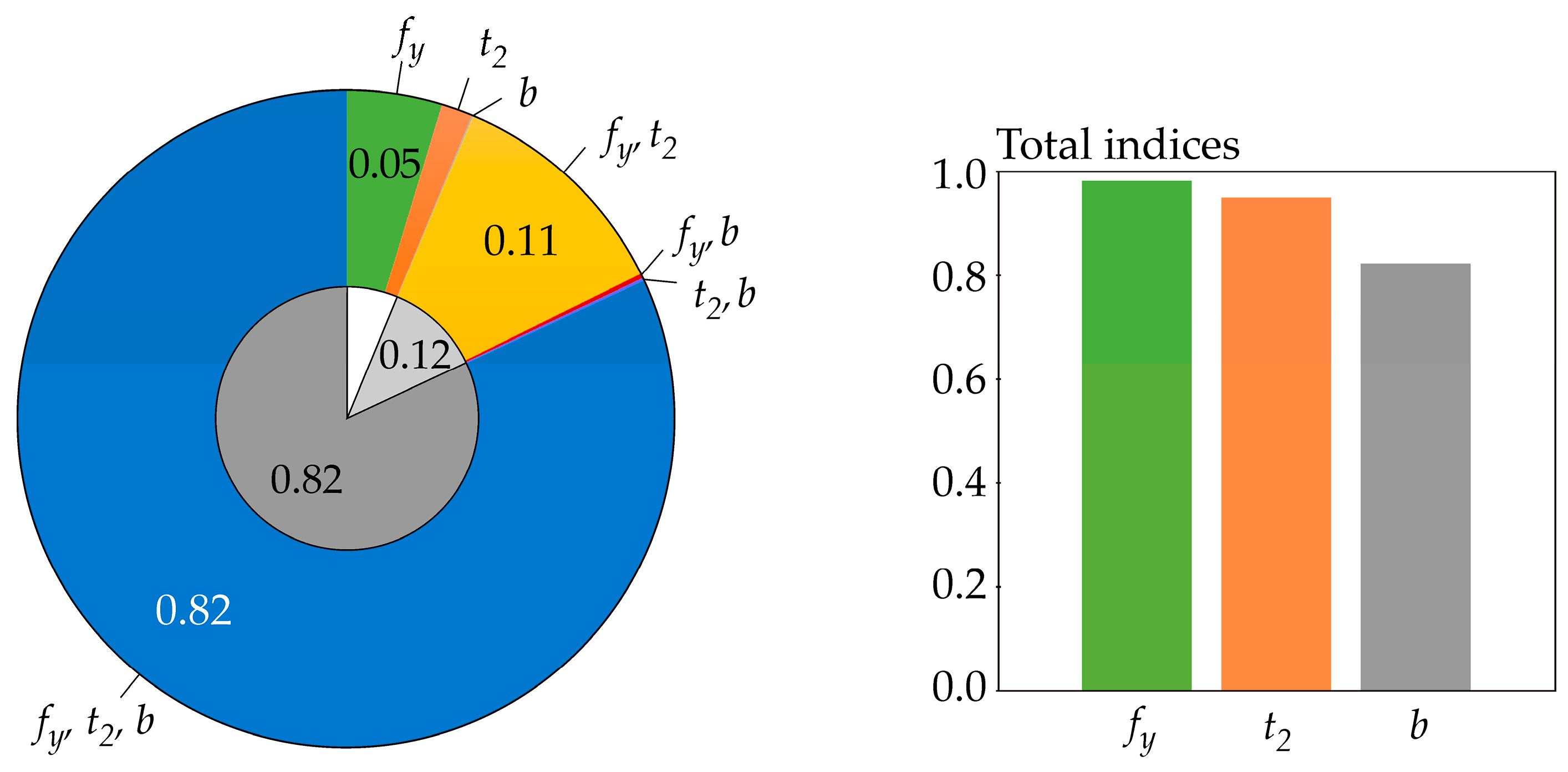
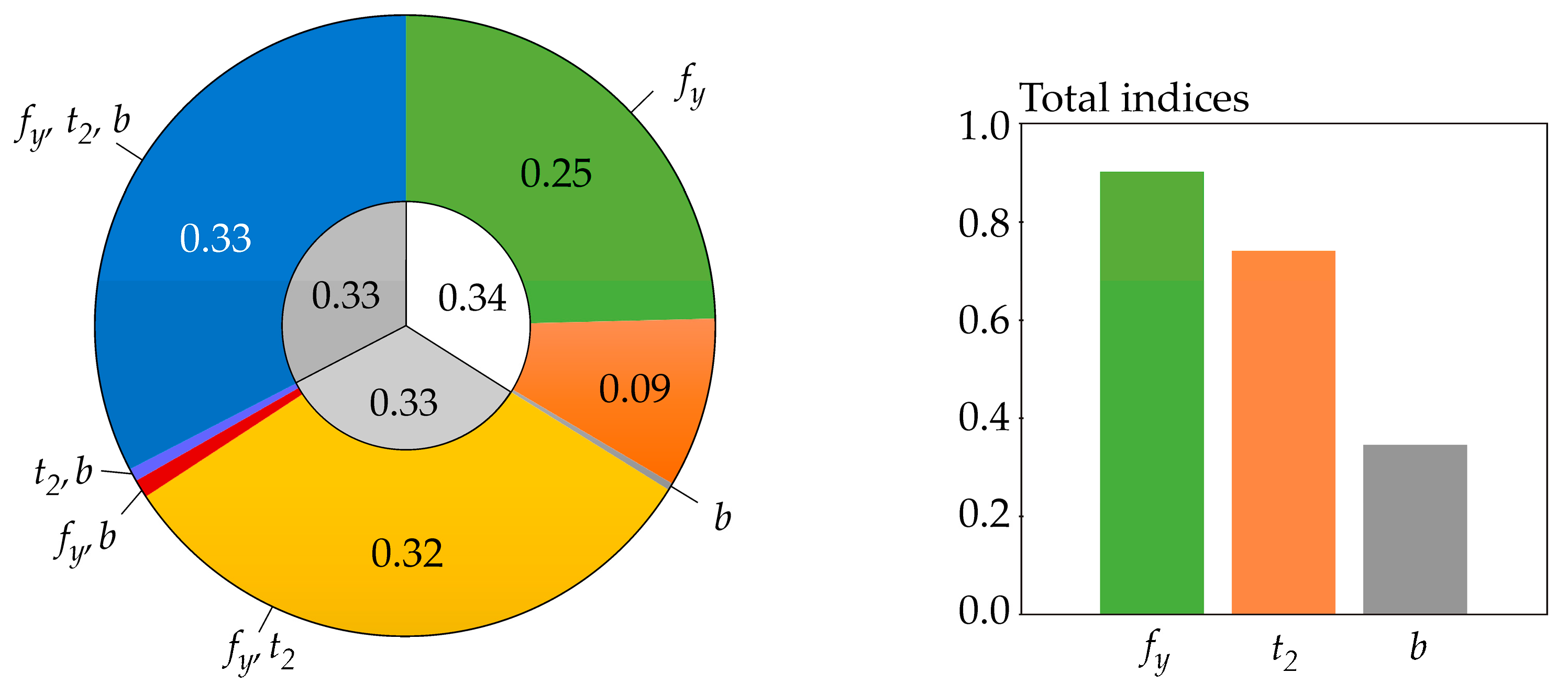
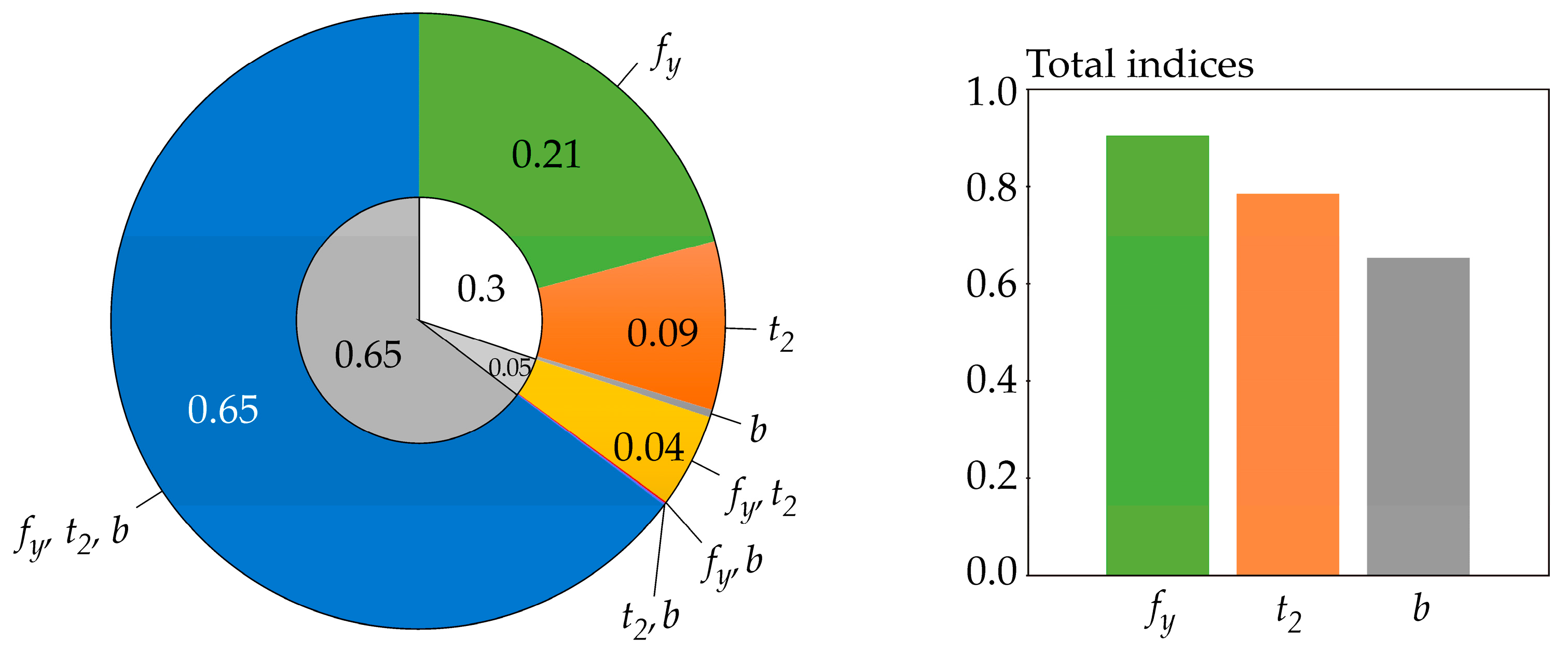
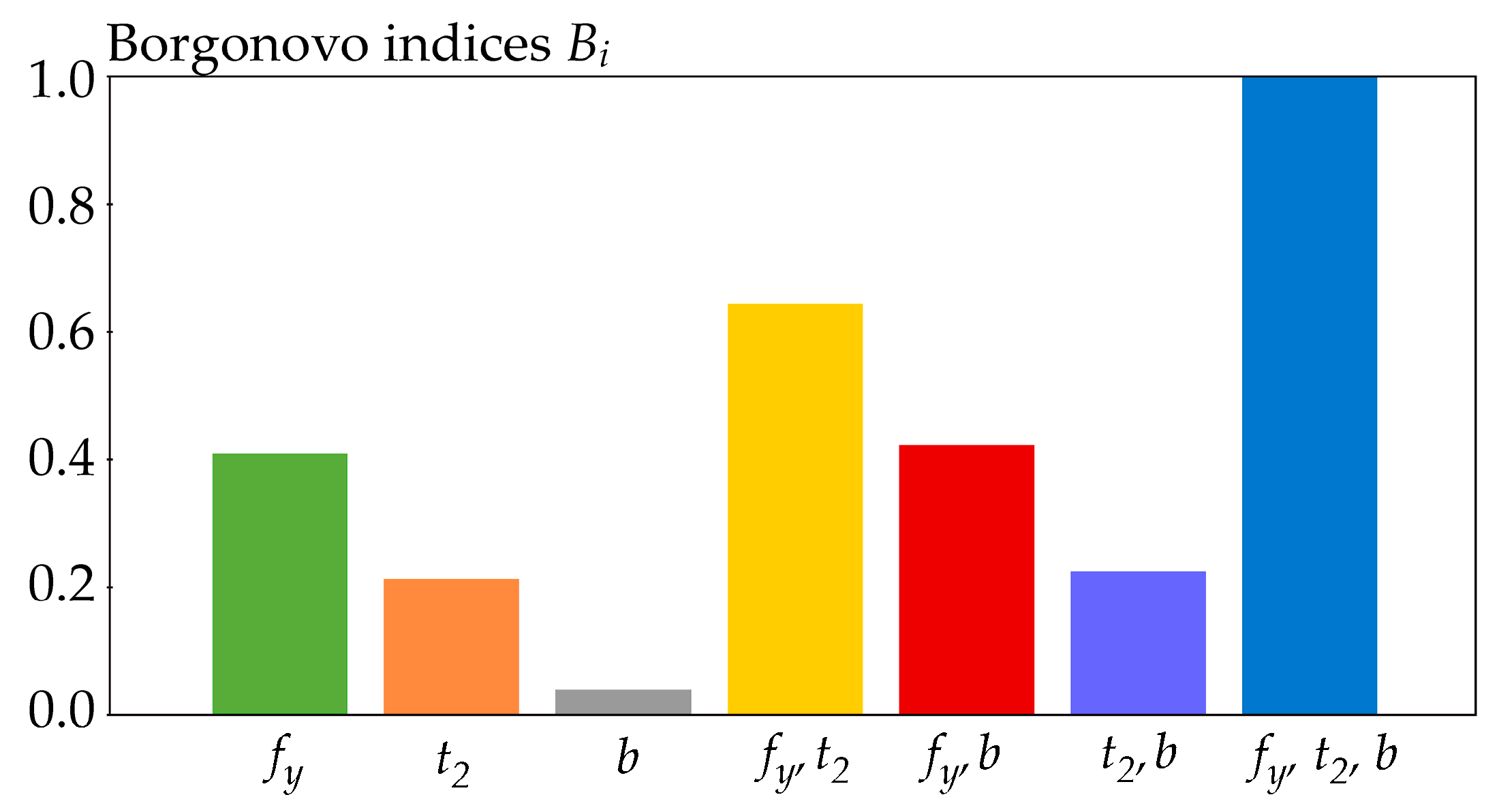
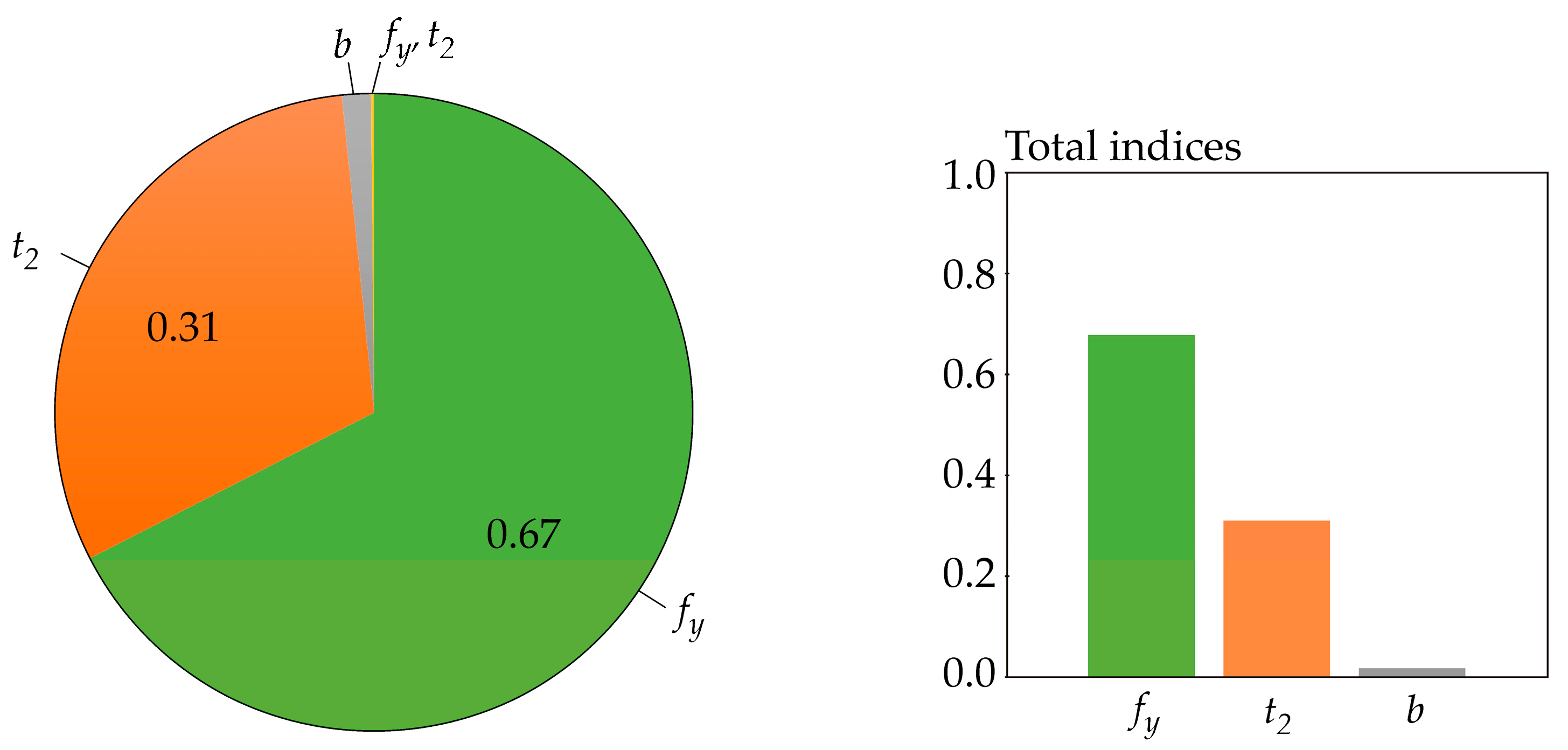
6.2. The Results of the Case Studies
7. Discussion
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sobol, I.M. Sensitivity estimates for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef] [PubMed]
- Castaings, W.; Borgonovo, E.; Morris, M.D.; Tarantola, S. Sampling strategies in density-based sensitivity analysis. Environ. Model Softw. 2012, 38, 13–26. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Modell. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E.; Rakovec, O.; Hill, M.C. Making the most out of a hydrological model data set: Sensitivity analyses to open the model black-box. Water Resour. Res. 2017, 53, 7933–7950. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. Distribution-based sensitivity analysis from a generic input-output sample. Environ. Model Softw. 2018, 108, 197–207. [Google Scholar] [CrossRef]
- Baroni, G.; Francke, T. An effective strategy for combining variance- and distribution-based global sensitivity analysis. Environ. Modell. Softw. 2020, 134, 104851. [Google Scholar] [CrossRef]
- Krykacz-Hausmann, B. Epistemic sensitivity analysis based on the concept of entropy. In Proceedings of the International Symposium on Sensitivity Analysis of Model Output, Madrid, Spain, 18–20 June 2001; pp. 31–35. [Google Scholar]
- Shannon, C.E. A Mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Liu, H.; Sudjianto, A.; Chen, W. Relative entropy based method for probabilistic sensitivity analysis in engineering design. J. Mech. Des. 2006, 128, 326–336. [Google Scholar] [CrossRef]
- Zhong, R.X.; Fu, K.Y.; Sumalee, A.; Ngoduy, D.; Lam, W.H.K. A cross-entropy method and probabilistic sensitivity analysis framework for calibrating microscopic traffic models. Transp. Res. Part C Emerg. Technol. 2016, 63, 147–169. [Google Scholar] [CrossRef]
- Tang, Z.C.; Lu, Z.Z.; Pan, W.; Zhang, F. An entropy-based global sensitivity analysis for the structures with both fuzzy variables and random variables. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2013, 227, 195–212. [Google Scholar]
- Shi, Y.; Lu, Z.; Zhou, Y. Global sensitivity analysis for fuzzy inputs based on the decomposition of fuzzy output entropy. Eng. Optim. 2018, 50, 1078–1096. [Google Scholar] [CrossRef]
- Yazdani, A.; Nicknam, A.; Dadras, E.Y.; Eftekhari, S.N. Entropy-based sensitivity analysis of global seismic demand of concrete structures. Eng. Struct. 2017, 146, 118–126. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, D.; Wu, J. Sensitivity analysis of the probability distribution of groundwater level series based on information entropy. Stoch. Environ. Res. Risk Assess. 2012, 26, 345–356. [Google Scholar] [CrossRef]
- Zhu, G.R.; Wang, X.H.; Huang, H.B.; Chen, H. Sensitivity analysis for shell-and-tube heat exchangers based on entropy production. Adv. Mat. Res. 2012, 516–517, 419–424. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Setiadi, Y. Sensitivity analysis of entropy-constrained designs of water distribution systems. Eng. Optim. 2008, 40, 439–457. [Google Scholar] [CrossRef]
- Lashkar-Ara, B.; Kalantari, N.; Sheikh Khozani, Z.; Mosavi, A. Assessing machine learning versus a mathematical model to estimate the transverse shear stress distribution in a rectangular channel. Mathematics 2021, 9, 596. [Google Scholar] [CrossRef]
- Zhou, C.; Cui, G.; Liang, W.; Liu, Z.; Zhang, L. A coupled macroscopic and mesoscopic creep model of soft marine soil using a directional probability entropy approach. J. Mar. Sci. Eng. 2021, 9, 224. [Google Scholar] [CrossRef]
- Pan, P.; Zhang, M.; Peng, W.; Chen, H.; Xu, G.; Liu, T. Thermodynamic evaluation and sensitivity analysis of a novel compressed air energy storage system incorporated with a coal-fired power plant. Entropy 2020, 22, 1316. [Google Scholar] [CrossRef] [PubMed]
- Lescauskiene, I.; Bausys, R.; Zavadskas, E.K.; Juodagalviene, B. VASMA weighting: Survey-based criteria weighting methodology that combines ENTROPY and WASPAS-SVNS to reflect the psychometric features of the VAS scales. Symmetry 2020, 12, 1641. [Google Scholar] [CrossRef]
- Hashemi, H.; Mousavi, S.M.; Zavadskas, E.K.; Chalekaee, A.; Turskis, Z. A New group decision model based on grey-intuitionistic fuzzy-ELECTRE and VIKOR for contractor assessment problem. Sustainability 2018, 10, 1635. [Google Scholar] [CrossRef]
- Cavallaro, F.; Zavadskas, E.K.; Raslanas, S. Evaluation of combined heat and power (CHP) systems using fuzzy shannon entropy and fuzzy TOPSIS. Sustainability 2016, 8, 556. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Esmaeili, A. Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets. J. Clean. Prod. 2016, 137, 213–229. [Google Scholar] [CrossRef]
- Liu, D.; Luo, Y.; Liu, Z. The linguistic picture fuzzy set and its application in multi-criteria decision-making: An illustration to the TOPSIS and TODIM methods based on entropy weight. Symmetry 2020, 12, 1170. [Google Scholar] [CrossRef]
- Maume-Deschamps, V.; Niang, I. Estimation of quantile oriented sensitivity indices. Stat. Probab. Lett. 2018, 134, 122–127. [Google Scholar] [CrossRef]
- Kucherenko, S.; Song, S.; Wang, L. Quantile based global sensitivity measures. Reliab. Eng. Syst. Saf. 2019, 185, 35–48253. [Google Scholar] [CrossRef]
- Kala, Z. Quantile-oriented global sensitivity analysis of design resistance. J. Civ. Eng. Manag. 2019, 25, 297–305. [Google Scholar] [CrossRef]
- Kala, Z. Quantile-based versus Sobol sensitivity analysis in limit state design. Structures 2020, 28, 2424–2430. [Google Scholar] [CrossRef]
- Kala, Z. From probabilistic to quantile-oriented sensitivity analysis: New indices of design quantiles. Symmetry 2020, 12, 1720. [Google Scholar] [CrossRef]
- Kala, Z. Global sensitivity analysis of quantiles: New importance measure based on superquantiles and subquantiles. Symmetry 2021, 13, 263. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Hao, W.; Feng, J.; Wang, B. Efficient sampling methods for global reliability sensitivity analysis. Comput. Phys. Commun. 2012, 183, 1728–1743. [Google Scholar] [CrossRef]
- Zhao, J.; Zeng, S.; Guo, J.; Du, S. Global reliability sensitivity analysis based on maximum entropy and 2-Layer polynomial chaos expansion. Entropy 2018, 20, 202. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liu, J.; Yan, Y.; Pandey, M. An effective approach for reliability-based sensitivity analysis with the principle of Maximum entropy and fractional moments. Entropy 2019, 21, 649. [Google Scholar] [CrossRef]
- Kala, Z. Global sensitivity analysis of reliability of structural bridge system. Eng. Struct. 2019, 194, 36–45. [Google Scholar] [CrossRef]
- Kala, Z. Estimating probability of fatigue failure of steel structures. Acta Comment. Univ. Tartu. Math. 2019, 23, 245–254. [Google Scholar] [CrossRef]
- Kala, Z. Sensitivity analysis in probabilistic structural design: A comparison of selected techniques. Sustainability 2020, 12, 4788. [Google Scholar] [CrossRef]
- Lei, J.; Lu, Z.; He, L. The single-loop Kriging model combined with Bayes’ formula for time-dependent failure probability based global sensitivity. Structures 2021, 32, 987–996. [Google Scholar] [CrossRef]
- Wang, P.; Li, H.; Huang, X.; Zhang, Z.; Xiao, S. Numerical decomposition for the reliability-oriented sensitivity with dependent variables using vine copulas. J. Mech. Des. 2021, 143, 081701. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Mardani, A.; Cavallaro, F.; Štreimikienė, D.; Khan, S.A.R. Pythagorean Fuzzy SWARA–VIKOR Framework for Performance Evaluation of Solar Panel Selection. Sustainability 2020, 12, 4278. [Google Scholar] [CrossRef]
- Mitrović Simić, J.; Stević, Ž.; Zavadskas, E.K.; Bogdanović, V.; Subotić, M.; Mardani, A. A Novel CRITIC-Fuzzy FUCOM-DEA-Fuzzy MARCOS model for safety evaluation of road sections based on geometric parameters of road. Symmetry 2020, 12, 2006. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Krishankumar, R.; Mardani, A.; Cavallaro, F.; Soundarapandian Ravichandran, K.; Balasubramanian, K. Hesitant fuzzy SWARA-complex proportional assessment approach for sustainable supplier selection (HF-SWARA-COPRAS). Symmetry 2020, 12, 1152. [Google Scholar] [CrossRef]
- Puška, A.; Nedeljković, M.; Hashemkhani Zolfani, S.; Pamučar, D. Application of interval fuzzy logic in selecting a sustainable supplier on the example of agricultural production. Symmetry 2021, 13, 774. [Google Scholar] [CrossRef]
- Wang, A.; Solomatine, D.P. Practical experience of sensitivity analysis: Comparing six methods, on three hydrological models, with three performance criteria. Water 2019, 11, 1062. [Google Scholar] [CrossRef]
- Štefaňák, J.; Kala, Z.; Miča, L.; Norkus, A. Global sensitivity analysis for transformation of Hoek-Brown failure criterion for rock mass. J. Civ. Eng. Manag. 2018, 24, 390–398. [Google Scholar] [CrossRef]
- Ching, D.S.; Safta, C.; Reichardt, T.A. Sensitivity-informed bayesian inference for home PLC network models with unknown parameters. Energies 2021, 14, 2402. [Google Scholar] [CrossRef]
- Rahn, S.; Gödel, M.; Fischer, R.; Köster, G. Dynamics of a simulated demonstration march: An efficient sensitivity analysis. Sustainability 2021, 13, 3455. [Google Scholar] [CrossRef]
- Martínez-Ruiz, A.; Ruiz-García, A.; Prado-Hernández, J.V.; López-Cruz, I.L.; Valencia-Islas, J.O.; Pineda-Pineda, J. Global sensitivity analysis and calibration by differential evolution algorithm of HORTSYST crop model for fertigation management. Water 2021, 13, 610. [Google Scholar] [CrossRef]
- Xu, N.; Luo, J.; Zuo, J.; Hu, X.; Dong, J.; Wu, T.; Wu, S.; Liu, H. Accurate suitability evaluation of large-scale roof greening based on RS and GIS methods. Sustainability 2020, 12, 4375. [Google Scholar] [CrossRef]
- Islam, A.B.M.; Karadoğan, E. Analysis of one-dimensional ivshin–pence shape memory alloy constitutive model for sensitivity and uncertainty. Materials 2020, 13, 1482. [Google Scholar] [CrossRef] [PubMed]
- Gamannossi, A.; Amerini, A.; Mazzei, L.; Bacci, T.; Poggiali, M.; Andreini, A. Uncertainty quantification of film cooling performance of an industrial gas turbine vane. Entropy 2020, 22, 16. [Google Scholar] [CrossRef] [PubMed]
- De Falco, A.; Resta, C.; Sevieri, G. Sensitivity analysis of frequency-based tie-rod axial load evaluation methods. Eng. Struct. 2021, 229, 111568. [Google Scholar] [CrossRef]
- Antucheviciene, J.; Kala, Z.; Marzouk, M.; Vaidogas, E.R. Solving civil engineering problems by means of fuzzy and stochastic MCDM methods: Current state and future research. Math. Probl. Eng. 2015, 2015, 362579. [Google Scholar] [CrossRef]
- Kala, Z.; Valeš, J. Sensitivity assessment and lateral-torsional buckling design of I-beams using solid finite elements. J. Constr. Steel Res. 2017, 139, 110–122. [Google Scholar] [CrossRef]
- Wen, Z.; Xia, Y.; Ji, Y.; Liu, Y.; Xiong, Z.; Lu, H. Study on risk control of water inrush in tunnel construction period considering uncertainty. J. Civ. Eng. Manag. 2019, 25, 757–772. [Google Scholar] [CrossRef]
- Strieška, M.; Koteš, P. Sensitivity of dose-response function for carbon steel under various conditions in Slovakia. Transp. Res. Procedia 2019, 40, 912–919. [Google Scholar] [CrossRef]
- Su, L.; Wang, T.; Li, H.; Chao, Y.; Wang, L. Multi-criteria decision making for identification of unbalanced bidding. J. Civ. Eng. Manag. 2020, 26, 43–52. [Google Scholar] [CrossRef]
- Rykov, V.; Kozyrev, D. On the reliability function of a double redundant system with general repair time distribution. Appl. Stoch. Models Bus Ind. 2019, 35, 191–197. [Google Scholar] [CrossRef]
- Luo, L.; Zhang, L.; Wu, G. Bayesian belief network-based project complexity measurement considering causal relationships. J. Civ. Eng. Manag. 2020, 26, 200–2015. [Google Scholar] [CrossRef]
- Strauss, A.; Moser, T.; Honeger, C.; Spyridis, P.; Frangopol, D.M. Likelihood of impact events in transport networks considering road conditions, traffic and routing elements properties. J. Civ. Eng. Manag. 2020, 26, 95–112. [Google Scholar] [CrossRef]
- Rykov, V.V.; Sukharev, M.G.; Itkin, V.Y. Investigations of the potential application of k-out-of-n systems in oil and gas industry objects. J. Mar. Sci. Eng. 2020, 8, 928. [Google Scholar] [CrossRef]
- Pan, L.; Novák, L.; Lehký, D.; Novák, D.; Cao, M. Neural network ensemble-based sensitivity analysis in structural engineering: Comparison of selected methods and the influence of statistical correlation. Comput. Struct. 2021, 242, 106376. [Google Scholar] [CrossRef]
- Schroeder, M.J. An Alternative to entropy in the measurement of information. Entropy 2004, 6, 388–412. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; John Wiley and Sons: Hoboken, NJ, USA, 1959. [Google Scholar]
- Gamboa, F.; Klein, T.; Lagnoux, A. Sensitivity analysis based on Cramér-von Mises distance. SIAM/ASA J. Uncertain. Quantif. 2018, 6, 522–548. [Google Scholar] [CrossRef]
- Kala, Z. Limit states of structures and global sensitivity analysis based on Cramér-von Mises distance. Int. J. Mech. 2020, 14, 107–118. [Google Scholar]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Kala, Z. Sensitivity assessment of steel members under compression. Eng. Struct. 2009, 31, 1344–1348. [Google Scholar] [CrossRef]
- Kala, Z. Global sensitivity analysis in stability problems of steel frame structures. J. Civ. Eng. Manag. 2016, 22, 417–424. [Google Scholar] [CrossRef]
- Kala, Z.; Valeš, J. Imperfection sensitivity analysis of steel columns at ultimate limit state. Arch. Civ. Mech. Eng. 2018, 18, 1207–1218. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: West Sussex, UK, 2008. [Google Scholar]
- Melcher, J.; Kala, Z.; Holický, M.; Fajkus, M.; Rozlívka, L. Design characteristics of structural steels based on statistical analysis of metallurgical products. J. Constr. Steel Res. 2004, 60, 795–808. [Google Scholar] [CrossRef]
- Kala, Z.; Melcher, J.; Puklický, L. Material and geometrical characteristics of structural steels based on statistical analysis of metallurgical products. J. Civ. Eng. Manag. 2009, 15, 299–307. [Google Scholar] [CrossRef]
- McKey, M.D.; Beckman, R.J.; Conover, W.J. A comparison of the three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Iman, R.C.; Conover, W.J. Small sample sensitivity analysis techniques for computer models with an application to risk assessment. Commun. Stat. Theory Methods 1980, 9, 1749–1842. [Google Scholar] [CrossRef]




| Characteristic | Index | Symbol | Mean Value μ | Standard Deviation σ |
|---|---|---|---|---|
| Yield Strength | 1 | fy | 412.68 MPa | 27.941 MPa |
| Thickness | 2 | t2 | 12 mm | 0.55 mm |
| Width | 3 | b | 100 mm | 1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kala, Z. Global Sensitivity Analysis Based on Entropy: From Differential Entropy to Alternative Measures. Entropy 2021, 23, 778. https://doi.org/10.3390/e23060778
Kala Z. Global Sensitivity Analysis Based on Entropy: From Differential Entropy to Alternative Measures. Entropy. 2021; 23(6):778. https://doi.org/10.3390/e23060778
Chicago/Turabian StyleKala, Zdeněk. 2021. "Global Sensitivity Analysis Based on Entropy: From Differential Entropy to Alternative Measures" Entropy 23, no. 6: 778. https://doi.org/10.3390/e23060778
APA StyleKala, Z. (2021). Global Sensitivity Analysis Based on Entropy: From Differential Entropy to Alternative Measures. Entropy, 23(6), 778. https://doi.org/10.3390/e23060778






