A New First-Order Integer-Valued Autoregressive Model with Bell Innovations
Abstract
1. Introduction
2. The BL-INAR(1) Model
2.1. The Bell Distribution
2.2. Definition and Properties of the BL-INAR(1) Process
3. Estimation of Parameters
3.1. Conditional Least Squares Estimation
3.2. Yule–Walker Estimation
3.3. Conditional Maximum Likelihood Estimation
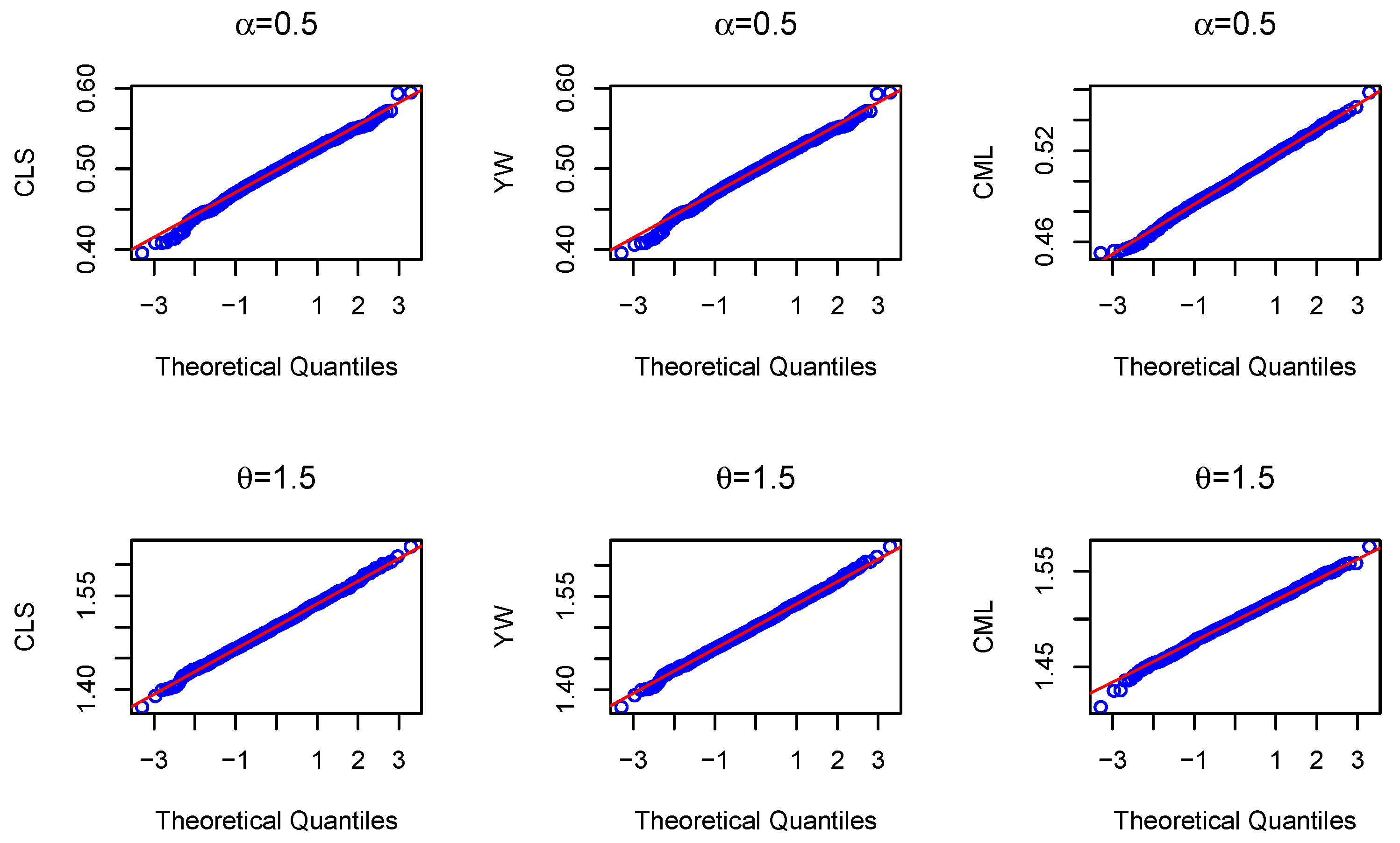
4. Simulation
5. Real Data Examples
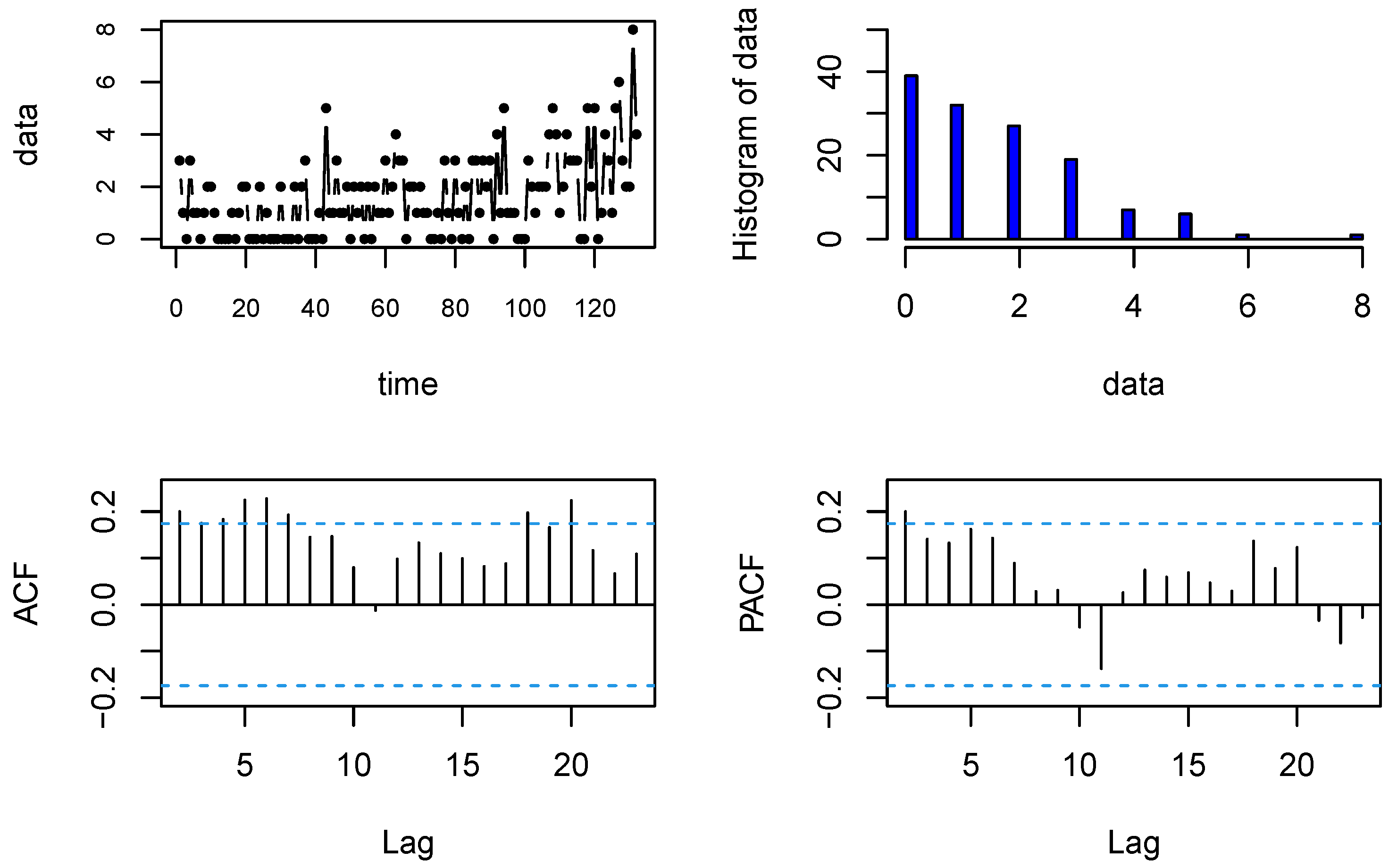
5.1. Disconduct Data
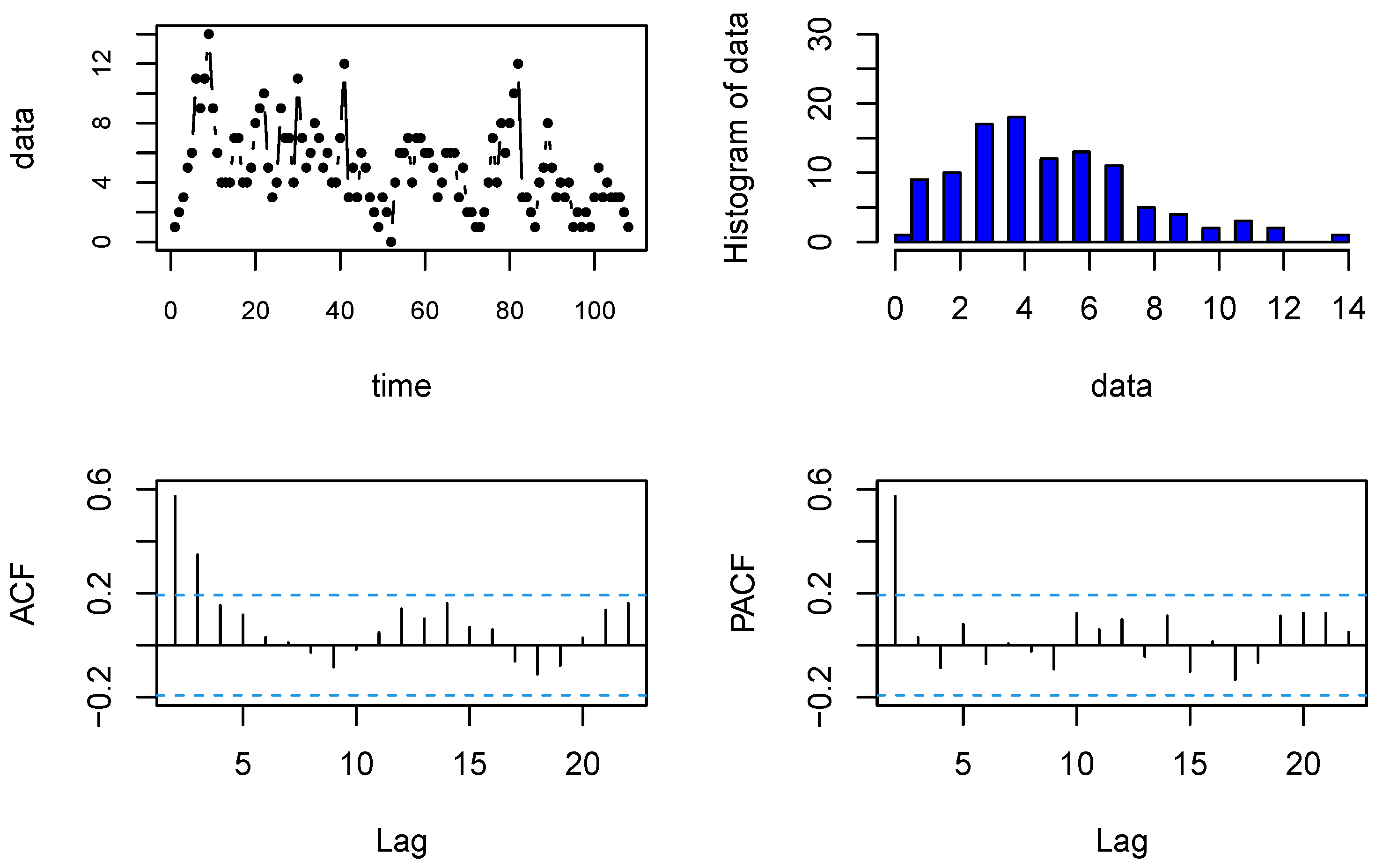
5.2. Strikes Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Theorem 2
Appendix A.2. Proof of Theorem 3
References
- McKenzie, E. Some simple models for discrete variate time series. Water Resour. Bull. 1985, 21, 645–650. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-order integer-valued autoregressive (INAR(1)) process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Steutel, F.W.; van Harn, K. Discrete analogues of self-decomposability and stability. Ann. Probab. 1979, 7, 893–899. [Google Scholar] [CrossRef]
- Alzaid, A.A.; Al-Osh, M.A. First-order integer-valued autoregressive process: Distributional and regression properties. Stat. Neerl. 1988, 42, 53–61. [Google Scholar] [CrossRef]
- Weiß, C.H. An Introduction to Discrete-Valued Time Series; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Ristić, M.M.; Bakouch, H.S.; Nastić, A.S. A new geometric first-order integer-valued autoregressive (NGINAR(1)) process. J. Stat. Plan. Inference 2009, 139, 2218–2226. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, F. A new extension of thinning-based integer-valued autoregressive models for count data. Entropy 2021, 23, 62. [Google Scholar] [CrossRef] [PubMed]
- Jung, R.C.; Ronning, G.; Tremayne, A.R. Estimation in conditional first order autoregression with discrete support. Stat. Pap. 2005, 46, 195–224. [Google Scholar] [CrossRef]
- Jazi, M.A.; Jones, G.; Lai, C.-D. First-order integer valued AR processes with zero inflated Poisson innovations. J. Time Ser. Anal. 2012, 33, 954–963. [Google Scholar] [CrossRef]
- Jazi, M.A.; Jones, G.; Lai, C.-D. Integer valued AR(1) with geometric innovations. J. Iran. Stat. Soc. 2012, 11, 173–190. [Google Scholar]
- Schweer, S.; Weiß, C.H. Compound Poisson INAR(1) processes: Stochastic properties and testing for overdispersion. Comput. Stat. Data Anal. 2014, 77, 267–284. [Google Scholar] [CrossRef]
- Livio, T.; Mamode Khan, N.; Bourgignon, M.; Bakouch, H.S. An INAR(1) model with Poisson–Lindley innovations. Econ. Bull. 2018, 38, 1505–1513. [Google Scholar]
- Bourguignon, M.; Rodrigues, J.; Santos-Neto, M. Extended Poisson INAR(1) processes with equidispersion, underdispersion and overdispersion. J. Appl. Stat. 2019, 46, 101–118. [Google Scholar] [CrossRef]
- Qi, X.; Li, Q.; Zhu, F. Modeling time series of count with excess zeros and ones based on INAR(1) model with zero-and-one inflated Poisson innovations. J. Comput. Appl. Math. 2019, 346, 572–590. [Google Scholar] [CrossRef]
- Cunha, E.T.D.; Bourguignon, M.; Vasconcellos, K.L.P. On shifted integer-valued autoregressive model for count time series showing equidispersion, underdispersion or overdispersion. Commun. Stat.-Theory Methods 2021. [Google Scholar] [CrossRef]
- Castellares, F.; Ferrari, S.L.P.; Lemonte, A.J. On the Bell distribution and its associated regression model for count data. Appl. Math. Model. 2018, 56, 172–185. [Google Scholar] [CrossRef]
- Akaike, H. Information theory as an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory; Petrov, B.N., Csaki, F., Eds.; Akadémiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Bozdogan, H. Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1978, 52, 345–370. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The Determination of the Order of an Autoregression. J. R. Stat. Soc. Ser. B 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Bell, E.T. Exponential polynomials. Ann. Math. 1934, 35, 258–277. [Google Scholar] [CrossRef]
- Batsidis, A.; Jiménez-Gamero, M.D.; Lemonte, A.J. On goodness-of-fit tests for the Bell distribution. Metrika 2020, 83, 297–319. [Google Scholar] [CrossRef]
- Castellares, F.; Lemonte, A.J.; Moreno–Arenas, G. On the two-parameter Bell–Touchard discrete distribution. Commun. Stat.-Theory Methods 2020, 49, 4834–4852. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Moreno-Arenas, G.; Castellares, F. Zero-inflated Bell regression models for count data. J. Appl. Stat. 2020, 47, 265–286. [Google Scholar] [CrossRef]
- Muhammad, A.; Muhammad, N.A.; Abdul, M. On the estimation of Bell regression model using ridge estimator. Commun. Stat.-Simul. Comput. 2021. [Google Scholar] [CrossRef]
- Du, J.G.; Li, Y. The integer valued autoregressive (INAR(p)) model. J. Times Ser. Anal. 1991, 12, 129–142. [Google Scholar]
- Fisher, R.A. The significance of deviations from expectation in a Poisson series. Biometrics 1950, 6, 17–24. [Google Scholar] [CrossRef]
- Tjøstheim, D. Estimation in nonlinear time series models. Stoch. Process. Their Appl. 1986, 21, 251–273. [Google Scholar] [CrossRef]
- Freeland, R.K.; McCabe, B. Asymptotic properties of CLS estimates in the Poisson AR(1) model. Stat. Probab. Lett. 2005, 73, 147–153. [Google Scholar] [CrossRef]
- Franke, J.; Seligmann, T. Conditional maximum likelihood estimates for INAR(1) processes and their application to modelling epileptic seizure counts. In Developments in Time Series Analysis; Rao, T.S., Ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1993; pp. 310–330. [Google Scholar]
- Ljung, G.M.; Box, G.E.P. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Weiß, C.H. The INARCH(1) model for overdispersed time series of Counts. Commun. Stat.-Simul. Comput. 2010, 39, 1269–1291. [Google Scholar] [CrossRef]


| T | ||||||
|---|---|---|---|---|---|---|
| (, ) = (0.25, 0.5) | ||||||
| 100 | 0.220445 | 0.507901 | 0.218464 | 0.508838 | 0.238497 | 0.500617 |
| (0.011615) | (0.003871) | (0.011564) | (0.003814) | (0.007120) | (0.003049) | |
| 250 | 0.240011 | 0.502610 | 0.239107 | 0.503039 | 0.246433 | 0.500099 |
| (0.004665) | (0.001520) | (0.004653) | (0.001501) | (0.002658) | (0.001146) | |
| 500 | 0.245254 | 0.500707 | 0.244710 | 0.500965 | 0.247766 | 0.499777 |
| (0.002286) | (0.000758) | (0.002284) | (0.000759) | (0.001300) | (0.000603) | |
| 1000 | 0.246458 | 0.500868 | 0.246197 | 0.500974 | 0.249120 | 0.499768 |
| (0.001195) | (0.000379) | (0.001197) | (0.000380) | (0.000714) | (0.000290) | |
| (, ) = (0.5, 0.5) | ||||||
| 100 | 0.475430 | 0.508229 | 0.469977 | 0.512782 | 0.495566 | 0.497046 |
| (0.010198) | (0.005396) | (0.010256) | (0.005296) | (0.004046) | (0.003083) | |
| 250 | 0.488517 | 0.504259 | 0.486491 | 0.505890 | 0.497636 | 0.499045 |
| (0.003895) | (0.002128) | (0.003911) | (0.002123) | (0.001723) | (0.001332) | |
| 500 | 0.493426 | 0.502160 | 0.492388 | 0.503029 | 0.498222 | 0.499355 |
| (0.001857) | (0.001026) | (0.001868) | (0.001025) | (0.000866) | (0.000643) | |
| 1000 | 0.496426 | 0.501635 | 0.495922 | 0.502043 | 0.499262 | 0.499936 |
| (0.000914) | (0.000530) | (0.000916) | (0.000529) | (0.000412) | (0.000322) | |
| (, ) = (0.75, 0.5) | ||||||
| 100 | 0.714977 | 0.535092 | 0.707308 | 0.543643 | 0.745993 | 0.500460 |
| (0.006966) | (0.011276) | (0.007639) | (0.011838) | (0.001321) | (0.003355) | |
| 250 | 0.736256 | 0.513360 | 0.733057 | 0.517222 | 0.748974 | 0.498915 |
| (0.002354) | (0.004357) | (0.002456) | (0.004432) | (0.000494) | (0.001352) | |
| 500 | 0.743674 | 0.505799 | 0.742084 | 0.507695 | 0.749245 | 0.499568 |
| (0.001052) | (0.001967) | (0.001079) | (0.001983) | (0.000243) | (0.000681) | |
| 1000 | 0.746006 | 0.504828 | 0.745283 | 0.505726 | 0.749925 | 0.500221 |
| (0.000546) | (0.001001) | (0.000554) | (0.001011) | (0.000132) | (0.000309) | |
| T | ||||||
|---|---|---|---|---|---|---|
| (, ) = (0.25, 1.5) | ||||||
| 100 | 0.230059 | 1.508538 | 0.227601 | 1.510489 | 0.252786 | 1.492707 |
| (0.010409) | (0.007500) | (0.010294) | (0.007323) | (0.004877) | (0.004375) | |
| 250 | 0.243290 | 1.503077 | 0.242313 | 1.503896 | 0.250278 | 1.498450 |
| (0.003994) | (0.002928) | (0.003976) | (0.002898) | (0.001810) | (0.001660) | |
| 500 | 0.244804 | 1.503143 | 0.244310 | 1.503531 | 0.249992 | 1.499429 |
| (0.001917) | (0.001459) | (0.001914) | (0.001451) | (0.000913) | (0.000829) | |
| 1000 | 0.248715 | 1.500420 | 0.248470 | 1.500628 | 0.251744 | 1.498222 |
| (0.000984) | (0.000745) | (0.000983) | (0.000745) | (0.000477) | (0.000422) | |
| (, ) = (0.5, 1.5) | ||||||
| 100 | 0.472192 | 1.522593 | 0.467254 | 1.528069 | 0.497401 | 1.497773 |
| (0.008714) | (0.011950) | (0.008913) | (0.011884) | (0.002653) | (0.004999) | |
| 250 | 0.489125 | 1.509054 | 0.487244 | 1.511225 | 0.499745 | 1.498361 |
| (0.003127) | (0.004609) | (0.003148) | (0.004598) | (0.000991) | (0.001856) | |
| 500 | 0.496116 | 1.502407 | 0.495032 | 1.503670 | 0.501865 | 1.496562 |
| (0.001650) | (0.002493) | (0.001660) | (0.002487) | (0.000584) | (0.001078) | |
| 1000 | 0.497904 | 1.501246 | 0.497432 | 1.501800 | 0.500976 | 1.498100 |
| (0.000826) | (0.001314) | (0.000827) | (0.001314) | (0.000274) | (0.000502) | |
| (, ) = (0.75, 1.5) | ||||||
| 100 | 0.721350 | 1.547389 | 0.713291 | 1.565523 | 0.749555 | 1.495159 |
| (0.005627) | (0.025790) | (0.006188) | (0.026764) | (0.000827) | (0.005581) | |
| 250 | 0.736975 | 1.522062 | 0.733930 | 1.529286 | 0.749880 | 1.497782 |
| (0.002181) | (0.011299) | (0.002278) | (0.011488) | (0.000343) | (0.002363) | |
| 500 | 0.742692 | 1.512717 | 0.741144 | 1.516338 | 0.749888 | 1.498329 |
| (0.000919) | (0.005007) | (0.000947) | (0.005076) | (0.000158) | (0.001101) | |
| 1000 | 0.747785 | 1.503485 | 0.747046 | 1.505296 | 0.750224 | 1.499187 |
| (0.000476) | (0.002670) | (0.000479) | (0.002670) | (0.000083) | (0.000541) | |
| Model | Parameters | AIC | BIC | CAIC | HQIC | Mean | Variance | RMSE |
|---|---|---|---|---|---|---|---|---|
| BL-INAR | 441.7380 | 447.5036 | 449.5036 | 444.0809 | 1.6201 | 2.5361 | 3.2205 | |
| P-INAR | 456.4653 | 462.2309 | 464.2309 | 458.8082 | 1.6197 | 2.1512 | 3.2497 | |
| G-INAR | 446.1416 | 451.9072 | 453.9072 | 448.4845 | 1.6207 | 3.2290 | 3.1803 | |
| PL-INAR | 444.3542 | 450.1198 | 452.1198 | 446.6971 | 1.6254 | 0.2928 | 3.1929 | |
| NB-INAR | 445.4351 | 454.0835 | 457.0835 | 448.9494 | 1.6201 | 2.5542 | 3.2233 | |
| ZIP-INAR | 442.7224 | 451.3708 | 454.3708 | 446.2367 | 1.6202 | 2.3903 | 3.2121 | |
| DP-INAR | 443.7622 | 452.4106 | 455.4106 | 447.2765 | 1.4900 | 2.6859 | 3.3155 | |
| GP-INAR | 445.8156 | 454.4640 | 457.4640 | 449.3300 | 1.6200 | 2.5386 | 3.2252 | |
| Model | Parameters | AIC | BIC | CAIC | HQIC | Mean | Variance | RMSE |
|---|---|---|---|---|---|---|---|---|
| BL-INAR | 468.1557 | 473.5199 | 475.5199 | 470.3307 | 4.9813 | 7.7408 | 2.2659 | |
| P-INAR | 473.0936 | 478.4578 | 480.4578 | 475.2686 | 4.9813 | 9.8110 | 2.3331 | |
| G-INAR | 475.3209 | 480.6852 | 482.6852 | 477.4960 | 4.9813 | 10.7361 | 2.2121 | |
| PL-INAR | 471.9345 | 477.2987 | 479.2987 | 474.1095 | 5.0016 | 1.8876 | 2.2489 | |
| NB-INAR | 469.6850 | 477.7314 | 480.7314 | 472.9476 | 4.9813 | 6.8573 | 2.2969 | |
| ZIP-INAR | 470.9985 | 479.0449 | 482.0449 | 474.2610 | 4.9813 | 6.6692 | 2.2663 | |
| DP-INAR | 469.5585 | 477.6048 | 480.6048 | 472.8210 | 4.9576 | 7.1420 | 2.2659 | |
| GP-INAR | 469.7467 | 477.7930 | 480.7930 | 473.0092 | 4.9813 | 6.8335 | 2.2986 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Zhu, F. A New First-Order Integer-Valued Autoregressive Model with Bell Innovations. Entropy 2021, 23, 713. https://doi.org/10.3390/e23060713
Huang J, Zhu F. A New First-Order Integer-Valued Autoregressive Model with Bell Innovations. Entropy. 2021; 23(6):713. https://doi.org/10.3390/e23060713
Chicago/Turabian StyleHuang, Jie, and Fukang Zhu. 2021. "A New First-Order Integer-Valued Autoregressive Model with Bell Innovations" Entropy 23, no. 6: 713. https://doi.org/10.3390/e23060713
APA StyleHuang, J., & Zhu, F. (2021). A New First-Order Integer-Valued Autoregressive Model with Bell Innovations. Entropy, 23(6), 713. https://doi.org/10.3390/e23060713





