1. Introduction
The rapidly growing securities market in China drives the participation and curiosity of investors. Investors’ reaction on information plays a central role in modern financial markets globally. As one of the key signals of a company’s profitability and sustainability, Dividend policy becomes an essential trigger of stock price movements. Despite what the Modigliani-Miller theorem states [
1], the effects of dividend policies are puzzling, especially in China.
China’s A-share market is an important global investment market. As of 1 December 2020, the total market value of China’s A-share listed companies in Shenzhen and Shanghai stocks reached 82.92 trillion yuan. In the global market, the total market value of A-share listed companies is second only to the United States, ranking second globally [
2]. Unlike other listed companies’ emphasis on cash dividends, there is a long-term phenomenon in China’s A-share market, called a “high stock dividend”. For every ten shares of holding, the company will transfer five shares or more to shareholders [
3], and its publication time is often concentrated in the annual report period. On 4 April 2018, the Shanghai Stock Exchange and the Shenzhen Stock Exchange announced the guidelines for disclosing listed companies’ high stock dividend information (Draft). This disclosure imposed strict restrictions on the reduction and sales of shares held by relevant shareholders, the company’s net profit, and the company’s earnings per share, accelerating the resulting downward trend in the number of high stock dividend distribution which began in 2016. Some research shows that the stock dividend announcements have a positive impact. In contrast, the cash dividend announcements negatively impact abnormal returns for Chinese companies [
4], and the intensity of high stock dividends is positively correlated with the scale of significant shareholders’ reduction [
5]. Part insiders may consciously take advantage of investors’ irrational preferences to achieve their rational self-interest motivations like stock sales in high stock dividends. High stock dividends have the feature of an instrument [
6]. Therefore, the prediction of stock dividend distribution is meaningful for alleviating the information asymmetry in the investment market, assisting investors in making investment decisions, and providing a decision-making basis for the market supervision department. That explains why a more accurate prediction on this particular phenomenon is valuable.
This study proposes a feature adaptive improved multi-layers ensemble model to boost prediction accuracy of “high stock dividends”. The following structure of this paper is as follows. In
Section 2, the previous results related to this study are reviewed, and the main contributions of stacking ensemble algorithm improving are also introduced.
Section 3 describes each part of the feature adaptive improved multi-layers ensemble model in detail, including the optimization of feature engineering, the adaptive matching of the base model and the feature subset, and the design of the second feature extraction layer. All model backtesting results with A-share historical data are analyzed in
Section 4 to evaluate the model’s predictive ability. Finally, the research is summarized, and the follow-up work is presented in
Section 5.
2. Literature Review
The previous studies discussed the phenomenon of high stock dividends mainly included three aspects: motivation, excess return, and prediction methods.
In the existing literature, there are several different views on the phenomenon. Most of the work was based on the aspects of traditional economics and behavioral economics. Under the traditional economics framework, some scholars analyzed the high stock dividend phenomenon from the perspective of the signaling theory [
7] and believed that the company’s management intended to pass the information of the company’s future performance to the investors through dividend policy. Many scholars demonstrated the effect of dividend policy on transmitting positive signals to the company’s operation [
8,
9,
10]. According to the optimal price theory put forward by other scholars, the excessive stock price will demand that small and medium-sized investors have more capital, which will restrict their trading behaviors. Split shares or dividend policies can reduce the stock price and improve liquidity, making the stock price be in a more reasonable range [
11,
12,
13]. In behavioral finance, a class of views supported the dividend catering theory, pointing out that when investors had irrational preferences, the company’s management had an incentive to cater to investors for proposing related dividend policies. Another group of researchers believed in price illusion theory, pointing out that nominal price changes due to stock dividend distribution can affect investors’ decision-making [
14].
Some scholars’ research focused on the excess return causing by high stock dividend. Eng et al. (2014) empirically found that the strengthening of stock split supervision would reduce the information asymmetry [
15], which made the return on the announcement day shift from high correlation with lagging profitability of the previous financial report to high correlation with future profitability. Furthermore, as Huang and Paul (2017) pointed out [
16], institutional investors preferred companies that paid dividends. There was often an inevitable excess return in the A-share market before and after the occurrence of a high stock dividend phenomenon [
17]. Therefore, the successful prediction of this phenomenon will help investors to build an effective event-driven strategy and obtain excess returns.
Another kind of research focused on the prediction of the stock dividends, but this kind of research was relatively unpopular. Ezell and Rubiales (1975) firstly used the idea of discrete dependent variable modeling to study the dividend policy prediction [
18]. Bae (2010) introduced decision tree, multi-layer perceptron, and support vector machine (SVM) models [
19]. Taking the data of Korean listed companies as an example, Bae found that the SVM model based on RBF kernel could accurately predict the dividend policy of South Korea. Xiong et al. (2012) used the logistic regression model to predict the high stock dividend phenomenon from 2007 to 2011 [
20]. Multi-layers perceptron was proposed by Dong and Zhao (2019) to predict the phenomenon of the high stock dividend distribution, which improved the accuracy rate by 12% based on the logistic regression model [
21].
According to the previous studies, there are still two aspects that should be improved: (1) Classical methods usually choose one method for feature selection. As we know, the selection principles of different single feature selection methods are different. As a result, the feature sets obtained by different methods are often different. In other words, some features can be selected by one method, but at the same time, they will be missed by another method. The single feature screening method has a specific feature omission risk. (2) Single-method models have strong prediction ability but relatively low generalization ability. Therefore, some studies use the stacking algorithm to integrate the base model’s output and improve the generalization ability. In this general stacking algorithm, the base model’s output is usually weighted or used as the input of a classification model to predict the final result. However, such a method lacks information extraction for the output of the base model, which limits the use efficiency of the feature information of the model and restricts the model’s predictive ability.
This paper proposes a feature adaptive improved multi-layers ensemble model, an improved stacking ensemble model. This study’s main contributions are as follows: (1) We use the equal weight feature comprehensive evaluation method to select the effective features. This method can take advantage of various single feature selection methods and reduce the risk of missing essential features. (2) Genetic algorithm is used to customize the optimal feature subset for each base model to improve each base model’s predictive ability, which is the basis for improving the overall predictive ability of the model. (3) With the inspiration of the deep tree model [
22], this paper uses the GBDT (Gradient Boosting Decision Tree) [
23] model as the feature information extraction layer of the base model output in the stacking algorithm [
24]. The base model output is mapped to the new space to achieve new features and use the new feature to make predictions through feature information extraction. This work improves the prediction accuracy of the model.
3. The Design of Feature Adaptive Improved Multi-Layers Ensemble Model
After summarizing the relevant literature, this section will discuss the design of the feature adaptive improved multi-layers ensemble model. The modeling process is divided into three parts: feature engineering, construction and selection of feature adaptive base models, and the multi-layer ensemble model.
This paper investigates the prediction of the “High Stock Dividend” phenomenon. Through identification of the A-listed companies with high stock dividend in the next six months as “1”, otherwise as “0”, the prediction observation can be transformed into a binary variable. Previous studies showed machine learning is effective when solving this kind of question, such as the rise and fall of stocks, debt default, etc. [
25,
26]. Feature selection plays an important role in machine learning prediction, and appropriate features can greatly improve the prediction ability of machine learning methods [
27]. There are two common feature selection methods [
28]: univariate methods (such as F value [
29], maximum information coefficient (MIC) value [
30], information value (IV) value [
31], etc.) and multivariate methods (such as recurrent feature elimination (RFE) [
32], etc.). All feature selection methods are based on a specific correlation or importance measurement method, but the relationship between variables is usually complex. Different feature selection methods may get different subsets [
33]. Some variables may be tail features in one method and head features in another, which means that univariate methods exist the risk of missing important features. For this reason, the ensemble feature selection method will be used in this model.
Since the single-method model is weak with generalization ability [
34], we decide to use the stacking ensemble model in this study. Stacking framework has been used in machine learning applications in different fields [
35,
36]. The idea of the framework is mainly divided into two parts. The first part integrates the first several layers of the model to achieve the generalization ability of the model as much as possible, and the second part integrates all the information and improving the robustness of the last layer. Due to the fact that the principles of different sub-models are different, their requirements for features may also be different to a certain degree. However, previous studies usually train and integrate different sub-models with the same selected feature dataset [
37], which makes some sub-models lack the input of important features in training, and it is difficult for sub-models to achieve optimal performance and ultimately affect the prediction ability of stacking method. To improve the performance of the stacking framework, based on feature selection, this paper will use a genetic algorithm [
38] to find the optimal feature subset of the corresponding model and train the model independently to achieve the consistency between the base model and the feature subset. The output of each base model can be regarded as a newly generated feature. To improve the efficiency of information utilization, we then need to cross these output features and extract new features. As an essential branch of machine learning, the tree model originated from the ID3 algorithm in 1986. After decades of development, tree models with good performance, such as CART (Classification and Regression Tree), C5.0, and others, have been proposed, making the tree model very popular. The tree model’s basic metrics include Gini impurity, Information gain, etc., which are based on the concept of entropy and information theory, which makes the tree model less demanding on the amount of data compared to other models. Because of this advantage, the tree model is well suited to act as the second feature extraction layer in “high stock dividend” prediction. The GBDT model is selected to generate new features from the base model’s output based on the feature cross-ability. Finally, Logistic Regression (LR) model is used to extract information from these features generated at the last level and outputs the final prediction results, which will improve the model’s generation ability.
As shown in
Figure 1, the first part of the model is feature engineering. In this part, the equal weight comprehensive feature evaluation method is used to find out the features related to high stock dividends, and the corresponding feature subset 1 is obtained. The feature subset 2 is then obtained by automatically expanding the feature subset 1 by the genetic programming method. The second part of the model is the construction and selection of the feature adaptive base model. In this paper, we use LR [
39], SVM [
40], Random Forest (RF) [
41], LightGBM (LGB) [
42], Multi-Layers Perceptron (MLP) [
43], and K-Nearest Neighbor (KNN) [
44] models with multiple datasets and feature subset combinations using feature adaptive selection algorism to form the feature adaptive base model. According to the base model comparison coefficient (formula 1) of the base models [
45], the base model with better performance and differentiated output results in the verification set in 2018 is selected. The specific steps are: (1) Calculate the numerator, which is the AUC [
46] of each base model in the validation dataset. (2) Select the model having the highest AUC as the target model. (3) Calculate the pearson correlation coefficient between the AUC of the target model and the AUC of the other base models. (4) Use the formula (1) to obtain the base model comparison coefficient, which will be used as the metrics to select the base models.
The last part of the model is the construction of a multi-layer ensemble model. In this paper, a multi-layer stacking ensemble model is designed to further improve the prediction and generalization ability based on the base models. Each part will be described in detail below.
3.1. Feature Engineering
The goal of feature engineering is to screen features in all directions (from the perspective of a linear relationship, nonlinear relationship, and model performance) without loss of model accuracy (AUC). The specific steps are as follows: (1) For single-factor analysis, using one-way ANOVA (F value) to investigate the linear relationship between features and target variables, and using family-wise error rate (FWE) error measure methods to investigate whether the features suitable under this inspection. (2) The maximum information coefficient (MIC) is used to investigate the arbitrary statistical relationship between features and target variables. The MIC value was scored with a fixed proportion (more than 50% quantile). (3) Firstly, the genetic algorithm is used to divide the features into boxes. The information value (IV) is used to check whether the features suitable under this inspection (more than 50% quantile). (4) Recursive feature elimination (RFE) with cross-validation was used to investigate the linear model’s importance and nonlinear model features by the LR model and the RF model with the L1 regular term. According to the output of RFE, whether the features scored under the inspection was evaluated (set to retain 50% features). After the above feature screening, each feature gets 5 groups of scores (1 point for each group). Finally, the final score of each feature is obtained by using the equal weight method. If the score is more than 4(including 4), it will be in the feature subset 1 with 48 features. Secondly, this paper uses genetic programming to mine features, which can automatically discover the potential relationship of features and get feature subset 2 with 100 features.
Considering the characteristics of the high stock dividend prediction problem, the model’s core evaluation indicators are determined as AUC and F1 score [
47]. On the one hand, the key index of the prediction is AUC, which comprehensively considers the positive and negative examples and reflects the degree of fitting of the model, which is suitable for the unbalanced two classification problem in this paper. However, the F1 score can comprehensively reflect the model’s accuracy and recall rate and comprehensively reflect its prediction ability.
3.2. The Construction and Screening of the Feature Adaptive Base Models
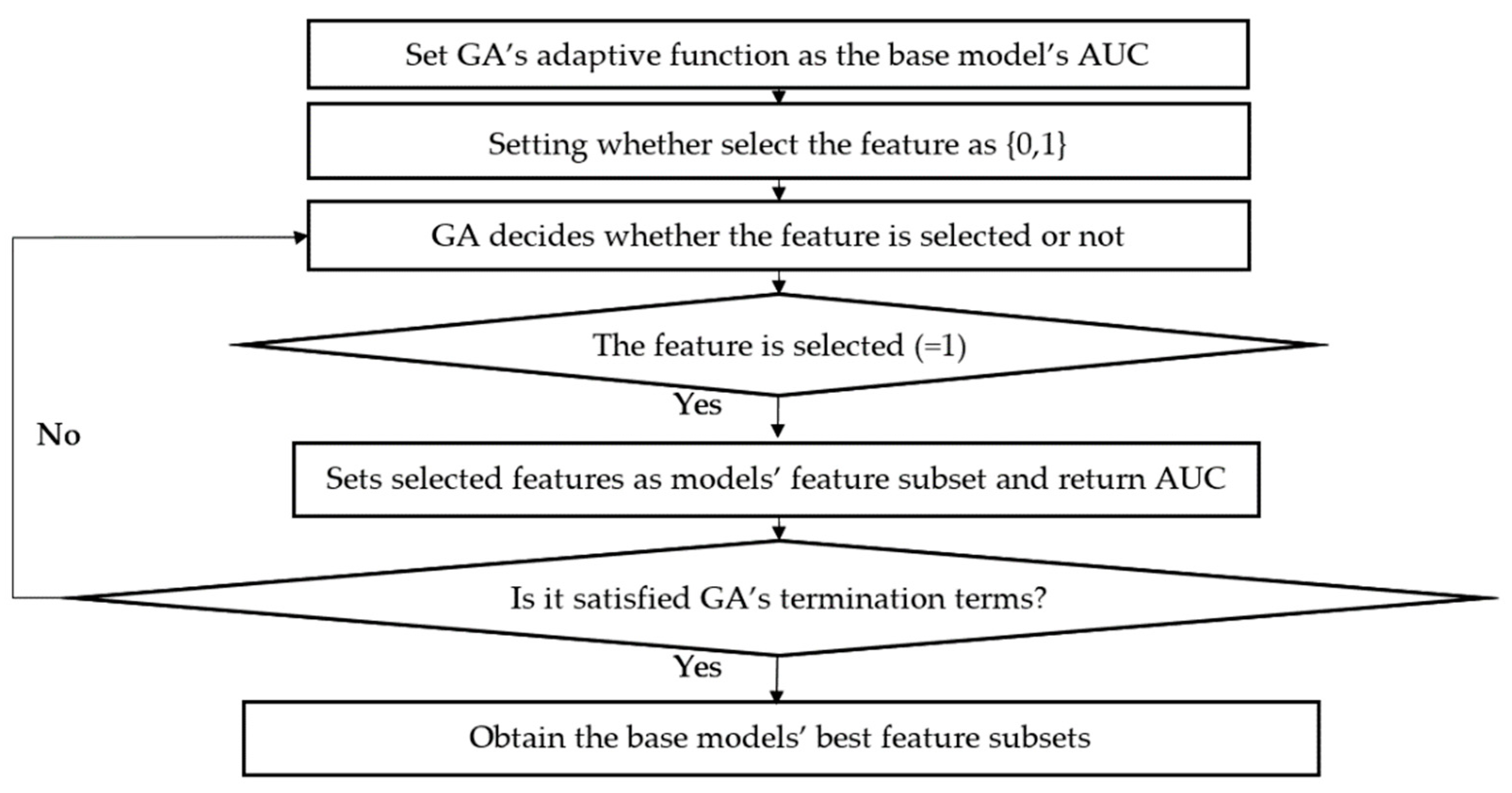
Based on the particle swarm optimization (PSO) feature selection algorithm proposed by Dai and Li [
48], this paper presents an adaptive feature selection algorithm. Considering that the RFE method only selects features from the perspective of feature importance, it does not take into account the promotion of feature subset on the model’s prediction ability. In this paper, the AUC returned by each base model is used as the adaptive function to be optimized, and the feature selection model is designed by using a genetic algorithm. The specific algorithm flow is shown in
Figure 2.
After the design of the adaptive feature selection algorithm, the model uses the instance hardness threshold to process the unbalanced data; LR, SVM, RF, LGB, MLP, and KNN are selected as the base models to be selected, and six sets of datasets are constructed with the sliding window method in
Figure 3. Then, 72 combinations (
) of different models, feature subsets, and datasets are combined with the adaptive feature improvement method to find the corresponding optimal feature subset (AUC is calculated by verification set when the algorithm is applied). Finally, taking 2018′s data as the verification set, the AUC of each combination is obtained, and the formula (1) is constructed (the model with the highest AUC is taken as a reference base).
3.3. Multi-Layer Ensemble Model
Based on the construction idea of the comparison coefficient of the base model (in the first layer of
Figure 1), this paper has screened out the basic model with strong expressive ability and a certain degree of difference. Because the corresponding dataset length and the feature subset are different, the model adopts a stacking framework to express each model’s advantages. For the second layer design of
Figure 1, traditional ensemble ideas often need the same length of datasets because of the different lengths. Simultaneously, some base models often fail to have the best “memory” ability, performance, and difference on the same dataset. Therefore, the model adopts the GBDT feature derivation framework and uses the LGB model to extract features further. The LGB model is used as the second layer of the stacking ensemble model, while the sample tree node information of LGB is extracted as the output of the second layer after the input of the predicted value of the base models. In the third layer of
Figure 1, all samples’ tree node information is used as the input of the LR model who has good robustness. The multi-layer stacking ensemble model integrates various datasets and feature subsets and uses the idea of deep learning to improve the prediction ability based on multiple strong learners. The memory ability of the machine learning model is explored as much as possible in the first layer. Then, the model’s generalization ability is improved by the second layer, and the risk of model over-fitting is reduced by using the third layer.
5. Conclusions
In this paper, based on equal weight comprehensive feature evaluation, GBDT, and stacking framework, the high stock dividend phenomenon’s existing prediction models are improved. A feature adaptive improved multi-layers ensemble model is proposed. This paper’s main contributions are as follows: (1) For the prediction of the high stock dividend phenomenon, the multi-layer stacking ensemble model constructed in this paper can predict the high stock dividend phenomenon accurately. Compared with the baseline model, the AUC is improved by 0.173, and the F1 score is increased by 0.303. (2) A complete comprehensive feature evaluation method and a model-based feature adaptive selection algorithm are proposed that can effectively select the feature subset which is more suitable for the corresponding model. (3) This paper proposes a multi-layer stacking ensemble model design, which can integrate models of different length datasets and feature subsets.
This paper’s practical significance is as follows: (1) From the investment perspective, this paper provides better prediction results than the existing methods, helping institutional investors better construct event-driven investment strategies on the high stock dividend issue. (2) From the perspective of policy, the existing policies are based on the previous scholars’ interpretation of the motivation behind the phenomenon of the high cash dividend. With the help of this paper’s high accuracy prediction model, regulators can conduct qualification screening for companies that may have a high stock dividend policy in the following year from November every year.
Although the model proposed in this paper has good prediction ability, there are still some limitations in this research, which will be possible future research directions. Firstly, this study uses the equal weight comprehensive feature evaluation method to filter the features that predict the “high stock dividend” phenomenon. Selected features increase the model’s information input consistency, but their interpretability is not provided. Feature interpretation under the stacking framework will be one of our future research works. Secondly, because the “high stock dividend” dataset is highly unbalanced in the securities market, the number of “high stock dividend” listed companies is far fewer than other listed companies. This current situation limits the predictive ability of the model. Some sampling methods have been used in this study’s data processing and have played some role in the improvement of model training. However, the research of this problem still requires better data balancing processing methods. Studying the sample structure of unbalanced data is also our future research agenda.