Minimum Message Length in Hybrid ARMA and LSTM Model Forecasting
Abstract
1. Introduction
2. ARIMA Modeling
3. Minimum Message Length
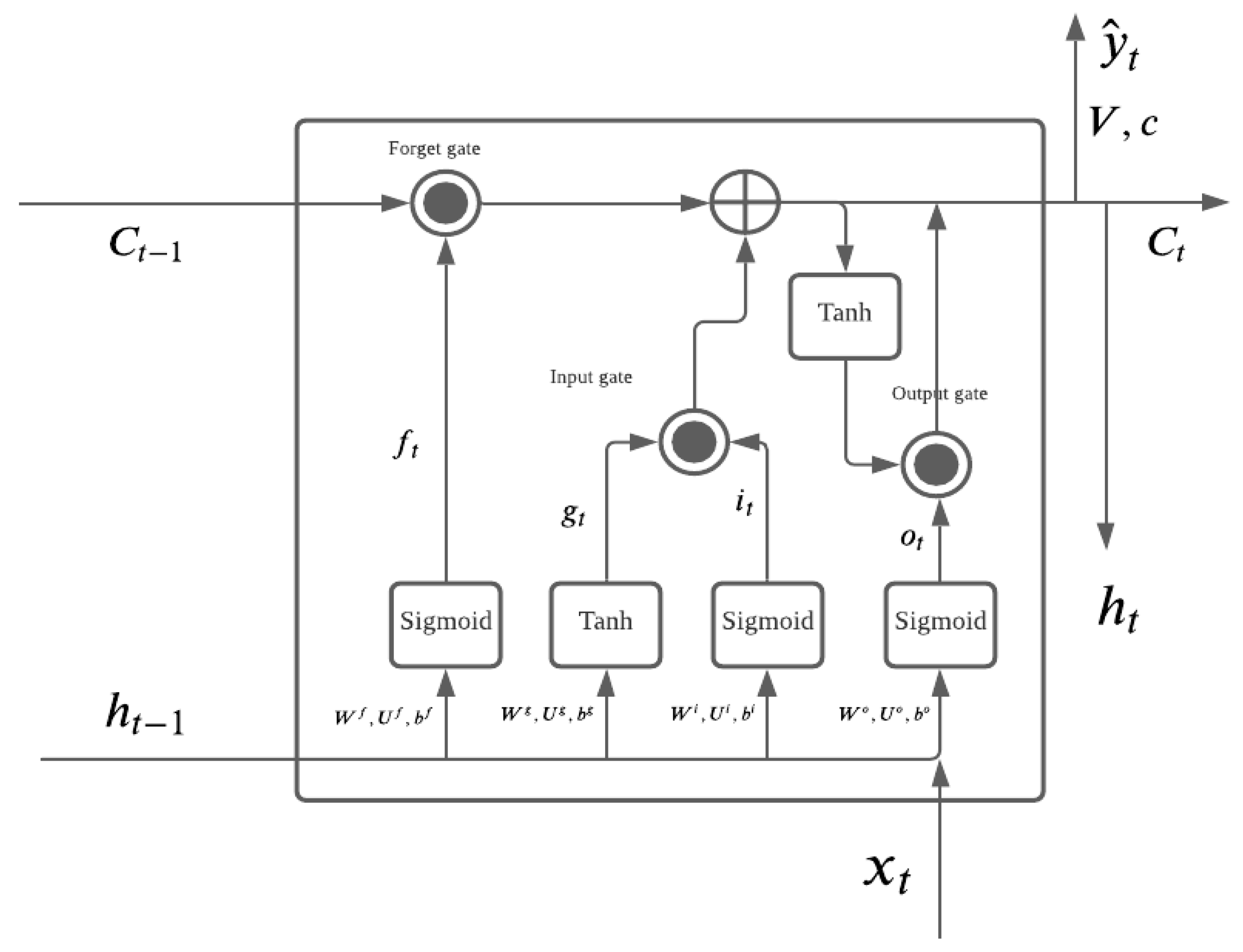
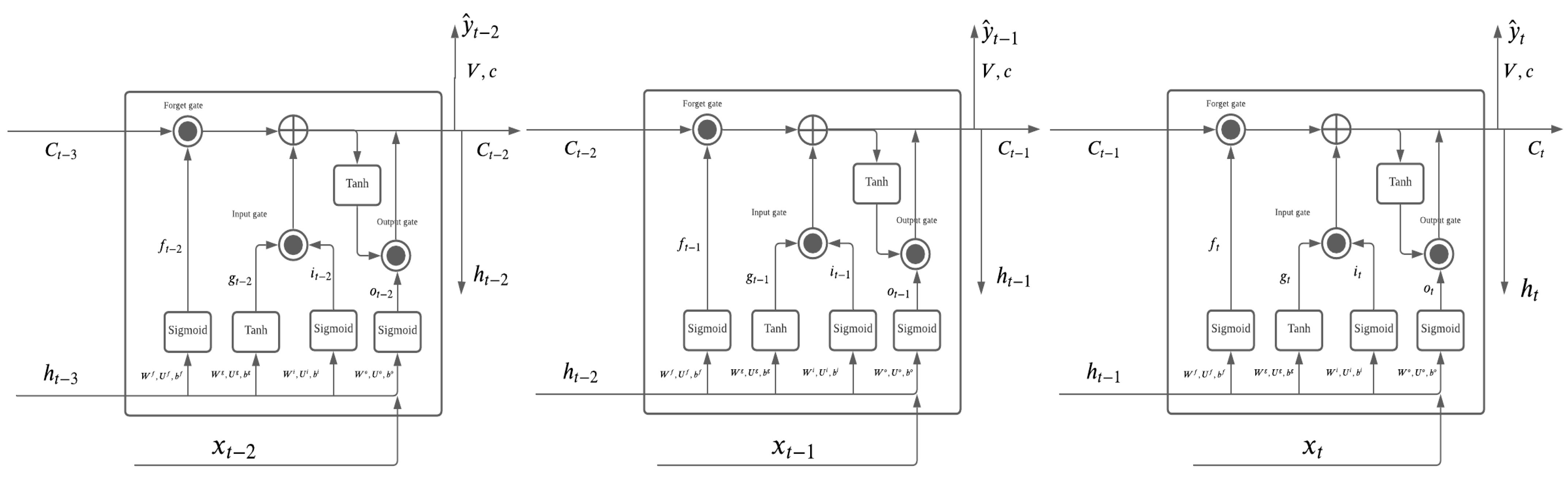
4. Long Short-Term Memory (LSTM)
- Forget gate: ;
- Input gate: ;
- Output gate: .
5. Hybrid ARMA-LSTM Model
| Algorithm 1 Algorithm 1 with the LSTM Model [17]. |
| Require: number of epochs = 10 while MA(q) order in order set selected by MML, AIC, BIC, and HQ do model.add(LSTM(30, return_sequences=True, input_shape=(q, 1))) model.add(LSTM(30, return_sequences=True)) model.add(LSTM(30)) model.add(Dense(1)) |
| Algorithm 2 Algorithm 2 with the Hybrid ARMA-LSTM Model. |
| Require: number of data n ≥ 0 while N ≤ number of different simulations do while n ≤ number of dataset in simulation do while i ∈ MA orders selected from MML, AIC, BIC, and HQ do if i ≠ 0 then Train LSTM model by the residuals of ARMA model Rolling forecast the residual by LSTM Calculate root mean squared error by Yt+1 else if i = 0 then Calculate root mean squared error by forecast from ARMA only |
6. Experiments
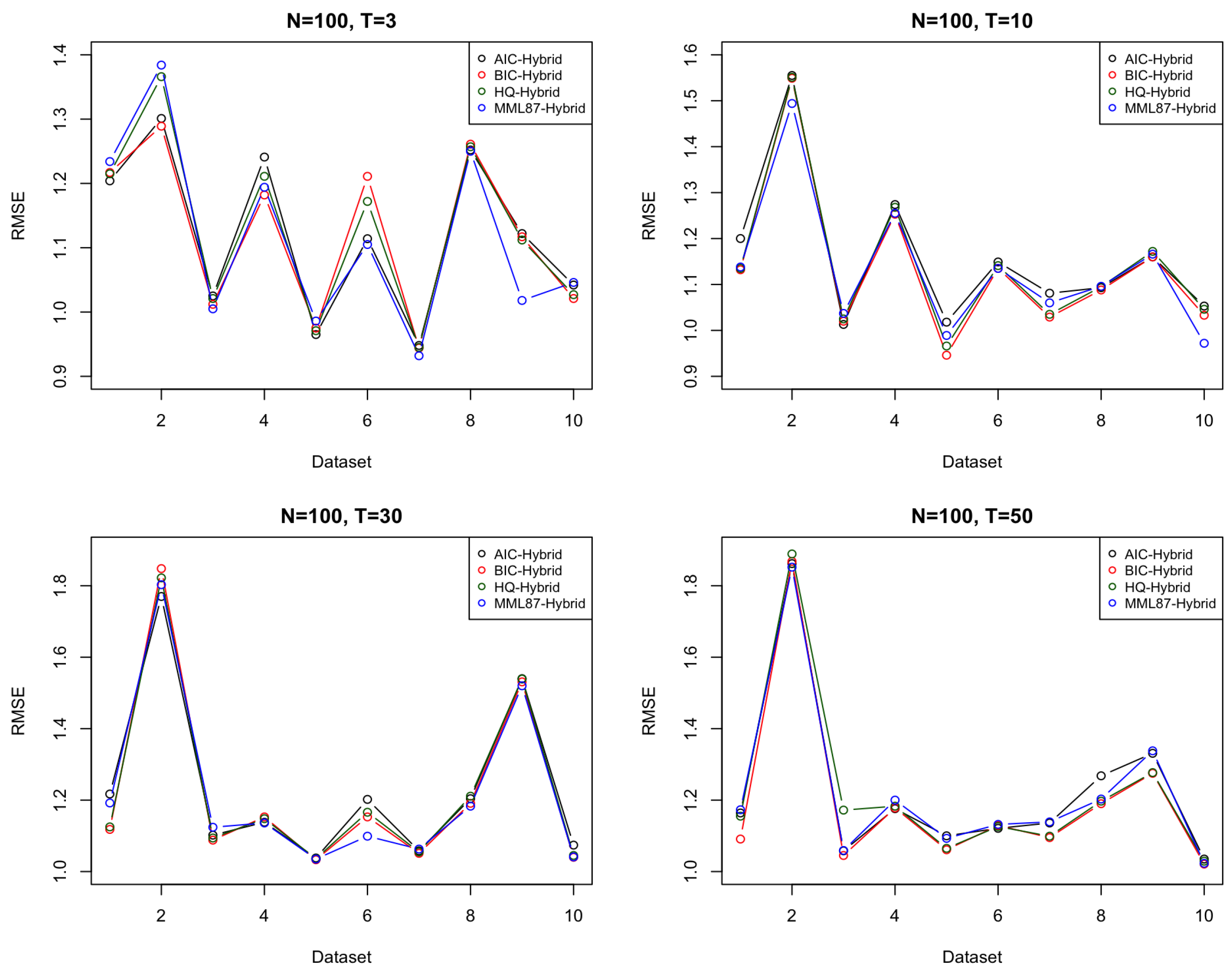
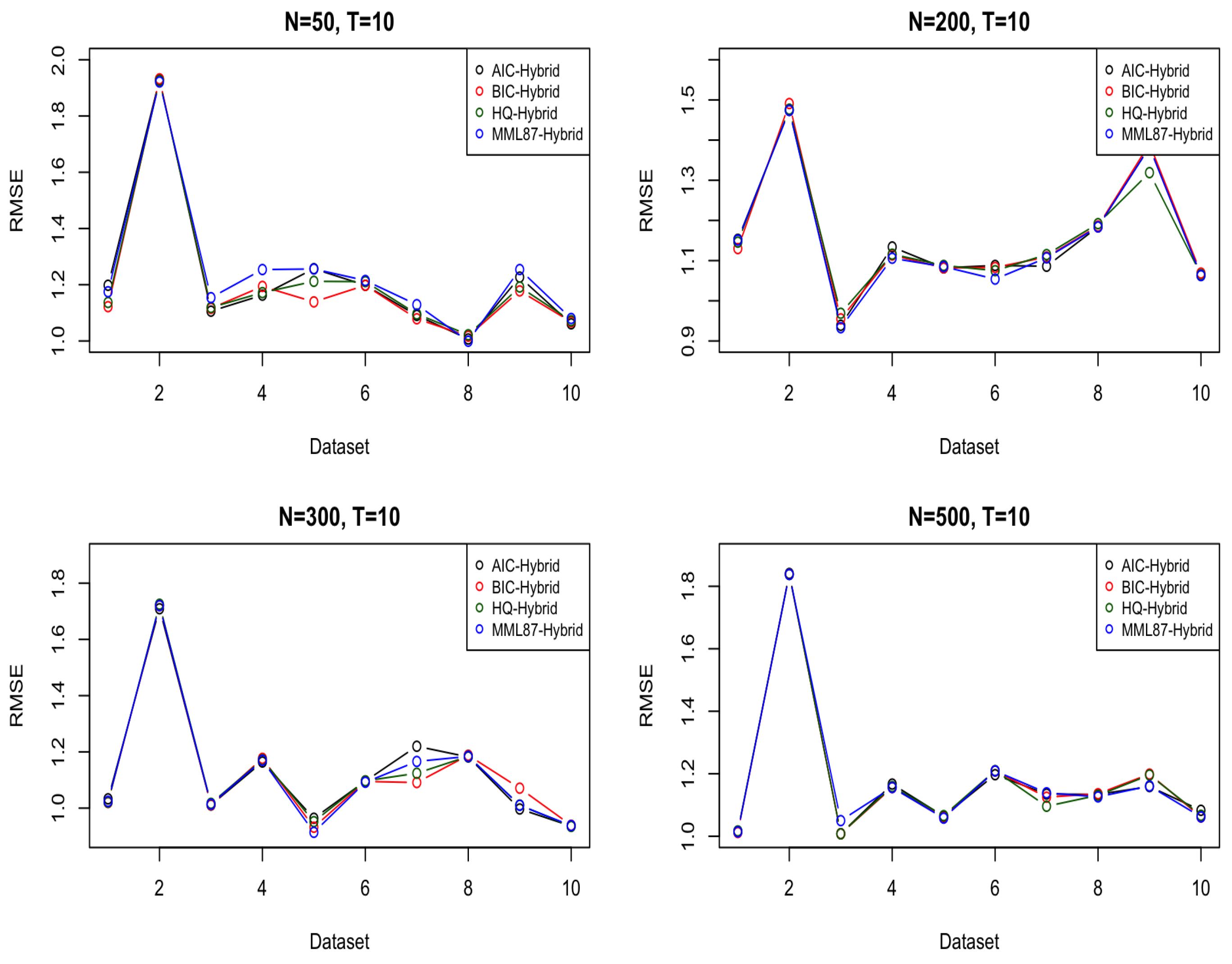
6.1. Simulated Dataset(s)
6.2. Financial Data-and Extension to ARIMA Models
6.3. PM2.5 Pollution Data
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 0.982 (0.646) | 1.108 (0.529) | 1.112 (0.499) | 1.033 (0.469) | 1.204 (0.308) | 1.217 (0.502) | 1.215 (0.511) | 1.234 (0.7) | |
| 1.133 (0.592) | 1.053 (0.669) | 1.172 (0.601) | 1.166 (0.635) | 1.301 (0.922) | 1.289 (0.95) | 1.366 (0.862) | 1.384 (0.838) | |
| 1.027 (0.423) | 1.024 (0.421) | 1.029 (0.445) | 1.023 (0.418) | 1.025 (0.408) | 1.012 (0.376) | 1.021 (0.411) | 1.005 (0.48) | |
| 1.333 (0.793) | 1.278 (0.841) | 1.286 (0.879) | 1.271 (0.848) | 1.241 (0.745) | 1.182 (0.711) | 1.211 (0.735) | 1.194 (0.674) | |
| 0.955 (0.377) | 0.956 (0.377) | 0.951 (0.375) | 0.944 (0.37) | 0.965 (0.341) | 0.975 (0.35) | 0.971 (0.351) | 0.986 (0.426) | |
| 1.293 (0.331) | 1.241 (0.296) | 1.245 (0.307) | 1.238 (0.296) | 1.114 (0.284) | 1.211 (0.266) | 1.172 (0.269) | 1.105 (0.259) | |
| 0.901 (0.483) | 0.916 (0.448) | 0.913 (0.451) | 0.871 (0.398) | 0.948 (0.397) | 0.944 (0.41) | 0.945 (0.413) | 0.932 (0.442) | |
| 1.207 (0.539) | 1.226 (0.515) | 1.224 (0.531) | 1.206 (0.513) | 1.252 (0.777) | 1.261 (0.778) | 1.257 (0.792) | 1.251 (0.772) | |
| 1.006 (0.54) | 0.907 (0.626) | 0.911 (0.642) | 0.903 (0.578) | 1.122 (0.538) | 1.117 (0.553) | 1.112 (0.564) | 1.018 (0.467) | |
| 1.026 (0.583) | 1.052 (0.553) | 1.054 (0.587) | 1.061 (0.559) | 1.042 (0.559) | 1.021 (0.592) | 1.027 (0.566) | 1.046 (0.53) | |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 1.234 (0.178) | 1.208 (0.165) | 1.206 (0.167) | 1.221 (0.293) | 1.201 (0.404) | 1.132 (0.184) | 1.135 (0.188) | 1.138 (0.317) | |
| 1.571 (0.375) | 1.553 (0.386) | 1.556 (0.391) | 1.398 (0.304) | 1.555 (1.109) | 1.549 (1.125) | 1.551 (1.123) | 1.494 (0.834) | |
| 1.025 (0.194) | 1.041 (0.203) | 1.044 (0.216) | 1.043 (0.193) | 1.013 (0.174) | 1.02 (0.182) | 1.025 (0.174) | 1.037 (0.265) | |
| 1.353 (0.438) | 1.327 (0.373) | 1.322 (0.391) | 1.325 (0.368) | 1.274 (0.213) | 1.257 (0.206) | 1.268 (0.211) | 1.255 (0.205) | |
| 0.947 (0.194) | 0.895 (0.129) | 0.918 (0.157) | 0.901 (0.134) | 1.018 (0.135) | 0.946 (0.116) | 0.966 (0.151) | 0.989 (0.154) | |
| 0.978 (0.266) | 1.06 (0.239) | 1.065 (0.225) | 1.048 (0.226) | 1.149 (0.328) | 1.137 (0.338) | 1.141 (0.352) | 1.135 (0.328) | |
| 1.083 (0.206) | 1.059 (0.2) | 1.063 (0.218) | 1.075 (0.179) | 1.081 (0.261) | 1.029 (0.179) | 1.035 (0.219) | 1.061 (0.128) | |
| 1.121 (0.192) | 1.112 (0.17) | 1.124 (0.186) | 1.104 (0.174) | 1.093 (0.212) | 1.088 (0.191) | 1.095 (0.252) | 1.096 (0.181) | |
| 1.279 (0.322) | 1.244 (0.296) | 1.264 (0.251) | 1.242 (0.29) | 1.169 (0.335) | 1.167 (0.327) | 1.172 (0.335) | 1.166 (0.306) | |
| 0.903 (0.078) | 0.867 (0.067) | 0.882 (0.059) | 0.877 (0.074) | 1.053 (0.231) | 1.033 (0.192) | 1.046 (0.188) | 0.972 (0.126) | |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 1.263 (0.167) | 1.252 (0.156) | 1.253 (0.173) | 1.256 (0.159) | 1.217 (0.295) | 1.118 (0.119) | 1.125 (0.133) | 1.192 (0.247) | |
| 2.641 (0.905) | 2.554 (0.838) | 2.631 (0.972) | 2.694 (0.961) | 1.771 (1.135) | 1.848 (0.739) | 1.822 (0.959) | 1.803 (1.373) | |
| 1.221 (0.139) | 1.186 (0.096) | 1.199 (0.121) | 1.184 (0.102) | 1.102 (0.084) | 1.088 (0.083) | 1.094 (0.089) | 1.124 (0.101) | |
| 1.044 (0.091) | 1.145 (0.108) | 1.093 (0.117) | 1.041 (0.088) | 1.138 (0.255) | 1.153 (0.211) | 1.148 (0.262) | 1.136 (0.256) | |
| 1.086 (0.181) | 1.066 (0.19) | 1.073 (0.195) | 1.061 (0.182) | 1.038 (0.172) | 1.036 (0.171) | 1.036 (0.188) | 1.035 (0.145) | |
| 1.112 (0.295) | 1.096 (0.309) | 1.139 (0.331) | 1.101 (0.306) | 1.202 (0.38) | 1.153 (0.328) | 1.166 (0.369) | 1.099 (0.264) | |
| 1.053 (0.22) | 1.038 (0.189) | 1.044 (0.167) | 1.035 (0.185) | 1.058 (0.14) | 1.051 (0.124) | 1.055 (0.139) | 1.063 (0.152) | |
| 1.263 (0.2) | 1.247 (0.194) | 1.251 (0.229) | 1.238 (0.21) | 1.204 (0.133) | 1.191 (0.114) | 1.211 (0.138) | 1.183 (0.152) | |
| 1.613 (0.27) | 1.679 (0.301) | 1.669 (0.343) | 1.599 (0.342) | 1.541 (0.884) | 1.531 (0.609) | 1.539 (0.915) | 1.521 (0.848) | |
| 1.092 (0.132) | 1.047 (0.234) | 1.052 (0.337) | 1.047 (0.114) | 1.074 (0.144) | 1.041 (0.117) | 1.045 (0.196) | 1.041 (0.115) | |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 1.189 (0.217) | 1.191 (0.228) | 1.193 (0.221) | 1.182 (0.222) | 1.164 (0.304) | 1.091 (0.212) | 1.155 (0.292) | 1.173 (0.241) | |
| 2.307 (0.458) | 2.308 (0.457) | 2.305 (0.464) | 2.298 (0.466) | 1.862 (1.169) | 1.868 (1.16) | 1.889 (1.171) | 1.852 (1.073) | |
| 1.113 (0.087) | 1.092 (0.103) | 1.095 (0.107) | 1.094 (0.104) | 1.058 (0.073) | 1.045 (0.096) | 1.172 (0.225) | 1.059 (0.139) | |
| 1.191 (0.096) | 1.189 (0.103) | 1.192 (0.107) | 1.191 (0.1) | 1.176 (0.24) | 1.178 (0.259) | 1.183 (0.285) | 1.201 (0.289) | |
| 1.094 (0.159) | 1.093 (0.157) | 1.095 (0.156) | 1.097 (0.155) | 1.101 (0.192) | 1.061 (0.144) | 1.065 (0.177) | 1.093 (0.115) | |
| 1.127 (0.06) | 1.123 (0.055) | 1.129 (0.057) | 1.125 (0.058) | 1.121 (0.134) | 1.129 (0.155) | 1.126 (0.143) | 1.132 (0.153) | |
| 1.188 (0.182) | 1.189 (0.188) | 1.185 (0.187) | 1.192 (0.186) | 1.136 (0.137) | 1.095 (0.181) | 1.099 (0.173) | 1.139 (0.113) | |
| 1.232 (0.165) | 1.221 (0.133) | 1.222 (0.137) | 1.212 (0.134) | 1.268 (0.457) | 1.19 (0.269) | 1.197 (0.234) | 1.203 (0.319) | |
| 1.593 (0.304) | 1.521 (0.199) | 1.533 (0.216) | 1.528 (0.209) | 1.331 (0.428) | 1.275 (0.234) | 1.277 (0.214) | 1.338 (0.383) | |
| 1.051 (0.083) | 1.033 (0.064) | 1.029 (0.096) | 1.032 (0.063) | 1.035 (0.055) | 1.021 (0.067) | 1.029 (0.077) | 1.023 (0.069) | |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 1.068 (0.147) | 1.071 (0.118) | 1.073 (0.125) | 1.067 (0.115) | 1.198 (0.222) | 1.122 (0.305) | 1.137 (0.336) | 1.175 (0.259) | |
| 1.994 (0.655) | 1.994 (0.655) | 2.056 (0.692) | 2.04 (0.705) | 1.93 (1.553) | 1.932 (1.563) | 1.926 (1.572) | 1.921 (1.566) | |
| 1.242 (0.213) | 1.242 (0.213) | 1.274 (0.252) | 1.235 (0.17) | 1.106 (0.193) | 1.116 (0.196) | 1.119 (0.189) | 1.154 (0.278) | |
| 1.185 (0.355) | 1.183 (0.359) | 1.196 (0.361) | 1.232 (0.476) | 1.163 (0.386) | 1.194 (0.499) | 1.172 (0.534) | 1.254 (0.601) | |
| 1.348 (0.557) | 1.254 (0.604) | 1.269 (0.661) | 1.304 (0.575) | 1.257 (0.499) | 1.139 (0.605) | 1.212 (0.657) | 1.256 (0.449) | |
| 1.283 (0.234) | 1.283 (0.234) | 1.281 (0.265) | 1.291 (0.233) | 1.198 (0.27) | 1.198 (0.27) | 1.211 (0.298) | 1.215 (0.285) | |
| 1.263 (0.461) | 1.251 (0.469) | 1.288 (0.477) | 1.044 (0.172) | 1.091 (0.264) | 1.079 (0.27) | 1.096 (0.288) | 1.129 (0.243) | |
| 0.987 (0.132) | 0.987 (0.132) | 0.989 (0.132) | 0.989 (0.137) | 1.007 (0.137) | 1.017 (0.126) | 1.022 (0.139) | 0.999 (0.138) | |
| 1.533 (0.457) | 1.426 (0.535) | 1.454 (0.561) | 1.464 (0.509) | 1.227 (0.442) | 1.178 (0.445) | 1.192 (0.496) | 1.254 (0.434) | |
| 1.101 (0.153) | 1.098 (0.151) | 1.111 (0.186) | 1.137 (0.185) | 1.061 (0.168) | 1.068 (0.175) | 1.072 (0.183) | 1.08 (0.117) | |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 1.244 (0.365) | 1.277 (0.42) | 1.286 (0.417) | 1.248 (0.404) | 1.153 (0.381) | 1.13 (0.376) | 1.146 (0.392) | 1.151 (0.353) | |
| 1.359 (0.445) | 1.359 (0.445) | 1.366 (0.462) | 1.359 (0.445) | 1.474 (0.813) | 1.491 (0.882) | 1.477 (0.893) | 1.474 (0.813) | |
| 0.927 (0.183) | 0.915 (0.172) | 0.916 (0.185) | 0.92 (0.182) | 0.939 (0.126) | 0.955 (0.15) | 0.969 (0.163) | 0.933 (0.128) | |
| 1.184 (0.41) | 1.191 (0.398) | 1.193 (0.366) | 1.189 (0.402) | 1.134 (0.368) | 1.114 (0.393) | 1.116 (0.407) | 1.106 (0.37) | |
| 1.137 (0.347) | 1.136 (0.347) | 1.129 (0.351) | 1.117 (0.355) | 1.082 (0.314) | 1.082 (0.316) | 1.088 (0.361) | 1.085 (0.325) | |
| 0.915 (0.198) | 1.038 (0.08) | 1.011 (0.081) | 0.991 (0.093) | 1.088 (0.184) | 1.083 (0.172) | 1.075 (0.199) | 1.054 (0.161) | |
| 1.199 (0.558) | 1.166 (0.557) | 1.174 (0.531) | 1.19 (0.562) | 1.086 (0.591) | 1.109 (0.507) | 1.115 (0.691) | 1.107 (0.732) | |
| 1.108 (0.196) | 1.101 (0.191) | 1.132 (0.615) | 1.129 (0.24) | 1.184 (0.358) | 1.186 (0.359) | 1.192 (0.379) | 1.184 (0.36) | |
| 1.581 (0.481) | 1.584 (0.475) | 1.584 (0.422) | 1.586 (0.48) | 1.383 (0.83) | 1.391 (0.802) | 1.396 (0.811) | 1.382 (0.832) | |
| 1.123 (0.263) | 1.101 (0.174) | 1.107 (0.155) | 1.101 (0.174) | 1.063 (0.234) | 1.069 (0.133) | 1.065 (0.129) | 1.063 (0.128) | |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 1.024 (0.312) | 1.028 (0.332) | 1.029 (0.321) | 1.031 (0.322) | 1.033 (0.316) | 1.02 (0.27) | 1.021 (0.291) | 1.024 (0.32) | |
| 2.008 (1.123) | 1.995 (1.024) | 1.996 (1.031) | 1.988 (1.028) | 1.709 (0.918) | 1.72 (0.896) | 1.725 (0.812) | 1.72 (0.854) | |
| 1.022 (0.144) | 1.025 (0.138) | 1.027 (0.132) | 1.016 (0.133) | 1.011 (0.125) | 1.012 (0.121) | 1.017 (0.126) | 1.014 (0.297) | |
| 1.172 (0.398) | 1.168 (0.383) | 1.171 (0.326) | 1.166 (0.384) | 1.164 (0.422) | 1.177 (0.443) | 1.172 (0.461) | 1.17 (0.413) | |
| 0.886 (0.198) | 0.868 (0.205) | 0.882 (0.217) | 0.865 (0.215) | 0.964 (0.261) | 0.932 (0.183) | 0.952 (0.191) | 0.914 (0.188) | |
| 1.07 (0.408) | 1.068 (0.412) | 1.065 (0.407) | 1.059 (0.401) | 1.096 (0.284) | 1.095 (0.289) | 1.097 (0.277) | 1.092 (0.284) | |
| 1.215 (0.445) | 1.191 (0.468) | 1.194 (0.462) | 1.184 (0.464) | 1.22 (0.621) | 1.091 (0.42) | 1.124 (0.468) | 1.166 (0.453) | |
| 1.191 (0.338) | 1.167 (0.308) | 1.172 (0.311) | 1.162 (0.278) | 1.182 (0.427) | 1.188 (0.473) | 1.184 (0.113) | 1.184 (0.433) | |
| 1.169 (0.225) | 1.159 (0.216) | 1.161 (0.232) | 1.152 (0.216) | 0.997 (0.131) | 1.071 (0.213) | 1.011 (0.159) | 1.01 (0.146) | |
| 0.874 (0.25) | 0.846 (0.249) | 0.852 (0.297) | 0.844 (0.247) | 0.936 (0.213) | 0.939 (0.197) | 0.935 (0.199) | 0.938 (0.196) | |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Order of Stationary ARMA | ARMA | ARMA-LSTM | ||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| 0.988 (0.229) | 0.966 (0.233) | 0.967 (0.252) | 0.968 (0.232) | 1.016 (0.178) | 1.012 (0.182) | 1.017 (0.169) | 1.014 (0.179) | |
| 1.546 (0.728) | 1.549 (0.713) | 1.552 (0.736) | 1.562 (0.703) | 1.841 (0.915) | 1.838 (0.875) | 1.838 (0.876) | 1.838 (0.877) | |
| 1.002 (0.37) | 1.017 (0.349) | 1.017 (0.355) | 1.016 (0.351) | 1.008 (0.329) | 1.008 (0.325) | 1.008 (0.334) | 1.05 (0.349) | |
| 1.156 (0.188) | 1.165 (0.176) | 1.163 (0.182) | 1.165 (0.176) | 1.167 (0.337) | 1.156 (0.355) | 1.159 (0.363) | 1.156 (0.355) | |
| 1.091 (0.175) | 1.093 (0.18) | 1.099 (0.175) | 1.09 (0.176) | 1.064 (0.225) | 1.06 (0.157) | 1.066 (0.173) | 1.058 (0.22) | |
| 1.23 (0.372) | 1.235 (0.364) | 1.235 (0.364) | 1.235 (0.364) | 1.197 (0.365) | 1.209 (0.393) | 1.21 (0.378) | 1.209 (0.393) | |
| 1.041 (0.272) | 1.07 (0.25) | 1.069 (0.261) | 1.063 (0.257) | 1.135 (0.342) | 1.053 (0.239) | 1.096 (0.298) | 1.139 (0.343) | |
| 1.253 (0.265) | 1.256 (0.265) | 1.261 (0.273) | 1.255 (0.266) | 1.134 (0.218) | 1.136 (0.214) | 1.131 (0.243) | 1.126 (0.235) | |
| 1.559 (0.363) | 1.551 (0.385) | 1.55 (0.374) | 1.541 (0.365) | 1.159 (0.331) | 1.199 (0.421) | 1.196 (0.411) | 1.161 (0.292) | |
| 1.073 (0.179) | 1.068 (0.188) | 1.071 (0.192) | 1.068 (0.188) | 1.083 (0.136) | 1.062 (0.167) | 1.067 (0.166) | 1.062 (0.167) | |
References
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. A comparison of ARIMA and LSTM in forecasting time series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar]
- Wallace, C.S.; Boulton, D.M. An information measure for classification. Comput. J. 1968, 11, 185–194. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The determination of the order of an autoregression. J. R. Stat. Soc. Ser. B Methodol. 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Dowe, D.L. Foreword re C. S. Wallace. Comput. J. 2008, 51, 523–560. [Google Scholar] [CrossRef]
- Wallace, C.S.; Dowe, D.L. Minimum message length and Kolmogorov complexity. Comput. J. 1999, 42, 270–283. [Google Scholar] [CrossRef]
- Wong, C.K.; Makalic, E.; Schmidt, D.F. Minimum message length inference of the Poisson and geometric models using heavy-tailed prior distributions. J. Math. Psychol. 2018, 83, 1–11. [Google Scholar] [CrossRef]
- Wallace, C.S.; Freeman, P.R. Estimation and inference by compact coding. J. R. Stat. Soc. Ser. B Methodol. 1987, 49, 240–252. [Google Scholar] [CrossRef]
- Fang, Z.; Dowe, D.L.; Peiris, S.; Rosadi, D. Minimum Message Length Autoregressive Moving Average Model Order Selection. arXiv 2021, arXiv:2110.03250. [Google Scholar]
- Schmidt, D.F. Minimum Message Length Inference of Autoregressive Moving Average Models. Ph.D. Thesis, Faculty of IT, Monash University, Melbourne, Australia, 2008. [Google Scholar]
- Fathi, O. Time Series Forecasting Using a Hybrid ARIMA and LSTM Model; Velvet Consulting: Paris, France, 2019. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis Prediction and Control; John Wiley and Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- De Gooijer, J.G.; Hyndman, R.J. 25 years of time series forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Wang, J.Q.; Du, Y.; Wang, J. LSTM based long-term energy consumption prediction with periodicity. Energy 2020, 197, 117197. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, Y.; Dai, F. A LSTM-based method for stock returns prediction: A case study of China stock market. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 2823–2824. [Google Scholar]
- Sak, M.; Dowe, D.L.; Ray, S. Minimum message length moving average time series data mining. In Proceedings of the In 2005 ICSC Congress on Computational Intelligence Methods and Applications, Istanbul, Turkey, 15–17 December 2005; 6p. [Google Scholar]
- Wallace, C.S. Statistical and Inductive Inference by Minimum Message Length; Springer: New York, NY, USA, 2005; pp. 93–100. [Google Scholar]
- Aho, K.; Derryberry, D.; Peterson, T. Model selection for ecologists: The worldviews of AIC and BIC. Ecology 2014, 95, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Grasa, A.A. Econometric Model Selection: A New Approach; Springer Science & Business Media: New York, NY, USA, 2013; Volume 16. [Google Scholar]
- Hernandez-Matamoros, A.; Fujita, H.; Hayashi, T.; Perez-Meana, H. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl. Soft Comput. 2020, 96, 106610. [Google Scholar] [CrossRef] [PubMed]
- Dissanayake, G.S.; Peiris, M.S.; Proietti, T. Fractionally differenced Gegenbauer processes with long memory: A review. Stat. Sci. 2018, 33, 413–426. [Google Scholar]
- Hunt, R.; Peiris, S.; Weber, N. A General Frequency Domain Estimation Method for Gegenbauer Processes. J. Time Ser. Econom. 2021, 13, 119–144. [Google Scholar]
- Dowe, D.L. MML, hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness. In Handbook of the Philosophy of Science; Volume 7: Philosophy of Statistics; Elsevier: New York, NY, USA, 2011; pp. 901–982. [Google Scholar]
- Baxter, R.A.; Dowe, D.L. Model selection in linear regression using the MML criterion. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 29–31 March 1994. [Google Scholar]
- Fitzgibbon, L.J.; Dowe, D.L.; Vahid, F. Minimum message length autoregressive model order selection. In Proceedings of the International Conference on Intelligent Sensing and Information Processing, Chennai, India, 4–7 January 2004; pp. 439–444. [Google Scholar]
- Schmidt, D.F. Minimum message length order selection and parameter estimation of moving average models. In Algorithmic Probability and Friends; Bayesian Prediction and Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2013; pp. 327–338. [Google Scholar]
- Wallace, C.S.; Dowe, D.L. Intrinsic classification by MML-the Snob program. In Proceedings of the 7th Australian Joint Conference on Artificial Intelligence World Scientific, Armidale, Australia, 1 January 1994; pp. 37–44. [Google Scholar]
- Wallace, C.S.; Dowe, D.L. MML clustering of multi-state, Poisson, von Mises circular and Gaussian distributions. Stat. Comput. 2000, 10, 73–83. [Google Scholar] [CrossRef]
- Dowe, D.L.; Allison, L.; Dix, T.I.; Hunter, L.; Wallace, C.S.; Edgoose, T. Circular clustering of protein dihedral angles by minimum message length. In Pacific Symposium on Biocomputing; World Scientific: Singapore, 1996; pp. 242–255. [Google Scholar]
- Oliver, J.J.; Dowe, D.L.; Wallace, C.S. Inferring decision graphs using the minimum message length principle. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, NSW, Australia, 16–18 November 1992; pp. 361–367. [Google Scholar]
- Tan, P.J.; Dowe, D.L. MML inference of decision graphs with multi-way joins and dynamic attributes. In Australasian Joint Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2003; pp. 269–281. [Google Scholar]
- Comley, J.W.; Dowe, D.L. General Bayesian networks and asymmetric languages. In Proceedings of the 2nd Hawaii International Conference on Statistics and Related Fields, Honolulu, HI, USA, 5–8 June 2003; 18p. [Google Scholar]
- Comley, J.W.; Dowe, D.L. Chapter 11: Minimum Message Length and Generalized Bayesian Nets with Asymmetric Languages. In Advances in Minimum Description Length: Theory and Applications; Grünwald, P.D., Myung, I.J., Pitt, M.A., Eds.; MIT Press: Cambridge, MA, USA, 2005; pp. 265–294. [Google Scholar]
- Saikrishna, V.; Dowe, D.L.; Ray, S. MML learning and inference of hierarchical Probabilistic Finite State Machines. In Applied Data Analytics: Principles and Applications; River Publishers: Aalborg, Denmark, 2020; pp. 291–325. [Google Scholar]
- Dowe, D.L.; Zaidi, N.A. Database normalization as a by-product of minimum message length inference. In Australasian Joint Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; pp. 82–91. [Google Scholar]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: New York, NY, USA, 2008; Volume 3. [Google Scholar]
- Solomonoff, R.J. Complexity-based induction systems: Comparisons and convergence theorems. IEEE Trans. Inf. Theory 1978, 24, 422–432. [Google Scholar] [CrossRef]
- Dowe, D.L. Introduction to Ray Solomonoff 85th memorial conference. In Algorithmic Probability and Friends. Bayesian Prediction and Artificial Intelligence; LNAI 7070; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–36. [Google Scholar]
- Makalic, E.; Allison, L.; Dowe, D.L. MML inference of single-layer neural networks. In Proceedings of the 3rd IASTED International Conferences Artificial Intelligence and Applications, Benalmadena, Spain, 8–10 September 2003; pp. 636–642. [Google Scholar]
- Fitzgibbon, L.J.; Dowe, D.L.; Allison, L. Univariate polynomial inference by Monte Carlo message length approximation. In International Conference Machine Learning; ICML: Sydney, Australia, 2002; pp. 147–154. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Chong, E.; Han, C.; Park, F.C. Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Syst. Appl. 2017, 83, 187–205. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, L.; Ren, Y.; Suganthan, P.N.; Amaratunga, G. Ensemble deep learning for regression and time series forecasting. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Ensemble Learning (CIEL), Orlando, FL, USA, 9–12 December 2014; pp. 1–6. [Google Scholar]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, J.; Bu, H.; Wu, J. Sentiment-aware stock market prediction: A deep learning method. In Proceedings of the 2017 International Conference on Service Systems and Service Management, Dalian, China, 16–18 June 2017; pp. 1–6. [Google Scholar]
- Zhang, X.; Tan, Y. Deep stock ranker: A LSTM neural network model for stock selection. In International Conference on Data Mining and Big Data; Springer: Cham, Switzerland, 2018; pp. 614–623. [Google Scholar]
- Bukhari, A.H.; Raja, M.A.Z.; Sulaiman, M.; Islam, S.; Shoaib, M.; Kumam, P. Fractional neuro-sequential ARFIMA-LSTM for financial market forecasting. IEEE Access 2020, 8, 71326–71338. [Google Scholar] [CrossRef]
- Cheng, T.; Gao, J.; Linton, O. Nonparametric Predictive Regressions for Stock Return Prediction; Working Paper; University of Cambridge: Cambridge, UK, 2019. [Google Scholar]
- Gao, J. Modelling long-range-dependent Gaussian processes with application in continuous-time financial models. J. Appl. Probab. 2004, 41, 467–482. [Google Scholar] [CrossRef][Green Version]
- Fama, E.F.; French, K.R. Dividend Yields and Expected Stock Returns; University of Chicago Press: Chicago, IL, USA, 2021; pp. 568–595. [Google Scholar]
- Keim, D.B.; Stambaugh, R.F. Predicting returns in the stock and bond markets. J. Financ. Econom. 1986, 17, 357–390. [Google Scholar] [CrossRef]
- Dowe, D.L.; Korb, K.B. Conceptual difficulties with the efficient market hypothesis: Towards a naturalized economics. In Proceedings of the Information, Statistics and Induction in Science Conference, World Scientific, Melbourne, Australia, 20–23 August 1996; pp. 212–223. [Google Scholar]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, New York, NY, USA, 8–12 June 2018; pp. 95–104. [Google Scholar]

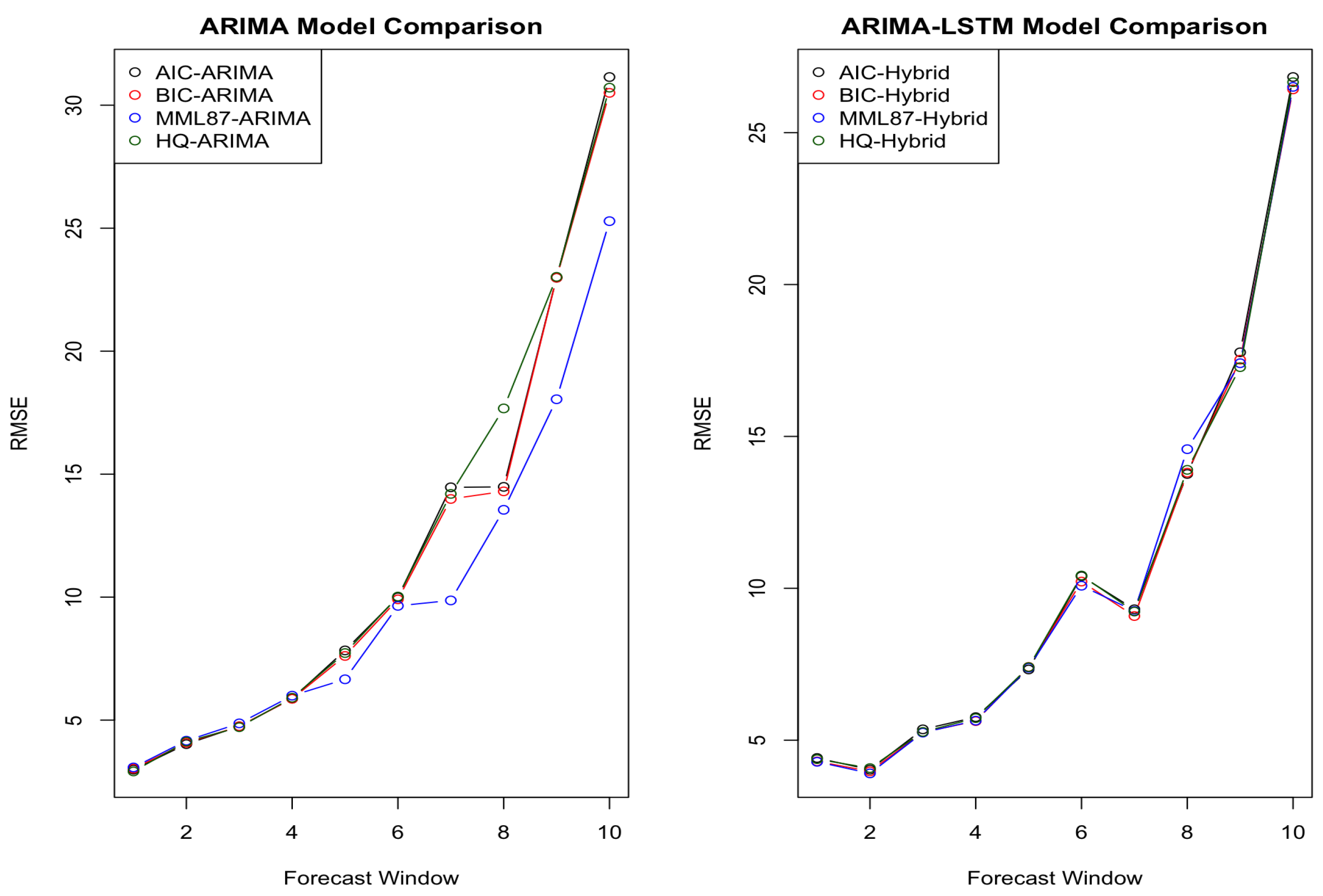
| No. of LSTM Time Steps | ||||
|---|---|---|---|---|
| 1 | 1.2519 | 1.3677 | 1.4962 | 1.3911 |
| 2 | 1.1794 | 1.2442 | 1.3863 | 1.2718 |
| 3 | 1.3372 | 1.6324 | 1.2256 | 1.3018 |
| 4 | 1.2195 | 1.2301 | 1.3284 | 1.3951 |
| 5 | 1.1341 | 1.6294 | 1.4276 | 1.4494 |
| Average of RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|
| ARMA | ARMA-LSTM | |||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| T = 3 | 1.086 | 1.076 | 1.090 | 1.072 | 1.121 | 1.123 | 1.134 | 1.115 |
| T = 10 | 1.149 | 1.136 | 1.144 | 1.121 | 1.159 | 1.136 | 1.143 | 1.134 |
| T = 30 | 1.338 | 1.331 | 1.340 | 1.325 | 1.234 | 1.221 | 1.224 | 1.220 |
| T = 50 | 1.308 | 1.296 | 1.297 | 1.295 | 1.225 | 1.195 | 1.219 | 1.221 |
| Average of RMSE (and Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| ARMA | ARMA-LSTM | |||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| N = 50 | 1.301 | 1.291 | 1.299 | 1.280 | 1.224 | 1.202 | 1.216 | 1.244 |
| N = 100 | 1.149 | 1.136 | 1.144 | 1.121 | 1.159 | 1.136 | 1.143 | 1.134 |
| N = 200 | 1.177 | 1.187 | 1.189 | 1.183 | 1.159 | 1.161 | 1.164 | 1.154 |
| N = 300 | 1.163 | 1.152 | 1.155 | 1.147 | 1.131 | 1.125 | 1.124 | 1.123 |
| N = 500 | 1.194 | 1.197 | 1.1984 | 1.196 | 1.180 | 1.173 | 1.179 | 1.181 |
| Mean | S.D | PACF1 | PACF2 | PACF3 | |
|---|---|---|---|---|---|
| AAPL | 66.440217 | 37.060808 | 0.996875 | 0.044454 | −0.004848 |
| BA | 258.704781 | 82.478194 | 0.995870 | −0.031231 | −0.061804 |
| CSCO | 40.585947 | 8.595774 | 0.994585 | 0.073202 | −0.016488 |
| GS | 227.095242 | 56.820929 | 0.993579 | 0.039741 | −0.043412 |
| IBM | 124.851224 | 10.369478 | 0.982339 | 0.070195 | −0.040622 |
| INTC | 46.269478 | 9.305502 | 0.992194 | 0.178757 | −0.053398 |
| JNJ | 130.715314 | 18.399352 | 0.993930 | 0.050988 | −0.031304 |
| JPM | 104.046116 | 24.467471 | 0.993854 | 0.067756 | −0.049235 |
| KO | 44.519034 | 6.089778 | 0.993828 | 0.031639 | −0.039178 |
| MMM | 173.550240 | 20.467854 | 0.991641 | 0.004475 | 0.026664 |
| Average of RMSE (& Standard Deviation) | ||||||||
|---|---|---|---|---|---|---|---|---|
| ARIMA | ARIMA-LSTM | |||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| T = 3 | 2.987 (3.446) | 3.027 (3.555) | 2.914 (3.567) | 3.075 (3.572) | 4.414 (4.75) | 4.302 (4.608) | 4.375 (4.757) | 4.289 (4.616) |
| T = 5 | 4.024 (5.091) | 4.077 (5.228) | 4.126 (5.218) | 4.163 (5.086) | 4.024 (5.45) | 3.966 (5.42) | 4.081 (5.739) | 3.907 (5.449) |
| T = 10 | 4.748 (4.707) | 4.747 (4.858) | 4.712 (4.815) | 4.868 (4.347) | 5.359 (5.429) | 5.261 (5.268) | 5.272 (5.443) | 5.249 (5.262) |
| T = 30 | 5.872 (6.797) | 5.867 (6.6) | 5.91 (6.576) | 5.994 (5.662) | 5.754 (4.822) | 5.628 (4.687) | 5.726 (4.776) | 5.643 (4.677) |
| T = 50 | 7.834 (7.511) | 7.609 (7.298) | 7.726 (7.269) | 6.659 (6.966) | 7.328 (6.787) | 7.411 (6.879) | 7.405 (6.789) | 7.384 (6.898) |
| T = 70 | 9.991 (9.491) | 9.909 (9.316) | 10.024 (9.173) | 9.645 (7.99) | 10.393 (8.048) | 10.221 (7.789) | 10.42 (8.061) | 10.085 (7.612) |
| T = 100 | 14.465 (17.187) | 13.991 (15.428) | 14.197 (13.637) | 9.866 (10.854) | 9.304 (9.256) | 9.087 (9.35) | 9.235 (9.396) | 9.253 (9.486) |
| T = 130 | 14.482 (9.714) | 14.301 (10.571) | 17.672 (13.139) | 13.551 (10.238) | 13.768 (10.598) | 13.811 (11.124) | 13.9 (11.516) | 14.581 (10.972) |
| T = 150 | 22.985 (28.173) | 22.985 (28.077) | 23.021 (28.071) | 18.045 (17.856) | 17.778 (16.771) | 17.526 (16.582) | 17.98 (16.734) | 17.461 (15.931) |
| T = 200 | 31.144 (37.567) | 30.502 (38.314) | 30.712 (38.322) | 30.286 (32.564) | 26.831 (31.63) | 26.424 (31.547) | 26.662 (31.645) | 26.507 (31.59) |
| No. Steps | T = 3 | T = 5 | T = 30 | T = 10 | T = 50 | T = 70 | T = 100 | T = 130 | T = 150 | T = 200 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8.5789 | 10.1965 | 56.7817 | 104.3681 | 123.4805 | 119.2673 | 151.1338 | 107.2951 | 114.8106 | 73.2335 |
| 3 | 5.7604 | 3.5166 | 3.6097 | 13.325 | 10.6368 | 31.9361 | 33.4419 | 26.0112 | 31.5578 | 26.6354 |
| 5 | 4.0695 | 3.0575 | 8.5064 | 11.9009 | 15.5075 | 17.3077 | 19.0942 | 48.0012 | 30.0622 | 36.6099 |
| 7 | 3.9708 | 6.4145 | 10.6368 | 6.8547 | 13.2163 | 16.5474 | 19.0724 | 32.7076 | 20.5954 | 44.1875 |
| 10 | 5.3985 | 6.4576 | 5.9597 | 13.8295 | 16.0972 | 20.6271 | 12.8859 | 28.2251 | 28.2803 | 25.5409 |
| Average of RMSE & Standard Deviation | ||||||||
|---|---|---|---|---|---|---|---|---|
| ARIMA | ARIMA-LSTM | |||||||
| AIC | BIC | HQ | MML87 | AIC | BIC | HQ | MML87 | |
| T = 3 | 26.805 (7.496) | 26.689 (7.532) | 26.569 (7.545) | 23.104 (7.843) | 25.768 (7.833) | 23.066 (8.693) | 24.791 (7.883) | 22.965 (6.711) |
| T = 5 | 28.036 (6.986) | 27.538 (6.805) | 27.479 (7.186) | 23.478 (8.426) | 24.636 (8.518) | 22.309 (7.596) | 24.113 (8.584) | 21.666 (7.424) |
| T = 10 | 30.633 (12.679) | 31.502 (12.283) | 31.585 (12.518) | 30.074 (14.917) | 26.970 (10.502) | 27.566 (13.487) | 27.924 (10.107) | 25.102 (9.855) |
| T = 30 | 40.730 (14.001) | 40.788 (13.372) | 40.157 (14.195) | 37.989 (19.180) | 31.022 (11.409) | 29.382 (12.196) | 31.689 (14.124) | 28.572 (12.229) |
| T = 50 | 39.097 (4.238) | 38.662 (4.660) | 39.007 (4.232) | 42.986 (6.062) | 35.639 (5.599) | 33.335 (5.184) | 36.036 (6.339) | 40.568 (9.24) |
| T = 70 | 34.004 (4.223) | 33.551 (4.105) | 34.773 (3.514) | 32.030 (9.404) | 48.942 (12.377) | 45.305 (10.567) | 49.723 (12.068) | 42.987 (8.705) |
| T = 100 | 32.002 (2.434) | 32.444 (2.425) | 31.170 (2.865) | 37.925 (4.444) | 56.024 (13.199) | 51.543 (12.714) | 59.705 (13.435) | 49.513 (11.45) |
| T = 130 | 44.023 (2.583) | 44.162 (2.576) | 43.635 (2.836) | 43.802 (1.853) | 36.183 (7.184) | 33.716 (4.591) | 39.401 (8.488) | 46.496 (7.168) |
| T = 150 | 44.463 (1.612) | 44.736 (1.862) | 43.928 (1.773) | 41.150 (5.221) | 32.574 (6.211) | 31.225 (4.301) | 30.923 (6.598) | 33.584 (7.679) |
| T = 200 | 42.150 (2.620) | 42.372 (2.522) | 41.863 (2.787) | 43.75 (4.07) | 46.711 (13.86) | 43.721 (11.349) | 53.393 (12.458) | 46.363 (12.472) |
| No. Steps | T = 3 | T = 5 | T = 10 | T = 30 | T = 50 | T = 70 | T = 100 | T = 130 | T = 150 | T = 200 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3.0976 | 5.7806 | 16.5048 | 47.8431 | 53.7436 | 67.2412 | 81.7044 | 92.6897 | 73.4192 | 71.5536 |
| 3 | 4.4983 | 8.1565 | 17.0462 | 34.0492 | 36.3896 | 47.2558 | 64.68533 | 90.7986 | 78.9972 | 78.5648 |
| 5 | 4.7719 | 9.2208 | 18.7955 | 33.6065 | 50.4786 | 56.7465 | 59.3666 | 75.4321 | 102.0098 | 88.1695 |
| 7 | 5.9126 | 9.8355 | 15.3696 | 25.8551 | 38.6874 | 53.06845 | 50.962 | 87.998 | 92.101 | 101.2337 |
| 10 | 8.4289 | 11.4749 | 11.4479 | 38.3303 | 44.5138 | 65.6299 | 70.6415 | 74.6879 | 90.1211 | 84.0196 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Dowe, D.L.; Peiris, S.; Rosadi, D. Minimum Message Length in Hybrid ARMA and LSTM Model Forecasting. Entropy 2021, 23, 1601. https://doi.org/10.3390/e23121601
Fang Z, Dowe DL, Peiris S, Rosadi D. Minimum Message Length in Hybrid ARMA and LSTM Model Forecasting. Entropy. 2021; 23(12):1601. https://doi.org/10.3390/e23121601
Chicago/Turabian StyleFang, Zheng, David L. Dowe, Shelton Peiris, and Dedi Rosadi. 2021. "Minimum Message Length in Hybrid ARMA and LSTM Model Forecasting" Entropy 23, no. 12: 1601. https://doi.org/10.3390/e23121601
APA StyleFang, Z., Dowe, D. L., Peiris, S., & Rosadi, D. (2021). Minimum Message Length in Hybrid ARMA and LSTM Model Forecasting. Entropy, 23(12), 1601. https://doi.org/10.3390/e23121601






