Quantum–Classical Correspondence Principle for Heat Distribution in Quantum Brownian Motion
Abstract
1. Introduction
2. The Caldeira–Leggett Model and the Heat Statistics
2.1. The Caldeira–Leggett Model
2.2. The Quantum Fluctuating Heat in the Relaxation Process
3. Results of the Characteristic Function of Heat
3.1. Quantum–Classical Correspondence Principle for Heat Statics and the Exchange Fluctuation Theorem of Heat
3.2. Long-Time Limit
3.3. Weak/Strong Coupling Limit in Finite Time
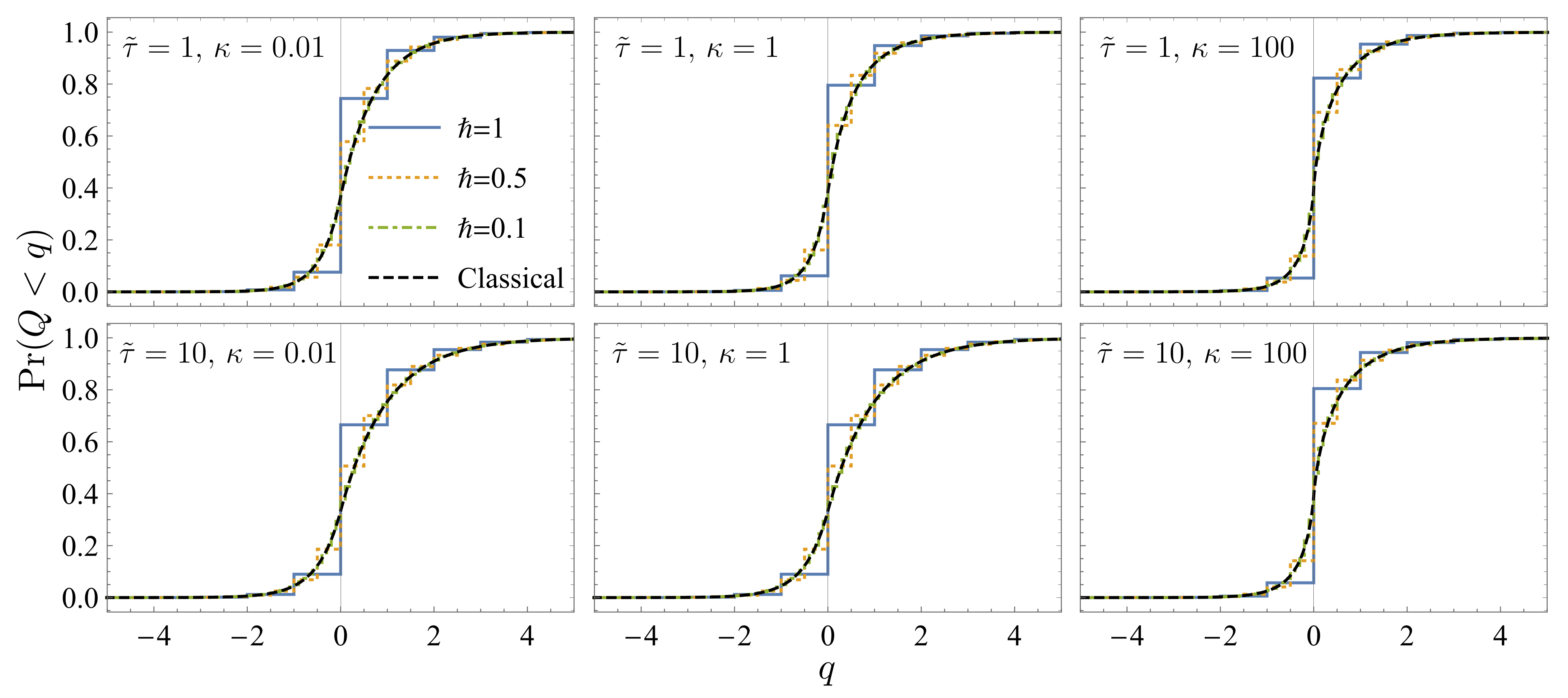
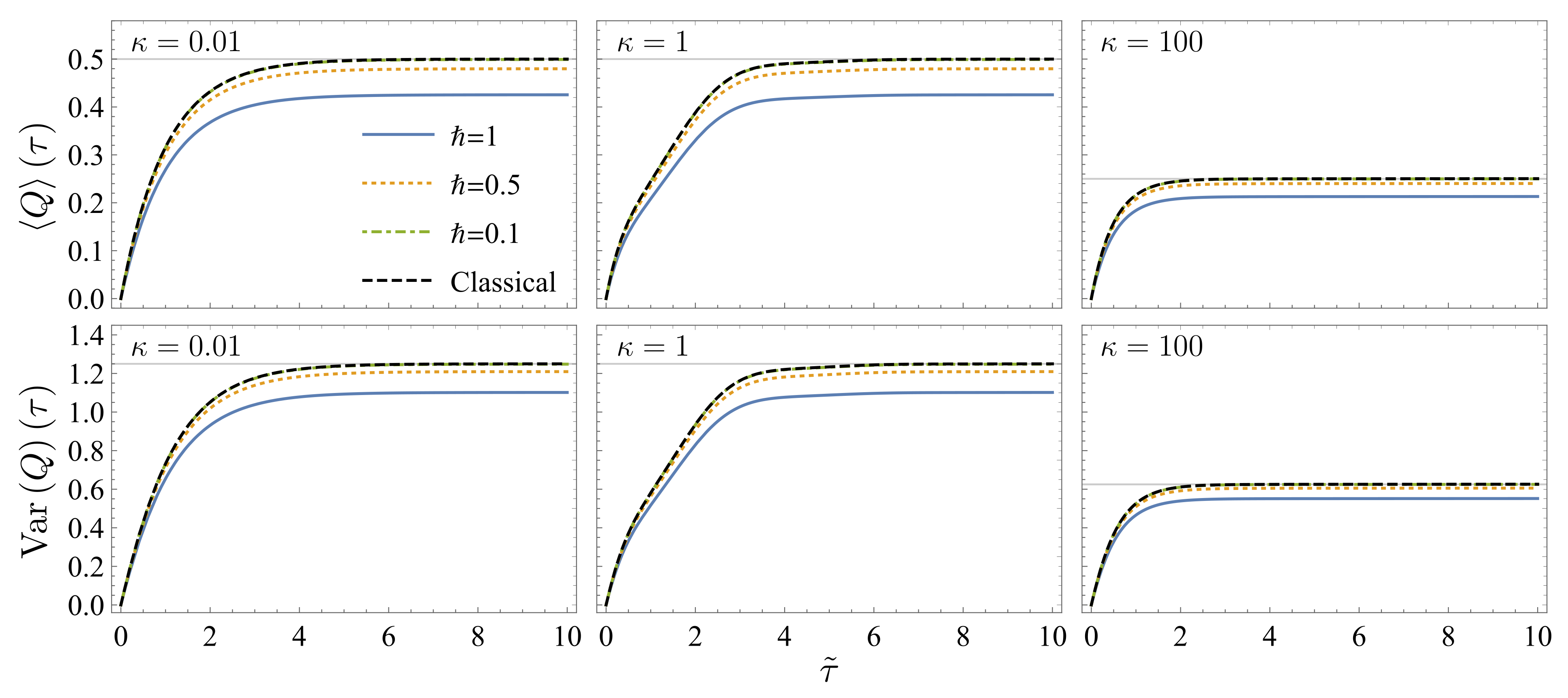
3.4. Numerical Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation to the Characteristic Function of Heat (17)
Appendix A.1.
Appendix A.2.
Appendix A.3. Calculation of the Integral
Appendix B. Classical Caldeira–Leggett Model
Appendix C. The Characteristic Function of Heat for the Classical Brownian Motion
Appendix C.1. The Long-Time Limit
Appendix C.2. The Underdamped Limit
Appendix C.3. The Overdamped Limit
Appendix D. The Characteristic Function of Heat for Complete Thermalization
References
- Gallavotti, G.; Cohen, E.G.D. Dynamical Ensembles in Nonequilibrium Statistical Mechanics. Phys. Rev. Lett. 1995, 74, 2694–2697. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C.; Wójcik, D.K. Classical and Quantum Fluctuation Theorems for Heat Exchange. Phys. Rev. Lett. 2004, 92, 230602. [Google Scholar] [CrossRef]
- Jarzynski, C. Equalities and Inequalities: Irreversibility and the Second Law of Thermodynamics at the Nanoscale. Annu. Rev. Condens. Matter Phys. 2011, 2, 329–351. [Google Scholar] [CrossRef]
- Sekimoto, K. Stochastic Energetics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Seifert, U. Entropy Production along a Stochastic Trajectory and an Integral Fluctuation Theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771–791. [Google Scholar] [CrossRef]
- Klages, R. Nonequilibrium Statistical Physics of Small Systems: Fluctuation Relations and Beyond; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nanoscale thermodynamics. Nat Commun 2013, 4, 2059. [Google Scholar] [CrossRef]
- Ciliberto, S. Experiments in Stochastic Thermodynamics: Short History and Perspectives. Phys. Rev. X 2017, 7, 021051. [Google Scholar] [CrossRef]
- Tasaki, H. Jarzynski Relations for Quantum Systems and Some Applications. arXiv 2000, arXiv:cond-mat.stat-mech/cond-mat/0009244. [Google Scholar]
- Kurchan, J. A Quantum Fluctuation Theorem. arXiv 2000, arXiv:cond-mat.stat-mech/cond-mat/0007360. [Google Scholar]
- Talkner, P.; Lutz, E.; Hänggi, P. Fluctuation theorems: Work is not an observable. Phys. Rev. E 2007, 75, 050102. [Google Scholar] [CrossRef] [PubMed]
- Deffner, S.; Lutz, E. Nonequilibrium work distribution of a quantum harmonic oscillator. Phys. Rev. E 2008, 77, 021128. [Google Scholar] [CrossRef] [PubMed]
- Liu, F. Calculating work in adiabatic two-level quantum Markovian master equations: A characteristic function method. Phys. Rev. E 2014, 90, 032121. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Gong, Z.; Wu, B.; Quan, H.T. Quantum-classical correspondence principle for work distributions in a chaotic system. Phys. Rev. E 2016, 93, 062108. [Google Scholar] [CrossRef]
- Funo, K.; Quan, H. Path Integral Approach to Quantum Thermodynamics. Phys. Rev. Lett. 2018, 121, 040602. [Google Scholar] [CrossRef]
- Salazar, D.S.P.; Lira, S.A. Stochastic thermodynamics of nonharmonic oscillators in high vacuum. Phys. Rev. E 2019, 99, 062119. [Google Scholar] [CrossRef]
- Jarzynski, C.; Quan, H.; Rahav, S. Quantum-Classical Correspondence Principle for Work Distributions. Phys. Rev. X 2015, 5, 031038. [Google Scholar] [CrossRef]
- Deffner, S.; Paz, J.P.; Zurek, W.H. Quantum work and the thermodynamic cost of quantum measurements. Phys. Rev. E 2016, 94, 010103(R). [Google Scholar] [CrossRef]
- García-Mata, I.; Roncaglia, A.J.; Wisniacki, D.A. Quantum-to-classical transition in the work distribution for chaotic systems. Phys. Rev. E 2017, 95, 050102. [Google Scholar] [CrossRef]
- Fei, Z.; Quan, H. Nonequilibrium Green’s Function’s Approach to the Calculation of Work Statistics. Phys. Rev. Lett. 2020, 124, 240603. [Google Scholar] [CrossRef] [PubMed]
- Qiu, T.; Fei, Z.; Pan, R.; Quan, H.T. Path-integral approach to the calculation of the characteristic function of work. Phys. Rev. E 2020, 101, 032111. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36–44. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Saito, K.; Dhar, A. Fluctuation Theorem in Quantum Heat Conduction. Phys. Rev. Lett. 2007, 99, 180601. [Google Scholar] [CrossRef] [PubMed]
- Dubi, Y.; Ventra, M.D. Colloquium: Heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 2011, 83, 131–155. [Google Scholar] [CrossRef]
- Thingna, J.; García-Palacios, J.L.; Wang, J.S. Steady-state thermal transport in anharmonic systems: Application to molecular junctions. Phys. Rev. B 2012, 85, 195452. [Google Scholar] [CrossRef]
- Wang, J.S.; Agarwalla, B.K.; Li, H.; Thingna, J. Nonequilibrium Green’s function method for quantum thermal transport. Front. Phys. 2014, 9, 673–697. [Google Scholar] [CrossRef]
- Thingna, J.; Manzano, D.; Cao, J. Dynamical signatures of molecular symmetries in nonequilibrium quantum transport. Sci. Rep. 2016, 6, 28027. [Google Scholar] [CrossRef]
- He, D.; Thingna, J.; Wang, J.S.; Li, B. Quantum thermal transport through anharmonic systems: A self-consistent approach. Phys. Rev. B 2016, 94, 155411. [Google Scholar] [CrossRef]
- Segal, D.; Agarwalla, B.K. Vibrational Heat Transport in Molecular Junctions. Ann. Phys. Chem. 2016, 67, 185–209. [Google Scholar] [CrossRef]
- Kilgour, M.; Agarwalla, B.K.; Segal, D. Path-integral methodology and simulations of quantum thermal transport: Full counting statistics approach. J. Chem. Phys. 2019, 150, 084111. [Google Scholar] [CrossRef]
- Wang, C.; Ren, J.; Cao, J. Unifying quantum heat transfer in a nonequilibrium spin-boson model with full counting statistics. Phys. Rev. A 2017, 95, 023610. [Google Scholar] [CrossRef]
- Aurell, E.; Donvil, B.; Mallick, K. Large deviations and fluctuation theorem for the quantum heat current in the spin-boson model. Phys. Rev. E 2020, 101, 052116. [Google Scholar] [CrossRef] [PubMed]
- Denzler, T.; Lutz, E. Heat distribution of a quantum harmonic oscillator. Phys. Rev. E 2018, 98, 052106. [Google Scholar] [CrossRef]
- Salazar, D.S.P.; Macêdo, A.M.S.; Vasconcelos, G.L. Quantum heat distribution in thermal relaxation processes. Phys. Rev. E 2019, 99, 022133. [Google Scholar] [CrossRef]
- Popovic, M.; Mitchison, M.T.; Strathearn, A.; Lovett, B.W.; Goold, J.; Eastham, P.R. Quantum Heat Statistics with Time-Evolving Matrix Product Operators. PRX Quantum 2021, 2, 020338. [Google Scholar] [CrossRef]
- Karsten Balzer, M.B. Nonequilibrium Green’s Functions Approach to Inhomogeneous Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Esposito, M.; Ochoa, M.A.; Galperin, M. Quantum Thermodynamics: A Nonequilibrium Green’s Function Approach. Phys. Rev. Lett. 2015, 114, 080602. [Google Scholar] [CrossRef] [PubMed]
- Polanco, C.A. Nonequilibrium Green’s functions (NEGF) in vibrational energy transport: A topical review. Nanoscale Microscale Thermophys. Eng. 2021, 25, 1–24. [Google Scholar] [CrossRef]
- Aron, C.; Biroli, G.; Cugliandolo, L.F. Symmetries of generating functionals of Langevin processes with colored multiplicative noise. J. Stat. Mech. 2010, 2010, P11018. [Google Scholar] [CrossRef]
- Mallick, K.; Moshe, M.; Orland, H. A field-theoretic approach to non-equilibrium work identities. J. Phys. A 2011, 44, 095002. [Google Scholar] [CrossRef]
- Carrega, M.; Solinas, P.; Braggio, A.; Sassetti, M.; Weiss, U. Functional integral approach to time-dependent heat exchange in open quantum systems: General method and applications. New J. Phys. 2015, 17, 045030. [Google Scholar] [CrossRef]
- Funo, K.; Quan, H.T. Path integral approach to heat in quantum thermodynamics. Phys. Rev. E 2018, 98, 012113. [Google Scholar] [CrossRef] [PubMed]
- Yeo, J. Symmetry and its breaking in a path-integral approach to quantum Brownian motion. Phys. Rev. E 2019, 100, 062107. [Google Scholar] [CrossRef]
- Fogedby, H.C. Heat fluctuations in equilibrium. J. Stat. Mech. Theory Exp. 2020, 2020, 083208. [Google Scholar] [CrossRef]
- Van Zon, R.; Cohen, E.G.D. Extended heat-fluctuation theorems for a system with deterministic and stochastic forces. Phys. Rev. E 2004, 69, 056121. [Google Scholar] [CrossRef]
- Imparato, A.; Peliti, L.; Pesce, G.; Rusciano, G.; Sasso, A. Work and heat probability distribution of an optically driven Brownian particle: Theory and experiments. Phys. Rev. E 2007, 76, 050101. [Google Scholar] [CrossRef]
- Fogedby, H.C.; Imparato, A. Heat distribution function for motion in a general potential at low temperature. J. Phys. A Math. Theor. 2009, 42, 475004. [Google Scholar] [CrossRef]
- Chatterjee, D.; Cherayil, B.J. Exact path-integral evaluation of the heat distribution function of a trapped Brownian oscillator. Phys. Rev. E 2010, 82, 051104. [Google Scholar] [CrossRef]
- Gomez-Solano, J.R.; Petrosyan, A.; Ciliberto, S. Heat Fluctuations in a Nonequilibrium Bath. Phys. Rev. Lett. 2011, 106, 200602. [Google Scholar] [CrossRef]
- Salazar, D.S.P.; Lira, S.A. Exactly solvable nonequilibrium Langevin relaxation of a trapped nanoparticle. J. Phys. A Math. Theor. 2016, 49, 465001. [Google Scholar] [CrossRef][Green Version]
- Pagare, A.; Cherayil, B.J. Stochastic thermodynamics of a harmonically trapped colloid in linear mixed flow. Phys. Rev. E 2019, 100, 052124. [Google Scholar] [CrossRef] [PubMed]
- Paraguassú, P.V.; Aquino, R.; Morgado, W.A.M. The Heat Distribution of the Underdamped Langevin Equation. arXiv 2021, arXiv:ond-mat.stat-mech/2102.09115. [Google Scholar]
- Gupta, D.; Sivak, D.A. Heat fluctuations in a harmonic chain of active particles. Phys. Rev. E 2021, 104, 024605. [Google Scholar] [CrossRef]
- Esposito, M.; Ochoa, M.A.; Galperin, M. Nature of heat in strongly coupled open quantum systems. Phys. Rev. B 2015, 92, 235440. [Google Scholar] [CrossRef]
- Talkner, P.; Hänggi, P. Open system trajectories specify fluctuating work but not heat. Phys. Rev. E 2016, 94, 022143. [Google Scholar] [CrossRef] [PubMed]
- Talkner, P.; Hänggi, P. Colloquium: Statistical mechanics and thermodynamics at strong coupling: Quantum and classical. Rev. Mod. Phys. 2020, 92, 041002. [Google Scholar] [CrossRef]
- Bez, W. Microscopic preparation and macroscopic motion of a Brownian particle. Z. Phys. B 1980, 39, 319–325. [Google Scholar] [CrossRef]
- Caldeira, A.; Leggett, A. Path integral approach to quantum Brownian motion. Phys. A 1983, 121, 587–616. [Google Scholar] [CrossRef]
- Caldeira, A.; Leggett, A. Quantum tunnelling in a dissipative system. Ann. Phys. 1983, 149, 374–456. [Google Scholar] [CrossRef]
- Unruh, W.G.; Zurek, W.H. Reduction of a wave packet in quantum Brownian motion. Phys. Rev. D 1989, 40, 1071–1094. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Weiss, U. Quantum Dissipative Systems; World Scientific Publishing Company: Singapore, 2008. [Google Scholar]
- Usually the quantum fluctuating heat is defined via two-point measurements over the heat bath. When the Hamiltonian of the system is time-independent, the internal energy change of the system is completely caused by the heat exchange. The quantum fluctuating heat can thus be alternatively defined via two-point measurements over the system, whose number of degrees of freedom is much smaller than that of the heat bath. Hence, the calculation of the heat statistics can be significantly simplified under this definition
- Yu, L.H.; Sun, C.P. Evolution of the wave function in a dissipative system. Phys. Rev. A 1994, 49, 592–595. [Google Scholar] [CrossRef]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Hillery, M.; O’Connell, R.; Scully, M.; Wigner, E. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121–167. [Google Scholar] [CrossRef]
- Polkovnikov, A. Phase space representation of quantum dynamics. Ann. Phys. 2010, 325, 1790–1852. [Google Scholar] [CrossRef]
- Fei, Z.; Quan, H.T.; Liu, F. Quantum corrections of work statistics in closed quantum systems. Phys. Rev. E 2018, 98, 012132. [Google Scholar] [CrossRef]
- Qian, Y.; Liu, F. Computing characteristic functions of quantum work in phase space. Phys. Rev. E 2019, 100, 062119. [Google Scholar] [CrossRef]
- Brodier, O.; Mallick, K.; de Almeida, A.M.O. Semiclassical work and quantum work identities in Weyl representation. J. Phys. A Math. Theor. 2020, 53, 325001. [Google Scholar] [CrossRef]
- Qiu, T.; Fei, Z.; Pan, R.; Quan, H.T. Quantum corrections to the entropy and its application in the study of quantum Carnot engines. Phys. Rev. E 2020, 101, 032113. [Google Scholar] [CrossRef]
- Qiu, T.; Quan, H.T. Quantum corrections to the entropy in a driven quantum Brownian motion model. Commun. Theor. Phys. 2021, 73, 095602. [Google Scholar] [CrossRef]
- Hu, B.L.; Paz, J.P.; Zhang, Y. Quantum Brownian motion in a general environment: Exact master equation with nonlocal dissipation and colored noise. Phys. Rev. D 1992, 45, 2843–2861. [Google Scholar] [CrossRef]
- Karrlein, R.; Grabert, H. Exact time evolution and master equations for the damped harmonic oscillator. Phys. Rev. E 1997, 55, 153–164. [Google Scholar] [CrossRef]
- Ford, G.W.; O’Connell, R.F. Exact solution of the Hu-Paz-Zhang master equation. Phys. Rev. D 2001, 64, 105020. [Google Scholar] [CrossRef]
- Salazar, D.S.P. Work distribution in thermal processes. Phys. Rev. E 2020, 101, 030101. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.H.; Chen, J.F.; Fei, Z.; Quan, H.T. A microscopic theory of Curzon-Ahlborn heat engine. arXiv 2021, arXiv:cond-mat.statmech/ 2108.04128. [Google Scholar]
- Cañizares, J.S.; Sols, F. Translational symmetry and microscopic preparation in oscillator models of quantum dissipation. Phys. A 1994, 212, 181–193. [Google Scholar] [CrossRef]
- Ju, K.K.; Guo, C.X.; Pan, X.Y. Initial-Slip Term Effects on the Dissipation-Induced Transition of a Simple Harmonic Oscillator. Chin. Phys. Lett. 2017, 34, 010301. [Google Scholar] [CrossRef]
- Kramers, H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Grabert, H.; Weiss, U.; Talkner, P. Quantum theory of the damped harmonic oscillator. Z. Phys. B 1984, 55, 87–94. [Google Scholar] [CrossRef]
- Strictly, the substitution requires to amend γn, Λnm, ξn, Δnm accordingly, but we only require q0(t) and p0(t) to calculate the characteristic function of heat, so we skip the further amendment.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-F.; Qiu, T.; Quan, H.-T. Quantum–Classical Correspondence Principle for Heat Distribution in Quantum Brownian Motion. Entropy 2021, 23, 1602. https://doi.org/10.3390/e23121602
Chen J-F, Qiu T, Quan H-T. Quantum–Classical Correspondence Principle for Heat Distribution in Quantum Brownian Motion. Entropy. 2021; 23(12):1602. https://doi.org/10.3390/e23121602
Chicago/Turabian StyleChen, Jin-Fu, Tian Qiu, and Hai-Tao Quan. 2021. "Quantum–Classical Correspondence Principle for Heat Distribution in Quantum Brownian Motion" Entropy 23, no. 12: 1602. https://doi.org/10.3390/e23121602
APA StyleChen, J.-F., Qiu, T., & Quan, H.-T. (2021). Quantum–Classical Correspondence Principle for Heat Distribution in Quantum Brownian Motion. Entropy, 23(12), 1602. https://doi.org/10.3390/e23121602





