1. Introduction
Wireless data traffic has grown exponentially over recent years with no foreseen saturation [
1]. To keep pace with connectivity requirements, one must carefully attend available resources with respect to three essential measures: reliability, latency, and complexity. As error correction codes (ECC) are well renowned as means to boost reliability, the research of practical schemes is crucial to meet demands.
One family of ECC that has had great impact on wireless standards is the convolutional codes (CC). Specifically, tail-biting convolutional codes (TBCC) [
2] were incorporated in the 4G Long-Term Evolution (LTE) standard [
3], and they are also considered for 5G hybrid turbo/LDPC code-based frameworks [
4].
The major practical difference between CC and TBCC lies in the termination constraint. Conventional CC encoding appends zeros bits to impose zero states; TBCC encoding requires no additional bits, avoiding the rate loss. Due to this rate loss aversion, TBCC dominates classical CC in the short-length regime: They achieve the minimum distance bound for a specified length block codes [
5]. Our work focuses on improving decoding performance of short length TBCC due to their significance.
Despite having great potential, the optimality of TBCC with respect to the reliability, latency, and complexity measures is not yet guaranteed. For example, TBCC suffer from increased complexity in the maximum-likelihood decoding as the initial state is unknown. Under TBCC encoding the Viterbi algorithm (VA) [
6] is not the maximum-likelihood decoder (MLD); the MLD operates by running a VA per initial state, outputting the most likely decoded codeword. Clearly, the complexity grows as the number of states.
To bridge the high complexity gap, several suboptimal and reduced complexity decoders have been proposed. Major works include the circular Viterbi algorithm (CVA) [
7] and the wrap-around Viterbi algorithm (WAVA) [
8]. Both methods utilize the circular nature of the trellis: They apply VA iteratively on the sequence of repeated log-likelihood ratios (LLR) values computed from the received channel word. The more repetitions employed, the lower the error rate is, yet at a cost of additional latency. Short-length codes require the additional repetitions, as indicated in [
7]: “it is very important that a sufficient number of symbol times be allowed for convergence. If the number is too small…the path chosen in this case will be circular but will not be the maximum likelihood path.”
Another common practice is to employ a list decoding scheme, for instance, the list Viterbi algorithm (LVA), along with cyclic redundancy check (CRC) code [
9,
10,
11]. According to this scheme, a list of the most likely decoded codewords, rather than a single codeword, is computed in the forward pass of the VA. The minimal path metric codeword that satisfies the CRC criterion is output. Both the decrement in error rate and the increase in complexity are proportional to the list size.
The additional repetitions and list size result in complexity overhead for short TBCC decoding. To mitigate this overhead, one may take a novel approach, rooted in a data-driven field: the machine learning (ML) based decoding.
Still a growing field, ML-based decoding attempts to bridge the gap between simple analytical models and the nonlinear observable reality. Contemporary literature is split between two different model choices: model-free and model-based. Model-free works include those in [
12,
13,
14], which leverage on state-of-the-art (SOTA) neural architectures with high neuronal capacity (i.e., ones that are able to implement many functions). On the other hand, under model-based approaches [
15,
16,
17,
18], a classical decoder is assigned learnable weights and trained to minimize a surrogate loss function. This approach suffers from high inductive bias due to the constrained architecture, leading to limited hypothesis space. Nonetheless, it generalizes better to longer codes than the model-free approach: Empirical simulations show that unrealistic fraction of codewords from the entire codebook must be fed to the network to achieve even moderate performance (see Figure 7 in [
12]). One notable model-based method by Shlezinger et al. is the ViterbiNet [
19]. This method compensates for nonlinearity in the channel with expectation-maximization clustering; an NN is utilized to approximate the marginal probability. This method holds great potential for dealing with nonlinear channels.
One recent innovation, referred to as the ensemble of decoders [
20], combined the benefits of model-based approach with the list decoding scheme. This ensemble is composed of learnable decoders, each one called an expert. Each expert is responsible for decoding channel words that lie in a unique part of the input space. A low-complexity gating function is employed to uniquely map each channel word to its respective decoder. The main intuition behind this divide-and-conquer approach is that combination of multiple
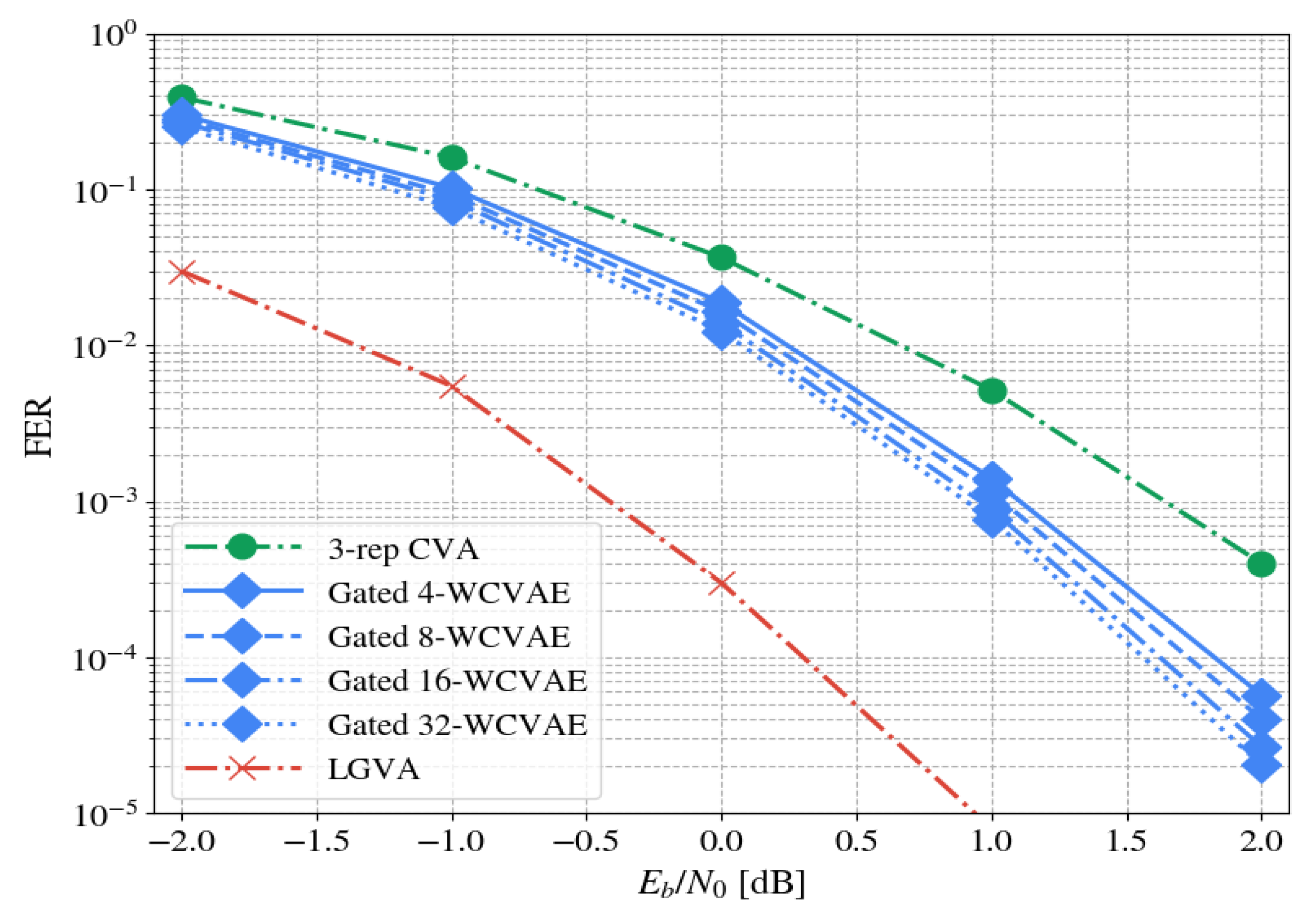
diverse members is expected to perform better than all individual basic algorithms that compose the ensemble. The paper shows this approach can achieve significant gains: Up to 1.25 dB on the benchmark.
The main contributions of this paper are the innovation of the model-based weighted circular Viterbi algorithm (WCVA) and its integration in the gated WCVAE, a designated ensemble of WCVA decoders, accompanied by a gating decoder. Next, we elaborate on the following major points.
WCVA—A parameterized CVA decoder, combining the optimality of the VA with a data-driven approach in
Section 3.1. Viterbi selections in the WCVA are based on the sums of weighted path metrics and the relevant branch metrics. The magnitude of a weight reflect the contribution of the corresponding path or branch to successful decoding of a noisy word.
Partition of the channel words space—We exploit the domain knowledge regarding the TBCC problem and partition the input space to different subsets of termination states in
Section 3.3; Each expert specializes on codewords that belong to a single subset.
Gating function—We reinforce the practical aspect of this scheme by introducing a low-complexity gating that acts as a filter, reducing the number of calls to each expert. The gating maps noisy words to a subgroup of experts based on the CRC checksum (see
Section 3.4).
Simulations of the proposed method on LTE-TBCC appear in
Section 4.
2. Background
2.1. Notation
Boldface upper-case and lower-case letters refer to matrices and vectors, respectively. Probability mass functions and probability density functions are denoted with . Subscripts refer to elements, with the ith element of the vector symbolized as , while superscripts in brackets, e.g., , index the jth vector in a sequence of vectors. A slice of a vector is denoted by . At last, is for the transpose operation and ‖·‖ is for the L1 norm. Throughout the paper, terms refer to indices.
2.2. Problem Formalization
Consider the block-wise transmission scenario of CC through the additive white Gaussian noise (AWGN) channel, see
Figure 1. Prior to transmission, the message word
is encoded twice: By an error detection code and by an error correction code. The CRC encodes
with systematic generator matrix
. Its parity check matrix is
. We denote the detection codeword by
and the codebook with
. Then, the CC encodes
with generator matrix
. As a result, the codeword
is a bits sequence
with
where
denotes the rate of the CC. For brevity, we denote
; the length of the CC calculated as
.
After encoding, the codeword
is BPSK-modulated (
,
) and
is transmitted through the channel with noise
. At the receiver, one decodes the LLR word
ℓ rather than
. The LLR values are approximated based on the bits i.i.d. assumption and Gaussian prior
. The decoder is represented by a function
that outputs the estimated detection codeword
. Our end goal is to find
that maximizes the a posteriori optimization problem:
Note that we solve for rather than as bit flips in either the systematic information bits or in the CRC bits are considered as errors.
2.3. Viterbi Decoding of CC
Naive solution of Equation (
1) is exponential in
. However, it can be simplified following Bayes:
where
is omitted, as this term is independent of
.
The time complexity of the solution to Equation (
2) is yet exponential, but may be further reduced to linear dependency in the memory’s length by following the well known Viterbi algorithm (VA) [
6]. We formulate notation for this algorithm in the following paragraphs.
Denote the memory of the CC by
and the state space by
. Convolutional codes can be represented by multiple temporal transitions, each one is a function of two arguments: the input bit and the current state. The trellis diagram is one convenient way to view these temporal relations, each trellis section is called a stage. We refer to the work in [
21] for a comprehensive tutorial regarding CC.
Let the sequence of states be represented by
. Following the properties of the CC, a 1-to-1 correspondence between the codeword
and the state sequence
exists:
Plugging the Markov property into the previous equation leads to:
where the last transition is due to the monotonic nature of the log function.
Next, denote the path metric
and the branch metric, representing the transition over a trellis edge, as
. Then, substituting these values into the last equation:
Taking a dynamic programming approach, the Viterbi algorithm solves Equation (
3) efficiently:
starting from
up to
, in an incremental fashion, with the initialization:
and
= 0. The constant
is called the LLR clipping parameter.
To output the decoded codeword , one has to perform the trace-back operation . This operation takes the LLR word along with a termination state and outputs the most likely decoded codeword: . Specifically, it calculates the sequence of states that follows the minimal values at each stage, starting from backwards. Then, the sequence is mapped to the corresponding estimated codeword . Under the classical zero-tail termination, is returned.
2.4. Circular Viterbi Decoding of TBCC
TBCC work under the assumption of equal start and end states. Their actual values are determined by the last bits. As such, the MLD with a list of size 1 is the decoded whose matching value is minimal, combining the decisions from multiple VA runs, one from each state .
As mentioned in
Section 1, the complexity of this MLD grows exponentially in the memory’s length. The CVA is a suboptimal decoder that exploits the circular nature of the TBCC trellis, executing VA for a specified number of repetitions, where each new VA is initialized with the end metrics of the previous repetitions. The CVA starts and ends its run at the zero state, being error prone near the zero tails.
Explicitly, the forward pass of the CVA follows Equation (
4) for
with
I denoting an odd number of replications. The same initialization as in Equation (
5) is used. The bits of the middle replication are the least error-prone, being farthest from the zero tails, thus returned:
for
.
3. A Data-Driven Approach to TBCC Decoding
This section describes our novel approach to decoding: Parameterization of the CVA decoder, and its integration into an ensemble composed from specialized experts and a low-complexity gating.
3.1. Weighted Circular Viterbi Algorithm
Nachmani et al. [
17] presented a weighted version of the classical Belief Propagation (BP) decoder [
22]. This learnable decoder is the deep unfolding of the BP [
23]. This weighted decoder outperforms the classical unweighted one by training over channel words, adjusting the weights to compensate for short cycles that are known to prevent convergence.
We follow the favorable model-based approach as well, parameterizing the branch metrics that correspond to edges of the trellis. We add another degree of freedom for each edge, assigning weights to the path metrics as well. Considering the complexity overhead, we only parameterize the middle replication. This formulation unfolds the middle replication of the CVA as a Neural Network (NN):
for
.
Our goal is to calculate parameters
that achieve termination states equal to the ground-truth start and end states. The exact equality criterion is non-differentiable; thus, we minimize the multi-class cross entropy loss, acting as a surrogate loss [
24]:
where
stands for the last learnable layer, and
being the softmax function:
This specific choice encourages the equality of the end states in the mid-replication to their ground-truth values. Note that the gradients back-propagate through the non-differentiable min criterion in Equation (
6) as in the maximum pooling operation: They only affect the state that achieved the minimum metric.
One fallacy of this approach is the similar importance for all edges, contrary to the BP, where not all edges are created equal (e.g., ones that participate in many short cycles). All edges are of the same importance as derived from the problem’s symmetry: Due to the unknown initial state, each state is equally likely.
This indicates that training this architecture may leave the weights as they are, or at worst even lead to divergence. To fully exploit the performance gained by the adjustment of the weights, one must first break the symmetry. We alter the uniform prior over the termination states by assigning only a subset of the termination states to a single decoder. We further elaborate on this proposition below.
3.2. Ensembles in Decoding
Ensembles [
25,
26] shine in data-driven applications: They exploit independence between the base models to enhance accuracy. The expressive power of the ensemble surpasses that of a single model. Thus, whereas a single model may fail to capture high-dimensional and nonlinear relations in the dataset, a combination of such models may succeed.
Nonetheless, ensembles also encompass computational complexity which is linear in the number of base learners, being unrealistic for practical considerations. To reduce complexity, our previous work [
20] suggests to employ a low complexity gating decoder. This decoder allows one to uniquely map each input word to a single most fitting decoder, keeping the overall computation complexity low. We further elaborate on the gated ensemble, referred to as gated WCVAE, in
Section 3.3 and gating in
Section 3.4.
3.3. Specialized-Experts Ensemble
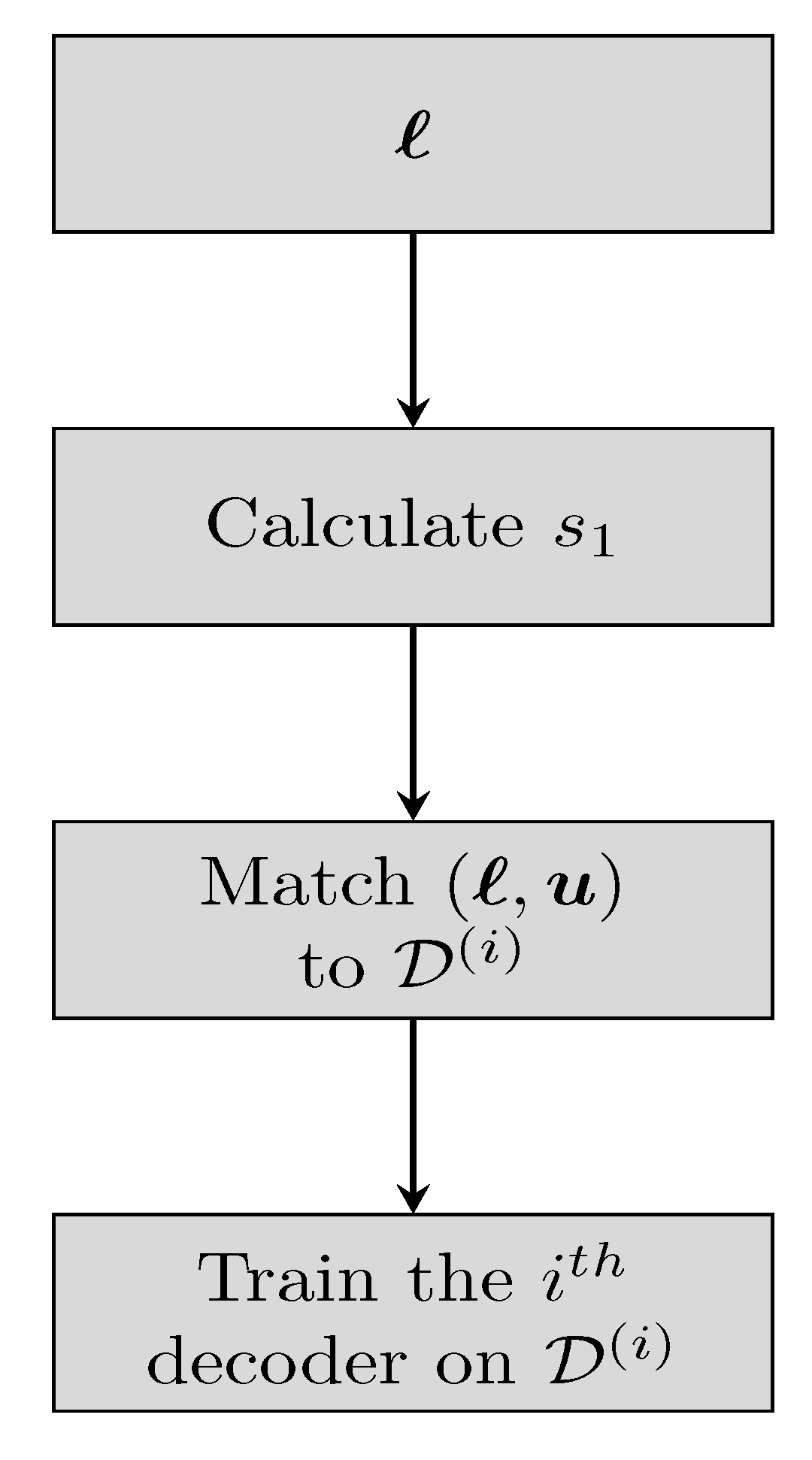
The WCVAE is an ensemble comprised of WCVA experts, each one specialized on words from a specific subset of termination states. We begin by discussing the forming of the experts in training, see
Figure 2 for the relevant flowchart.
3.4. Gating
Let the number of trainable WCVA decoders in the WCVAE be
, with each decoder possessing
I repetitions. To form the experts, we first simulate many message words randomly, each message word is encoded and transmitted through the channel. The initial state of a transmitted word
, known in training, is denoted by
as before. Then, we add the tuple
to the dataset representing the subset of states that include state
:
with
and
is yet the memory of the CC. Each dataset accumulates a high number of words by the above procedure.
All the WCVA decoders are trained as in the guidelines of
Section 3.1, with one exception: The
ith decoder is trained with the corresponding
. Subsequently,
specialized experts are formed, each one specializes on decoding words affiliated to a specific subset of termination states. Each codeword has equal probability to appear, thus the distribution over the termination states is uniform. We further elaborate on the intuition to this particular division of close-by states in
Section 4.4.
One common practice is to separate TBCC decoding into an initial state estimation followed by decoding. For example, Fedorenko et al. [
27] run a soft-input soft-output (SISO) decoder prior to LVA decoding. This prerun determines the most reliable starting state.
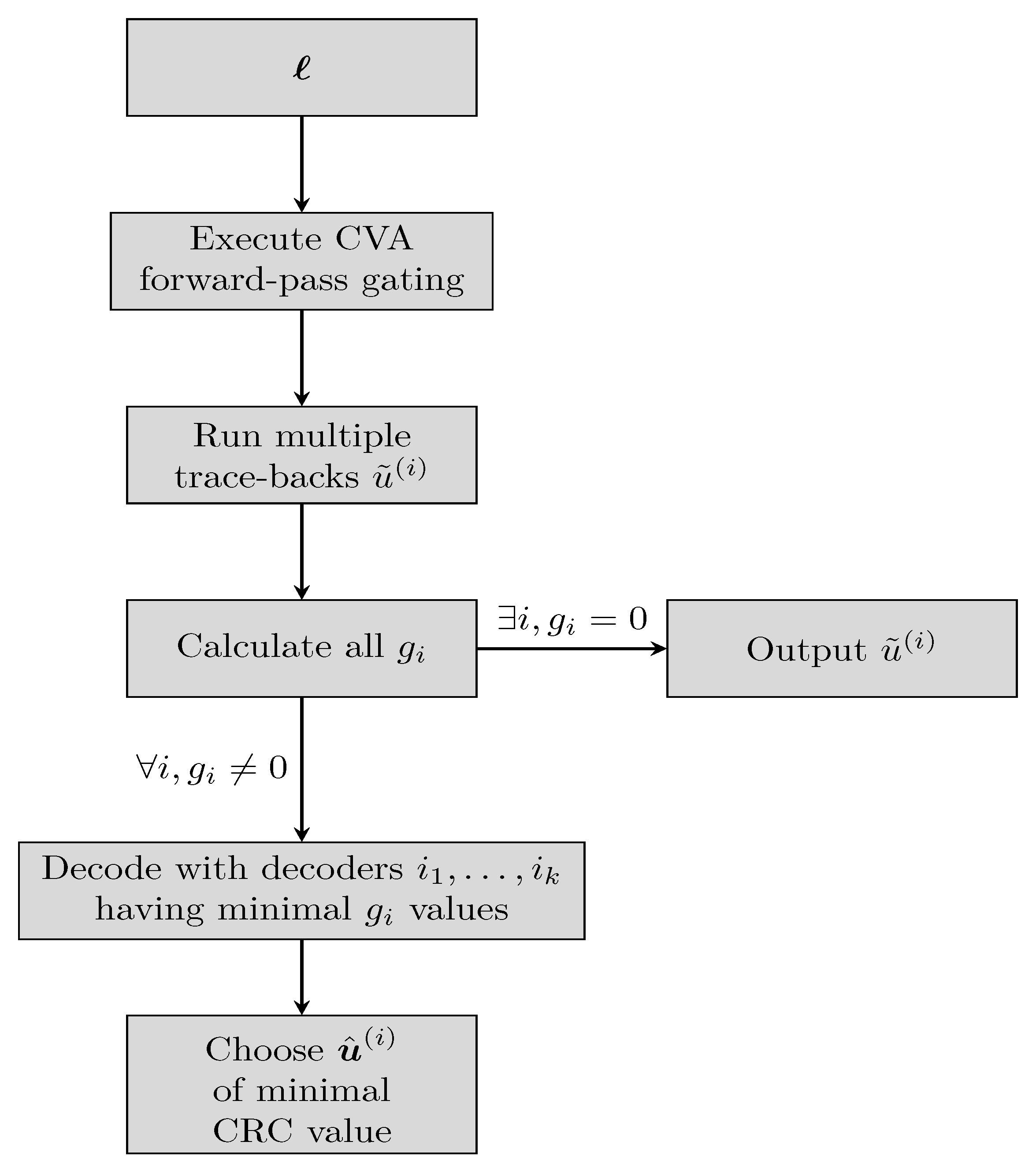
Similarly, our work presents a gating decoder which acts as a coarse state estimation. The gating is composed of two parts: a single forward pass of the CVA and a multiple trace-backs phase. We only employ the gating in the evaluation phase; Check
Figure 3 for the complete flow.
First, a forward pass of a CVA is executed on the input word
ℓ, as in Equation (
4). As all states are equiprobable, the initialization is chosen as
instead of Equation (
5). After calculating
for every state and stage, the trace-back
runs
times, each time starting from a different state. The starting states are spread uniformly over
, with the decoded words given as
Notice that the trace-back is a cheap operation, compared to the forward pass [
7]. Next, the value of the CRC syndrome is calculated for each trace-back:
with
indicating that no error has occurred (or is detectable). In case that a single
is zero, the corresponding decoded word
is output. If more than one
is zero, the decoded word is chosen randomly among all candidates. Only if no
i exists such that
, the word
ℓ continues for additional decoding at the ensemble.
Note that each computed value is correlative with the ascription of the word ℓ to the termination state . Though the ground-truth termination state may not necessarily have the minimum , this minimal value still hints that the ground-truth state is close by. As a result, decoding with the decoder corresponding to the minimal is satisfactory. If multiple share the same minimal value then decoders decode the word, choosing the output of minimal CRC value among the candidates.
5. Discussion
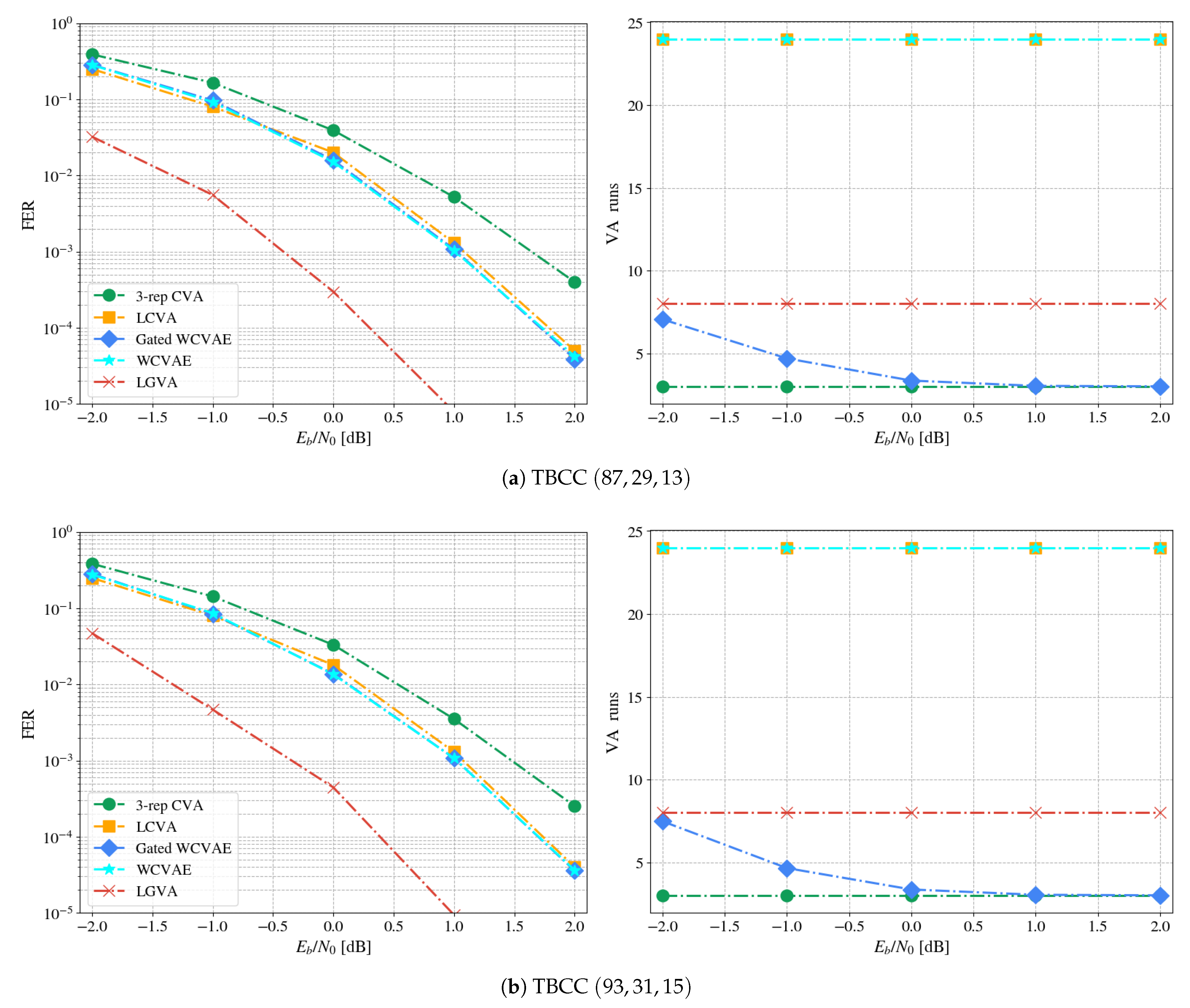
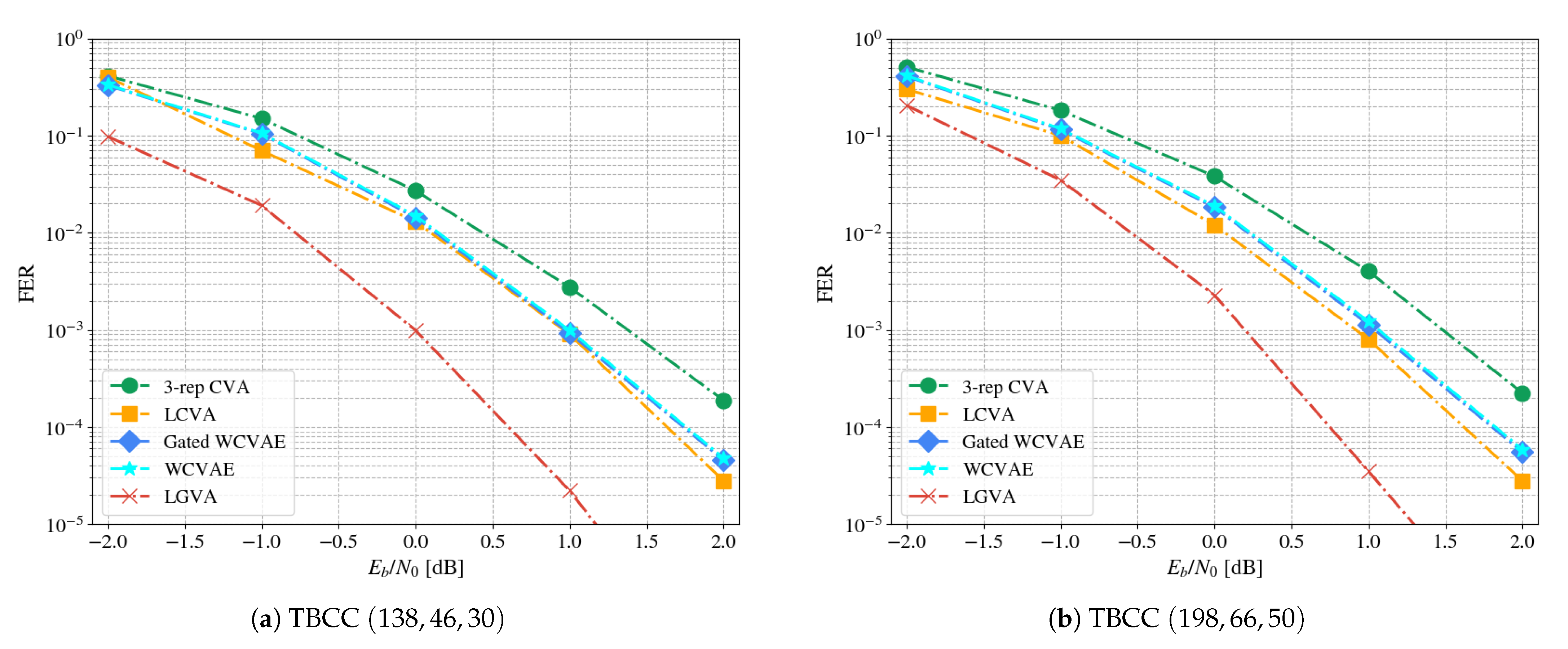
This work follows the model-based approach and applies it for TBCC decoding, starting with the parameterization of the common CVA decoder. Its parameterization relies on domain knowledge to effectively exploit the decoder: A classical low-complexity CVA acts as a gating decoder, filtering easy to decode channel words and directing harder ones to fitting experts; Each expert is specialized in decoding words that belong to a specific subset of termination states. This solution improves the overall performance, compared to a single decoder, as well as reduces the complexity in a data-driven fashion.
Future directions are to extend the ensemble approach to more use cases, such as different codes and various learnable decoders. For example, an ensemble tailored for polar codes, with a CRC-based gating, is one idea we intend to explore. This scenario is indeed practical, as 5G standard incorporates polar codes accompanied by CRC codes. Another direction is the theoretical study and analysis of the input space, e.g., the regions of the pseudo-codewords [
5] and tailbits errors [
7]. This could direct the training of the learnable decoder to surpass current results.