Signal Fluctuations and the Information Transmission Rates in Binary Communication Channels
Abstract
1. Introduction
- (1)
- between signal Information Transmission Rates (also Mutual Information) and signal correlations [40]. I show that neural binary coding cannot be captured by straightforward correlations among input and output signals.
- (2)
- between signals information transmission rates and signal firing rates (spikes’ frequencies) [41]. By examining this dependence, I have found the conditions in which temporal coding rather than rate coding is used. It turned out that this possibility depends on the parameter characterizing the transition from state to state.
- (3)
- between information transmission rates of signals (which are (auto)correlated) coming from Markov information sources and information transmission rates of signals coming from corresponding (to this Markov processes) Bernoulli processes. Here, “corresponding” means limiting the Bernoulli process with stationary distributions of these Markov processes [42]. I have shown in the case of correlated signals that the loss of information is relatively small, and thus temporal codes, which are more energetically efficient, can replace rate codes effectively. These results were confirmed by experiments.
2. Theoretical Background and Methods
2.1. Shannon’s Entropy and Information Transmission Rate
2.2. Information Sources
2.2.1. Information Sources—Markov Processes
2.2.2. Information Sources—Bernoulli Process Case
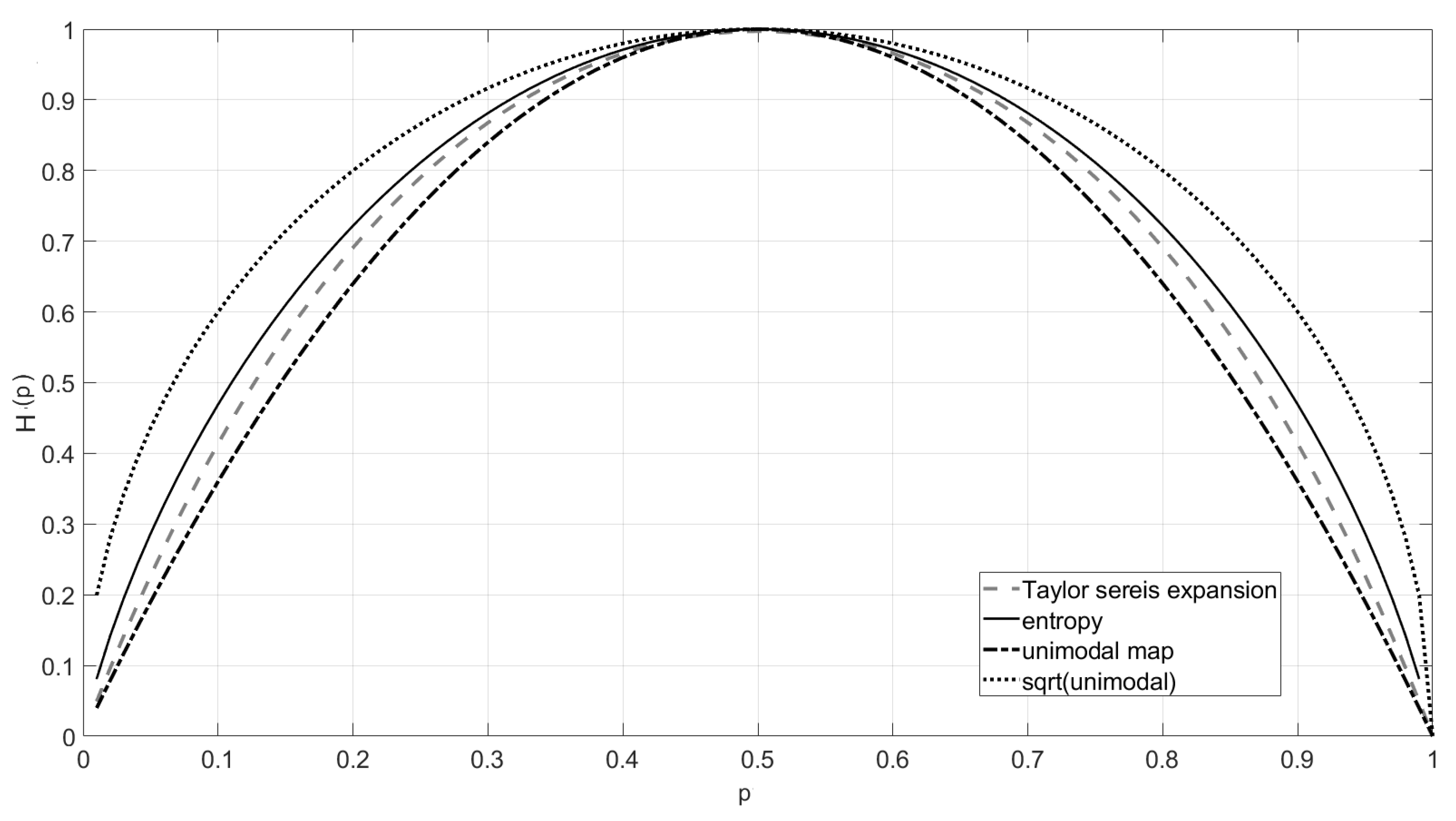
2.2.3. Generalized Entropy Variants
2.3. Fluctuations Measure
3. Results
3.1. Information against Fluctuations for Two-States Markov Processes—General Case
3.1.1. Standard Deviation in the Markov Process Case
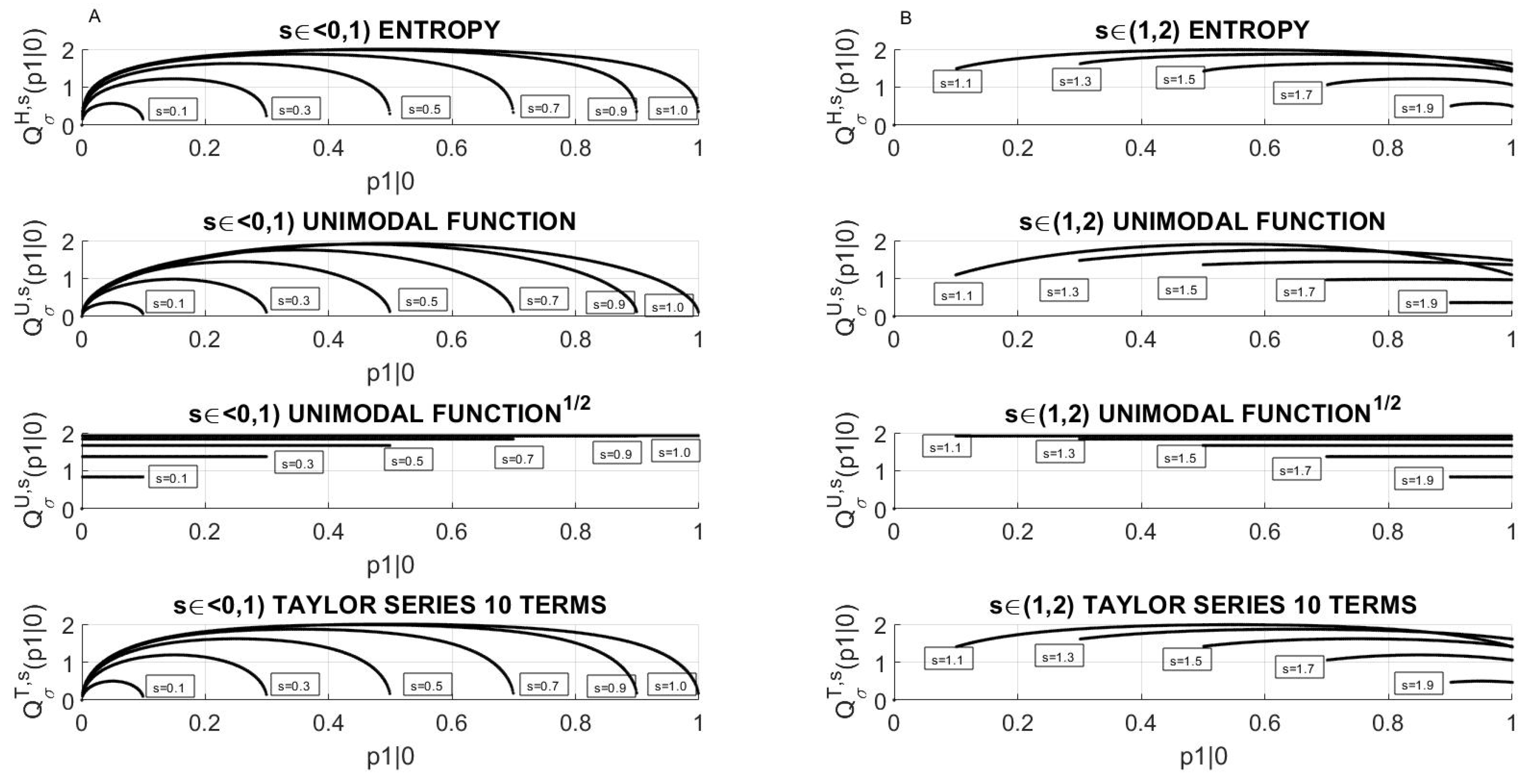
3.1.2. Relation between Information Transmission Rate of Markov Process and Its Standard Deviation
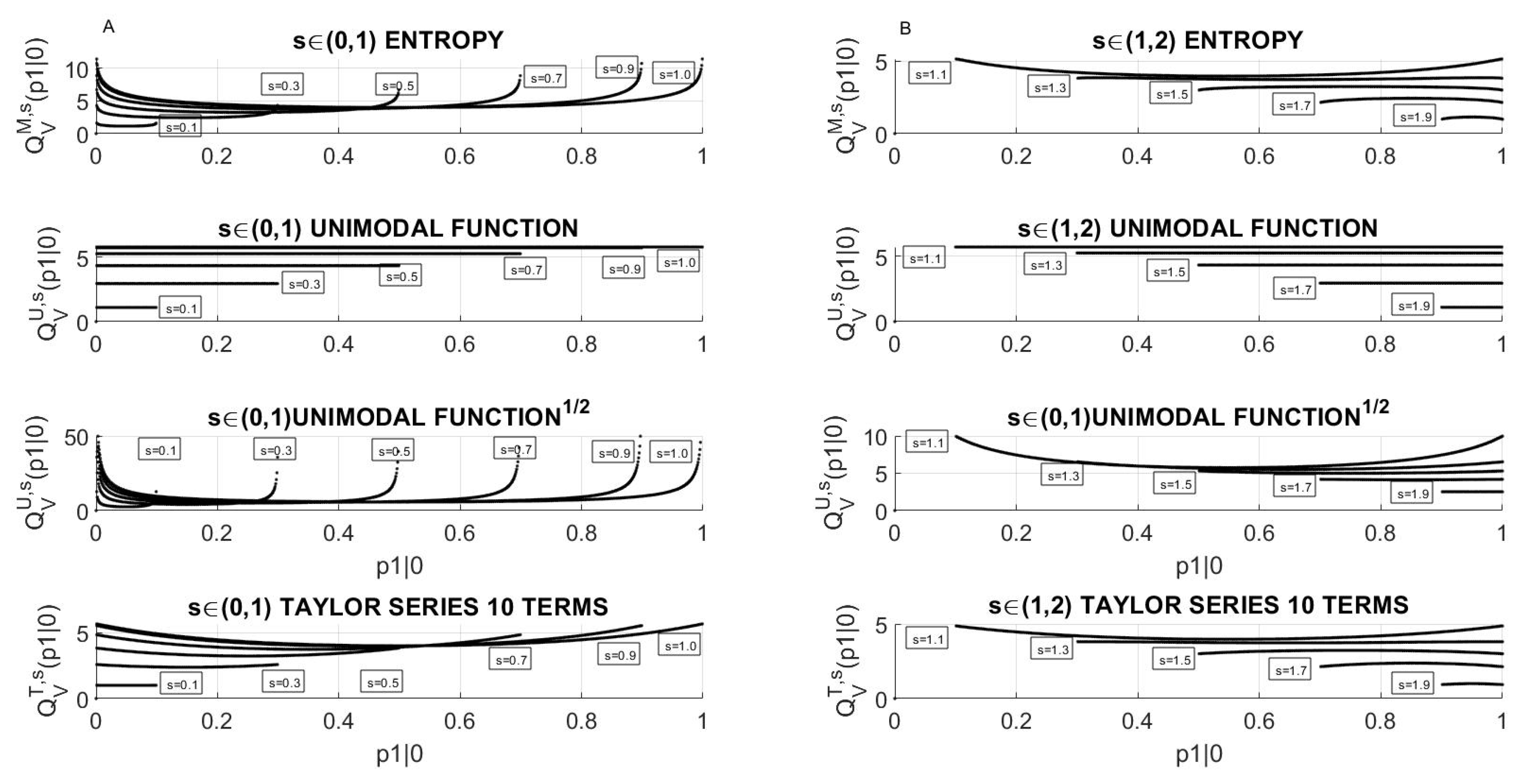
3.1.3. Relation between Information Transmission Rate of Markov Process and Its Variation
4. Discussion and Conclusions
Funding
Conflicts of Interest
References
- Huk, A.C.; Hart, E. Parsing signal and noise in the brain. Science 2019, 364, 236–237. [Google Scholar] [PubMed]
- Mainen, Z.F.; Sejnowski, T.J. Reliability of spike timing in neocortical neurons. Science 1995, 268, 1503–1506. [Google Scholar] [CrossRef] [PubMed]
- van Hemmen, J.L.; Sejnowski, T. 23 Problems in Systems Neurosciences; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Deco, G.; Jirsa, V.; McIntosh, A.R.; Sporns, O.; Kötter, R. Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. USA 2009, 106, 10302–10307. [Google Scholar] [CrossRef] [PubMed]
- Fraiman, D.; Chialvo, D.R. What kind of noise is brain noise: Anomalous scaling behavior of the resting brain activity fluctuations. Front. Physiol. 2012, 3, 1–11. [Google Scholar] [CrossRef]
- Gardella, C.; Marre, O.; Mora, T. Modeling the correlated activity of neural populations: A review. Neural Comput. 2019, 31, 233–269. [Google Scholar] [CrossRef]
- Adrian, E.D.; Zotterman, Y. The impulses produced by sensory nerve endings. J. Physiol. 1926, 61, 49–72. [Google Scholar] [CrossRef]
- MacKay, D.; McCulloch, W.S. The limiting information capacity of a neuronal link. Bull. Math. Biol. 1952, 14, 127–135. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Rieke, F.; Warland, D.D.; de Ruyter van Steveninck, R.R.; Bialek, W. Spikes: Exploring the Neural Code; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ash, R.B. Information Theory; John Wiley and Sons: New York, NY, USA, 1965. [Google Scholar]
- Teich, M.C.; Khanna, S.M. Pulse-number distribution for the neural spike train in the cat’s auditory nerve. J. Acoust. Soc. Am. 1985, 77, 1110–1128. [Google Scholar] [CrossRef]
- Daley, D.H.; Vere-Jones, D. An Introduction to the Theory of Point Processes: Volume I: Elementary Theory and Methods; Springer: Berlin, Germany, 2003. [Google Scholar]
- Werner, G.; Mountcastle, V.B. Neural activity in mechanoreceptive cutaneous afferents: Stimulusresponse relations, weber functions, and information transmission. J. Neurophysiol. 1965, 28, 359–397. [Google Scholar] [CrossRef]
- Tolhurst, D.J.; Movshon, J.A.; Thompson, I.D. The dependence of response amplitude and variance of cat visual cortical neurones on stimulus contrast. Exp. Brain Res. 1981, 41, 414–419. [Google Scholar] [CrossRef] [PubMed]
- de Ruyter van Steveninck, R.R.; Lewen, G.D.; Strong, S.P.; Koberle, R.; Bialek, W. Reproducibility and variability in neural spike trains. Science 1997, 275, 1805–1808. [Google Scholar] [CrossRef] [PubMed]
- Ross, S.M. Stochastic Processes; Wiley-Interscience: New York, NY, USA, 1996. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; Tata McGraw-Hill Education: New York, NY, USA, 2002. [Google Scholar]
- Kass, R.E.; Ventura, V. A spike-train probability model. Neural Comput. 2001, 13, 1713–1720. [Google Scholar] [CrossRef] [PubMed]
- Radons, G.; Becker, J.D.; Dülfer, B.; Krüger, J. Analysis, classification, and coding of multielectrode spike trains with hidden Markov models. Biol. Cybern. 1994, 71, 359–373. [Google Scholar] [CrossRef]
- Berry, M.J.; Meister, M. Refractoriness and neural precision. J. Neurosci. 1998, 18, 2200–2211. [Google Scholar] [CrossRef]
- Bouchaud, J.P. Fluctuations and response in financial markets: The subtle nature of ‘random’ price changes. Quant. Financ. 2004, 4, 176–190. [Google Scholar] [CrossRef]
- Knoblauch, A.; Palm, G. What is signal and what is noise in the brain? Biosystems 2005, 79, 83–90. [Google Scholar] [CrossRef][Green Version]
- Mishkovski, I.; Biey, M.; Kocarev, L. Vulnerability of complex networks. J. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 341–349. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Prokopowicz, P. The use of ordered fuzzy numbers for modeling changes in dynamic processe. Inf. Sci. 2019, 470, 1–14. [Google Scholar] [CrossRef]
- Zhang, M.L.; Qu, H.; Xie, X.R.; Kurths, J. Supervised learning in spiking, neural networks with noise-threshold. Neurocomputing 2017, 219, 333–349. [Google Scholar] [CrossRef]
- Lin, Z.; Ma, D.; Meng, J.; Chen, L. Relative ordering learning in spiking neural network for pattern recognition. Neurocomputing 2018, 275, 94–106. [Google Scholar] [CrossRef]
- Antonietti, A.; Monaco, J.; D’Angelo, E.; Pedrocchi, A.; Casellato, C. Dynamic redistribution of plasticity in a cerebellar spiking neural network reproducing an associative learning task perturbed by tms. Int. J. Neural Syst. 2018, 28, 1850020. [Google Scholar] [CrossRef] [PubMed]
- Kim, R.; Li, Y.; Sejnowski, T.J. Simple framework for constructing functional spiking recurrent neural networks. Proc. Natl. Acad. Sci. USA 2019, 116, 22811–22820. [Google Scholar] [CrossRef]
- Sobczak, F.; He, Y.; Sejnowski, T.J.; Yu, X. Predicting the fmri signal fluctuation with recurrent neural networks trained on vascular network dynamics. Cereb. Cortex 2020, 31, 826–844. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, H.; Liu, R.; Wu, B.; Wang, Y.M.; Pan, G. Activity-dependent neuron model for noise resistance. Neurocomputing 2019, 357, 240–247. [Google Scholar] [CrossRef]
- van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley Series Probability and Statistics; John Wiley and Sons: New York, NY, USA, 1958. [Google Scholar]
- Salinas, E.; Sejnowski, T.J. Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci. 2001, 2, 539–550. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Salinas, S.R.A. Introduction to Statistical Physics; Springer: Berlin, Germany, 2000. [Google Scholar]
- Kittel, C. Elementary Statistical Physics; Dovel Publications, INC.: Mineola, NY, USA, 2004. [Google Scholar]
- Pregowska, A.; Szczepanski, J.; Wajnryb, E. Mutual information against correlations in binary communication channels. BMC Neurosci. 2015, 16, 32. [Google Scholar] [CrossRef]
- Pregowska, A.; Szczepanski, J.; Wajnryb, E. Temporal code versus rate code for binary Information Sources. Neurocomputing 2016, 216, 756–762. [Google Scholar] [CrossRef]
- Pregowska, A.; Kaplan, E.; Szczepanski, J. How Far can Neural Correlations Reduce Uncertainty? Comparison of Information Transmission Rates for Markov and Bernoulli Processes. Int. J. Neural Syst. 2019, 29. [Google Scholar] [CrossRef]
- Amigo, J.M.; Szczepański, J.; Wajnryb, E.; Sanchez-Vives, M.V. Estimating the entropy rate of spike trains via Lempel-Ziv complexity. Neural Comput. 2004, 16, 717–736. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W.; Rieke, F.; Van Steveninck, R.D.R.; Warl, D. Reading a neural code. Science 1991, 252, 1854–1857. [Google Scholar] [CrossRef] [PubMed]
- Collet, P.; Eckmann, J.P. Iterated Maps on the Interval as Dynamical Systems; Reports on Progress in Physics; Birkhauser: Basel, Switzerland, 1980. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Renyi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; pp. 547–561. [Google Scholar]
- Amigo, J.M. Permutation Complexity in Dynamical Systems: Ordinal Patterns, Permutation Entropy and All That; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Crumiller, M.; Knight, B.; Kaplan, E. The measurement of information transmitted by a neural population: Promises and challenges. Entropy 2013, 15, 3507–3527. [Google Scholar] [CrossRef]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T. An Introduction to Transfer Entropy, Information Flow in Complex Systems; Springer: Berlin, Germany, 2016. [Google Scholar]
- Amigo, J.M.; Balogh, S.G.; Hernandez, S. A Brief Review of Generalized Entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef] [PubMed]
- Jetka, T.; Nienałtowski, K.; Filippi, S.; Stumpf, M.P.H.; Komorowski, M. An information-theoretic framework for deciphering pleiotropic and noisy biochemical signaling. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pregowska, A. Signal Fluctuations and the Information Transmission Rates in Binary Communication Channels. Entropy 2021, 23, 92. https://doi.org/10.3390/e23010092
Pregowska A. Signal Fluctuations and the Information Transmission Rates in Binary Communication Channels. Entropy. 2021; 23(1):92. https://doi.org/10.3390/e23010092
Chicago/Turabian StylePregowska, Agnieszka. 2021. "Signal Fluctuations and the Information Transmission Rates in Binary Communication Channels" Entropy 23, no. 1: 92. https://doi.org/10.3390/e23010092
APA StylePregowska, A. (2021). Signal Fluctuations and the Information Transmission Rates in Binary Communication Channels. Entropy, 23(1), 92. https://doi.org/10.3390/e23010092