Structural Statistical Quantifiers and Thermal Features of Quantum Systems
Abstract
1. Introduction
1.1. LMC Structural Quantifiers
1.2. Thermal Uncertainty Relations (TURs)
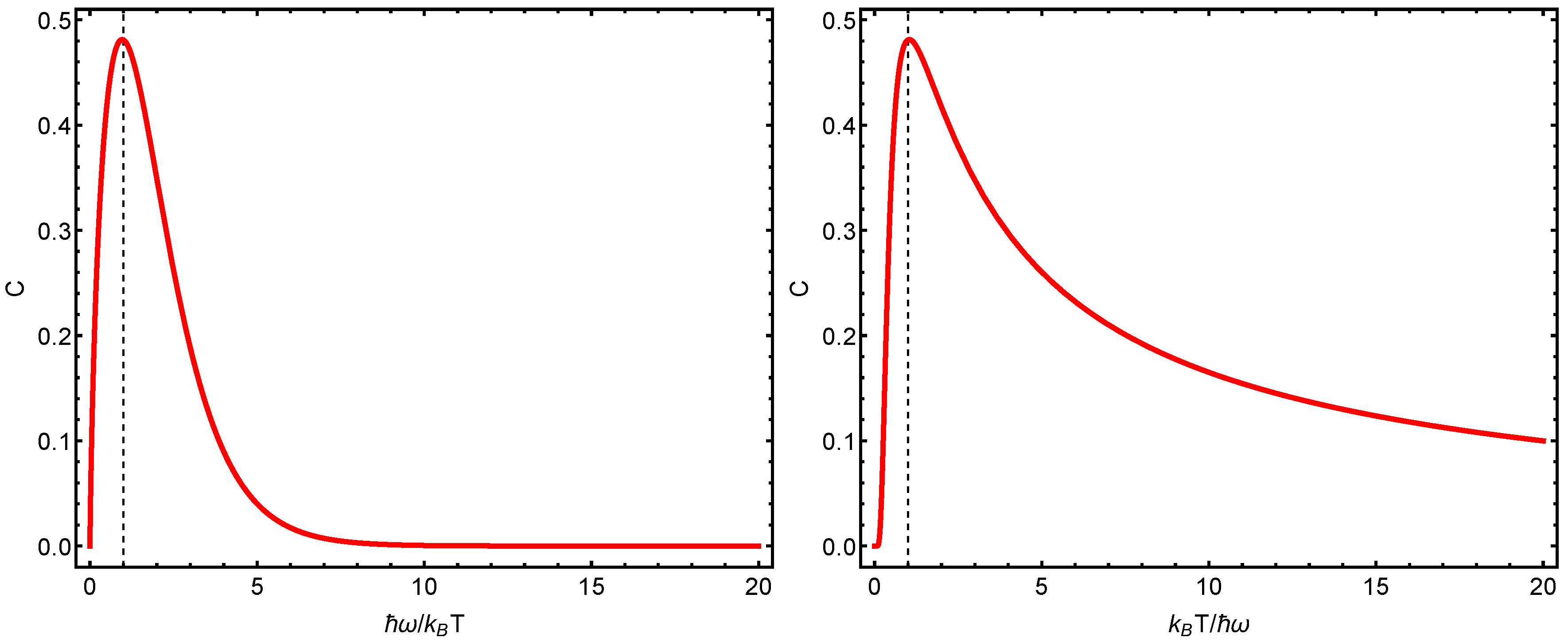
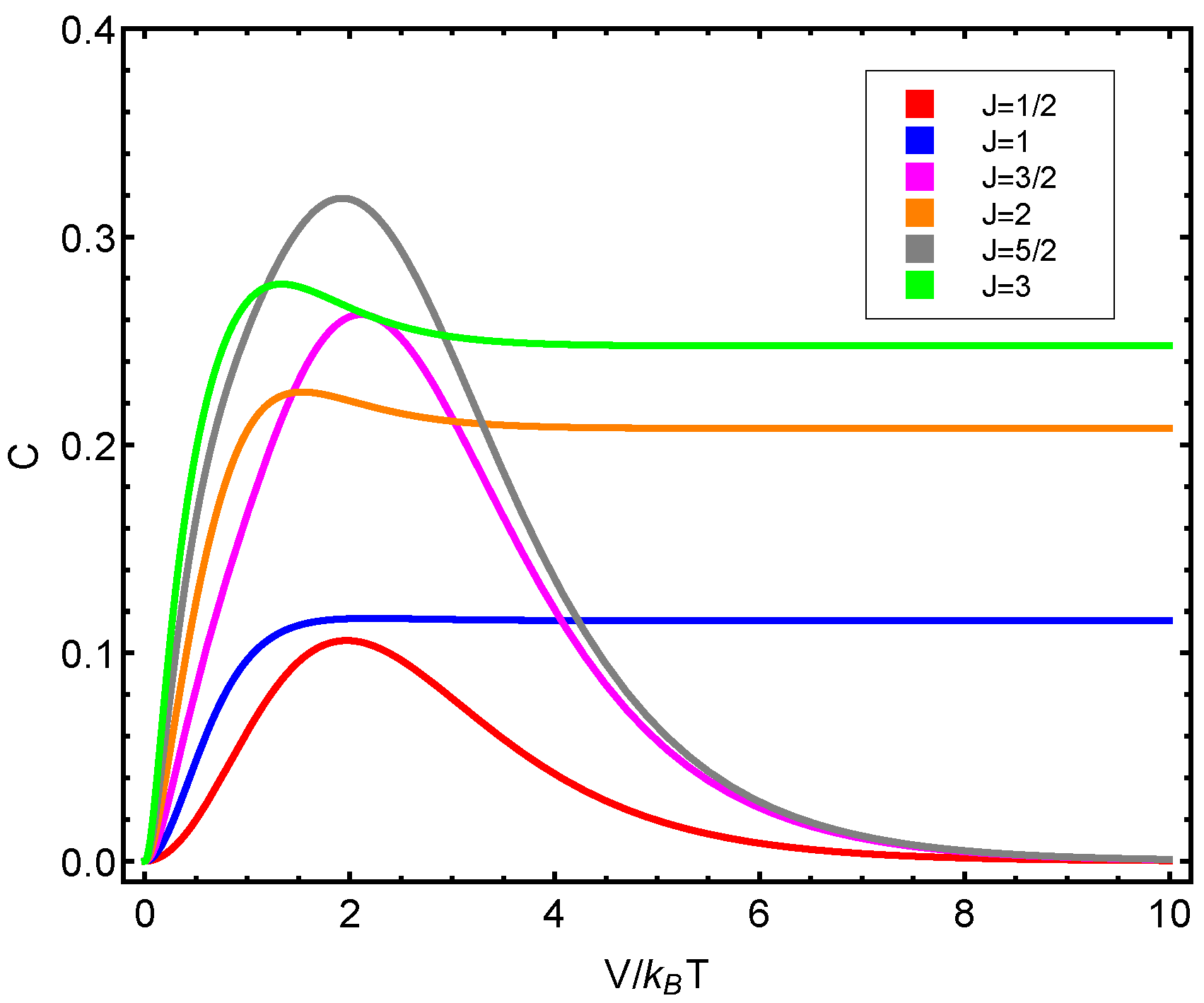
2. The Thermal Quantum Case
3. A Strict Bound Relating D to Quantum Uncertainties
4. Extending Bridges to a Semi-Classical Environment
4.1. Introduction: Coherent States and Husimi Distributions
4.2. HO Specialization
5. HO–Semi-Classical Thermal Treatment and Uncertainty Relations
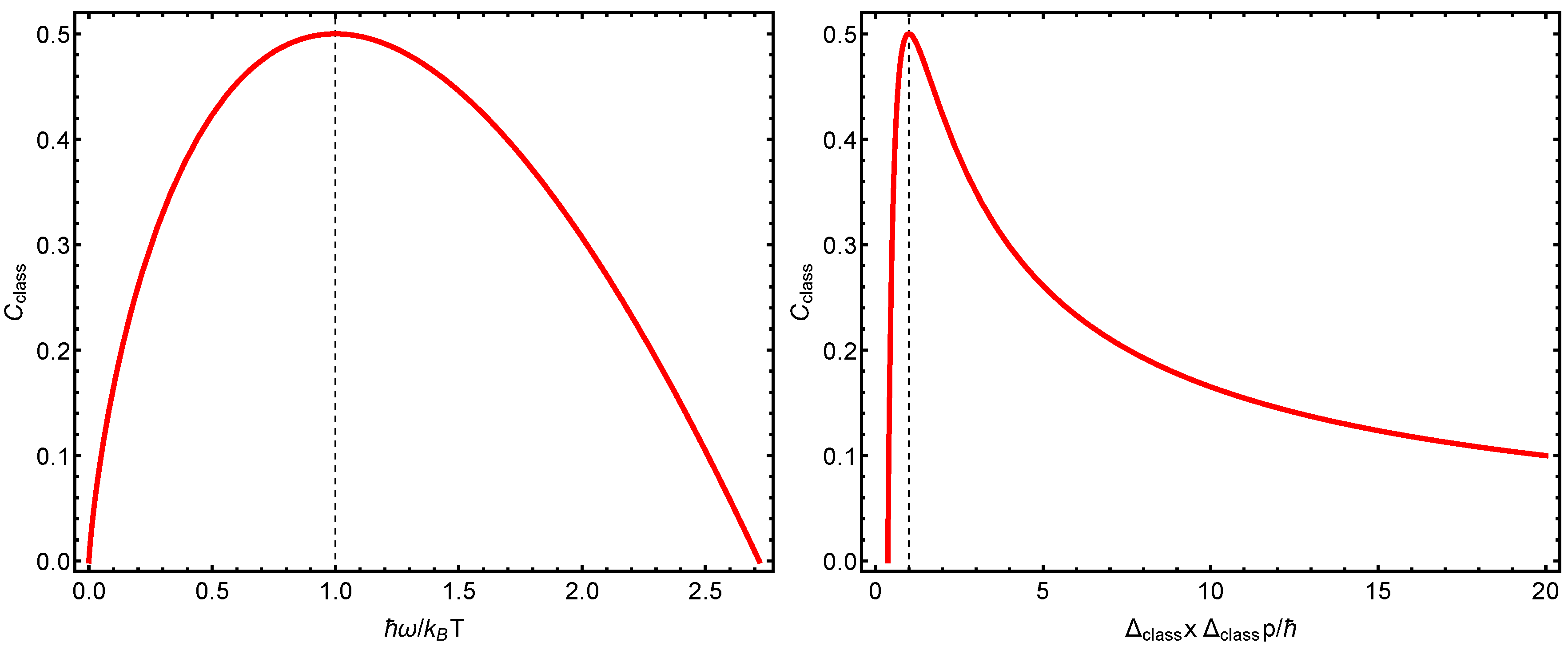
6. Possible Classical Extension
7. Application to a Nuclear Physics Model
7.1. The Model
7.2. Second Quantization Language
7.3. Hamiltonian H for Our Model
7.4. Phase Transitions
7.5. Finite Temperature
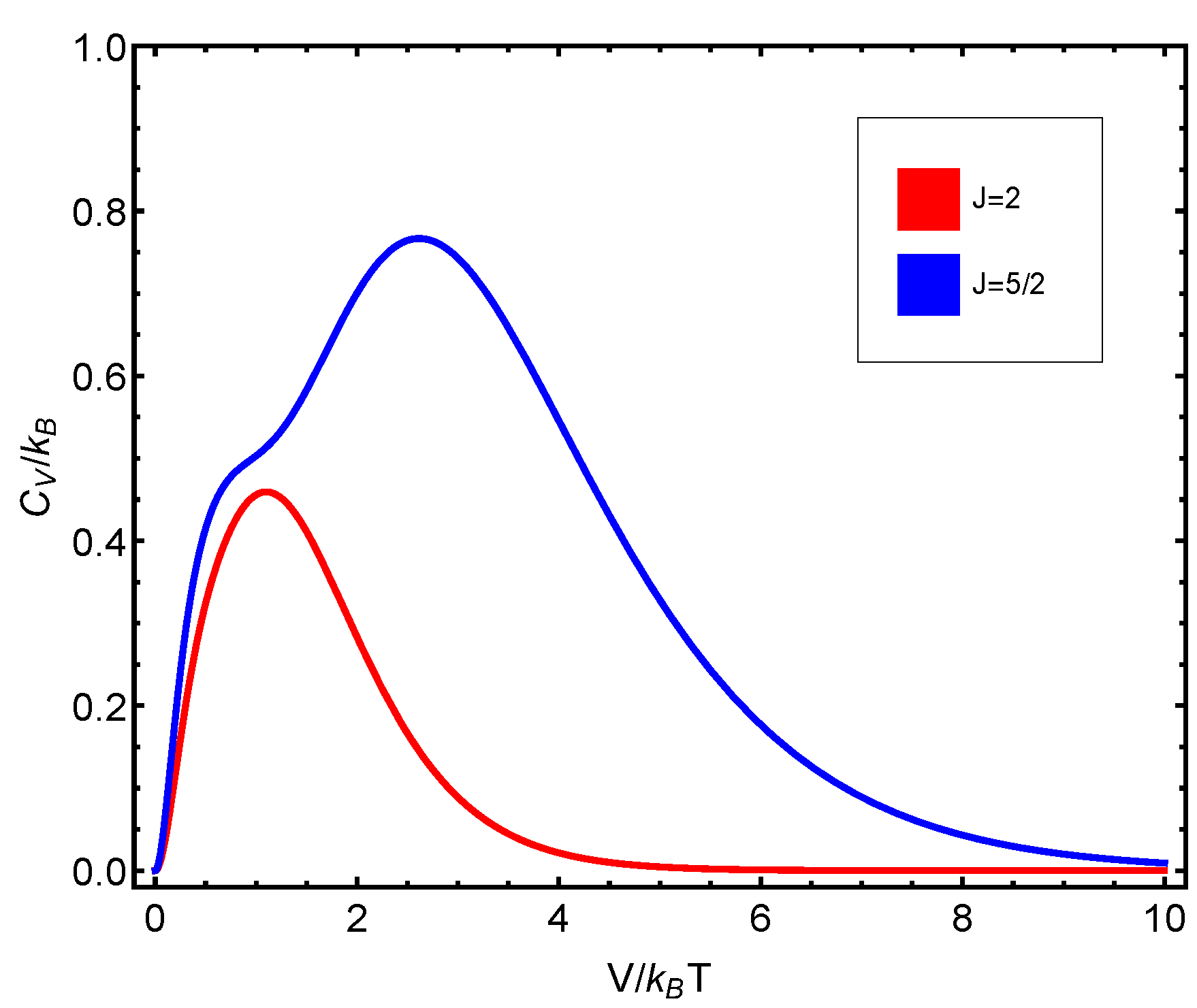
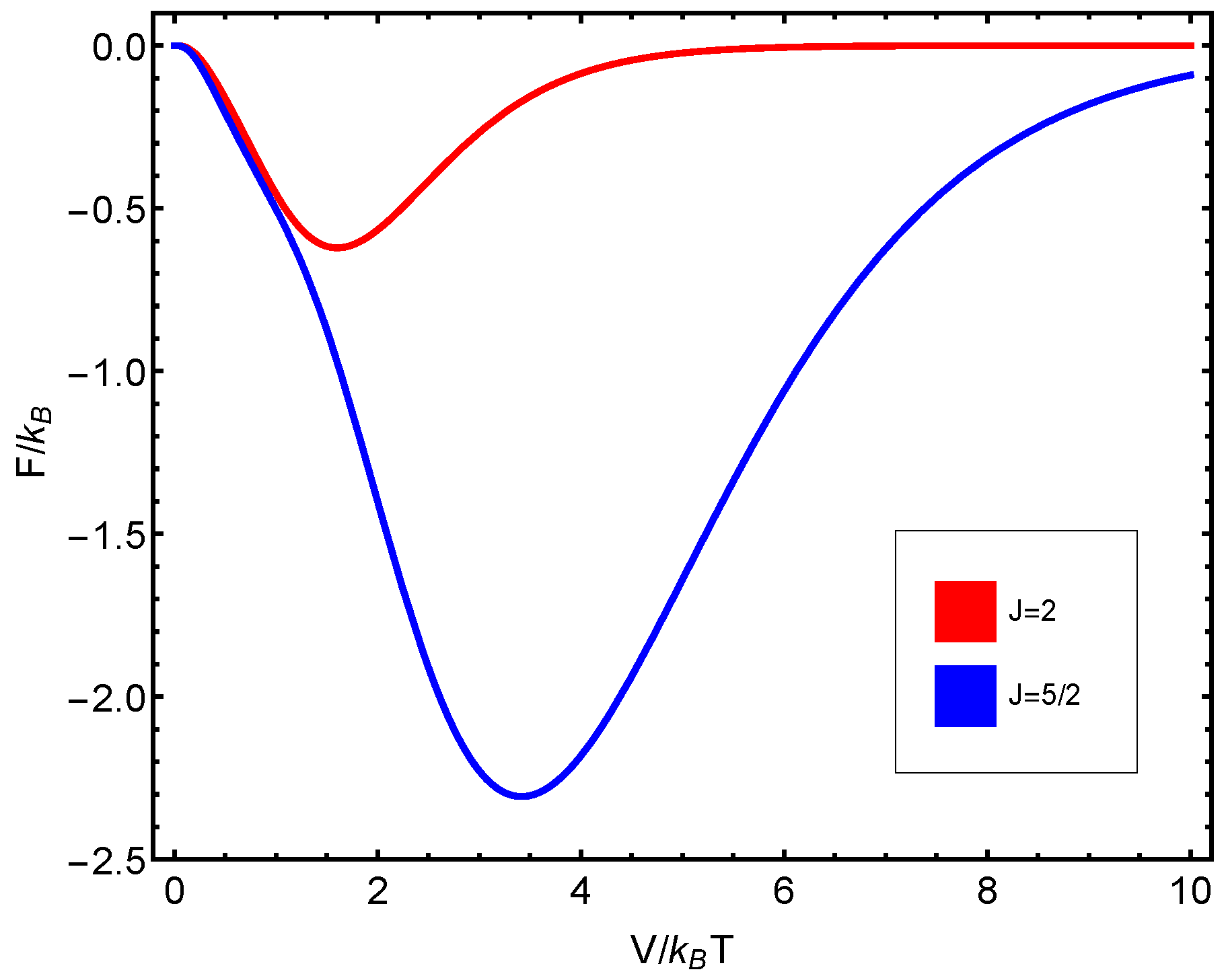
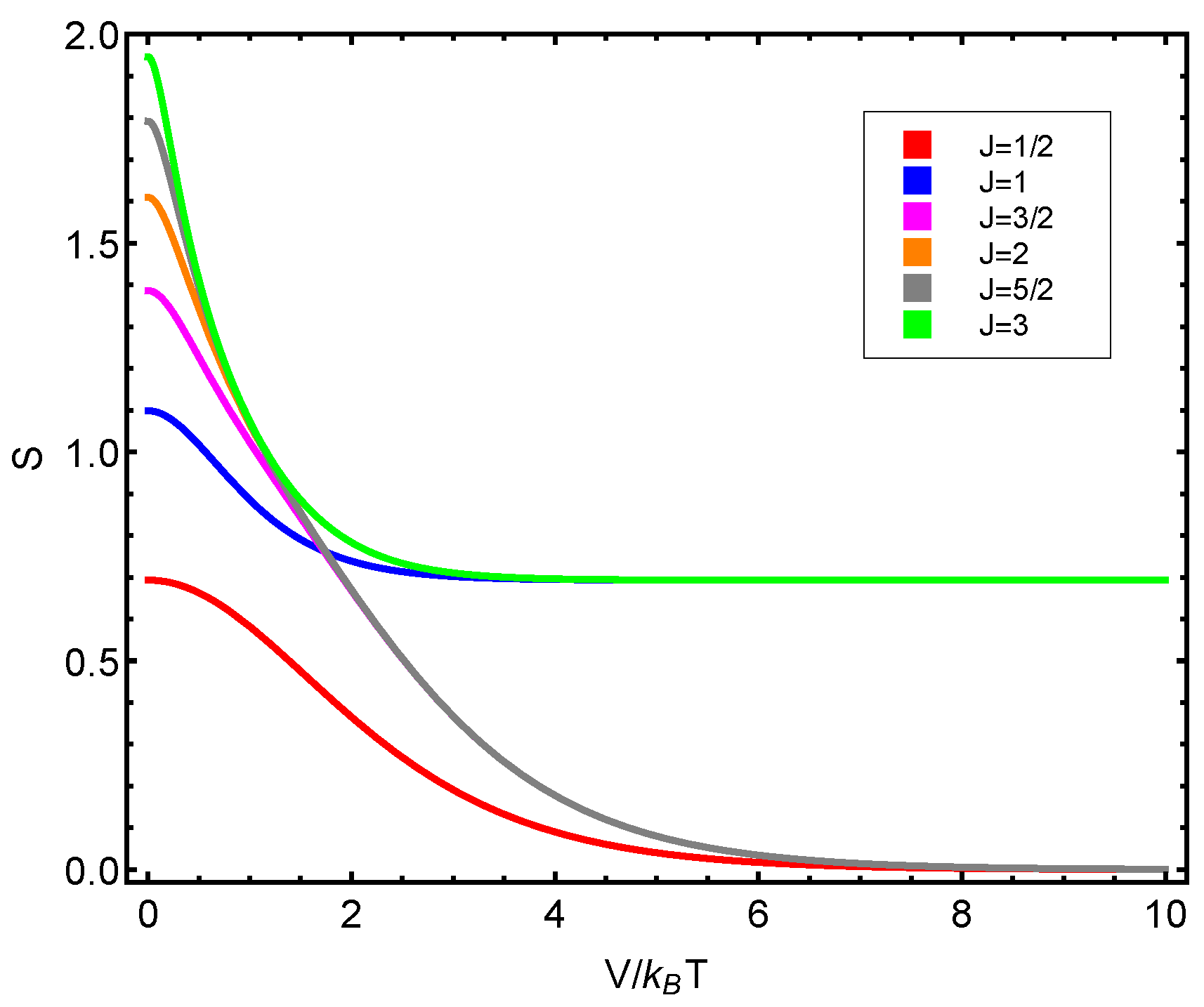
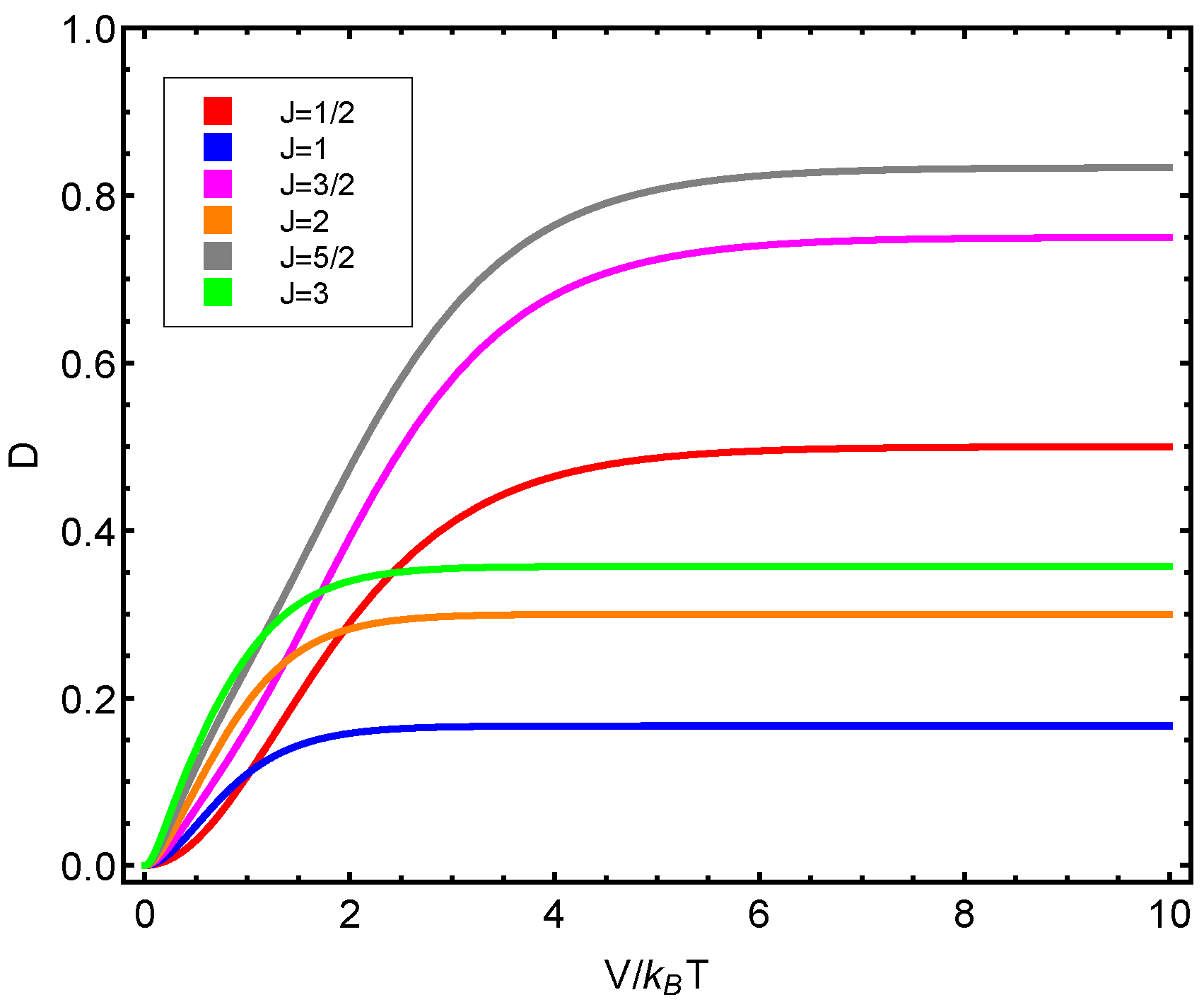
7.6. Application Results
8. Conclusions
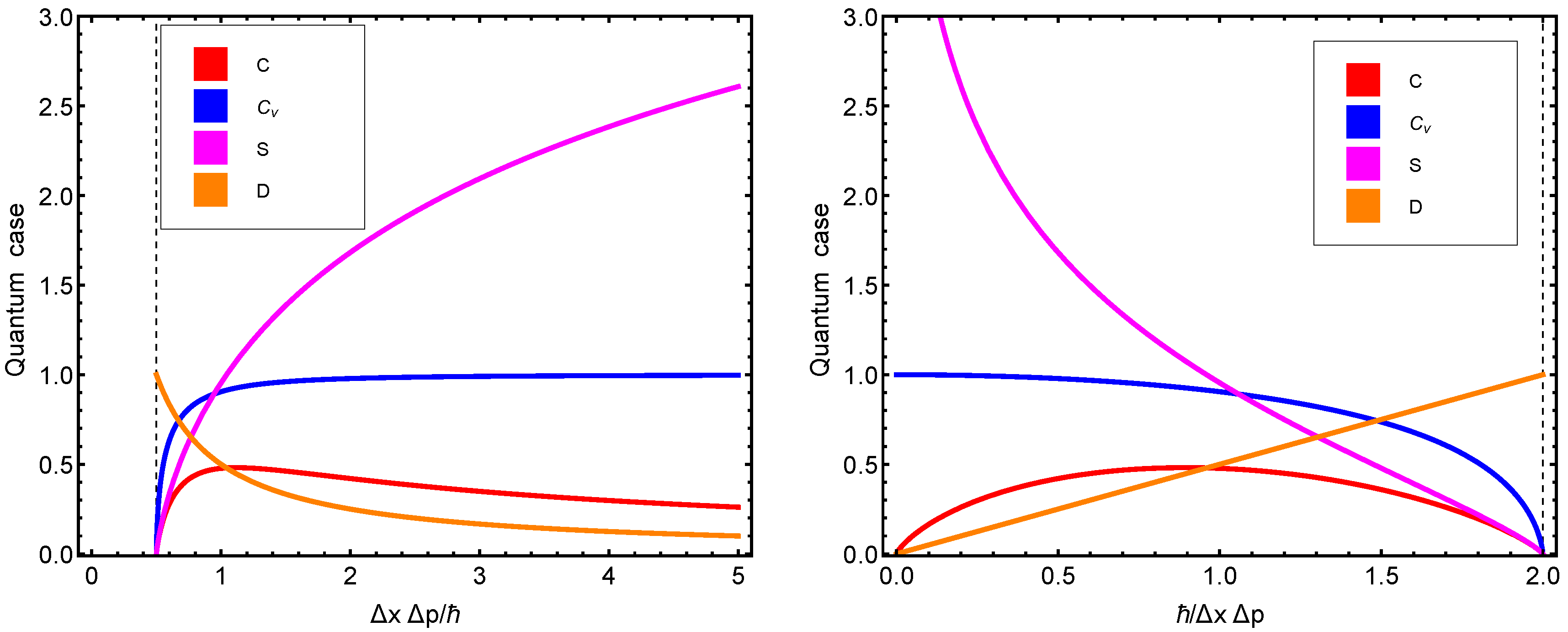
- At the minimum minimorum uncertainty value, the entropy, specific heat, and structural quantifier C all vanish.
- There is a strong connection between the disequilibrium D and the thermal uncertainty (TU). As D grows, the TU decreases. The TU is minimal for pure states where .
- Note that all quantities involved in (15) are observable (in principle), so we are dealing with a relation that has its counterpart in nature.
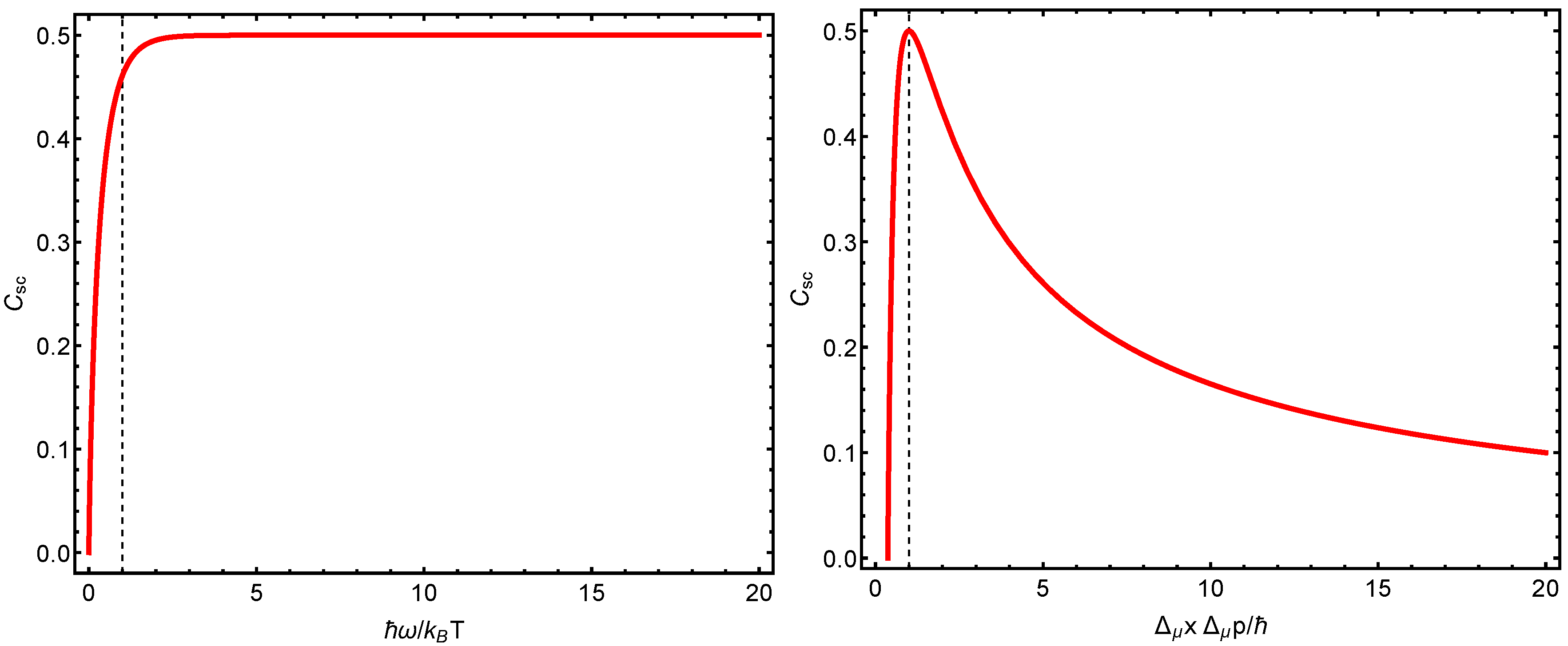
- The Wehrl structural quantifier attains its maximum values at the same place at which the quantal structural quantifier C does so.
- This place corresponds to the maximum possible semi-classical localization in phase space.
- Wehrl’s structural quantifier grows from zero at null vibrational energy (VE) until the VE attains half of the thermal–kinetic energy, and then remains constant.
- can be regarded as the phase-space localization error e (in its natural units) that accompanies the Husimi distribution.
- The Wehrl structural quantifier becomes a maximum in these circumstances.
- We emphasize that attains its constant classical value as soon as the thermal energy equals the vibrational one.
- The three different structural quantifiers, C, at play in this work behave in a remarkably similar fashion, as shown in the last graphs.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LMC | Lopez-Rioz, Mancini, and Calbet |
| LMCTSQ | Lopez-Rioz, Mancini, and Calbet thermal structural quantifiers |
| TUR | Thermal uncertainty relation |
| HO | Harmonic oscillator |
| MM | Minimum minimorum |
| TQF | Thermal quantum quantifiers |
| HD | Husimi distributions |
| DD | Density distribution |
| LM | Lipkin model |
Appendix A. Mathematics Program

References
- Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; Lopez-Rosa, S.; Flores-Gallegos, N. Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 2010, 12, 7108–7116. [Google Scholar] [CrossRef] [PubMed]
- Toranzo, I.V.; Dehesa, J.S. Entropy and complexity properties of the d-dimensional blackbody radiation. Eur. Phys. J. D 2014, 68, 316. [Google Scholar] [CrossRef]
- Bouvrie, P.A.; Angulo, J.C.; Dehesa, J.S. Entropy and complexity analysis of Dirac-delta-like quantum potentials. Physica A 2011, 390, 2215–2228. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Pennnini, F.; Plastino, A. Disequilibrium, thermodynamic relations, and Rényi’s entropy. Phys. Lett. A 2017, 381, 212–215. [Google Scholar] [CrossRef]
- López-Ruiz, R. Complexity in Some Physical System. Int. J. Bifurc. Chaos 2001, 11, 2669–2673. [Google Scholar] [CrossRef]
- Anteneodo, C.; Plastino, A.R. Some features of the López-Ruiz-Mancini-Calbet (LMC) statistical measure of complexity. Phys. Lett. A 1996, 223, 348–354. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Rudnicki, L.; Toranzo, I.V.; Sánchez-Moreno, P.; Dehesa, J.S. Monotone measures of statistical structural quantifier. Phys. Lett. A 2016, 380, 377–380. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Zunino, L.; Lenzi, E.K.; Santoro, P.A.; Mendes, R.S. Complexity-Entropy Causality Plane as a Complexity Measure for Two-Dimensional Patterns. PLoS ONE 2012, 7, e40689. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.; Calbet, X. A Statistical Measure of structural quantifier in Concepts and recent advances in generalized information measures and statistics. In Bentham Science Books; Kowalski, A., Rossignoli, R., Curado, E.M.C., Eds.; Bentham Science Publishers: New York, NY, USA, 2013; pp. 147–168. [Google Scholar]
- Sen, K.D. (Ed.) Statistical Structural Quantifier, Applications in Electronic Structure; Springer: Berlin, Germany, 2011. [Google Scholar]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized statistical structural quantifier measures: Geometrical and analytical properties. Physica A 2006, 369, 439–462. [Google Scholar] [CrossRef]
- Ghosh, P.; Nath, D. Complexity analysis of two families of orthogonal functions. Int. J. Quant. Chem. 2019, 119, e25964. [Google Scholar] [CrossRef]
- Fulop, A. Statistical complexity of the time dependent damped L84 model. Chaos 2019, 29, 083105. [Google Scholar] [CrossRef] [PubMed]
- Plastino, A.; Moszkowski, S.M. Simplified model for illustrating Hartree-Fock in a Lipkin-model problem. Nuovo Cimento 1978, 47, 470–474. [Google Scholar] [CrossRef]
- Kruse, M.K.G.; Miller, H.G.; Plastino, A.; Plastino, A.R. Thermodynamics’ third law and quantum phase transitions. Physica A 2010, 389, 2533–2540. [Google Scholar] [CrossRef]
- Kruse, M.K.G.; Miller, H.G.; Plastino, A.; Plastino, A.R. Thermodynamic Detection of Quantum Phase Transitions. Int. J. Mod. Phys. B 2010, 24, 5027–5036. [Google Scholar] [CrossRef]
- Cambiaggio, M.C.; Plastino, A.; Szybisz, L. Constrained Hartree-Fock and quasi-spin projection. Nucl. Phys. 1980, 344, 233–248. [Google Scholar] [CrossRef]
- Zander, C.; Plastino, A.; Plastino, A.R. Quantum entanglement in a many-body system exhibiting multiple quantum phase transitions. Braz. J. Phys. 2009, 39, 464–467. [Google Scholar] [CrossRef]
- Kruse, M.K.G.; Miller, H.G.; Plastino, A.; Plastino, A.R. Aspects of quantum phase transitions. arXiv 2008, arXiv:0809.3514. [Google Scholar]
- Lipkin, H.J.; Meshkov, N.; Glick, A.J. Validity of many-body approximation methods for a solvable model: (III). Diagram summations. Nucl. Phys. 1965, 62, 211–224. [Google Scholar] [CrossRef]
- Plastino, A.R.; Ferri, G.L.; Rocca, M.C.; Plastino, A. Information-Based Numerical Distancesbetween Equilibrium and Non-EquilibriumStates. Angelo Plastino J. Mod. Phys. 2020, 11, 1031–1043. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Statistical quantifiers for few-fermion’ systems. Physica A 2018, 491, 305–312. [Google Scholar] [CrossRef]
- Peltier, S.M.; Plastino, A. A density-matrix approach to critical phenomena. Nucl. Phys. 1984, 430, 397–408. [Google Scholar] [CrossRef]
- Nagata, S. Linkage between thermodynamic quantities and the uncertainty relation in harmonic oscillator model. Results Phys. 2016, 6, 946–951. [Google Scholar] [CrossRef][Green Version]
- Rosenfeld, L. Ergodic Theories; Caldirola, P., Ed.; Academic Press: New York, NY, USA, 1961. [Google Scholar]
- Mandelbrot, B. The role of sufficiency and of estimation in thermodynamics. Ann. Math. Stat. 1962, 33, 1021–1038. [Google Scholar] [CrossRef]
- Mandelbrot, B. An outline of a purely phenomenological theory of statistical thermodynamics–I: Canonical ensembles. IRE Trans. Inform. Theory 1956, 2, 190–203. [Google Scholar] [CrossRef]
- Mandelbrot, B. On the derivation of statistical thermodynamics from purely phenomenological principles. J. Math. Phys. 1964, 5, 164–171. [Google Scholar] [CrossRef]
- Lavenda, B.H. Thermodynamic uncertainty relations and irreversibility. Int. J. Theor. Phys. 1987, 26, 1069–1084. [Google Scholar] [CrossRef]
- Lavenda, B.H. Bayesian approach to thermostatistics. Int. J. Theor. Phys. 1988, 27, 451–472. [Google Scholar] [CrossRef]
- Lavenda, B.H. On the phenomenological basis of statistical thermodynamics. J. Phys. Chem. Solids 1988, 49, 685–693. [Google Scholar] [CrossRef]
- Uffink, J.; van Lith, J. Thermodynamic uncertainty relations. Found. Phys. 1999, 29, 655–692. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A.; Plastino, A.R.; Casas, M. How fundamental is the character of thermal uncertainty relations? Phys. Lett. A 2002, 302, 156–162. [Google Scholar] [CrossRef]
- Pathria, R.K. Statistical Mechanics; Pergamon Press: Exeter, UK, 1993. [Google Scholar]
- Dodonov, V.V. Quantum variances. J. Opt. BA 2001, 4, S98. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rep. Math. Phys. 1978, 16, 221. [Google Scholar] [CrossRef]
- Gnuzmann, S.; Życzkowski, K. Renyi-Wehrl entropies as measures of localization in phase space. J. Phys. A 2001, 34, 101233. [Google Scholar]
- Anderson, A.; Halliwell, J.J. Information-theoretic measure of uncertainty due to quantum and thermal fluctuations. Phys. Rev. D 1993, 48, 275. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Klauder, J.R.; Skagerstam, B.S. Coherent States; World Scientific: Singapore, 1985. [Google Scholar]
- Schnack, J. Thermodynamics of the harmonic oscillator using coherent states. Europhys. Lett. 1999, 45, 647. [Google Scholar] [CrossRef]
- Katz, A. Principles of Statistical Mechanics: The Information Theory Approach; Freeman and Co.: San Francisco, CA, USA, 1967. [Google Scholar]
- Husimi, K. Some formal properties of the density matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264–314. [Google Scholar]
- Lieb, E.H. Proof of an Entropy Conjecture of Wehrl. Commun. Math. Phys. 1978, 62, 35–41. [Google Scholar] [CrossRef]
- Pennini, F.; Plastino, A. Heisenberg-Fisher thermal uncertainty measure. Phys. Rev. E 2004, 69, 057101. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O. ; Zubairy, Quantum Optics; Cambridge University Press: Cambridge, NY, USA, 1997. [Google Scholar]
- Pennini, F.; Plastino, A. Power-law distributions and Fisher’s information measure. Physica A 2004, 334, 132–138. [Google Scholar] [CrossRef]
- Reif, F. Fundamentals of Statistical and Thermal Physics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Satuła, W.; Dobaczewski, J.; Nazarewicz, W. Odd-even staggering of nuclear masses: Pairing or shape effect? Phys. Rev. Lett. 1998, 81, 3599. [Google Scholar] [CrossRef]
- Dugett, T.; Bonche, P.; Heenen, P.H. Pairing correlations. II. Microscopic analysis of odd-even mass staggering in nuclei. J. Meyer 2001, 65, 014311. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin, Germany, 1980. [Google Scholar]
- Xu, F.R.; Wyss, R.; Walker, P.M. Mean-field and blocking effects on odd-even mass differences and rotational motion of nuclei. Phys. Rev. C 1999, 60, 051301(R). [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pennini, F.; Plastino, A.; Plastino, A.R.; Hernando, A. Structural Statistical Quantifiers and Thermal Features of Quantum Systems. Entropy 2021, 23, 19. https://doi.org/10.3390/e23010019
Pennini F, Plastino A, Plastino AR, Hernando A. Structural Statistical Quantifiers and Thermal Features of Quantum Systems. Entropy. 2021; 23(1):19. https://doi.org/10.3390/e23010019
Chicago/Turabian StylePennini, Flavia, Angelo Plastino, Angel Ricardo Plastino, and Alberto Hernando. 2021. "Structural Statistical Quantifiers and Thermal Features of Quantum Systems" Entropy 23, no. 1: 19. https://doi.org/10.3390/e23010019
APA StylePennini, F., Plastino, A., Plastino, A. R., & Hernando, A. (2021). Structural Statistical Quantifiers and Thermal Features of Quantum Systems. Entropy, 23(1), 19. https://doi.org/10.3390/e23010019





