Coupling between Blood Pressure and Subarachnoid Space Width Oscillations during Slow Breathing
Abstract
1. Introduction
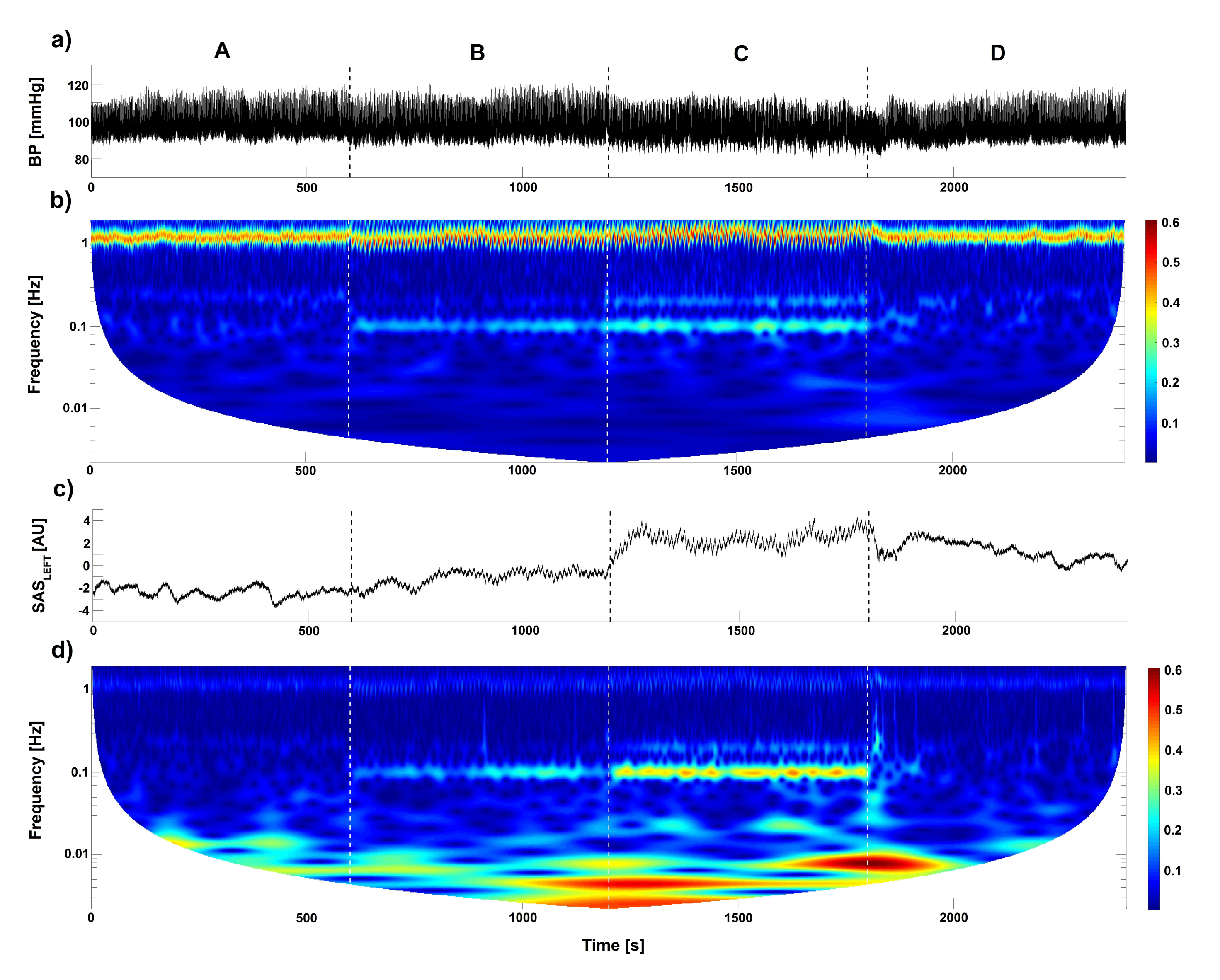
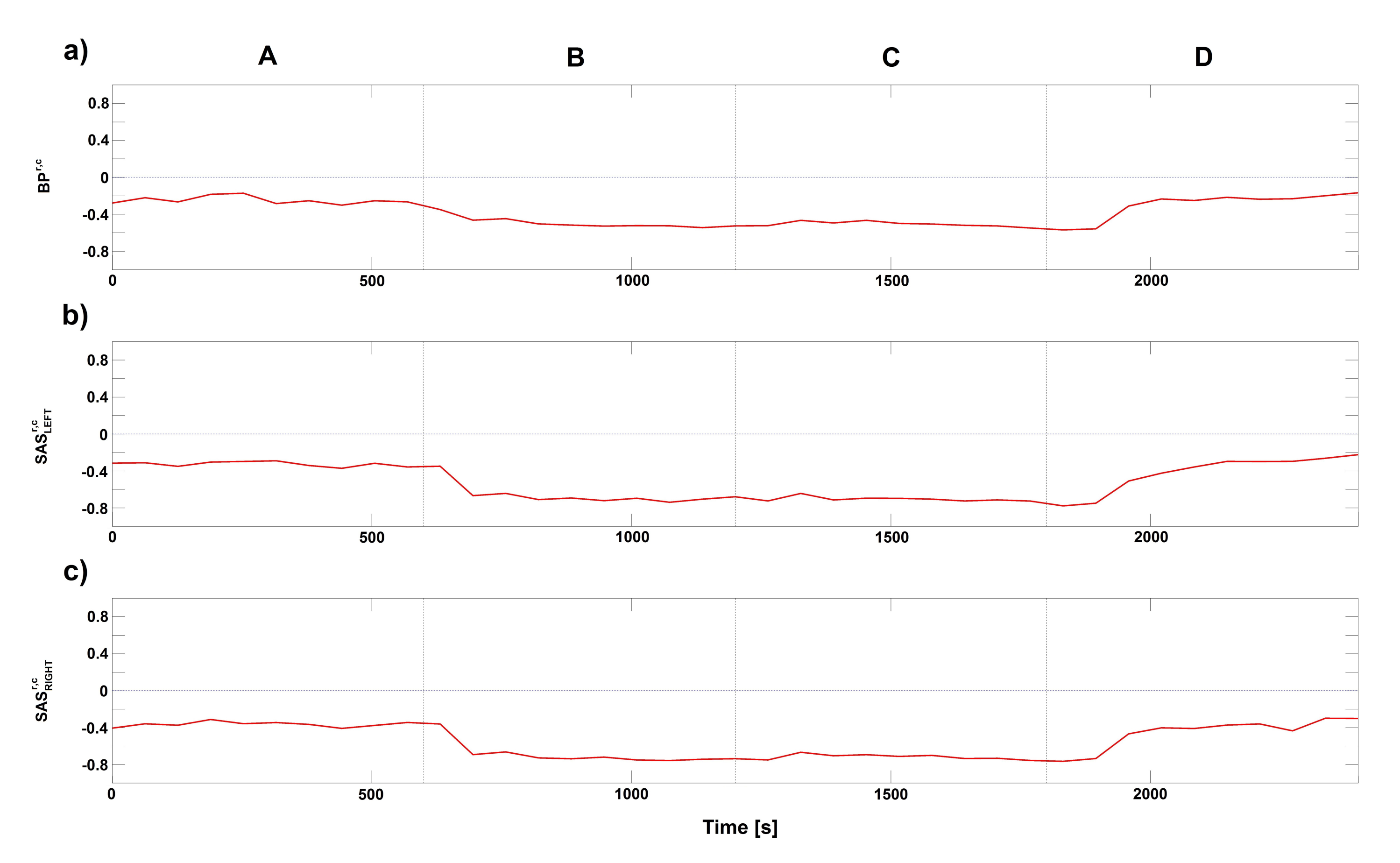
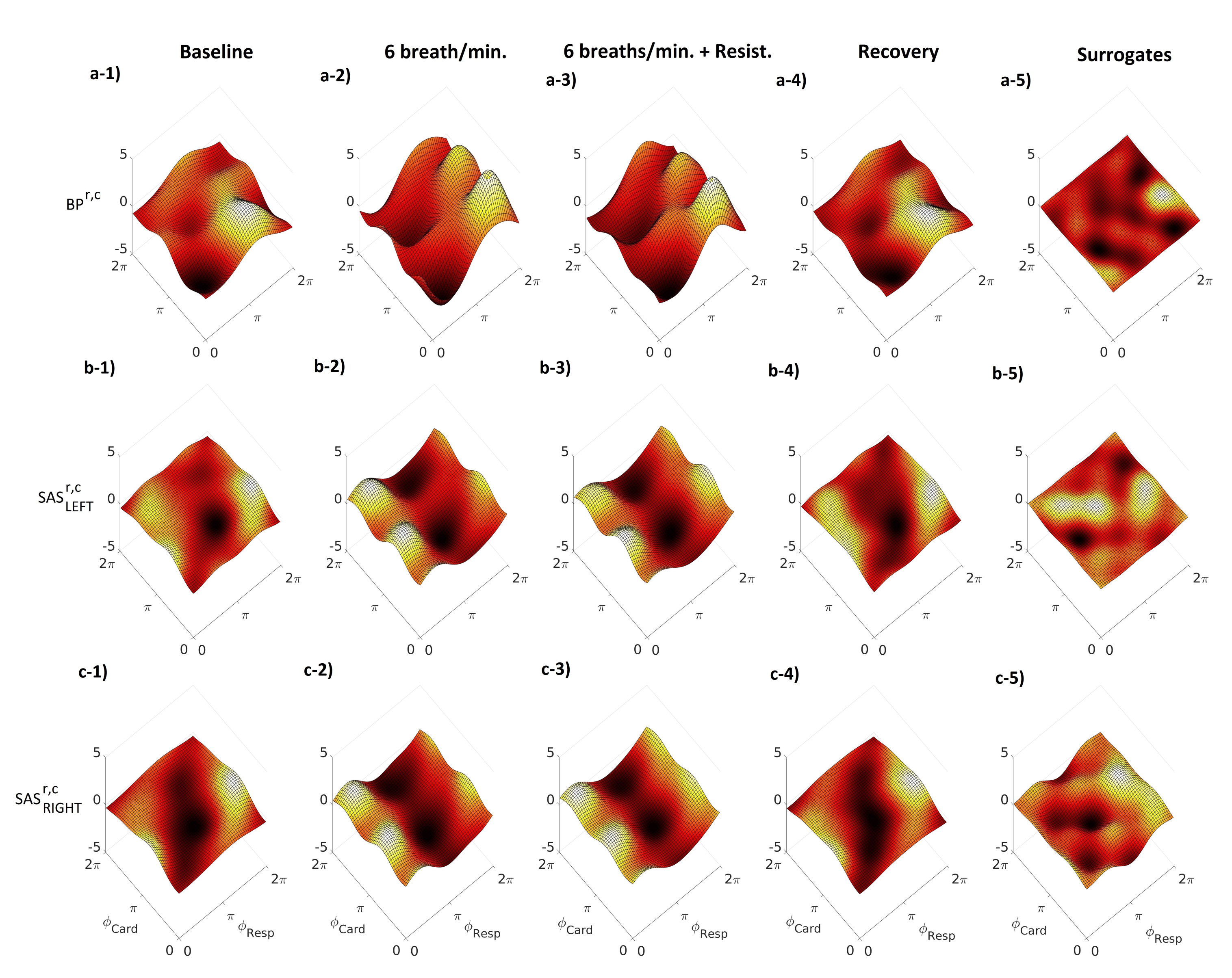
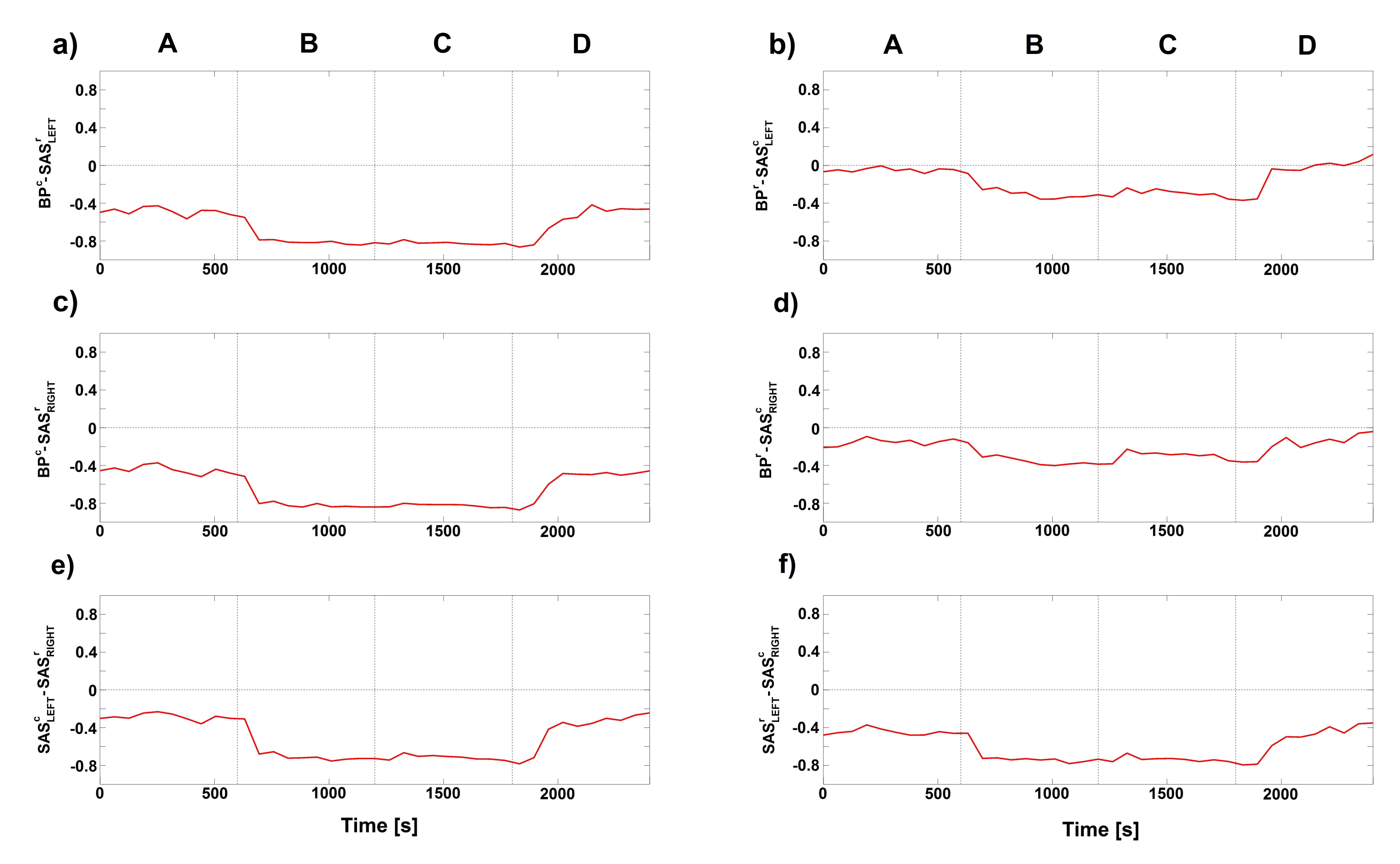
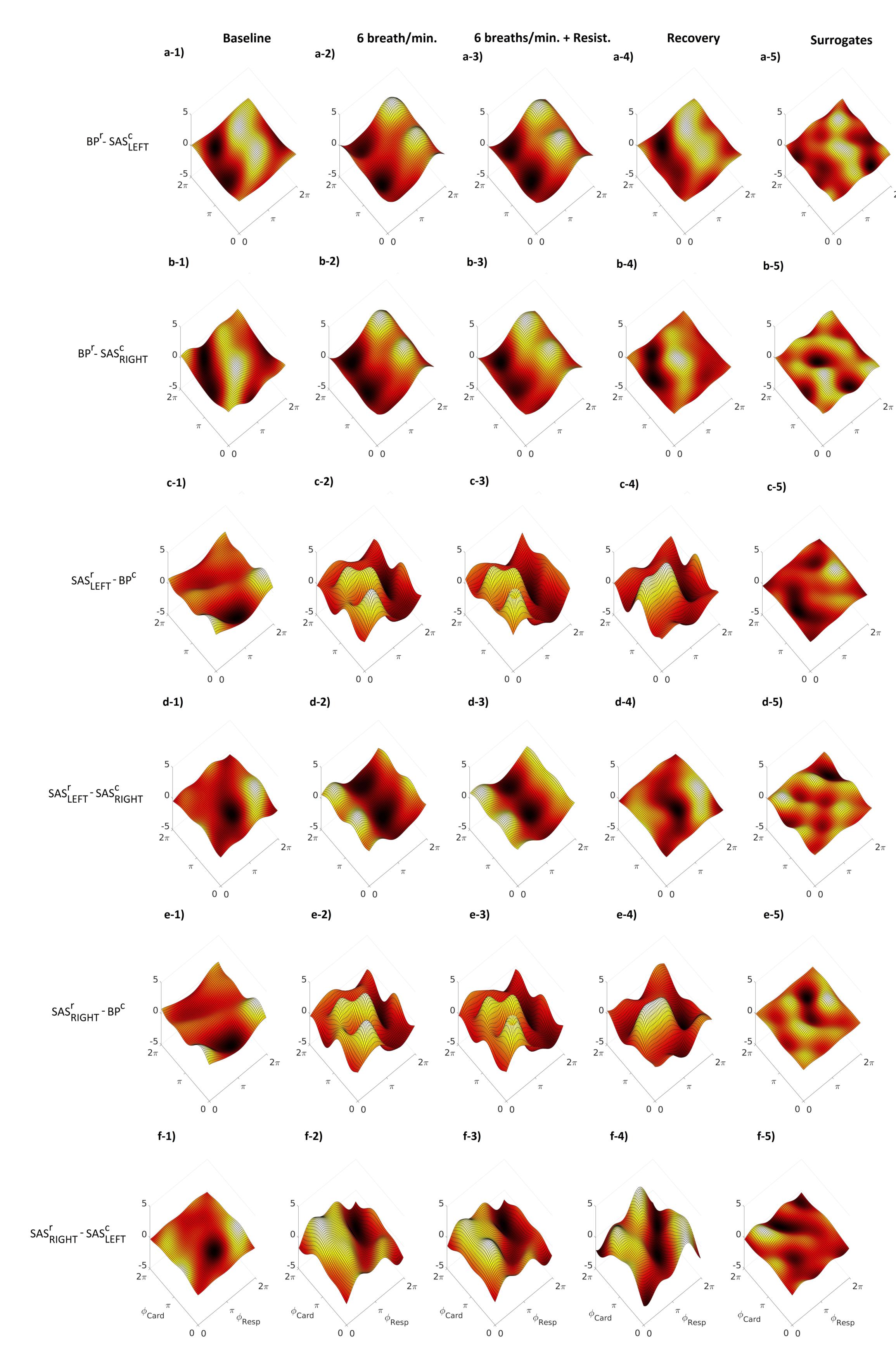
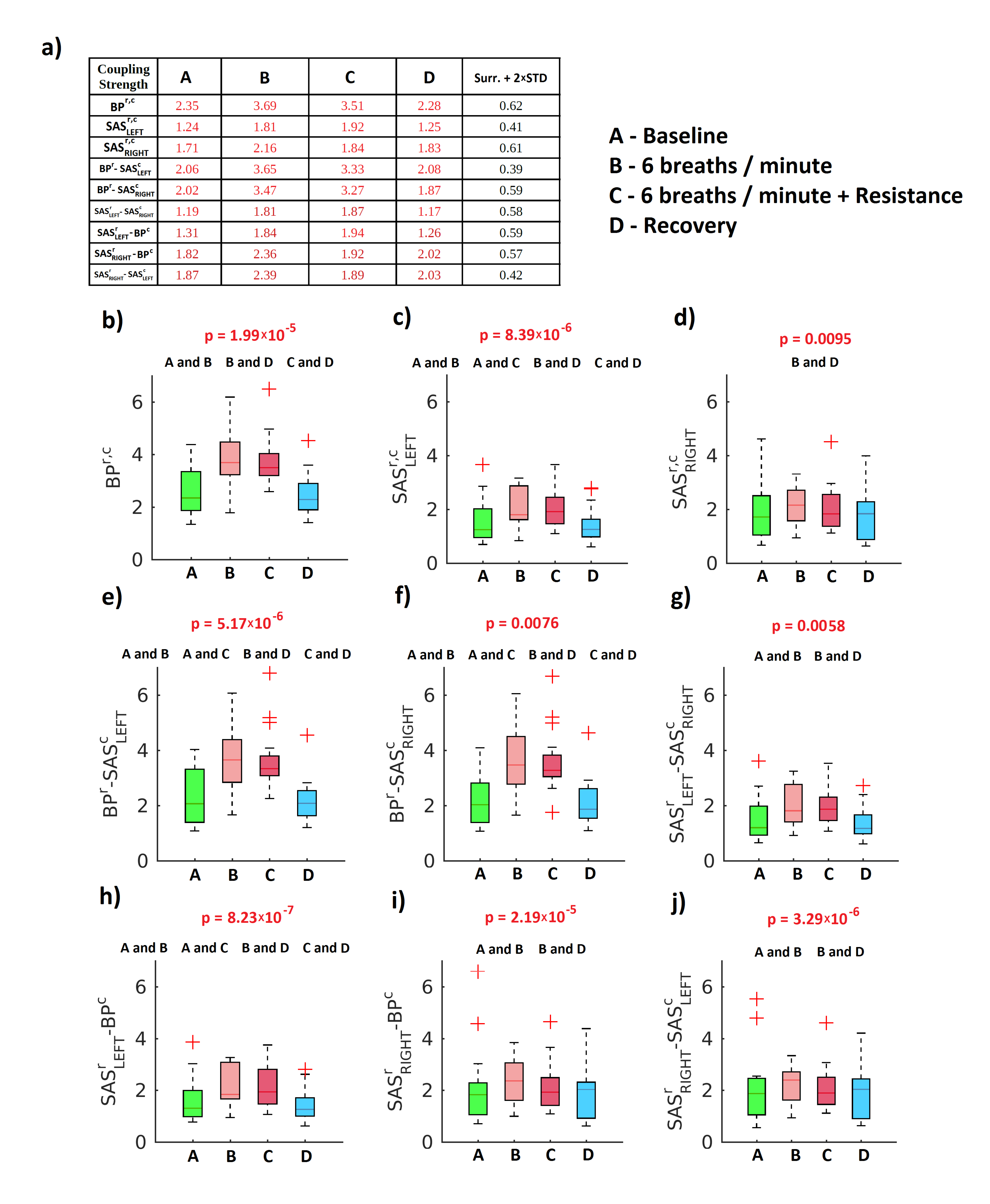
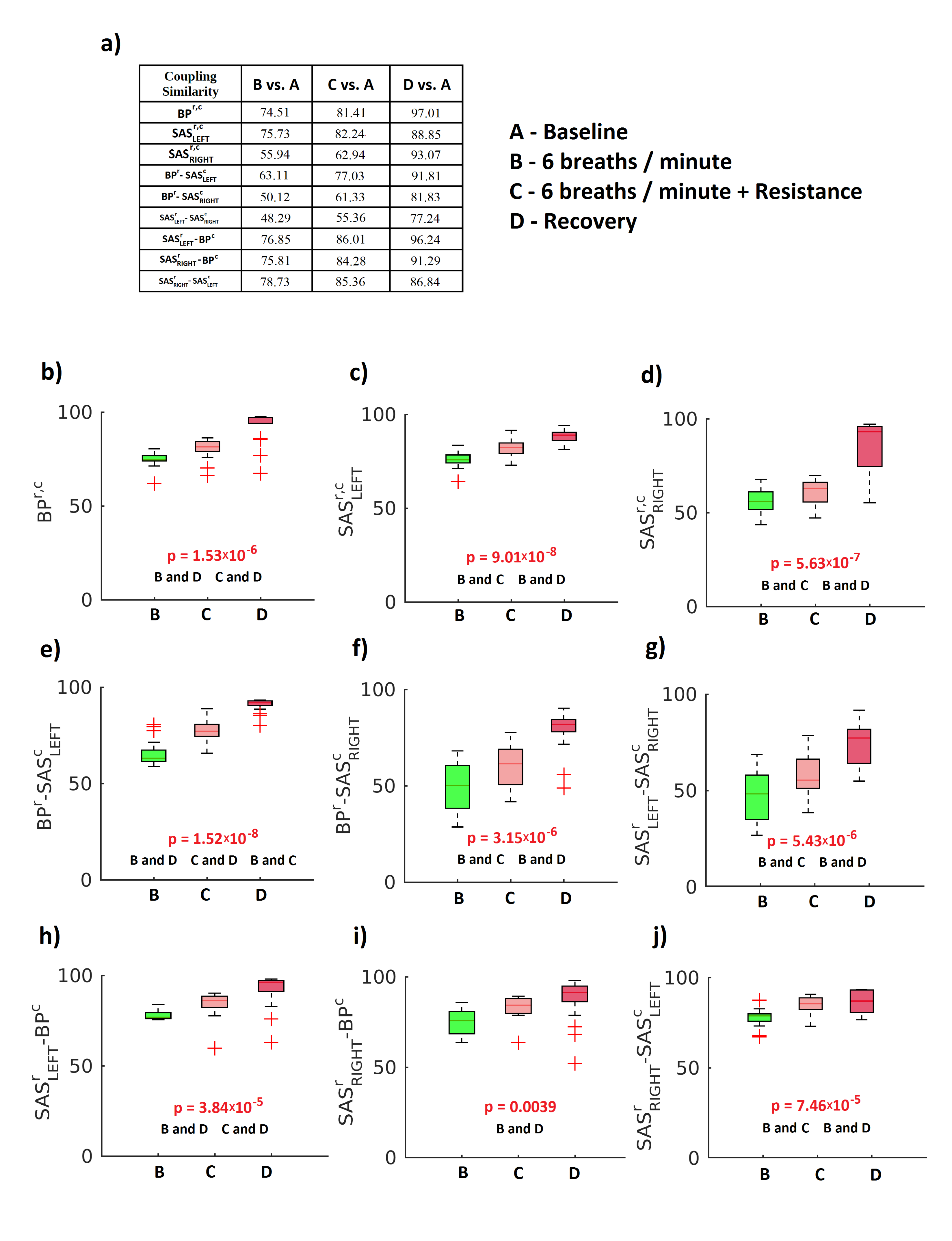
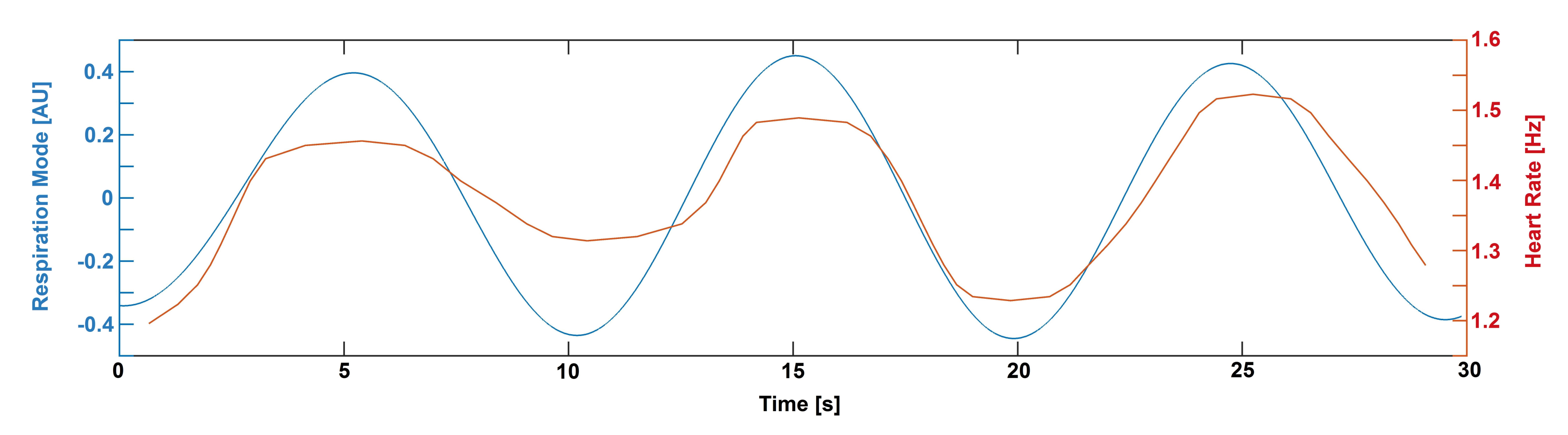
2. Results
3. Discussion
4. Materials and Methods
4.1. Subjects
4.2. Experimental Design
4.3. Measurements
4.4. Mathematical Analysis
4.4.1. Wavelet Analysis
4.4.2. Decomposition and Preprocessing
4.4.3. Modelling of Coupling Functions
4.4.4. Statistical Analysis and Surrogates
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ludwig, C. Beiträge zur Kenntniss des Einflusses der Respirationsbewegungen auf den Blutlauf im Aortensysteme. Arch. Anat. Physiol. 1847, 13, 242–302. [Google Scholar]
- Hirsch, J.A.; Bishop, B. Respiratory sinus arrhythmia in humans: How breathing patterns modulate heart rate. J. Physiol. 1981, 241, H620–H629. [Google Scholar] [CrossRef] [PubMed]
- Angelone, A.; Coulter, N.A. Respiratory sinus arrhythmia: A frequency dependent phenomenon. J. Appl. Physiol. 1964, 19, 479–482. [Google Scholar] [CrossRef] [PubMed]
- Vaschillo, E.G.; Vaschillo, B.; Lehrer, P.M. Characteristics of resonance in heart rate variability stimulated by biofeedback. Appl. Psychophysiol. Biofeedback 2006, 31, 129–142. [Google Scholar] [CrossRef] [PubMed]
- Zaccaro, A.; Piarulli, A.; Laurino, M.; Garbella, E.; Menicucci, D.; Neri, B.; Gemignani, A. How Breath-Control Can Change Your Life: A Systematic Review on Psycho-Physiological Correlates of Slow Breathing. Front. Hum. Neurosci. 2018, 12, 353. [Google Scholar] [CrossRef] [PubMed]
- Gruszecki, M.; Nuckowska, M.K.; Szarmach, A.; Radkowski, M.; Szalewska, D.; Waskow, M.; Szurowska, E.; Frydrychowski, A.F.; Demkow, U.; Winklewski, P.J. Oscillations of subarachnoid space width as a potential marker of cerebrospinal fluid pulsatility. Adv. Exp. Med. Biol. 2018, 1070, 37–47. [Google Scholar]
- Winklewski, P.J.; Wolf, J.; Gruszecki, M.; Wszedybyl-Winklewska, M.; Narkiewicz, K. Current understanding of the effects of inspiratory resistance on the interactions between systemic blood pressure, cerebral perfusion, intracranial pressure, and cerebrospinal fluid dynamics. J. Appl. Physiol. 2019, 127, 1206–1214. [Google Scholar] [CrossRef]
- Plucinski, J.; Frydrychowski, A.F.; Kaczmarek, J.; Juzwa, W. Theoretical foundations for noninvasive measurement of variations in the width of the subarachnoid space. J. Biomed. Opt. 2000, 5, 291–299. [Google Scholar] [CrossRef]
- Frydrychowski, A.F.; Guminski, W.; Rojewski, M.; Kaczmarek, J.; Juzwa, W. Technical foundations for noninvasive assessment of changes in the width of the subarachnoid space with near-infrared transillumination-backscattering sounding (NIR-TBSS). IEEE Trans. Biomed. Eng. 2002, 49, 887–904. [Google Scholar] [CrossRef]
- Plucinski, J.; Frydrychowski, A.F. New aspects in assessment of changes in width of subarachnoid space with near-infrared transillumination/backscattering sounding, part 1: Monte Carlo numerical modeling. J. Biomed. Opt. 2007, 12, 044015. [Google Scholar] [CrossRef]
- Frydrychowski, A.F.; Plucinski, J. New aspects in assessment of changes in width of subarachnoid space with near-infrared transillumination/backscattering sounding, part 2: Clinical verification in the patient. J. Biomed. Opt. 2007, 12, 044016. [Google Scholar] [CrossRef] [PubMed]
- Frydrychowski, A.F.; Szarmach, A.; Czaplewski, B.; Winklewski, P.J. Subarachnoid space: New tricks by an old dog. PLoS ONE 2012, 7, e37529. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nuckowska, M.K.; Gruszecki, M.; Kot, J.; Wolf, J.; Guminski, W.; Frydrychowski, A.F.; Wtorek, J.; Narkiewicz, K.; Winklewski, P.J. Impact of slow breathing on the blood pressure and subarachnoid space width oscillations in humans. Sci. Rep. 2019, 9, 6232. [Google Scholar] [CrossRef] [PubMed]
- Stankovski, T.; Pereira, T.; McClintock, P.V.E.; Stefanovska, A. Coupling functions: Universal insights into dynamical interaction mechanisms. Rev. Mod. Phys. 2017, 89, 045001. [Google Scholar] [CrossRef]
- Stankovski, T.; Pereira, T.; McClintock, P.V.E.; Stefanovska, A. Coupling Functions: Dynamical Interaction Mechanisms in the Physical, Biological and Social Sciences. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2019, 377, 20190039. [Google Scholar] [CrossRef] [PubMed]
- Kralemann, B.; Frühwirth, M.; Pikovsky, A.; Rosenblum, M.; Kenner, T.; Schaefer, J.; Moser, M. In vivo cardiac phase response curve elucidates human respiratory heart rate variability. Nat. Commun. 2013, 4, 2418. [Google Scholar] [CrossRef]
- Kiss, I.Z.; Zhai, Y.; Hudson, J.L. Predicting Mutual Entrainment of Oscillators with Experiment-Based Phase Models. Phys. Rev. Lett. 2005, 94, 248301. [Google Scholar] [CrossRef]
- Tokuda, I.T.; Jain, S.; Kiss, I.Z.; Hudson, J.L. Inferring Phase Equations from Multivariate Time Series. Phys. Rev. Lett. 2007, 99, 064101. [Google Scholar] [CrossRef]
- Levnajić, Z.; Pikovsky, A. Network Reconstruction from Random Phase Resetting. Phys. Rev. Lett. 2011, 107, 034101. [Google Scholar] [CrossRef]
- Stankovski, T.; Duggento, A.; McClintock, P.V.E.; Stefanovska, A. Inference of Time-Evolving Coupled Dynamical Systems in the Presence of Noise. Phys. Rev. Lett. 2012, 109, 024101. [Google Scholar] [CrossRef]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. Neuroimage 2003, 19, 1273. [Google Scholar] [CrossRef]
- Kiss, I.Z.; Rusin, C.G.; Kori, H.; Hudson, J.L. Engineering complex dynamical structures: Sequential patterns and desynchronization. Science 2007, 316, 1886. [Google Scholar] [CrossRef] [PubMed]
- Moon, W.; Wettlaufer, J.S. Coupling functions in climate. Philos. Trans. R. Soc. A 2019, 377, 20190006. [Google Scholar] [CrossRef] [PubMed]
- Stankovski, T.; McClintock, P.V.E.; Stefanovska, A. Coupling functions enable secure communications. Phys. Rev. X 2014, 4, 011026. [Google Scholar] [CrossRef]
- Kralemann, B.; Cimponeriu, L.; Rosenblum, M.; Pikovsky, A.; Mrowka, R. Phase dynamics of coupled oscillators reconstructed from data. Phys. Rev. E 2008, 77, 066205. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, S.; Spaiser, V.; Mann, R.P.; Sumpter, D.J.T. Bayesian Dynamical Systems Modelling in the Social Sciences. PLoS ONE 2014, 9, e86468. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Iatsenko, D.; Bernjak, A.; Stankovski, T.; Shiogai, Y.; Owen-Lynch, P.J.; Clarkson, P.B.M.; McClintock, P.V.E.; Stefanovska, A. Evolution of cardiorespiratory interactions with age. Phil. Trans. R. Soc. Lond. A 2013, 371, 20110622. [Google Scholar] [CrossRef]
- Ticcinelli, V.; Stankovski, T.; Iatsenko, D.; Bernjak, A.; Bradbury, A.; Gallagher, A.; Clarkson, P.B.M.; McClintock, P.V.E.; Stefanovska, A. Coherence and coupling functions reveal microvascular impairment in treated hypertension. Front. Physiol. 2017, 8, 749. [Google Scholar] [CrossRef]
- Lukarski, D.; Ginovska, M.; Spasevska, H.; Stankovski, T. Time Window Determination for Inference of Time-Varying Dynamics: Application to Cardiorespiratory Interaction. Front. Physiol. 2020, in press. [Google Scholar] [CrossRef]
- Stankovski, T.; Petkoski, S.; Raeder, J.; Smith, A.F.; McClintock, P.V.E.; Stefanovska, A. Alterations in the coupling functions between cortical and cardio–respiratory oscillations due to anæsthesia with propofol and sevoflurane. Phil. Trans. R. Soc. A 2016, 374, 20150186. [Google Scholar] [CrossRef]
- Stankovski, T.; Ticcinelli, V.; McClintock, P.V.E.; Stefanovska, A. Neural Cross-Frequency Coupling Functions. Front. Syst. Neurosci. 2017, 11. [Google Scholar] [CrossRef] [PubMed]
- Onojima, T.; Goto, T.; Mizuhara, H.; Aoyagi, T. A dynamical systems approach for estimating phase interactions between rhythms of different frequencies from experimental data. PLoS Comput. Biol. 2018, 14, e1005928. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K.; Aoyagi, T.; Kitano, K. Bayesian Estimation of Phase Dynamics Based on Partially Sampled Spikes Generated by Realistic Model Neurons. Front. Comput. Neurosci. 2018, 11, 116. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Huo, C.; Wang, B.; Li, W.; Xu, G.; Liu, Q.; Li, Z. Alterations in the coupling functions between cerebral oxyhaemoglobin and arterial blood pressure signals in post-stroke subjects. PLoS ONE 2018, 13, e0195936. [Google Scholar] [CrossRef]
- Stankovski, T.; Cooke, W.; Rudas, L.; Stefanovska, A.; Eckberg, D. Time-frequency methods and voluntary ramped-frequency breathing: A powerful combination for exploration of human neurophysiological mechanisms. J. Appl. Physiol. 2013, 115, 1806–1821. [Google Scholar] [CrossRef]
- Bateman, G.A. Pulse-wave encephalopathy: A comparative study of the hydrodynamics of leukoaraiosis and normal-pressure hydrocephalus. Neuroradiology 2002, 44, 740–748. [Google Scholar] [CrossRef]
- Wszedybyl-Winklewska, M.; Wolf, J.; Szarmach, A.; Winklewski, P.J.; Szurowska, E.; Narkiewicz, K. Central sympathetic nervous system reinforcement in obstructive sleep apnoea. Sleep Med. Rev. 2018, 39, 143–154. [Google Scholar] [CrossRef]
- Avolio, A.; Kim, M.O.; Adji, A.; Gangoda, S.; Avadhanam, B.; Tan, I.; Butlin, M. Cerebral haemodynamics: Effects of systemic arterial pulsatile function and hypertension. Curr. Hypertens. Rep. 2018, 20, 20. [Google Scholar] [CrossRef]
- Bedussi, B.; Almasian, M.; de Vos, J.; VanBavel, E.; Bakker, E.N. Paravascular spaces at the brain surface: Low resistance pathways for cerebrospinal fluid flow. J. Cereb. Blood Flow Metab. 2018, 38, 719–726. [Google Scholar] [CrossRef]
- Mestre, H.; Tithof, J.; Du, W.; Song, T.; Peng, W.; Sweeney, A.M.; Olveda, G.; Thomas, J.H.; Nedergaard, M.; Kelley, D.H. Flow of cerebrospinal fluid is driven by arterial pulsations and is reduced in hypertension. Nat. Commun. 2018, 9, 4878. [Google Scholar] [CrossRef]
- Dreha-Kulaczewski, S.; Joseph, A.A.; Merboldt, K.D.; Ludwig, H.C.; Gartner, J.; Frahm, J. Identification of the Upward Movement of Human CSF In Vivo and its Relation to the Brain Venous System. J. Neurosci. 2017, 37, 2395–2402. [Google Scholar] [CrossRef] [PubMed]
- Wardlaw, J.M.; Benveniste, H.; Nedergaard, M.; Zlokovic, B.V.; Mestre, H.; Lee, H.; Doubal, F.N.; Brown, R.; Ramirez, J.; MacIntosh, B.J.; et al. Perivascular spaces in the brain: Anatomy, physiology and pathology. Nat. Rev. Neurol. 2020, 16, 137–153. [Google Scholar] [CrossRef] [PubMed]
- Tyler, W.J. The mechanobiology of brain function. Nat. Rev. Neurosci. 2012, 13, 867–878. [Google Scholar] [CrossRef] [PubMed]
- Roesmann, K.; Dellert, T.; Junghoefer, M.; Kissler, J.; Zwitserlood, P.; Zwanzger, P.; Dobel, C. The causal role of prefrontal hemispheric asymmetry in valence processing of words—Insights from a combined cTBS-MEG study. Neuroimage 2019, 191, 367–379. [Google Scholar] [CrossRef]
- Kiviniemi, V.; Wang, X.; Korhonen, V.; Keinanen, T.; Tuovinen, T.; Autio, J.; LeVan, P.; Keilholz, S.; Zang, Y.F.; Hennig, J.; et al. Flow of cerebrospinal fluid is driven by arterial pulsations and is reduced in hypertension. J. Cereb. Blood Flow Metab. 2016, 36, 1033–1045. [Google Scholar] [CrossRef]
- Schaller, B. Physiology of cerebral venous blood flow: From experimental data in animals to normal function in humans. Brain Res. Rev. 2004, 46, 243–260. [Google Scholar] [CrossRef]
- Guild, S.J.; Saxena, U.A.; McBryde, F.D.; Malpas, S.C.; Ramchandra, R. Intracranial pressure influences the level of sympathetic tone. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2018, 315, R1049–R1053. [Google Scholar] [CrossRef]
- Schmidt, E.A.; Despas, F.; Pavy-Le Traon, A.; Czosnyka, Z.; Pickard, J.D.; Rahmouni, K.; Pathak, A.; Senard, J.M. Intracranial Pressure Is a Determinant of Sympathetic Activity. Front. Physiol. 2018, 9, 11. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Song, G.; Poon, C.S. Modulation of Hering-Breuer reflex by ventrolateral pons. Adv. Exp. Med. Biol. 2008, 605, 387–392. [Google Scholar]
- St Croix, C.M.; Morgan, B.J.; Wetter, T.J.; Dempsey, J.A. Fatiguing inspiratory muscle work causes reflex sympathetic activation in humans. J. Physiol. 2000, 529, 493–504. [Google Scholar] [CrossRef]
- Winklewski, P.J.; Tkachenko, Y.; Mazur, K.; Kot, J.; Gruszecki, M.; Guminski, W.; Czuszynski, K.; Wtorek, J.; Frydrychowski, A.F.; Drvis, I.; et al. Effect of maximal apnoea easy-going and struggle phases on subarachnoid width and pial artery pulsation in elite breath-hold divers. PLoS ONE 2015, 10, e0135751. [Google Scholar] [CrossRef] [PubMed]
- Rickards, C.A.; Ryan, K.L.; Cooke, W.H.; Lurie, K.G.; Convertino, V.A. Inspiratory resistance delays the reporting of symptoms with central hypovolemia: Association with cerebral blood flow. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2007, 293, R243–R250. [Google Scholar] [CrossRef]
- Russo, M.A.; Santarelli, D.M.; O’Rourke, D. The physiological effects of slow breathing in the healthy human. Breathe 2012, 13, 298–309. [Google Scholar] [CrossRef] [PubMed]
- Radaelli, A.; Raco, R.; Perfetti, P.; Viola, A.; Azzellino, A.; Signorini, M.G.; Ferrari, A.U. Effects of slow, controlled breathing on baroreceptor control of heart rate and blood pressure in healthy men. J. Hypertens. 2004, 22, 1361–1370. [Google Scholar] [CrossRef] [PubMed]
- Joseph, C.N.; Porta, C.; Casucci, G.; Casiraghi, N.; Maffeis, M.; Rossi, M.; Bernardi, L. Slow breathing improves arterial baroreflex sensitivity and decreases blood pressure in essential hypertension. Hypertension 2005, 46, 714–718. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, L.; Bandinelli, G.; Wdowczyc-Szulc, J. Effect of rosary prayer and yoga mantras on autonomic cardiovascular rhythms: Comparative study. BMJ 2001, 323, 1446. [Google Scholar] [CrossRef]
- Rosengård-Bärlund, M.; Bernardi, L.; Holmqvist, J.; Debarbieri, G.; Mäntysaari, M.; Af Björkesten, C.G. Deep breathing improves blunted baroreflex sensitivity even after 30 years of type 1 diabetes. Diabetologia 2011, 54, 1862. [Google Scholar]
- Lachowska, K.; Bellwon, J.; Narkiewicz, K.; Gruchała, M.; Hering, D. Long-term effects of device-guided slow breathing in stable heart failure patients with reduced ejection fraction. Clin. Res. Cardiol. 2019, 108, 48–60. [Google Scholar] [CrossRef]
- Mestre, H.; Du, T.; Sweeney, A.M.; Liu, G.; Samson, A.J.; Peng, W.; Mortensen, K.N.; Stæger, F.F.; Bork, P.A.R.; Bashford, L.; et al. Cerebrospinal fluid influx drives acute ischemic tissue swelling. Science 2020, 13, 367. [Google Scholar] [CrossRef]
- Smelyanskiy, V.N.; Luchinsky, D.G.; Stefanovska, A.; McClintock, P.V.E. Inference of a Nonlinear Stochastic Model of the Cardiorespiratory Interaction. Phys. Rev. Lett. 2005, 94, 098101. [Google Scholar] [CrossRef]
- Bernjak, A.; Stefanovska, A.; McClintock, P.V.E.; Owen-Lynch, P.J.; Clarkson, P.B.M. Coherence between fluctuations in blood flow and oxygen saturation. Fluct. Noise Lett. 2012, 11, 1240013. [Google Scholar] [CrossRef]
- Stefanovska, A.; Bračič, M.; Kvernmo, H.D. Wavelet analysis of oscillations in the peripheral blood circulation measured by laser Doppler technique. IEEE Trans. Biomed. Eng. 1999, 46, 1230–1239. [Google Scholar] [CrossRef] [PubMed]
- Selesnick, I.W.; Burrus, C.S. Generalized digital Butterworth filter design. IEEE Trans. Signal Process. 1998, 46, 1688–1694. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Duggento, A.; Luchinsky, D.G.; Smelyanskiy, V.N.; Khovanov, I.; McClintock, P.V.E. Inferential framework for nonstationary dynamics. I. Theory. Phys. Rev. E 2008, 77, 061106. [Google Scholar] [CrossRef] [PubMed]
- Wilting, J.; Lehnertz, K. Bayesian inference of interaction properties of noisy dynamical systems with time-varying coupling: Capabilities and limitations. Eur. Phys. J. B 2015, 88, 193. [Google Scholar] [CrossRef]
- Bahraminasab, A.; Ghasemi, F.; Stefanovska, A.; McClintock, P.V.E.; Kantz, H. Direction of Coupling from Phases of Interacting Oscillators: A Permutation Information Approach. Phys. Rev. Lett. 2008, 100, 084101. [Google Scholar] [CrossRef]
- Jamšek, J.; Paluš, M.; Stefanovska, A. Detecting couplings between interacting oscillators with time-varying basic frequencies: Instantaneous wavelet bispectrum and information theoretic approach. Phys. Rev. E 2010, 81, 036207. [Google Scholar] [CrossRef]
- Jirsa, V.; Müller, V. Cross-frequency coupling in real and virtual brain networks. Front. Comput. Neurosci. 2013, 7, 78. [Google Scholar] [CrossRef]
- Paluš, M.; Stefanovska, A. Direction of coupling from phases of interacting oscillators: An information-theoretic approach. Phys. Rev. E 2003, 67, 055201. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S. Detecting direction of coupling in interacting oscillators. Phys. Rev. E 2001, 64, 045202. [Google Scholar] [CrossRef]
- Varela, F.; Lachaux, J.P.; Rodriguez, E.; Martinerie, J. The brainweb: Phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2001, 2, 045202. [Google Scholar] [CrossRef] [PubMed]
- Von Toussaint, U. Bayesian inference in physics. Rev. Mod. Phys. 2011, 83, 943. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization—A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Duggento, A.; Stankovski, T.; McClintock, P.V.E.; Stefanovska, A. Dynamical Bayesian inference of time-evolving interactions: From a pair of coupled oscillators to networks of oscillators. Phys. Rev. E 2012, 86, 061126. [Google Scholar] [CrossRef] [PubMed]
- Kralemann, B.; Pikovsky, A.; Rosenblum, M. Reconstructing phase dynamics of oscillator networks. Chaos 2011, 21, 025104. [Google Scholar] [CrossRef] [PubMed]
- Stankovski, T.; Duggento, A.; McClintock, P.V.E.; Stefanovska, A. A tutorial on time-evolving dynamical Bayesian inference. Eur. Phys. J. Spec. Top. 2014, 223, 2685. [Google Scholar] [CrossRef]
- Stankovski, T.; Ticcinelli, V.; McClintock, P.V.E.; Stefanovska, A. Coupling functions in networks of oscillators. New J. Phys. 2015, 17, 035002. [Google Scholar] [CrossRef]
- Lancaster, G.; Iatsenko, D.; Pidde, A.; Ticcinelli, V.; Stefanovska, A. Surrogate data for hypothesis testing of physical systems. Phys. Rep. 2018, 748, 1–60. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruszecka, A.; Nuckowska, M.K.; Waskow, M.; Kot, J.; Winklewski, P.J.; Guminski, W.; Frydrychowski, A.F.; Wtorek, J.; Bujnowski, A.; Lass, P.; et al. Coupling between Blood Pressure and Subarachnoid Space Width Oscillations during Slow Breathing. Entropy 2021, 23, 113. https://doi.org/10.3390/e23010113
Gruszecka A, Nuckowska MK, Waskow M, Kot J, Winklewski PJ, Guminski W, Frydrychowski AF, Wtorek J, Bujnowski A, Lass P, et al. Coupling between Blood Pressure and Subarachnoid Space Width Oscillations during Slow Breathing. Entropy. 2021; 23(1):113. https://doi.org/10.3390/e23010113
Chicago/Turabian StyleGruszecka, Agnieszka, Magdalena K. Nuckowska, Monika Waskow, Jacek Kot, Pawel J. Winklewski, Wojciech Guminski, Andrzej F. Frydrychowski, Jerzy Wtorek, Adam Bujnowski, Piotr Lass, and et al. 2021. "Coupling between Blood Pressure and Subarachnoid Space Width Oscillations during Slow Breathing" Entropy 23, no. 1: 113. https://doi.org/10.3390/e23010113
APA StyleGruszecka, A., Nuckowska, M. K., Waskow, M., Kot, J., Winklewski, P. J., Guminski, W., Frydrychowski, A. F., Wtorek, J., Bujnowski, A., Lass, P., Stankovski, T., & Gruszecki, M. (2021). Coupling between Blood Pressure and Subarachnoid Space Width Oscillations during Slow Breathing. Entropy, 23(1), 113. https://doi.org/10.3390/e23010113





