Exploring the Possibility of a Recovery of Physics Process Properties from a Neural Network Model
Abstract
1. Introduction
2. Results
2.1. The Jet Generator
2.2. The Neyman–Pearson Lemma
2.3. Recovering the Original Probability Distribution
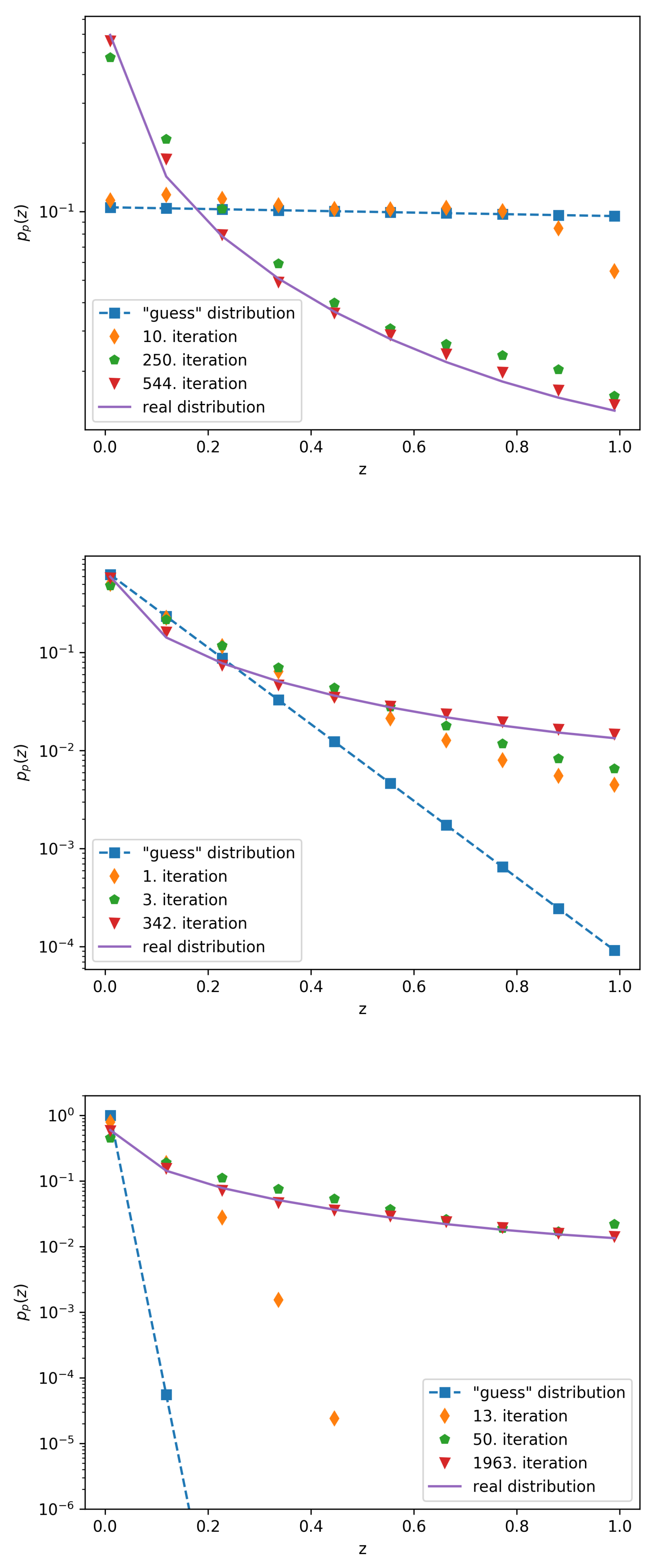
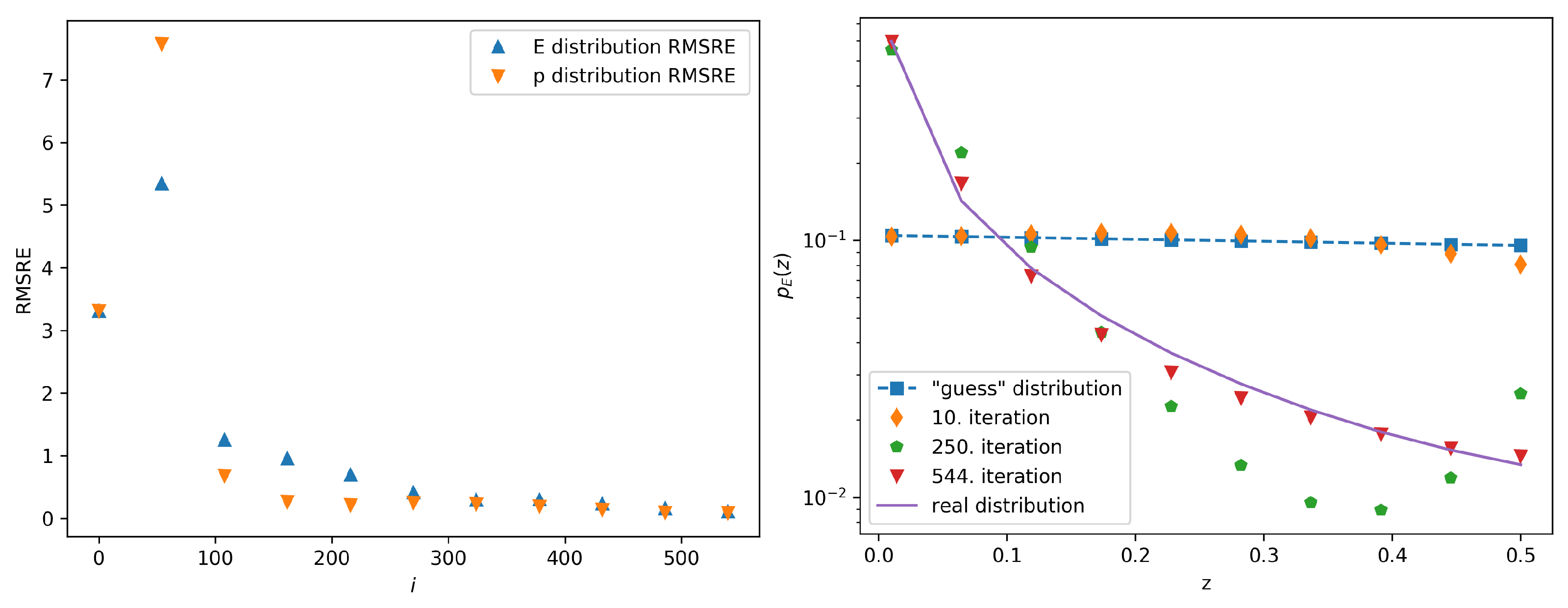
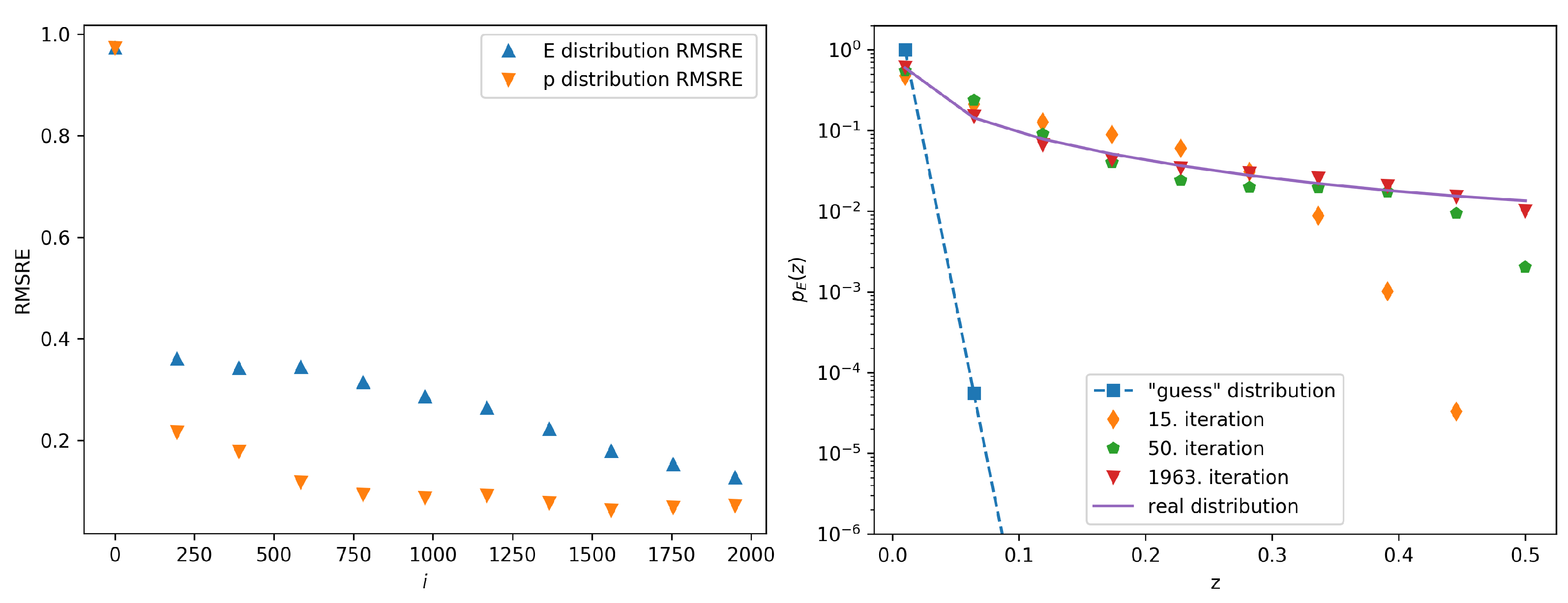
2.4. Calculation Results and Errors
3. Discussion
4. Materials and Methods
4.1. The Jet Generator
- We start with a particle at rest with a given rest mass, here taken to be 100 (the units are inconsequential in the calculation).
- The particle decays into two new particles. The energies and the momenta of these particles are determined by a probability distribution. To generate the real data we use a distribution already known in particle physics, given by:The energy of the decay particle E equals , with being the energy of the decaying particle. Note that the probability diverges as z approaches zero, so the distribution is limited by a lower boundary on z both due to physical and computational reasons. is a constant that ensures that the integral of the probability distribution equals 1 and depends on the lower boundary set on z. In our simulation, we set the minimum z to 10, making equal to .The momentum of the decay particle is limited with the total energy of the particle. We determine the momentum by sampling the same probability distribution as for the energy, but now we set the momentum p equal to , with E being the energy of the decay particle. To differentiate between these z distributions, we write and when deemed necessary.The spatial distribution of the decay products is uniform in space. This means that, observed from the rest frame of the decaying particle, the probability that either one of the decay products flies off in a certain infinitesimal solid angle is uniform. Physically speaking, the angles and are sampled from uniform distributions on intervals and , respectively.The energy, the momentum and the direction of the second particle are determined by the laws of conservation of energy and momentum. In other words, when looking at energy, and , since the original momentum in the center of mass system is zero. These facts also save computational time due to symmetry, since we can sample for the energy of the first particle in the interval , instead of placing the upper limit for z to 1.
- After the first decay, the procedure repeats iteratively, i.e., we repeat step 2 for both decay products from the previous step. The only difference compared to the previous step is that we now perform the calculations for each particle in its center of mass frame and then transform the obtained quantities back to the laboratory frame, which coincides with the center of mass frame of the original particle.Once the total number of particles exceeds a pre-determined threshold (in our case set to 32), we disregard the lowest energy particles. We do this both to reduce the computational time and because we determined that these particles do not influence our end result in a significant manner.The decay procedure stops when either of two conditions is met; if the decay particle mass falls below 0.1, or a certain number of decays has been reached. In the simulations, we limited the number of decays in a single branch to 50. For simplicity, all the decays are considered to happen in the same point in space.
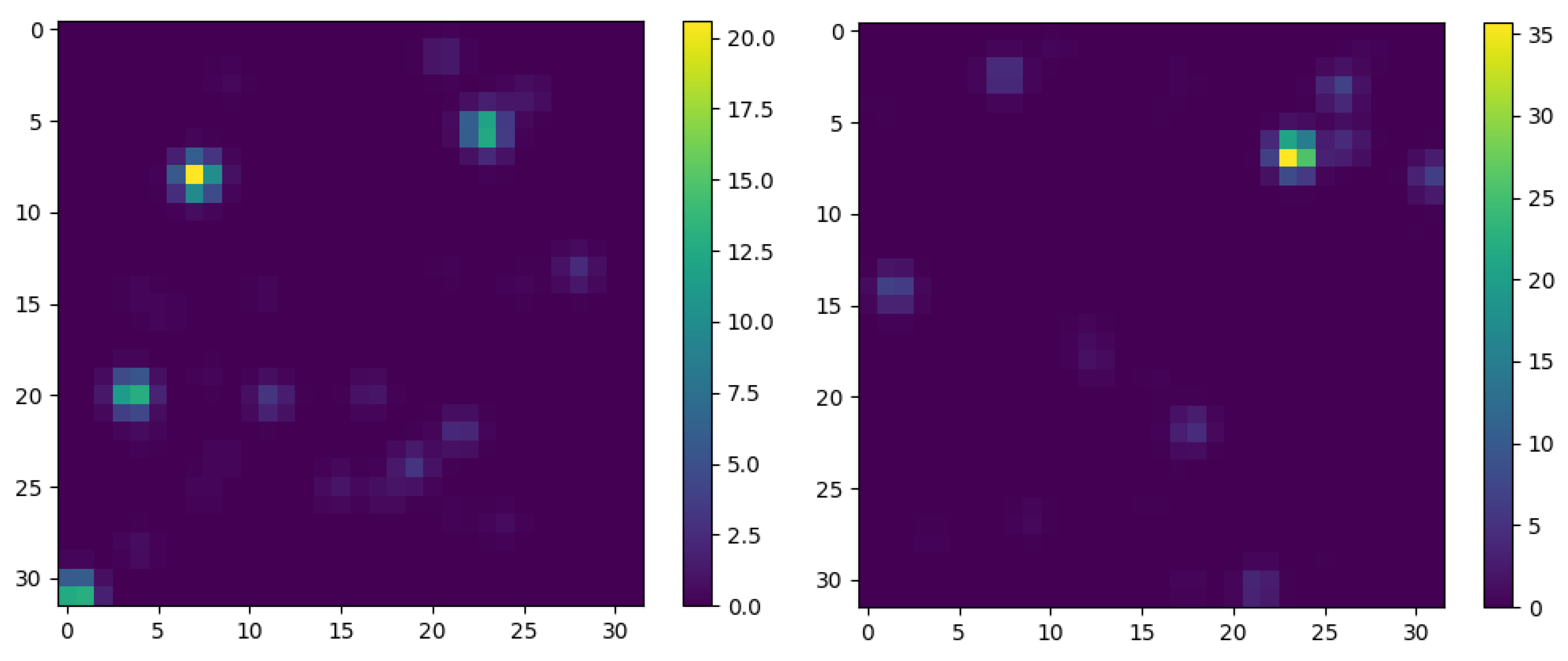
- The list of final decay particles now forms a list that contains the energies, the momenta and the directions of the n particles. We call this entity a jet. The jet has a maximum of 32 particles in its final state stemming from a maximum of 1 + 2 + 4 + 8 + 16 + 45·32 = 1471 decays. Hence, the full description of a jet is given by a maximum of 1471 parameters, 1471 parameters and 1471 pairs of angles (, ).To create the final representation of the jet which will be fed to a classifier, we create a histogram whose axes represent the direction of a particle in space. The histogram has 32 × 32 pixels with axes representing the polar angle and the azimuthal angle of a particle. The color of a pixel in the histogram corresponds to either the energy or the momentum of the particle traveling in that direction in space. We distribute the deposited energy and momentum as Gaussian distributions in the histograms, with the Gaussian of equal to 1 pixel centralized at the pixel corresponding to a direction of a certain particle. This mimics the physics situation in real life, where the readout from a detector always consists of a signal and a background noise. In fact, even when simulating data in a deterministic way, this effect is taken into account [12]. Lastly, the energy and momentum histograms are stacked to create an image with dimensions 32 × 32 × 2. An example of the jet generator tree with modified parameters is given in the appendix. Two examples of jet images are given on Figure 1 in the main body of the text.
4.2. The Classifier
4.3. The Algorithm Used to Recover the Underlying Probability Distributions
4.3.1. Generating the Data From the Obtained Distributions
4.3.2. Training the CNN Classifier
4.3.3. Calculation of the Probability Distributions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| QCD | Quantum Chromodynamics |
| LHC | Large Hadron Collider |
| RMSRE | Root mean square relative error |
| CNN | Convolutional Neural Network |
| AUC | Area Under the Curve |
Appendix A. An Example of a Generated Jet

Appendix B. Supplementary Results
References
- Sjostrand, T.; Mrenna, S.; Skands, P. PYTHIA 6.4 Physics and Manual. arXiv 2006, arXiv:hep-ph/0603175. [Google Scholar] [CrossRef]
- Neyman, J.; Pearson, E.S. On the problem of the most efficient tests of statistical hypotheses. Philos. Trans. R. Soc. Lond. A 1933, 231, 694–706. [Google Scholar]
- Streit, R.L. A neural network for optimum Neyman-Pearson classification. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; pp. 685–690. [Google Scholar]
- Tong, X.; Feng, Y.; Li, J.J. Neyman-Pearson classification algorithms and NP receiver operating characteristics. Sci. Adv. 2018, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- Altarelli, G.; Parisi, G. Asymptotic freedom in parton language. NPB 1977, 126, 298–318. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. NAT 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A. Neural Networks and Deep Learning. Available online: neuralnetworksanddeeplearning.com/ (accessed on 1 September 2020).
- Göçken, M.; Mehmet özçalici, M.; Boru, A.; Dosdoğru, A.T. Integrating metaheuristics and Artificial Neural Networks for improved stock price prediction. ESA 2016, 44, 320–331. [Google Scholar] [CrossRef]
- Li, M.F.; Tang, X.P.; Wu, W.; Liu, H.B. General models for estimating daily global solar radiation for different solar radiation zones in mainland China. ECM 2013, 70, 139–148. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 1 September 2020).
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Asai, D.; Banerjee, S.; Barrand, G. Geant4—A simulation toolkit. NIM A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jercic, M.; Poljak, N. Exploring the Possibility of a Recovery of Physics Process Properties from a Neural Network Model. Entropy 2020, 22, 994. https://doi.org/10.3390/e22090994
Jercic M, Poljak N. Exploring the Possibility of a Recovery of Physics Process Properties from a Neural Network Model. Entropy. 2020; 22(9):994. https://doi.org/10.3390/e22090994
Chicago/Turabian StyleJercic, Marko, and Nikola Poljak. 2020. "Exploring the Possibility of a Recovery of Physics Process Properties from a Neural Network Model" Entropy 22, no. 9: 994. https://doi.org/10.3390/e22090994
APA StyleJercic, M., & Poljak, N. (2020). Exploring the Possibility of a Recovery of Physics Process Properties from a Neural Network Model. Entropy, 22(9), 994. https://doi.org/10.3390/e22090994





