1. Introduction
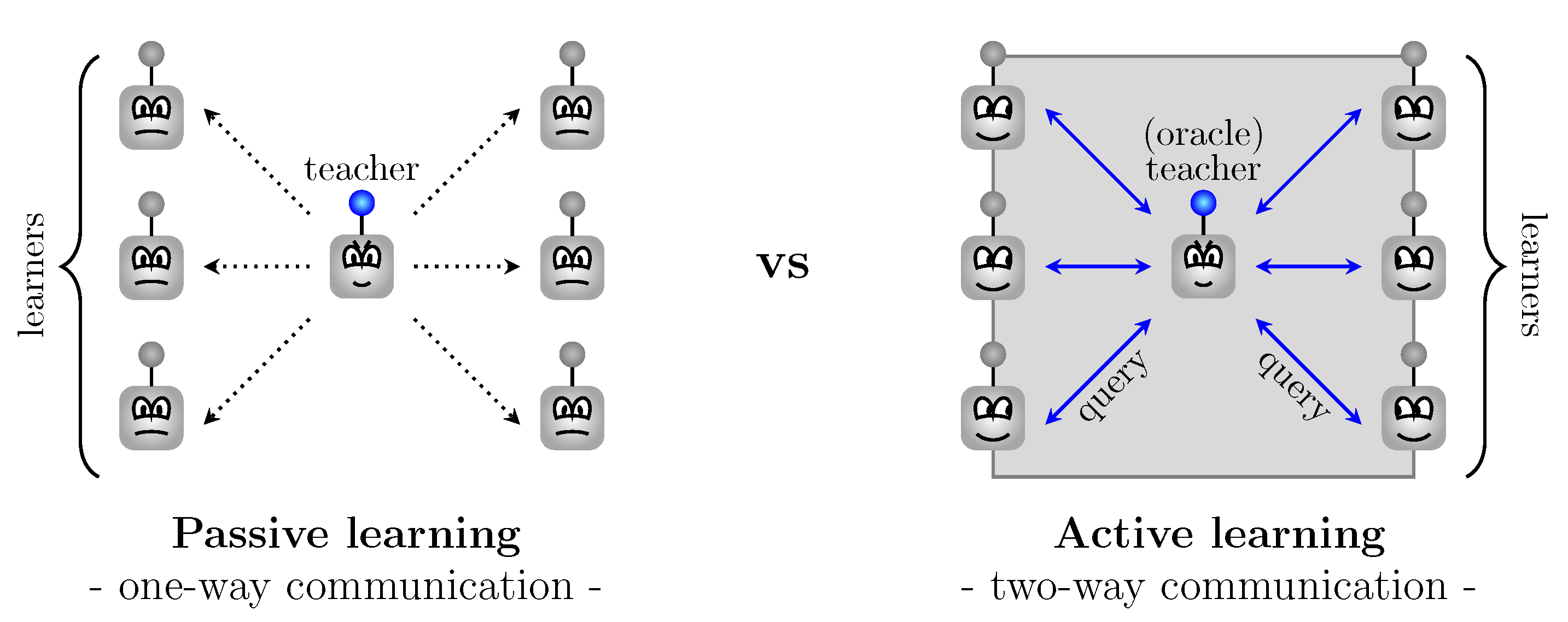
The passive learning technique normally requires an enormous amount of labeled data that has to provide the correct answers (see
Figure 1). An active learning environment guarantees better performance while training on less, but carefully chosen, data which reduces the costs of both annotating and analyzing large data sets [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10]. In uncertainty sampling, which has been reported to be successful in numerous scenarios and settings [
11,
12], a machine requests instances which cause uncertainty. This leads to the optimal leveraging of both new and existing data [
13].
The process of querying the information imitates a classroom instructional method that actively engages learners in the learning process [
14,
15,
16]. They replace or adapt their knowledge and understanding based on prior knowledge in response to learning opportunities provided by a teacher. This contrasts with a model of instruction whereby knowledge is transmitted from the teacher to learners, which typically presents passive learning. Active learning in an educational setting integrates a variety of strategies and instructional models chosen by a teacher to contribute to learners’ knowledge [
17].
Hence, machine active learning strategies are still expected to be more versatile and self-sustaining. In particular, deep neural networks demonstrate remarkable performance on particular supervised learning tasks but are not good at telling when they are not sure while working in an active learning environment. The output from the softmax layer usually tends to be overconfident. Besides, deep neural networks have grown so complex that it seems practically impossible to follow their decision-making process [
18].
In this study, we intend to inspect humans and machines reasoning processes [
19,
20,
21,
22,
23] in order to understand how machines make predictions in an active learning environment. Rather than improving performance, we explored whether we can explain how machines come to decisions by imitating human-like reasoning in multiple-choice testing [
24,
25,
26,
27,
28,
29]. We suggest a new uncertainty sampling strategy based on the four-parameter logistic item response theory (4PL IRT) [
24] we call Information Capacity. The strategy guarantees the performance similar to the most common uncertainty sampling techniques—Least Confidence and Entropy Sampling—but allows creating more transparent knowledge models in deep learning.
In deep neural networks, we have little visibility into the understanding of how models come to conclusions. This happens because we do not know how learning is supposed to work. While training a model, we iterate with better data, better configurations, better algorithms, and more computational power, although we have little knowledge why that model converges slowly and generalizes poorly. As a result, we do not have much control over rebuilding that model—it is not transparent [
18,
30,
31].
Information Capacity brings with it a new interpretation of learning processes to enlighten “black-box” models. In contrast to Least Confidence and Entropy Sampling, the proposed strategy relies on neural network architectures to model learners’ behavior, where neurons or network weights of network classifiers are considered to be a group of learners with different proficiency in classifying learning items. Information Capacity ensures more flexible deep architectures with explainable and controllable learning behavior, not restricted to connectionist models.
2. Results
2.1. Design of Experiments
We built a SGD-based CNN classifier with two convolutional layers with a ReLU activation and one dropout layer ending with a softmax layer in PyTorch. The first convolutional layer filters the input image with the square kernel of size 5. The second convolutional layer takes as input the pooled output of the first convolutional layer with a stride of 2 pixels and the square kernel of size 5. An SGD optimizer with learning rate 0.01 and momentum 0.5 was trained on with and tested with .
We tested the CNN model on the MNIST and Fashion MNIST datasets. From each dataset we randomly took examples for training and examples for testing. The active learning environment was created with three labeled pool with fifty rounds and hundred queried examples .
The proposed Information Capacity strategy was implemented in line with the two baseline algorithms—Least Confidence and Entropy Sampling. Each experiment was repeated in order to produce statistically significant estimates.
2.2. Analysis of Experiments
The parameters of the proposed strategy in training the model defined clearly interpretable behavior of learners during multiple-choice testing. The learners (network weights) guessed correctly with the probability on the item (labeled example) i of the difficulty . We assumed that there was no penalty for guessing announced. The item discrimination parameter reflects how well an item discriminates among the learners located at different points along the continuum. These values for parameters are chosen to minimize the maximum of the information capacity of the items in L but, at the same time, avoid possible inaccuracies caused by machine precision when the informativeness measure values are approaching zero and become imperceptible for different classes.
Implemented guessing behavior reflects “noise” in information. Therefore, a nonzero
reduced the amount information available for locating learners on the
continuum. In addition, answering the item
i, the learners with locations at
did not have a success probability equal to 1 but
due to partial forgetting. The locations
present lower level learners, while the locations
describe higher level learners. The given values for the parameters
define the behavior of learners responding to the items in accord with the item information function (see
Section 3) that presents the amount of information each item provides.
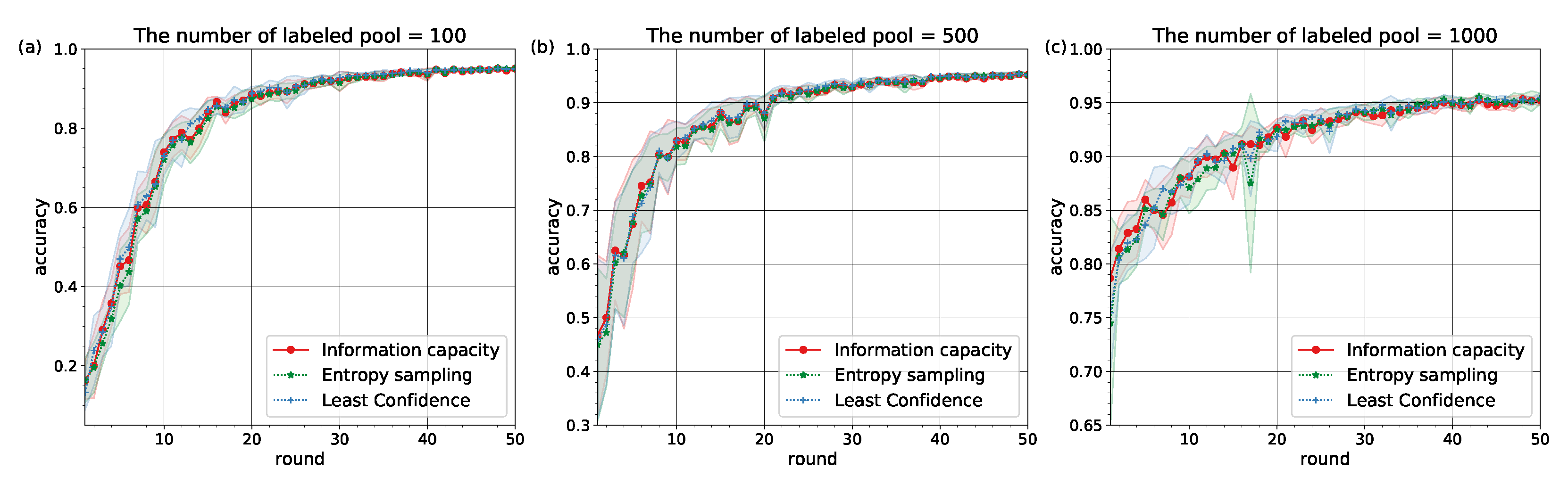
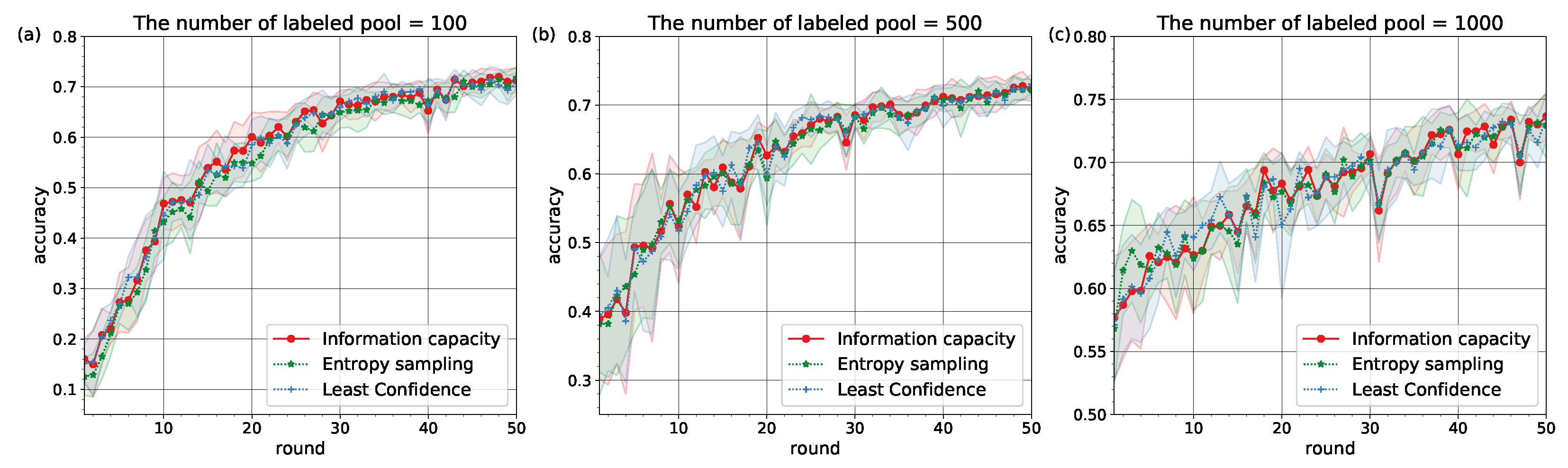
The experiments confirmed that Information Capacity with pre-defined learning behavior can represent the baseline active learning strategies (see
Figure 2 and
Figure 3). The values of accuracy on testing over rounds
are given in
Table 1 and
Table 2.
The similarity in learning behavior for different subsets of the MNIST and Fashion MNIST datasets pointed to the conclusion that Information Capacity relies on neural network architectures to model learners’ behavior. It can be explained by the fact that decisions on classification tasks are made at the output layer of a network, but depended on weights (learners) which were set at hidden layers. With increasing amount of labeled pool
the similarities between the accuracy curves for different strategies become stronger (see
Table 1 and
Table 2).
We applied a one-sided Wilcoxon test [
44] with Bonferroni correction [
45,
46] for each round to confirm a lack of statistically significant differences between the three strategies in the accuracy values on testing. Since the
p-value for each round turned out to be close to 1, we have a sufficient reason to accept the null hypothesis. Consequently, the similarities between the accuracy curves in
Figure 2 and
Figure 3 are statistically significant.
2.3. Discussion
We took Least Confidence and Entropy Sampling for comparison for two reasons. First, these active learning strategies are used as baseline sampling techniques for more complex approaches adopted in deep active learning. Second, Information Capacity shares some similarity with them—it finds which range over all possible labels (Entropy Sampling) with the least information capacity (Least Confidence).
As progress on improving performance in deep learning has come at the cost of transparency, we find this approach particularly beneficial. Information Capacity allows learners to exhibit different learning behaviors with regard to the IRT hyperparameters. In the experiments, they were chosen in a certain way to rule out the reasoning behind the Least Confidence and Entropy Sampling strategies. In particular, we modeled uncertainty with a group of learners, who adopted both guessing and forgetting strategies ( and ) to classify “hard” items (). In addition, it was difficult to assess how strong or weak the learners were ( or ) because the value of discrimination factor was low . No penalty for guessing delivered less predictable behavioral observations.
As we have seen, Least Confidence and Entropy Sampling can be interpreted by the scenario in which each learner (neuron) in a neural network shares the same behavior. Considering the complexity of deep networks, these backbone strategies seem limited. For increasing the transparency of deep learning process, different combinations of the IRT parameters can be used to construct a variety of educational scenarios and learning strategies with strong or weak learners including learning in groups [
47,
48,
49].
The analysis of different neural network architectures with regard to learning behaviors is beyond the scope of this study. However, we hope that our presentation of neural networks will encourage further research exploring novel neural networks building groups of learners with learning behavior which is not limited to gradient-based methods and primitive connectionist models.
3. Materials and Methods
3.1. Problem Statement
Let
be a feature space and
be a label space. Let
be an unknown underlying distribution, where
,
. We use labeled training set
of
m labeled training samples to select a prediction function
,
so as to minimize the risk
, where
is a given loss function. For any labeled set
L (training and testing), the empirical risk over
L is given by:
In a pool-based setting [
7,
33], an active learner chooses examples from a set
of unlabeled samples according to a query function
S. Query functions often select points based on information inferred from the current model
, the existing training set
, and the current pool
. The aim is to accurately train the model for a given number of labeled points
.
We consider a class of learning behaviors during testing, where each behavior represents a hypothesis class containing all learners , where s defines a set of parameters in a testing framework for making behavioral observations.
3.2. Testing Framework
We are interested in measuring classification proficiencies of a group of learners (neurons or network weights). Although it seems impossible to directly observe the level of proficiency (working knowledge), we can infer its existence through behavioral observations in a classroom. The learners are given an instrument containing several items (labeled examples) i.e., multiple-choice tests [
27,
28,
50,
51,
52]. The responses to this instrument constitute the behavioral observations.
Item Response Theory [
24,
28,
53,
54,
55,
56] suggests a variety of models to assess the distance between the learner and the item locations as it clearly defines the learner’s correct response. This means that items located toward the right side have difficulty
. They require a learner to have greater proficiency
to correctly answer items located on the right side than items located on the left side. In general, items located below 0 are “easy” while items above 0 are “hard”.
In this study, we focused on the four-parameter logistic item response theory (4PL IRT) model which can be presented as [
24]:
where
is the probability of providing the correct response
to an item
i by a learner
j with the location (ability)
. From the definition (
1) we can see that the rate of success mainly depends on the relationship between the item’s parameters and learners’ proficiency.
3.3. Information Capacity
So far, we considered the estimation of a learner’s location from its uncertainty. Let us now take the opposite side and define a query strategy S.
The instrument’s items—labeled examples—contain a certain amount of information that can be used for estimating the learner location parameters. We assume that each item contributes information to reduce the uncertainty about a learner’s location independent of the other items of the instrument. The amount of information items provide can be presented using the Fisher information as [
24,
57,
58]:
where
is the asymptotic variance error of the estimate
. The log likelihood function for a learner
j’s response vector is equal to:
where
. The items’ capacity is defined as the maximum of the information function
.
The definition (
2) can be rewritten with regard to (
1) in the explicit form as:
The detailed derivation of the Equation (
4) is given in
Appendix A.
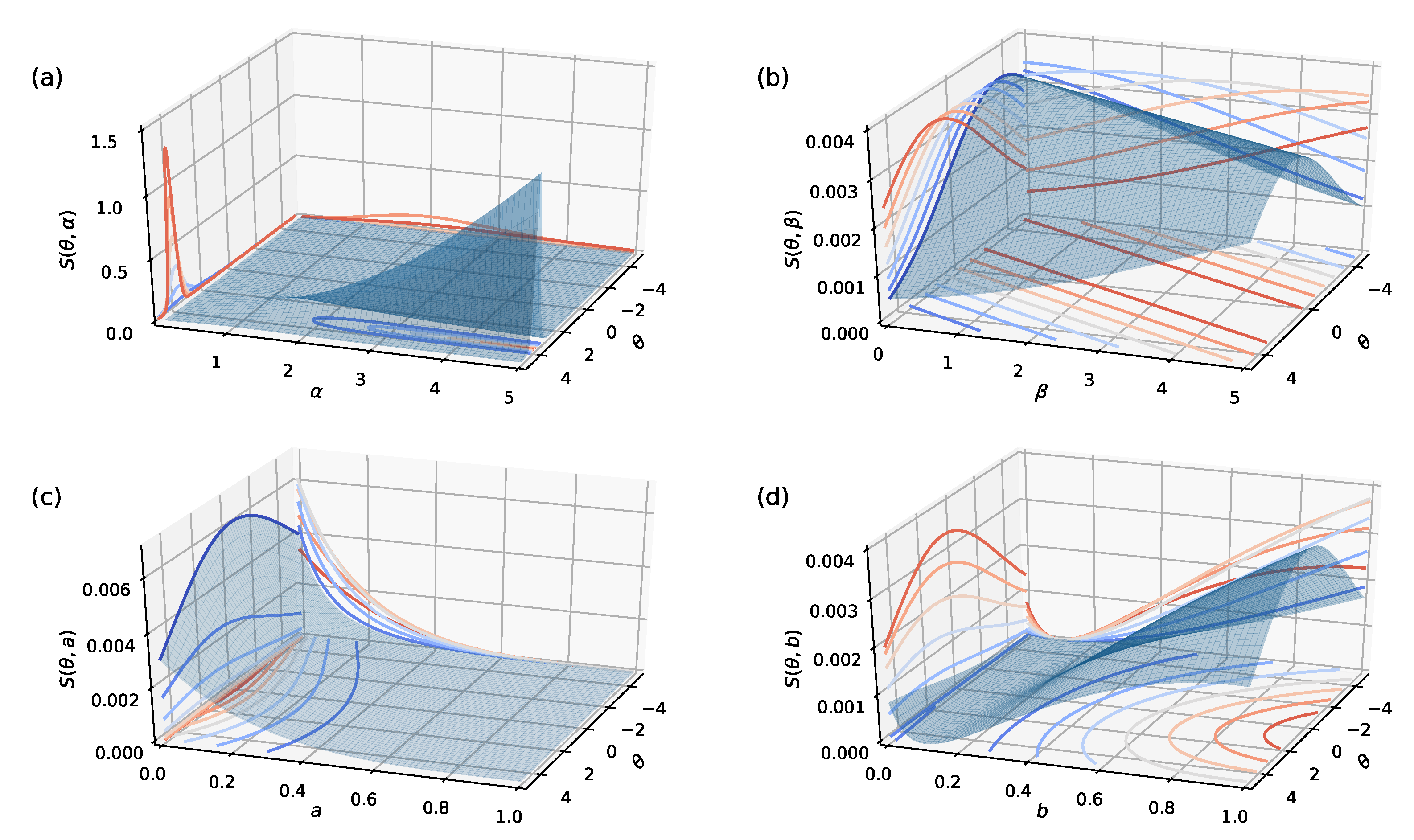
Figure 4 illustrates the projections of the information function with fixed values
,
,
,
described in
Section 2.2.
A new pool-based strategy—we refer to as Information Capacity—suggests estimating the information capacity for unlabelled instances based on the definition (
4).
Figure 5 depicts the proposed pool-based strategy for measuring the items capacity
S with regard to the items’ difficulty
, learners’ locations
, strategies
and
, and penalty announcement
p in a classroom. The strategy is aimed at “moving” learners along the difficulty axis while keeping high values for the capacity axis. The learners query the examples with the lowest information capacity. For clarity, the algorithm represents the proposed pool-based active learning with the Information Capacity strategy (see Algorithm 1). The differences in implementation in comparison with the traditional active learning framework are highlighted in blue.
| Algorithm 1 Pool-based active learning with Information Capacity strategy |
- 1:
procedureInformationCapacity(, ) - 2:
Initialize a labeled training set L; - 3:
Initialize an unlabeled training pool ; - 4:
Initialize a learning behavior of learners B with regard to a set of parameters ; - 5:
Train a group of learners on the labeled set L; - 6:
Measure performance of the group of learners on the test set ; - 7:
Initialize several rounds and several queried examples ; - 8:
for do - 9:
Estimate the probabilities with regard to ( 1) based on the learning behavior B; - 10:
Sort the unlabeled items in U according to ( 4) based on the probabilities from the step 9; - 11:
Query the items with the smallest of the maximum capacity S in a ; - 12:
; - 13:
; - 14:
Retrain a group of learners on the labeled set L; - 15:
Measure performance of the group of learners on the test set ; - 16:
end for - 17:
return The performance of the learners with the interpretation of their learning behavior.
|
4. Conclusions
We present Information Capacity, which is an uncertainty sampling strategy that effectively integrates human- and machine-reasoning processes. The strategy allows embedding into the models different learning behaviors with regard to the parameters of the 4PL IRT model. The experiments on the MNIST and Fashion MNIST datasets with the same CNN model indicate that Information Capacity performs similarly to Least Confidence and Entropy Sampling but brings more transparency into a deep learning process.
We considered the neurons or network weights of the CNN classifier at the last hidden layer as a group of learners with different proficiency in classifying learning items, i.e., images. The pre-defined parameters of the Information Capacity strategy defined their learning behavior: the learners had a success probability due to partial forgetting while they guessed correctly with the probability on the item i of the difficulty , which discriminated the learners with the factor .
The equivalence of the parameters for different subsets of the MNIST and Fashion MNIST datasets revealed that the model architecture greatly influences learning behavior. As a direction for further research, we suggest modeling learning behaviors with different network architectures. While keeping equally good performance due to the similarity between different strategies, it seems desirable to optimize neural network architectures and learning processes.
Author Contributions
All coauthors contributed equally to the paper. Conceptualization, methodology and investigation, I.K., T.L. and T.Š.; software, I.K.; validation; T.L. and T.Š.; formal analysis, I.K. and T.L.; writing—original draft, I.K.; writing—review and editing, T.L. and T.Š.; T.Š.: supervision and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Centre of Excellence project “DATACROSS”, co-financed by the Croatian Government and the European Union through the European Regional Development Fund—the Competitiveness and Cohesion Operational Programme (KK.01.1.1.01.0009) and the Ministry of Education and Science of the Russian Federation (grant No. 074-U01).
Acknowledgments
The authors would like to thank the reviewers for valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Derivation of the Equation (4)
Let us denote
. The derivative of the model (
1) can be defined as
Extracting the definition (
1) from (
A1) gives
Let us now define the probability of getting an incorrect response:
From the Equation (
A3), it follows that
Taking into account (
A4), we can rewrite (
A1) as follows:
Substituting (
A5) into the definition (
2) immediately gives (
4).
References
- Bachman, P.; Sordoni, A.; Trischler, A. Learning algorithms for active learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Fazakis, N.; Kanas, V.G.; Aridas, C.K.; Karlos, S.; Kotsiantis, S. Combination of active learning and semi-supervised learning under a self-training scheme. Entropy 2019, 21, 988. [Google Scholar] [CrossRef]
- Hsu, W.-N.; Lin, H.-T. Active learning by learning. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Huang, S.; Jin, R.; Zhou, Z. Active learning by querying informative and representative examples. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1936–1949. [Google Scholar] [CrossRef] [PubMed]
- Konyushkova, K.; Raphael, S.; Fua, P. Learning active learning from data. In Proceedings of the Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ramirez-Loaiza, M.E.; Sharma, M.; Kumar, G.; Bilgic, M. Active learning: An empirical study of common baselines. Data Min. Knowl. Discov. 2017, 31, 287–313. [Google Scholar] [CrossRef]
- Settles, B. Active Learning Literature Survey. In Computer Sciences Technical Report; University of Wisconsin–Madison: Madison, WI, USA, 2009. [Google Scholar]
- Sourati, J.; Akcakaya, M.; Dy, J.G.; Leen, T.K.; Erdogmus, D. Classification Active Learning Based on Mutual Information. Entropy 2016, 18, 51. [Google Scholar] [CrossRef]
- Sourati, J.; Akcakaya, M.; Leen, T.K.; Erdogmus, D.; Dy, J.G. A probabilistic active learning algorithm based on Fisher information ratio. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2023–2029. [Google Scholar] [CrossRef]
- Wu, J.; Sheng, V.S.; Zhang, J.; Li, H.; Dadakova, T.; Swisher, C.L.; Cui, Z.; Zhao, P. Multi-label active learning algorithms for image classification: Overview and future promise. ACM Comput. Surv. 2020, 53, 1–35. [Google Scholar] [CrossRef]
- Joshi, A.J.; Porikli, F.; Papanikolopoulos, N. Multi-class active learning for image classification. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Yang, Y.; Ma, Z.; Nie, F.; Chang, X.; Hauptmann, A.G. Multi-Class active learning by uncertainty sampling with diversity maximization. Int. J. Comput. Vis. 2015, 113, 113–127. [Google Scholar] [CrossRef]
- Hanneke, S. Activized Learning: Transforming passive to active with improved label complexity. J. Mach. Learn. Res. 2012, 13, 1469–1587. [Google Scholar]
- Bonwell, C.; Eison, J. Active Learning: Creating Excitement in the Classroom; Jossey-Bass: San Francisco, CA, USA, 1991. [Google Scholar]
- Cook, B.R.; Babon, A. Active learning through online quizzes: Better learning and less (busy) work. J. Geogr. High. Educ. 2017, 41, 24–38. [Google Scholar] [CrossRef]
- Prince, M. Does Active Learning Work? A review of the research. J. Eng. Educ. 2004, 93, 223–231. [Google Scholar] [CrossRef]
- Aubrey, K.; Riley, A. Understanding and Using Educational Theories; Sage Publications Ltd.: Newbury Park, CA, USA, 2015. [Google Scholar]
- Mascharka, D.; Tran, P.; Soklaski, R.; Majumdar, A. Transparency by design: Closing the gap between performance and interpretability in visual reasoning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Castro, R.; Kalish, C.; Nowak, R.; Qian, R.; Rogers, T.; Zhu, X. Human active learning. In Proceedings of the Twenty-Second Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–11 December 2008. [Google Scholar]
- Lake, B.M.; Salakhutdinov, R.; Tenenbaum, J.B. Human-level concept learning through probabilistic program induction. Science 2015, 350, 1332–1338. [Google Scholar] [CrossRef] [PubMed]
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building machines that learn and think like people. Behav. Brain Sci. 2017, 40, e253. [Google Scholar] [CrossRef] [PubMed]
- Mastorakis, G. Human-like machine learning: Limitations and suggestions. arXiv 2018, arXiv:1811.06052v1. [Google Scholar]
- Wilson, R.C.; Shenhav, A.; Straccia, M.; Cohen, J.D. The Eighty Five Percent Rule for optimal learning. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- De Ayala, R.J. The Theory and Practice of Item Response Theory (Methodology in the Social Sciences); The Guilford Press: New York, NY, USA, 2009. [Google Scholar]
- Gierl, M.J.; Bulut, O.; Guo, Q.; Zhang, X. Developing, analyzing, and using distractors for multiple-choice tests in education: A comprehensive review. Rev. Educ. Res. 2017, 87, 1082–1116. [Google Scholar] [CrossRef]
- Hakel, M.D. (Ed.) Beyond Multiple Choice: Evaluating Alternatives to Traditional Testing for Selection; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 1998. [Google Scholar]
- Lee, C.J. The test taker’s fallacy: How students guess answers on multiple-choice tests. Behav. Decis. Mak. 2019, 32, 140–151. [Google Scholar] [CrossRef]
- Lord, F.M. Applications of Item Response Theory to Practical Testing Problems; Erlbaum: Hillsdale, NJ, USA, 1980. [Google Scholar]
- Thissen, D.; Steinberg, L.; Fitzpatrick, A.R. Multiple-choice models: The distractors are also part of the item. J. Educ. Meas. 1989, 26, 161–176. [Google Scholar] [CrossRef]
- Mittelstadt, B.; Russell, C.; Wachter, S. Explaining explanations in AI. In Proceedings of the Fairness, Accountability, and Transparency (FAT*), Atlanta, GA, USA, 29–31 January 2019; pp. 279–288. [Google Scholar]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Gal, Y.; Islam, R.; Ghahramani, Z. Deep Bayesian active learning with image data. In Proceedings of the 34th International Conference on MachineLearning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Geifman, Y.; El-Yaniv, R. Deep active learning with a neural architecture search. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Ouali, Y.; Hudelot, C.; Tami, M. An overview of deep semi-supervised learning. arXiv 2020, arXiv:2006.05278v1. [Google Scholar]
- Sener, O.; Savarese, S. Active learning for convolutional neural networks: A core-set approach. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, D.; Shang, Y. A new active labeling method for deep learning. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 112–119. [Google Scholar]
- Budd, S.; Robinson, E.C.; Kainz, B. A survey on active learning and human-in-the-loop deep learning for medical image analysis. arXiv 2019, arXiv:1910.02923v1. [Google Scholar]
- Chen, Y.; Filho, T.S.; Prudencio, R.B.C.; Diethe, T.; Flach, P. β3-IRT: A new item response model and its applications. arXiv 2019, arXiv:1903.04016. Available online: https://arxiv.org/abs/1903.04016 (accessed on 3 June 2019).
- Martinez-Plumed, F.; Prudencio, R.B.C.; Martinez-Uso, A.; Hernandez-Orallo, J. Item response theory in AI: Analysing machine learning classifiers at the instance Level. Artif. Intell. 2019, 271, 18–42. [Google Scholar] [CrossRef]
- Whitehill, J.; Ruvolo, P.; Wu, T.; Bergsma, J.; Movellan, J. Whose vote should count more: Optimal integration of labels from labelers of unknown expertise. In Proceedings of the Advances in Neural Information Processing Systems 22 (NIPS 2009), Vancouver, BC, Canada, 7–10 December 2009. [Google Scholar]
- Yeung, C.K. Deep-IRT: Make deep learning based knowledge tracing explainable using item response theory. arXiv 2019, arXiv:1904.11738. [Google Scholar]
- Lalor, J.P.; Wu, H.; Yu, H. CIFT: Crowd-informed fine-tuning to improve machine learning ability. arXiv 2017, arXiv:1702.08563v2. [Google Scholar]
- Ravi, S.; Larochelle, H. Meta-Learning for Batch Mode Active Learning. 2018. Available online: https://openreview.net/forum?id=r1PsGFJPz (accessed on 4 June 2018).
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple comparisons among means. J. Am. Stat. Assoc. 1961, 56, 52–64. [Google Scholar] [CrossRef]
- Perneger, T.V. What’s wrong with Bonferroni adjustments. BMJ 1998, 316, 1236–1238. [Google Scholar] [CrossRef]
- Kulikovskikh, I.M.; Prokhorov, S.A.; Suchkova, S.A. Promoting collaborative learning through regulation of guessing in clickers. Comput. Hum. Behav. 2017, 75, 81–91. [Google Scholar] [CrossRef]
- Le, H.; Janssen, J.; Wubbels, T. Collaborative learning practices: Teacher and student perceived obstacles to effective student collaboration. Camb. J. Educ. 2018, 48, 103–122. [Google Scholar] [CrossRef]
- Sawyer, J.; Obeid, R. Cooperative and collaborative learning: Getting the best of both words. In How We Teach Now: The GSTA Guide to Student-Centered Teaching; Obeid, R., Schwartz, A., Shane-Simpson, C., Brooks, P.J., Eds.; Society for the Teaching of Psychology: Washington, DC, USA, 2018; pp. 163–177. [Google Scholar]
- Liu, C.W.; Wang, W.C. Unfolding IRT models for Likert-type items with a don’t know option. Appl. Psychol. Meas. 2016, 49, 517–533. [Google Scholar] [CrossRef]
- Liu, C.W.; Wang, W.C. A general unfolding IRT model for multiple response styles. Appl. Psychol. Meas. 2019, 43, 195–210. [Google Scholar] [CrossRef] [PubMed]
- Sideridis, G.; Tsaousis, I.; Harbi, K.A. Improving measures via examining the behavior of distractors in multiple-choice tests: Assessment and remediation. Educ. Psychol. Meas. 2016, 77, 82–103. [Google Scholar] [CrossRef] [PubMed]
- Bonifay, W. Multidimensional Item Response Theory (Quantitative Applications in the Social Sciences); SAGE Publications: Newbury Park, CA, USA, 2020. [Google Scholar]
- DeMars, C.E. “Guessing” parameter estimates for multidimensional Item Response Theory models. Educ. Psychol. Meas. 2007, 67, 433–446. [Google Scholar] [CrossRef]
- Gin, B.; Sim, N.; Skrondal, A.; Rabe-Hesketh, S. A dyadic IRT model. arXiv 2019, arXiv:1906.01100v1. [Google Scholar]
- Reckase, M.D. Multidimensional Item Response Theory; Springer: New York, NY, USA, 2009. [Google Scholar]
- Frieden, B.R. Science from Fisher Information: A Unification; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).