Achievable Information Rates for Probabilistic Amplitude Shaping: An Alternative Approach via Random Sign-Coding Arguments
Abstract
1. Introduction
2. Related Work and Our Contribution
2.1. Notation
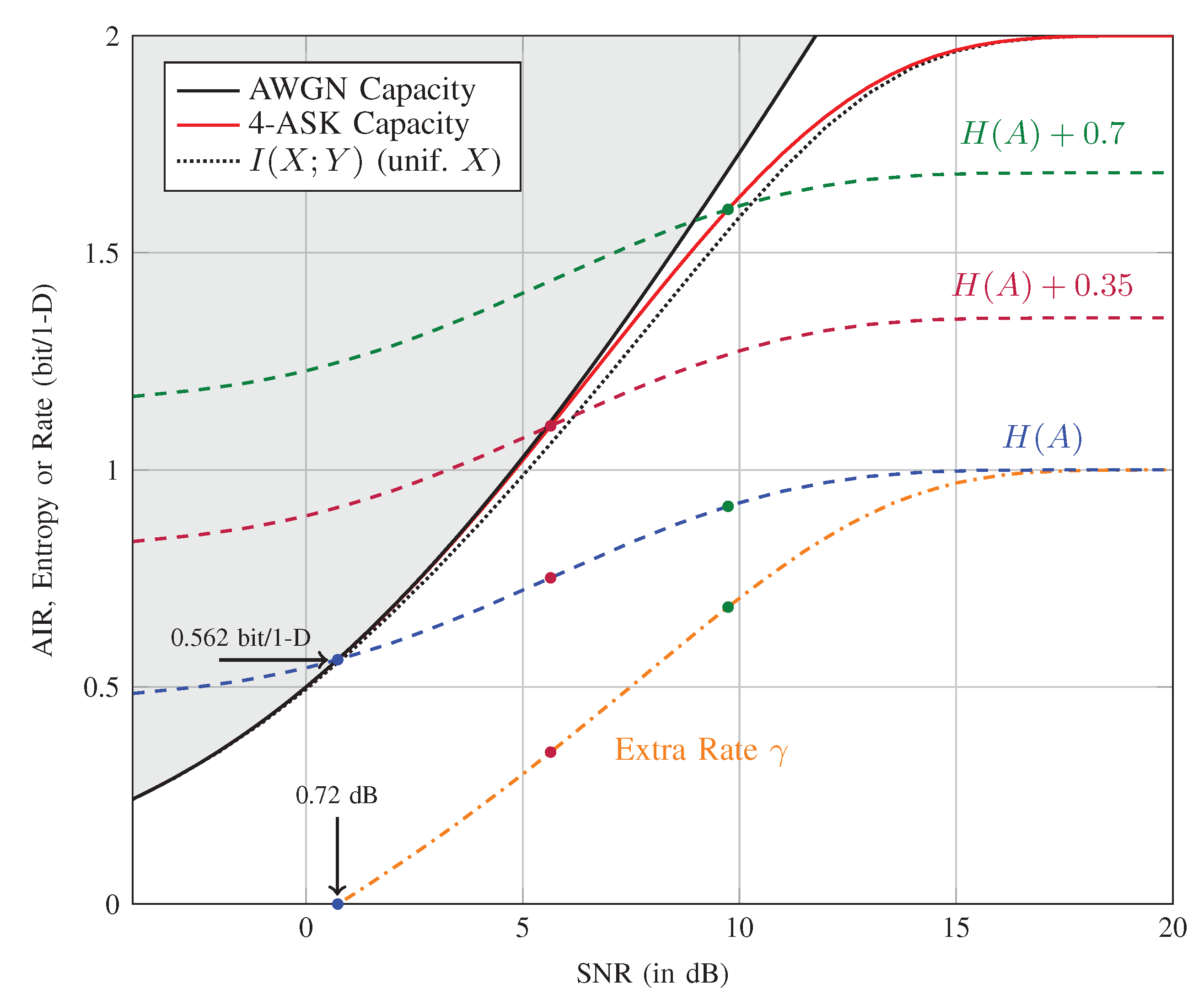
2.2. Achievable Information Rates
2.3. Probabilistic Amplitude Shaping: Model
2.4. Probabilistic Amplitude Shaping: Achievable Rates
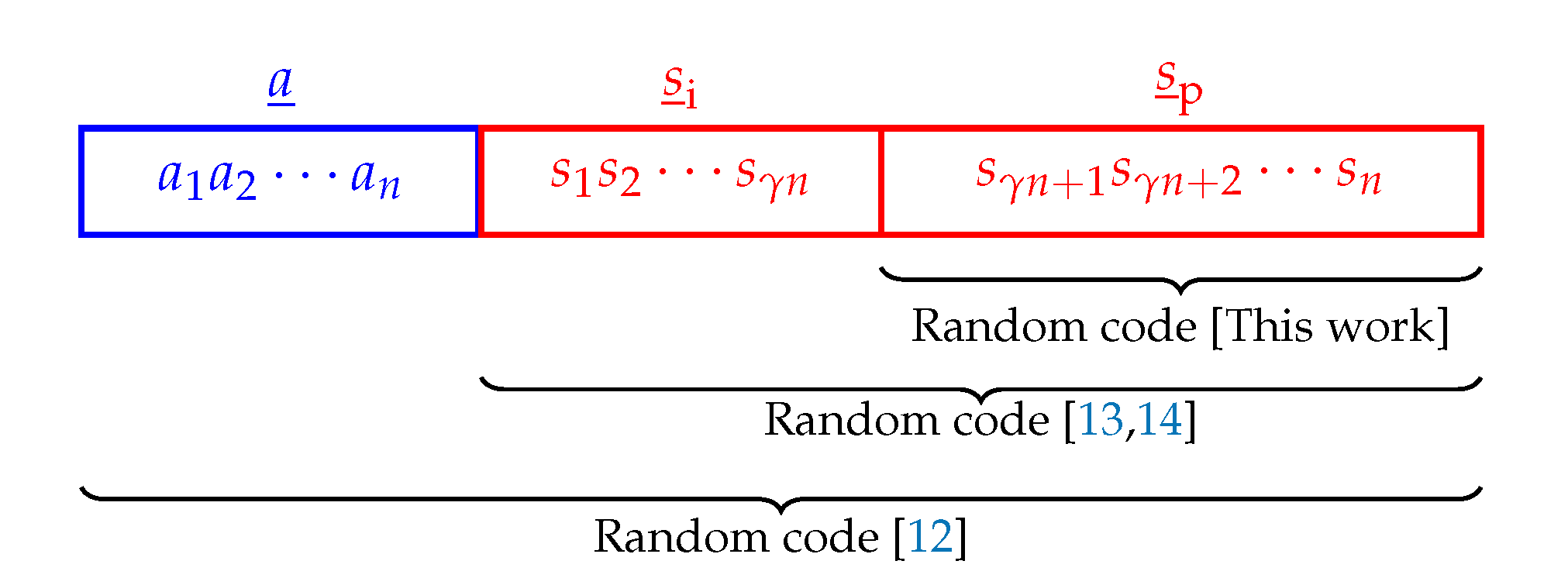
2.5. Our Contribution
3. Preliminaries
3.1. Memoryless Channels
3.2. Typical Sequences
- P1:
- For ,
- P2:
- For n large enough,
- P3:
- holds for all n, while holds for n large enough.
4. Random Sign-Coding Experiment
4.1. Random Sign-Coding Setup
- A shaping layer that produces for every message index , a length-n shaped amplitude sequence where the mapping is one-to-one. The set of amplitude sequences is assumed to be shaped, but uncoded.
- An additional -bit (uniform) information string in the form of a sign sequence part for every message index .
- A coding layer that extends the sign sequence part by adding a second (uniform) sign sequence part of length- for all and . This is obtained by using an encoder that produces redundant signs in the set from and . Here, .
4.2. Shaping Layer
4.3. Decoding Rules
5. Achievable Information Rates of Sign-Coding
5.1. Sign-Coding with Symbol-Metric Decoding
5.2. Sign-Coding with Bit-Metric Decoding
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix A.1. Proof of P1
Appendix A.2. Proof of P2
Appendix A.3. Proof of P3
Appendix B. Proofs of Theorems 1, 2, 3, and 4
Appendix B.1. Proof of Theorem 1
Appendix B.2. Proof of Theorem 2
- (A40)
- follows from and from the fact that is uniform; more precisely, .
- (A41)
- is obtained by splitting into and .
- (A42)
- follows for n sufficiently large and for from:and from ,
- (A43)
- follows from summing over instead of over and over instead of for . Moreover, it follows from summing over instead of for and .
- (A44)
- follows from substituting for and for .
- (A46)
- is obtained by working out the summations over in the first part and in the second part. Moreover, we replaced with .
- (A47)
- (A48)
- follows from (15), and its extension to jointly typical triplets; more precisely, .
Appendix B.3. Proof of Theorem 3
- (A61)
- follows for n sufficiently large and for from , which can be shown in a similar way as (A31) was derived.
- (A62)
- follows from summing over instead of over and over instead of over for .
- (A63)
- is obtained by working out the summations over , and .
- (A64)
- (A65)
Appendix B.4. Proof of Theorem 4
- (A75)
- follows for n sufficiently large and for from and from ,
- (A76)
- follows from summing over instead of over and over instead of for . Moreover, it follows from summing over instead of for and ,
- (A77)
- follows from substituting for and for .
- (A78)
- is obtained by working out the summations over in the first part and in the second part.
- (A79)
- (A80)
References
- Imai, H.; Hirakawa, S. A new multilevel coding method using error-correcting codes. IEEE Trans. Inf. Theory 1977, 23, 371–377. [Google Scholar] [CrossRef]
- Wachsmann, U.; Fischer, R.F.H.; Huber, J.B. Multilevel codes: Theoretical concepts and practical design rules. IEEE Trans. Inf. Theory 1999, 45, 1361–1391. [Google Scholar] [CrossRef]
- Ungerböck, G. Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory 1982, 28, 55–67. [Google Scholar] [CrossRef]
- Zehavi, E. 8-PSK trellis codes for a Rayleigh channel. IEEE Trans. Commun. 1992, 40, 873–884. [Google Scholar] [CrossRef]
- Caire, G.; Taricco, G.; Biglieri, E. Bit-interleaved coded modulation. IEEE Trans. Inf. Theory 1998, 44, 927–946. [Google Scholar] [CrossRef]
- IEEE Standard for Information Technology—Telecommunications and Information Exchange between Systems Local and Metropolitan Area Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications; IEEE Std 802.11-2016 (Revision of IEEE Std 802.11-2012); IEEE Standards Association: Piscataway, NJ, USA, 2016; pp. 1–3534. [CrossRef]
- Digital Video Broadcasting (DVB); 2nd Generation Framing Structure, Channel Coding and Modulation Systems for Broadcasting, Interactive Services, News Gathering and Other Broadband Satellite Applications (DVB-S2); European Telecommun. Standards Inst. (ETSI) Standard EN 302 307, Rev. 1.2.1; European Telecommunications Standards Institute: Valbonne, France, 2009.
- Böcherer, G.; Steiner, F.; Schulte, P. Bandwidth efficient and rate-matched low-density parity-check coded modulation. IEEE Trans. Commun. 2015, 63, 4651–4665. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Buchali, F.; Steiner, F.; Böcherer, G.; Schmalen, L.; Schulte, P.; Idler, W. Rate adaptation and reach increase by probabilistically shaped 64-QAM: An experimental demonstration. J. Lightw. Technol. 2016, 34, 1599–1609. [Google Scholar] [CrossRef]
- Idler, W.; Buchali, F.; Schmalen, L.; Lach, E.; Braun, R.; Böcherer, G.; Schulte, P.; Steiner, F. Field trial of a 1 Tb/s super-channel network using probabilistically shaped constellations. J. Lightw. Technol. 2017, 35, 1399–1406. [Google Scholar] [CrossRef]
- Böcherer, G. Achievable rates for probabilistic shaping. arXiv 2018, arXiv:1707.01134. [Google Scholar]
- Böcherer, G. Principles of Coded Modulation. Habilitation Thesis, TUM Department of Electrical and Computer Engineering Technical University of Munich, Munich, Germany, 2018. [Google Scholar]
- Amjad, R.A. Information rates and error exponents for probabilistic amplitude shaping. In Proceedings of the 2018 IEEE Information Theory Workshop (ITW), Guangzhou, China, 25–29 November 2018. [Google Scholar]
- Gallager, R.G. Information Theory and Reliable Communication; John Wiley & Sons: New York, NY, USA, 1968. [Google Scholar]
- Kramer, G. Topics in multi-user information theory. Found. Trends Commun. Inf. Theory 2008, 4, 265–444. [Google Scholar] [CrossRef]
- Kaplan, G.; Shamai, S. Information rates and error exponents of compound channels with application to antipodal signaling in a fading environment. AËU Archiv für Elektronik und Übertragungstechnik 1993, 47, 228–239. [Google Scholar]
- Merhav, N.; Kaplan, G.; Lapidoth, A.; Shamai, S. On information rates for mismatched decoders. IEEE Trans. Inf. Theory 1994, 40, 1953–1967. [Google Scholar] [CrossRef]
- Szczecinski, L.; Alvarado, A. Bit-Interleaved Coded Modulation: Fundamentals, Analysis, and Design; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Martinez, A.; Guillén i Fàbregas, A.; Caire, G.; Willems, F.M.J. Bit-interleaved coded modulation revisited: A mismatched decoding perspective. IEEE Trans. Inf. Theory 2009, 55, 2756–2765. [Google Scholar] [CrossRef]
- Guillén i Fàbregas, A.; Martinez, A. Bit-Interleaved Coded Modulation with Shaping. In Proceedings of the 2010 IEEE Information Theory Workshop, Dublin, Ireland, 30 August–3 September 2010. [Google Scholar]
- Alvarado, A.; Brännström, F.; Agrell, E. High SNR bounds for the BICM capacity. In Proceedings of the 2011 IEEE Information Theory Workshop, Paraty, Brazil, 16–20 October 2011. [Google Scholar]
- Peng, L. Fundamentals of Bit-Interleaved Coded Modulation and Reliable Source Transmission. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2012. [Google Scholar]
- Böcherer, G. Probabilistic signal shaping for bit-metric decoding. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014. [Google Scholar]
- Böcherer, G. Probabilistic signal shaping for bit-metric decoding. arXiv 2014, arXiv:1401.6190. [Google Scholar]
- Böcherer, G. Achievable rates for shaped bit-metric decoding. arXiv 2016, arXiv:1410.8075. [Google Scholar]
- Schulte, P.; Böcherer, G. Constant composition distribution matching. IEEE Trans. Inf. Theory 2016, 62, 430–434. [Google Scholar] [CrossRef]
- Fehenberger, T.; Millar, D.S.; Koike-Akino, T.; Kojima, K.; Parsons, K. Multiset-partition distribution matching. IEEE Trans. Commun. 2019, 67, 1885–1893. [Google Scholar] [CrossRef]
- Schulte, P.; Steiner, F. Divergence-optimal fixed-to-fixed length distribution matching with shell mapping. IEEE Wirel. Commun. Lett. 2019, 8, 620–623. [Google Scholar] [CrossRef]
- Gültekin, Y.C.; van Houtum, W.J.; Koppelaar, A.; Willems, F.M.J. Enumerative sphere shaping for wireless communications with short packets. IEEE Trans. Wirel. Commun. 2020, 19, 1098–1112. [Google Scholar] [CrossRef]
- Amjad, R.A. Information Rates and Error Exponents for Probabilistic Amplitude Shaping. arXiv 2018, arXiv:1802.05973. [Google Scholar]
- Shulman, N.; Feder, M. Random coding techniques for nonrandom codes. IEEE Trans. Inf. Theory 1999, 45, 2101–2104. [Google Scholar] [CrossRef]
- Yeung, R. Information Theory and Network Coding; Springer: Boston, MA, USA, 2008. [Google Scholar]



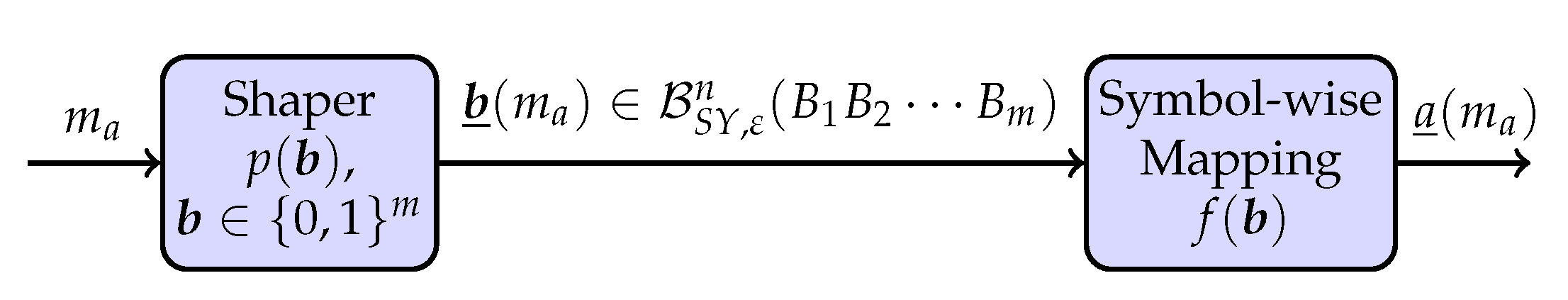
| A | 7 | 5 | 3 | 1 | 1 | 3 | 5 | 7 |
| S | −1 | −1 | −1 | −1 | 1 | 1 | 1 | 1 |
| X | −7 | −5 | −3 | −1 | 1 | 3 | 5 | 7 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gültekin, Y.C.; Alvarado, A.; Willems, F.M.J. Achievable Information Rates for Probabilistic Amplitude Shaping: An Alternative Approach via Random Sign-Coding Arguments. Entropy 2020, 22, 762. https://doi.org/10.3390/e22070762
Gültekin YC, Alvarado A, Willems FMJ. Achievable Information Rates for Probabilistic Amplitude Shaping: An Alternative Approach via Random Sign-Coding Arguments. Entropy. 2020; 22(7):762. https://doi.org/10.3390/e22070762
Chicago/Turabian StyleGültekin, Yunus Can, Alex Alvarado, and Frans M. J. Willems. 2020. "Achievable Information Rates for Probabilistic Amplitude Shaping: An Alternative Approach via Random Sign-Coding Arguments" Entropy 22, no. 7: 762. https://doi.org/10.3390/e22070762
APA StyleGültekin, Y. C., Alvarado, A., & Willems, F. M. J. (2020). Achievable Information Rates for Probabilistic Amplitude Shaping: An Alternative Approach via Random Sign-Coding Arguments. Entropy, 22(7), 762. https://doi.org/10.3390/e22070762