Multi-Domain Entropy-Random Forest Method for the Fusion Diagnosis of Inter-Shaft Bearing Faults with Acoustic Emission Signals
Abstract
1. Introduction
2. Multi-Domain Entropy Approach for Feature Extraction
2.1. Information Entropy Theory
2.2. Extraction of Information Entropy Features in Many Analytical Domains
2.2.1. Time Domain Information Entropy Features
2.2.2. Frequency Domain Information Entropy Feature
2.2.3. Time-Frequency Domain Information Entropy Features
2.3. Multi-Domain Entropy
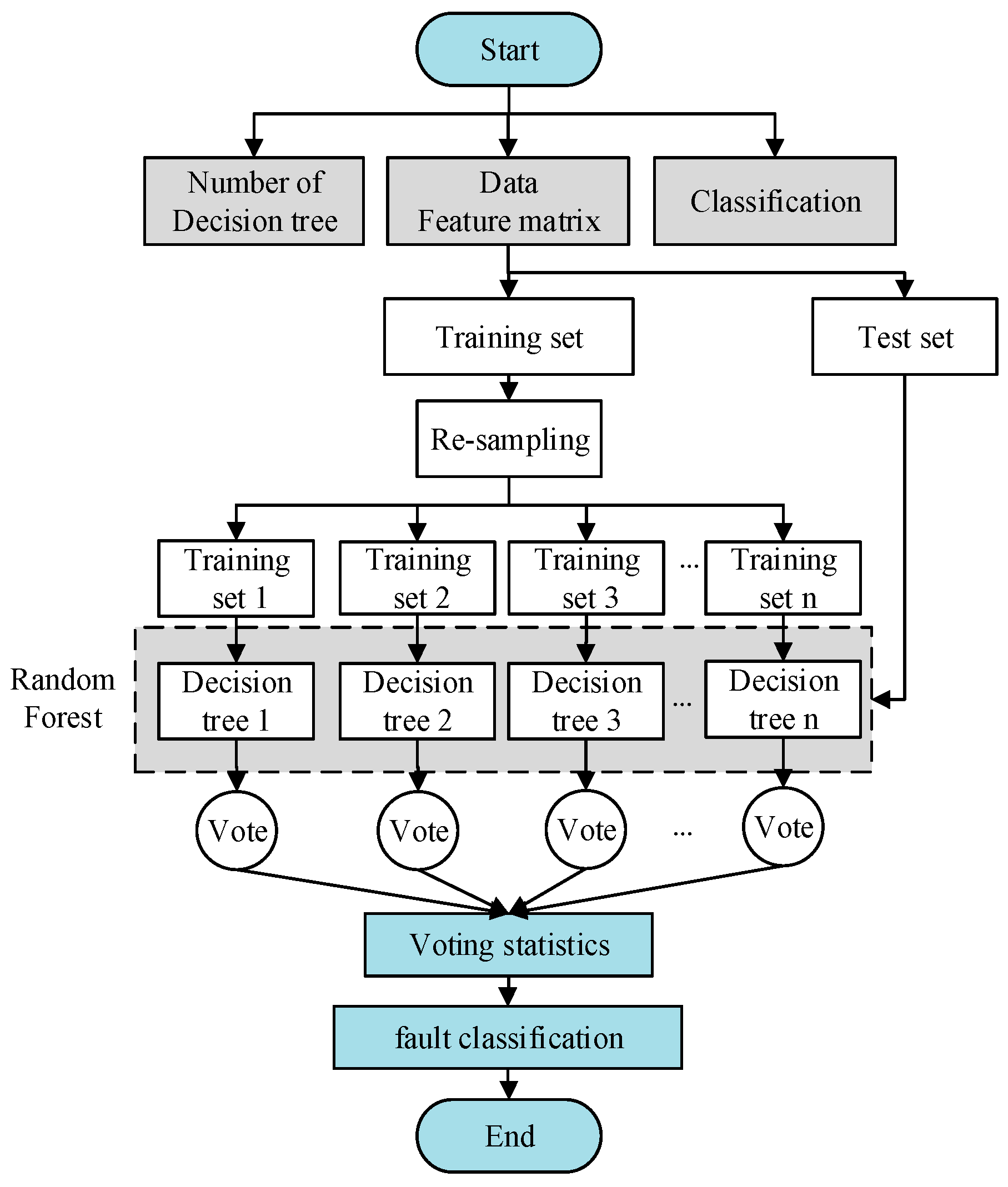
3. Random Forest Method for Fault Diagnosis
3.1. Random Forest Algorithm Building
3.2. Random Forest Performance Evaluation
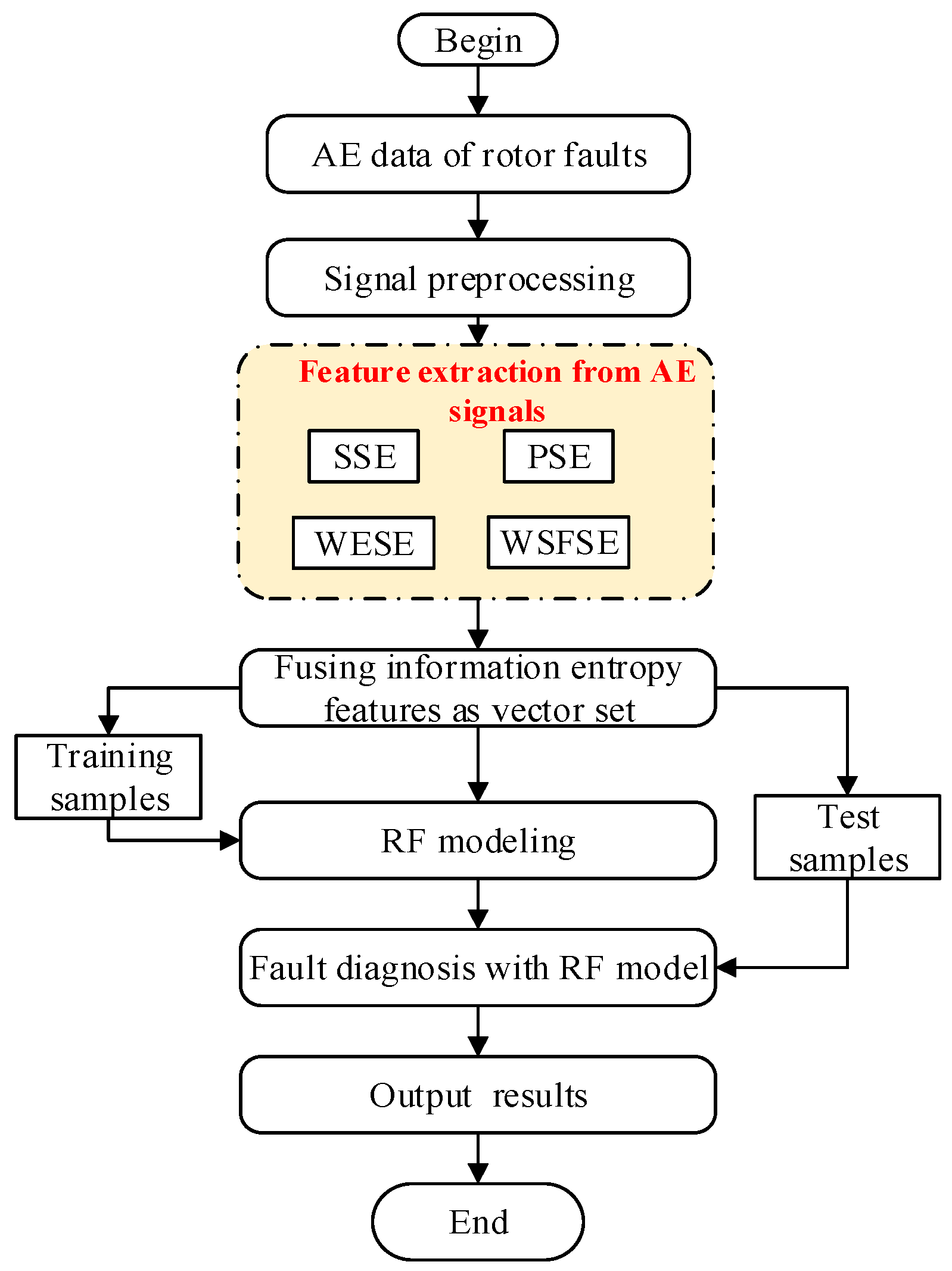
4. Multi-Domain Entropy-Random Forest Method for Fault Diagnosis
5. Fusion Diagnosis of Inter-Shaft Bearing Faults
5.1. Rolling Bearing Faults Simulation Experiment
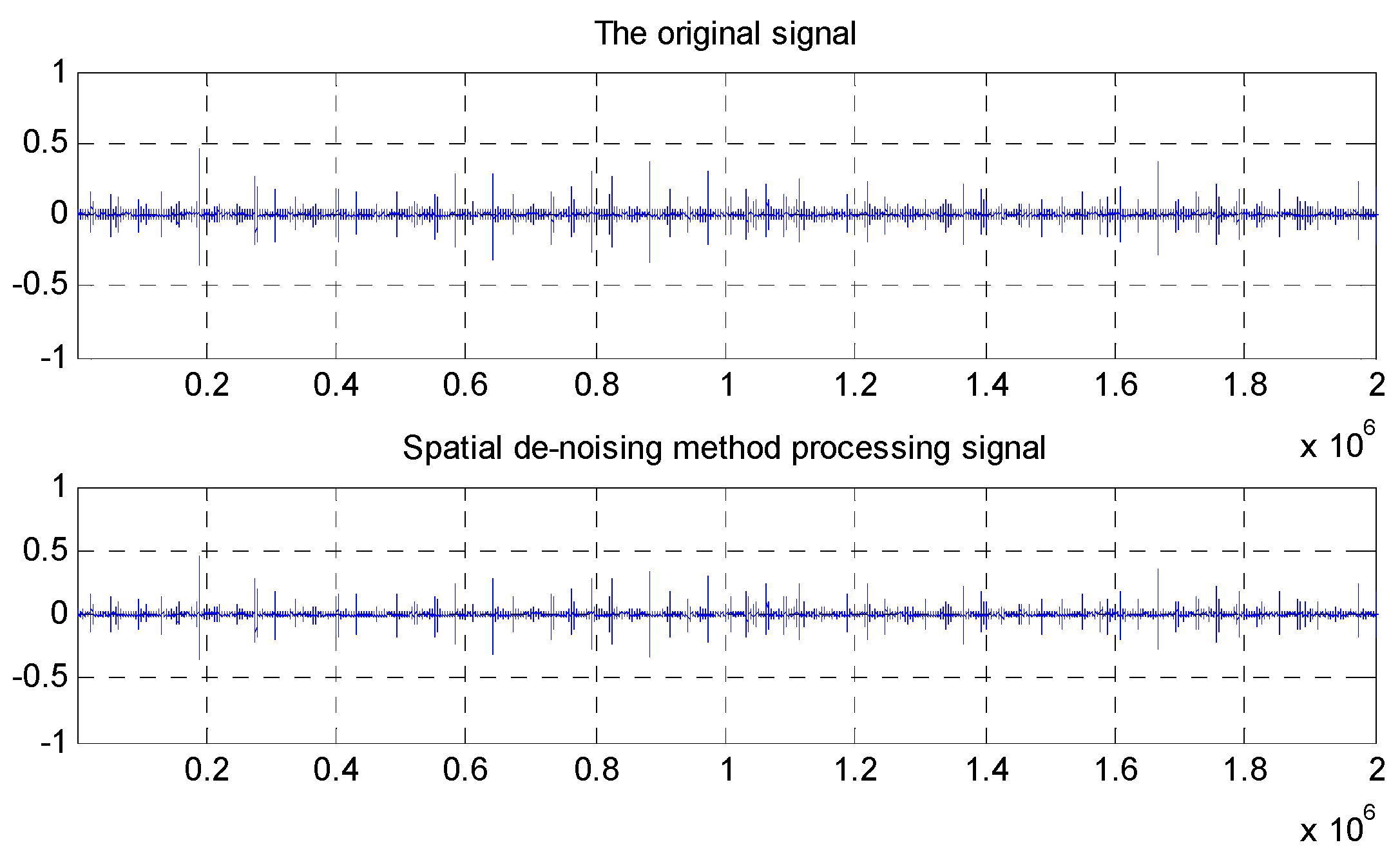
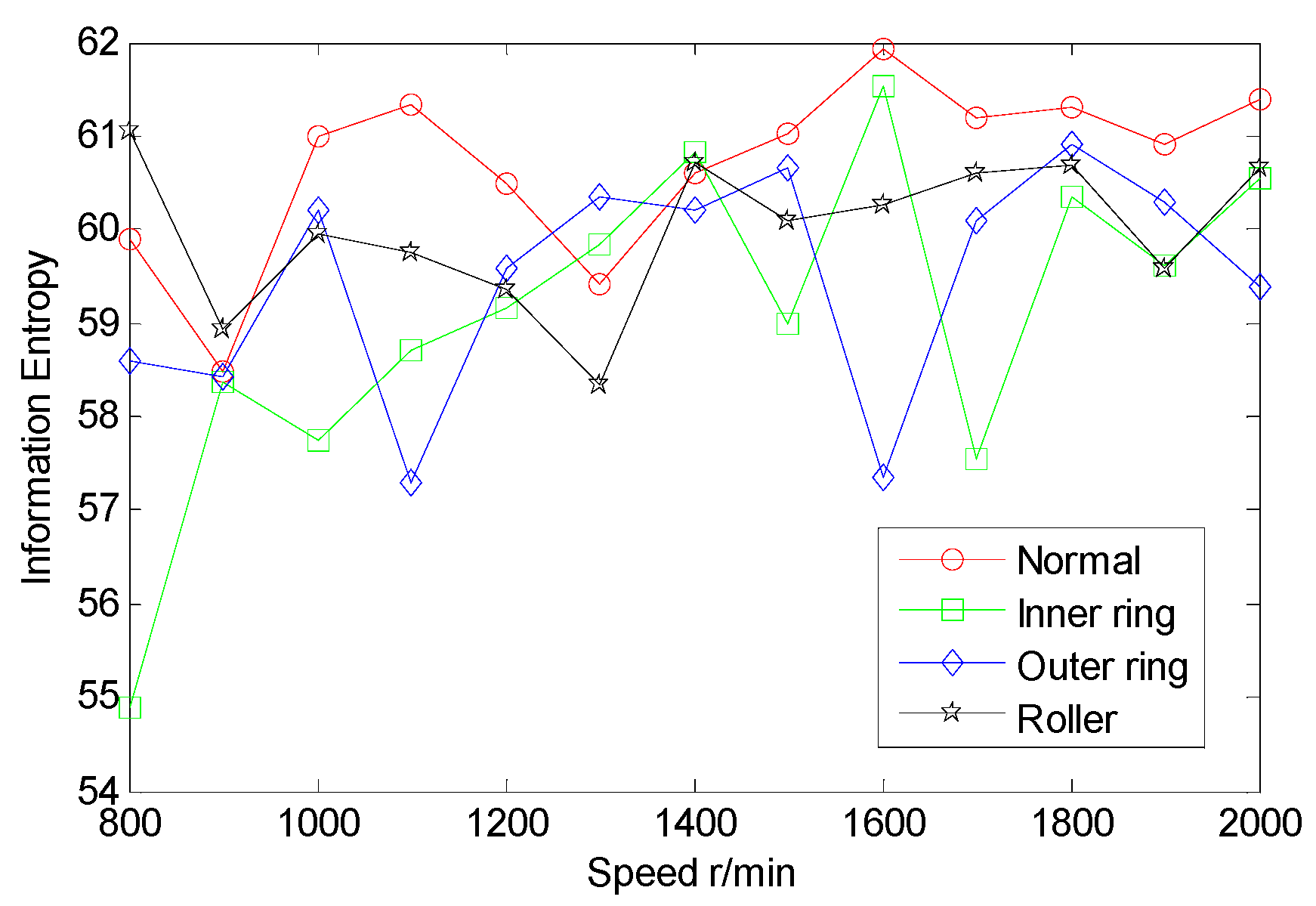
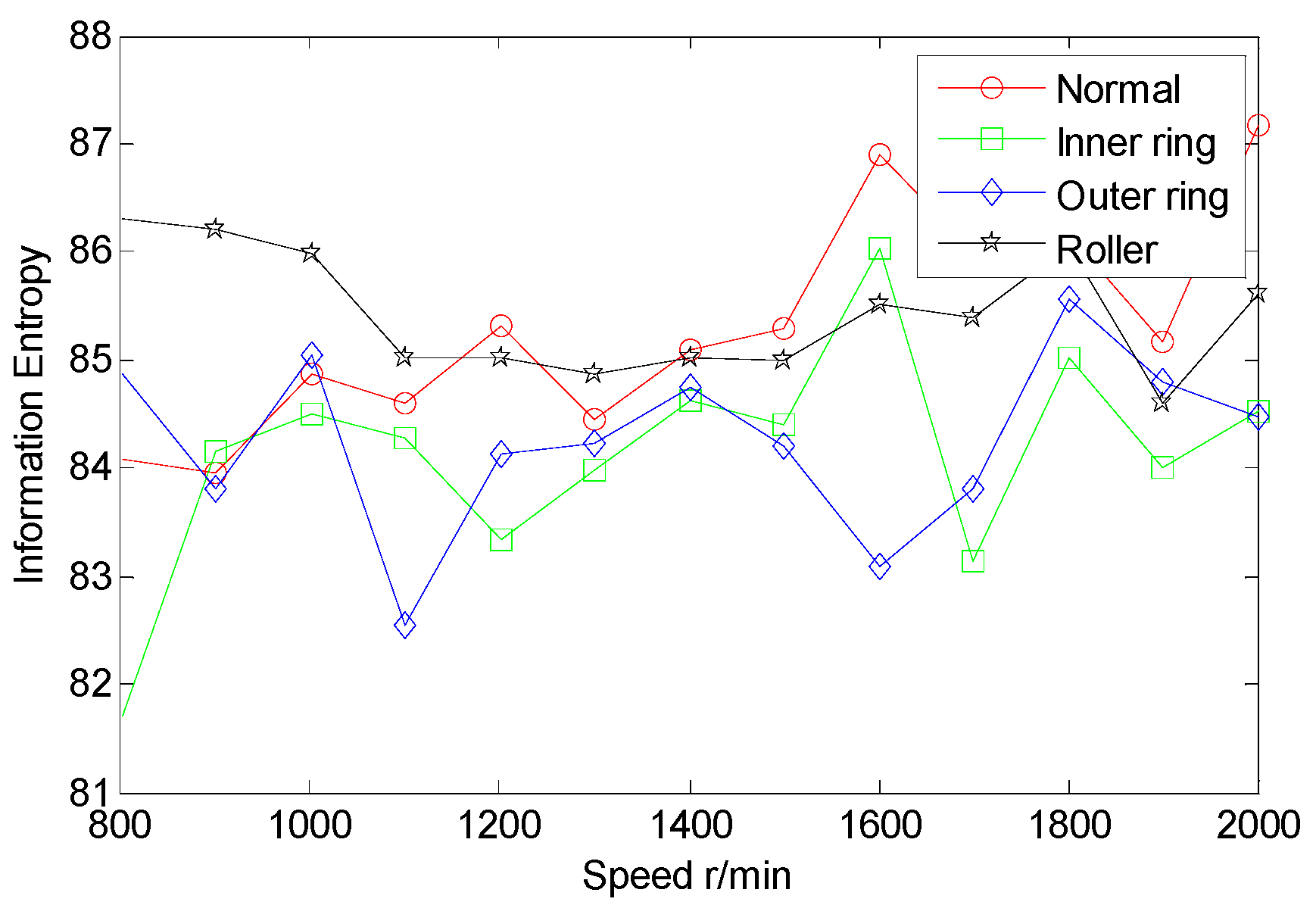
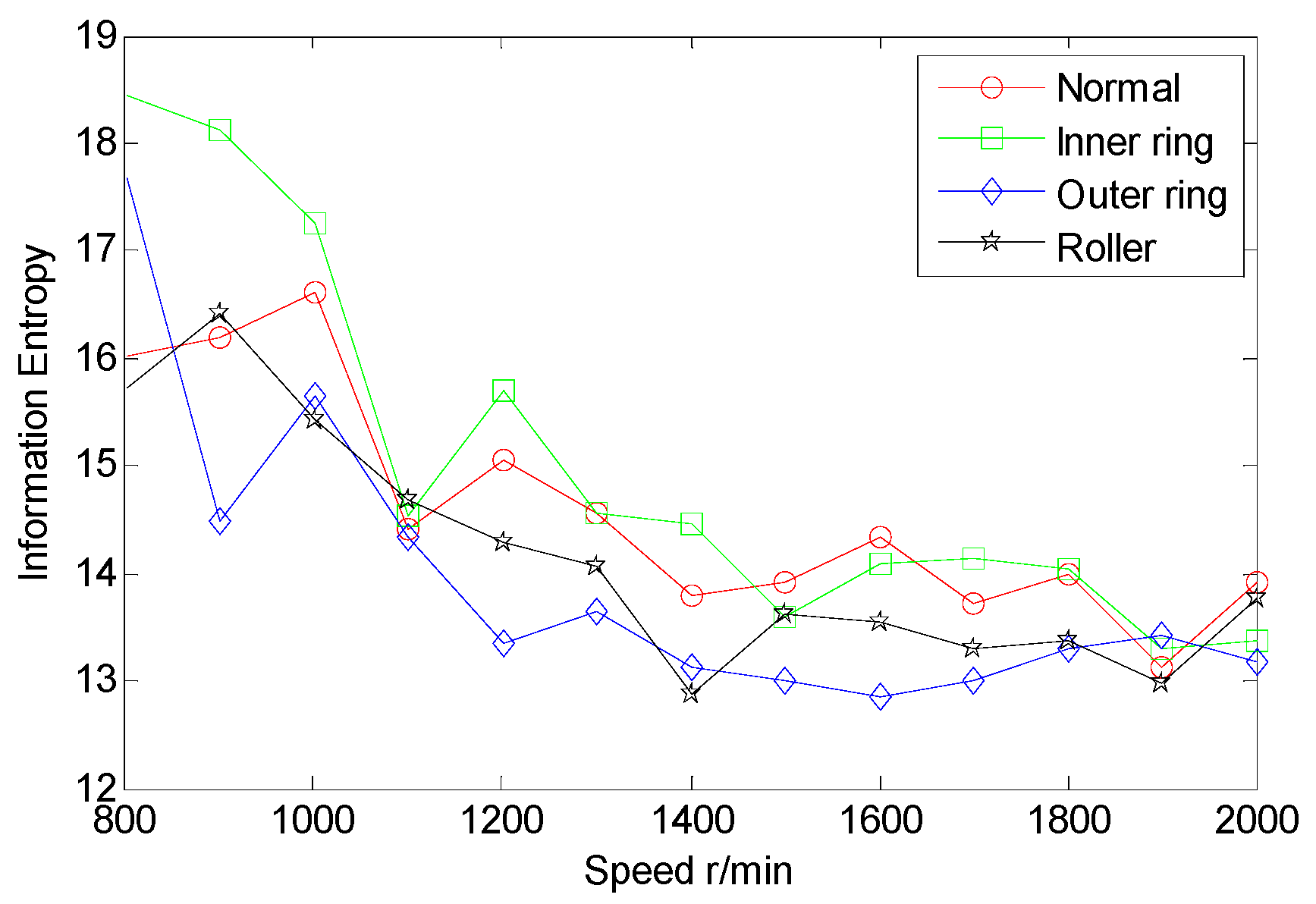
5.2. Extraction of Many Information Entropy Features of AE Signals
5.3. Extraction of Multi-Domain Entropy Features of AE Signals
5.4. Fusion Diagnosis of Inter-Shaft Bearing Faults with MDERF Method
5.4.1. MDERF Modeling
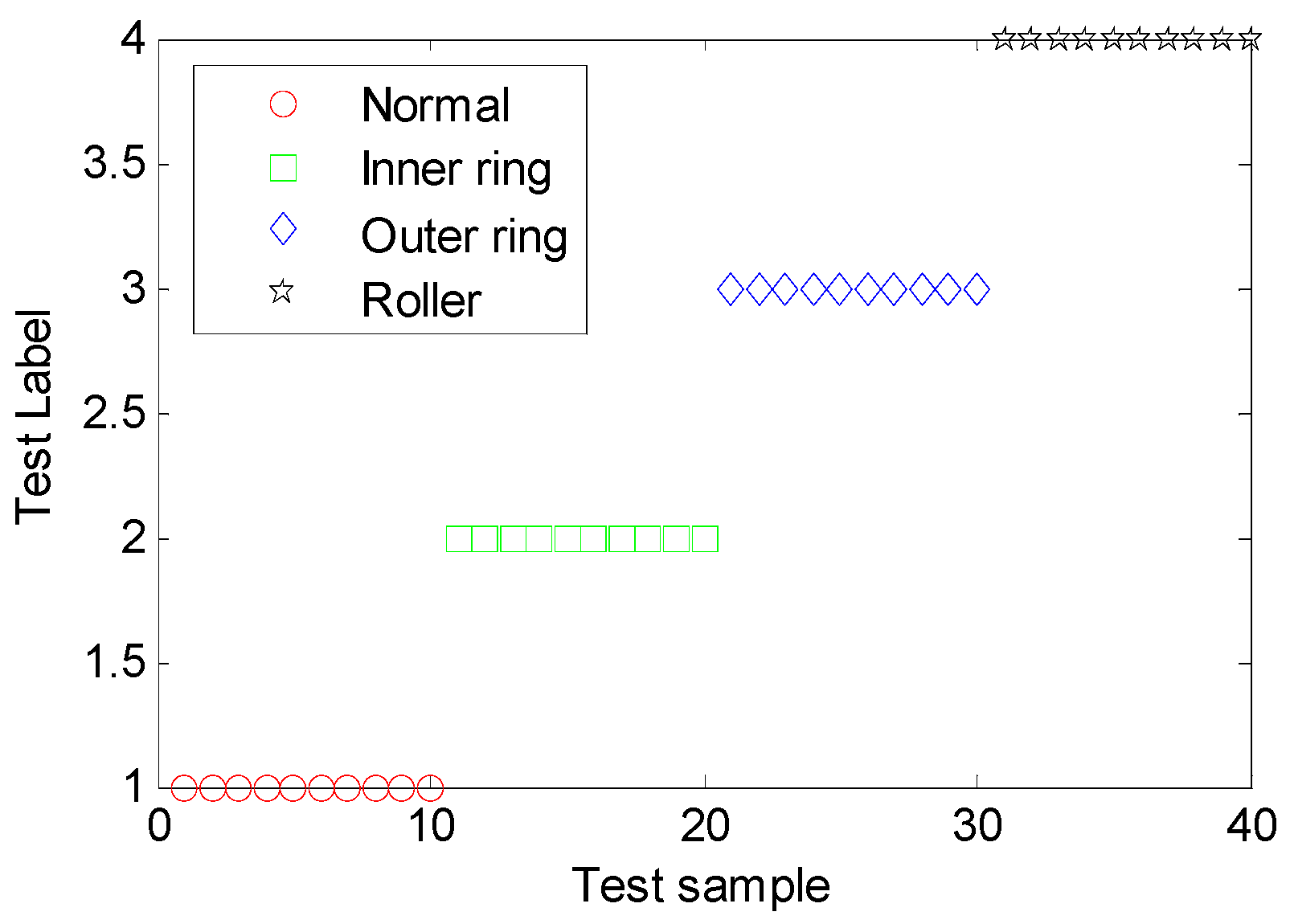
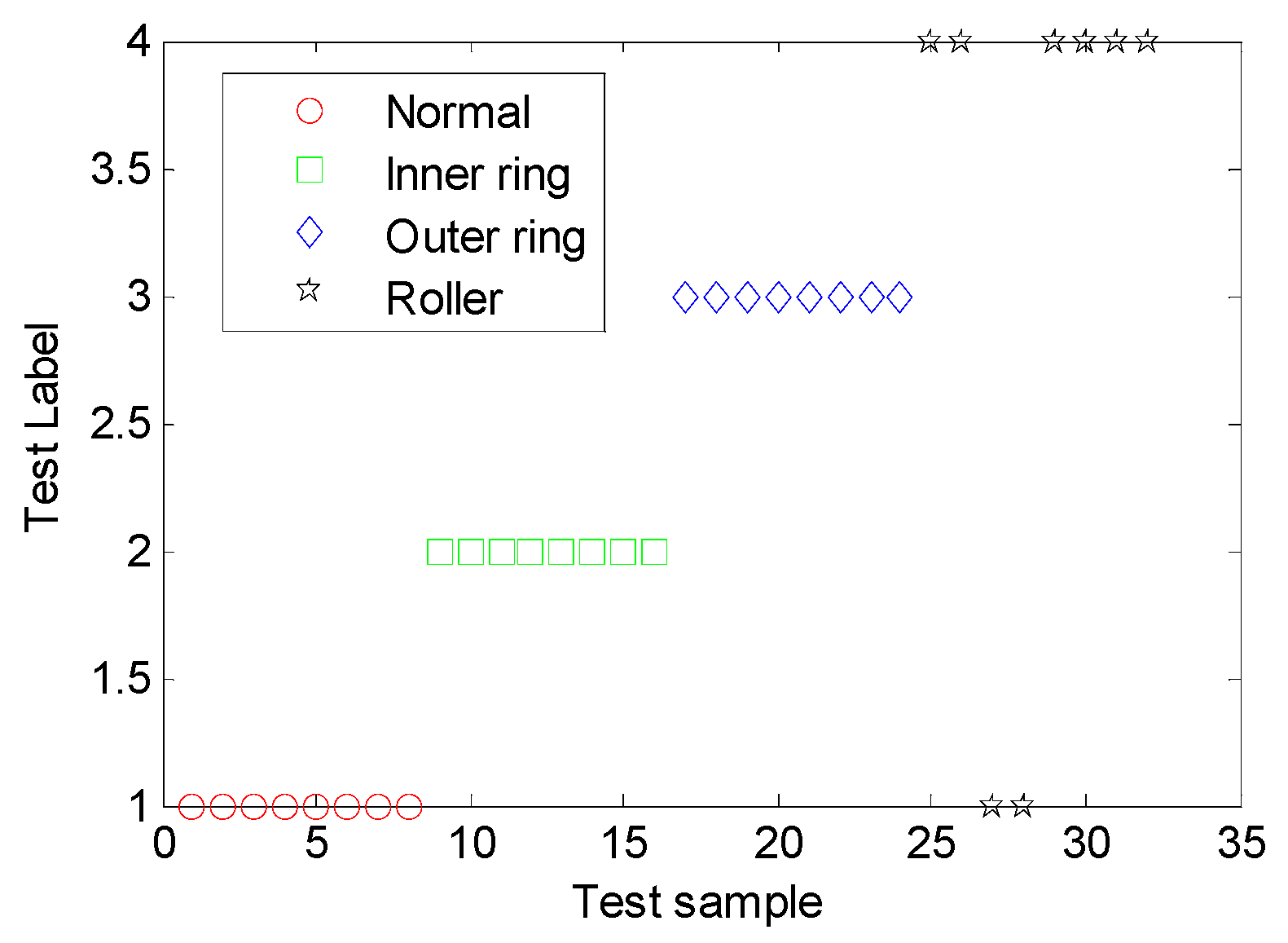
5.4.2. Validation of MDERF Method
Learning Ability Verification
Generalization Ability Verification
5.5. Method Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fei, C.W.; Lu, C.; Liem, R.P. Decomposed-coordinated surrogate modelling strategy for compound function approximation and a turbine blisk reliability evaluation. Aerosp. Sci. Technol. 2019, 95, 105466. [Google Scholar] [CrossRef]
- Caesarendra, W.; Kosasih, B.; Tieu, A.K.; Zhu, H.T.; Moodie, C.A.S.; Zhu, Q. Acoustic emission-based condition monitoring methods: Review and application for low speed slew bearing. Mech. Syst. Signal Process. 2016, 72–73, 134–159. [Google Scholar] [CrossRef]
- Hsieh, N.K.; Lin, W.Y.; Young, H.T. High-speed spindle fault diagnosis with the empirical mode decomposition and multiscale entropy method. Entropy 2015, 17, 2170–2183. [Google Scholar] [CrossRef]
- Romero-Troncoso, R.J.; Saucedo-Gallaga, R.; Cabal-Yepez, E.; Garcia-Perez, A.; Osornio-Rios, Q.A.; Alvarez-Salas, R.; Miranda-Vidales, H.; Huber, N. FPGA-based online detection of multiple combined faults in induction motors through information entropy and fuzzy inference. IEEE Trans. Ind. Electron. 2011, 58, 5263–5270. [Google Scholar] [CrossRef]
- Yu, X.T.; Lu, W.X.; Chu, F.L. Fault diagnostics based on pattern spectrum entropy and proximal support vector machine. Key Eng. Mater. 2009, 413–414, 607–612. [Google Scholar] [CrossRef]
- Ai, Y.T.; Guan, J.Y.; Fei, C.W.; Tian, J.; Zhang, F.L. Fusion information entropy method of rolling bearing fault diagnosis based on n-dimensional characteristic parameter distance. Mech. Syst. Signal Process. 2017, 88, 123–136. [Google Scholar] [CrossRef]
- Hernandez-Vargas, M.; Cabal-Yepez, E.; Garcia-Perez, A.; Romero-Troncoso, R.J. Novel methodology for broken-rotor-bar and bearing faults detection through SVD and information entropy. J. Sci. Ind. Res. 2012, 71, 589–593. [Google Scholar]
- Fei, C.W.; Bai, G.C.; Tang, W.Z. Quantitative diagnosis of rotor vibration fault using process power spectrum entropy and support vector machine method. J. Shock Vib. 2014, 2014, 957531. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.W.; Fei, C.W.; Bu, S.Q. Improved decomposed-coordinated Kriging modeling strategy for dynamic probabilistic analysis of multi-component structures. IEEE Trans. Reliab. 2019, 1–18. [Google Scholar] [CrossRef]
- Zhang, W.B.; Zhou, J.Z. Fault diagnosis for rolling element bearings based on feature space reconstruction and multiscale permutation entropy. Entropy 2019, 21, 519. [Google Scholar] [CrossRef]
- Ju, B.; Zhang, H.J.; Liu, Y.B.; Liu, F.; Lu, S.L.; Dai, Z.J. A feature extraction method using improved multi-scale entropy for rolling bearing fault diagnosis. Entropy 2018, 20, 212. [Google Scholar] [CrossRef]
- Ge, M.T.; Wang, J.; Ren, X.Y. Fault diagnosis of rolling bearings based on EWT and KDEC. Entropy 2017, 19, 633. [Google Scholar] [CrossRef]
- Zhao, H.M.; Sun, M.; Deng, W.; Yang, X.H. A new feature extraction method based on EEMD and multi-scale fuzzy entropy for motor bearing. Entropy 2017, 19, 14. [Google Scholar] [CrossRef]
- Gao, Y.D.; Villecco, F.; Li, M.; Song, W.Q. Multi-scale permutation entropy based on improved LMD and HMM for rolling bearing diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Song, L.K.; Bai, G.C.; Fei, C.W.; Tang, W.Z. Multi-failure probabilistic design for turbine bladed disks using neural network regression with distributed collaborative strategy. Aerosp. Sci. Technol. 2019, 92, 464–477. [Google Scholar] [CrossRef]
- Gómez-Peñate, S.; Valencia-Palomo, G.; López-Estrada, F.-R.; Astorga-Zaragoza, C.-M.; Osornio-Rios, R.A.; Santos-Ruiz, I. Sensor fault diagnosis based on a H∞ sliding mode and unknown input observer for Takagi-Sugeno systems with uncertain premise variables. Asian J. Control. 2019, 21, 339–353. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Song, L.Y.; Tomita, M.; Chen, P. Automatic fault detection and isolation method for roller bearing using hybrid-GA and sequential fuzzy inference. Sensors 2019, 19, 3553. [Google Scholar] [CrossRef]
- Santos-Ruiz, I.; López-Estrada, F.R.; Puig, V.; Pérez-Pérez, E.J.; Mina-Antonio, J.D.; Valencia-Palomo, G. Diagnosis of fluid leaks in pipelines using dynamic PCA. IFAC-PapersOnLine 2018, 51, 373–380. [Google Scholar] [CrossRef]
- Amandeep, S.; Anand, P. Gearbox fault diagnosis under fluctuating load conditions with independent angular re-sampling technique, continuous wavelet transform and multilayer perceptron neural network. IET Sci. Meas. Technol. 2017, 11, 220–225. [Google Scholar]
- Paliwal, D.; Choudhury, A.; Tingarikar, G. Wavelet and scalar indicator based fault assessment approach for rolling element bearings. Procedia Mater. Sci. 2014, 5, 2347–2355. [Google Scholar] [CrossRef][Green Version]
- Hu, G.S.; Zhu, F.F.; Ren, Z. Power quality disturbance identification using wavelet packet energy entropy and weighted support vector machines. Expert Syst. Appl. 2008, 35, 143–149. [Google Scholar] [CrossRef]
- Bradley, E.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC: New York, NY, USA, 1998; pp. 15–17. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Charles, J.S. CART: Classification and regression trees. Encycl. Ecol. 1983, 1, 582–588. [Google Scholar]
- Masetic, Z.; Subasi, A. Congestive heart failure detection using random forest classifier. Comput. Methods Programs Biomed. 2016, 130, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. Mach. Learn. 2012, 45, 157–176. [Google Scholar]
- Yang, B.S.; Di, X.; Han, T. Random forests classifier for machine fault diagnosis. J. Mech. Sci. Technol. 2008, 22, 1716–1725. [Google Scholar] [CrossRef]
- Fei, C.W.; Bai, G.C. Wavelet correlation feature scale entropy and fuzzy support vector machine approach for aeroengine whole-body vibration fault diagnosis. Shock Vib. 2013, 20, 341–349. [Google Scholar] [CrossRef]
- Zhang, Z.H. Introduction to machine learning: K-nearest neighbors. Ann. Transl. Med. 2016, 4, 2–18. [Google Scholar] [CrossRef]
- De’ath, G.; Fabricius, K.E. Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology 2000, 81, 3178–3192. [Google Scholar] [CrossRef]
- Xia, F.; Liu, C.; Li, Y. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]



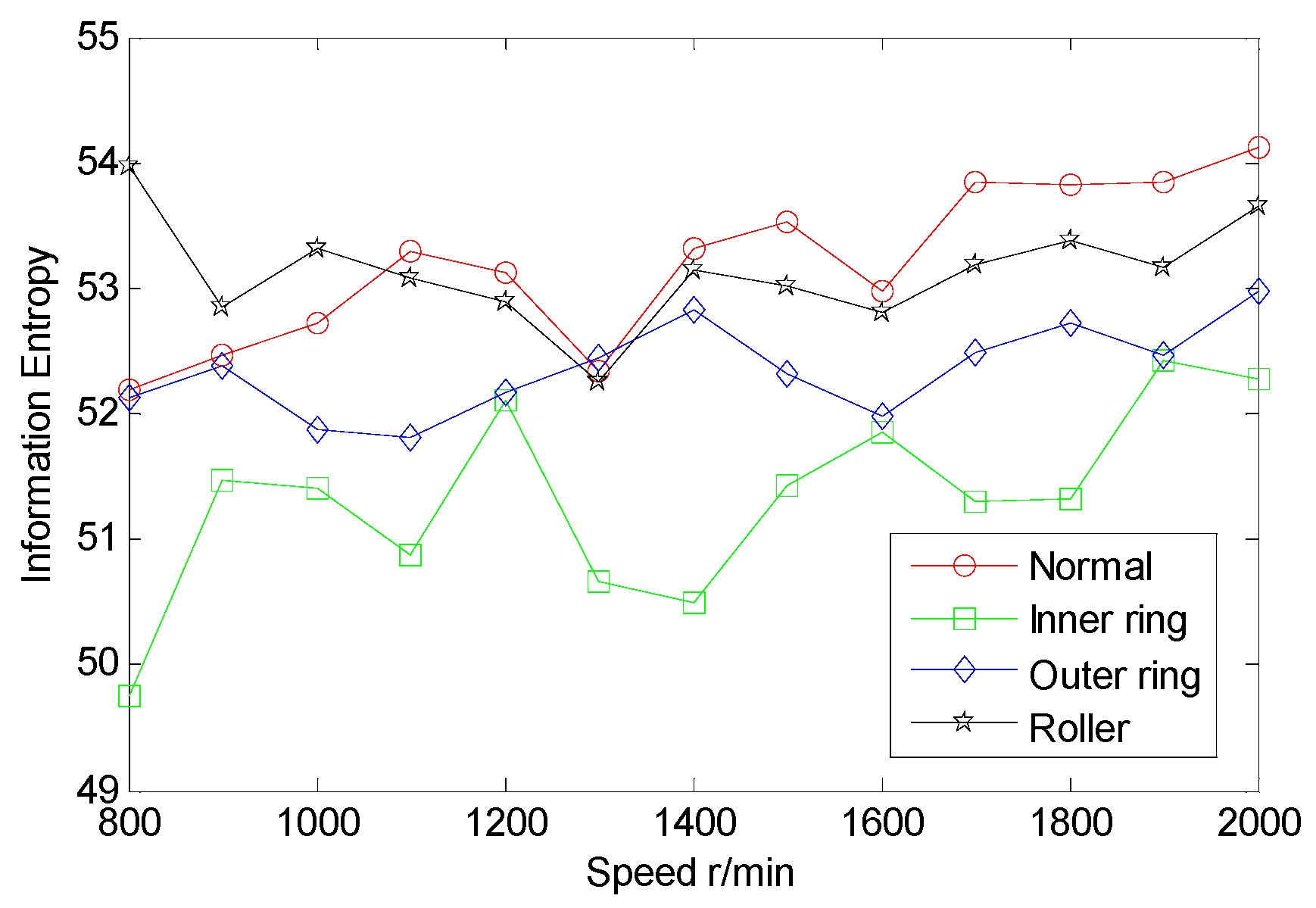
| Fault Type | Sample Number | Vector of Multi-Domain Entropy Point | Type No. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Normal | 1 | 51.22 | 52.18 | 52.03 | 53.28 | 53.22 | 52.93 | 52.75 | 1 |
| 53.29 | 53.32 | 53.67 | 53.56 | 54.07 | 53.66 | ||||
| 2 | 51.36 | 52.55 | 52.40 | 53.30 | 53.22 | 53.04 | 52.80 | 1 | |
| 53.08 | 53.26 | 53.89 | 53.32 | 53.65 | 54.02 | ||||
| Inner ring fault | 1 | 51.57 | 52.30 | 52.18 | 51.27 | 51.72 | 51.54 | 51.41 | 2 |
| 51.99 | 53.11 | 51.67 | 52.39 | 52.08 | 53.37 | ||||
| 2 | 51.35 | 51.47 | 51.13 | 51.14 | 51.43 | 51.04 | 51.88 | 2 | |
| 50.88 | 51.99 | 51.10 | 51.87 | 52.65 | 52.93 | ||||
| Outer ring fault | 1 | 52.85 | 53.17 | 51.50 | 52.12 | 52.14 | 52.30 | 52.54 | 3 |
| 52.13 | 52.40 | 52.04 | 52.44 | 52.59 | 53.26 | ||||
| 2 | 52.93 | 52.47 | 51.78 | 52.36 | 52.60 | 51.98 | 52.76 | 3 | |
| 52.37 | 52.06 | 51.84 | 52.34 | 52.64 | 52.94 | ||||
| Roller fault | 1 | 52.84 | 53.49 | 52.54 | 51.97 | 52.92 | 52.45 | 52.48 | 4 |
| 52.45 | 52.35 | 52.06 | 52.72 | 53.24 | 53.03 | ||||
| 2 | 53.19 | 53.04 | 52.89 | 52.13 | 52.53 | 52.69 | 52.51 | 4 | |
| 52.53 | 52.90 | 52.29 | 52.57 | 52.90 | 53.08 | ||||
| Confusion Matrix | Real | Precision | ||||
|---|---|---|---|---|---|---|
| Normal | Inner Ring Fault | Outer Ring Fault | Roller Fault | |||
| Predict | Normal | 10 | 0 | 0 | 0 | 100% |
| Inner ring fault | 0 | 10 | 0 | 0 | ||
| Outer ring fault | 0 | 0 | 10 | 0 | ||
| Roller fault | 0 | 0 | 0 | 10 | ||
| Confusion Matrix | Real | Precision | ||||
|---|---|---|---|---|---|---|
| Normal | Inner Ring Fault | Outer Ring Fault | Roller Fault | |||
| Predict | Normal | 8 | 0 | 0 | 2 | 93.75% |
| Inner ring fault | 0 | 8 | 0 | 0 | ||
| Outer ring fault | 0 | 0 | 8 | 0 | ||
| Roller fault | 0 | 0 | 0 | 6 | ||
| Algorithm | Precision |
|---|---|
| SVM | 80.45% |
| KNN | 78.25% |
| CART | 85.46% |
| GBDT | 87.23% |
| RF | 93.75% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Liu, L.; Zhang, F.; Ai, Y.; Wang, R.; Fei, C. Multi-Domain Entropy-Random Forest Method for the Fusion Diagnosis of Inter-Shaft Bearing Faults with Acoustic Emission Signals. Entropy 2020, 22, 57. https://doi.org/10.3390/e22010057
Tian J, Liu L, Zhang F, Ai Y, Wang R, Fei C. Multi-Domain Entropy-Random Forest Method for the Fusion Diagnosis of Inter-Shaft Bearing Faults with Acoustic Emission Signals. Entropy. 2020; 22(1):57. https://doi.org/10.3390/e22010057
Chicago/Turabian StyleTian, Jing, Lili Liu, Fengling Zhang, Yanting Ai, Rui Wang, and Chengwei Fei. 2020. "Multi-Domain Entropy-Random Forest Method for the Fusion Diagnosis of Inter-Shaft Bearing Faults with Acoustic Emission Signals" Entropy 22, no. 1: 57. https://doi.org/10.3390/e22010057
APA StyleTian, J., Liu, L., Zhang, F., Ai, Y., Wang, R., & Fei, C. (2020). Multi-Domain Entropy-Random Forest Method for the Fusion Diagnosis of Inter-Shaft Bearing Faults with Acoustic Emission Signals. Entropy, 22(1), 57. https://doi.org/10.3390/e22010057






