Frequency Dependence of the Entanglement Entropy Production in a System of Coupled Driven Nonlinear Oscillators
Abstract
1. Introduction
2. System of Interest
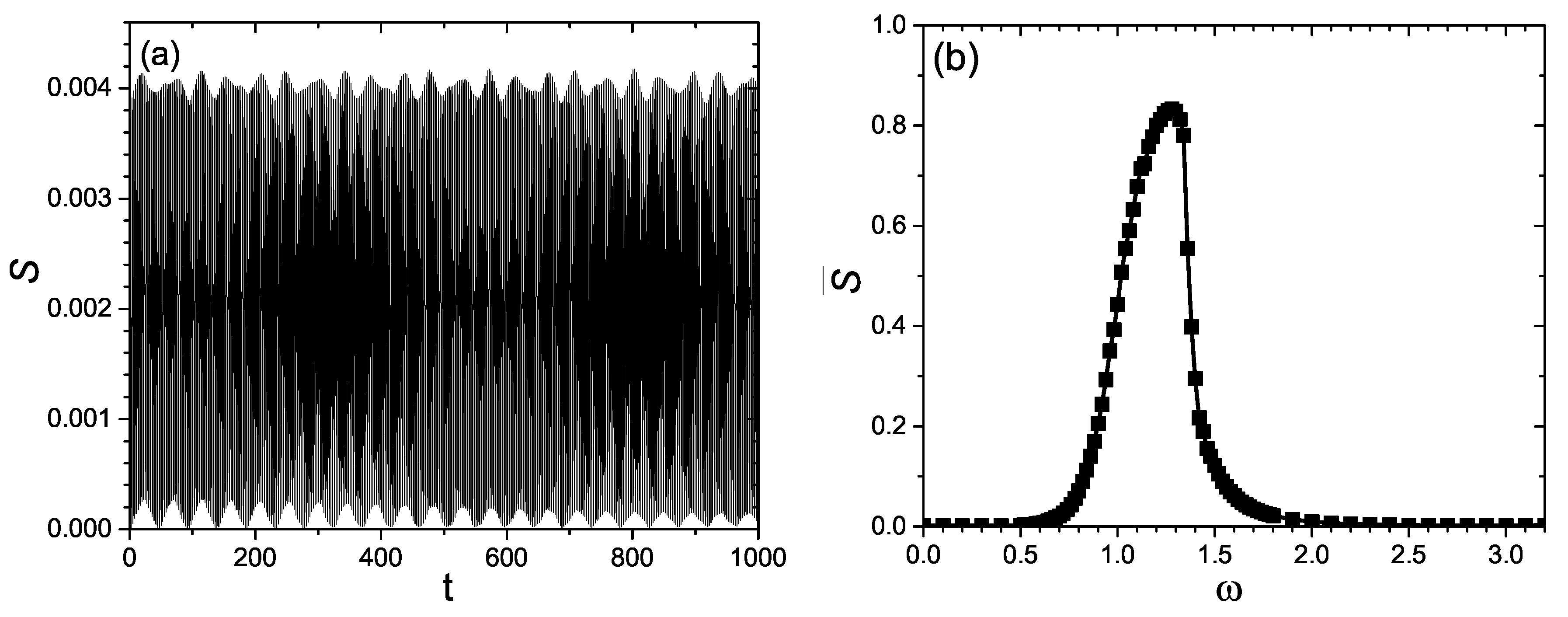
3. Entanglement Entropy and Its Frequency Response
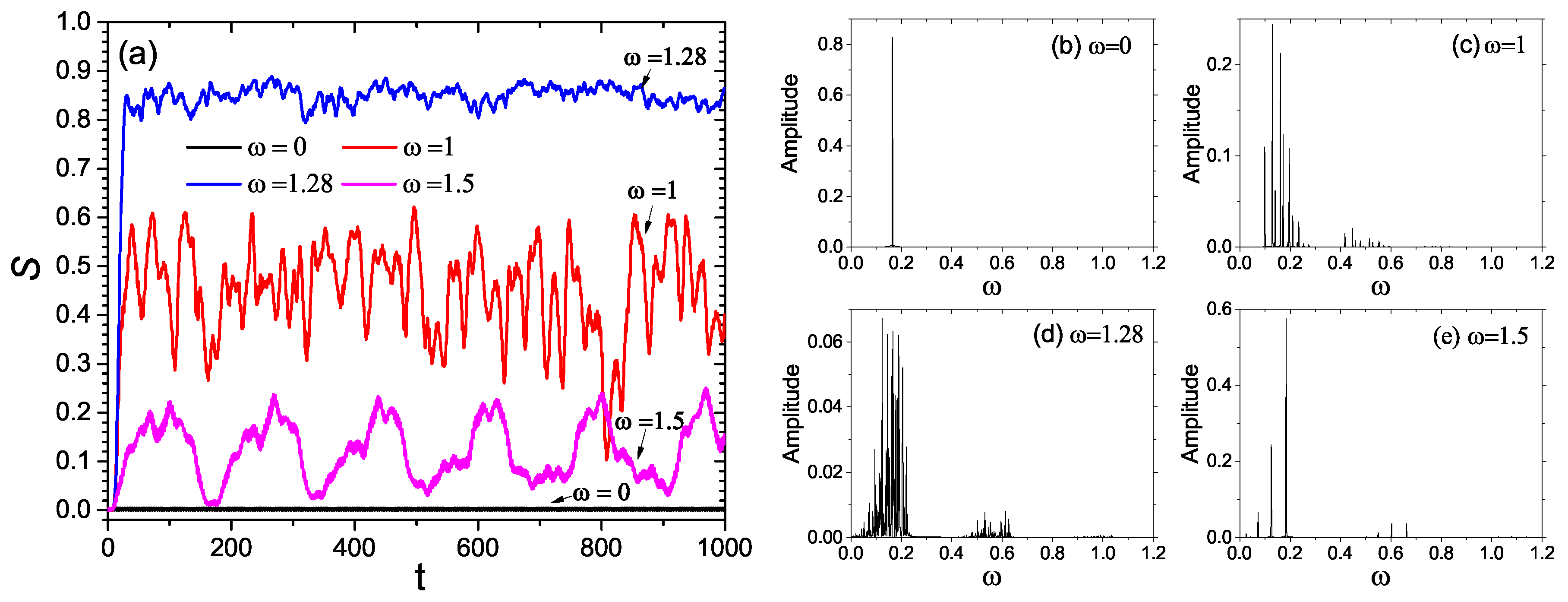
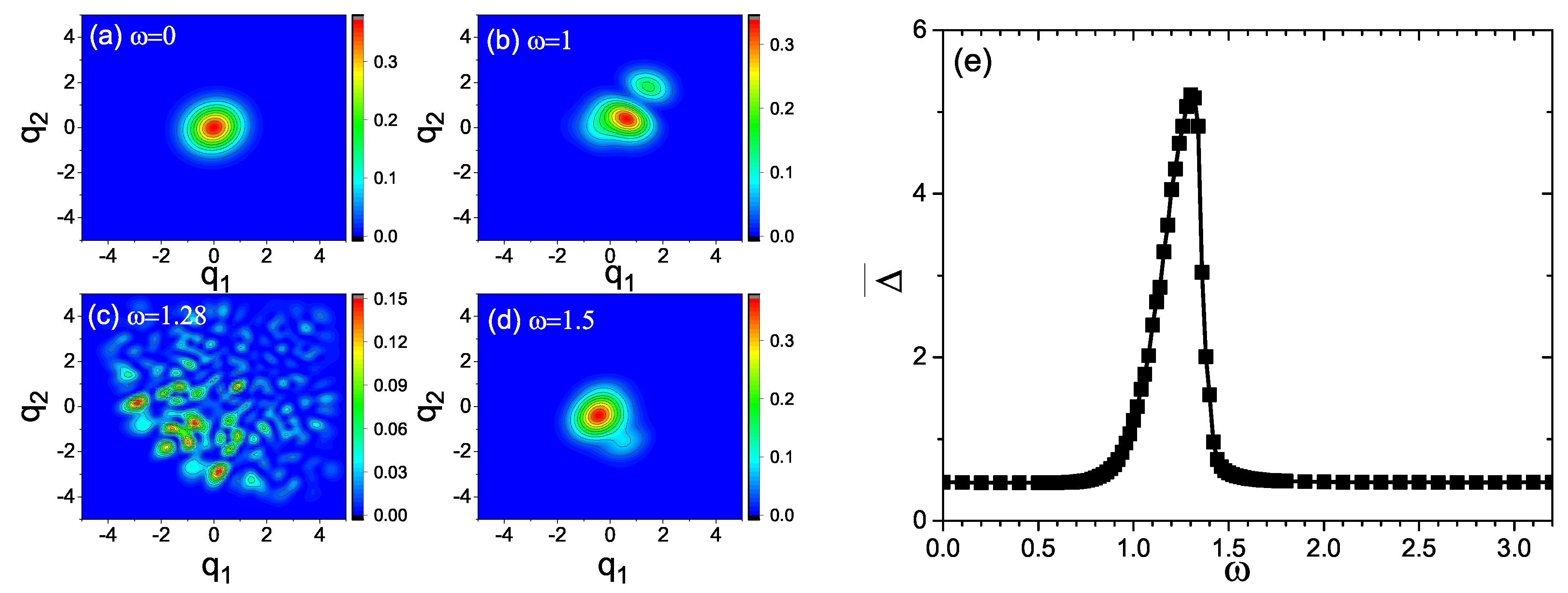
4. Entropy Production during the Quantum Evolution
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2011; pp. 571–580. [Google Scholar]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Eleuch, H.; Hassouni, Y. Beam splitting and entanglement generation: Excited coherent states. Quant. Inf. Process. 2013, 12, 69–82. [Google Scholar] [CrossRef]
- Mohamed, A.B.; Eleuch, H. Non-classical effects in cavity QED containing a nonlinear optical medium and a quantum well: Entanglement and non-Gaussanity. Eur. Phys. J. D 2015, 69, 191. [Google Scholar] [CrossRef]
- Mohamed, A.B.A.; Eleuch, H. Quantum correlation control for two semiconductor microcavities connected by an optical fiber. Phys. Scr. 2017, 92, 065101. [Google Scholar] [CrossRef]
- Berrada, K.; Eleuch, H.; Hassouni, Y. Asymptotic dynamics of quantum discord in open quantum systems. J. Phys. B 2011, 44, 145503. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H.; Das, S. Semiconductor cavity QED with squeezed light: Nonlinear regime. Phys. Rev. A 2011, 84, 053817. [Google Scholar] [CrossRef]
- Vacanti, G.; Paternostro, M.; Palma, G.M.; Kim, M.S.; Vedral, V. Non-classicality of optomechanical devices in experimentally realistic operating regimes. Phys. Rev. A 2013, 88, 1023–1027. [Google Scholar] [CrossRef]
- Rips, S.; Kiffner, M.; Wilsonrae, I.; Hartmann, M.J. Steady-state negative wigner functions of nonlinear nanomechanical oscillators. New J. Phys. 2012, 4, 023042. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Poot, M.; Zant, H.S.J.V.D. Mechanical systems in the quantum regime. Phys. Rep. 2012, 511, 273–335. [Google Scholar] [CrossRef]
- Kaltenbaek, R.; Kiesel, N.; Romero-Isart, O.; Schwab, K.C.; Johann, U.; Aspelmeyer, M. Macroscopic quantum resonators (MAQRO): 2015 Update. Exp. Astron. 2015, 34, 123–164. [Google Scholar] [CrossRef]
- Yukihiro, T.; Hiroya, T.; Dykman, M.I. Driven nonlinear nanomechanical resonators as digital signal detectors. Sci. Rep. 2018, 8, 11284. [Google Scholar]
- Peano, V.; Thorwart, M. Macroscopic quantum effects in a strongly driven nanomechanical resonator. Phys. Rev. B 2005, 70, 155–163. [Google Scholar] [CrossRef]
- Imboden, M.; Williams, O.; Mohanty, P. Nonlinear dissipation in diamond nanoelectromechanical resonators. Appl. Phys. Lett. 2013, 102, 103502. [Google Scholar] [CrossRef]
- Rips, S.; Wilsonrae, I.; Hartmann, M.J. Nonlinear nanomechanical resonators for quantum optoelectromechanics. Phys. Rev. A 2014, 89, 58–61. [Google Scholar] [CrossRef]
- Almog, R.; Zaitsev, S.; Shtempluck, O.; Buks, E. Noise squeezing in a nanomechanical duffing resonator. Phys. Rev. Lett. 2007, 98, 078103. [Google Scholar] [CrossRef] [PubMed]
- Ong, F.R.; Boissonneault, M.; Mallet, F.; Palacioslaloy, A.; Dewes, A.; Doherty, A.C.; Blais, A.; Bertet, P.; Vion, D.; Esteve, D. Circuit QED with a nonlinear resonator: Ac-stark shift and dephasing. Phys. Rev. Lett. 2011, 106, 167002. [Google Scholar] [CrossRef] [PubMed]
- Murch, K.W.; Vijay, R.; Barth, I.; Naaman, O.; Aumentado, J.; Friedland, L.; Siddiqi, I. Quantum fluctuations in the chirped pendulum. Nat. Phys. 2011, 7, 105–108. [Google Scholar] [CrossRef]
- Yang, C.P.; Chu, S.I.; Han, S. Possible realization of entanglement, logical gates, and quantum-information transfer with superconducting-quantum-interference-device qubits in cavity qed. Phys. Rev. A 2003, 67, 042311. [Google Scholar] [CrossRef]
- Stannigel, K.; Komar, P.; Habraken, S.J.M.; Bennett, S.D.; Lukin, M.D.; Zoller, P.; Rabl, P. Optomechanical quantum information processing with photons and phonons. Phys. Rev. Lett. 2012, 109, 013603. [Google Scholar] [CrossRef]
- Cleland, A.N.; Geller, M.R. Superconducting qubit storage and entanglement with nanomechanical resonators. Phys. Rev. Lett. 2004, 93, 070501. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, D.S.; Fillaux, F. Incoherent elastic-neutron-scattering study of the vibrational dynamics and spin-related symmetry of protons in the crystal. Phys. Rev. B 1999, 59, 4134. [Google Scholar] [CrossRef]
- Audenaert, K.; Eisert, J.; Werner, R.F. Entanglement properties of the harmonic chain. Phys. Rev. A 2002, 66, 042327. [Google Scholar] [CrossRef]
- Fillaux, D.F. Quantum entanglement and nonlocal proton transfer dynamics in dimers of formic acid and analogues. Chem. Phys. Lett. 2005, 408, 302. [Google Scholar] [CrossRef]
- Chung, N.N.; Chew, L.Y. Two-step approach to the dynamics of coupled anharmonic oscillators. Phys. Rev. A 2009, 80, 012103. [Google Scholar] [CrossRef]
- Qiao, G.J.; Gao, H.X.; Liu, H.D.; Yi, X.X. Quantum synchronization of two mechanical oscillators in coupled optomechanical systems with Kerr nonlinearity. Sci. Rep. 2018, 8, 15614. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Sarma, A.K. Entanglement dynamics of two coupled mechanical oscillators in modulated optomechanics. Phys. Rev. A 2018, 97, 022336. [Google Scholar] [CrossRef]
- Ralph, T.C.; Gilchris, A.; Milburn, G.J.; Munro, W.J.; Glancy, S. Quantum computation with optical coherent states. Phys. Rev. A 2003, 68, 042319. [Google Scholar] [CrossRef]
- Jaffe, C.; Brumer, P. Classical Liouville mechanics and intramolecular relaxation dynamics. J. Phys. Chem. 1984, 88, 4829–4839. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Path integral approach to quantum brownian motion. Physica A 1983, 121, 587–616. [Google Scholar] [CrossRef]
- Rabinovich, M.I.; Trubetskov, D.I. Oscillations and Waves: In Linear and Nonlinear Systems; Kluver Academic Publisher: Dordrecht, The Netherlands, 1989; pp. 286–297. [Google Scholar]
- Lefebvrebrion, H.; Field, R. The Spectra and Dynamics of Diatomic Molecules Revised and Enlarged Edition; Elsevier: San Diego, CA, USA, 2004; pp. 27–47. [Google Scholar]
- Bracewell, R. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1985; pp. 112–113. [Google Scholar]
- Louisell, W.H. Quantum Statistical Properties of Radiation; Wiley: New York, NY, USA, 1973; pp. 331–468. [Google Scholar]
- Duan, L.-M.; Guo, G.-C. Preserving coherence in quantum computation by pairing the quantum bits. Phys. Rev. Lett. 1997, 79, 1953. [Google Scholar] [CrossRef]
- Eleuch, H.; Guérin, S.; Jauslin, H. Effects of an environment on a cavity-quantum-electrodynamics system controlled by bichromatic adiabatic passage. Phys. Rev. A 2012, 85, 13830. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Resonances in open quantum systems. Phys. Rev. A 2017, 95, 022117. [Google Scholar] [CrossRef]
- Eleuch, H.; Rotter, I. Open quantum systems and Dicke superradiance. Eur. Phys. J. D 2014, 68, 74. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2004, 76, 1267. [Google Scholar] [CrossRef]
- Berrada, K.; El Baz, M.; Eleuch, H.; Hassouni, Y. A comparative study of negativity and concurrence based on spin coherent states. Int. J. Mod. Phys. C 2010, 21, 291. [Google Scholar] [CrossRef]
- Bogoliubov, N.N. A New method in the theory of superconductivity. I. J. Exp. Theor. Phys. 1958, 34, 58. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 1961, 124, 246. [Google Scholar] [CrossRef]
- Arraut, I. The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry 2019, 11, 803. [Google Scholar] [CrossRef]
- Nambu, Y. From Yukawa’s Pion to spontaneous symmetry breaking. J. Phys. Soc. Jpn. 2007, 76, 111002. [Google Scholar] [CrossRef]
- Arraut, I. The Nambu-Goldstone theorem in non-relativistic systems. Int. J. Mod. Phys. 2017, A32, 1750127. [Google Scholar] [CrossRef]
- Arraut, I. The origin of the mass of the Nambu-Goldstone bosons. Int. J. Mod. Phys. 2018, A33, 1850041. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Li, J.; Feng, J.; Zhang, H. The Phase Transition in a Bistable Duffing System Driven by Lèvy Noise. J. Stat. Phys. 2015, 158, 120–131. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.-H.; Yan, Z.-Y. Frequency Dependence of the Entanglement Entropy Production in a System of Coupled Driven Nonlinear Oscillators. Entropy 2019, 21, 889. https://doi.org/10.3390/e21090889
Zhang S-H, Yan Z-Y. Frequency Dependence of the Entanglement Entropy Production in a System of Coupled Driven Nonlinear Oscillators. Entropy. 2019; 21(9):889. https://doi.org/10.3390/e21090889
Chicago/Turabian StyleZhang, Shi-Hui, and Zhan-Yuan Yan. 2019. "Frequency Dependence of the Entanglement Entropy Production in a System of Coupled Driven Nonlinear Oscillators" Entropy 21, no. 9: 889. https://doi.org/10.3390/e21090889
APA StyleZhang, S.-H., & Yan, Z.-Y. (2019). Frequency Dependence of the Entanglement Entropy Production in a System of Coupled Driven Nonlinear Oscillators. Entropy, 21(9), 889. https://doi.org/10.3390/e21090889




