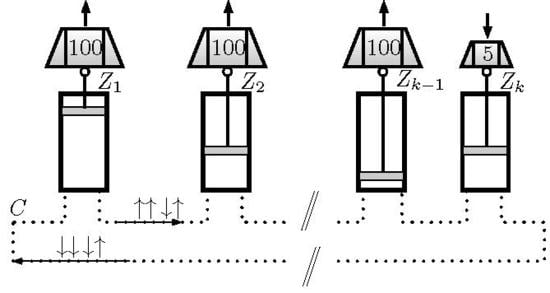
Entropy Distribution in a Quantum Informational Circuit of Tunable Szilard Engines
Abstract
1. Introduction
2. Antecedents
3. Reference Quantum Szilard Engine
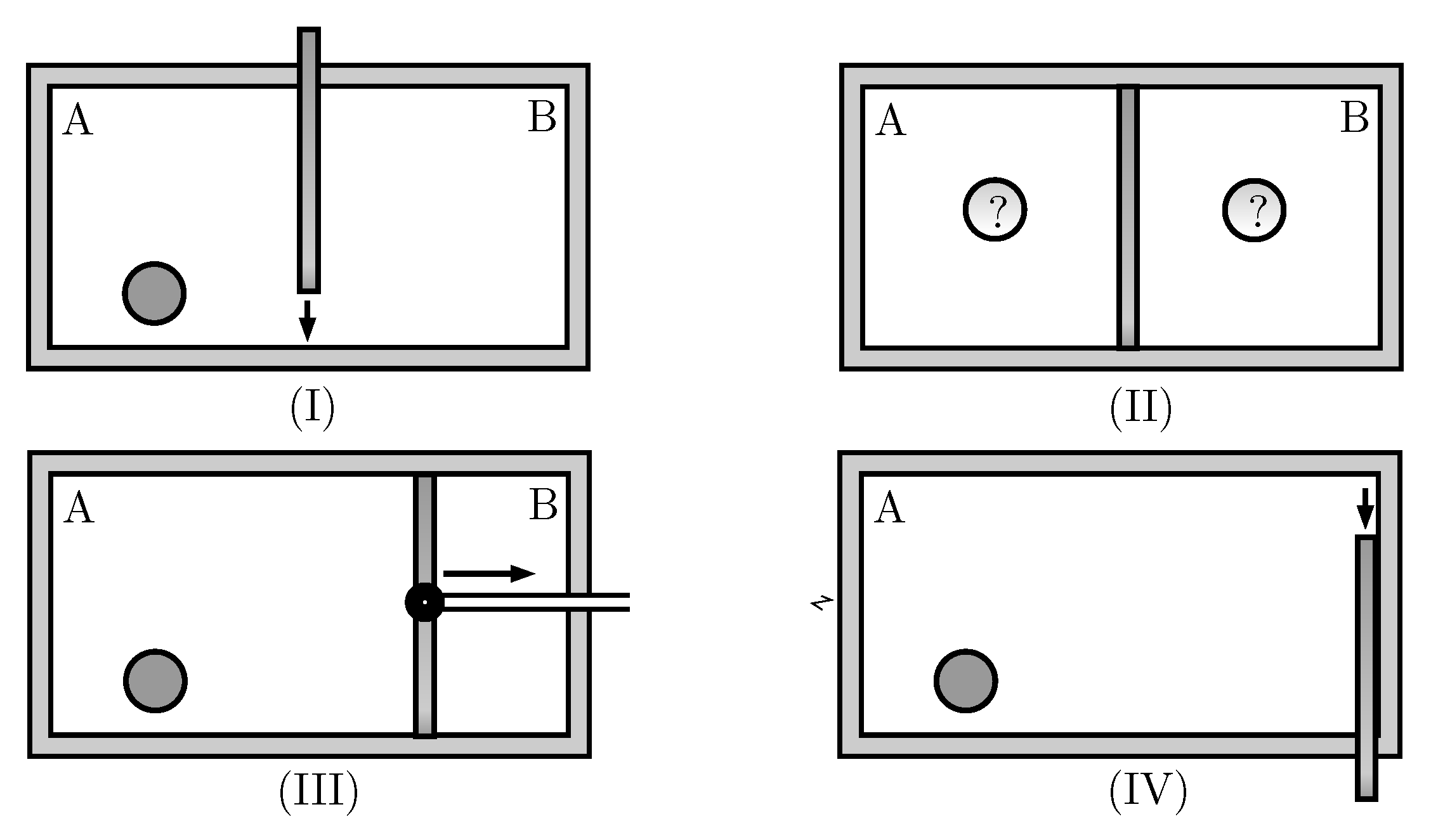
- (I)
- Insertion of the wall in the middle of the box.
- (II)
- Measurement of which side of the wall the particle is on.
- (III)
- Expansion of the wall until if the particle is on the left side, or until , otherwise.
- (IV)
- Removal of the wall.
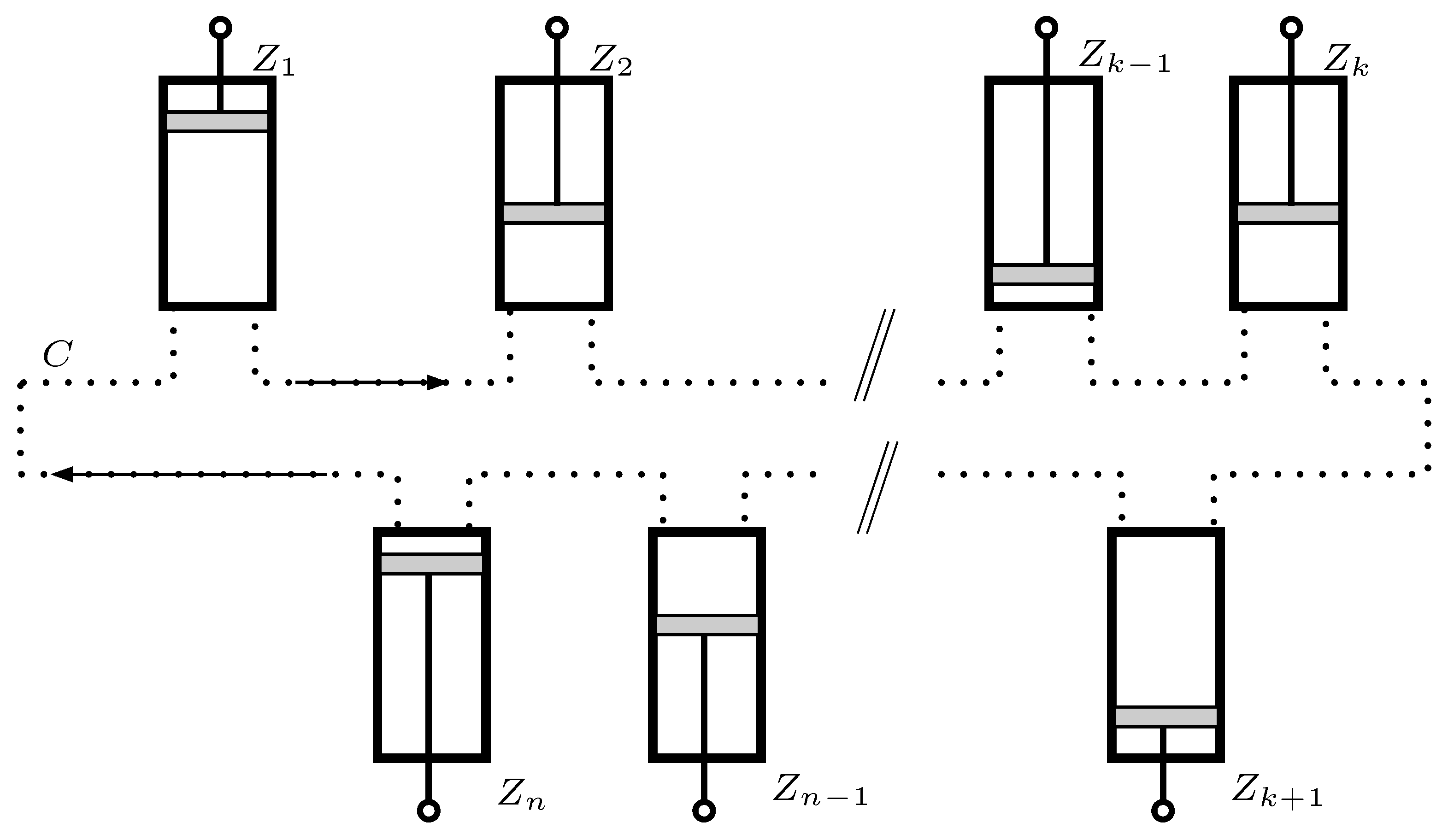
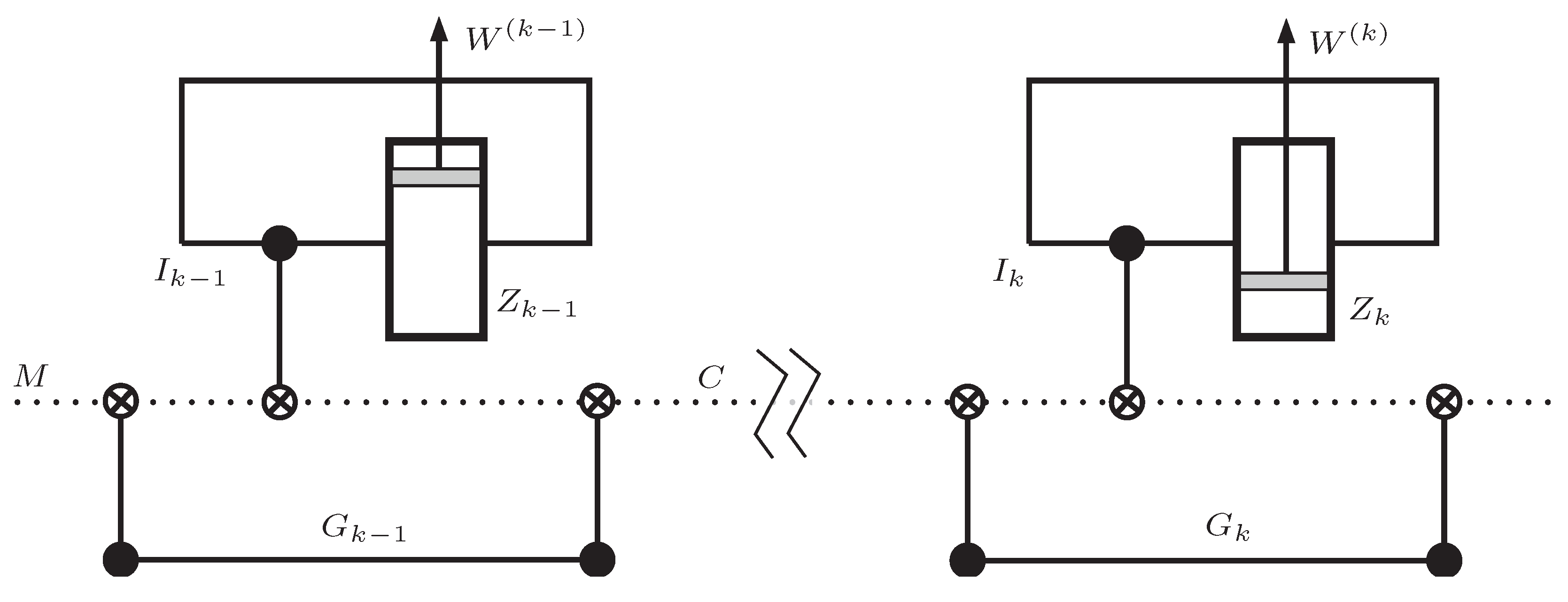
4. Protected Information Transmission with GHZ States
5. Partial Information Cycles for Motors and Generators
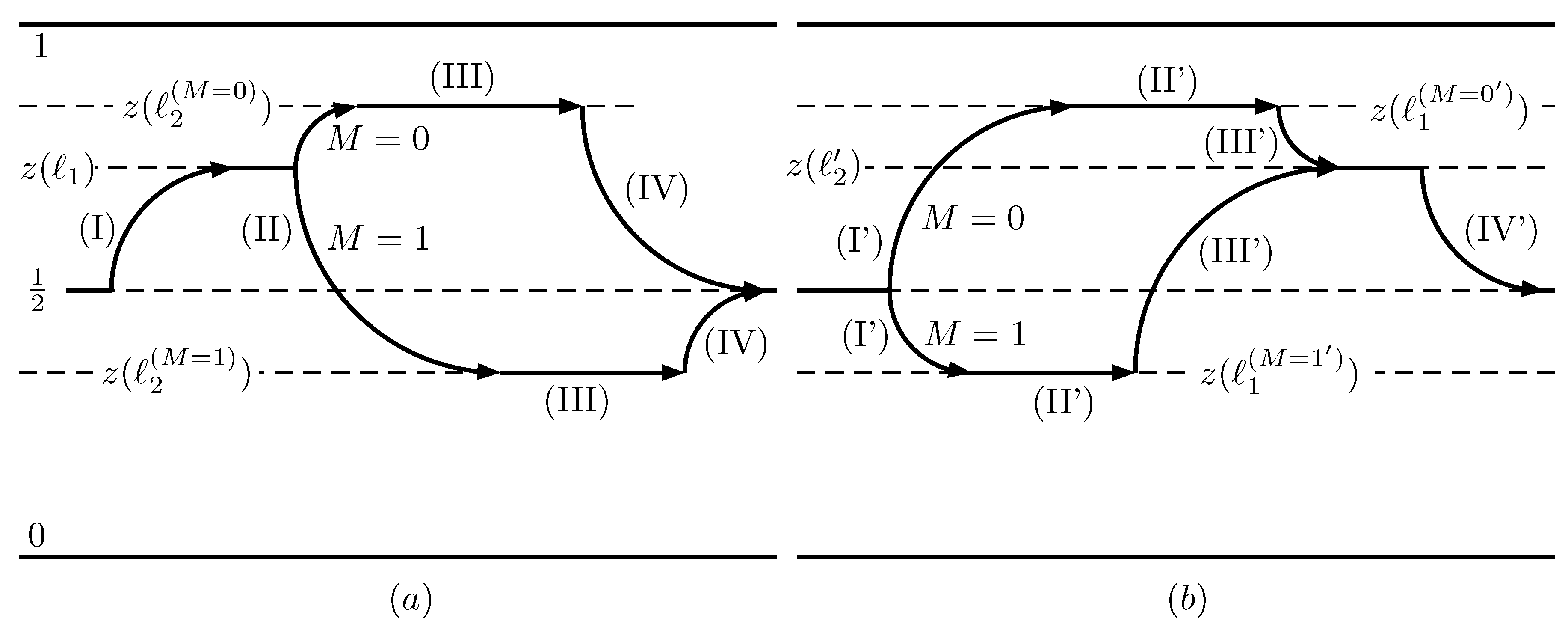
- (I)
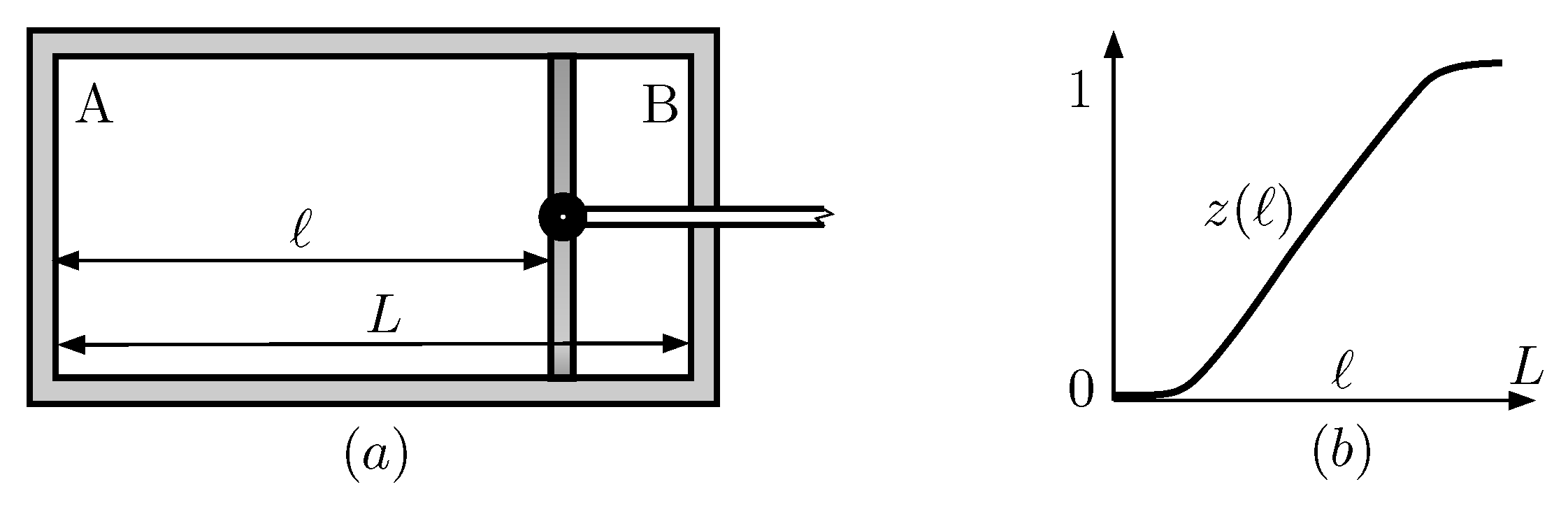
- Insertion. Instead of reinserting the wall in the middle of the box, we consider the case where it is reintroduced at an arbitrary position, determined by the value of ℓ. It is assumed that . Considering the left-right symmetry of the cylinder, this restriction does not imply a loss of generality. At the end of this stage there is no tunneling between the left and the right compartments.
- (II)
- Measurement. We assume that the fresh qubit M which is used to host the result of the measurement enters a partially mixed state. The which-side qubit I, defined in Appendix B and determined by the left () or right () situation of the particle, enters the stage in a statewhere and only depends on . It is the probability of finding the particle on the left side at the end of the insertion process. It can be computed from the partition function for the particle in a cylindrical box given in Appendix A. Precisely, , whereIn the original RefQSZ, the measurement was perfect, which is equivalent to having a pure initial state for M; it also assumed that , which implied .
- (III)
- Expansion. Considering that the left/right measurement is not completely certain, the expansion will stop at a suitable value of ℓ, controlled by the result of the measurement.
- (IV)
- Removal. This stage differs from the RQuSZE only in that the wall is pulled-out at , instead of at or . The positions are chosen so that the extraction is reversible. Therefore, they are determined by the equations:where are the conditional probabilities for the particle to be on the left side for , respectively. They are derived in Section 6 and written in Equation (12).
- (I’)
- Insertion. The position of the insertion is controlled by M. This creates a correlation between M and the left/right position of the particle.
- (II’)
- Compression. The wall is displaced from its initial position to a final value of .
- (III’)
- Erasure. A CNOT gate, controlled by the position of the particle, is applied to M. As a consequence, some of the entropy of M is transferred to I and their joint state factorizes.
- (IV’)
- Removal. The wall is pulled-out at .
6. Qubit Processing by A Cylinder
- (a)
- Motor. In the first stage, the introduction of the wall at sets the state of I to be partially mixed and is given by Equation (6).Next, in stage (II), the M qubit is used as target in a CNOT gate controlled by the which-side qubit I. After the CNOT gate, the joint state of qubits I,M readsThe M qubit then controls the final position in the expansion stage. Its two states have probabilities , that are given byThe states of I, conditioned on M are:whereare the conditional probabilities of I given M, in the computational basis.The M qubit leaves the cycle in the statewhich, after definingbecomeswhich leads to the relation between as a function of
- (b)
- Generator. This mode is essentially the inverse of the motor mode. However, for the sake of disambiguation, we outline it in detail. The objective of the process is to output the M qubit in statewhen its input state isassuming . With the benefit of hindsight, after the description of the motor mode, we determine a set of relevant parameters for the generator mode. Looking at Equation (16), we definewhich always lies in the interval . From Equation (14) we defineand from Equation (11),States determine as the positions for a reversible reintroduction of the wall, so that it is controlled in Stage (I’) by qubit M. Accordingly, with probabilities , the I qubit exits (I’) in states , respectively.The next stage is still controlled by M and leads to a position of the wall given by . It is determined by the condition that if the wall was reinserted at , the reduced state of I would beThen, after the CNOT on M controlled by I, the joint state factorizes intowhich is ready for a reversible wall removal at .
7. Work Evaluation
- (a)
- Motor. After addition of the (I), (III) and (IV) contributions, we arrive atFollowing the measurement, there are two possible states for the particle, , with probabilities , respectively. The average work expected when iswhile if , it iswhere is the entropy of the P state before the CNOT, and conditioned to , after the CNOT gate.Consequently, the average value of the work per cycle yieldswhere the first contribution cancels, because . Thus,We can derive another equation by considering that the CNOT gate preserves the entropy of the M-P system. Before the CNOT, M,P are independent. Therefore,On the other hand, after the CNOT, the two possible states of P: occur with probabilities . Then,where is the entropy of the M-P system after the CNOT, and is the well-known Shannon entropy function. After equating Equations (31) and (32), and substituting for , we arrive at:which, combined with Equation (30), yieldswhere represents the entropy increment of M in the cycle.As has been shown, the CNOT gate plays a central role in the obtention of the average work per cycle. The following remarks may shed some additional intuition on the previous derivation. The only contribution to the energy of the system, before and after the CNOT, comes from the particle, because the M qubit is assumed to have a completely degenerate Hamiltonian. Accordingly, only the reduced state of the particle is relevant. Note that it is not changed by the CNOT gate. However, this does not imply that the energies of the conditional states are equal. Considering the entropy, the distinctive character of the CNOT stems from the fact that it is the only interaction that exchanges information between the particle and the M qubits. Despite the overall entropy being conserved by the gate, the conditional states and show different values and the entropy of M is raised. This increment is the prize paid for the obtained work.
- (b)
- Generator. Considering that the generator and motor modes are the reverse of one another, Equation (34) applies. The only obvious difference is that in the generator mode, are both negative.
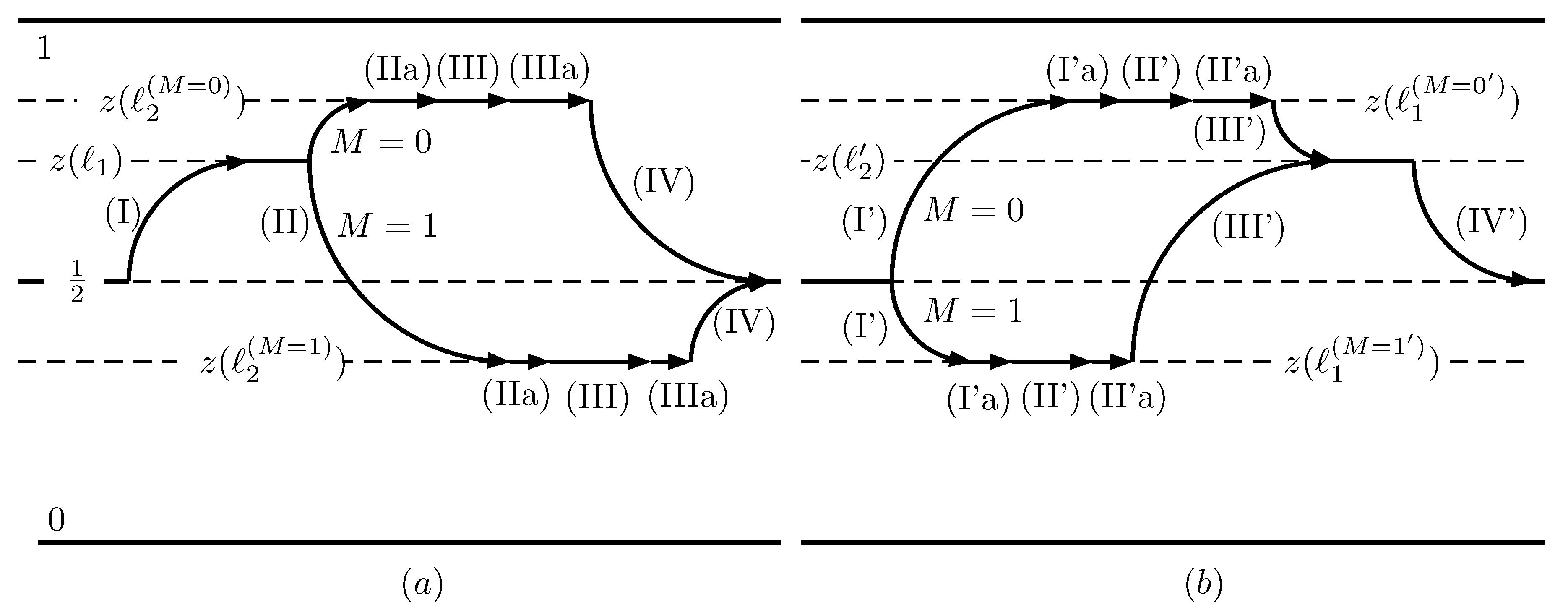
8. Force Matching Tweak
- A new stage (IIa) known as Precompression is defined between (II) and (III). The wall is moved from to a suitable position , controlled by M and keeping the load disengaged.
- Stage (III) now proceeds from to . The load is engaged only in this stage, and the values of are also controlled by M.
- A second new stage (IIIa), called Relaxation, follows (III). The wall is moved to defined in Section 5, keeping the load disengaged.
- A new stage (I’a) that we also call Precompression is defined between (I’) and (II’). The wall is moved to a suitable position , keeping the load (in the generator mode the load acts supplying energy, as a pump in a hydraulic system) disengaged. The value of is controlled by M.
- Stage (II’) now proceeds from to . The load is engaged only in this stage and the value of is also controlled by M.
- A second new stage (II’a), also called Relaxation, follows (II’). Te wall is moved to keeping the load disengaged.
9. Carnot Cycles with Szilard Cylinders
10. Discussion
11. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Energies of a Particle in A Cylindrical Compartment
Appendix B. Location Qubit
Appendix C. Employment of A CNOT Gate to Locate the Particle
References
- Kim, S.; Sagawa, T.; Liberato, S.D.; Ueda, M. Quantum Szilard Engine. Phys. Rev. Lett. 2011, 106, 070401. [Google Scholar] [CrossRef] [PubMed]
- Carnot, S. Réflexions sur la Puissance Motrice du feu et sur les Machines Propres à Développer Cette Puissance; Bachelier: Paris, France, 1824. (In French) [Google Scholar]
- Thomson, W. XV.—On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule’s Equivalent of a Thermal Unit, and M. Regnault’s Observations on Steam. Earth Env. Sci. Trans. R. Soc. Edinburgh 1853, 20, 261–288. [Google Scholar] [CrossRef]
- Maxwell, J.C. Theory of Heat; Longmans, Green, and Co.: London, UK, 1871. [Google Scholar]
- Szilard, L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Zeitschrift für Physik 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Bennett, C.H. Demons, Engines and the Second Law. Sci. Am. 1987, 257, 108–117. [Google Scholar] [CrossRef]
- Zurek, W.H. Maxwell’s Demon, Szilard’s Engine and Quantum Measurements. arXiv 2003, arXiv:quant-ph/0301076. [Google Scholar]
- Kish, L.B.; Granqvist, C.G. Energy requirement of control: Comments on Szilard’s engine and Maxwell’s demon. EPL (Europhy. Lett.) 2012, 98, 68001. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bérut, A.; Arakelyan, A.; Petrosyan, A.; Ciliberto, S.; Dillenschneider, R.; Lutz, E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 2012, 483, 187–189. [Google Scholar] [CrossRef]
- Parrondo, J.M.R.; Horowitz, J.M.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131. [Google Scholar] [CrossRef]
- Deffner, S.; Jarzynski, C. Information Processing and the Second Law of Thermodynamics: An Inclusive, Hamiltonian Approach. Phys. Rev. X 2013, 3, 041003. [Google Scholar] [CrossRef]
- Lorenzo, S.; McCloskey, R.; Ciccarello, F.; Paternostro, M.; Palma, G.M. Landauer’s Principle in Multipartite Open Quantum System Dynamics. Phys. Rev. Lett. 2015, 115, 120403. [Google Scholar] [CrossRef] [PubMed]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Mandal, D.; Jarzynski, C. Work and information processing in a solvable model of Maxwell’s demon. Proc. Natl. Acad. Sci. USA 2012, 109, 11641–11645. [Google Scholar] [CrossRef] [PubMed]
- Mandal, D.; Quan, H.T.; Jarzynski, C. Maxwell’s Refrigerator: An Exactly Solvable Model. Phys. Rev. Lett. 2013, 111, 030602. [Google Scholar] [CrossRef] [PubMed]
- Barato, A.C.; Seifert, U. Stochastic thermodynamics with information reservoirs. Phys. Rev. E 2014, 90, 042150. [Google Scholar] [CrossRef] [PubMed]
- Chapman, A.; Miyake, A. How an autonomous quantum Maxwell demon can harness correlated information. Phys. Rev. E 2015, 92, 062125. [Google Scholar] [CrossRef]
- Manzano, G.; Plastina, F.; Zambrini, R. Optimal Work Extraction and Thermodynamics of Quantum Measurements and Correlations. Phys. Rev. Lett. 2018, 121, 120602. [Google Scholar] [CrossRef]
- Boyd, A.B.; Mandal, D.; Crutchfield, J.P. Identifying functional thermodynamics in autonomous Maxwellian ratchets. New J. Phys. 2016, 18, 023049. [Google Scholar] [CrossRef]
- Stevens, J.; Deffner, S. Quantum to classical transition in an information ratchet. Phys. Rev. E 2019, 99, 042129. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W. Quantum Discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 2002, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Oppenheim, J.; Horodecki, M.; Horodecki, P.; Horodecki, R. Thermodynamical Approach to Quantifying Quantum Correlations. Phys. Rev. Lett. 2002, 89, 180402. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Quantum discord and Maxwell’s demons. Phys. Rev. A 2003, 67, 012320. [Google Scholar] [CrossRef]
- De Liberato, S.; Ueda, M. Carnot’s theorem for nonthermal stationary reservoirs. Phys. Rev. E 2011, 84, 051122. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kim, K.; Sagawa, T.; Kim, S. Heat engine driven by purely quantum information. Phys. Rev. Lett. 2013, 111, 230402. [Google Scholar] [CrossRef] [PubMed]
- Dann, R.; Kosloff, R. Quantum Signatures in the Quantum Carnot Cycle. arXiv 2019, arXiv:1906.06946. [Google Scholar]
- Gardas, B.; Deffner, S. Thermodynamic universality of quantum Carnot engines. Phys. Rev. E 2015, 92, 042126. [Google Scholar] [CrossRef] [PubMed]
- Alicki, R.; Kosloff, R. Introduction to Quantum Thermodynamics: History and Prospects. In Thermodynamics in the Quantum Regime: Fundamental Aspects and New Directions; Binder, F., Correa, L.A., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 1–33. [Google Scholar] [CrossRef]
- Lloyd, S. Quantum-mechanical Maxwell’s demon. Phys. Rev. A 1997, 56, 3374–3382. [Google Scholar] [CrossRef]
- Piechocinska, B. Information erasure. Phys. Rev. A 2000, 61, 062314. [Google Scholar] [CrossRef]
- Scully, M.O. Extracting Work from a Single Thermal Bath via Quantum Negentropy. Phys. Rev. Lett. 2001, 87, 220601. [Google Scholar] [CrossRef]
- Scully, M.O.; Rostovtsev, Y.; Sariyanni, Z.E.; Zubairy, M.S. Using quantum erasure to exorcize Maxwell’s demon: I. Concepts and context. Phys. E Low-Dimens. Syst. Nanostructures 2005, 29, 29–39. [Google Scholar] [CrossRef]
- Sariyanni, Z.E.; Rostovtsev, Y.; Zubairy, M.S.; Scully, M.O. Using quantum erasure to exorcize Maxwell’s demon: III. Implementation. Phys. E Low-Dimens. Syst. Nanostructures 2005, 29, 47–52. [Google Scholar] [CrossRef]
- Rostovtsev, Y.; Sariyanni, Z.E.; Zubairy, M.S.; Scully, M.O. Using quantum erasure to exorcise Maxwell’s demon: II. Analysis. Phys. E Low-Dimens. Syst. Nanostructures 2005, 29, 40–46. [Google Scholar] [CrossRef]
- Quan, H.T.; Wang, Y.D.; Liu, Y.X.; Sun, C.P.; Nori, F. Maxwell’s Demon Assisted Thermodynamic Cycle in Superconducting Quantum Circuits. Phys. Rev. Lett. 2006, 97, 180402. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Segal, D. Minimal model of a heat engine: Information theory approach. Phys. Rev. E 2010, 82, 011120. [Google Scholar] [CrossRef] [PubMed]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyuki, E.; Sano, M. Information heat engine: Converting information to energy by feedback control. Nat. Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Rio, L.D.; Aberg, J.; Renner, R.; Dahlsten, O.; Vedral, V. The thermodynamic meaning of negative entropy. Nature 2011, 474, 61–63. [Google Scholar] [CrossRef]
- Plesch, M.; Dahlsten, O.; Goold, J.; Vedral, V. Comment on “Quantum Szilard Engine”. Phys. Rev. Lett. 2013, 111, 188901. [Google Scholar] [CrossRef]
- Funo, K.; Watanabe, Y.; Ueda, M. Thermodynamic work gain from entanglement. Phys. Rev. A 2013, 88, 052319. [Google Scholar] [CrossRef]
- Diaz de la Cruz, J.M.; Martin-Delgado, M.A. Quantum-information engines with many-body states attaining optimal extractable work with quantum control. Phys. Rev. A 2014, 89, 032327. [Google Scholar] [CrossRef]
- Vidrighin, M.D.; Dahlsten, O.; Barbieri, M.; Kim, M.S.; Vedral, V.; Walmsley, I.A. Photonic Maxwell’s Demon. Phys. Rev. Lett. 2016, 116, 050401. [Google Scholar] [CrossRef] [PubMed]
- Hewgill, A.; Ferraro, A.; De Chiara, G. Quantum correlations and thermodynamic performances of two-qubit engines with local and common baths. Phys. Rev. A 2018, 98, 042102. [Google Scholar] [CrossRef]
- Paneru, G.; Lee, D.Y.; Tlusty, T.; Pak, H.K. Lossless Brownian Information Engine. Phys. Rev. Lett. 2018, 120, 020601. [Google Scholar] [CrossRef] [PubMed]
- Seah, S.; Nimmrichter, S.; Scarani, V. Work production of quantum rotor engines. New J. Phys. 2018, 20, 043045. [Google Scholar] [CrossRef]
- Uzdin, R. Coherence-Induced Reversibility and Collective Operation of Quantum Heat Machines via Coherence Recycling. Phys. Rev. Appl. 2016, 6, 024004. [Google Scholar] [CrossRef]
- Vedral, V. The role of relative entropy in quantum information theory. Rev. Mod. Phys. 2002, 74, 197–234. [Google Scholar] [CrossRef]
- Hasegawa, H.; Ishikawa, J.; Takara, K.; Driebe, D. Generalization of the second law for a nonequilibrium initial state. Phys. Lett. A 2010, 374, 1001–1004. [Google Scholar] [CrossRef]
- Sagawa, T. Second Law-Like Inequalities with Quantum Relative Entropy: An Introduction. In Lectures on Quantum Computing, Thermodynamics and Statistical Physics; World Scientific: Singapore, 2013; pp. 125–190. [Google Scholar]
- Brandao, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef]
- Brillouin, L. The Negentropy Principle of Information. J. Appl. Phys. 1953, 24, 1152–1163. [Google Scholar] [CrossRef]
- Maruyama, K.; Nori, F.; Vedral, V. Colloquium: The physics of Maxwell’s demon and information. Rev. Mod. Phys. 2009, 81, 1–23. [Google Scholar] [CrossRef]
- Quan, H.T.; Liu, Y.x.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [PubMed]
- Abah, O.; Roßnagel, J.; Jacob, G.; Deffner, S.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Single-Ion Heat Engine at Maximum Power. Phys. Rev. Lett. 2012, 109, 203006. [Google Scholar] [CrossRef] [PubMed]
- Ludovico, M.F.; Arrachea, L.; Moskalets, M.; Sánchez, D. Periodic Energy Transport and Entropy Production in Quantum Electronics. Entropy 2016, 18, 419. [Google Scholar] [CrossRef]
- Kosloff, R.; Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 2017, 19, 136. [Google Scholar] [CrossRef]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Galindo, A.; Martin-Delgado, M.A. Information and computation: Classical and quantum aspects. Rev. Mod. Phys. 2002, 74, 347–423. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Quantum and Information Thermodynamics: A Unifying Framework Based on Repeated Interactions. Phys. Rev. X 2017, 7, 021003. [Google Scholar] [CrossRef]
- Zurek, W.H. Eliminating ensembles from equilibrium statistical physics: Maxwell’s demon, Szilard’s engine, and thermodynamics via entanglement. Phys. Rep. 2018, 755, 1. [Google Scholar] [CrossRef]
- Safranek, D.; Deffner, S. Quantum Zeno effect in correlated qubits. Phys. Rev. A 2018, 98, 032308. [Google Scholar] [CrossRef]
- Diaz de la Cruz, J.M.; Martin-Delgado, M.A. Enhanced Energy Distribution for Quantum Information Heat Engines. Entropy 2016, 18, 335. [Google Scholar] [CrossRef]
- Diaz de la Cruz, J.M.; Martin-Delgado, M.A. Quantum Information Remote Carnot Engines and Voltage Transformers. Entropy 2019, 21, 127. [Google Scholar] [CrossRef]
- Aydin, A.; Sisman, A. Quantum shape effects and novel thermodynamic behaviors at nanoscale. Phys. Lett. A 2019, 383, 655. [Google Scholar] [CrossRef]
- Aydin, A.; Sisman, A.; Kosloff, R. Landauer’s Principle in a Quantum Szilard Engine Without Maxwell’s Demon. arXiv 2019, arXiv:1908.04400. [Google Scholar]
- Arfken, G.; Weber, H. Mathematical Methods for Physicists; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
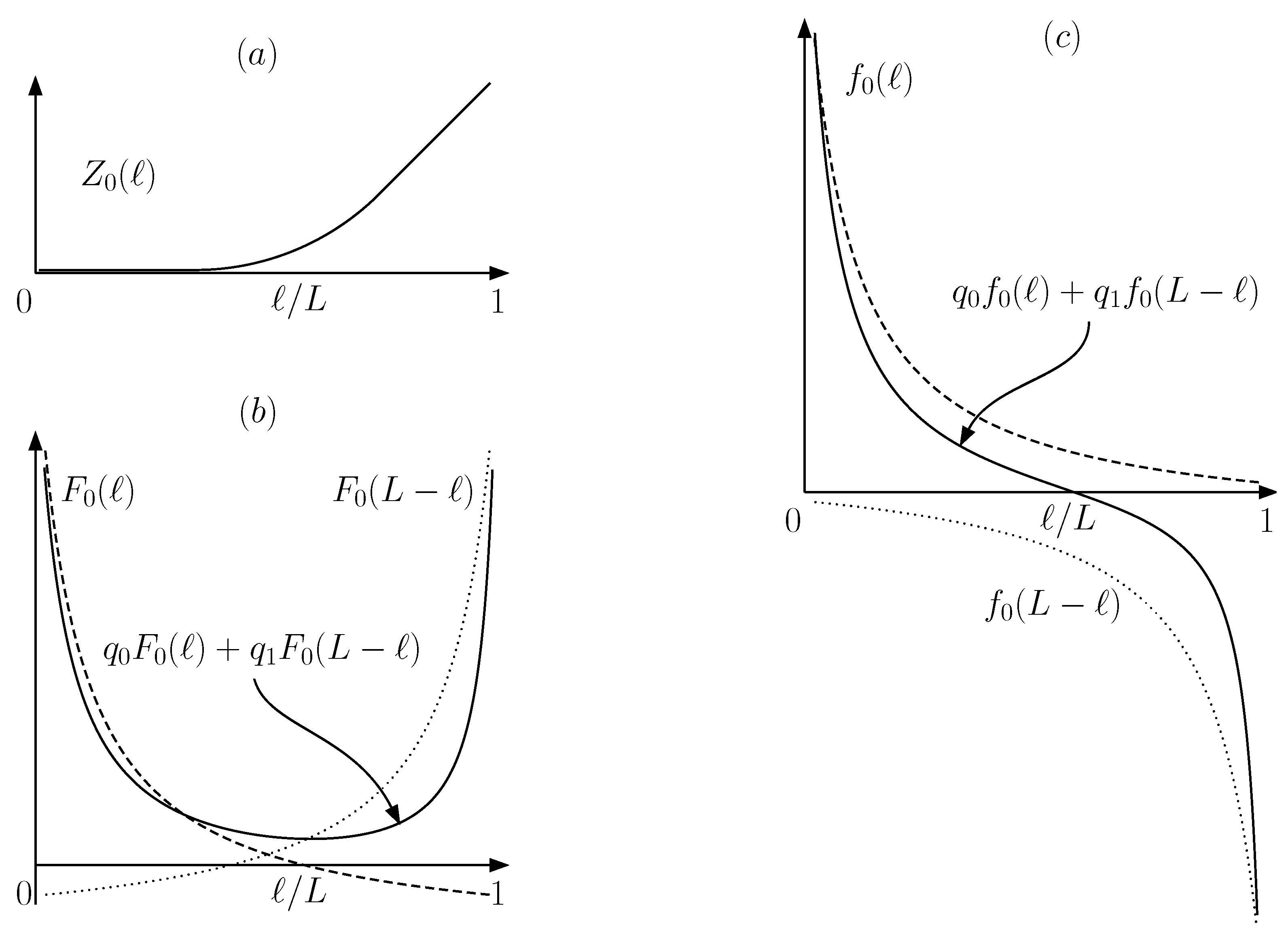
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diazdelacruz, J. Entropy Distribution in a Quantum Informational Circuit of Tunable Szilard Engines. Entropy 2019, 21, 980. https://doi.org/10.3390/e21100980
Diazdelacruz J. Entropy Distribution in a Quantum Informational Circuit of Tunable Szilard Engines. Entropy. 2019; 21(10):980. https://doi.org/10.3390/e21100980
Chicago/Turabian StyleDiazdelacruz, Jose. 2019. "Entropy Distribution in a Quantum Informational Circuit of Tunable Szilard Engines" Entropy 21, no. 10: 980. https://doi.org/10.3390/e21100980
APA StyleDiazdelacruz, J. (2019). Entropy Distribution in a Quantum Informational Circuit of Tunable Szilard Engines. Entropy, 21(10), 980. https://doi.org/10.3390/e21100980