Pragmatic Hypotheses in the Evolution of Science
Abstract
1. Introduction
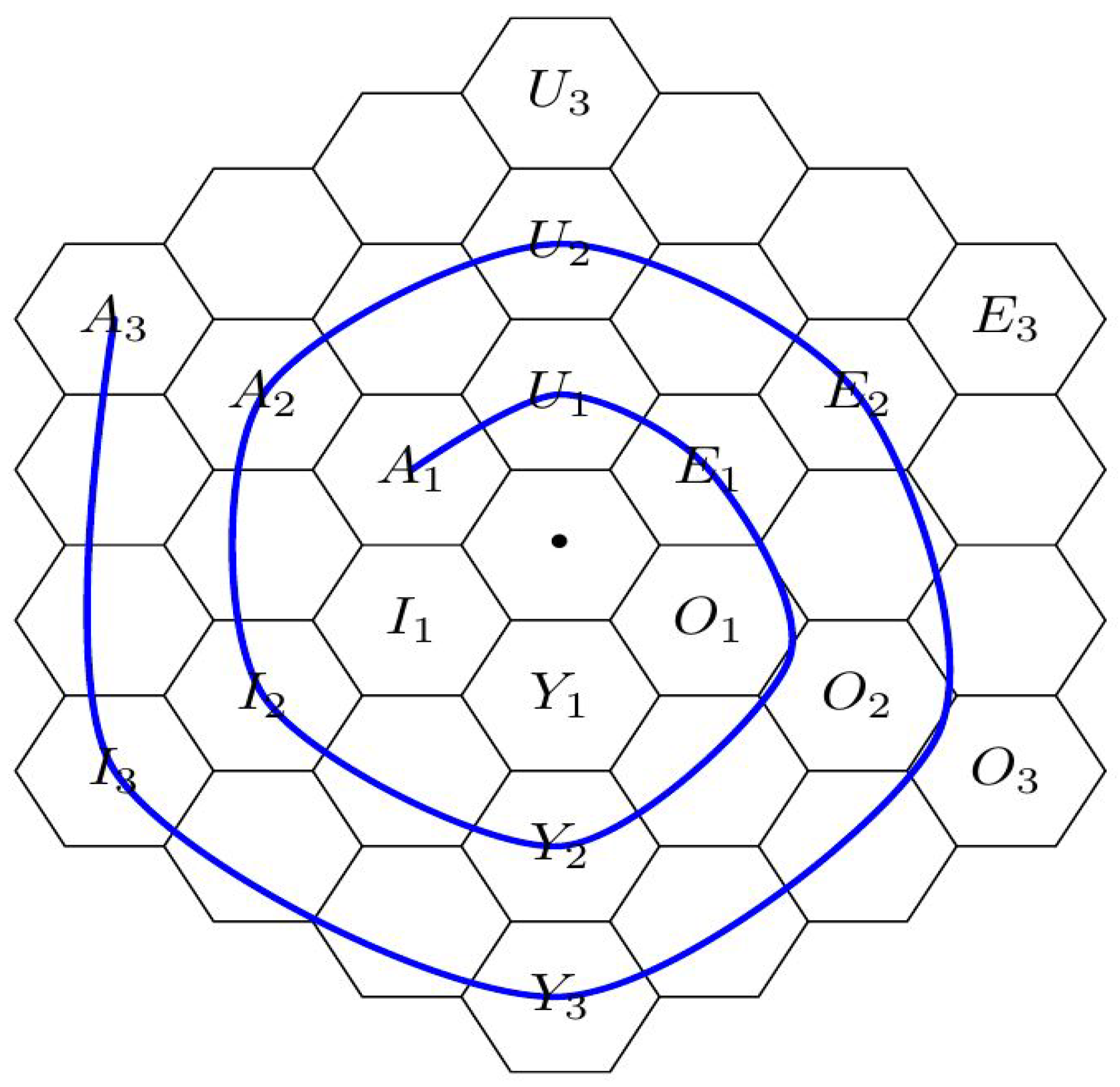
2. Gallais’ Hexagonal Spirals and the Evolution of Science
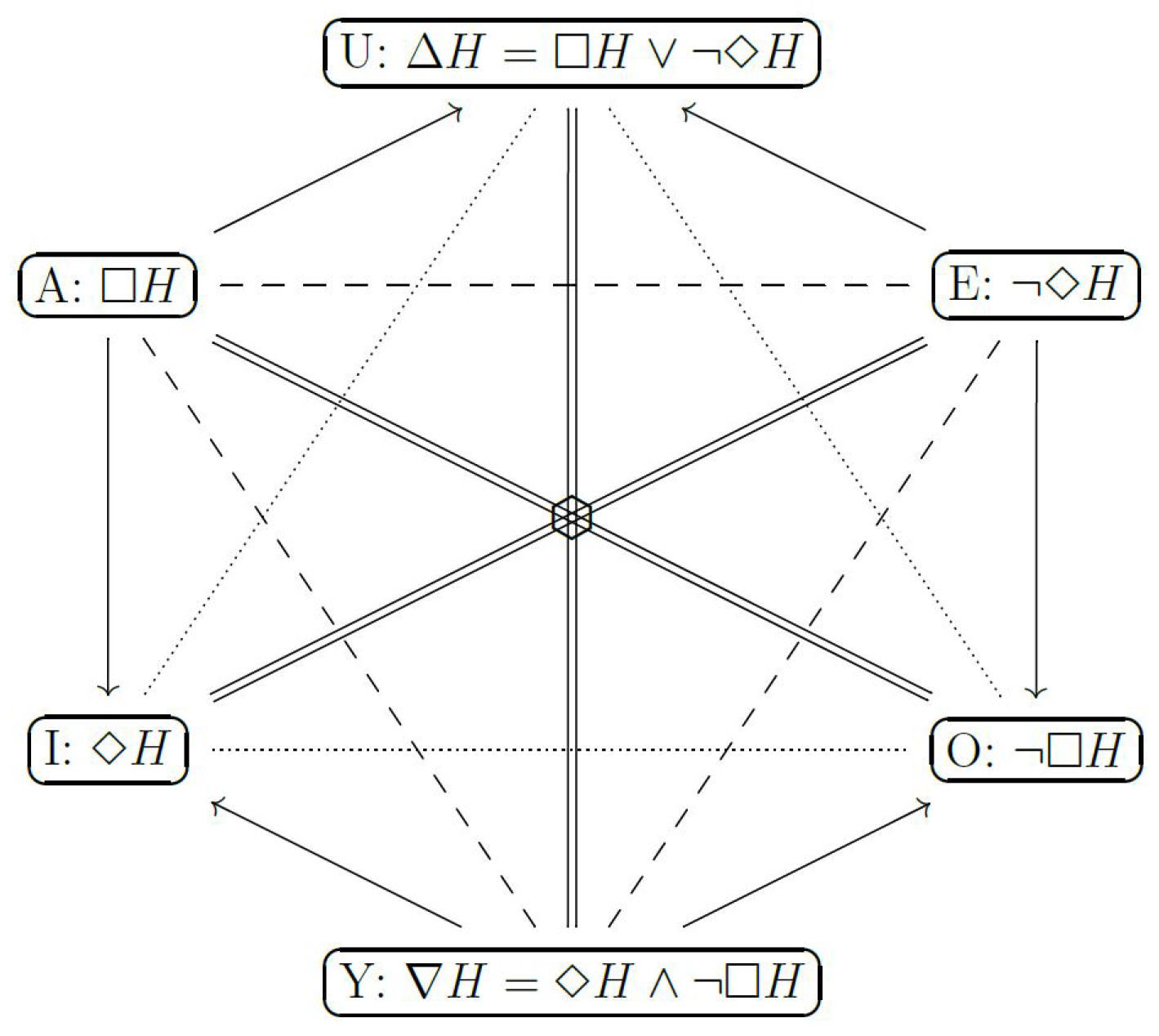
- - Extant thesis: This vertex represents a standing paradigm, an accepted theory using well-known formalisms and familiar concepts, relying on accredited experimental means and methods, etc. In fact, the concepts of a current paradigm may become so familiar and look so natural that they become part of a reified ontology. That is, there is a perceived correspondence between concepts of the theory and “dinge-an-sich” (things-in-themselves) as seen in nature [29,30].
- - Analysis: This vertex represents the moment when some hypotheses of the standing theory are put in question. At this moment, possible alternatives to the standing hypotheses may still be only vaguely defined.
- - Antithesis: This vertex represents the moment when some laws of the standing theory have to be rejected. Such a rejection of old laws may put in question the entire world-view of the current paradigm, opening the way for revolutionary ideas, as described in the next vertex.
- - Apothesis/ Prosthesis: This vertex is the locus of revolutionary freedom. Alternative models are considered, and specific (precise) forms investigated. There is intellectual freedom to set aside and dispose of (apothesis) old preconceptions, prejudices and stereotypes, and also to explore and investigate new paths, to put together (prosthesis) and try out new concepts and ideas.
- - Synthesis: It is at this vertex that new laws are formulated; this is the point of Eureka moment(s). A selection of old and and new concepts seem to click into place, fitting together in the form of new laws, laws that are able to explain new phenomena and incorporate objects of an expanded reality.
- - Enthesis: At this vertex new laws, concepts and methods must enter and be integrated into a consistent and coherent system. At this stage many tasks are performed in order to combine novel and traditional pieces or to accommodate original and conventional components into an well-integrated framework. Finally, new experimental means and methods are developed and perfected, allowing the new laws to be corroborated.
- - New Thesis: At this vertex, the new theory is accepted as the standard paradigm that succeeds the preceding one (). Acceptance occurs after careful determination of fundamental constants and calibration factors (including their known precision), metrological and instrumentational error bounds, etc. At later stages of maturity, equivalent theoretical frameworks may be developed using alternative formalisms and ontologies. For example, analytical mechanics offers variational alternatives that are (almost) equivalent to the classical formulation of Newtonian mechanics [31]. Usually, these alternative worldviews reinforce the trust and confidence on the underlying laws. Nevertheless, the existence of such alternative perspectives may also foster exploratory efforts and investigative works in the next cycle in evolution.
3. Pragmatic Hypotheses
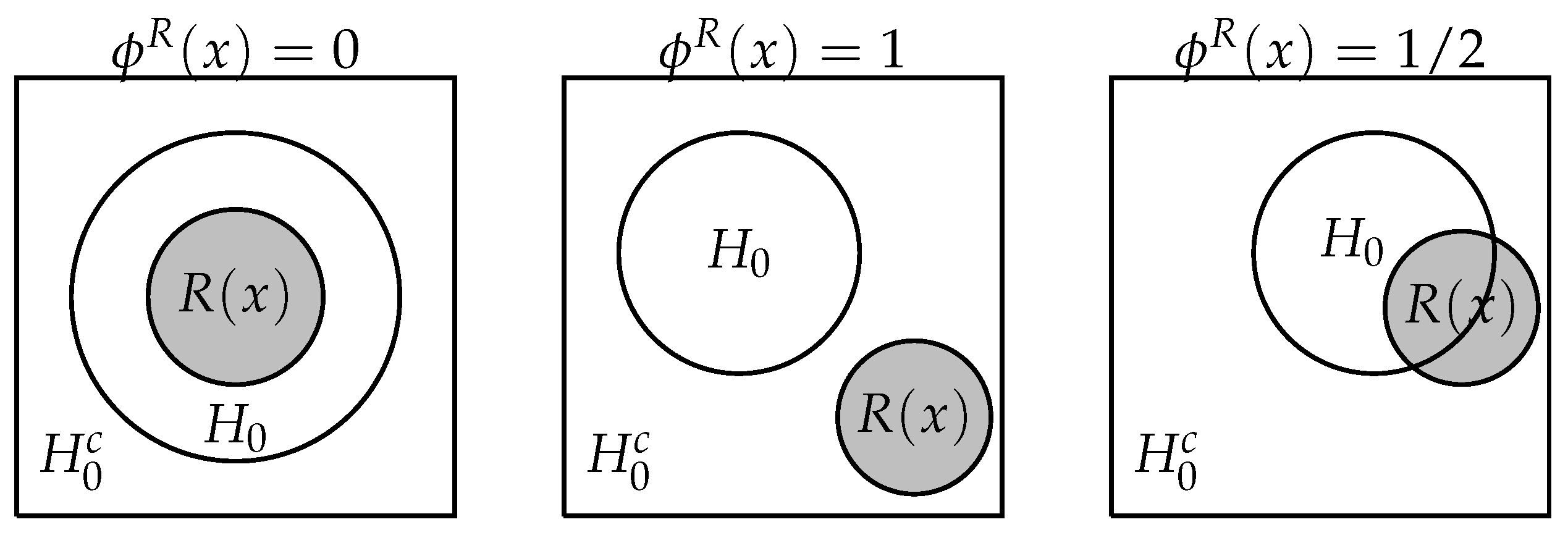
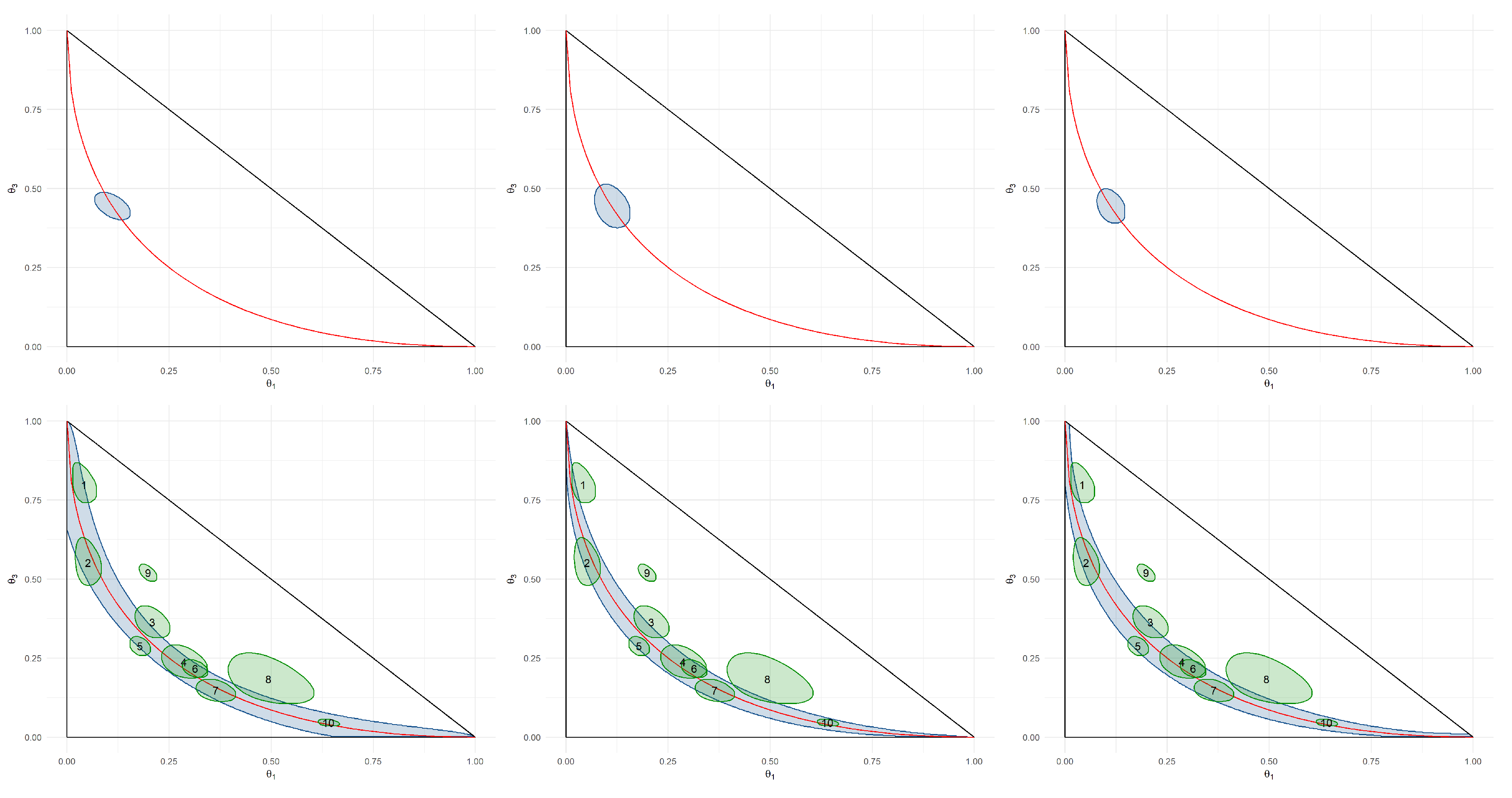
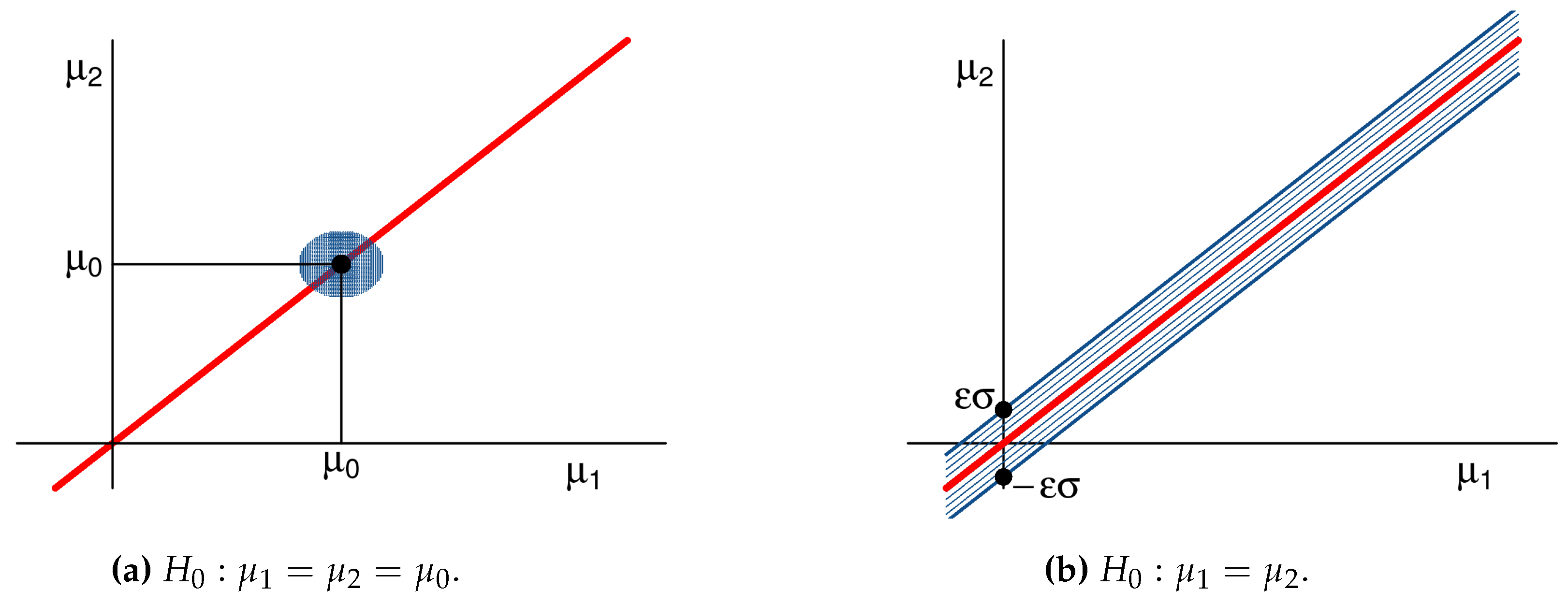
3.1. Singleton Hypotheses
3.2. Composite Hypotheses
- If for some , then .
- If for every and , then .
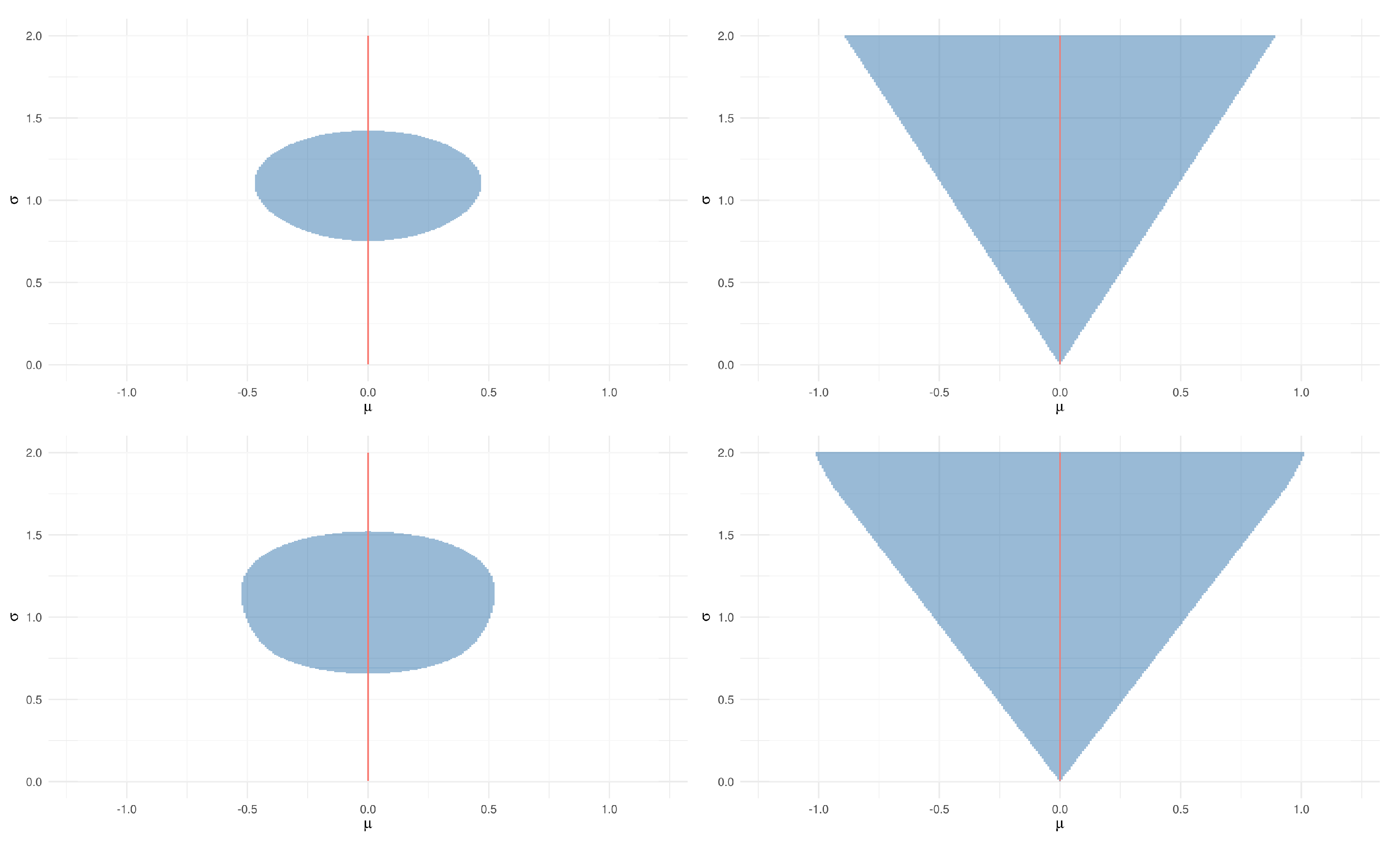
4. Applications
5. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs
References
- Izbicki, R.; Esteves, L.G. Logical consistency in simultaneous statistical test procedures. Log. J. IGPL. 2015, 23, 732–758. [Google Scholar] [CrossRef]
- Esteves, L.G.; Izbicki, R.; Stern, J.M.; Stern, R.B. The logical consistency of simultaneous agnostic hypothesis tests. Entropy 2016, 18, 256. [Google Scholar] [CrossRef]
- Stern, J.; Izbicki, R.; Esteves, L.; Stern, R. Logically-Consistent Hypothesis Testing and the Hexagon of Oppositions. Log. J. IGPL 2017, 25, 741–757. [Google Scholar] [CrossRef]
- Blanché, R. Structures Intellectuelles: Essai sur l’Organisation Systématique des Concepts; Vrin: Paris, France, 1966. (In French) [Google Scholar]
- Béziau, J.Y. The power of the hexagon. Log. Univers. 2012, 6, 1–43. [Google Scholar] [CrossRef]
- Béziau, J.Y. Opposition and order. In New Dimensions of the Square of Opposition; Béziau, J.Y., Gan-Krzywoszynska, K., Eds.; Philosophia Verlag: Munich, Germany, 2015; pp. 1–11. [Google Scholar]
- Carnielli, W.; Pizzi, C. Modalities and Multimodalities (Logic, Epistemology, and the Unity of Science); Springer: Berlin, Germany, 2008. [Google Scholar]
- Dubois, D.; Prade, H. On several representations of an uncertain body of evidence. In Fuzzy Information and Decision Processes; Gupta, M., Sanchez, E., Eds.; Elsevier: Amsterdam, The Netherlands, 1982; pp. 167–181. [Google Scholar]
- Dubois, D.; Prade, H. From Blanché’s Hexagonal Organization of Concepts to Formal Concept Analysis and Possibility Theory. Log. Univers. 2012, 6, 149–169. [Google Scholar] [CrossRef]
- Gallais, P.; Pollina, V. Hegaxonal and Spiral Structure in Medieval Narrative. Yale Fr. Stud. 1974, 51, 115–132. [Google Scholar] [CrossRef]
- Gallais, P. Dialectique Du Récit Mediéval: Chrétien de Troyes et l’Hexagone Logique; Rodopi: Amsterdam, The Netherlands, 1982. (In French) [Google Scholar]
- Stern, J.M. Symmetry, Invariance and Ontology in Physics and Statistics. Symmetry 2011, 3, 611–635. [Google Scholar] [CrossRef]
- Stern, J.M. Continuous versions of Haack’s Puzzles: Equilibria, Eigen-States and Ontologies. Log. J. IGPL 2017, 25, 604–631. [Google Scholar] [CrossRef]
- DeGroot, M.H.; Schervish, M.J. Probability and Statistics; Pearson Education: London, UK, 2012. [Google Scholar]
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Bucher, J.L. The Metrology Handbook, 2nd ed.; ASQ Quality Press: Milwaukee, WI, USA, 2012. [Google Scholar]
- Czichos, H.; Saito, T.; Smith, L. Springer Handbook of Metrology and Testing, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Cohen, R.; Crowe, K.; DuMond, J. The Fundamental Constants of Physics; CODATA/Interscience Publishers: Geneva, Switzerland, 1957. [Google Scholar]
- Cohen, R. Mathematical Analysis of the Universal Physical Constants. Il Nuovo Cimento 1957, 6, 187–214. [Google Scholar] [CrossRef]
- Lévy-Leblond, J. On the conceptual nature of the physical constants. Il Nuovo Cimento 1977, 7, 187–214. [Google Scholar]
- Pakkan, M.; Akman, V. Hypersolver: A graphical tool for commonsense set theory. Inform. Sci. 1995, 85, 43–61. [Google Scholar] [CrossRef]
- Akman, V.; Pakkan, M. Nonstandard set theories and information management. J. Intell. Inf. Syst. 1996, 6, 5–31. [Google Scholar] [CrossRef][Green Version]
- Wainwright, M.J. Stochastic Processes on Graphs with Cycles: Geometric and Variational Approaches. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, April 2002. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Heidelberg, Germany, 2006. [Google Scholar]
- Iordanov, B. HyperGraphDB: A generalized graph database. In International Conference on Web-Age Information Management; Springer: Berlin, Germany, 2010; pp. 25–36. [Google Scholar]
- Gelman, A.; Vehtari, A.; Jylänki, P.; Sivula, T.; Tran, D.; Sahai, S.; Blomstedt, P.; Cunningham, J.P.; Schiminovich, D.; Robert, C. Expectation propagation as a way of life: A framework for Bayesian inference on partitioned data. arXiv 2014, arXiv:1412.4869. [Google Scholar]
- Greimas, A. Structural Semantics: An Attempt at a Method; University of Nebraska Press: Lincoln, NE, USA, 1983. [Google Scholar]
- Propp, V. Morphology of the Folktale; University of Texas Press: Austin, TX, USA, 2000. [Google Scholar]
- Stern, J.M. Jacob’s Ladder and Scientific Ontologies. Cybern. Human Knowing 2014, 21, 9–43. [Google Scholar]
- Stern, J.M. Constructive Verification, Empirical Induction, and Falibilist Deduction: A Threefold Contrast. Information 2011, 2, 635–650. [Google Scholar] [CrossRef]
- Abraham, R.; Marsden, J.E. Foundations of Mechanics; Addison-Wesley: Boston, MA, USA, 2013. [Google Scholar]
- Hawking, S. The Illustrated On the Shoulders of Giants: The Great Works of Physics and Astronomy; Running Press: Philadelphia, PA, USA, 2004. [Google Scholar]
- Stern, J.M.; Nakano, F. Optimization Models for Reaction Networks: Information Divergence, Quadratic Programming and Kirchhoff’s Laws. Axioms 2014, 3, 109–118. [Google Scholar] [CrossRef]
- Coscrato, V.; Izbicki, R.; Stern, R.B. Agnostic tests can control the type I and type II errors simultaneously. Braz. J. Probab. Stat. 2019. Available online: https://www.imstat.org/wp-content/uploads/2019/01/BJPS431.pdf (accessed on 9 September 2019).
- Izbicki, R.; Fossaluza, V.; Hounie, A.G.; Nakano, E.Y.; de Braganca Pereira, C.A. Testing allele homogeneity: The problem of nested hypotheses. BMC Genet. 2012, 13, 103. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, G.M.; Esteves, L.G.; Fossaluza, V.; Izbicki, R.; Wechsler, S. A bayesian decision-theoretic approach to logically-consistent hypothesis testing. Entropy 2015, 17, 6534–6559. [Google Scholar] [CrossRef]
- Fossaluza, V.; Izbicki, R.; da Silva, G.M.; Esteves, L.G. Coherent hypothesis testing. Am. Statist. 2017, 71, 242–248. [Google Scholar] [CrossRef]
- Pereira, C.A.B.; Stern, J.M.; Wechsler, S. Can a Signicance Test be Genuinely Bayesian? Bayesian Anal. 2008, 3, 79–100. [Google Scholar] [CrossRef]
- Stern, J.M.; Pereira, C.A.D.B. Bayesian Epistemic Values: Focus on Surprise, Measure Probability! Log. J. IGPL. 2014, 22, 236–254. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury Press: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Wechsler, S.; Izbicki, R.; Esteves, L.G. A Bayesian look at nonidentifiability: A simple example. Am. Statist 2013, 67, 90–93. [Google Scholar] [CrossRef]
- Coscrato, V.; Esteves, L.G.; Izbicki, R.; Stern, R.B. Interpretable hypothesis tests. arXiv 2019, arXiv:1904.06605. [Google Scholar]
- Hardy, G. Mendelian proportions in a mixed population. 1908. Yale J. Biol. Med. 2003, 76, 79. [Google Scholar] [PubMed]
- Brentani, H.; Nakano, E.Y.; Martins, C.B.; Izbicki, R.; Pereira, C.A.d.B. Disequilibrium coefficient: A Bayesian perspective. Stat. Appl. Genet. Mol. 2011, 10. [Google Scholar] [CrossRef]
- Chow, S.C.; Song, F.; Bai, H. Analytical similarity assessment in biosimilar studies. AAPS J. 2016, 18, 670–677. [Google Scholar] [CrossRef][Green Version]
| Vertex | Orbital Astronomy | Chemical Affinity |
|---|---|---|
| - Enthesis/ - Thesis | Ptolemaic/Copernican cycles and epicycles | Geoffroy affinity table and highest rank substitution |
| - Analysis | Circular or oval orbits? | Ordinal or numeric affinity? |
| - Antithesis | Non-circular orbits | Non-ordinal affinity |
| - Apothesis /Prosthesis | Elliptic planetary orbits, focal centering of sun | Integer affinity values, for arithmetic recombination |
| - Synthesis | Kepler laws! | Morveau rules and tables! |
| - Enthesis - Thesis | Vortex physics theories, Keplerian astronomy | Affinity + stoichiometry substitution reactions |
| - Analysis | Tangential or radial forces? | Total or partial reaction? |
| - Antithesis | Non-tangential forces | Non-total substitutions |
| - Apothesis/Prosthesis | Radial attraction forces, inverse square of distance | Reversible reactions, equilibrium conditions |
| - Synthesis | Newton laws! | Mass-Action kinetics! |
| - Enthesis/ - Thesis | Newtonian mechanics & variational equivalents | Thermodynamic theories for reaction networks |
| AA | AD | DD | Decision | |
|---|---|---|---|---|
| 1 | 4 | 18 | 94 | Agnostic |
| 2 | 6 | 53 | 74 | Accept |
| 3 | 57 | 118 | 100 | Agnostic |
| 4 | 58 | 97 | 48 | Agnostic |
| 5 | 120 | 361 | 194 | Agnostic |
| 6 | 206 | 309 | 142 | Accept |
| 7 | 110 | 148 | 44 | Accept |
| 8 | 34 | 22 | 12 | Agnostic |
| 9 | 198 | 282 | 520 | Reject |
| 10 | 641 | 314 | 45 | Accept |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esteves, L.G.; Izbicki, R.; Stern, J.M.; Stern, R.B. Pragmatic Hypotheses in the Evolution of Science. Entropy 2019, 21, 883. https://doi.org/10.3390/e21090883
Esteves LG, Izbicki R, Stern JM, Stern RB. Pragmatic Hypotheses in the Evolution of Science. Entropy. 2019; 21(9):883. https://doi.org/10.3390/e21090883
Chicago/Turabian StyleEsteves, Luis Gustavo, Rafael Izbicki, Julio Michael Stern, and Rafael Bassi Stern. 2019. "Pragmatic Hypotheses in the Evolution of Science" Entropy 21, no. 9: 883. https://doi.org/10.3390/e21090883
APA StyleEsteves, L. G., Izbicki, R., Stern, J. M., & Stern, R. B. (2019). Pragmatic Hypotheses in the Evolution of Science. Entropy, 21(9), 883. https://doi.org/10.3390/e21090883






