Electron Traversal Times in Disordered Graphene Nanoribbons
Abstract
1. Introduction
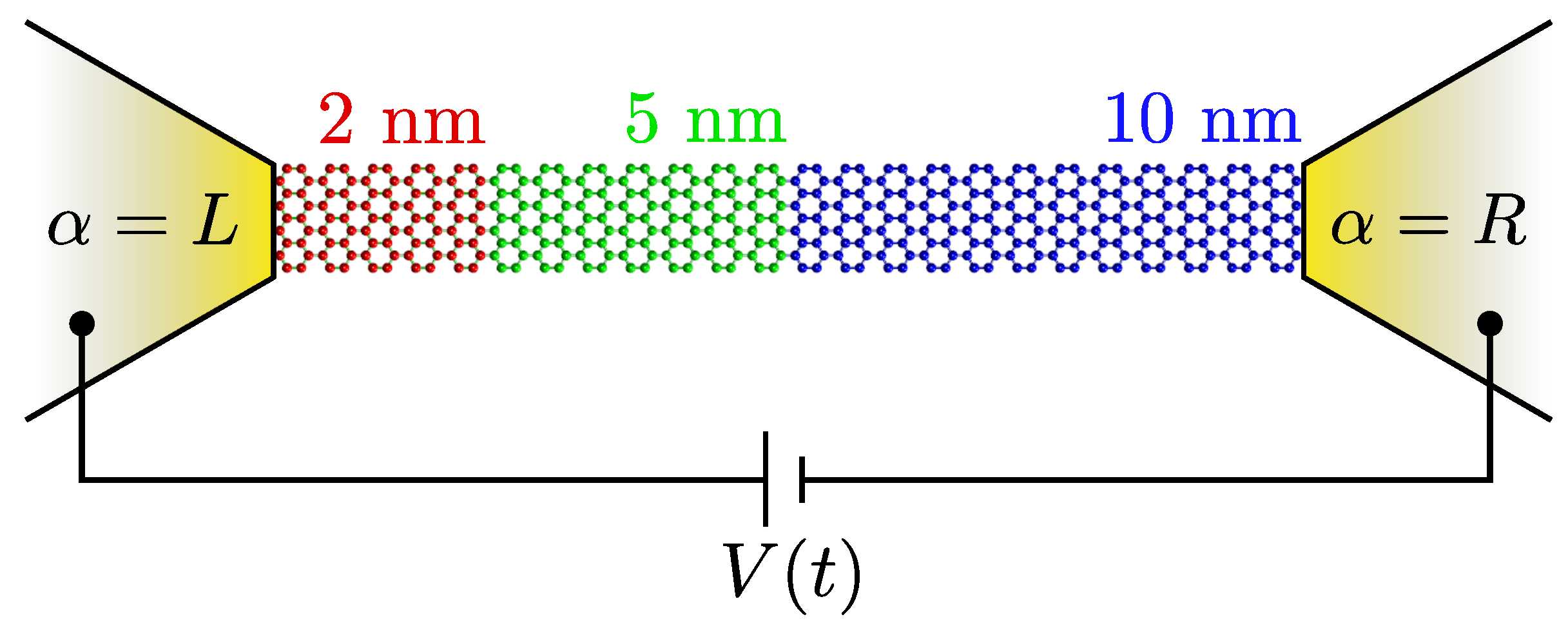
2. Model and Method
3. Results and Discussion
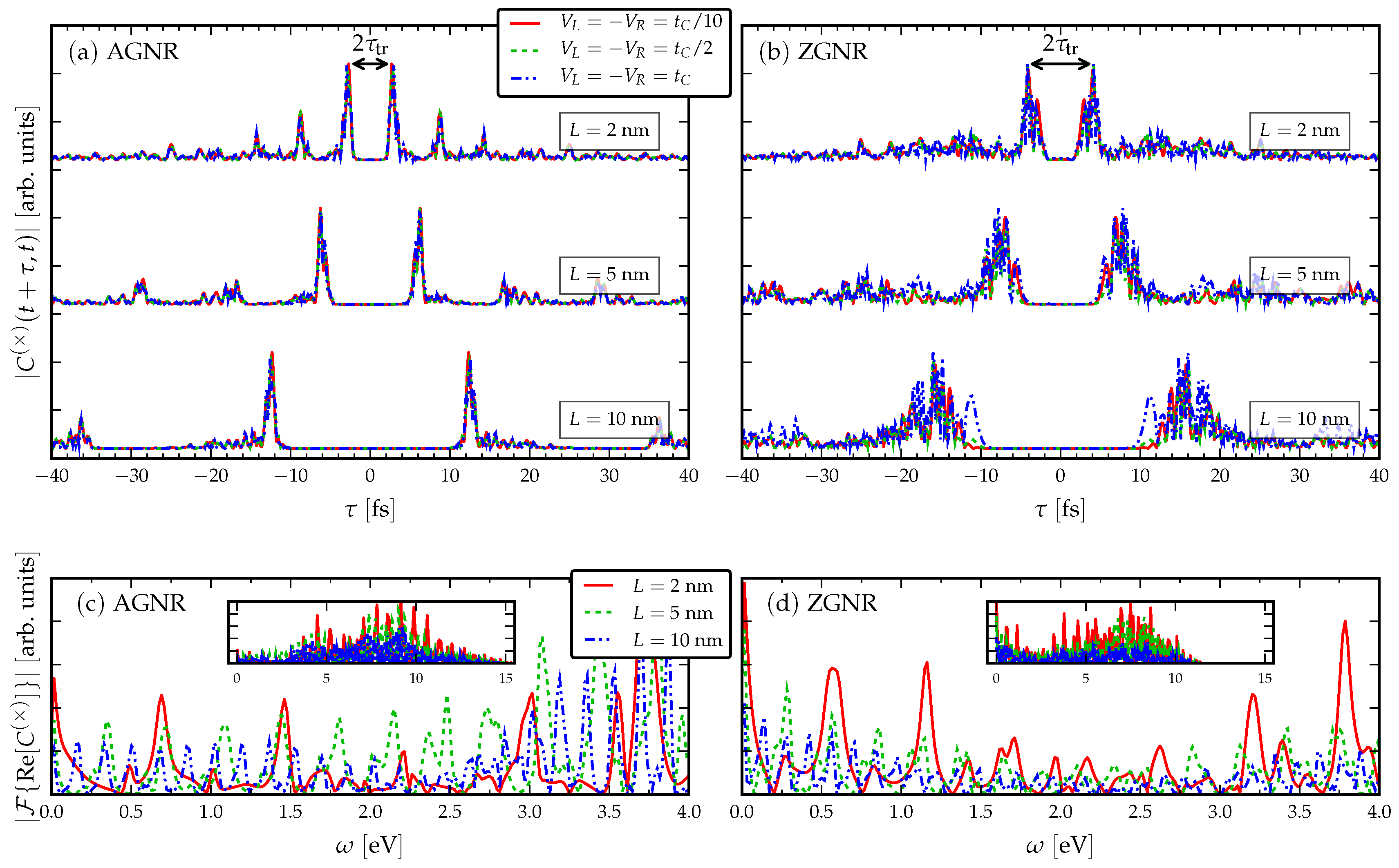
3.1. Response to a dc Drive
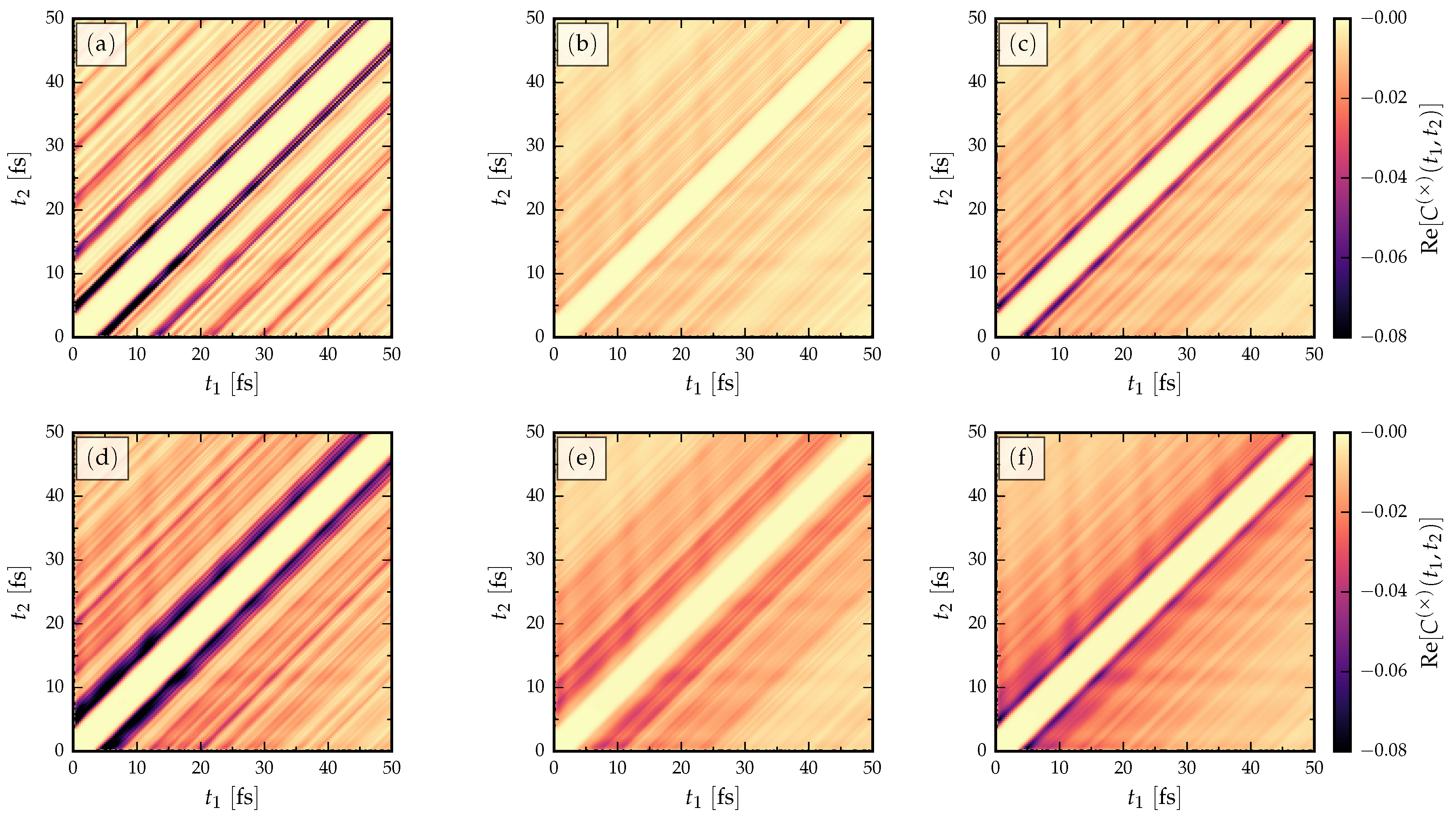
- The signal is more clear for the AGNR than ZGNR. In the AGNR case, the propagating wavefront is coherent [35], so that there is less spread in the resonant traversal time signal than in the corresponding ZGNR case. This relates to the shape of the propagating wavefront, since in AGNR it is flat, whereas in ZGNR it has a triangular shape [35]. The back-and-forth internal reflections of the wavepackets between the electrode interfaces have a fairly regular structure in AGNR which results in a clear signal in the current cross-correlation. This means devices based on ZGNR have a less well-defined operational frequency.
- The current cross-correlations are mostly independent of the strength of the applied voltage. The voltage may affect the shape of the curves slightly, but not the location of the main resonance. This can be related to the group velocity of electrons crossing the GNR, , which should not depend on a k-independent shift in the energy dispersion [34].
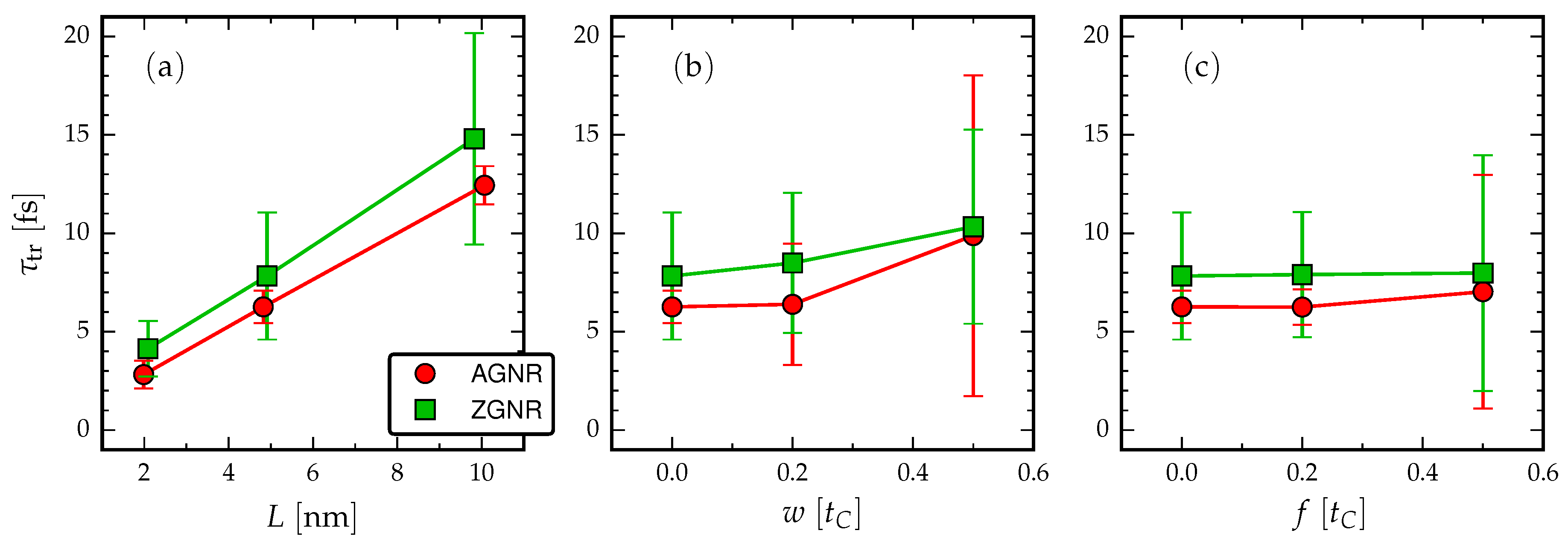
- Evidently, there is a roughly linear increase of the time-difference between the first maxima with increasing L, due to the time taken for the propagating electron wavefront to cross the structure. The time-difference between the first maxima is related to the traversal time of information through the GNRs via Equation (4).
- Increasing the length in the AGNR does not increase the number of resonant peaks in the cross-correlations, but in ZGNR it leads to a broader range of resonances clustered about a mean traversal time. This dependence on the orientation of the GNR then affects the spread of operational device frequencies.
- The low-frequency regions of the Fourier transforms show resonant frequencies at where n is a positive integer and is some intrinsic frequency depending on the length of the GNR. In particular, by increasing the length of the GNR more transport channels are opened in the bias window, and therefore more peaks appear in the Fourier spectra.
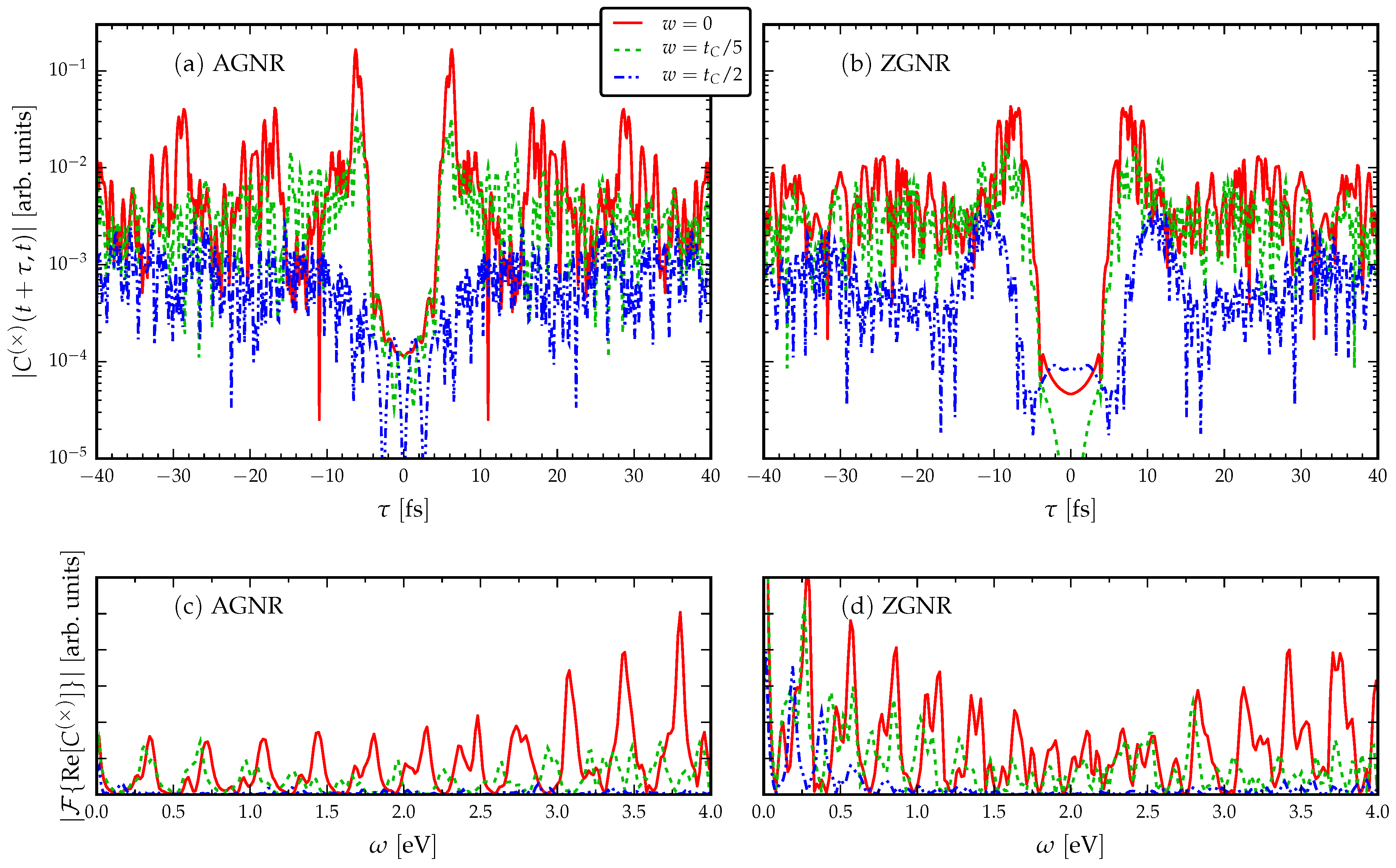
3.2. The Role of Disorder
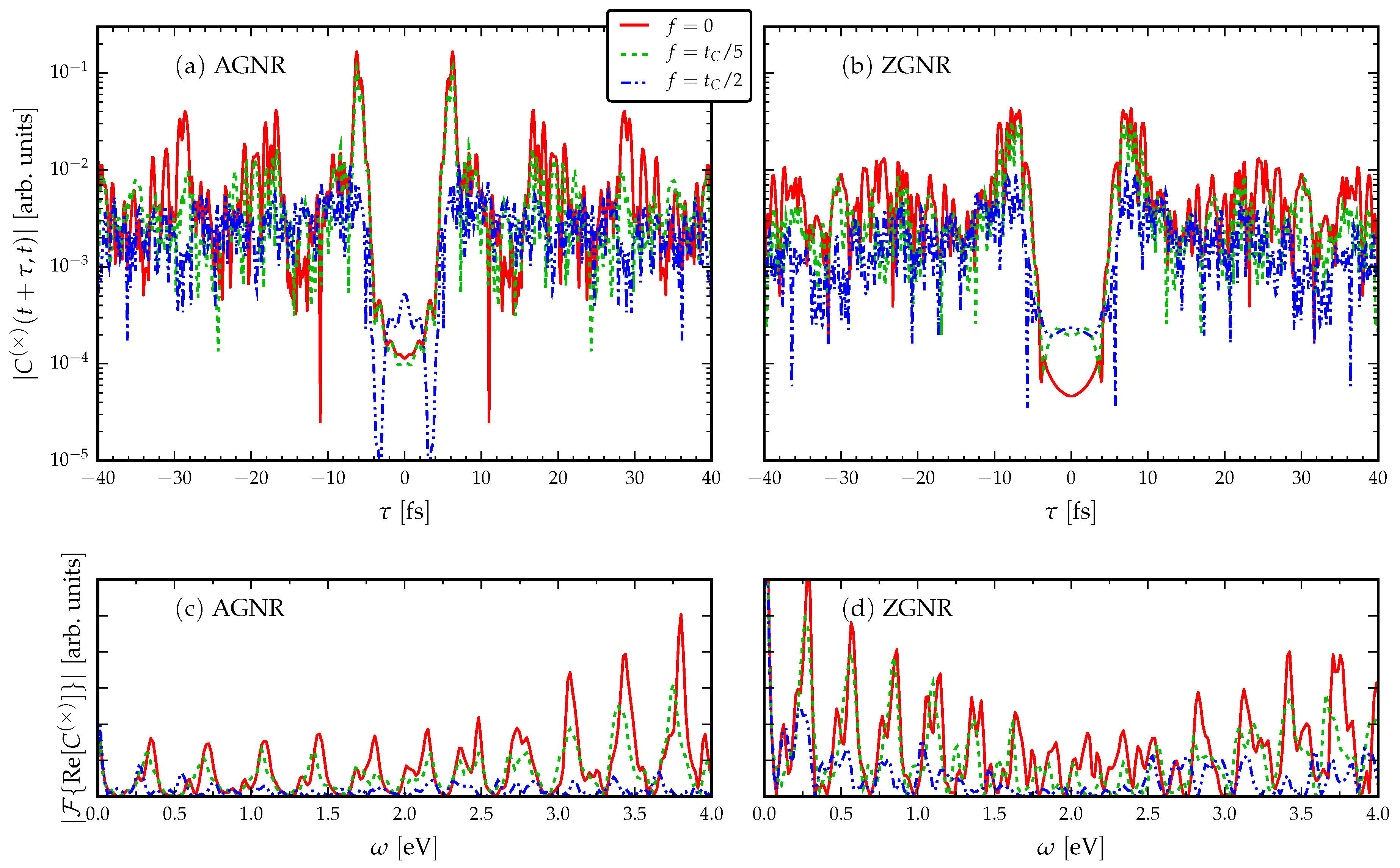
3.3. Response to an ac Drive
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dragoman, D.; Dragoman, M. Time flow in graphene and its implications on the cutoff frequency of ballistic graphene devices. J. Appl. Phys. 2011, 110, 014302. [Google Scholar] [CrossRef]
- Lin, Y.M.; Jenkins, K.A.; Valdes-Garcia, A.; Small, J.P.; Farmer, D.B.; Avouris, P. Operation of graphene transistors at gigahertz frequencies. Nano Lett. 2009, 9, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.; Bai, J.; Cheng, R.; Lin, Y.C.; Jiang, S.; Qu, Y.; Huang, Y.; Duan, X. Sub-100 nm channel length graphene transistors. Nano Lett. 2010, 10, 3952–3956. [Google Scholar] [CrossRef] [PubMed]
- Büttiker, M.; Landauer, R. Traversal time for tunneling. Phys. Rev. Lett. 1982, 49, 1739. [Google Scholar] [CrossRef]
- Hauge, E.; Støvneng, J. Tunneling times: A critical review. Rev. Mod. Phys. 1989, 61, 917. [Google Scholar] [CrossRef]
- Landauer, R.; Martin, T. Barrier interaction time in tunneling. Rev. Mod. Phys. 1994, 66, 217. [Google Scholar] [CrossRef]
- Collins, S.; Lowe, D.; Barker, J. The quantum mechanical tunnelling time problem-revisited. J. Phys. C Solid State 1987, 20, 6213. [Google Scholar] [CrossRef]
- Baz’, A.I. A quantum mechanical calculation of collision time. Sov. J. Nucl. Phys. 1967, 5, 161. [Google Scholar]
- Rybachenko, V.F. Time of penetration of a particle through a potential barrier. In In the Intermissions…Collected Works on Research into the Essentials of Theoretical Physics in Russian Federal Nuclear Center, Arzamas-16; Trutnev, Y.A., Ed.; World Scientific: Singapore, 1998. [Google Scholar] [CrossRef]
- Winful, H.G. Tunneling time, the Hartman effect, and superluminality: A proposed resolution of an old paradox. Phys. Rep. 2006, 436, 1–69. [Google Scholar] [CrossRef]
- Yamada, N. Speakable and Unspeakable in the Tunneling Time Problem. Phys. Rev. Lett. 1999, 83, 3350. [Google Scholar] [CrossRef]
- Sokolovski, D. Path integral approach to space-time probabilities: A theory without pitfalls but with strict rules. Phys. Rev. D 2013, 87, 076001. [Google Scholar] [CrossRef]
- Landsman, A.S.; Keller, U. Attosecond science and the tunnelling time problem. Phys. Rep. 2015, 547, 1–24. [Google Scholar] [CrossRef]
- Landsman, A.S.; Weger, M.; Maurer, J.; Boge, R.; Ludwig, A.; Heuser, S.; Cirelli, C.; Gallmann, L.; Keller, U. Ultrafast resolution of tunneling delay time. Optica 2014, 1, 343–349. [Google Scholar] [CrossRef]
- Camus, N.; Yakaboylu, E.; Fechner, L.; Klaiber, M.; Laux, M.; Mi, Y.; Hatsagortsyan, K.Z.; Pfeifer, T.; Keitel, C.H.; Moshammer, R. Experimental Evidence for Quantum Tunneling Time. Phys. Rev. Lett. 2017, 119, 023201. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, C.; Landsman, A.S.; Keller, U. Attoclock revisited on electron tunnelling time. J. Mod. Opt. 2019, 66, 1052–1070. [Google Scholar] [CrossRef]
- Gao, W.; Shu, J.; Reichel, K.; Nickel, D.V.; He, X.; Shi, G.; Vajtai, R.; Ajayan, P.M.; Kono, J.; Mittleman, D.M.; et al. High-contrast terahertz wave modulation by gated graphene enhanced by extraordinary transmission through ring apertures. Nano Lett. 2014, 14, 1242–1248. [Google Scholar] [CrossRef] [PubMed]
- Koppens, F.; Mueller, T.; Avouris, P.; Ferrari, A.; Vitiello, M.; Polini, M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 2014, 9, 780. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.C.; Cao, T.; Chen, C.; Pedramrazi, Z.; Haberer, D.; De Oteyza, D.G.; Fischer, F.R.; Louie, S.G.; Crommie, M.F. Molecular bandgap engineering of bottom-up synthesized graphene nanoribbon heterojunctions. Nat. Nanotechnol. 2015, 10, 156. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, X.; Zhang, L.; Lee, S.; Dai, H. Chemically derived, ultrasmooth graphene nanoribbon semiconductors. Science 2008, 319, 1229–1232. [Google Scholar] [CrossRef] [PubMed]
- Kimouche, A.; Ervasti, M.M.; Drost, R.; Halonen, S.; Harju, A.; Joensuu, P.M.; Sainio, J.; Liljeroth, P. Ultra-narrow metallic armchair graphene nanoribbons. Nat. Commun. 2015, 6, 10177. [Google Scholar] [CrossRef]
- Carbonell-Sanromà, E.; Garcia-Lekue, A.; Corso, M.; Vasseur, G.; Brandimarte, P.; Lobo-Checa, J.; de Oteyza, D.G.; Li, J.; Kawai, S.; Saito, S.; et al. Electronic Properties of Substitutionally Boron-Doped Graphene Nanoribbons on a Au(111) Surface. J. Phys. Chem. C 2018, 122, 16092–16099. [Google Scholar] [CrossRef]
- Li, J.; Sanz, S.; Corso, M.; Choi, D.J.; Peña, D.; Frederiksen, T.; Pascual, J.I. Single spin localization and manipulation in graphene open-shell nanostructures. Nat. Commun. 2019, 10, 200. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Friedrich, N.; Merino, N.; de Oteyza, D.G.; Peña, D.; Jacob, D.; Pascual, J.I. Electrically Addressing the Spin of a Magnetic Porphyrin through Covalently Connected Graphene Electrodes. Nano Lett. 2019, 19, 3288–3294. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.M.; Dimitrakopoulos, C.; Jenkins, K.A.; Farmer, D.B.; Chiu, H.Y.; Grill, A.; Avouris, P. 100-GHz transistors from wafer-scale epitaxial graphene. Science 2010, 327, 662. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Lin, Y.M.; Bol, A.A.; Jenkins, K.A.; Xia, F.; Farmer, D.B.; Zhu, Y.; Avouris, P. High-frequency, scaled graphene transistors on diamond-like carbon. Nature 2011, 472, 74. [Google Scholar] [CrossRef]
- Cheng, R.; Bai, J.; Liao, L.; Zhou, H.; Chen, Y.; Liu, L.; Lin, Y.C.; Jiang, S.; Huang, Y.; Duan, X. High-frequency self-aligned graphene transistors with transferred gate stacks. Proc. Natl. Acad. Sci. USA 2012, 109, 11588–11592. [Google Scholar] [CrossRef]
- Yu, C.; He, Z.; Song, X.; Liu, Q.; Gao, L.; Yao, B.; Han, T.; Gao, X.; Lv, Y.; Feng, Z.; et al. High-Frequency Flexible Graphene Field-Effect Transistors with Short Gate Length of 50 nm and Record Extrinsic Cut-Off Frequency. Phys. Status Solidi RRL 2018, 12, 1700435. [Google Scholar] [CrossRef]
- Areshkin, D.A.; Gunlycke, D.; White, C.T. Ballistic transport in graphene nanostrips in the presence of disorder: Importance of edge effects. Nano Lett. 2007, 7, 204–210. [Google Scholar] [CrossRef]
- Dauber, J.; Terrés, B.; Volk, C.; Trellenkamp, S.; Stampfer, C. Reducing disorder in graphene nanoribbons by chemical edge modification. Appl. Phys. Lett. 2014, 104, 083105. [Google Scholar] [CrossRef]
- Mucciolo, E.R.; Castro Neto, A.H.; Lewenkopf, C.H. Conductance quantization and transport gaps in disordered graphene nanoribbons. Phys. Rev. B 2009, 79, 075407. [Google Scholar] [CrossRef]
- Mucciolo, E.R.; Lewenkopf, C.H. Disorder and electronic transport in graphene. J. Phys. Condens. Matter 2010, 22, 273201. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Wang, X. Singularity of density of states induced by random bond disorder in graphene. Phys. Lett. A 2016, 380, 2233–2236. [Google Scholar] [CrossRef]
- Ridley, M.; MacKinnon, A.; Kantorovich, L. Partition-free theory of time-dependent current correlations in nanojunctions in response to an arbitrary time-dependent bias. Phys. Rev. B 2017, 95, 165440. [Google Scholar] [CrossRef]
- Tuovinen, R.; Perfetto, E.; Stefanucci, G.; van Leeuwen, R. Time-dependent Landauer-Büttiker formula: Application to transient dynamics in graphene nanoribbons. Phys. Rev. B 2014, 89, 085131. [Google Scholar] [CrossRef]
- Da Rocha, C.G.; Tuovinen, R.; van Leeuwen, R.; Koskinen, P. Curvature in graphene nanoribbons generates temporally and spatially focused electric currents. Nanoscale 2015, 7, 8627–8635. [Google Scholar] [CrossRef]
- Tuovinen, R.; Sentef, M.A.; Gomes da Rocha, C.; Ferreira, M. Time-resolved impurity-invisibility in graphene nanoribbons. Nanoscale 2019, 11, 12296. [Google Scholar] [CrossRef]
- Ludwig, A.W.W.; Fisher, M.P.A.; Shankar, R.; Grinstein, G. Integer quantum Hall transition: An alternative approach and exact results. Phys. Rev. B 1994, 50, 7526. [Google Scholar] [CrossRef]
- Kawarabayashi, T.; Hatsugai, Y.; Aoki, H. Quantum Hall Plateau Transition in Graphene with Spatially Correlated Random Hopping. Phys. Rev. Lett. 2009, 103, 156804. [Google Scholar] [CrossRef]
- Chen, A.; Ilan, R.; de Juan, F.; Pikulin, D.I.; Franz, M. Quantum Holography in a Graphene Flake with an Irregular Boundary. Phys. Rev. Lett. 2018, 121, 036403. [Google Scholar] [CrossRef]
- Cini, M. Time-dependent approach to electron transport through junctions: General theory and simple applications. Phys. Rev. B 1980, 22, 5887. [Google Scholar] [CrossRef]
- Stefanucci, G.; Almbladh, C.O. Time-dependent partition-free approach in resonant tunneling systems. Phys. Rev. B 2004, 69, 195318. [Google Scholar] [CrossRef]
- Ridley, M.; Tuovinen, R. Formal equivalence between partitioned and partition-free quenches in quantum transport. J. Low Temp. Phys. 2018, 191, 380–392. [Google Scholar] [CrossRef]
- Zhu, Y.; Maciejko, J.; Ji, T.; Guo, H.; Wang, J. Time-dependent quantum transport: Direct analysis in the time domain. Phys. Rev. B 2005, 71, 075317. [Google Scholar] [CrossRef]
- Verzijl, C.J.O.; Seldenthuis, J.S.; Thijssen, J.M. Applicability of the wide-band limit in DFT-based molecular transport calculations. J. Chem. Phys. 2013, 138, 094102. [Google Scholar] [CrossRef] [PubMed]
- Covito, F.; Eich, F.G.; Tuovinen, R.; Sentef, M.A.; Rubio, A. Transient Charge and Energy Flow in the Wide-Band Limit. J. Chem. Theory Comput. 2018, 14, 2495–2504. [Google Scholar] [CrossRef]
- Ridley, M.; Gull, E.; Cohen, G. Lead Geometry and Transport Statistics in Molecular Junctions. J. Chem. Phys. 2019, 150, 244107. [Google Scholar] [CrossRef] [PubMed]
- Reich, S.; Maultzsch, J.; Thomsen, C.; Ordejón, P. Tight-binding description of graphene. Phys. Rev. B 2002, 66, 035412. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Hancock, Y.; Uppstu, A.; Saloriutta, K.; Harju, A.; Puska, M.J. Generalized tight-binding transport model for graphene nanoribbon-based systems. Phys. Rev. B 2010, 81, 245402. [Google Scholar] [CrossRef]
- Joost, J.P.; Schlünzen, N.; Bonitz, M. Femtosecond Electron Dynamics in Graphene Nanoribbons—A Nonequilibrium Green Functions Approach Within an Extended Hubbard Model. Phys. Status Solidi B 2019, 1800498. [Google Scholar] [CrossRef]
- Datta, S.S.; Strachan, D.R.; Khamis, S.M.; Johnson, A.T.C. Crystallographic Etching of Few-Layer Graphene. Nano Lett. 2008, 8, 1912–1915. [Google Scholar] [CrossRef] [PubMed]
- Papaefthimiou, V.; Florea, I.; Baaziz, W.; Janowska, I.; Doh, W.H.; Begin, D.; Blume, R.; Knop-Gericke, A.; Ersen, O.; Pham-Huu, C.; et al. Effect of the Specific Surface Sites on the Reducibility of a-Fe2O3/Graphene Composites by Hydrogen. J. Phys. Chem. C 2013, 117, 20313–20319. [Google Scholar] [CrossRef]
- Wang, Z.F.; Li, Q.; Zheng, H.; Ren, H.; Su, H.; Shi, Q.W.; Chen, J. Tuning the electronic structure of graphene nanoribbons through chemical edge modification: A theoretical study. Phys. Rev. B 2007, 75, 113406. [Google Scholar] [CrossRef]
- Lu, Y.H.; Wu, R.Q.; Shen, L.; Yang, M.; Sha, Z.D.; Cai, Y.Q.; He, P.M.; Feng, Y.P. Effects of edge passivation by hydrogen on electronic structure of armchair graphene nanoribbon and band gap engineering. Appl. Phys. Lett. 2009, 94, 122111. [Google Scholar] [CrossRef]
- Landauer, R. Electrical resistance of disordered one-dimensional lattices. Philos. Mag. 1970, 21, 863. [Google Scholar] [CrossRef]
- Büttiker, M. Four-terminal phase-coherent conductance. Phys. Rev. Lett. 1986, 57, 1761. [Google Scholar] [CrossRef] [PubMed]
- Tuovinen, R.; van Leeuwen, R.; Perfetto, E.; Stefanucci, G. Time-dependent Landauer–Büttiker formula for transient dynamics. J. Phys. Conf. Ser. 2013, 427, 012014. [Google Scholar] [CrossRef]
- Ridley, M.; MacKinnon, A.; Kantorovich, L. Current through a multilead nanojunction in response to an arbitrary time-dependent bias. Phys. Rev. B 2015, 91, 125433. [Google Scholar] [CrossRef]
- Ridley, M.; MacKinnon, A.; Kantorovich, L. Calculation of the current response in a nanojunction for an arbitrary time-dependent bias: Application to the molecular wire. J. Phys. Conf. Ser. 2016, 696, 012017. [Google Scholar] [CrossRef]
- Ridley, M.; MacKinnon, A.; Kantorovich, L. Fluctuating-bias controlled electron transport in molecular junctions. Phys. Rev. B 2016, 93, 205408. [Google Scholar] [CrossRef]
- Tuovinen, R.; Säkkinen, N.; Karlsson, D.; Stefanucci, G.; van Leeuwen, R. Phononic heat transport in the transient regime: An analytic solution. Phys. Rev. B 2016, 93, 214301. [Google Scholar] [CrossRef]
- Tuovinen, R.; van Leeuwen, R.; Perfetto, E.; Stefanucci, G. Time-dependent Landauer–Büttiker formalism for superconducting junctions at arbitrary temperatures. J. Phys. Conf. Ser. 2016, 696, 012016. [Google Scholar] [CrossRef]
- Tuovinen, R.; Perfetto, E.; van Leeuwen, R.; Stefanucci, G.; Sentef, M.A. Distinguishing Majorana Zero Modes from Impurity States through Time-Resolved Transport. arXiv 2019, arXiv:1902.05821. [Google Scholar]
- Ridley, M.; Tuovinen, R. Time-dependent Landauer-Büttiker approach to charge pumping in ac-driven graphene nanoribbons. Phys. Rev. B 2017, 96, 195429. [Google Scholar] [CrossRef]
- Février, P.; Gabelli, J. Tunneling time probed by quantum shot noise. Nat. Commun. 2018, 9, 4940. [Google Scholar] [CrossRef] [PubMed]
- Fertig, H. Traversal-time distribution and the uncertainty principle in quantum tunneling. Phys. Rev. Lett. 1990, 65, 2321. [Google Scholar] [CrossRef] [PubMed]
- Pollak, E.; Miller, W.H. New physical interpretation for time in scattering theory. Phys. Rev. Lett. 1984, 53, 115. [Google Scholar] [CrossRef]
- Gopar, V.A. Shot noise fluctuations in disordered graphene nanoribbons near the Dirac point. Phys. E 2016, 77, 23–28. [Google Scholar] [CrossRef]
- Stefanucci, G.; van Leeuwen, R. Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Deng, G.W.; Wei, D.; Li, S.X.; Johansson, J.; Kong, W.C.; Li, H.O.; Cao, G.; Xiao, M.; Guo, G.C.; Nori, F.; et al. Coupling two distant double quantum dots with a microwave resonator. Nano Lett. 2015, 15, 6620–6625. [Google Scholar] [CrossRef] [PubMed]
- Miao, F.; Wijeratne, S.; Zhang, Y.; Coskun, U.C.; Bao, W.; Lau, C.N. Phase-Coherent Transport in Graphene Quantum Billiards. Science 2007, 317, 1530–1533. [Google Scholar] [CrossRef]
- Galperin, M.; Ratner, M.A.; Nitzan, A. Molecular transport junctions: Vibrational effects. J. Phys. Condens. Matter 2007, 19, 103201. [Google Scholar] [CrossRef]
- Swenson, D.W.; Cohen, G.; Rabani, E. A semiclassical model for the non-equilibrium quantum transport of a many-electron Hamiltonian coupled to phonons. Mol. Phys. 2012, 110, 743–750. [Google Scholar] [CrossRef]
- Härtle, R.; Cohen, G.; Reichman, D.R.; Millis, A.J. Decoherence and lead-induced interdot coupling in nonequilibrium electron transport through interacting quantum dots: A hierarchical quantum master equation approach. Phys. Rev. B 2013, 88, 235426. [Google Scholar] [CrossRef]
- Galperin, M.; Nitzan, A.; Ratner, M.A. Inelastic tunneling effects on noise properties of molecular junctions. Phys. Rev. B 2006, 74, 075326. [Google Scholar] [CrossRef]
- Souza, F.M.; Jauho, A.P.; Egues, J.C. Spin-polarized current and shot noise in the presence of spin flip in a quantum dot via nonequilibrium Green’s functions. Phys. Rev. B 2008, 78, 155303. [Google Scholar] [CrossRef]
- Myöhänen, P.; Stan, A.; Stefanucci, G.; van Leeuwen, R. Kadanoff-Baym approach to quantum transport through interacting nanoscale systems: From the transient to the steady-state regime. Phys. Rev. B 2009, 80, 115107. [Google Scholar] [CrossRef]
- Lynn, R.A.; van Leeuwen, R. Development of non-equilibrium Green’s functions for use with full interaction in complex systems. J. Phys. Conf. Ser. 2016, 696, 012020. [Google Scholar] [CrossRef]
- Miwa, K.; Chen, F.; Galperin, M. Towards Noise Simulation in Interacting Nonequilibrium Systems Strongly Coupled to Baths. Sci. Rep. 2017, 7, 9735. [Google Scholar] [CrossRef]
- Cabra, G.; Di Ventra, M.; Galperin, M. Local-noise spectroscopy for nonequilibrium systems. Phys. Rev. B 2018, 98, 235432. [Google Scholar] [CrossRef]
- Shepelyansky, D.L. Coherent Propagation of Two Interacting Particles in a Random Potential. Phys. Rev. Lett. 1994, 73, 2607. [Google Scholar] [CrossRef]
- Vojta, T.; Epperlein, F.; Schreiber, M. Do Interactions Increase or Reduce the Conductance of Disordered Electrons? It Depends! Phys. Rev. Lett. 1998, 81, 4212. [Google Scholar] [CrossRef]
- Karlsson, D.; Hopjan, M.; Verdozzi, C. Disorder and interactions in systems out of equilibrium: The exact independent-particle picture from density functional theory. Phys. Rev. B 2018, 97, 125151. [Google Scholar] [CrossRef]
- Eich, F.G.; Di Ventra, M.; Vignale, G. Density-Functional Theory of Thermoelectric Phenomena. Phys. Rev. Lett. 2014, 112, 196401. [Google Scholar] [CrossRef] [PubMed]
- Eich, F.G.; Principi, A.; Di Ventra, M.; Vignale, G. Luttinger-field approach to thermoelectric transport in nanoscale conductors. Phys. Rev. B 2014, 90, 115116. [Google Scholar] [CrossRef]
- Eich, F.G.; Di Ventra, M.; Vignale, G. Temperature-driven transient charge and heat currents in nanoscale conductors. Phys. Rev. B 2016, 93, 134309. [Google Scholar] [CrossRef]
- Eich, F.G.; Ventra, M.D.; Vignale, G. Functional theories of thermoelectric phenomena. J. Phys. Condens. Matter 2016, 29, 063001. [Google Scholar] [CrossRef] [PubMed]
- Ridley, M.; Singh, V.N.; Gull, E.; Cohen, G. Numerically exact full counting statistics of the nonequilibrium Anderson impurity model. Phys. Rev. B 2018, 97, 115109. [Google Scholar] [CrossRef]
- Kemper, A.F.; Sentef, M.A.; Moritz, B.; Freericks, J.K.; Devereaux, T.P. Direct observation of Higgs mode oscillations in the pump-probe photoemission spectra of electron-phonon mediated superconductors. Phys. Rev. B 2015, 92, 224517. [Google Scholar] [CrossRef]
- Sentef, M.A.; Kemper, A.F.; Georges, A.; Kollath, C. Theory of light-enhanced phonon-mediated superconductivity. Phys. Rev. B 2016, 93, 144506. [Google Scholar] [CrossRef]
- Kemper, A.F.; Sentef, M.A.; Moritz, B.; Devereaux, T.P.; Freericks, J.K. Review of the Theoretical Description of Time-Resolved Angle-Resolved Photoemission Spectroscopy in Electron-Phonon Mediated Superconductors. Ann. Phys. 2017, 529, 1600235. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ridley, M.; Sentef, M.A.; Tuovinen, R. Electron Traversal Times in Disordered Graphene Nanoribbons. Entropy 2019, 21, 737. https://doi.org/10.3390/e21080737
Ridley M, Sentef MA, Tuovinen R. Electron Traversal Times in Disordered Graphene Nanoribbons. Entropy. 2019; 21(8):737. https://doi.org/10.3390/e21080737
Chicago/Turabian StyleRidley, Michael, Michael A. Sentef, and Riku Tuovinen. 2019. "Electron Traversal Times in Disordered Graphene Nanoribbons" Entropy 21, no. 8: 737. https://doi.org/10.3390/e21080737
APA StyleRidley, M., Sentef, M. A., & Tuovinen, R. (2019). Electron Traversal Times in Disordered Graphene Nanoribbons. Entropy, 21(8), 737. https://doi.org/10.3390/e21080737




