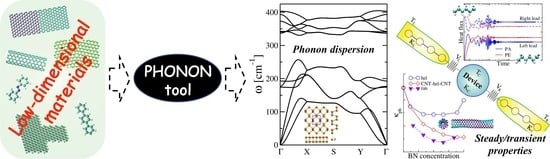
Quantum Phonon Transport in Nanomaterials: Combining Atomistic with Non-Equilibrium Green’s Function Techniques
Abstract
1. Introduction
2. DFTB-Based Quantum Transport
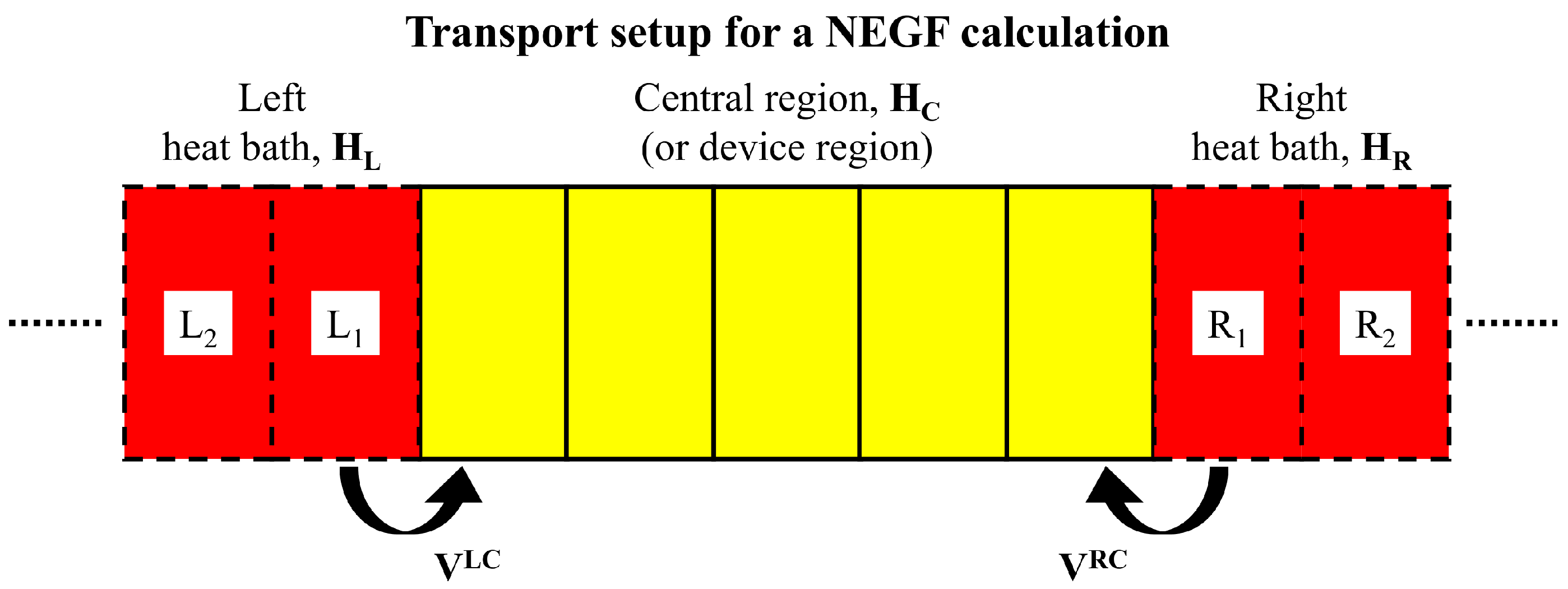
2.1. Ballistic Phonon Transport
- -
- The lesser GF, .
- -
- The greater GF, .
- -
- The retarded GF, .
- -
- The advanced GF, .
- -
- The time-ordered GF, .
- -
- The anti-time-ordered GF, .
2.2. Density Functional Tight-Binding
2.3. Application of the DFTB-Based PHONON Tool
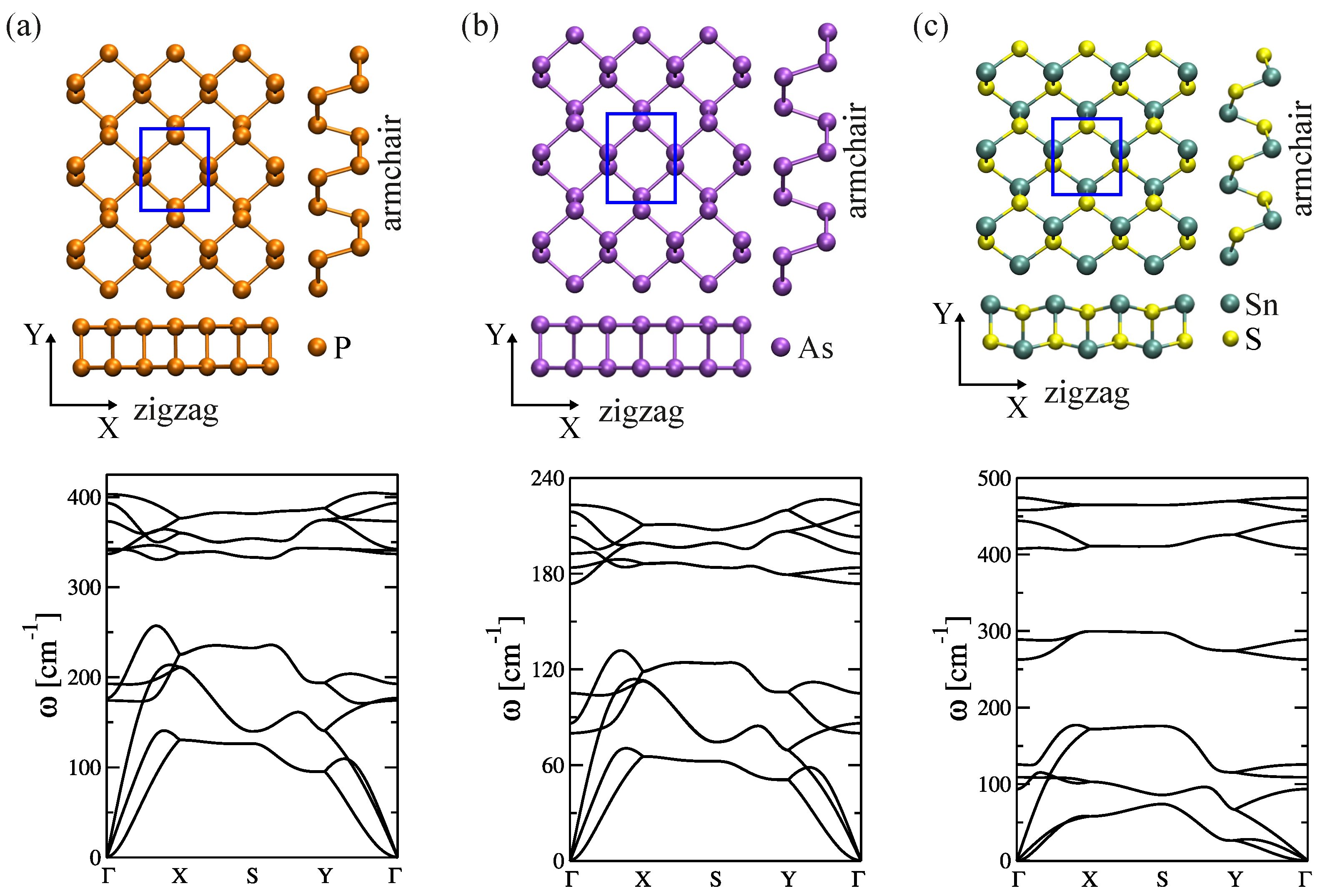
2.3.1. 2D Orthorhombic Materials
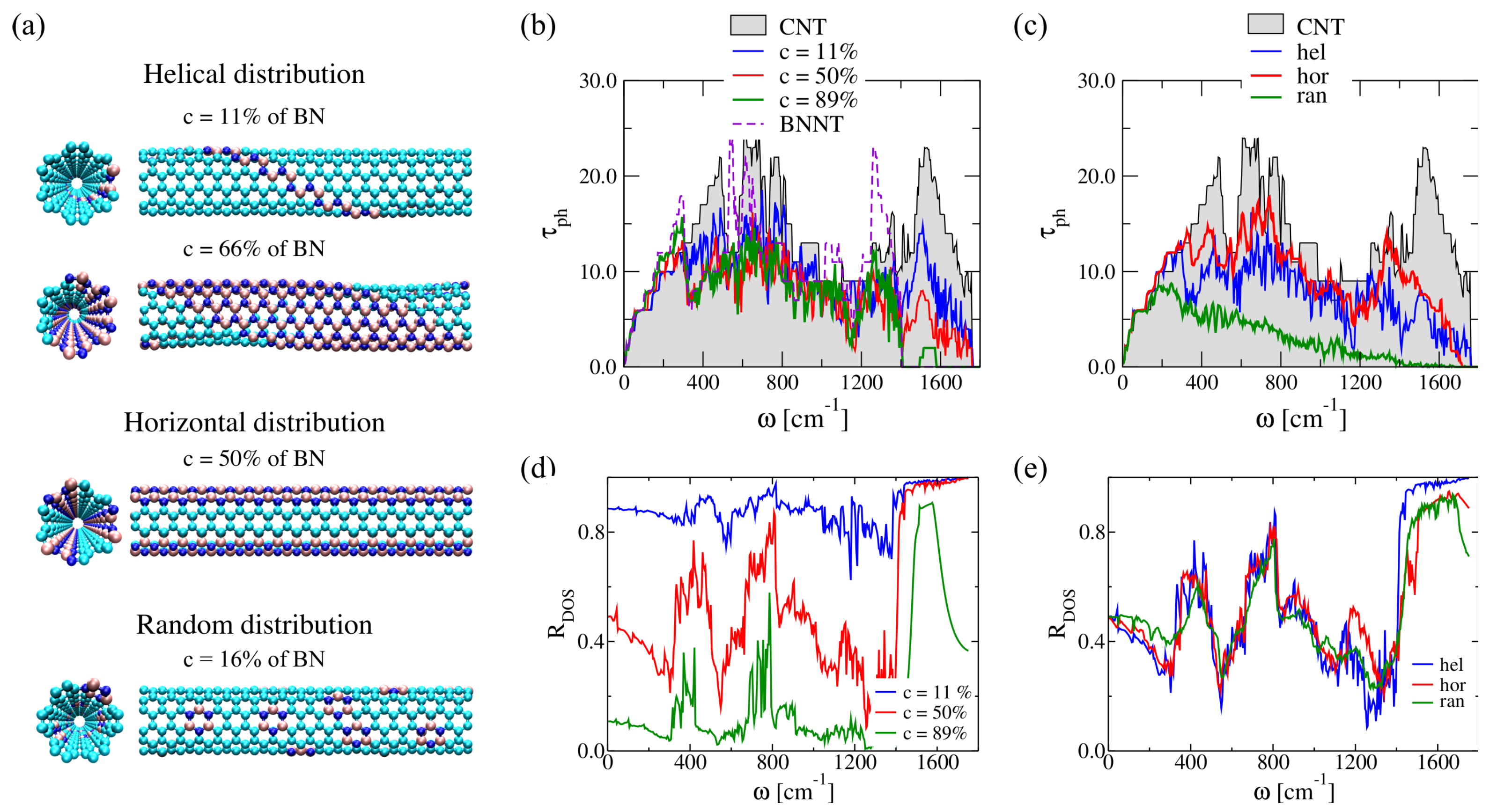
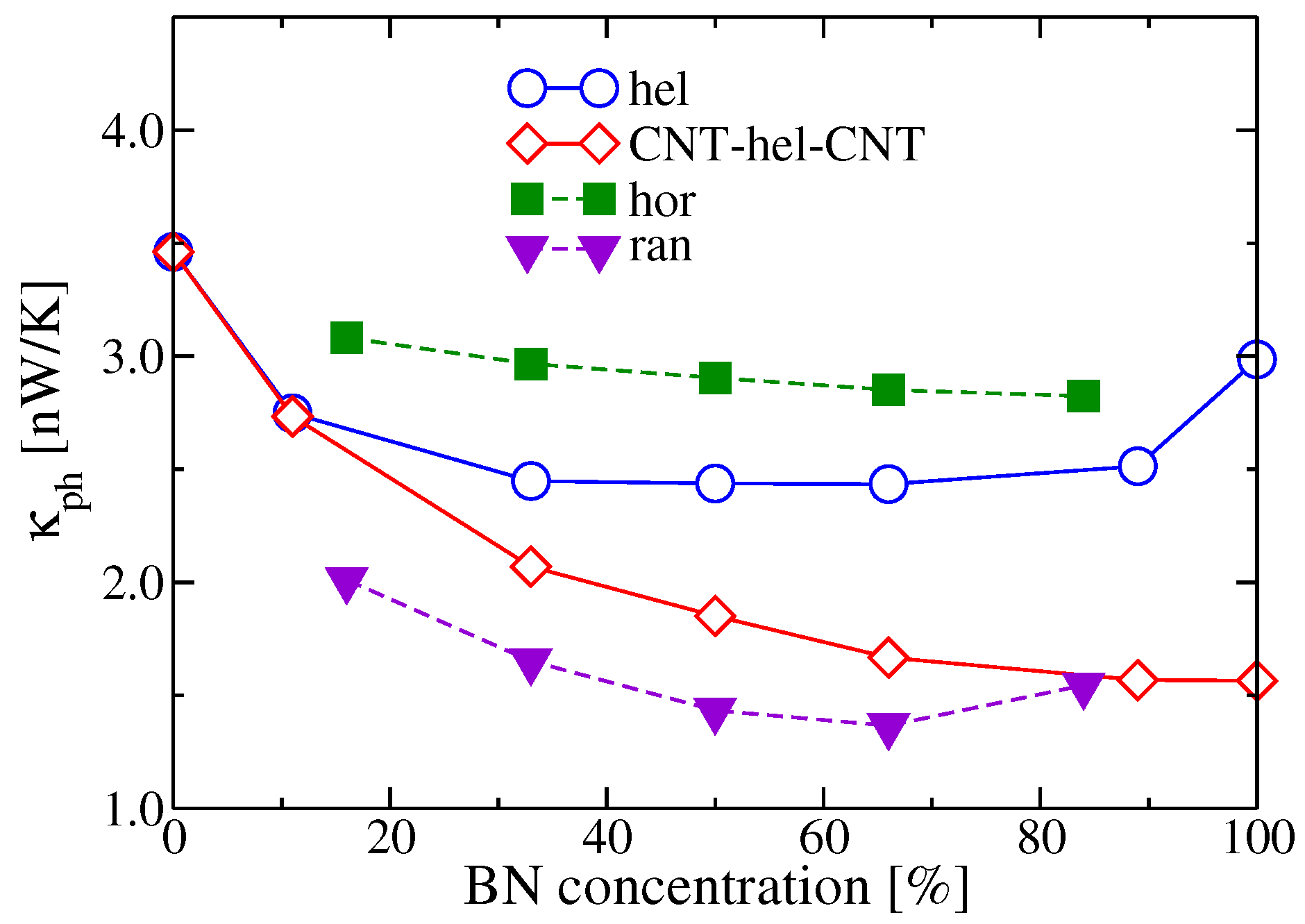
2.3.2. Doping Influence on BNC Heteronanotubes
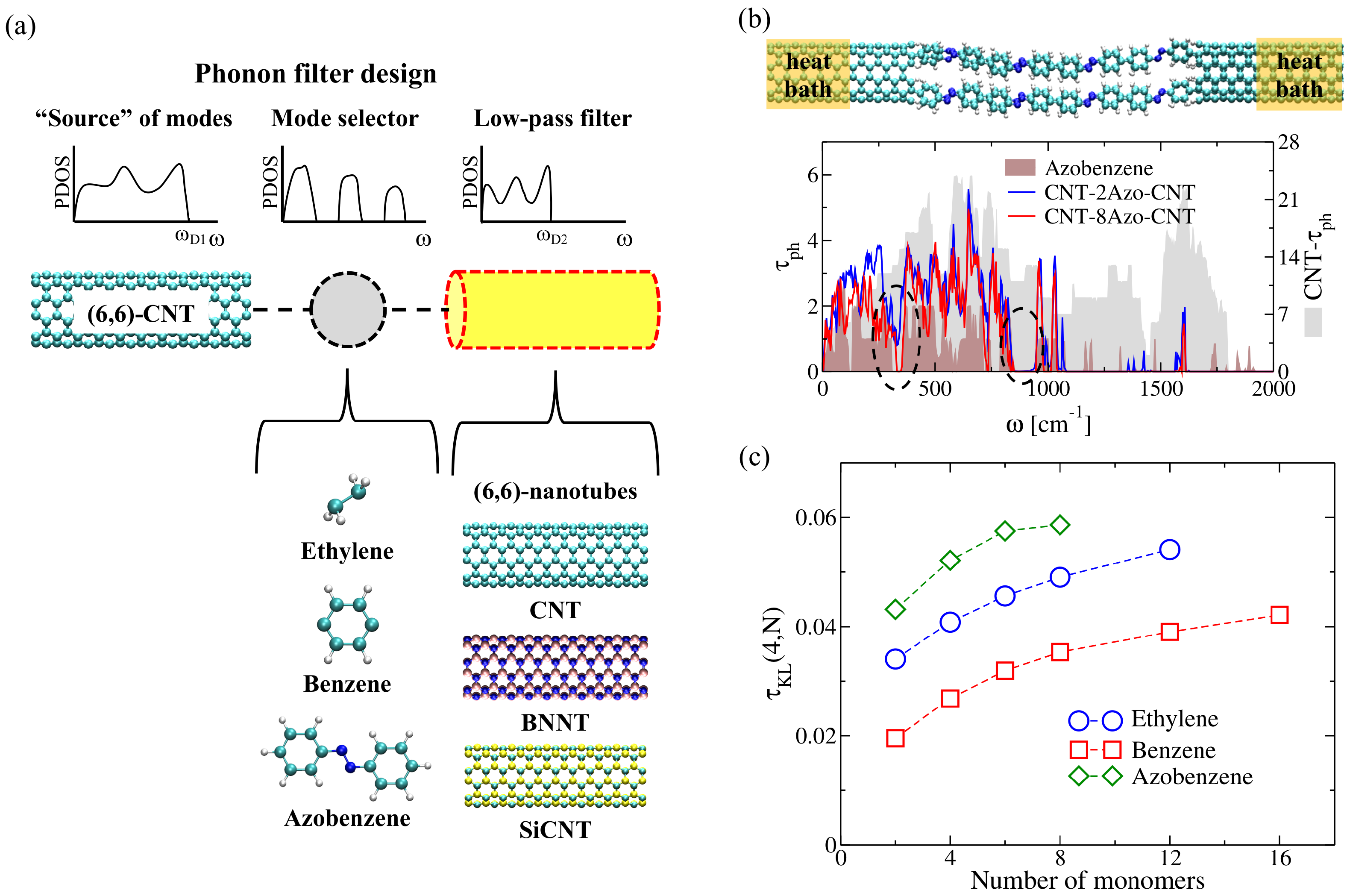
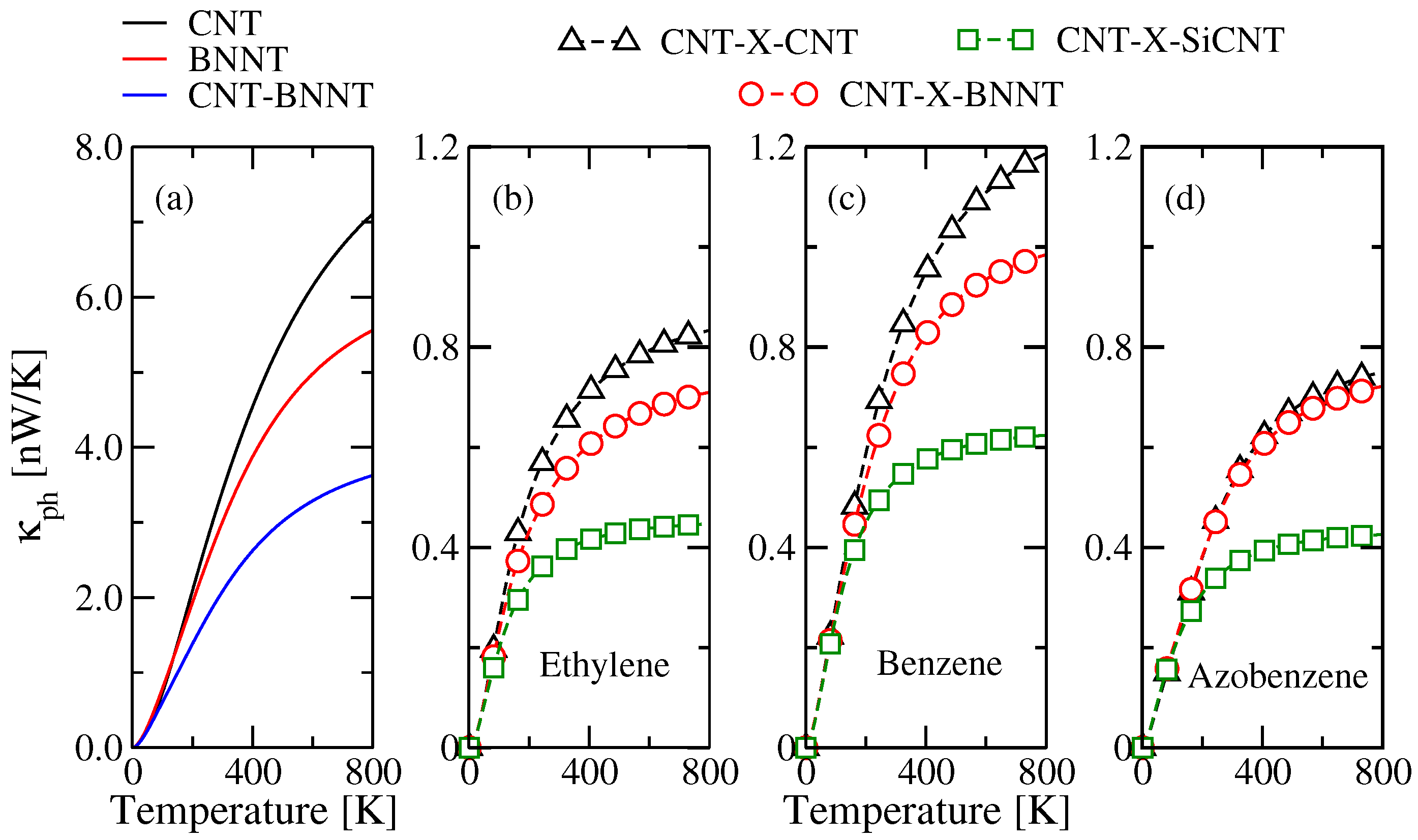
2.3.3. Selective Molecular-Scale Phonon Filtering
3. Atomistic Framework for Time-Dependent Thermal Transport
3.1. Auxiliary-Mode Approach
3.2. Applications of TD-NEGF Approach
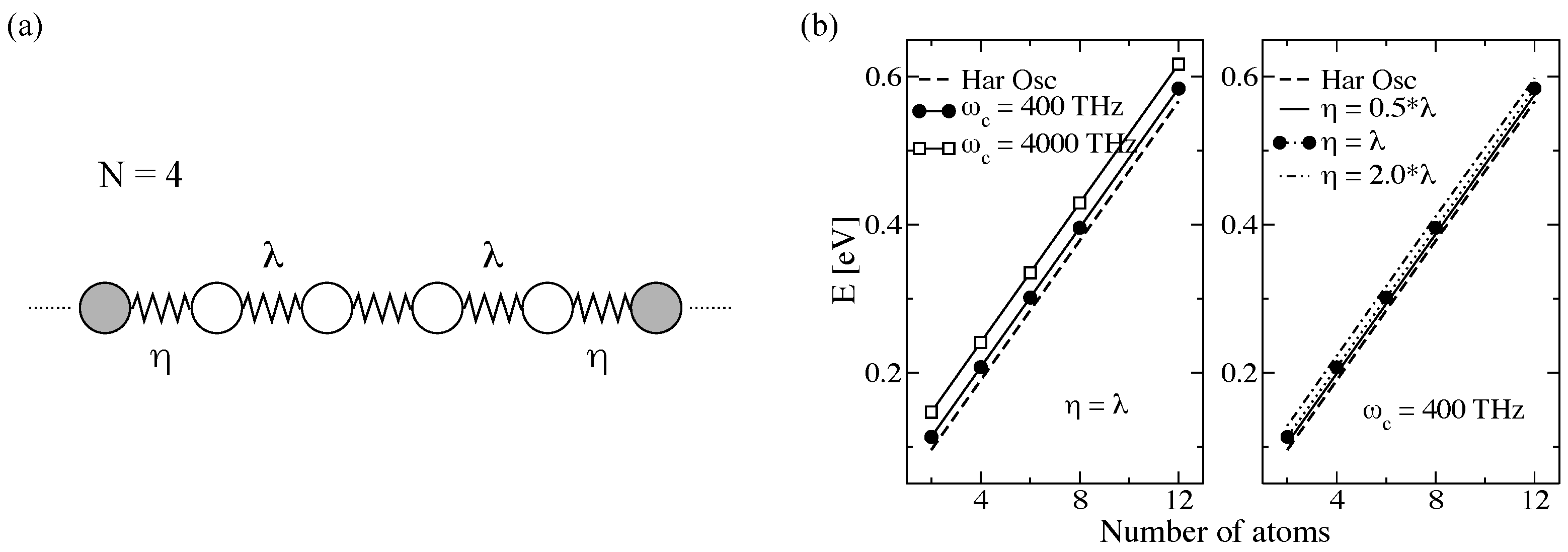
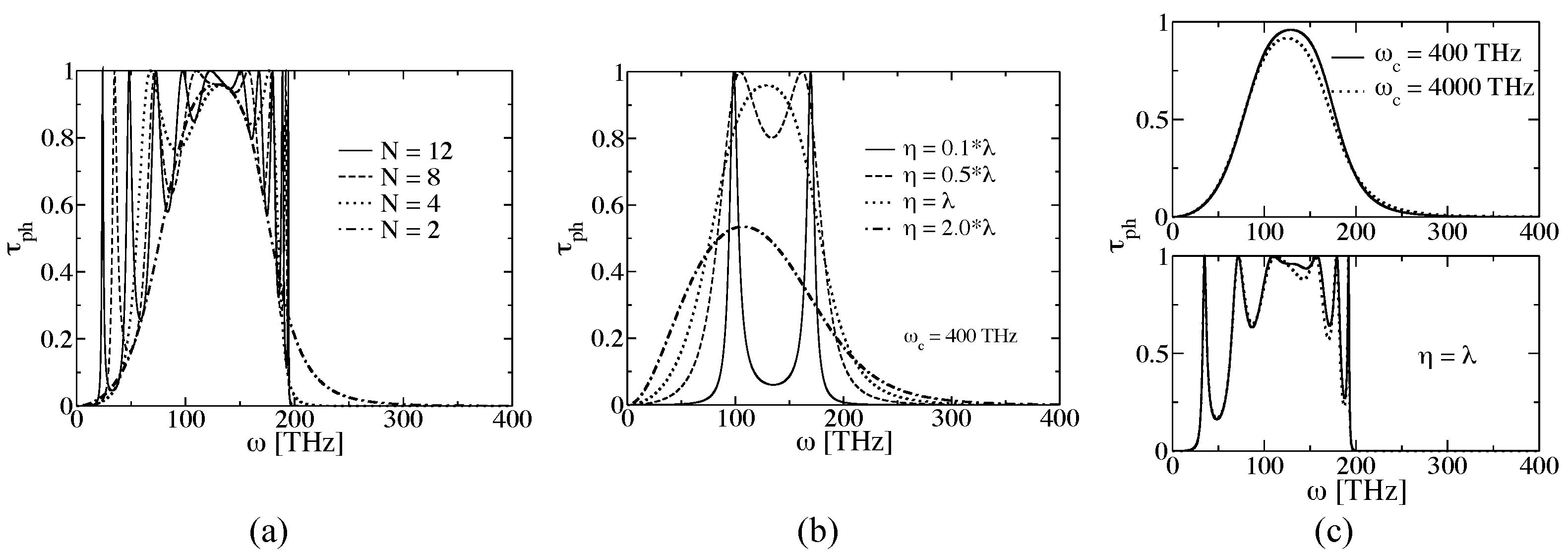
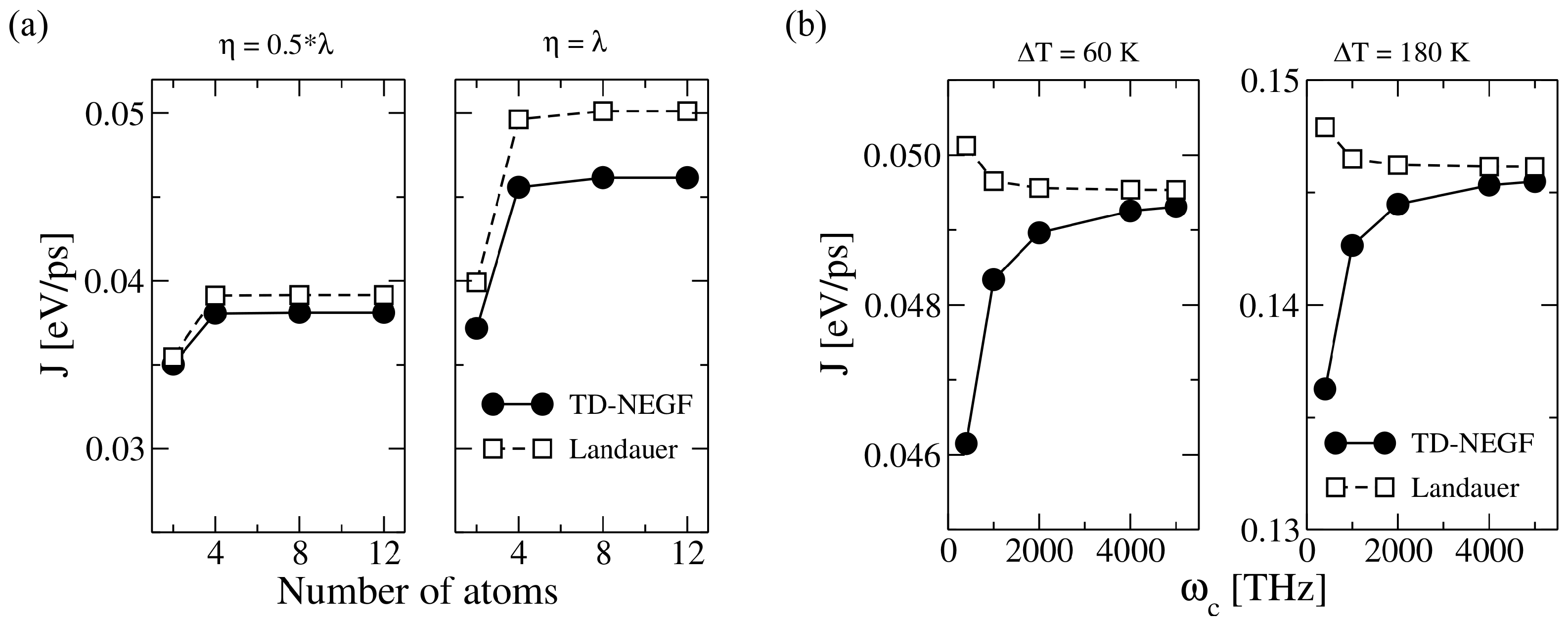
3.2.1. Proof-of-Principle: One-Dimensional Atomic Chain
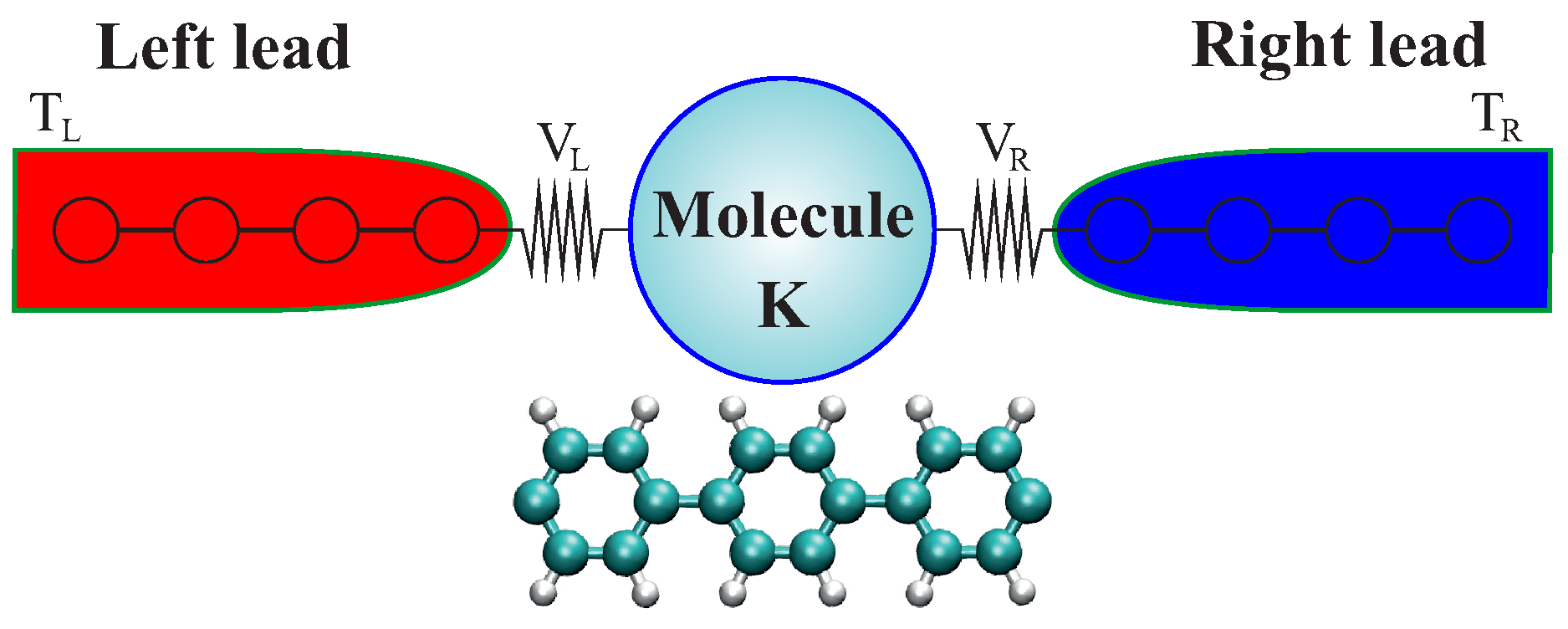
3.2.2. Atomistic System: Carbon-Based Molecular Junctions
4. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CNT | Carbon nanotube |
| DFT | Density functional theory |
| DFTB | Density functional tight-binding |
| DOS | Density of states |
| EOM | Equation of motion |
| GF | Green’s functions |
| LDOS | Local density of states |
| NEGF | Non-equilibrium Green’s functions |
| NEMD | Non-equilibrium molecular dynamics |
| MD | Molecular dynamics |
| PA | Poly-acetylene |
| PE | Poly-ethylene |
| TD | Time-dependent |
References
- Moore, A.L.; Shi, L. Emerging challenges and materials for thermal management of electronics. Mater. Today 2014, 17, 163–174. [Google Scholar] [CrossRef]
- Li, N.; Ren, J.; Wang, L.; Zhang, G.; Hänggi, P.; Li, B. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 2012, 84, 1045–1066. [Google Scholar] [CrossRef]
- Dubi, Y.; Di Ventra, M. Colloquium: Heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 2011, 83, 131–155. [Google Scholar] [CrossRef]
- Volz, S.; Ordonez-Miranda, J.; Shchepetov, A.; Prunnila, M.; Ahopelto, J.; Pezeril, T.; Vaudel, G.; Gusev, V.; Ruello, P.; Weig, E.M.; et al. Nanophononics: State of the art and perspectives. Eur. Phys. J. B 2016, 89, 15. [Google Scholar] [CrossRef]
- Balandin, A.A.; Nika, D.L. Phononics in low-dimensional materials. Mater. Today 2012, 15, 266–275. [Google Scholar] [CrossRef]
- Sklan, S.R. Splash, pop, sizzle: Information processing with phononic computing. AIP Adv. 2015, 5, 053302. [Google Scholar] [CrossRef]
- Pop, E. Energy dissipation and transport in nanoscale devices. Nano Res. 2010, 3, 147–169. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, G.; Khan, J.M.; Balandin, A.A. Graphene quilts for thermal management of high-power GaN transistors. Nat. Commun. 2012, 3, 827. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105. [Google Scholar] [CrossRef]
- Biswas, K.; He, J.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Dravid, V.P.; Kanatzidis, M.G. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 2012, 489, 414. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- McNeil, R.P.G.; Kataoka, M.; Ford, C.J.B.; Barnes, C.H.W.; Anderson, D.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A. On-demand single-electron transfer between distant quantum dots. Nature 2011, 477, 439. [Google Scholar] [CrossRef] [PubMed]
- Hermelin, S.; Takada, S.; Yamamoto, M.; Tarucha, S.; Wieck, A.D.; Saminadayar, L.; Bäuerle, C.; Meunier, T. Electrons surfing on a sound wave as a platform for quantum optics with flying electrons. Nature 2011, 477, 435. [Google Scholar] [CrossRef] [PubMed]
- Rossignol, C.; Chigarev, N.; Ducousso, M.; Audoin, B.; Forget, G.; Guillemot, F.; Durrieu, M.C. In-vitro picosecond ultrasonics in a single cell. Appl. Phys. Lett. 2008, 93, 123901. [Google Scholar] [CrossRef]
- Rego, L.G.C.; Kirczenow, G. Quantized thermal conductance of dielectric quantum wires. Phys. Rev. Lett. 1998, 81, 232–235. [Google Scholar] [CrossRef]
- Schwab, K.; Henriksen, E.A.; Worlock, J.M.; Roukes, M.L. Measurement of the quantum of thermal conductance. Nature 2000, 404, 974–977. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Jeong, W.; Hur, S.; Matt, M.; Klöckner, J.C.; Pauly, F.; Nielaba, P.; Cuevas, J.C.; Meyhofer, E.; Reddy, P. Quantized thermal transport in single-atom junctions. Science 2017, 355, 1192–1195. [Google Scholar] [CrossRef] [PubMed]
- Mosso, N.; Drechsler, U.; Menges, F.; Nirmalraj, P.; Karg, S.; Riel, H.; Gotsmann, B. Heat transport through atomic contacts. Nat. Nanotechnol. 2017, 12, 430. [Google Scholar] [CrossRef]
- Tavakoli, A.; Lulla, K.; Crozes, T.; Mingo, N.; Collin, E.; Bourgeois, O. Heat conduction measurements in ballistic 1D phonon waveguides indicate breakdown of the thermal conductance quantization. Nat. Commun. 2018, 9, 4287. [Google Scholar] [CrossRef]
- Sikora, A.; Ftouni, H.; Richard, J.; Hébert, C.; Eon, D.; Omnés, F.; Bourgeois, O. Highly sensitive thermal conductivity measurements of suspended membranes (SiN and diamond) using a 3ω-Völklein method. Rev. Sci. Instrum. 2012, 83, 054902, Erratum in 2013, 84, 029901. [Google Scholar] [CrossRef]
- Regner, K.T.; Sellan, D.P.; Su, Z.; Amon, C.H.; McGaughey, A.J.H.; Malen, J.A. Broadband phonon mean free path contributions to thermal conductivity measured using frequency domain thermoreflectance. Nat. Commun. 2013, 4, 1640. [Google Scholar] [CrossRef] [PubMed]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Mahan, G.D.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793–818. [Google Scholar] [CrossRef]
- Kim, K.; Jeong, W.; Lee, W.; Reddy, P. Ultra-high vacuum scanning thermal microscopy for nanometer resolution quantitative thermometry. ACS Nano 2012, 6, 4248–4257. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Chung, J.; Won, J.; Kwon, O.; Lee, J.S.; Park, S.H.; Choi, Y.K. Quantitative scanning thermal microscopy using double scan technique. Appl. Phys. Lett. 2008, 93, 203115. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, Z.; Qin, G.; Yang, J.Y.; Ouyang, T.; Hu, M. Methodology perspective of computing thermal transport in low-dimensional materials and nanostructures: The old and the new. ACS Omega 2018, 3, 3278–3284. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Jund, P.; Jullien, R. Molecular-dynamics calculation of the thermal conductivity of vitreous silica. Phys. Rev. B 1999, 59, 13707–13711. [Google Scholar] [CrossRef]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comp. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Fugallo, G.; Lazzeri, M.; Paulatto, L.; Mauri, F. Ab initio variational approach for evaluating lattice thermal conductivity. Phys. Rev. B 2013, 88, 045430. [Google Scholar] [CrossRef]
- Dove, M.; Dove, M.; Hochella, M.; Liebermann, R.; Putnis, A. Introduction to Lattice Dynamics; Cambridge Topics in Mineral Physics and Chemistry; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Mingo, N.; Yang, L. Phonon transport in nanowires coated with an amorphous material: An atomistic Green’s function approach. Phys. Rev. B 2003, 68, 245406. [Google Scholar] [CrossRef]
- Zhang, W.; Fisher, T.S.; Mingo, N. The atomistic Green’s function method: An efficient simulation approach for nanoscale phonon transport. Numer. Heat Transf. Part B Fundam. 2007, 51, 333–349. [Google Scholar] [CrossRef]
- Zhang, W.; Mingo, N.; Fisher, T.S. Simulation of phonon transport across a non-polar nanowire junction using an atomistic Green’s function method. Phys. Rev. B 2007, 76, 195429. [Google Scholar] [CrossRef]
- Wang, J.S.; Agarwalla, B.K.; Li, H.; Thingna, J. Nonequilibrium Green’s function method for quantum thermal transport. Front. Phys. 2014, 9, 673–697. [Google Scholar] [CrossRef]
- Wingert, M.C.; Kwon, S.; Hu, M.; Poulikakos, D.; Xiang, J.; Chen, R. Sub-amorphous thermal conductivity in ultrathin crystalline silicon nanotubes. Nano Lett. 2015, 15, 2605–2611. [Google Scholar] [CrossRef]
- Wang, Y.; Vallabhaneni, A.; Hu, J.; Qiu, B.; Chen, Y.P.; Ruan, X. Phonon lateral confinement enables thermal rectification in asymmetric single-material nanostructures. Nano Lett. 2014, 14, 592–596. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Gong, X.; Xu, B.; Hu, M. Decouple electronic and phononic transport in nanotwinned structures: A new strategy for enhancing the figure-of-merit of thermoelectrics. Nanoscale 2017, 9, 9987–9996. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.S. Dimensional crossover of thermal conductance in nanowires. Appl. Phys. Lett. 2007, 90, 241908. [Google Scholar] [CrossRef]
- Hu, J.; Ruan, X.; Chen, Y.P. Thermal conductivity and thermal rectification in graphene nanoribbons: A molecular dynamics study. Nano Lett. 2009, 9, 2730–2735. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, X.; Wang, J.S.; Gu, B.L.; Duan, W. Thermal transport in graphene junctions and quantum dots. Phys. Rev. B 2010, 81, 195425. [Google Scholar] [CrossRef]
- Balandin, A.; Wang, K.L. Effect of phonon confinement on the thermoelectric figure of merit of quantum wells. J. Appl. Phys. 1998, 84, 6149–6153. [Google Scholar] [CrossRef]
- Kazan, M.; Guisbiers, G.; Pereira, S.; Correia, M.R.; Masri, P.; Bruyant, A.; Volz, S.; Royer, P. Thermal conductivity of silicon bulk and nanowires: Effects of isotopic composition, phonon confinement, and surface roughness. J. Appl. Phys. 2010, 107, 083503. [Google Scholar] [CrossRef]
- Park, W.; Romano, G.; Ahn, E.C.; Kodama, T.; Park, J.; Barako, M.T.; Sohn, J.; Kim, S.J.; Cho, J.; Marconnet, A.M.; et al. Phonon conduction in silicon nanobeam labyrinths. Sci. Rep. 2017, 7, 6233. [Google Scholar] [CrossRef] [PubMed]
- Seol, J.H.; Jo, I.; Moore, A.L.; Lindsay, L.; Aitken, Z.H.; Pettes, M.T.; Li, X.; Yao, Z.; Huang, R.; Broido, D.; et al. Two-dimensional phonon transport in supported graphene. Science 2010, 328, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M.R.; Graczykowski, B.; Reparaz, J.S.; El Sachat, A.; Sledzinska, M.; Alzina, F.; Sotomayor Torres, C.M. Two-dimensional phononic crystals: Disorder matters. Nano Lett. 2016, 16, 5661–5668. [Google Scholar] [CrossRef] [PubMed]
- Anufriev, R.; Ramiere, A.; Maire, J.; Nomura, M. Heat guiding and focusing using ballistic phonon transport in phononic nanostructures. Nat. Commun. 2017, 8, 15505. [Google Scholar] [CrossRef] [PubMed]
- Segal, D.; Nitzan, A. Molecular heat pump. Phys. Rev. E 2006, 73, 026109. [Google Scholar] [CrossRef]
- Ren, J.; Hänggi, P.; Li, B. Berry-phase-induced heat pumping and its impact on the fluctuation theorem. Phys. Rev. Lett. 2010, 104, 170601. [Google Scholar] [CrossRef]
- Galperin, M.; Saito, K.; Balatsky, A.V.; Nitzan, A. Cooling mechanisms in molecular conduction junctions. Phys. Rev. B 2009, 80, 115427. [Google Scholar] [CrossRef]
- Segal, D.; Nitzan, A. Spin-boson thermal rectifier. Phys. Rev. Lett. 2005, 94, 034301. [Google Scholar] [CrossRef]
- Segal, D. Heat flow in nonlinear molecular junctions: Master equation analysis. Phys. Rev. B 2006, 73, 205415. [Google Scholar] [CrossRef]
- Wei, D.; Obstbaum, M.; Ribow, M.; Back, C.H.; Woltersdorf, G. Spin Hall voltages from AC and DC spin currents. Nat. Commun. 2014, 5, 3768. [Google Scholar] [CrossRef]
- Bocklage, L. Coherent THz transient spin currents by spin pumping. Phys. Rev. Lett. 2017, 118, 257202. [Google Scholar] [CrossRef]
- Croy, A.; Saalmann, U. Propagation scheme for nonequilibrium dynamics of electron transport in nanoscale devices. Phys. Rev. B 2009, 80, 245311. [Google Scholar] [CrossRef]
- Popescu, B.; Woiczikowski, P.B.; Elstner, M.; Kleinekathöfer, U. Time-dependent view of sequential transport through molecules with rapidly fluctuating bridges. Phys. Rev. Lett. 2012, 109, 176802. [Google Scholar] [CrossRef]
- Popescu, B.S.; Croy, A. Efficient auxiliary-mode approach for time-dependent nanoelectronics. New J. Phys. 2016, 18, 093044. [Google Scholar] [CrossRef]
- Kurth, S.; Stefanucci, G.; Almbladh, C.O.; Rubio, A.; Gross, E.K.U. Time-dependent quantum transport: A practical scheme using density functional theory. Phys. Rev. B 2005, 72, 035308. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, F.; Yam, C.Y.; Mo, Y.; Chen, G. Time-dependent density-functional theory for open systems. Phys. Rev. B 2007, 75, 195127. [Google Scholar] [CrossRef]
- Oppenländer, C.; Korff, B.; Niehaus, T.A. Higher harmonics and ac transport from time dependent density functional theory. J. Comput. Electron. 2013, 12, 420–427. [Google Scholar] [CrossRef][Green Version]
- Biele, R.; D’Agosta, R.; Rubio, A. Time-dependent thermal transport theory. Phys. Rev. Lett. 2015, 115, 056801. [Google Scholar] [CrossRef]
- Sena-Junior, M.I.; Lima, L.R.F.; Lewenkopf, C.H. Phononic heat transport in nanomechanical structures: Steady-state and pumping. J. Phys. A Math. Theor. 2017, 50, 435202. [Google Scholar] [CrossRef]
- Tuovinen, R.; Säkkinen, N.; Karlsson, D.; Stefanucci, G.; van Leeuwen, R. Phononic heat transport in the transient regime: An analytic solution. Phys. Rev. B 2016, 93, 214301. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, J.; Lü, J.T. Quantum thermal transport in nanostructures. Eur. Phys. J. B 2008, 62, 381–404. [Google Scholar] [CrossRef]
- Sevinçli, H.; Roche, S.; Cuniberti, G.; Brandbyge, M.; Gutierrez, R.; Medrano Sandonas, L. Green function, quasi-classical Langevin and Kubo–Greenwood methods in quantum thermal transport. J. Phys. Condens. Matter 2019, 31, 273003. [Google Scholar] [CrossRef]
- Stefanucci, G.; van Leeuwen, R. Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Martin, P.C.; Schwinger, J. Theory of many-particle systems. I. Phys. Rev. 1959, 115, 1342–1373. [Google Scholar] [CrossRef]
- Kadanoff, L.; Baym, G. Quantum Statistical Mechanics: Green’s Function Methods in Equilibrium and Nonequilibrium Problems; Frontiers in Physics; Benjamin, W.A., Ed.; Reading Mass: New York, NY, USA, 1962. [Google Scholar]
- Keldysh, L.V. Diagram technique for nonequilibrium processes. Zh. Eksp. Teor. Fiz. 1964, 47, 1515–1527. [Google Scholar]
- Wagner, M. Expansions of nonequilibrium Green’s functions. Phys. Rev. B 1991, 44, 6104–6117. [Google Scholar] [CrossRef]
- Jauho, A.P.; Wingreen, N.S.; Meir, Y. Time-dependent transport in interacting and noninteracting resonant-tunneling systems. Phys. Rev. B 1994, 50, 5528–5544. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge Studies in Semiconductor Physi; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ozpineci, A.; Ciraci, S. Quantum effects of thermal conductance through atomic chains. Phys. Rev. B 2001, 63, 125415. [Google Scholar] [CrossRef]
- Yamamoto, T.; Watanabe, K. Nonequilibrium Green’s function approach to phonon transport in defective carbon nanotubes. Phys. Rev. Lett. 2006, 96, 255503. [Google Scholar] [CrossRef]
- Dhar, A. Heat transport in low-dimensional systems. Adv. Phys. 2008, 57, 457–537. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, J.; Zeng, N. Nonequilibrium Green’s function approach to mesoscopic thermal transport. Phys. Rev. B 2006, 74, 033408. [Google Scholar] [CrossRef]
- Wang, J.S.; Zeng, N.; Wang, J.; Gan, C.K. Nonequilibrium Green’s function method for thermal transport in junctions. Phys. Rev. E 2007, 75, 061128. [Google Scholar] [CrossRef]
- Mingo, N. Anharmonic phonon flow through molecular-sized junctions. Phys. Rev. B 2006, 74, 125402. [Google Scholar] [CrossRef]
- Galperin, M.; Nitzan, A.; Ratner, M.A. Heat conduction in molecular transport junctions. Phys. Rev. B 2007, 75, 155312. [Google Scholar] [CrossRef]
- Medrano Sandonas, L. Computational Modeling of Thermal Transport in Low-Dimensional Materials. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, July 2018. [Google Scholar]
- Gang, Z. Nanoscale Energy Transport and Harvesting: A Computational Study; Jenny Stanford Publishing: Singapore, 2015. [Google Scholar]
- Kubo, R. The fluctuation–dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Velev, J.; Butler, W. On the equivalence of different techniques for evaluating the Green function for a semi-infinite system using a localized basis. J. Phys. Condens. Matter 2004, 16, R637. [Google Scholar] [CrossRef]
- Sancho, M.P.L.; Sancho, J.M.L.; Sancho, J.M.L.; Rubio, J. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F Met. Phys. 1985, 15, 851. [Google Scholar] [CrossRef]
- Parr, R.; Weitao, Y. Density-Functional Theory of Atoms and Molecules; International Series of Monographs on Chemistry; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kim, K.; Jordan, K.D. Comparison of Density Functional and MP2 Calculations on the Water Monomer and Dimer. J. Phys. Chem. 1994, 98, 10089–10094. [Google Scholar] [CrossRef]
- Walter, T. Semiempirical quantum-chemical methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 4, 145–157. [Google Scholar]
- Seifert, G.; Eschrig, H.; Bierger, W. An approximation variant of LCAO-X-ALPHA methods. Z. Phys. Chem. 1986, 267, 529. [Google Scholar]
- Foulkes, W.M.C.; Haydock, R. Tight-binding models and density-functional theory. Phys. Rev. B 1989, 39, 12520–12536. [Google Scholar] [CrossRef]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Erdogan, E.; Popov, I.H.; Enyashin, A.N.; Seifert, G. Transport properties of MoS2 nanoribbons: Edge priority. Eur. Phys. J. B 2012, 85, 33. [Google Scholar] [CrossRef]
- Ghorbani-Asl, M.; Borini, S.; Kuc, A.; Heine, T. Strain-dependent modulation of conductivity in single-layer transition-metal dichalcogenides. Phys. Rev. B 2013, 87, 235434. [Google Scholar] [CrossRef]
- Sevincli, H.; Sevik, C.; Cagin, T.; Cuniberti, G. A bottom-up route to enhance thermoelectric figures of merit in graphene nanoribbons. Sci. Rep. 2013, 3, 1228. [Google Scholar] [CrossRef]
- Erdogan, E.; Popov, I.; Rocha, C.G.; Cuniberti, G.; Roche, S.; Seifert, G. Engineering carbon chains from mechanically stretched graphene-based materials. Phys. Rev. B 2011, 83, 041401. [Google Scholar] [CrossRef]
- Witek, H.A.; Morokuma, K. Systematic study of vibrational frequencies calculated with the self-consistent charge density functional tight-binding method. J. Comput. Chem. 2004, 25, 1858–1864. [Google Scholar] [CrossRef]
- Oviedo, M.B.; Negre, C.F.A.; Sanchez, C.G. Dynamical simulation of the optical response of photosynthetic pigments. Phys. Chem. Chem. Phys. 2010, 12, 6706–6711. [Google Scholar] [CrossRef]
- Scholz, R.; Luschtinetz, R.; Seifert, G.; Jägeler-Hoheisel, T.; Körner, C.; Leo, K.; Rapacioli, M. Quantifying charge transfer energies at donor-acceptor interfaces in small-molecule solar cells with constrained DFTB and spectroscopic methods. J. Phys. Condens. Matter 2013, 25, 473201. [Google Scholar] [CrossRef]
- Seifert, G.; Joswig, J.O. Density-functional tight binding—An approximate density-functional theory method. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 456–465. [Google Scholar] [CrossRef]
- Elstner, M.; Seifert, G. Density functional tight binding. Philos. Trans. R. Soc. A 2014, 372. [Google Scholar] [CrossRef]
- Gaus, M.; Cui, Q.; Elstner, M. Density functional tight binding: Application to organic and biological molecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 49–61. [Google Scholar] [CrossRef]
- Porezag, D.; Frauenheim, T.; Köhler, T.; Seifert, G.; Kaschner, R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [Google Scholar] [CrossRef]
- Hazebroucq, S.; Picard, G.S.; Adamo, C.; Heine, T.; Gemming, S.; Seifert, G. Density-functional-based molecular-dynamics simulations of molten salts. J. Chem. Phys. 2005, 123, 134510. [Google Scholar] [CrossRef]
- Elstner, M. SCC-DFTB: What is the proper degree of self-consistency? J. Phys. Chem. A 2007, 111, 5614–5621. [Google Scholar] [CrossRef]
- Liang, R.; Swanson, J.M.J.; Voth, G.A. Benchmark study of the SCC-DFTB approach for a biomolecular proton channel. J. Chem. Theory Comput. 2014, 10, 451–462. [Google Scholar] [CrossRef]
- Gaus, M.; Cui, Q.; Elstner, M. DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [Google Scholar] [CrossRef]
- Witek, H.A.; Irle, S.; Morokuma, K. Analytical second-order geometrical derivatives of energy for the self-consistent-charge density-functional tight-binding method. J. Chem. Phys. 2004, 121, 5163–5170. [Google Scholar] [CrossRef]
- Huang, P.; Zhu, H.; Jing, L.; Zhao, Y.; Gao, X. Graphene covalently binding aryl groups: Conductivity increases rather than decreases. ACS Nano 2011, 5, 7945–7949. [Google Scholar] [CrossRef]
- Erni, R.; Rossell, M.D.; Nguyen, M.T.; Blankenburg, S.; Passerone, D.; Hartel, P.; Alem, N.; Erickson, K.; Gannett, W.; Zettl, A. Stability and dynamics of small molecules trapped on graphene. Phys. Rev. B 2010, 82, 165443. [Google Scholar] [CrossRef]
- Du, A.; Chen, Y.; Zhu, Z.; Lu, G.; Smith, S.C. C-BN single-walled nanotubes from hybrid connection of BN/C nanoribbons: Prediction by ab initio density functional calculations. J. Am. Chem. Soc. 2009, 131, 1682–1683. [Google Scholar] [CrossRef]
- Yu, Q.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.; Su, Z.; Cao, H.; Liu, Z.; Pandey, D.; Wei, D.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443–449. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Louie, S.G. Electronic transport in polycrystalline graphene. Nat. Mater. 2010, 9, 806–809. [Google Scholar] [CrossRef]
- Guo, H.; Lu, N.; Dai, J.; Wu, X.; Zeng, X.C. Phosphorene nanoribbons, phosphorus nanotubes, and van der Waals multilayers. J. Phys. Chem. C 2014, 118, 14051–14059. [Google Scholar] [CrossRef]
- Bissett, M.A.; Tsuji, M.; Ago, H. Strain engineering the properties of graphene and other two-dimensional crystals. Phys. Chem. Chem. Phys. 2014, 16, 11124–11138. [Google Scholar] [CrossRef]
- Castellanos-Gomez, A.; Singh, V.; van der Zant, H.S.J.; Steele, G.A. Mechanics of freely-suspended ultrathin layered materials. Ann. Phys. 2015, 527, 27–44. [Google Scholar] [CrossRef]
- Medrano Sandonas, L.; Gutierrez, R.; Pecchia, A.; Dianat, A.; Cuniberti, G. Thermoelectric properties of functionalized graphene grain boundaries. J. Self-Assem. Mol. Electron. 2015, 3, 1–20. [Google Scholar]
- Medrano Sandonas, L.; Teich, D.; Gutierrez, R.; Lorenz, T.; Pecchia, A.; Seifert, G.; Cuniberti, G. Anisotropic thermoelectric response in two-dimensional puckered structures. J. Phys. Chem. C 2016, 120, 18841–18849. [Google Scholar] [CrossRef]
- Medrano Sandonas, L.; Gutierrez, R.; Pecchia, A.; Seifert, G.; Cuniberti, G. Tuning quantum electron and phonon transport in two-dimensional materials by strain engineering: A Green’s function based study. Phys. Chem. Chem. Phys. 2017, 19, 1487–1495. [Google Scholar] [CrossRef]
- Medrano Sandonas, L.; Sevincli, H.; Gutierrez, R.; Cuniberti, G. First-principle-based phonon transport properties of nanoscale graphene grain boundaries. Adv. Sci. 2018, 5, 1700365. [Google Scholar] [CrossRef]
- Medrano Sandonas, L.; Cuba-Supanta, G.; Gutierrez, R.; Landauro, C.V.; Rojas-Tapia, J.; Cuniberti, G. Doping engineering of thermoelectric transport in BNC heteronanotubes. Phys. Chem. Chem. Phys. 2019, 21, 1904–1911. [Google Scholar] [CrossRef]
- Medrano Sandonas, L.; Rodriguez Mendez, A.; Gutierrez, R.; Ugalde, J.M.; Mujica, V.; Cuniberti, G. Selective transmission of phonons in molecular junctions with nanoscopic thermal baths. J. Phys. Chem. C 2019, 123, 9680–9687. [Google Scholar] [CrossRef]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tomanek, D.; Ye, P.D. Phosphorene: An unexplored 2D semiconductor with a high hole mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef]
- Zhu, Z.; Guan, J.; Liu, D.; Tománek, D. Designing isoelectronic counterparts to layered group V semiconductors. ACS Nano 2015, 9, 8284–8290. [Google Scholar] [CrossRef]
- Fei, R.; Li, W.; Li, J.; Yang, L. Giant piezoelectricity of monolayer group IV monochalcogenides: SnSe, SnS, GeSe, and GeS. Appl. Phys. Lett. 2015, 107, 173104. [Google Scholar] [CrossRef]
- Shengli, Z.; Zhong, Y.; Yafei, L.; Zhongfang, C.; Haibo, Z. Atomically thin arsenene and antimonene: Semimetal-semiconductor and indirect-direct band-gap transitions. Angew. Chem. Inter. Ed. 2015, 54, 3112–3115. [Google Scholar]
- Jain, A.; McGaughey, A.J.H. Strongly anisotropic in-plane thermal transport in single-layer black phosphorene. Sci. Rep. 2015, 5, 8501. [Google Scholar] [CrossRef]
- Qin, G.; Yan, Q.B.; Qin, Z.; Yue, S.Y.; Hu, M.; Su, G. Anisotropic intrinsic lattice thermal conductivity of phosphorene from first principles. Phys. Chem. Chem. Phys. 2015, 17, 4854–4858. [Google Scholar] [CrossRef]
- Kamal, C.; Ezawa, M. Arsenene: Two-dimensional buckled and puckered honeycomb arsenic systems. Phys. Rev. B 2015, 91, 085423. [Google Scholar] [CrossRef]
- Zeraati, M.; Vaez Allaei, S.M.; Abdolhosseini Sarsari, I.; Pourfath, M.; Donadio, D. Highly anisotropic thermal conductivity of arsenene: An ab-initio study. Phys. Rev. B 2016, 93, 085424. [Google Scholar] [CrossRef]
- Kamal, C.; Chakrabarti, A.; Ezawa, M. Direct band gaps in group IV-VI monolayer materials: Binary counterparts of phosphorene. Phys. Rev. B 2016, 93, 125428. [Google Scholar] [CrossRef]
- Liu, T.H.; Chang, C.C. Anisotropic thermal transport in phosphorene: Effects of crystal orientation. Nanoscale 2015, 7, 10648–10654. [Google Scholar] [CrossRef]
- Fei, R.; Faghaninia, A.; Soklaski, R.; Yan, J.A.; Lo, C.; Yang, L. Enhanced thermoelectric efficiency via orthogonal electrical and thermal conductances in phosphorene. Nano Lett. 2014, 14, 6393–6399. [Google Scholar] [CrossRef]
- Stephan, O.; Ajayan, P.M.; Colliex, C.; Redlich, P.; Lambert, J.M.; Bernier, P.; Lefin, P. Doping Graphitic and Carbon Nanotube Structures with Boron and Nitrogen. Science 1994, 266, 1683–1685. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C. Mechanical properties of hybrid boron nitride–carbon nanotubes. J. Phys. D Appl. Phys. 2016, 49, 155305. [Google Scholar] [CrossRef]
- Zhong, R.L.; Xu, H.L.; Su, Z.M. Connecting effect on the first hyperpolarizability of armchair carbon-boron-nitride heteronanotubes: Pattern versus proportion. Phys. Chem. Chem. Phys. 2016, 18, 13954–13959. [Google Scholar] [CrossRef]
- Alam, H.; Ramakrishna, S. A review on the enhancement of figure of merit from bulk to nano-thermoelectric materials. Nano Energy 2013, 2, 190–212. [Google Scholar] [CrossRef]
- Frauenheim, T.; Seifert, G.; Elsterner, M.; Hajnal, Z.; Jungnickel, G.; Porezag, D.; Suhai, S.; Scholz, R. A Self-consistent charge density-functional based tight-binding method for predictive materials simulations in physics, chemistry and biology. Phys. Status Solidi B 2000, 217, 41–62. [Google Scholar] [CrossRef]
- Seifert, G. Tight-binding density functional theory: An approximate Kohn-Sham DFT scheme. J. Phys. Chem. A 2007, 111, 5609–5613. [Google Scholar] [CrossRef]
- Machado, M.; Kar, T.; Piquini, P. The influence of the stacking orientation of C and BN stripes in the structure, energetics, and electronic properties of BC2N nanotubes. Nanotechnology 2011, 22, 205706. [Google Scholar] [CrossRef]
- Carvalho, A.C.M.; Bezerra, C.G.; Lawlor, J.A.; Ferreira, M.S. Density of states of helically symmetric boron carbon nitride nanotubes. J. Phys. Condens. Matter 2014, 26, 015303. [Google Scholar] [CrossRef]
- Li, Q.; Duchemin, I.; Xiong, S.; Solomon, G.C.; Donadio, D. Mechanical tuning of thermal transport in a molecular junction. J. Phys. Chem. C 2015, 119, 24636–24642. [Google Scholar] [CrossRef]
- Sasikumar, K.; Keblinski, P. Effect of chain conformation in the phonon transport across a Si-polyethylene single-molecule covalent junction. J. Appl. Phys. 2011, 109, 114307. [Google Scholar] [CrossRef]
- Lyeo, H.K.; Cahill, D.G. Thermal conductance of interfaces between highly dissimilar materials. Phys. Rev. B 2006, 73, 144301. [Google Scholar] [CrossRef]
- Nika, D.L.; Pokatilov, E.P.; Balandin, A.A.; Fomin, V.M.; Rastelli, A.; Schmidt, O.G. Reduction of lattice thermal conductivity in one-dimensional quantum-dot superlattices due to phonon filtering. Phys. Rev. B 2011, 84, 165415. [Google Scholar] [CrossRef]
- Li, X.; Yang, R. Effect of lattice mismatch on phonon transmission and interface thermal conductance across dissimilar material interfaces. Phys. Rev. B 2012, 86, 054305. [Google Scholar] [CrossRef]
- Luckyanova, M.N.; Garg, J.; Esfarjani, K.; Jandl, A.; Bulsara, M.T.; Schmidt, A.J.; Minnich, A.J.; Chen, S.; Dresselhaus, M.S.; Ren, Z.; et al. Coherent phonon heat conduction in superlattices. Science 2012, 338, 936–939. [Google Scholar] [CrossRef]
- Medrano Sandonas, L.; Croy, A.; Gutierrez, R.; Cuniberti, G. Atomistic framework for time-dependent thermal transport. J. Phys. Chem. C 2018, 122, 21062–21068. [Google Scholar] [CrossRef]
- Ulrich, W. Quantum Dissipative Systems, 2nd ed.; Series in Modern Condensed Matter Physics; World Scientific Publishing Company: Singapore, 1999. [Google Scholar]
- De Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Ritschel, G.; Eisfeld, A. Analytic representations of bath correlation functions for ohmic and superohmic spectral densities using simple poles. J. Chem. Phys. 2014, 141, 094101. [Google Scholar] [CrossRef] [PubMed]
- Meier, C.; Tannor, D.J. Non-Markovian evolution of the density operator in the presence of strong laser fields. J. Chem. Phys. 1999, 111, 3365. [Google Scholar] [CrossRef]
- Hu, J.; Xu, R.X.; Yan, Y. Communication: Padé spectrum decomposition of Fermi function and Bose function. J. Chem. Phys. 2010, 133, 101106. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian—09; Revision E.01; Gaussian. Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Pecchia, A.; Di Carlo, A.; Gagliardi, A.; Sanna, S.; Frauenheim, T.; Gutierrez, R. Incoherent electron-phonon scattering in octanethiols. Nano Lett. 2004, 4, 2109–2114. [Google Scholar] [CrossRef]
- Penazzi, G.; Pecchia, A.; Gupta, V.; Frauenheim, T. A self energy model of dephasing in molecular junctions. J. Phys. Chem. C 2016, 120, 16383–16392. [Google Scholar] [CrossRef]
- Markussen, T.; Palsgaard, M.; Stradi, D.; Gunst, T.; Brandbyge, M.; Stokbro, K. Electron-phonon scattering from Green’s function transport combined with molecular dynamics: Applications to mobility predictions. Phys. Rev. B 2017, 95, 245210. [Google Scholar] [CrossRef]
- Frederiksen, T.; Paulsson, M.; Brandbyge, M.; Jauho, A.P. Inelastic transport theory from first principles: Methodology and application to nanoscale devices. Phys. Rev. B 2007, 75, 205413. [Google Scholar] [CrossRef]
- Viljas, J.K.; Cuevas, J.C.; Pauly, F.; Häfner, M. Electron-vibration interaction in transport through atomic gold wires. Phys. Rev. B 2005, 72, 245415. [Google Scholar] [CrossRef]
| Systems | Transport Direction | Other Works (ZZ, AC) [Å] | |
|---|---|---|---|
| ZZ [Å] | AC [Å] | ||
| Phosphorene | 3.49 | 4.34 | (3.28, 4.43) [126] (3.32, 4.58) [127] |
| Arsenene | 3.81 | 4.75 | (3.68, 4.77) [128] (3.69, 4.77) [129] |
| SnS monolayer | 3.93 | 4.51 | (4.03, 4.26) [124] (4.01, 4.35) [130] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medrano Sandonas, L.; Gutierrez, R.; Pecchia, A.; Croy, A.; Cuniberti, G. Quantum Phonon Transport in Nanomaterials: Combining Atomistic with Non-Equilibrium Green’s Function Techniques. Entropy 2019, 21, 735. https://doi.org/10.3390/e21080735
Medrano Sandonas L, Gutierrez R, Pecchia A, Croy A, Cuniberti G. Quantum Phonon Transport in Nanomaterials: Combining Atomistic with Non-Equilibrium Green’s Function Techniques. Entropy. 2019; 21(8):735. https://doi.org/10.3390/e21080735
Chicago/Turabian StyleMedrano Sandonas, Leonardo, Rafael Gutierrez, Alessandro Pecchia, Alexander Croy, and Gianaurelio Cuniberti. 2019. "Quantum Phonon Transport in Nanomaterials: Combining Atomistic with Non-Equilibrium Green’s Function Techniques" Entropy 21, no. 8: 735. https://doi.org/10.3390/e21080735
APA StyleMedrano Sandonas, L., Gutierrez, R., Pecchia, A., Croy, A., & Cuniberti, G. (2019). Quantum Phonon Transport in Nanomaterials: Combining Atomistic with Non-Equilibrium Green’s Function Techniques. Entropy, 21(8), 735. https://doi.org/10.3390/e21080735