Symmetry Properties of Mixed and Heat Photo-Assisted Noise in the Quantum Hall Regime
Abstract
1. Introduction
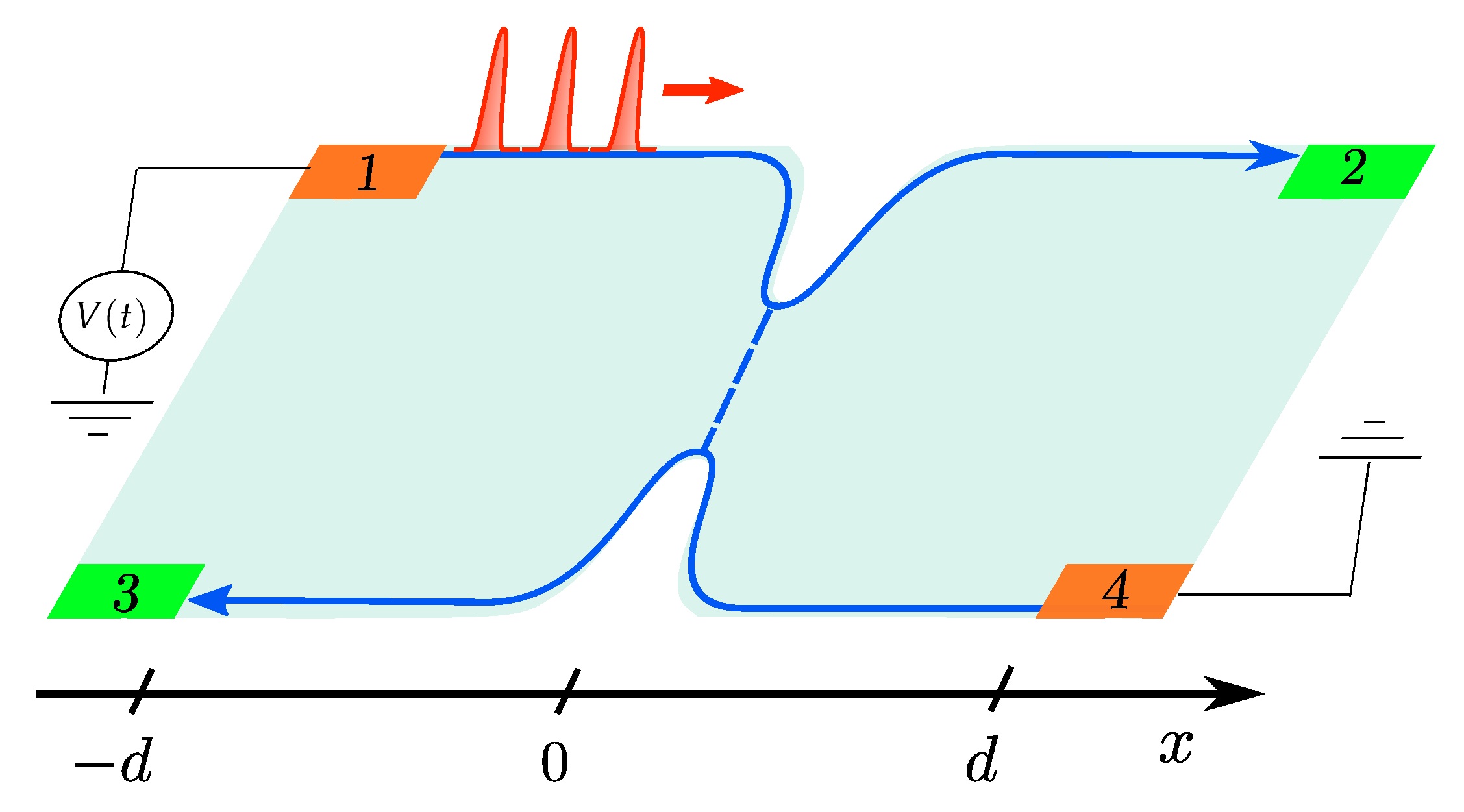
2. Model
3. Charge Current
4. Heat Current
5. Mixed Noise and Heat Noise
6. Results
6.1. Heat Current
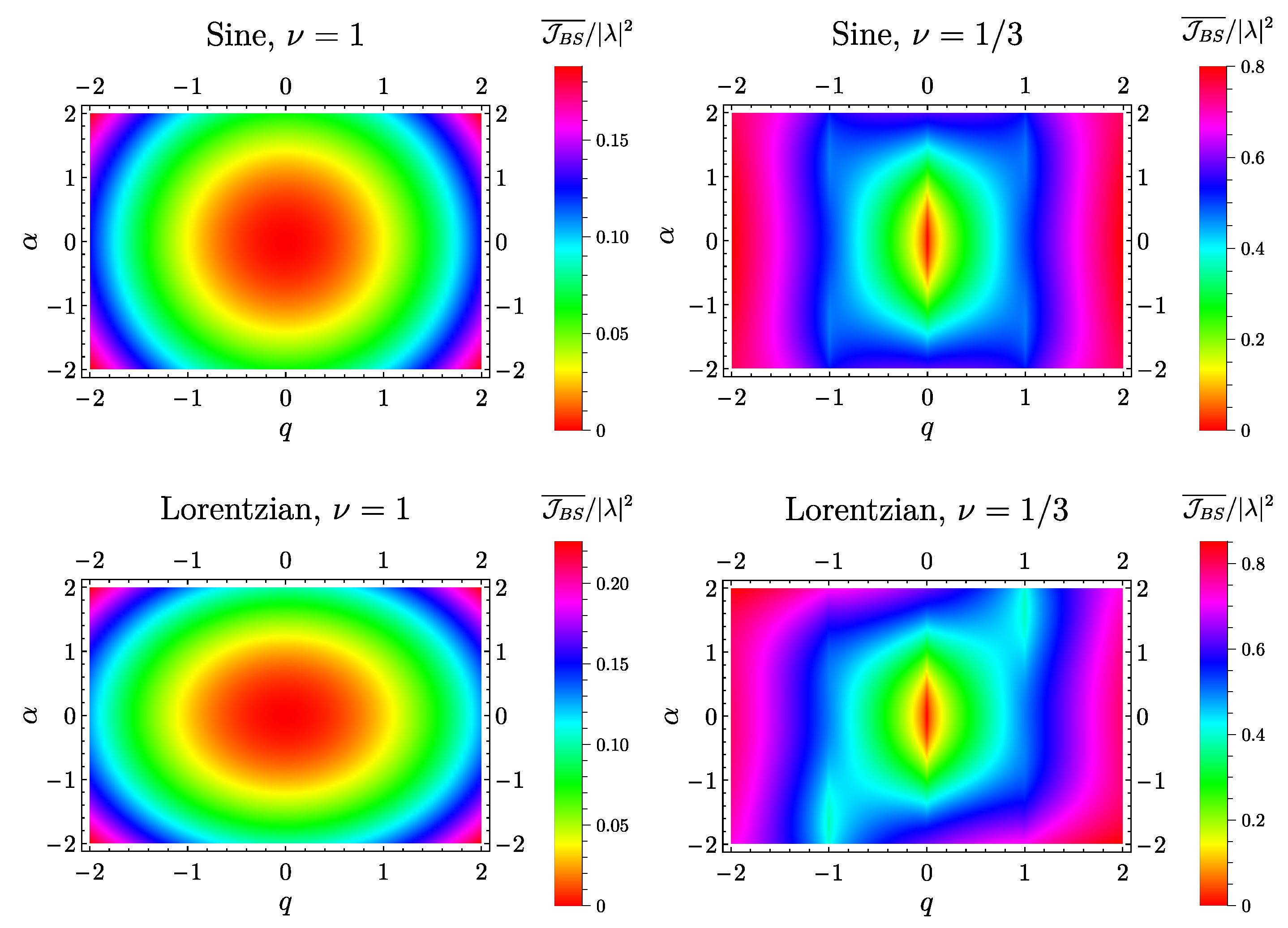
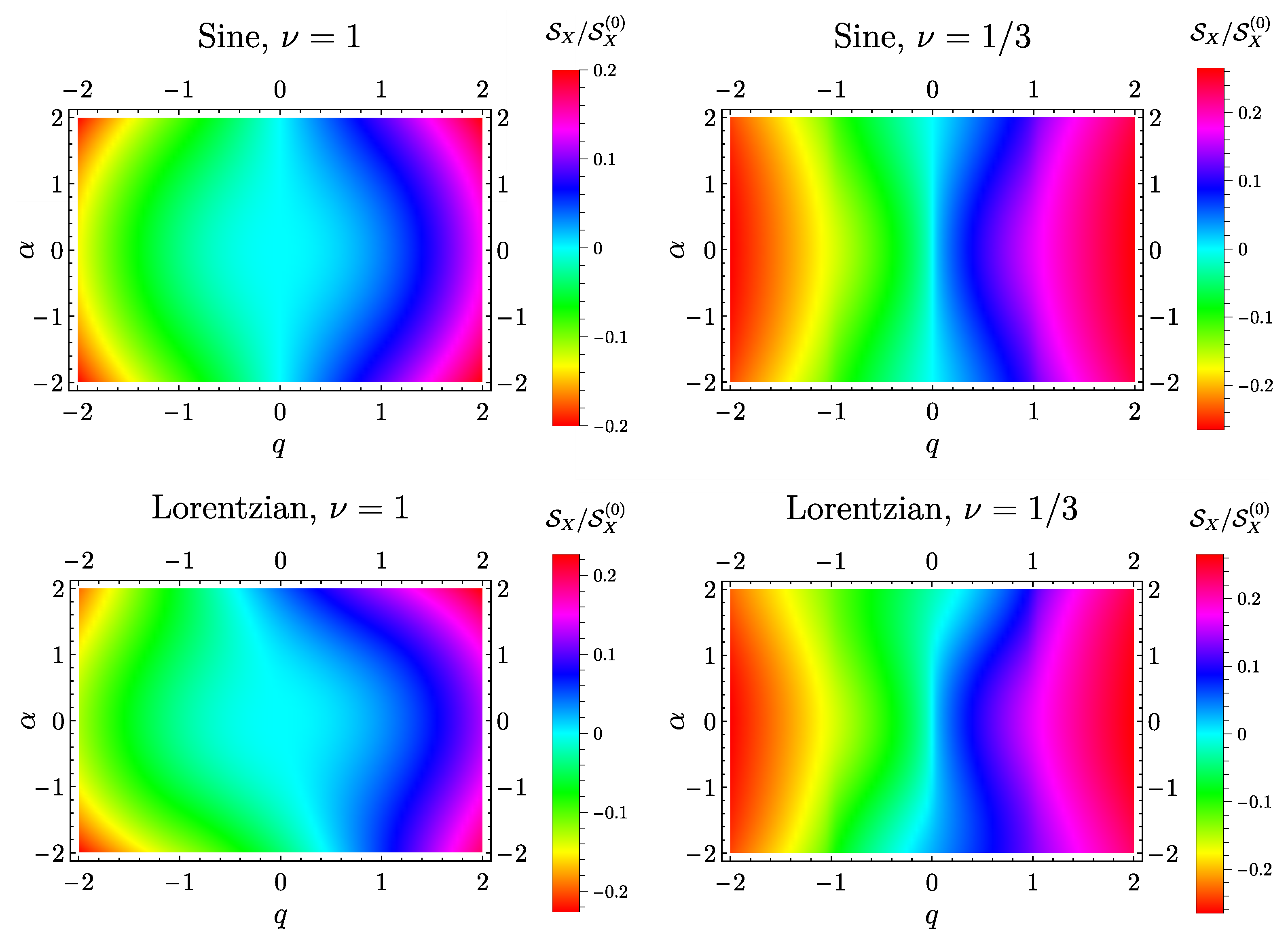
6.2. Mixed Noise
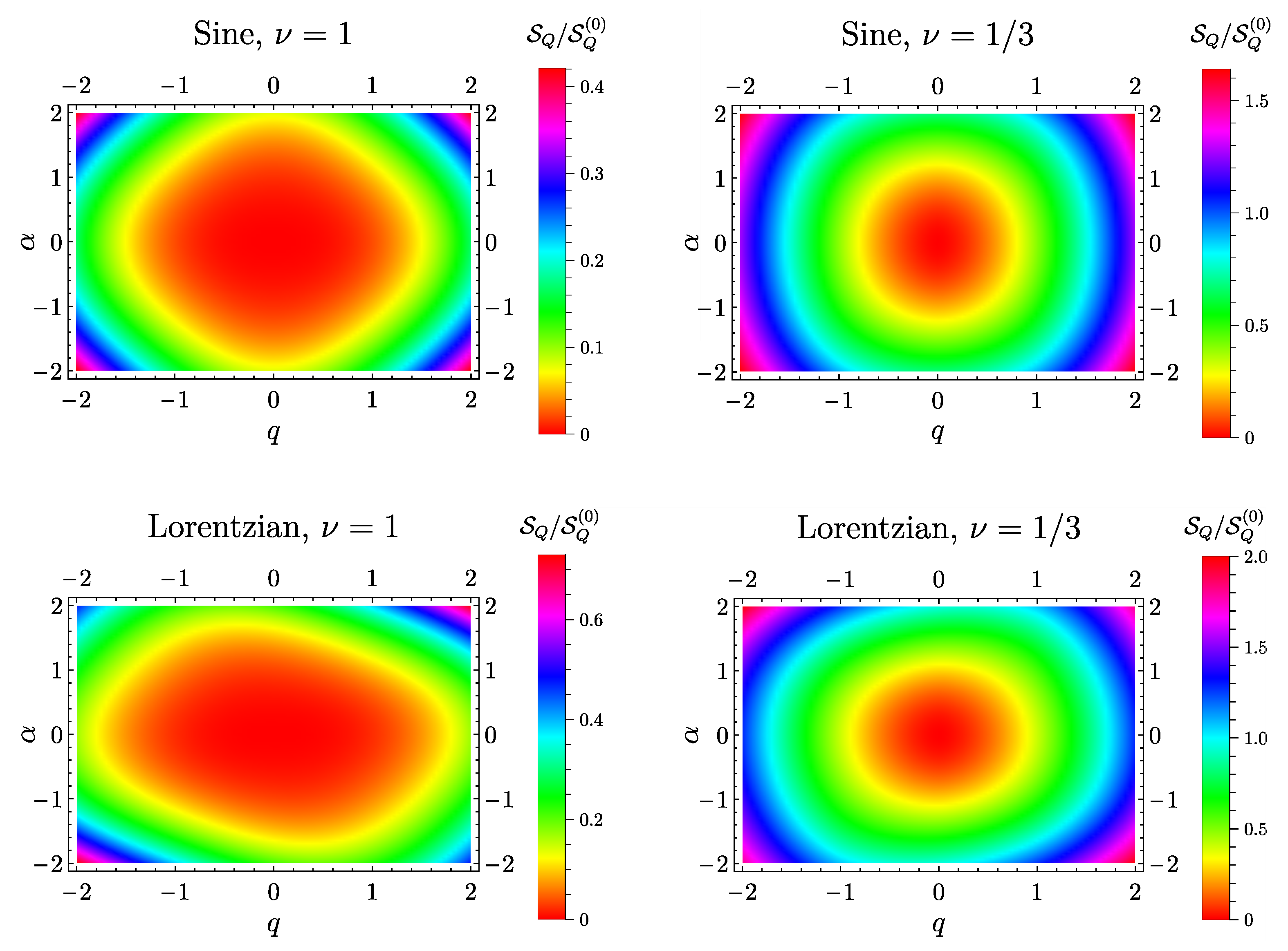
6.3. Heat Noise
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FQH | Fractional Quantum Hall |
| QPC | Quantum Point Contact |
| EQO | Electron Quantum Optics |
References
- Grenier, C.; Hervé, R.; Fève, G.; Degiovanni, P. Electron quantum optics in quantum Hall edge channels. Mod. Phys. Lett. B 2011, 25, 1053. [Google Scholar] [CrossRef]
- Bocquillon, E.; Freulon, V.; Parmentier, F.D.; Berroir, J.-M.; Plaçais, B.; Wahl, C.; Rech, J.; Jonckheere, T.; Martin, T.; Grenier, C.; et al. Electron quantum optics in ballistic chiral conductors. Ann. Phys. 2014, 526, 1. [Google Scholar] [CrossRef]
- Bäuerle, C.; Glattli, D.C.; Meunier, T.; Portier, F.; Roche, P.; Roulleau, P.; Takada, S.; Waintal, X. Coherent control of single electrons: A review of current progress. Rep. Prog. Phys. 2018, 81, 056503. [Google Scholar] [CrossRef] [PubMed]
- Fève, G.; Mahé, A.; Berroir, J.-M.; Kontos, T.; Plaçais, B.; Glattli, D.C.; Cavanna, A.; Etienne, B.; Jin, Y. An on-demand coherent single-electron source. Science 2007, 316, 1169. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, D.; Rech, J.; Jonckheere, T.; Martin, T. Single quasiparticle and electron emitter in the fractional quantum Hall regime. Phys. Rev. B 2015, 91, 205409. [Google Scholar] [CrossRef]
- Büttiker, M.; Thomas, H.; Prêtre, A. Mesoscopic capacitors. Phys. Lett. A 1993, 180, 364. [Google Scholar] [CrossRef]
- Moskalets, M.; Samuelsson, P.; Büttiker, M. Quantized Dynamics of a Coherent Capacitor. Phys. Rev. Lett. 2008, 100, 086601. [Google Scholar] [CrossRef]
- Ludovico, M.L.; Arrachea, L.; Moskalets, M.; Sanchez, D. Periodic energy transport and entropy production in quantum electronics. Entropy 2016, 18, 419. [Google Scholar] [CrossRef]
- Alomar, M.I.; Lim, J.S.; Sanchez, D. Coulomb-blockade effect in nonlinear mesoscopic capacitors. Phys. Rev. B 2016, 94, 165425. [Google Scholar] [CrossRef]
- Levitov, L.S.; Lee, H.W.; Lesovik, G.B. Electron counting statistics and coherent states of electric current. J. Math. Phys. 1996, 37, 4845. [Google Scholar] [CrossRef]
- Ivanov, D.; Lee, H.W.; Levitov, L.S. Coherent states of alternating current. Phys. Rev. B 1997, 56, 6839. [Google Scholar] [CrossRef]
- Keeling, J.; Klich, I.; Levitov, L.S. Minimal Excitation States of Electrons in One-Dimensional Wires. Phys. Rev. Lett. 2006, 97, 116403. [Google Scholar] [CrossRef]
- Glattli, D.C.; Roulleau, P. Levitons for electron quantum optics. Phys. Status Solidi B 2017, 254, 1600650. [Google Scholar] [CrossRef]
- Dubois, J.; Jullien, T.; Portier, F.; Roche, P.; Cavanna, A.; Jin, Y.; Wegscheider, W.; Roulleau, P.; Glattli, D.C. Minimal excitation states for electron quantum optics using levitons. Nature 2013, 502, 659. [Google Scholar] [CrossRef]
- Crépieux, A.; Devillard, P.; Martin, T. Photoassisted current and shot noise in the fractional quantum Hall effect. Phys. Rev. B 2004, 69, 205302. [Google Scholar] [CrossRef]
- Dubois, J.; Jullien, T.; Grenier, C.; Degiovanni, P.; Roulleau, P.; Glattli, D.C. Integer and fractional charge Lorentzian voltage pulses analyzed in the framework of photon-assisted shot noise. Phys. Rev. B 2013, 88, 085301. [Google Scholar] [CrossRef]
- Rech, J.; Ferraro, D.; Jonckheere, T.; Vannucci, L.; Sassetti, M.; Martin, T. Minimal Excitations in the Fractional Quantum Hall Regime. Phys. Rev. Lett. 2017, 118, 076801. [Google Scholar] [CrossRef]
- Acciai, M.; Carrega, M.; Rech, J.; Jonckheere, T.; Martin, T.; Sassetti, M. Probing interactions via non-equilibrium momentum distribution and noise in integer quantum Hall systems at ν = 2. Phys. Rev. B 2018, 98, 035426. [Google Scholar] [CrossRef]
- Ronetti, F.; Vannucci, L.; Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T.; Sassetti, M. Crystallization of levitons in the fractional quantum Hall regime. Phys. Rev. B 2018, 98, 075401. [Google Scholar] [CrossRef]
- Ferraro, D.; Ronetti, F.; Vannucci, L.; Acciai, M.; Rech, J.; Jockheere, T.; Martin, T.; Sassetti, M. Hong-Ou-Mandel characterization of multiply charged Levitons. Eur. Phys. J. Spec. Top. 2018, 227, 1345. [Google Scholar] [CrossRef]
- Hanbury-Brown, R.; Twiss, R.Q. Correlation between photons in two coherent beams of light. Nature 1956, 177, 27. [Google Scholar] [CrossRef]
- Bocquillon, E.; Parmentier, F.D.; Grenier, C.; Berroir, J.-M.; Degiovanni, P.; Glattli, D.C.; Plaçais, B.; Cavanna, A.; Jin, Y.; Fève, G. Electron Quantum Optics: Partitioning Electrons One by One. Phys. Rev. Lett. 2012, 108, 196803. [Google Scholar] [CrossRef]
- Calzona, A.; Acciai, M.; Carrega, M.; Cavaliere, F.; Sassetti, M. Time-resolved energy dynamics after single electron injection into an interacting helical liquid. Phys. Rev. B 2016, 94, 035404. [Google Scholar] [CrossRef]
- Giazotto, F.; Heikkilä, T.T.; Luukanen, A.; Savin, A.M.; Pekola, J.P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 2006, 78, 217. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum Thermodynamics. Contemp. Phys. 2016, 57, 545. [Google Scholar] [CrossRef]
- Sànchez, R.; Sothmann, B.; Jordan, A.N. Chiral Thermoelectrics with Quantum Hall Edge States. Phys. Rev. Lett. 2015, 114, 146801. [Google Scholar] [CrossRef]
- Sànchez, R.; Sothmann, B.; Jordan, A.N. Heat diode and engine based on quantum Hall edge states. New J. Phys. 2015, 17, 075006. [Google Scholar] [CrossRef]
- Samuelsson, P.; Kheradsoud, S.; Sothmann, B. Optimal Quantum Interference Thermoelectric Heat Engine with Edge States. Phys. Rev. Lett. 2017, 118, 256801. [Google Scholar] [CrossRef]
- Thierschmann, H.; Sànchez, R.; Sothmann, B.; Arnold, F.; Heyn, C.; Hansen, W.; Buhmann, H.; Molenkamp, L.W. Three terminal energy harvester with coupled quantum dots. Nat. Nanotechnol. 2015, 10, 854. [Google Scholar] [CrossRef]
- Juergens, S.; Haupt, F.; Moskalets, M.; Splettstoesser, J. Thermoelectric performance of a driven double quantum dot. Phys. Rev. B 2013, 87, 245423. [Google Scholar] [CrossRef]
- Erdman, P.A.; Mazza, F.; Bosisio, R.; Benenti, G.; Fazio, R.; Taddei, F. Thermoelectric properties of an interacting quantum dot based heat engine. Phys. Rev. B 2017, 95, 245432. [Google Scholar] [CrossRef]
- Mazza, F.; Bosisio, R.; Benenti, G.; Giovannetti, V.; Fazio, R.; Taddei, F. Thermoelectric efficiency of three terminal quantum thermal machines. New J. Phys. 2014, 16, 085001. [Google Scholar] [CrossRef]
- Ferraro, D.; Campisi, M.; Andolina, G.M.; Pellegrini, V.; Polini, M. High-Power Collective Charging of a Solid-State Quantum Battery. Phys. Rev. Lett. 2018, 120, 117702. [Google Scholar] [CrossRef]
- Vannucci, L.; Ronetti, F.; Dolcetto, G.; Carrega, M.; Sassetti, M. Interference-induced thermoelectric switching and heat rectification in quantum Hall junctions. Phys. Rev. B 2015, 92, 075446. [Google Scholar] [CrossRef]
- Ronetti, F.; Vannucci, L.; Dolcetto, G.; Carrega, M.; Sassetti, M. Spin-thermoelectric transport induced by interactions and spin-flip processes in two-dimensional, topological insulators. Phys. Rev. B 2016, 93, 165414. [Google Scholar] [CrossRef]
- Ronetti, F.; Carrega, M.; Ferraro, D.; Rech, J.; Jonckheere, T.; Martin, T.; Sassetti, M. Polarized heat current generated by quantum pumping in two-dimensional topological insulators. Phys. Rev. B 2017, 95, 115412. [Google Scholar] [CrossRef]
- Ludovico, M.F.; Lim, J.S.; Moskalets, M.; Arrachea, L.; Sànchez, D. Dynamical energy transfer in ac-driven quantum systems. Phys. Rev. B 2014, 89, 161306(R). [Google Scholar] [CrossRef]
- Ludovico, M.F.; Moskalets, M.; Sànchez, D.; Arrachea, L. Dynamics of energy transport and entropy production in ac driven quantum electron systems. Phys. Rev. B 2016, 94, 035436. [Google Scholar] [CrossRef]
- Ludovico, M.F.; Arrachea, L.; Moskalets, M.; Sànchez, D. Probing the energy reactance with adiabatically driven quantum dots. Phys. Rev. B 2018, 97, 041416(R). [Google Scholar] [CrossRef]
- Erlingsson, S.I.; Manolescu, A.; Nemnes, G.A.; Bandarson, J.H.; Sanchez, D. Reversal of Thermoelectric Current in Tubular Nanowires. Phys. Rev. Lett. 2017, 119, 036804. [Google Scholar] [CrossRef]
- Mazza, F.; Valentini, S.; Bosisio, R.; Benenti, G.; Giovannetti, V.; Fazio, R.; Taddei, F. Separation of heat and charge currents for boosted thermoelectric conversion. Phys. Rev. B 2015, 91, 245435. [Google Scholar] [CrossRef]
- Carrega, M.; Solinas, P.; Braggio, A.; Sassetti, M.; Weiss, U. Functional integral approach to time-dependent heat exchange in open quantum systems: General method and applications. New J. Phys. 2015, 17, 045030. [Google Scholar] [CrossRef]
- Carrega, M.; Solinas, P.; Sassetti, M.; Weiss, U. Energy Exchange in Driven Open Quantum Systems at Strong Coupling. Phys. Rev. Lett. 2016, 116, 240403. [Google Scholar] [CrossRef]
- Moskalets, M.; Haack, G. Heat and charge transport measurements to access single-electron quantum characteristics. Phys. Status Solidi B 2017, 254, 1600616. [Google Scholar] [CrossRef]
- Crépieux, A.; Michelini, F. Mixed, charge and heat noises in thermoelectric nanosystems. J. Phys. Condens. Matter 2014, 27, 015302. [Google Scholar] [CrossRef]
- Crépieux, A.; Michelini, F. Heat-charge mixed noise and thermoelectric efficiency fluctuations. J. Stat. Mech. 2016, 2016, 054015. [Google Scholar] [CrossRef]
- Battista, F.; Haupt, F.; Splettstoesser, J. Correlations between charge and energy current in ac-driven coherent conductors. J. Phys. Conf. Ser. 2014, 568, 052008. [Google Scholar] [CrossRef]
- Battista, F.; Moskalets, M.; Albert, M.; Samuelsson, P. Quantum Heat Fluctuations of Single-Particle Sources. Phys. Rev. Lett. 2013, 110, 126602. [Google Scholar] [CrossRef]
- Battista, F.; Haupt, F.; Splettstoesser, J. Energy and power fluctuations in ac-driven coherent conductors. Phys. Rev. B 2014, 90, 085418. [Google Scholar] [CrossRef]
- Vannucci, L.; Ronetti, F.; Rech, J.; Ferraro, D.; Jonckheere, T.; Martin, T.; Sassetti, M. Minimal excitation states for heat transport in driven quantum Hall systems. Phys. Rev. B 2017, 95, 245415. [Google Scholar] [CrossRef]
- Dashti, N.; Misiorny, M.; Samuelsson, P.; Splettstoesser, J. Probing charge- and heat-current noise by frequency dependent fluctuations in temperature and potential. Phys. Rev. Appl. 2018, 10, 024007. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations. Phys. Rev. Lett. 1983, 50, 1395. [Google Scholar] [CrossRef]
- Vannucci, L.; Ronetti, F.; Ferraro, D.; Rech, J.; Jonckheere, T.; Martin, T.; Sassetti, M. Photoassisted shot noise spectroscopy at fractional filling factor. J. Phys. Conf. Ser. 2018, 969, 012143. [Google Scholar] [CrossRef]
- Wen, X.-G. Topological orders and edge excitations in fractional quantum Hall states. Adv. Phys. 1995, 44, 405. [Google Scholar] [CrossRef]
- Kane, C.L.; Fisher, M.P.A. Nonequilibrium noise and fractional charge in the quantum Hall effect. Phys. Rev. Lett. 1994, 72, 724. [Google Scholar] [CrossRef]
- Kane, C.L.; Fisher, M.P.A. Transport in a one-channel Luttinger liquid. Phys. Rev. Lett. 1992, 68, 1220. [Google Scholar] [CrossRef]
- Kane, C.L.; Fisher, M.P.A. Thermal Transport in a Luttinger Liquid. Phys. Rev. Lett. 1996, 76, 3192. [Google Scholar] [CrossRef]
- Voit, J. One-dimensional Fermi liquids. Rep. Prog. Phys. 1995, 58, 977. [Google Scholar] [CrossRef]
- Von Delft, J.; Schoeller, H. Bosonization for beginners—Refermionization for experts. Ann. Phys. (Leipzig) 1998, 7, 225. [Google Scholar] [CrossRef]
- Ferraro, D.; Braggio, A.; Magnoli, N.; Sassetti, M. Neutral modes’ edge state dynamics through quantum point contacts. New J. Phys. 2010, 12, 013012. [Google Scholar] [CrossRef]
- Ferraro, D.; Ronetti, F.; Rech, J.; Jonckheere, T.; Sassetti, M.; Martin, T. Enhancing photon squeezing one leviton at a time. Phys. Rev. B 2018, 97, 155135. [Google Scholar] [CrossRef]
- Chamon, C.; Freed, D.E.; Kivelson, S.A.; Sondhi, S.L.; Wen, X.-G. Two point-contact interferometer for quantum Hall systems. Phys. Rev. B 1997, 55, 2331. [Google Scholar] [CrossRef]
- Dolcetto, G.; Barbarino, S.; Ferraro, D.; Magnoli, N.; Sassetti, M. Tunneling between helical edge states through extended contacts. Phys. Rev. B 2012, 85, 195138. [Google Scholar] [CrossRef]
- Braggio, A.; Sassetti, M.; Kramer, B. Control of spin in quantum dots with non-Fermi liquid correlations. Phys. Rev. Lett. 2001, 87, 146802. [Google Scholar] [CrossRef]
- Dolcetto, G.; Sassetti, M.; Schmidt, T.L. Edge physics in two-dimensional topological insulators. Riv. Nuovo Cimento 2016, 39, 113. [Google Scholar]
- Ronetti, F.; Vannucci, L.; Ferraro, D.; Jonckheere, T.; Rech, J.; Martin, T.; Sassetti, M. Hong-Ou-Mandel heat noise in the quantum Hall regime. Phys. Rev. B 2019, 99, 205406. [Google Scholar] [CrossRef]
- Kane, C.L.; Fisher, M.P.A. Quantized thermal transport in the fractional quantum hall effect. Phys. Rev. B 1997, 55, 15832. [Google Scholar] [CrossRef]
- Slobodeniuk, A.O.; Levkivskyi, I.P.; Sukhorukov, E.V. Equilibration of quantum Hall edge states by an Ohmic contact. Phys. Rev. B 2013, 88, 165307. [Google Scholar] [CrossRef]
- Blanter, Y.M.; Büttiker, M. Shot noise in mesoscopic conductors. Phys. Rep. 2000, 336, 1. [Google Scholar] [CrossRef]
- Ferraro, D.; Wahl, C.; Rech, J.; Jonckheere, T.; Martin, T. Electronic Hong-Ou-Mandel interferometry in two-dimensional topological insulators. Phys. Rev. B 2014, 89, 075407. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ronetti, F.; Acciai, M.; Ferraro, D.; Rech, J.; Jonckheere, T.; Martin, T.; Sassetti, M. Symmetry Properties of Mixed and Heat Photo-Assisted Noise in the Quantum Hall Regime. Entropy 2019, 21, 730. https://doi.org/10.3390/e21080730
Ronetti F, Acciai M, Ferraro D, Rech J, Jonckheere T, Martin T, Sassetti M. Symmetry Properties of Mixed and Heat Photo-Assisted Noise in the Quantum Hall Regime. Entropy. 2019; 21(8):730. https://doi.org/10.3390/e21080730
Chicago/Turabian StyleRonetti, Flavio, Matteo Acciai, Dario Ferraro, Jérôme Rech, Thibaut Jonckheere, Thierry Martin, and Maura Sassetti. 2019. "Symmetry Properties of Mixed and Heat Photo-Assisted Noise in the Quantum Hall Regime" Entropy 21, no. 8: 730. https://doi.org/10.3390/e21080730
APA StyleRonetti, F., Acciai, M., Ferraro, D., Rech, J., Jonckheere, T., Martin, T., & Sassetti, M. (2019). Symmetry Properties of Mixed and Heat Photo-Assisted Noise in the Quantum Hall Regime. Entropy, 21(8), 730. https://doi.org/10.3390/e21080730




