Generalized Master Equation Approach to Time-Dependent Many-Body Transport
Abstract
1. Introduction
2. Formalism
2.1. Generalized Master Equation for Hybrid Systems
2.2. ‘Hybrid’ States and Diagonalization Procedure
2.3. Numerical Implementation and Observables
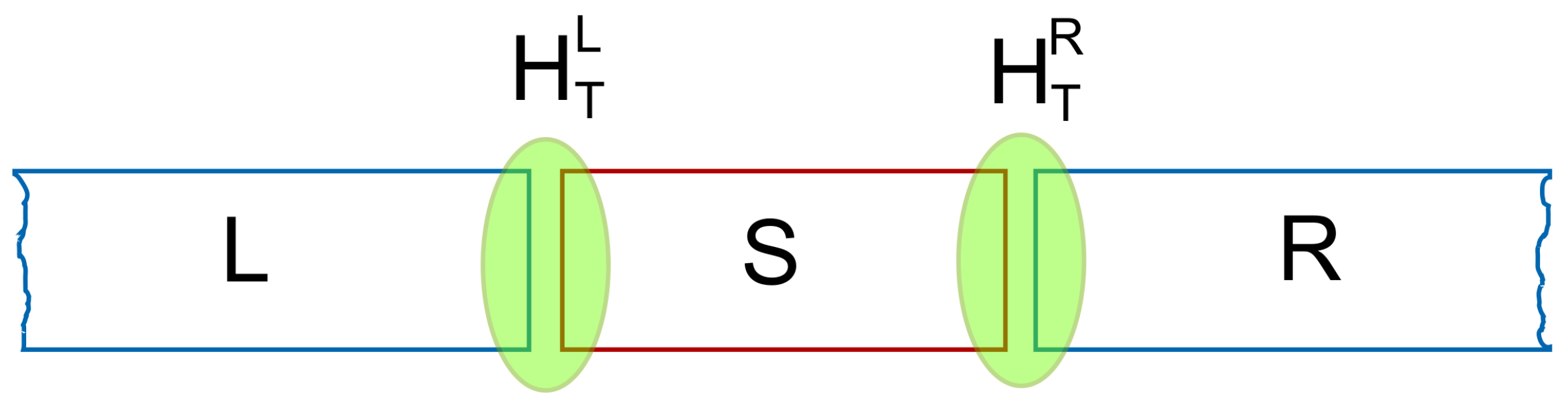
2.4. Coupling between Leads and Central System
3. Many-Body Effects in the Transient Regime
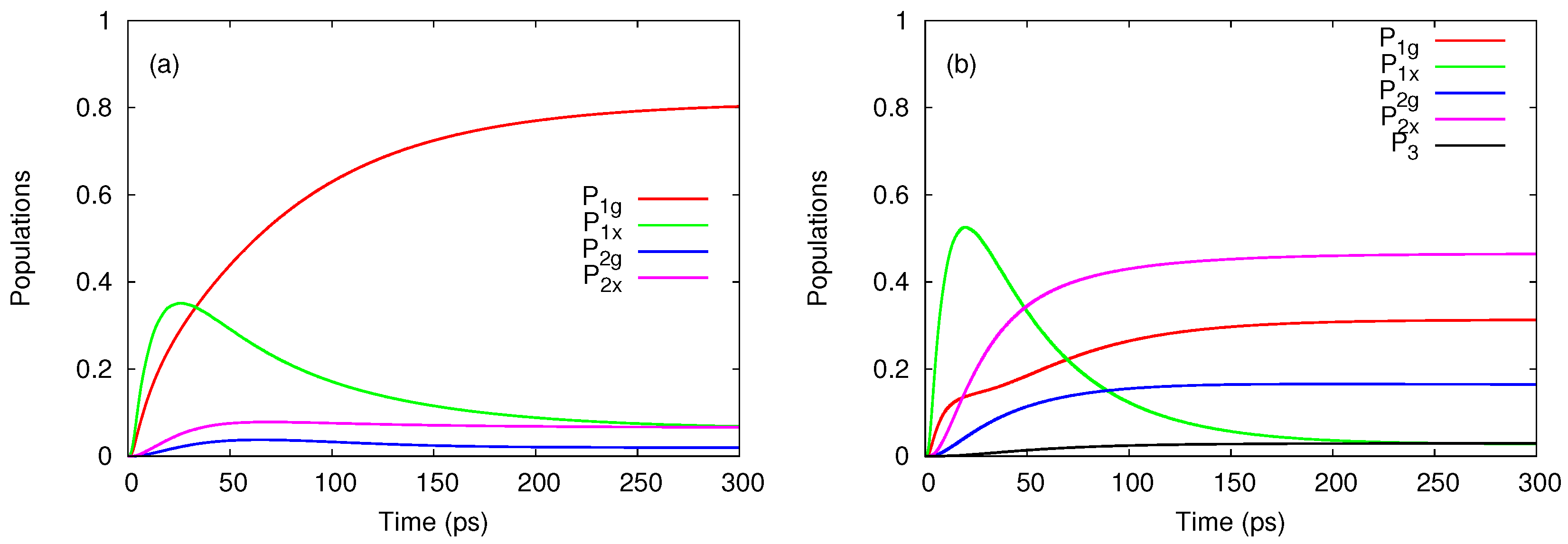
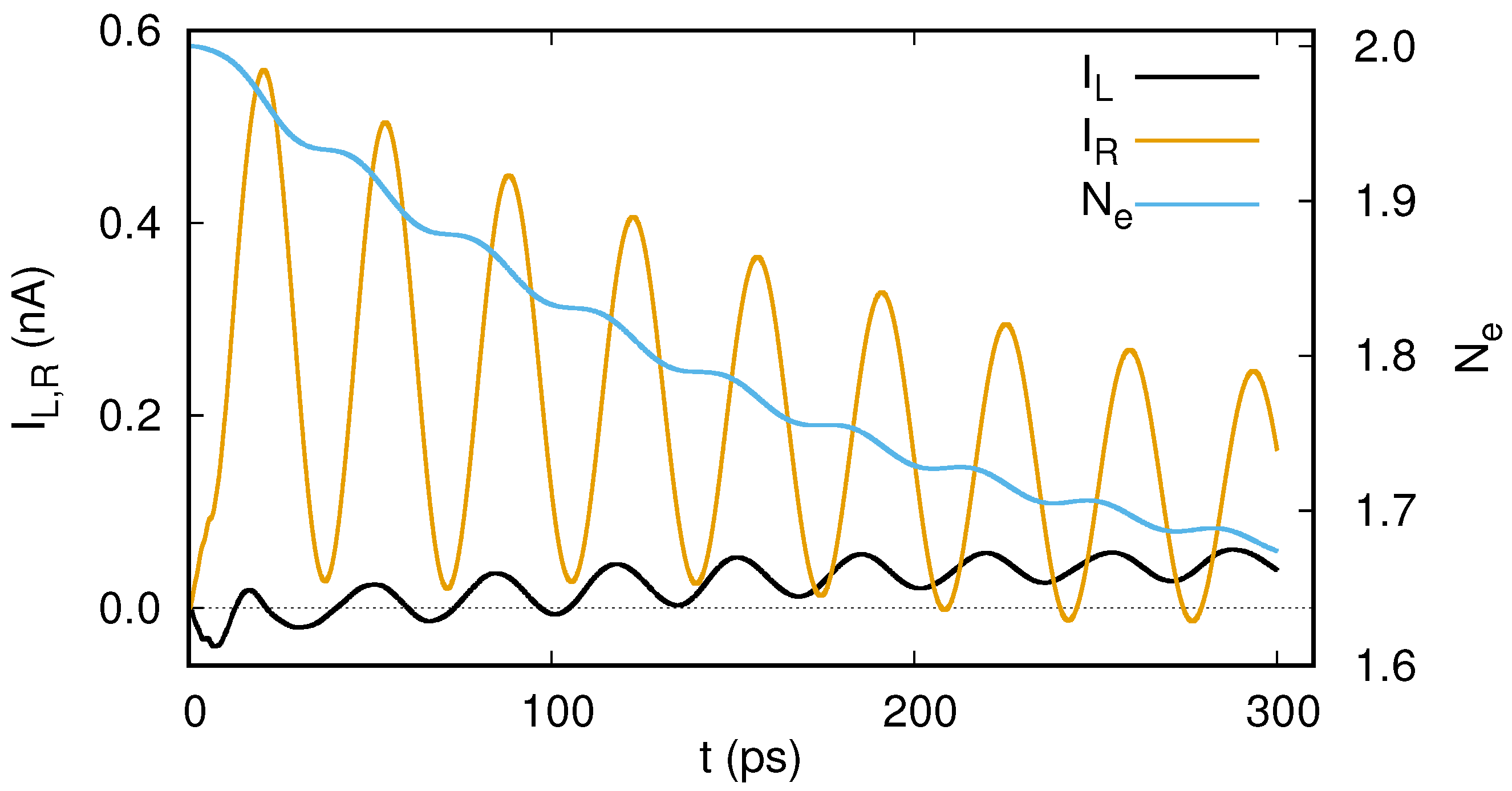
3.1. Transient Charging of Excited States
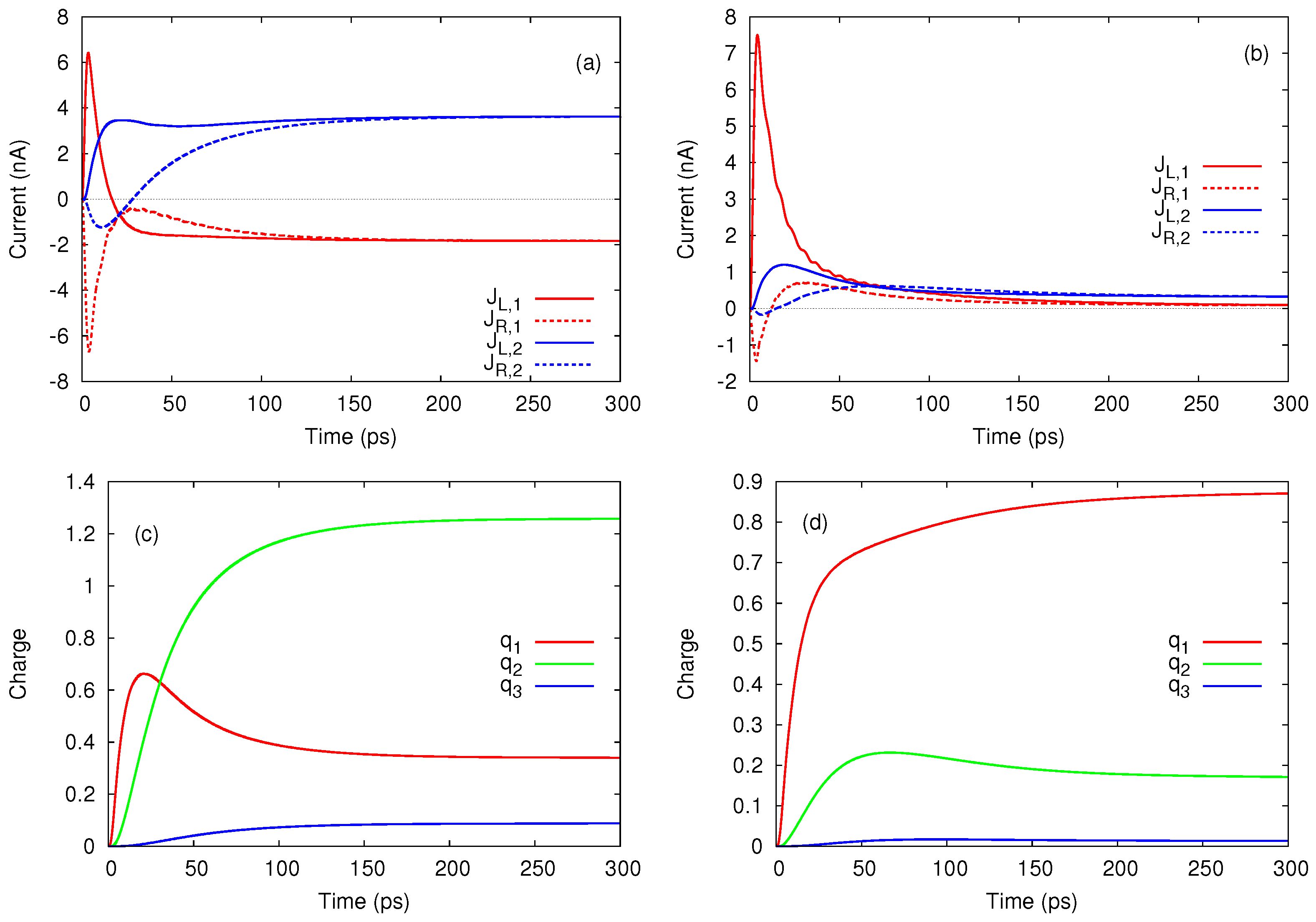
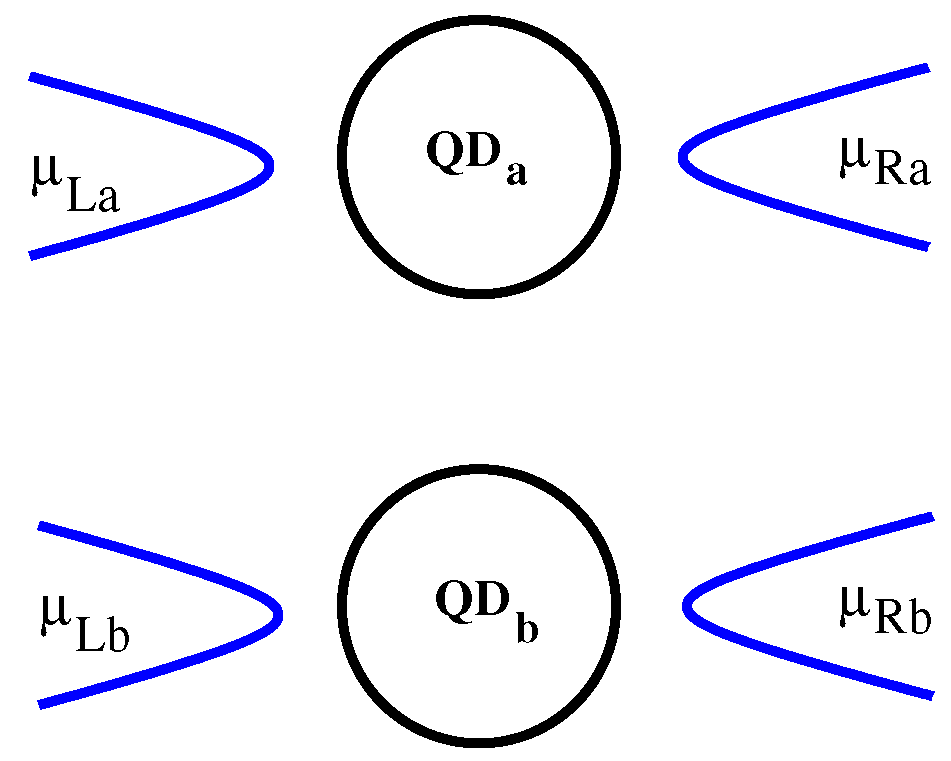
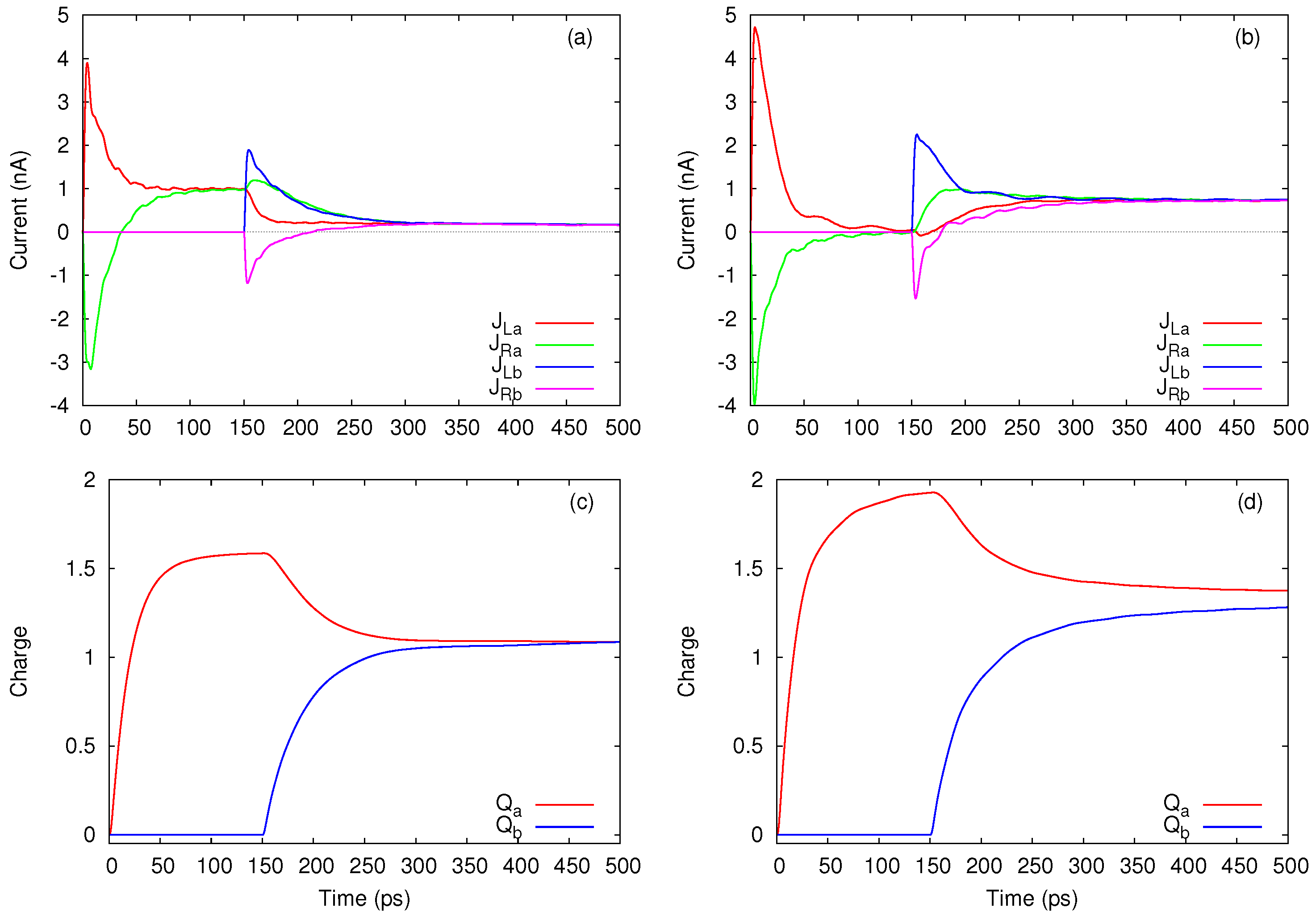
3.2. Coulomb Switching of Transport in Parallel Quantum Dots
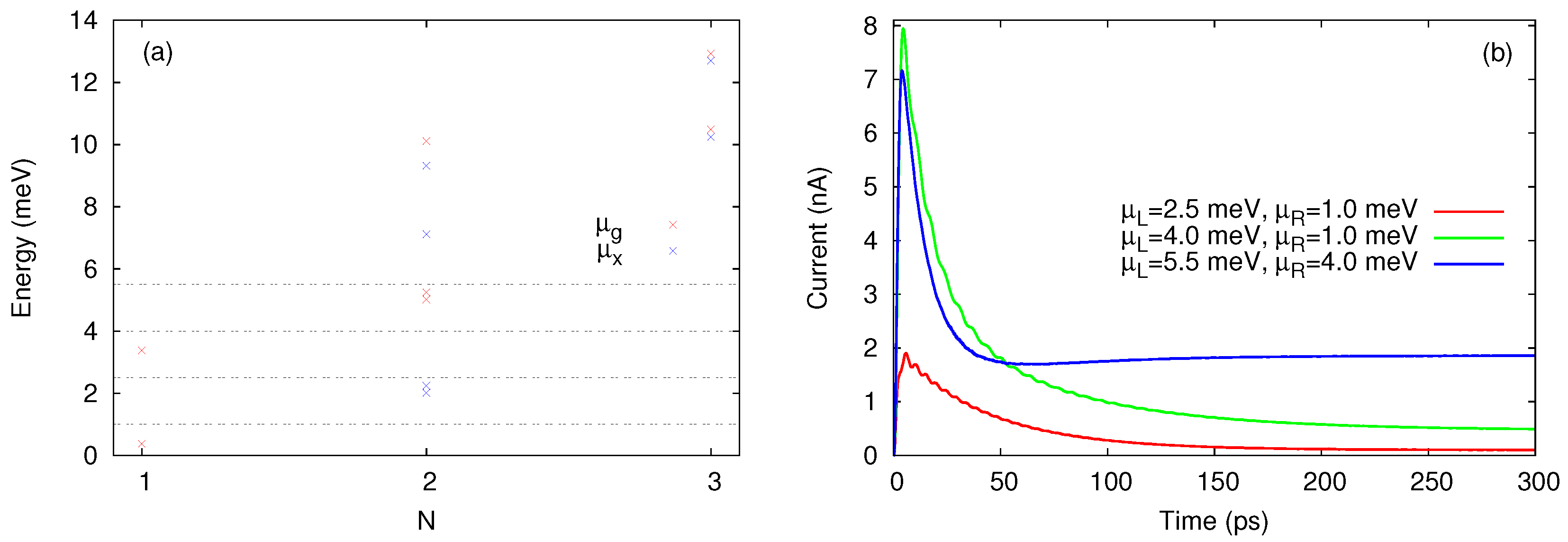
4. Thermoelectric Transport
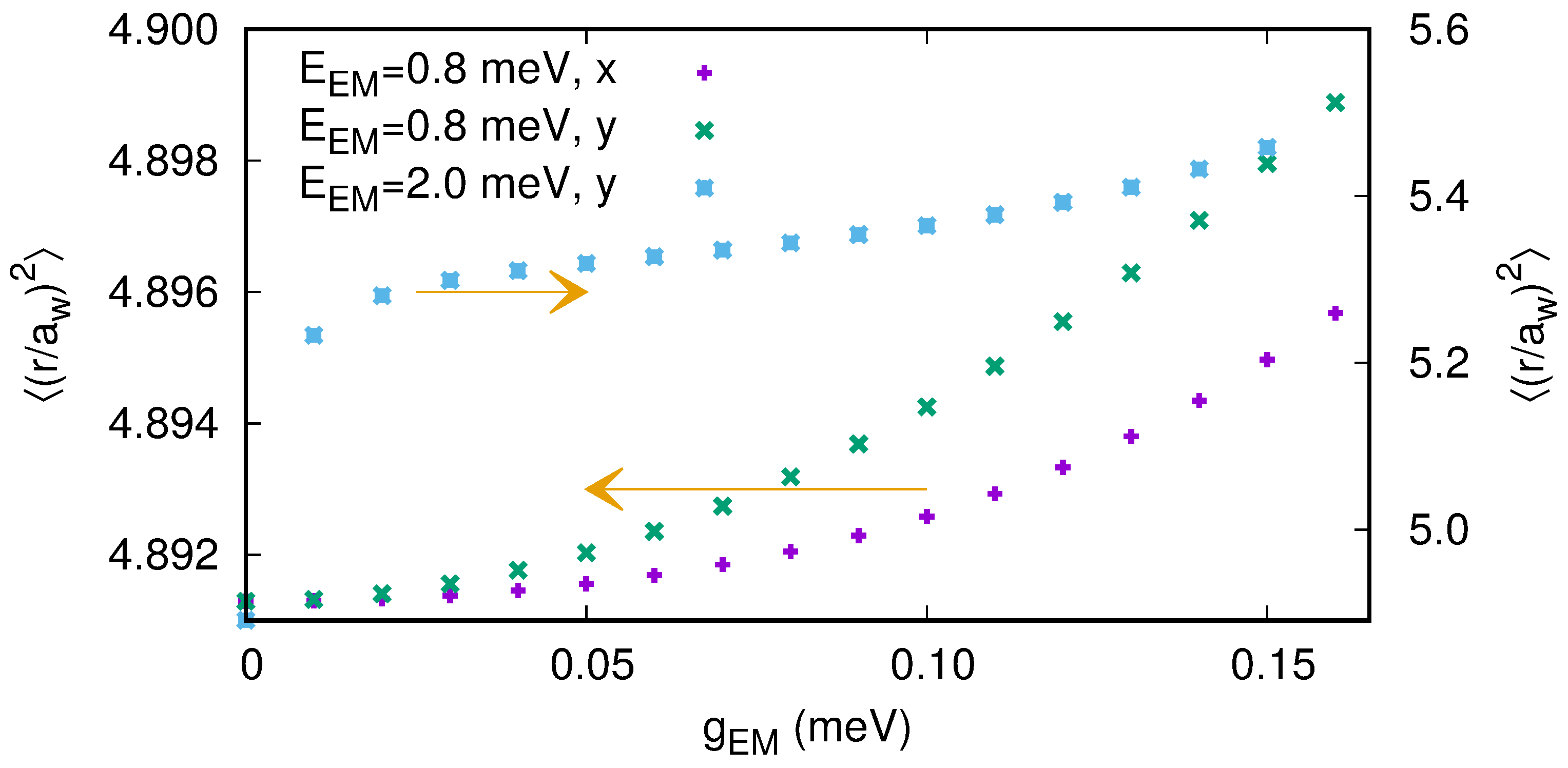
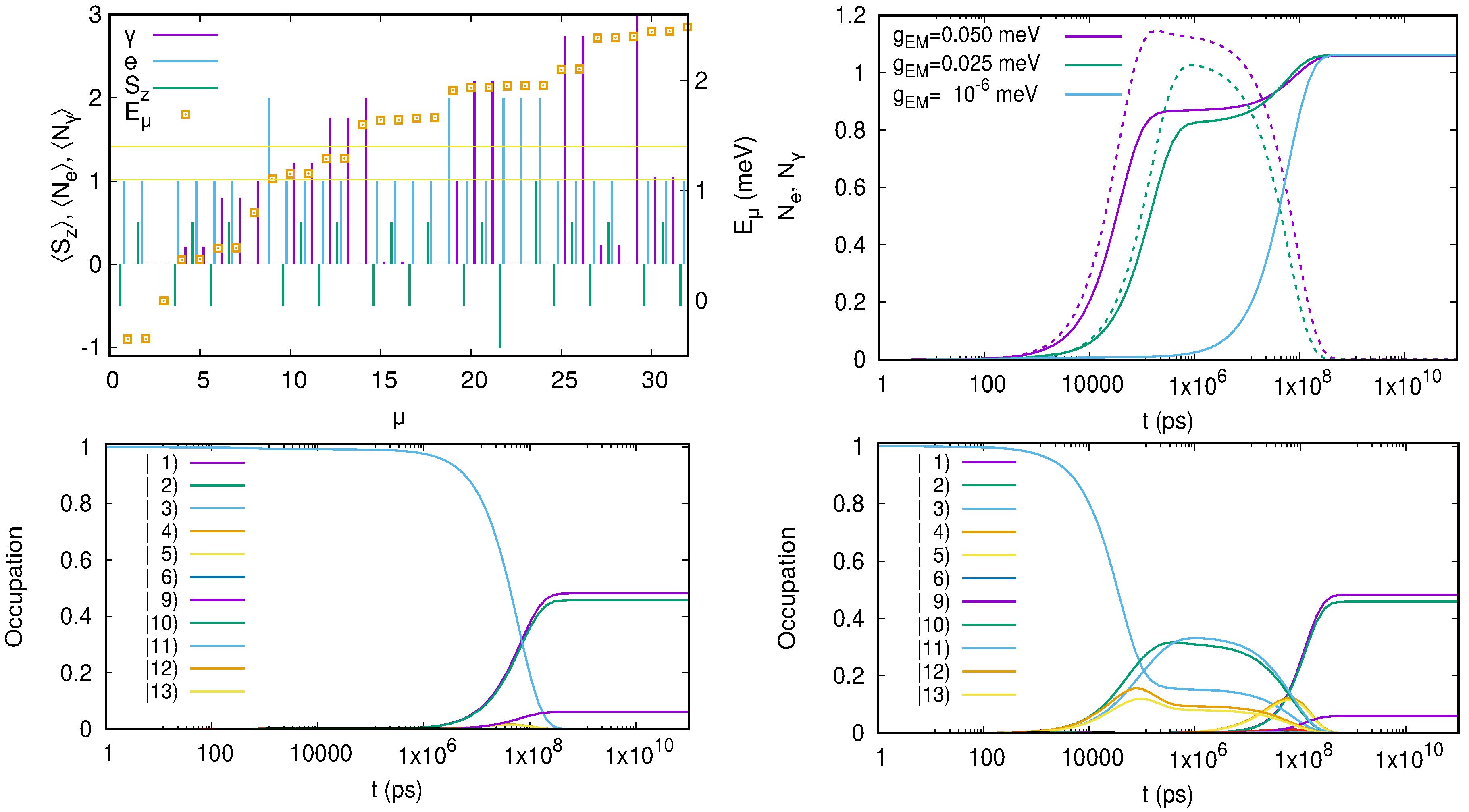
5. Electron Transport through Photon Cavities
5.1. The Electron-Photon Coupling
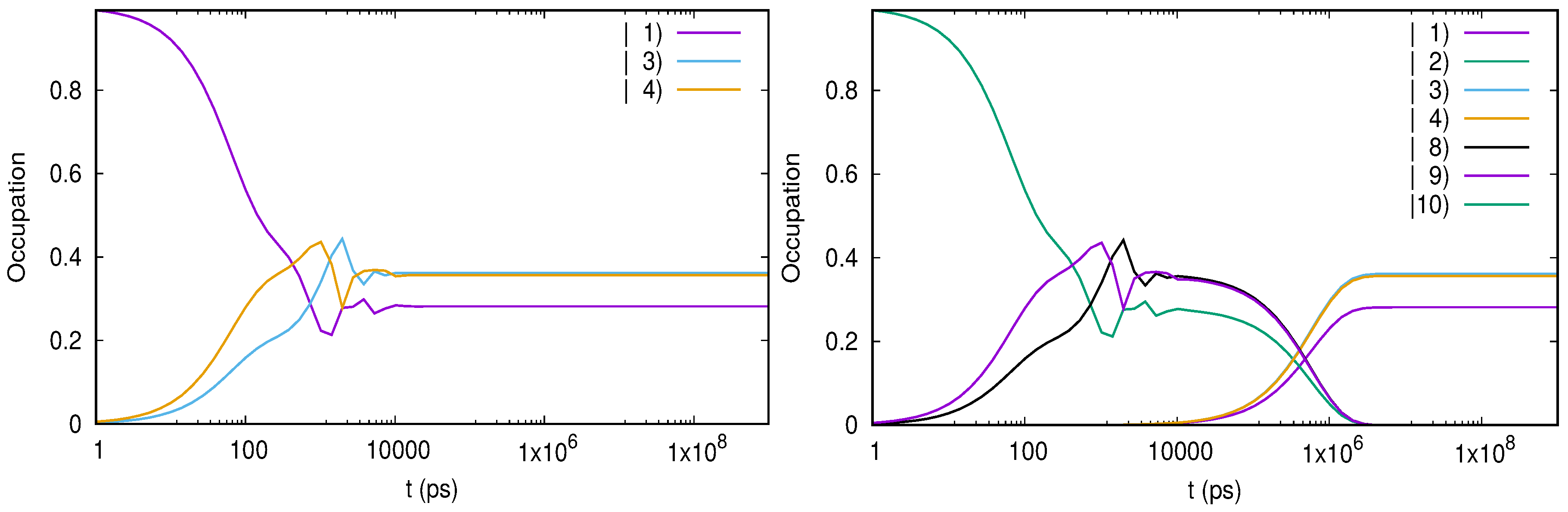
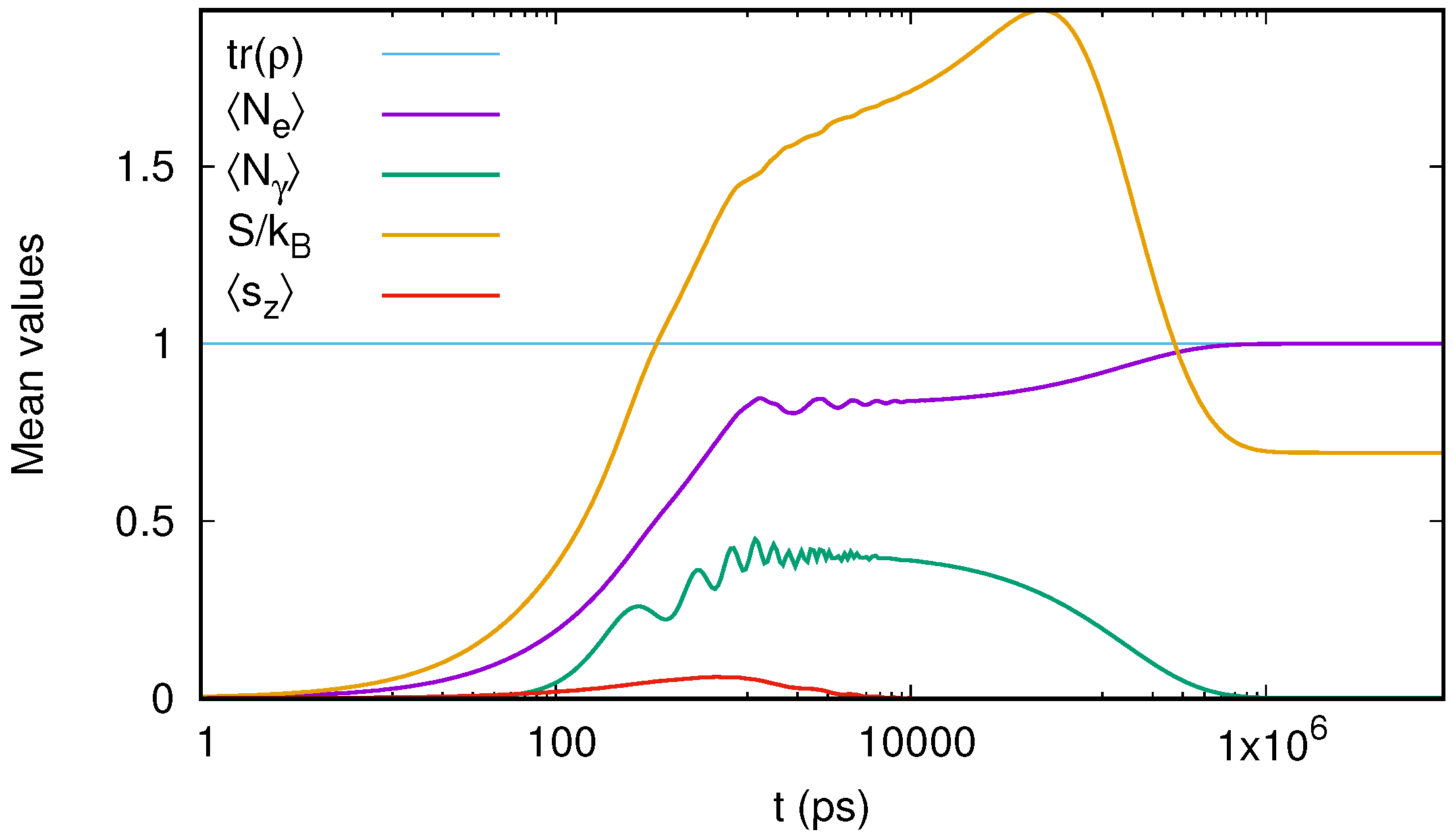
5.2. Results
6. Steady-State
6.1. The Steady-State Limit
6.2. Results
7. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Di Ventra, M. Electrical Transport in Nanoscale Systems; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Jahnke, F. Quantum Optics with Semiconductor Nanostructures; Woodhead Publishing Series in Electronic and Optical Materials; Elsevier Science: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Chow, W.W.; Jahnke, F. On the physics of semiconductor quantum dots for applications in lasers and quantum optics. Prog. Quantum Electron. 2013, 37, 109–184. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar] [CrossRef]
- Bloch, F. Generalized Theory of Relaxation. Phys. Rev. 1957, 105, 1206–1222. [Google Scholar] [CrossRef]
- Wangsness, R.K.; Bloch, F. The Dynamical Theory of Nuclear Induction. Phys. Rev. 1953, 89, 728–739. [Google Scholar] [CrossRef]
- Redfield, A.G. The Theory of Relaxation Processes. Adv. Magn. Reson. 1965, 1, 1–32. [Google Scholar]
- Scully, M.O.; Zubairy, M.S. Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Carmichael, H.J. Statistical Methods in Quantum Optics 1: Master Equations and Fokker-Planck Equations; Springer: Berlin, Germany, 2003. [Google Scholar]
- Timm, C. Tunneling through molecules and quantum dots: Master-equation approaches. Phys. Rev. B 2008, 77, 195416. [Google Scholar] [CrossRef]
- Elenewski, J.E.; Gruss, D.; Zwolak, M. Communication: Master equations for electron transport: The limits of the Markovian limit. J. Chem. Phys. 2017, 147, 151101. [Google Scholar] [CrossRef]
- Moldoveanu, V.; Manolescu, A.; Gudmundsson, V. Geometrical effects and signal delay in time-dependent transport at the nanoscale. New J. Phys. 2009, 11, 073019. [Google Scholar] [CrossRef]
- Vaz, E.; Kyriakidis, J. Transient dynamics of confined charges in quantum dots in the sequential tunneling regime. Phys. Rev. B 2010, 81, 085315. [Google Scholar] [CrossRef]
- Moldoveanu, V.; Manolescu, A.; Tang, C.S.; Gudmundsson, V. Coulomb interaction and transient charging of excited states in open nanosystems. Phys. Rev. B 2010, 81, 155442. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Lin, Y.Y.; Tang, C.S.; Moldoveanu, V.; Bardarson, J.H.; Manolescu, A. Transport through a quantum ring, dot, and barrier embedded in a nanowire in magnetic field. Phys. Rev. B 2005, 71, 235302. [Google Scholar] [CrossRef]
- Torfason, K.; Manolescu, A.; Molodoveanu, V.; Gudmundsson, V. Excitation of collective modes in a quantum flute. Phys. Rev. B 2012, 85, 245114. [Google Scholar] [CrossRef]
- Moldoveanu, V.; Manolescu, A.; Gudmundsson, V. Dynamic correlations induced by Coulomb interactions in coupled quantum dots. Phys. Rev. B 2010, 82, 085311. [Google Scholar] [CrossRef]
- Bulnes Cuetara, G.; Esposito, M.; Gaspard, P. Fluctuation theorems for capacitively coupled electronic currents. Phys. Rev. B 2011, 84, 165114. [Google Scholar] [CrossRef]
- Harbola, U.; Esposito, M.; Mukamel, S. Quantum master equation for electron transport through quantum dots and single molecules. Phys. Rev. B 2006, 74, 235309. [Google Scholar] [CrossRef]
- Cohen, G.; Rabani, E. Memory effects in nonequilibrium quantum impurity models. Phys. Rev. B 2011, 84, 075150. [Google Scholar] [CrossRef]
- Härtle, R.; Cohen, G.; Reichman, D.R.; Millis, A.J. Decoherence and lead-induced interdot coupling in nonequilibrium electron transport through interacting quantum dots: A hierarchical quantum master equation approach. Phys. Rev. B 2013, 88, 235426. [Google Scholar] [CrossRef]
- Esposito, M.; Galperin, M. Transport in molecular states language: Generalized quantum master equation approach. Phys. Rev. B 2009, 79, 205303. [Google Scholar] [CrossRef]
- Galperin, M.; Nitzan, A.; Ratner, M.A. Inelastic transport in the Coulomb blockade regime within a nonequilibrium atomic limit. Phys. Rev. B 2008, 78, 125320. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- Kulkarni, M.; Cotlet, O.; Türeci, H.E. Cavity-coupled double-quantum dot at finite bias: Analogy with lasers and beyond. Phys. Rev. B 2014, 90, 125402. [Google Scholar] [CrossRef]
- Viennot, J.J.; Delbecq, M.R.; Dartiailh, M.C.; Cottet, A.; Kontos, T. Out-of-equilibrium charge dynamics in a hybrid circuit quantum electrodynamics architecture. Phys. Rev. B 2014, 89, 165404. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Stehlik, J.; Eichler, C.; Gullans, M.J.; Taylor, J.M.; Petta, J.R. Semiconductor double quantum dot micromaser. Science 2015, 347, 285. [Google Scholar] [CrossRef] [PubMed]
- Viennot, J.J.; Dartiailh, M.C.; Cottet, A.; Kontos, T. Coherent coupling of a single spin to microwave cavity photons. Science 2015, 349, 408–411. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.Y.; Stehlik, J.; Mi, X.; Hartke, T.R.; Gullans, M.J.; Petta, J.R. On-Chip Quantum-Dot Light Source for Quantum-Device Readout. Phys. Rev. Appl. 2018, 9, 014030. [Google Scholar] [CrossRef]
- Beaudoin, F.; Gambetta, J.M.; Blais, A. Dissipation and ultrastrong coupling in circuit QED. Phys. Rev. A 2011, 84, 043832. [Google Scholar] [CrossRef]
- Dinu, I.V.; Moldoveanu, V.; Gartner, P. Many-body effects in transport through a quantum-dot cavity system. Phys. Rev. B 2018, 97, 195442. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Jonasson, O.; Tang, C.S.; Goan, H.S.; Manolescu, A. Time-dependent transport of electrons through a photon cavity. Phys. Rev. B 2012, 85, 075306. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Sitek, A.; yi Lin, P.; Abdullah, N.R.; Tang, C.S.; Manolescu, A. Coupled Collective and Rabi Oscillations Triggered by Electron Transport through a Photon Cavity. ACS Photonics 2015, 2, 930–934. [Google Scholar] [CrossRef]
- Cirio, M.; De Liberato, S.; Lambert, N.; Nori, F. Ground State Electroluminescence. Phys. Rev. Lett. 2016, 116, 113601. [Google Scholar] [CrossRef]
- Cirio, M.; Shammah, N.; Lambert, N.; De Liberato, S.; Nori, F. Multielectron Ground State Electroluminescence. Phys. Rev. Lett. 2019, 122, 190403. [Google Scholar] [CrossRef] [PubMed]
- Schachenmayer, J.; Genes, C.; Tignone, E.; Pupillo, G. Cavity-Enhanced Transport of Excitons. Phys. Rev. Lett. 2015, 114, 196403. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Poot, M.; van der Zant, H.S. Mechanical systems in the quantum regime. Phys. Rep. 2012, 511, 273–335. [Google Scholar] [CrossRef]
- Tanatar, B.; Moldoveanu, V.; Dragomir, R.; Stanciu, S. Interaction and Size Effects in Open Nano-Electromechanical Systems. Phys. Status Solidi (b) 2019, 256, 1800443. [Google Scholar] [CrossRef]
- Settineri, A.; Macrí, V.; Ridolfo, A.; Di Stefano, O.; Kockum, A.F.; Nori, F.; Savasta, S. Dissipation and thermal noise in hybrid quantum systems in the ultrastrong-coupling regime. Phys. Rev. A 2018, 98, 053834. [Google Scholar] [CrossRef]
- Zueco, D.; García-Ripoll, J. Ultrastrongly dissipative quantum Rabi model. Phys. Rev. A 2019, 99, 013807. [Google Scholar] [CrossRef]
- Jonasson, O.; Tang, C.S.; Goan, H.S.; Manolescu, A.; Gudmundsson, V. Nonperturbative approach to circuit quantum electrodynamics. Phys. Rev. E 2012, 86, 046701. [Google Scholar] [CrossRef]
- Schinabeck, C.; Erpenbeck, A.; Härtle, R.; Thoss, M. Hierarchical quantum master equation approach to electronic-vibrational coupling in nonequilibrium transport through nanosystems. Phys. Rev. B 2016, 94, 201407. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Gainar, C.; Tang, C.S.; Moldoveanu, V.; Manolescu, A. Time-dependent transport via the generalized master equation through a finite quantum wire with an embedded subsystem. New J. Phys. 2009, 11, 113007. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Jonasson, O.; Arnold, T.; Tang, C.S.; Goan, H.S.; Manolescu, A. Stepwise introduction of model complexity in a generalized master equation approach to time-dependent transport. Fortschr. Phys. 2013, 61, 305. [Google Scholar] [CrossRef]
- Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Magnetic-field-influenced nonequilibrium transport through a quantum ring with correlated electrons in a photon cavity. Phys. Rev. B 2013, 87, 035314. [Google Scholar] [CrossRef]
- Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Excitation spectra of a quantum ring embedded in a photon cavity. J. Opt. 2015, 17, 015201. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Gudmundsson, V. Time-dependent magnetotransport in an interacting double quantum wire with window coupling. Phys. Rev. B 2010, 82, 195325. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Delocalization of electrons by cavity photons in transport through a quantum dot molecule. Phys. E Low-dimens. Syst. Nanostruct. 2014, 64, 254–262. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Sitek, A.; Abdullah, N.R.; Tang, C.S.; Manolescu, A. Cavity-photon contribution to the effective interaction of electrons in parallel quantum dots. Ann. Phys. 2016. [Google Scholar] [CrossRef]
- Vargiamidis, V.; Valassiades, O.; Kyriakos, D.S. Lippmann-Schwinger equation approach to scattering in quantum wires. Phys. Stat. Sol. 2003, 236, 597. [Google Scholar] [CrossRef]
- Bardarson, J.H.; Magnusdottir, I.; Gudmundsdottir, G.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Coherent electronic transport in a multimode quantum channel with Gaussian-type scatterers. Phys. Rev. B 2004, 70, 245308. [Google Scholar] [CrossRef]
- Arnold, T. The Influence of Cavity Photons on the Transient Transport of Correlated Electrons through a Quantum Ring with Magnetic Field and Spin-Orbit Interaction. Ph.D. Thesis, University of Iceland, Reykjavík, Iceland, 2014. [Google Scholar]
- Fujisawa, T.; Austing, D.G.; Tokura, Y.; Hirayama, Y.; Tarucha, S. Electrical pulse measurement, inelastic relaxation, and non-equilibrium transport in a quantum dot. J. Phys. Condens. Matter 2003, 15, R1395–R1428. [Google Scholar] [CrossRef][Green Version]
- Naser, B.; Ferry, D.K.; Heeren, J.; Reno, J.L.; Bird, J.P. Large capacitance in the nanosecond-scale transient response of quantum point contacts. Appl. Phys. Lett. 2006, 89, 083103. [Google Scholar] [CrossRef]
- Lai, W.T.; Kuo, D.M.; Li, P.W. Transient current through a single germanium quantum dot. Phys. E Low-dimens. Syst. Nanostruct. 2009, 41, 886–889. [Google Scholar] [CrossRef]
- Kaestner, B.; Kashcheyevs, V. Non-adiabatic quantized charge pumping with tunable-barrier quantum dots: A review of current progress. Rep. Prog. Phys. 2015, 78, 103901. [Google Scholar] [CrossRef] [PubMed]
- Moldoveanu, V.; Manolescu, A.; Gudmundsson, V. Theoretical investigation of modulated currents in open nanostructures. Phys. Rev. B 2009, 80, 205325. [Google Scholar] [CrossRef]
- Moldoveanu, V.; Dinu, I.V.; Tanatar, B.; Moca, C.P. Quantum turnstile operation of single-molecule magnets. New J. Phys. 2015, 17, 083020. [Google Scholar] [CrossRef]
- Moldoveanu, V.; Cornean, H.D.; Pillet, C.A. Nonequilibrium steady states for interacting open systems: Exact results. Phys. Rev. B 2011, 84, 075464. [Google Scholar] [CrossRef]
- Cornean, H.D.; Neidhardt, H.; Zagrebnov, V.A. The Effect of Time-Dependent Coupling on Non-Equilibrium Steady States. Ann. Henri Poincaré 2009, 10, 61–93. [Google Scholar] [CrossRef][Green Version]
- Narozhny, B.N.; Levchenko, A. Coulomb drag. Rev. Mod. Phys. 2016, 88, 025003. [Google Scholar] [CrossRef]
- Sánchez, R.; López, R.; Sánchez, D.; Büttiker, M. Mesoscopic Coulomb Drag, Broken Detailed Balance, and Fluctuation Relations. Phys. Rev. Lett. 2010, 104, 076801. [Google Scholar] [CrossRef] [PubMed]
- Kaasbjerg, K.; Jauho, A.P. Correlated Coulomb Drag in Capacitively Coupled Quantum-Dot Structures. Phys. Rev. Lett. 2016, 116, 196801. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.S.; Sánchez, D.; López, R. Engineering drag currents in Coulomb coupled quantum dots. New J. Phys. 2018, 20, 023038. [Google Scholar] [CrossRef]
- Zhou, C.; Guo, H. Coulomb drag between quantum wires: A nonequilibrium many-body approach. Phys. Rev. B 2019, 99, 035423. [Google Scholar] [CrossRef]
- Sánchez, R.; Thierschmann, H.; Molenkamp, L.W. Single-electron thermal devices coupled to a mesoscopic gate. New J. Phys. 2017, 19, 113040. [Google Scholar] [CrossRef]
- Bhandari, B.; Chiriacò, G.; Erdman, P.A.; Fazio, R.; Taddei, F. Thermal drag in electronic conductors. Phys. Rev. B 2018, 98, 035415. [Google Scholar] [CrossRef]
- Sánchez, D.; López, R. Nonlinear phenomena in quantum thermoelectrics and heat. C. R. Phys. 2016, 17, 1060–1071. [Google Scholar] [CrossRef]
- Sierra, M.A.; Sánchez, D. Strongly nonlinear thermovoltage and heat dissipation in interacting quantum dots. Phys. Rev. B 2014, 90, 115313. [Google Scholar] [CrossRef]
- Torfason, K.; Manolescu, A.; Erlingsson, S.I.; Gudmundsson, V. Thermoelectric current and Coulomb-blockade plateaus in a quantum dot. Physica E 2013, 53, 178–185. [Google Scholar] [CrossRef][Green Version]
- Sánchez, D.; Linke, H. Focus on Thermoelectric Effects in Nanostructures. New J. Phys. 2014, 16, 110201. [Google Scholar] [CrossRef]
- Beenakker, C.W.J.; Staring, A.A.M. Theory of the thermopower of a quantum dot. Phys. Rev. B 1992, 46, 9667–9676. [Google Scholar] [CrossRef]
- Staring, A.A.M.; Molenkamp, L.W.; Alphenaar, B.W.; van Houten, H.; Buyk, O.J.A.; Mabesoone, M.A.A.; Beenakker, C.W.J.; Foxon, C.T. Coulomb-Blockade Oscillations in the Thermopower of a Quantum Dot. Europhys. Lett. 1993, 22, 57. [Google Scholar] [CrossRef]
- Dzurak, A.; Smith, C.; Pepper, M.; Ritchie, D.; Frost, J.; Jones, G.; Hasko, D. Observation of Coulomb blockade oscillations in the thermopower of a quantum dot. Solid State Commun. 1993, 87, 1145–1149. [Google Scholar] [CrossRef]
- Svensson, S.F.; Persson, A.I.; Hoffmann, E.A.; Nakpathomkun, N.; Nilsson, H.A.; Xu, H.Q.; Samuelson, L.; Linke, H. Lineshape of the thermopower of quantum dots. New J. Phys. 2012, 14, 033041. [Google Scholar] [CrossRef]
- Reddy, P.; Jang, S.Y.; Segalman, R.A.; Majumdar, A. Thermoelectricity in Molecular Junctions. Science 2007, 315, 1568–1571. [Google Scholar] [CrossRef] [PubMed]
- Svensson, S.F.; Hoffmann, E.A.; Nakpathomkun, N.; Wu, P.M.; Xu, H.Q.; Nilsson, H.A.; Sánchez, D.; Kashcheyevs, V.; Linke, H. Nonlinear thermovoltage and thermocurrent in quantum dots. New J. Phys. 2013, 15, 105011. [Google Scholar] [CrossRef]
- Zimbovskaya, N.A. The effect of Coulomb interactions on nonlinear thermovoltage and thermocurrent in quantum dots. J. Chem. Phys. 2015, 142, 244310. [Google Scholar] [CrossRef] [PubMed]
- Stanciu, A.E.; Nemnes, G.A.; Manolescu, A. Thermoelectric Effects in Nanostructured Quantum Wires in the Non-Linear Temperature Regime. Rom. J. Phys. 2015, 60, 716. [Google Scholar]
- Erlingsson, S.; Manolescu, A.; Nemnes, G.; Bardarson, J.; Sanchez, D. Reversal of Thermoelectric Current in Tubular Nanowires. Phys. Rev. Lett. 2017, 119, 036804. [Google Scholar] [CrossRef] [PubMed]
- Thorgilsson, G.; Erlingsson, S.I.; Manolescu, A. Thermoelectric current in tubular nanowires in transverse electric and magnetic fields. J. Phys. Conf. Ser. 2017, 906, 012021. [Google Scholar] [CrossRef]
- Erlingsson, S.I.; Bardarson, J.H.; Manolescu, A. Thermoelectric current in topological insulator nanowires with impurities. Beilstein J. Nanotechnol. 2018, 9, 1156. [Google Scholar] [CrossRef]
- Zhang, Q.; Lou, M.; Li, X.; Reno, J.L.; Pan, W.; Watson, J.D.; Manfra, M.J.; Kono, J. Collective non-perturbative coupling of 2D electrons with high-quality-factor terahertz cavity photons. Nat. Phys. 2016, 12, 1005. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Abdullah, N.R.; Sitek, A.; Goan, H.S.; Tang, C.S.; Manolescu, A. Time-dependent current into and through multilevel parallel quantum dots in a photon cavity. Phys. Rev. B 2017, 95, 195307. [Google Scholar] [CrossRef]
- Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Impact of a circularly polarized cavity photon field on the charge and spin flow through an Aharonov-Casher ring. Phys. E Low-dimens. Syst. Nanostruct. 2014, 60, 170–182. [Google Scholar] [CrossRef]
- Feranchuk, I.D.; Komarov, L.I.; Ulyanenkov, A.P. Two-level system in a one-mode quantum field: Numerical solution on the basis of the operator method. J. Phys. A Math. Gen. 1996, 29, 4035. [Google Scholar] [CrossRef]
- Li, X.H.; Wang, K.L.; Liu, T. Ground State of Jaynes–Cummings Model: Comparison of Solutions with and without the Rotating-Wave Approximation. Chin. Phys. Lett. 2009, 26, 044212. [Google Scholar]
- Jonasson, O.; Tang, C.S.; Goan, H.S.; Manolescu, A.; Gudmundsson, V. Quantum magneto-electrodynamics of electrons embedded in a photon cavity. New J. Phys. 2012, 14, 013036. [Google Scholar] [CrossRef]
- Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Effects of geometry and linearly polarized cavity photons on charge and spin currents in a quantum ring with spin-orbit interactions. Eur. Phys. J. B 2014, 87, 113. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Electron transport through a quantum dot assisted by cavity photons. J. Phys. Condens. Matter 2013, 25, 465302. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Optical switching of electron transport in a waveguide-QED system. Phys. E Low-dimens. Syst. Nanostruct. 2016, 84, 280–284. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Competition of static magnetic and dynamic photon forces in electronic transport through a quantum dot. J. Phys. Condens. Matter 2016, 28, 375301. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Effects of photon field on heat transport through a quantum wire attached to leads. Phys. Lett. A 2018, 382, 199–204. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Cavity-Photon Controlled Thermoelectric Transport through a Quantum Wire. ACS Photonics 2016, 3, 249–254. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Spin-dependent heat and thermoelectric currents in a Rashba ring coupled to a photon cavity. Phys. E Low-dimens. Syst. Nanostruct. 2018, 95, 102–107. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Photon-induced tunability of the thermospin current in a Rashba ring. J. Phys. Condens. Matter 2018, 30, 145303. [Google Scholar] [CrossRef] [PubMed]
- Abdulla, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Manifestation of the Purcell effect in current transport through a dot-cavity-QED system. Nanomaterials 2019, 9, 1023. [Google Scholar] [CrossRef] [PubMed]
- Jonsson, T.H.; Manolescu, A.; Goan, H.S.; Abdullah, N.R.; Sitek, A.; Tang, C.S.; Gudmundsson, V. Efficient determination of the Markovian time-evolution towards a steady-state of a complex open quantum system. Comput. Phys. Commun. 2017, 220, 81. [Google Scholar] [CrossRef]
- Petersen, K.B.; Pedersen, M.S. The Matrix Cookbook. Version 20121115. 2012. Available online: http://www2.imm.dtu.dk/pubdb/views/publication_details.php?id=3274 (accessed on 25 July 2019).
- Weidlich, W. Liouville-space formalism for quantum systems in contact with reservoirs. Z. Phys. 1971, 241, 325. [Google Scholar] [CrossRef]
- Nakano, R.; Hatano, N.; Petrosky, T. Nontrivial Eigenvalues of the Liouvillian of an Open Quantum System. Int. J. Theor. Phys. 2010, 50, 1134–1142. [Google Scholar] [CrossRef][Green Version]
- Petrosky, T. Complex Spectral Representation of the Liouvillian and Kinetic Theory in Nonequilibrium Physics. Prog. Theor. Phys. 2010, 123, 395–420. [Google Scholar] [CrossRef]
- Swain, S. Master equation derivation of quantum regression theorem. J. Phys. A Math. Gen. 1981, 14, 2577. [Google Scholar] [CrossRef]
- Walls, D.; Milburn, G.J. Quantum Optics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Goan, H.S.; Chen, P.W.; Jian, C.C. Non-Markovian finite-temperature two-time correlation functions of system operators: Beyond the quantum regression theorem. J. Chem. Phys. 2011, 134, 124112. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Abdullah, N.R.; Sitek, A.; Goan, H.S.; Tang, C.S.; Manolescu, A. Current correlations for the transport of interacting electrons through parallel quantum dots in a photon cavity. Phys. Lett. A 2018, 382, 1672–1678. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Jonsson, T.H.; Bernodusson, M.L.; Abdullah, N.R.; Sitek, A.; Goan, H.S.; Tang, C.S.; Manolescu, A. Regimes of radiative and nonradiative transitions in transport through an electronic system in a photon cavity reaching a steady state. Ann. Phys. 2016, 529, 1600177. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Abdullah, N.R.; Sitek, A.; Goan, H.S.; Tang, C.S.; Manolescu, A. Electroluminescence caused by the transport of interacting electrons through parallel quantum dots in a photon cavity. Ann. Phys. 2018. [Google Scholar] [CrossRef]
- De Liberato, S.; Gerace, D.; Carusotto, I.; Ciuti, C. Extracavity quantum vacuum radiation from a single qubit. Phys. Rev. A 2009, 80, 053810. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Gestsson, H.; Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Moldoveanu, V. Coexisting spin and Rabi-oscillations at intermediate time in electron transport through a photon cavity. Beilstein J. Nanotechnol. 2018, 10, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Oscillations in electron transport caused by multiple resonances in a quantum dot-QED system in the steady-state regime. arXiv 2019, arXiv:1903.03655. [Google Scholar]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. The photocurrent generated by photon replica states of an off-resonantly coupled dot-cavity system. arXiv 2019, arXiv:1904.04888. [Google Scholar]
- Purcell, E.M. Spontaneous Emission Probabilities at Radio Frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Moldoveanu, V. Cavity-photon induced high order transitions between ground states of quantum dots. arXiv 2019, arXiv:1905.10883. [Google Scholar]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Thermoelectric Inversion in a Resonant Quantum Dot-Cavity System in the Steady-State Regime. Nanomaterials 2019, 9. [Google Scholar] [CrossRef] [PubMed]
- Stefanucci, G.; van Leeuwen, R. Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Deng, C.; Orgiazzi, J.L.; Shen, F.; Ashhab, S.; Lupascu, A. Observation of Floquet States in a Strongly Driven Artificial Atom. Phys. Rev. Lett. 2015, 115, 133601. [Google Scholar] [CrossRef] [PubMed]
- Koski, J.V.; Landig, A.J.; Pályi, A.; Scarlino, P.; Reichl, C.; Wegscheider, W.; Burkard, G.; Wallraff, A.; Ensslin, K.; Ihn, T. Floquet Spectroscopy of a Strongly Driven Quantum Dot Charge Qubit with a Microwave Resonator. Phys. Rev. Lett. 2018, 121, 043603. [Google Scholar] [CrossRef] [PubMed]
- Pagel, D.; Fehske, H. Non-Markovian dynamics of few emitters in a laser-driven cavity. Phys. Rev. A 2017, 96, 041802. [Google Scholar] [CrossRef]
- Szczygielski, K.; Alicki, R. Markovian theory of dynamical decoupling by periodic control. Phys. Rev. A 2015, 92, 022349. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moldoveanu, V.; Manolescu, A.; Gudmundsson, V. Generalized Master Equation Approach to Time-Dependent Many-Body Transport. Entropy 2019, 21, 731. https://doi.org/10.3390/e21080731
Moldoveanu V, Manolescu A, Gudmundsson V. Generalized Master Equation Approach to Time-Dependent Many-Body Transport. Entropy. 2019; 21(8):731. https://doi.org/10.3390/e21080731
Chicago/Turabian StyleMoldoveanu, Valeriu, Andrei Manolescu, and Vidar Gudmundsson. 2019. "Generalized Master Equation Approach to Time-Dependent Many-Body Transport" Entropy 21, no. 8: 731. https://doi.org/10.3390/e21080731
APA StyleMoldoveanu, V., Manolescu, A., & Gudmundsson, V. (2019). Generalized Master Equation Approach to Time-Dependent Many-Body Transport. Entropy, 21(8), 731. https://doi.org/10.3390/e21080731




