Multifractal Spectrum Curvature of RR Tachograms of Healthy People and Patients with Congestive Heart Failure, a New Tool to Assess Health Conditions
Abstract
1. Introduction
2. Methods
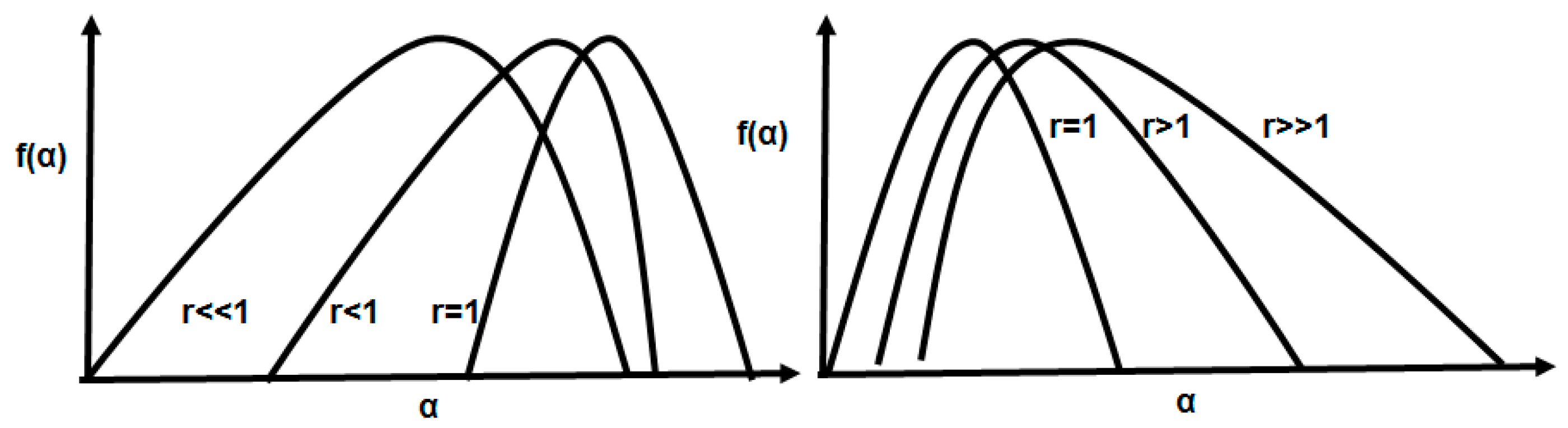
2.1. The Multifractal Spectrum Width and Symmetry
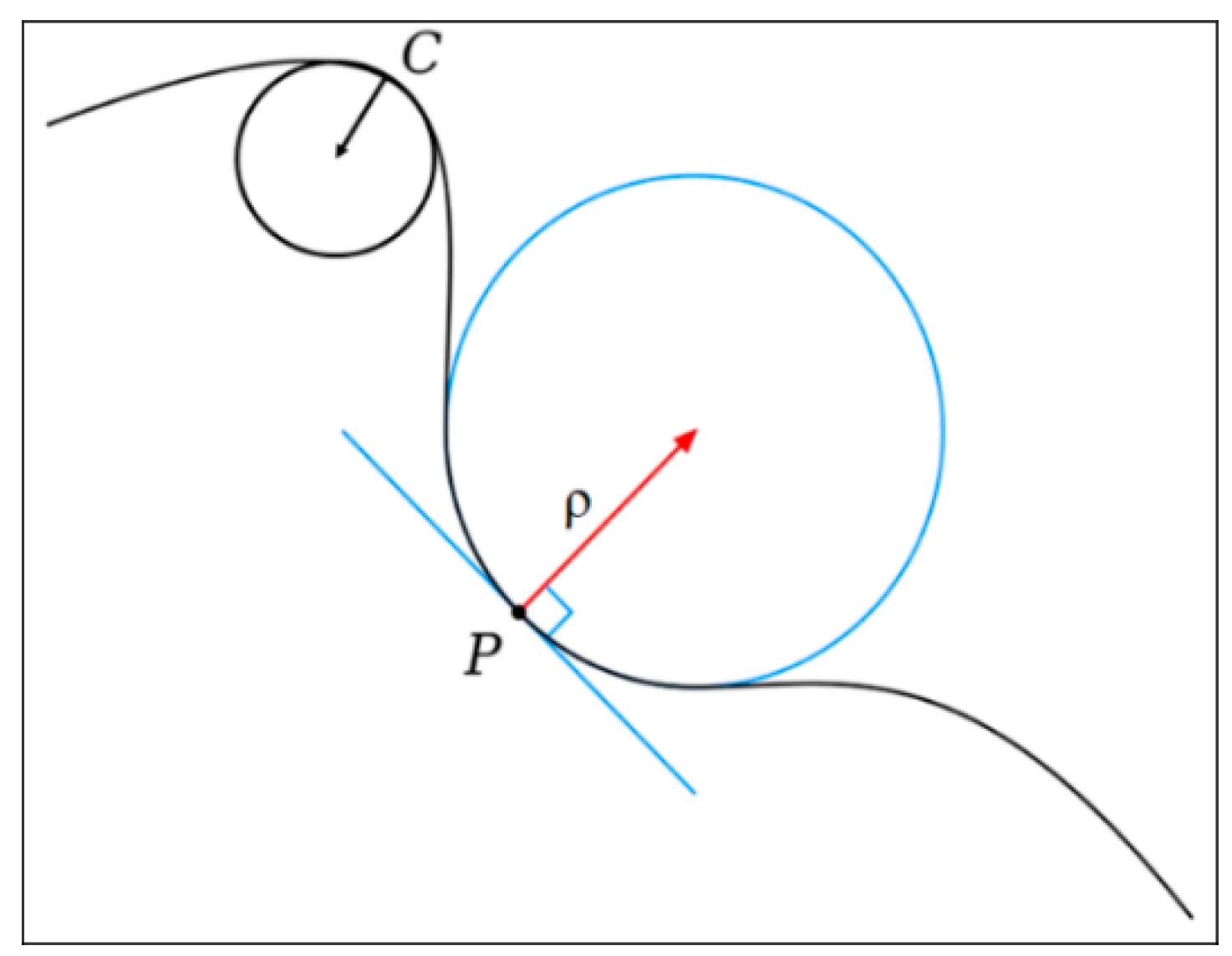
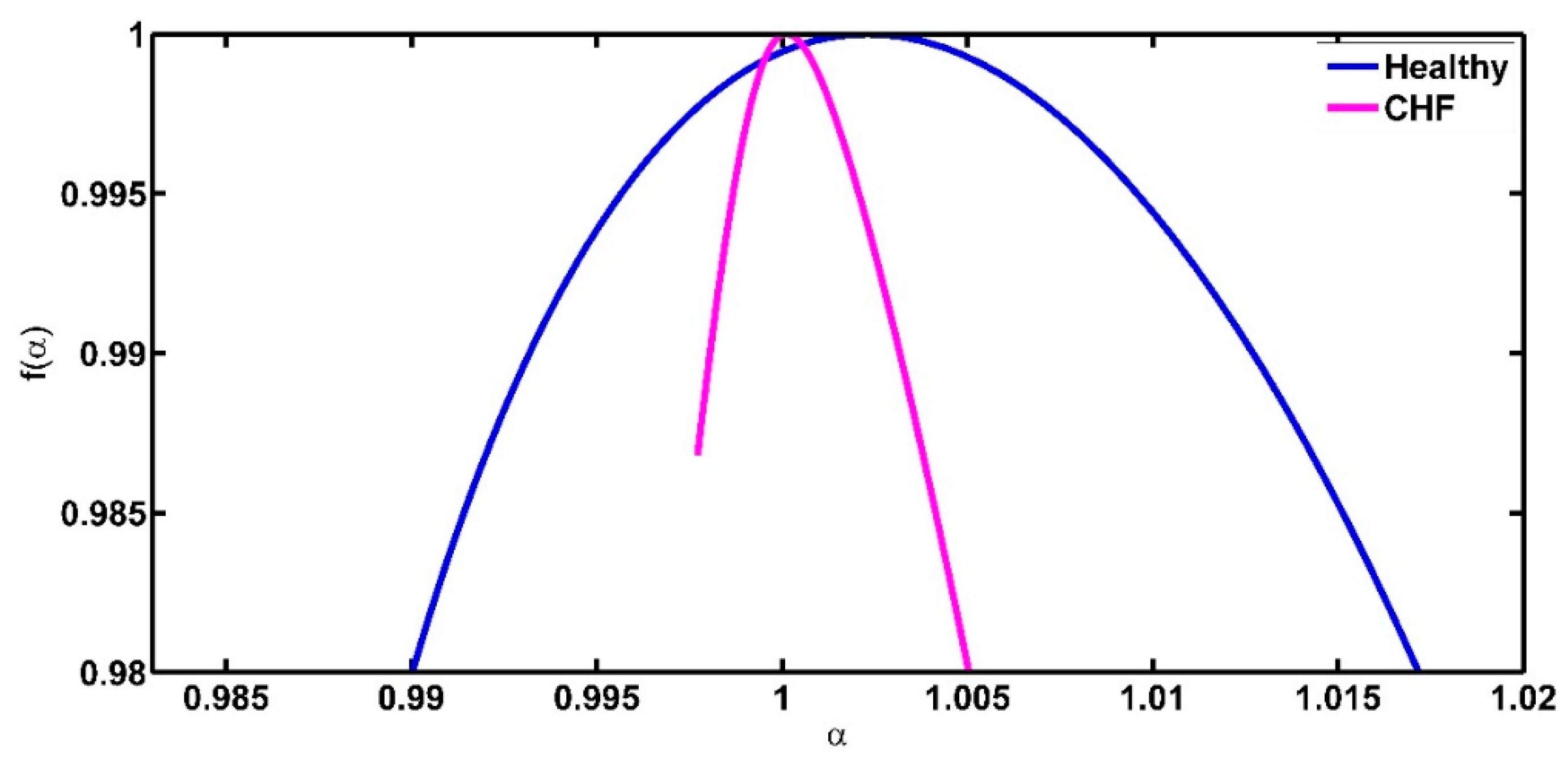
2.2. Curvature
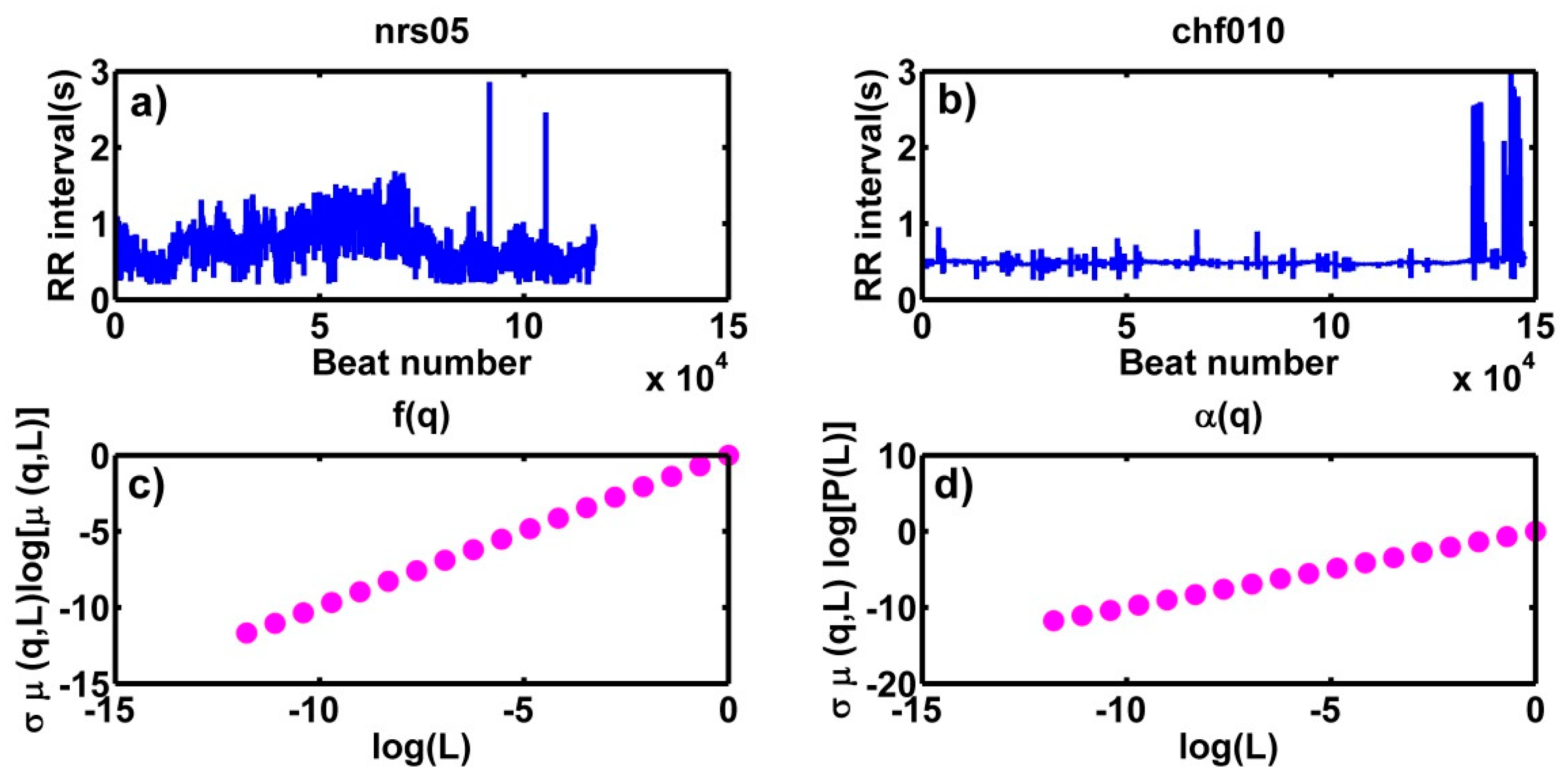
3. Databases
4. Results
4.1. On the Symmetry of the Spectra
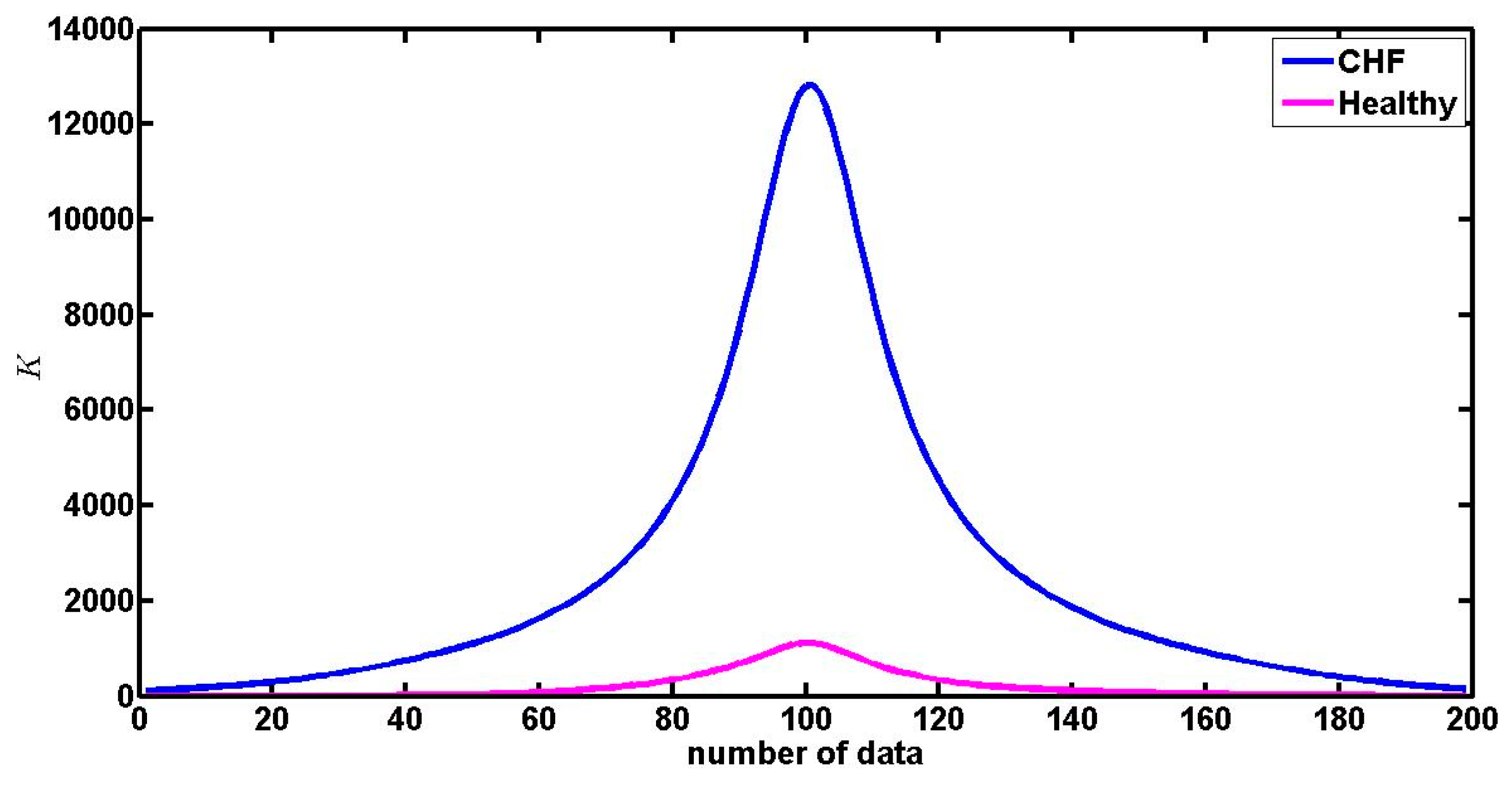
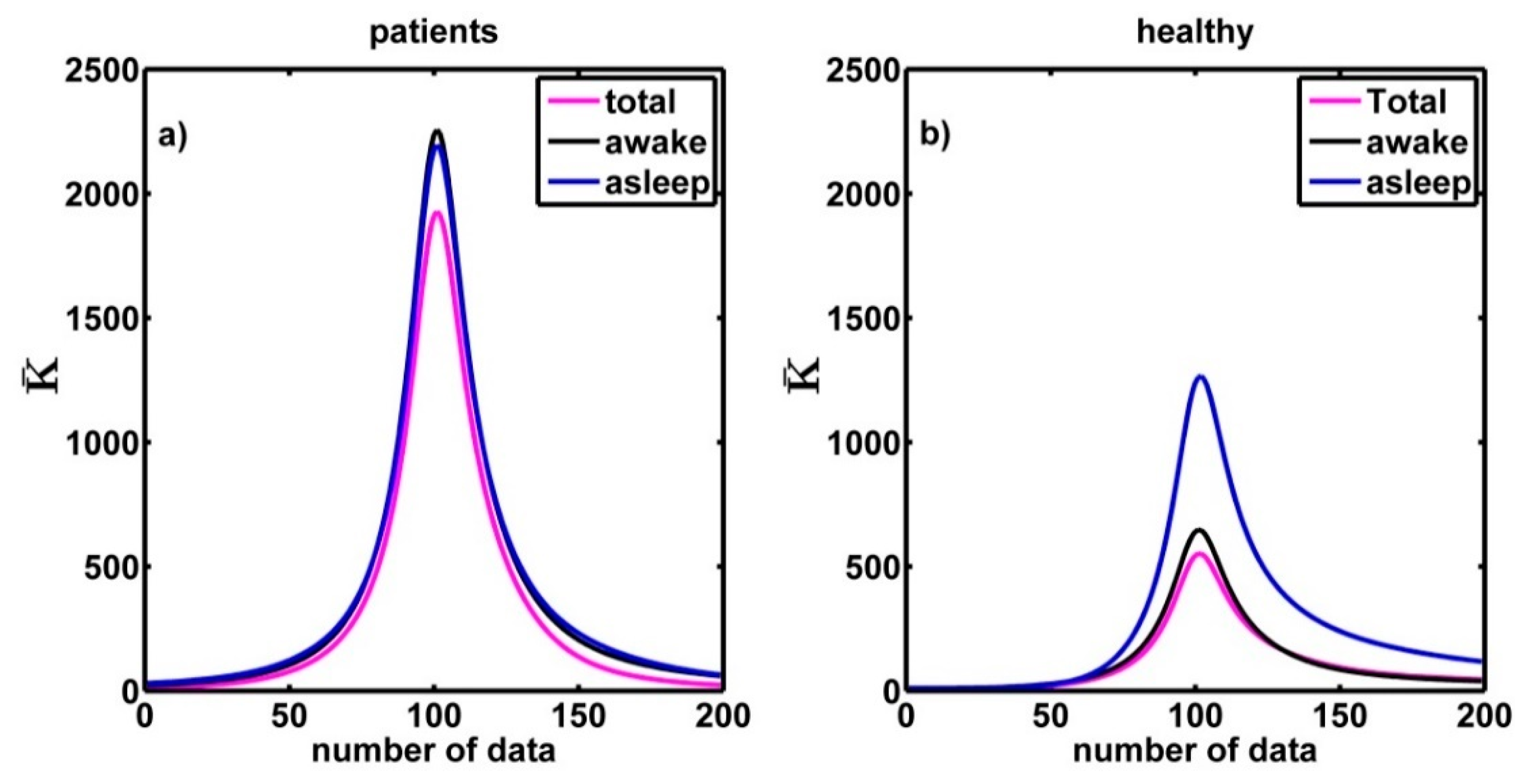
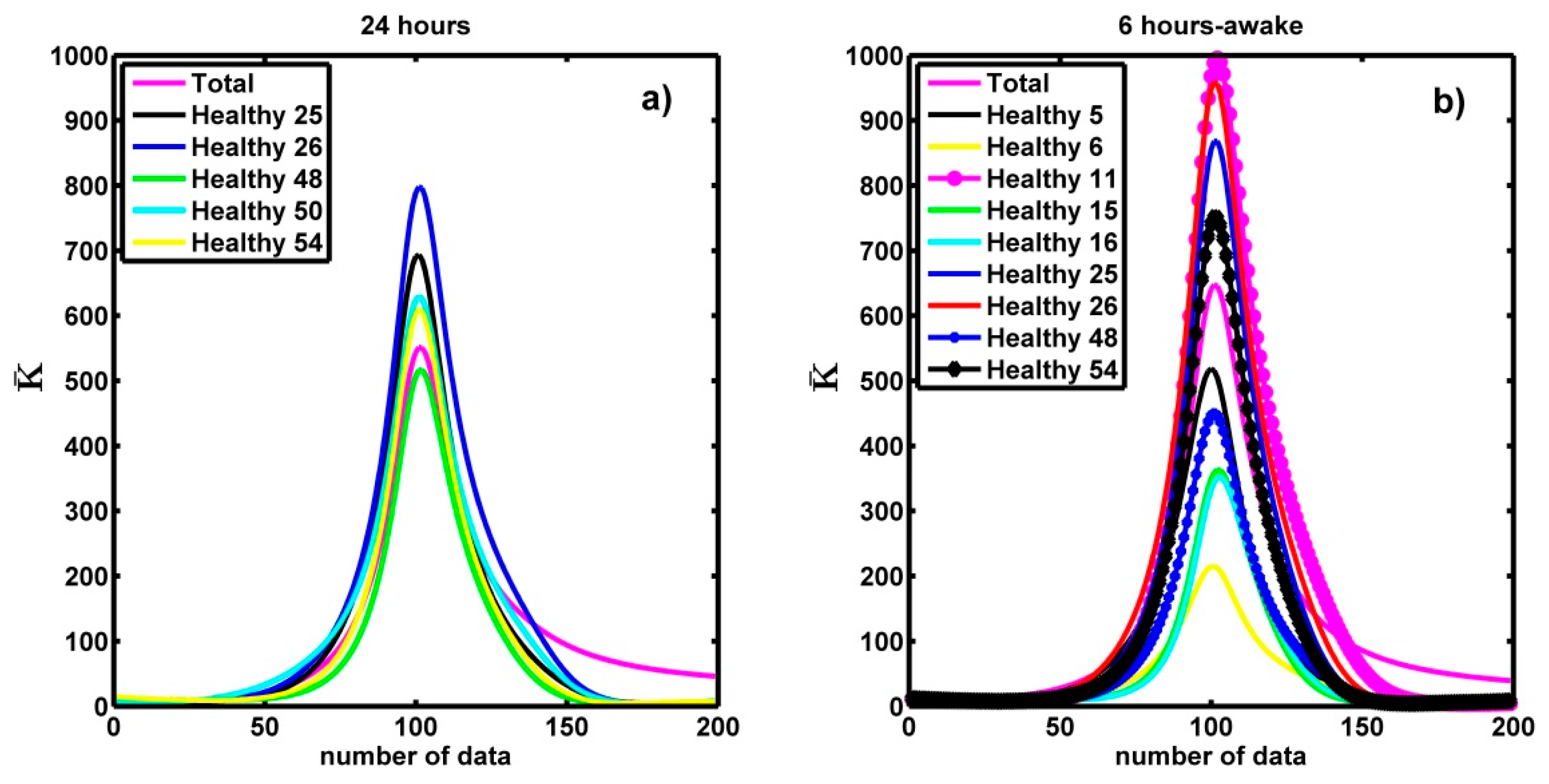
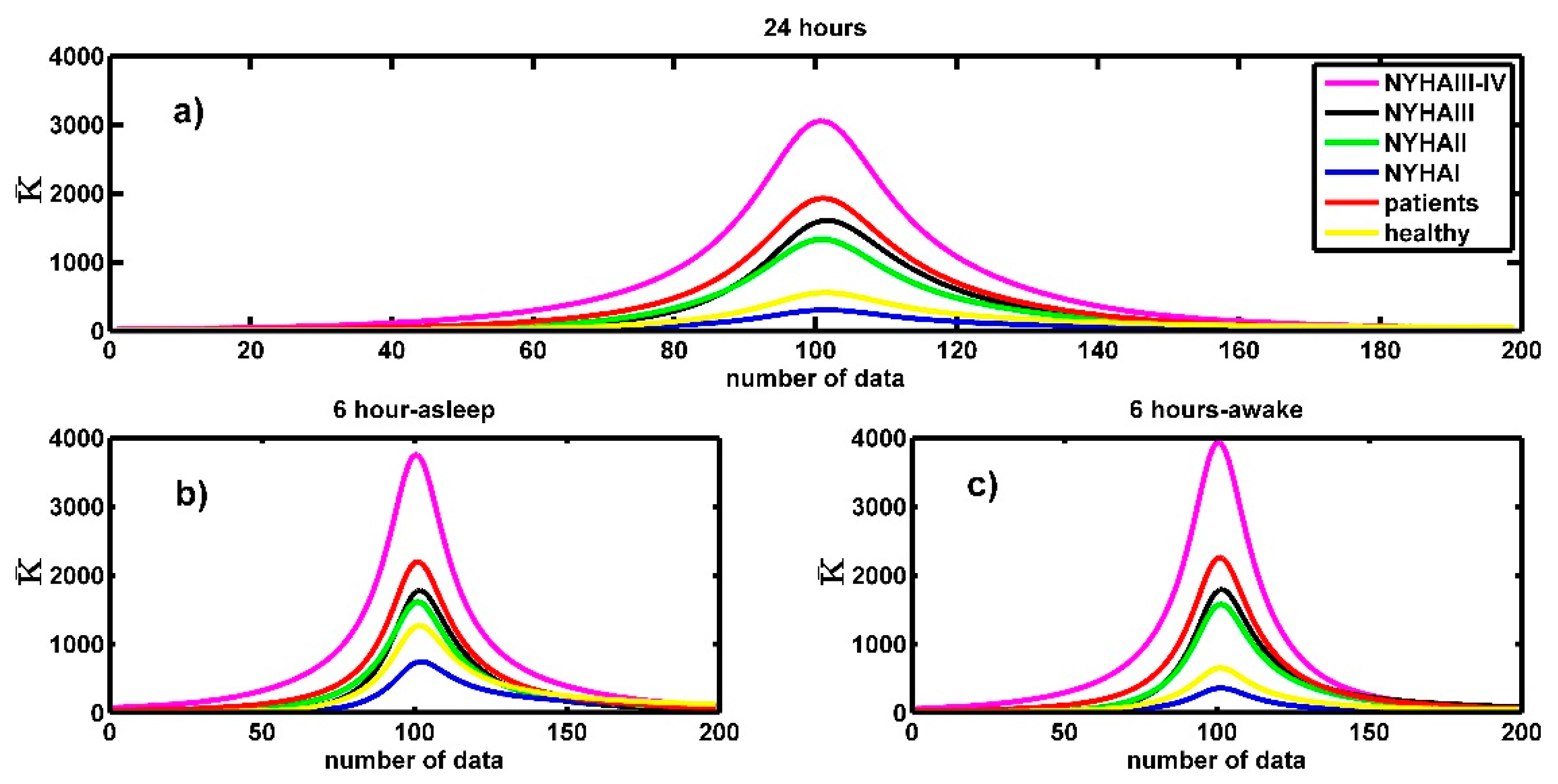
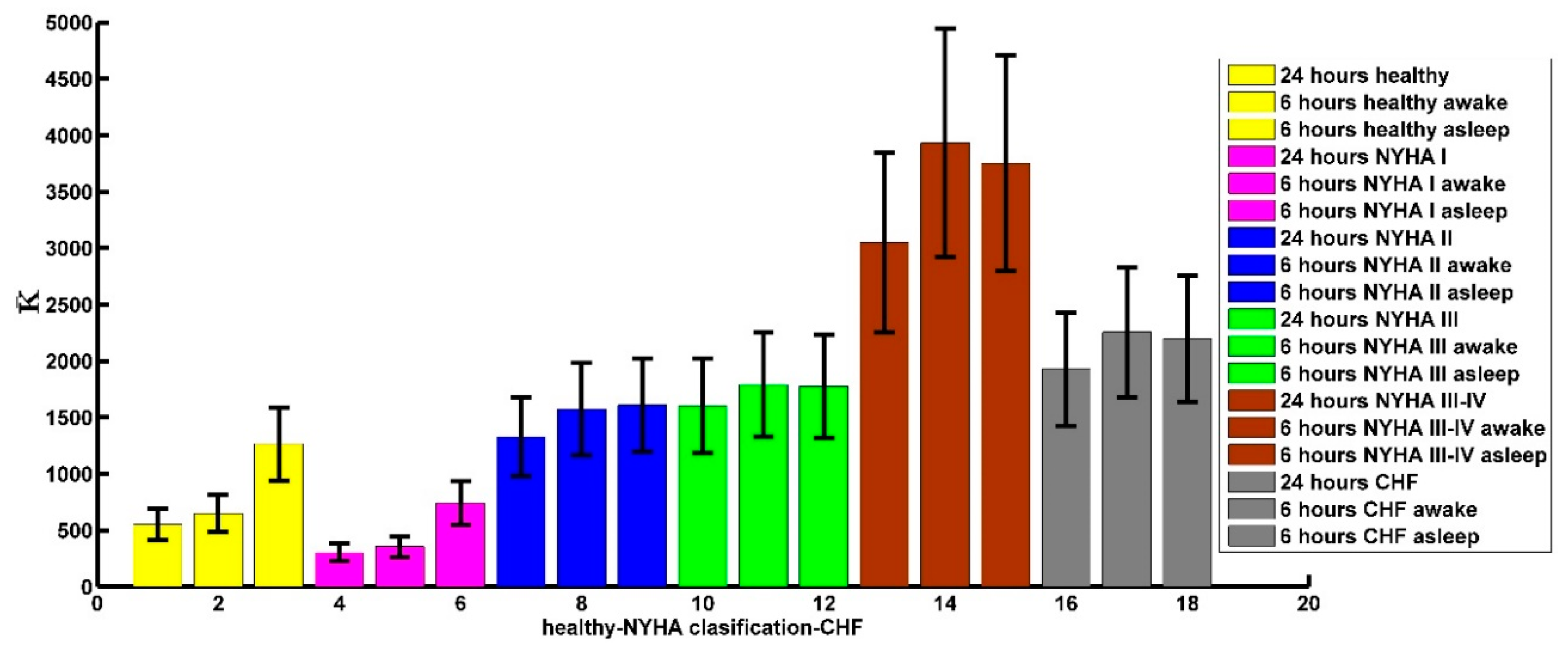
4.2. On the Curvature of the Spectra around the Maximum
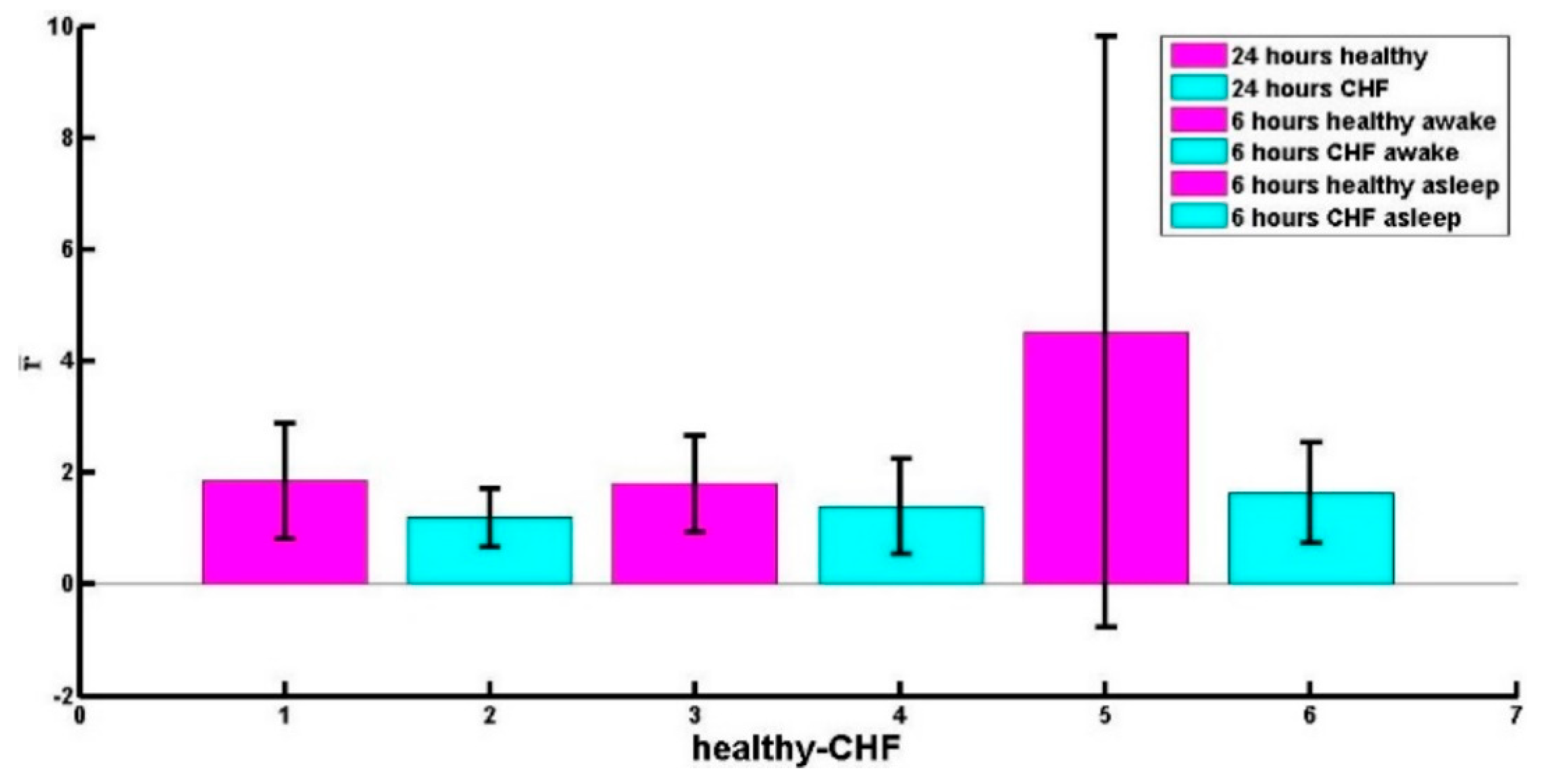
4.3. The Symmetry and the Curvature
4.4. The Curvature and the NYHA Classification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kwapień, J.; Drożdż, S. Physical approach to complex systems. Phys. Rep. 2012, 515, 115–226. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Nunes-Amaral, L.A.; Goldberger, A.L.; Stanley, H.E. Stochastic Feedback and the Regulation of Biological Rhythms. Europhys. Lett. 1998, 43, 363–368. [Google Scholar] [CrossRef] [PubMed]
- Bernaola-Galván, P.; Ivanov, P.C.; Nunes-Amaral, L.A.; Stanley, H.E. Scale Invariance in the Nonstationarity of Human Heart Rate. Phys. Rev. Lett. 2001, 87, 168105. [Google Scholar] [CrossRef] [PubMed]
- Nunes-Amaral, L.A.; Ivanov, P.C.; Aoyagi, N.; Hidaka, I.; Tomono, S.; Goldberger, A.L.; Stanley, H.E.; Yamamoto, Y. Behavioral-independent features of complex heartbeat dynamics. Phys. Rev. Lett. 2001, 86, 6026–6029. [Google Scholar] [CrossRef] [PubMed]
- Stanley, H.E.; Amaral, L.A.N.; Goldberger, A.L.; Havlin, S.; Ivanov, P.C.; Peng, C.K. Statistical physics and physiology: Monofractal and multifractal approaches. Phys. A Stat. Mech. Its Appl. 1999, 270, 309–324. [Google Scholar] [CrossRef]
- Salat, H.; Murcio, R.; Arcaute, E. Multifractal methodology. Phys. A Stat. Mech. Its Appl. 2017, 473, 467–487. [Google Scholar] [CrossRef]
- Lopes, R.; Betrouni, N. Fractal and Multifractal Analysis: A Review. Med Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, P.C.; Goldberger, A.L.; Stanley, H.E. Fractal and Multifractal Approaches in Physiology. In The Science of Disasters; Bunde, A., Knopp, J., Schellnhuber, H.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 218–257. [Google Scholar]
- Stanley, H.E.; Meakin, P. Multifractal phenomena in physics and chemistry. Nature 1988, 335, 405–409. [Google Scholar] [CrossRef]
- Murcio, R.; Masucci, A.P.; Arcaute, E.; Batty, M. Multifractal to monofractal evolution of the London street network. Phys. Rev. E 2015, 92, 062130. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Amaral, L.A.N.; Goldberger, A.L.; Havlin, S.; Rosemblum, M.G.; Struzik, Z.R.; Stanley, H.E. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Amaral, L.A.N.; Goldberger, A.L.; Havlin, S.; Rosenblum, M.G.; Stanley, H.E.; Struzik, Z.R. From 1/f noise to multifractal cascades in heartbeat dynamics. Chaos 2001, 11, 641–652. [Google Scholar] [CrossRef] [PubMed]
- Shekatkar, S.M.; Kotriwar, Y.; Harikrishnan, K.P.; Ambika, G. Detecting abnormality in heart dynamics from multifractal analysis of ECG signals. Sci. Rep. 2017, 7, 15127. [Google Scholar] [CrossRef] [PubMed]
- Makowiec, D.; Rynkiewicz, A.; Galaska, R.; Wdowczyk-Szulc, J.; Zarczynska-Buchowiecka, M. Reading multifractal spectra: Aging by multifractal analysis of heart rate. EPL 2011, 94, 68005. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Hausdorff, J.M.; Ivanov, P.C.; Peng, C.-K.; Stanley, H.E. Fractal dynamics in physiology: Alterations with disease and aging. Proc. Natl. Acad. Sci. USA 2002, 99, 2466–2472. [Google Scholar] [CrossRef] [PubMed]
- Curto-Risso, P.L.; Medina, A.; Hernández, A.C.; Guzmán-Vargas, L.; Angulo-Brown, F. Monofractal and multifractal analysis of simulated heat release fluctuations in a spark ignition heat engine. Phys. A 2010, 389, 5662–5670. [Google Scholar] [CrossRef]
- Tadić, B.; Mijatović, S.; Janićević, S.; Spasojević, D.; Rodgers, G.J. The critical Barkhausen avalanches in thin random-field ferromagnets with an open boundary. Sci. Rep. 2019, 9, 6340. [Google Scholar] [CrossRef] [PubMed]
- Tadić, B.; Dankulov, M.M.; Melnik, R. Mechanisms of self-organized criticality in social processes of knowledge creation. Phys. Rev. E 2017, 96, 032307. [Google Scholar] [CrossRef] [PubMed]
- Voss, B.A.; Schulz, S.; Schroeder, R.; Baumert, M.; Caminal, P. Methods derived from nonlinear dynamics for analyzing heart rate variability. Phil. Trans. R. Soc. A 2009, 367, 277–296. [Google Scholar] [CrossRef] [PubMed]
- Guzmán-Vargas, L.; Muñoz-Diosdado, A.; Angulo-Brown, F. Influence of the loss of time-constants repertoire in pathologic heartbeat dynamics. Phys. A Stat. Mech. Its Appl 2005, 348, 304–316. [Google Scholar]
- Ivanov, P.C.; Bunde, A.; Amaral, L.A.N.; Havlin, S.; Fritsch-Yelle, J.; Baevsky, R.M.; Stanley, H.E.; Goldberger, A.L. Sleep–wake differences in scaling behavior of the human heartbeat: Analysis of terrestrial and long-term space flight data. Europhys. Lett. 1999, 48, 594–600. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Ashkenazy, Y.; Ivanov, P.C.; Bunde, A.; Havlin, S.; Penzel, T.; Peter, J.h.; Stanley, H.E. Characterization of sleep stages by correlations in the magnitude and sign of heartbeat increments. Phys. Rev. E 2002, 65, 051908. [Google Scholar] [CrossRef] [PubMed]
- Karasik, R.; Sapir, N.; Ashkenazy, Y.; Ivanov, P.C.; Dvir, I.; Lavie, P.; Havlin, S. Correlation differences in heartbeat fluctuations during rest and exercise. Phys. Rev. E 2002, 66, 062902. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, P.C. Scale-invariant aspects of cardiac dynamics across sleep stages and circadian phases. IEEE Eng. Med. Biol. Mag. 2007, 26, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Ivanov, P.C.; Hilton, M.F.; Chen, Z.; Ayers, R.T.; Stanley, H.E.; Shea, S.A. Endogenous circadian rhythm in an index of cardiac vulnerability independent of changes in behavior. Proc. Natl. Acad. Sci. USA 2004, 101, 18223–18227. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Diosdado, A.; Correa, J.L.d.; Angulo-Brown, F.; Calleja-Quevedo, E. Fractal analysis of human gait: Old and young, healthy and ill subjects. Revista Mexicana de Fisica 2005, 51, 14–21. [Google Scholar]
- Muñoz-Diosdado, A.; Hernández, L.R.; Aguilar-Molina, A.M.; Zamora-Justo, J.A.; Gutiérrez-Calleja, R.A.; Virgilio-González, C.D. Multifractal analysis and the NYHA index. AIP Conf. Proc. 2014, 1626, 155–158. [Google Scholar]
- Ivanov, P.C.; Ma, Q.D.Y.; Bartsch, R.P.; Hausdorff, J.M.; Nunes-Amaral, L.A.; Schulte-Frohlinde, V.; Stanley, H.E.; Yoneyama, M. Levels of Complexity in Scale-Invariant Neural Signals. Phys. Rev. E 2009, 79, 041920. [Google Scholar] [CrossRef] [PubMed]
- Ponard, G.C.; Kondratyev, A.A.; Kucera, J.P. Mechanisms of Intrinsic Beating Variability in Cardiac Cell Cultures and Model Pacemaker Networks. Biophys. J. 2007, 92, 3734–3752. [Google Scholar] [CrossRef] [PubMed]
- Guzmán-Vargas, L.; Angulo-Brown, F. Simple model of the aging effect in heart interbeat time series. Phys. Rev. E. 2003, 67, 052901. [Google Scholar] [CrossRef] [PubMed]
- Jameson, J.L.; Fauci, A.S.; Kasper, D.L.; Hauser, S.L.; Longo; Loscalzo, J. Harrison’s Principles of Internal Medicine, 20th ed.; McGraw-Hill Education: New York, NY, USA, 2018; Volumes 1 and 2. [Google Scholar]
- Shah, S.J. Heart Failure. Available online: https://www.merckmanuals.com/professional/cardiovascular-disorders/heart-failure/heart-failure (accessed on 7 June 2019).
- Raphael, C.; Briscoe, C.; Davies, J.; Whinnett, Z.I.; Manisty, C.; Sutton, R.; Mayet, J.; Francis, D.P. Limitations of the New York Heart Association functional classification system and self-reported walking distances in chronic heart failure. Heart 2007, 93, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Chhabra, B.; Jensen, R.V. Direct determination of the f(α) singularity spectrum. Phys. Rev. Lett. 1989, 62, 1327–1330. [Google Scholar] [CrossRef] [PubMed]
- Kline, M. Calculus: An Intuitive and Physical Approach, 2nd ed.; Dover Publications: Mineola, NY, USA, 1998; pp. 456–461. [Google Scholar]
- Spiegel, M.R.; Lipschitz, S. Schaum’s Outline of Vector Analysis, 1st ed.; McGraw-Hill Education: New York, NY, USA, 1969. [Google Scholar]
- Goldberger, L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.-G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Havlin, S.; Ivanov, P.C. Modeling transient correlations in heartbeat dynamics during sleep. Europhys. Lett. 2003, 62, 147–153. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, D.J.; Burden, A.M. Numerical Analysis, 10th ed.; Cencage Learning: Independence, KY, USA, 2016. [Google Scholar]
- King, J. MATLAB 6 for Engineers: Hands-On Tutorial; R.T. Edwards Inc.: Philadelphia, PA, USA, 2001. [Google Scholar]
- Sharma, B.; Owens, R.; Malhotra, A. Sleep in Congestive Heart Failure. Med Clin. North Am. 2010, 94, 447–464. [Google Scholar] [CrossRef] [PubMed]
| Healthy | CHF | |
|---|---|---|
| 24 h RR time series. | Right skewed (49 subjects) r = 1.9 ± 1.0 | Right skewed (25 patients) r = 1.5 ± 0.5 |
| Left skewed (5 subjects) r = 0.9 ± 0.05 | Left skewed (19 patients) r = 0.8 ± 0.16 | |
| 6 h RR time series asleep | Right skewed (54 subjects) r = 4.5 ± 5.3 | Right skewed (25 patients) r = 1.9 ± 0.8 |
| Left skewed (0 subjects) | Left skewed (19 patients) r = 0.7 ± 0.18 | |
| 6 h RR time series awake | Right skewed (45 subjects) r = 2.0 ± 0.8 | Right skewed (31 patients) r = 1.9 ± 0.8 |
| Left skewed (9 subjects) r = 0.8 ± 0.08 | Left skewed (9 patients) r = 0.7 ± 0.2 |
| Person | r | Person | r | Person | r |
|---|---|---|---|---|---|
| nsr01(64F) | 1.85 | nsr19(65F) | 1.69 | nsr37(63M) | 2.56 |
| nsr02(67M) | 1.52 | nsr20(58F) | 1.14 | nsr38(62M) | 1.23 |
| nsr03(67F) | 1.14 | nsr21(59M) | 2.19 | nsr39(70F) | 1.49 |
| nsr04(62F) | 2.05 | nsr22(68M) | 3.38 | nsr40(63F) | 3.34 |
| nsr05(62F) | 1.80 | nsr23(66F) | 1.97 | nsr41(64F) | 1.28 |
| nsr06(64M) | 2.66 | nsr24(63F) | 2.07 | nsr42(68F) | 2.21 |
| nsr07(76M) | 2.12 | nsr25(75M) | 0.92 | nsr43(66M) | 1.87 |
| nsr08(64F) | 1.76 | nsr26(72M) | 0.83 | nsr44(65F) | 1.57 |
| nsr09(66M) | 1.22 | nsr27(64M) | 4.47 | nsr45(67F) | 1.76 |
| nsr10(61F) | 1.71 | nsr28(65M) | 2.20 | nsr46(63F) | 1.82 |
| nsr11(65F) | 1.04 | nsr29(63M) | 1.44 | nsr47(28.5M) | 1.01 |
| nsr12(66M) | 2.94 | nsr30(70F) | 6.65 | nsr48(38M) | 0.88 |
| nsr13(63F) | 1.34 | nsr31(67M) | 2.35 | nsr49(39M) | 1.06 |
| nsr14(65F) | 1.40 | nsr32(68M) | 1.81 | nsr50(29M) | 0.83 |
| nsr15(74M) | 1.34 | nsr33(65M) | 3.93 | nsr51(40M) | 1.15 |
| nsr16(73F) | 1.24 | nsr34(67M) | 2.75 | nsr52(39M) | 1.05 |
| nsr17(71F) | 1.40 | nsr35(66M) | 1.18 | nsr53(35M) | 1.69 |
| nsr18(68M) | 1.27 | nsr36(60F) | 1.24 | nsr54(35M) | 0.94 |
| Person | Awake | Asleep | Patient | Awake | Asleep |
|---|---|---|---|---|---|
| nsr01 | 1.88 | 3.17 | chf001 | 1.45 | 1.56 |
| nsr02 | 1.52 | 2.90 | chf002 | 1.06 | 0.62 |
| nsr03 | 1.19 | 3.01 | chf004 | 1.44 | 1.16 |
| nsr04 | 1.58 | 4.09 | chf005 | 0.63 | 1.43 |
| nsr05 | 0.72 | 2.99 | chf006 | No data | 1.85 |
| nsr06 | 0.92 | 3.09 | chf007 | 2.91 | 1.06 |
| nsr07 | 1.34 | 20.70 | chf008 | 3.67 | 1.94 |
| nsr08 | 2.28 | 3.36 | chf010 | 1.04 | 0.28 |
| nsr09 | 1.41 | 3.99 | chf011 | 1.70 | 1.51 |
| nsr10 | 1.04 | 3.06 | chf012 | 1.02 | 1.20 |
| nsr11 | 0.95 | 3.10 | chf013 | 0.30 | 1.02 |
| nsr12 | 3.05 | 3.19 | chf014 | 0.89 | 1.01 |
| nsr13 | 1.61 | 2.46 | chf015 | 0.62 | 1.05 |
| nsr14 | 1.47 | 2.86 | chf201 | 2.70 | 1.15 |
| nsr15 | 0.95 | 31.86 | chf202 | 0.80 | 0.70 |
| nsr16 | 0.83 | 1.65 | chf203 | 2.84 | 3.71 |
| nsr17 | 1.03 | 1.57 | chf204 | 2.13 | 1.60 |
| nsr18 | 2.15 | 1.45 | chf205 | 0.61 | 0.47 |
| nsr19 | 2.06 | 2.32 | chf207 | 0.75 | 1.28 |
| nsr20 | 1.32 | 1.45 | chf208 | 2.56 | 1.62 |
| nsr21 | 1.01 | 2.38 | chf209 | No data | 0.80 |
| nsr22 | 3.10 | 3.67 | chf210 | 2.45 | 2.01 |
| nsr23 | 1.14 | 1.74 | chf211 | 0.82 | 2.51 |
| nsr24 | 4.15 | 1.55 | chf212 | 0.44 | 0.66 |
| nsr25 | 0.79 | 1.85 | chf213 | 0.89 | 2.65 |
| nsr26 | 0.75 | 8.41 | chf214 | 0.98 | 1.51 |
| nsr27 | 2.41 | 2.80 | chf215 | 2.45 | 0.75 |
| nsr28 | 2.30 | 3.50 | chf216 | 2.48 | 1.89 |
| nsr29 | 1.05 | 2.92 | chf217 | 1.30 | 3.63 |
| nsr30 | 2.53 | 17.01 | chf218 | 0.82 | 3.28 |
| nsr31 | 1.82 | 2.73 | chf219 | 1.10 | 2.20 |
| nsr32 | 1.18 | 3.40 | chf220 | 0.91 | 1.25 |
| nsr33 | 3.59 | 6.52 | chf221 | 0.82 | 2.18 |
| nsr34 | 1.93 | 9.43 | chf223 | 0.64 | 1.09 |
| nsr35 | 1.94 | 1.49 | chf224 | 1.56 | 2.60 |
| nsr36 | 3.52 | 4.53 | chf225 | 0.68 | 0.98 |
| nsr37 | 3.80 | 3.16 | chf226 | 2.45 | 3.17 |
| nsr38 | 1.98 | 2.40 | chf227 | 1.20 | 2.56 |
| nsr39 | 2.81 | 3.48 | chf228 | 1.12 | 3.01 |
| nsr40 | 2.57 | 5.39 | chf229 | 0.53 | 0.69 |
| nsr41 | 1.69 | 1.22 | |||
| nsr42 | 2.12 | 1.40 | |||
| nsr43 | 3.22 | 3.07 | |||
| nsr44 | 2.14 | 2.45 | |||
| nsr45 | 2.17 | 4.09 | |||
| nsr46 | 1.05 | 3.73 | |||
| nsr47 | 1.85 | 2.87 | |||
| nsr48 | 0.86 | 2.91 | |||
| nsr49 | 1.14 | 14.96 | |||
| nsr050 | 1.25 | 2.76 | |||
| nsr051 | 1.52 | 3.88 | |||
| nsr052 | 1.28 | 3.09 | |||
| nsr053 | 2.52 | 2.91 | |||
| nsr054 | 0.86 | 3.86 |
| Patient | r | Patient | r | Patient | r |
|---|---|---|---|---|---|
| chf001(III-IV, 71M) | 1.09 | chf201(III, 55M) | 1.51 | chf216(II, 58U) | 0.94 |
| chf002(III-IV, 61F) | 1.05 | chf202(III, 59F) | 0.85 | chf217(I, 50U) | 1.99 |
| chf003(III-IV, 63M) | 1.73 | chf203(III, 68M) | 1.25 | chf218(I, 72U) | 1.04 |
| chf004(III-IV, 54M) | 1.18 | chf204(III, 62M) | 1.62 | chf219(III, 62U) | 1.39 |
| chf005(III-IV, 59F) | 0.72 | chf205(III, 39M) | 0.47 | chf220(II, 64U) | 1.02 |
| chf006(III-IV, UM) | 1.89 | chf206(III, 38F) | 0.91 | chf221(I, 37U) | 1.11 |
| chf007(III-IV, 48M) | 2.41 | chf207(III, 62M) | 0.82 | chf222(III, 63U) | 0.76 |
| chf008(III-IV, 51M) | 2.51 | chf208(III, 62M) | 0.77 | chf223(III, 56U) | 0.87 |
| chf009(III-IV, 63F) | 0.87 | chf209(III, 65M) | 0.88 | chf224(II, 35U) | 1.85 |
| chf010(III-IV, 22M) | 1.03 | chf210(III, 43M) | 2.02 | chf225(III, 66U) | 0.78 |
| chf011(III-IV, 54F) | 1.54 | chf211(II, 34U) | 1.48 | chf226(II, 51U) | 2.44 |
| chf012(III-IV, 61M) | 0.89 | chf212(II, 54U) | 0.41 | chf227(III, 64U) | 1.27 |
| chf013(III-IV, 63M) | 0.71 | chf213(I, 53U) | 1.34 | chf228(III, 31U) | 1.25 |
| chf014(III-IV, 61M) | 1.01 | chf214(II, 79U) | 0.89 | chf229(III,58U) | 0.54 |
| chf015(III-IV, 53M) | 0.60 | chf215(II, 43U) | 0.86 |
| Time Series of 6 h | Awake | Asleep |
|---|---|---|
| NYHA I | 325 ± 57 | 706 ± 131 |
| NYHA II | 1434 ± 270 | 1442 ± 276 |
| NYHA III | 1649 ± 304 | 1651 ± 300 |
| NYHA III-IV | 3419 ± 890 | 3054 ± 801 |
| healthy people | 587 ± 108 | 1177 ± 220 |
| CHF patients | 1986 ± 380 | 1971 ± 377 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar-Molina, A.M.; Angulo-Brown, F.; Muñoz-Diosdado, A. Multifractal Spectrum Curvature of RR Tachograms of Healthy People and Patients with Congestive Heart Failure, a New Tool to Assess Health Conditions. Entropy 2019, 21, 581. https://doi.org/10.3390/e21060581
Aguilar-Molina AM, Angulo-Brown F, Muñoz-Diosdado A. Multifractal Spectrum Curvature of RR Tachograms of Healthy People and Patients with Congestive Heart Failure, a New Tool to Assess Health Conditions. Entropy. 2019; 21(6):581. https://doi.org/10.3390/e21060581
Chicago/Turabian StyleAguilar-Molina, Ana María, Fernando Angulo-Brown, and Alejandro Muñoz-Diosdado. 2019. "Multifractal Spectrum Curvature of RR Tachograms of Healthy People and Patients with Congestive Heart Failure, a New Tool to Assess Health Conditions" Entropy 21, no. 6: 581. https://doi.org/10.3390/e21060581
APA StyleAguilar-Molina, A. M., Angulo-Brown, F., & Muñoz-Diosdado, A. (2019). Multifractal Spectrum Curvature of RR Tachograms of Healthy People and Patients with Congestive Heart Failure, a New Tool to Assess Health Conditions. Entropy, 21(6), 581. https://doi.org/10.3390/e21060581





