1. Introduction
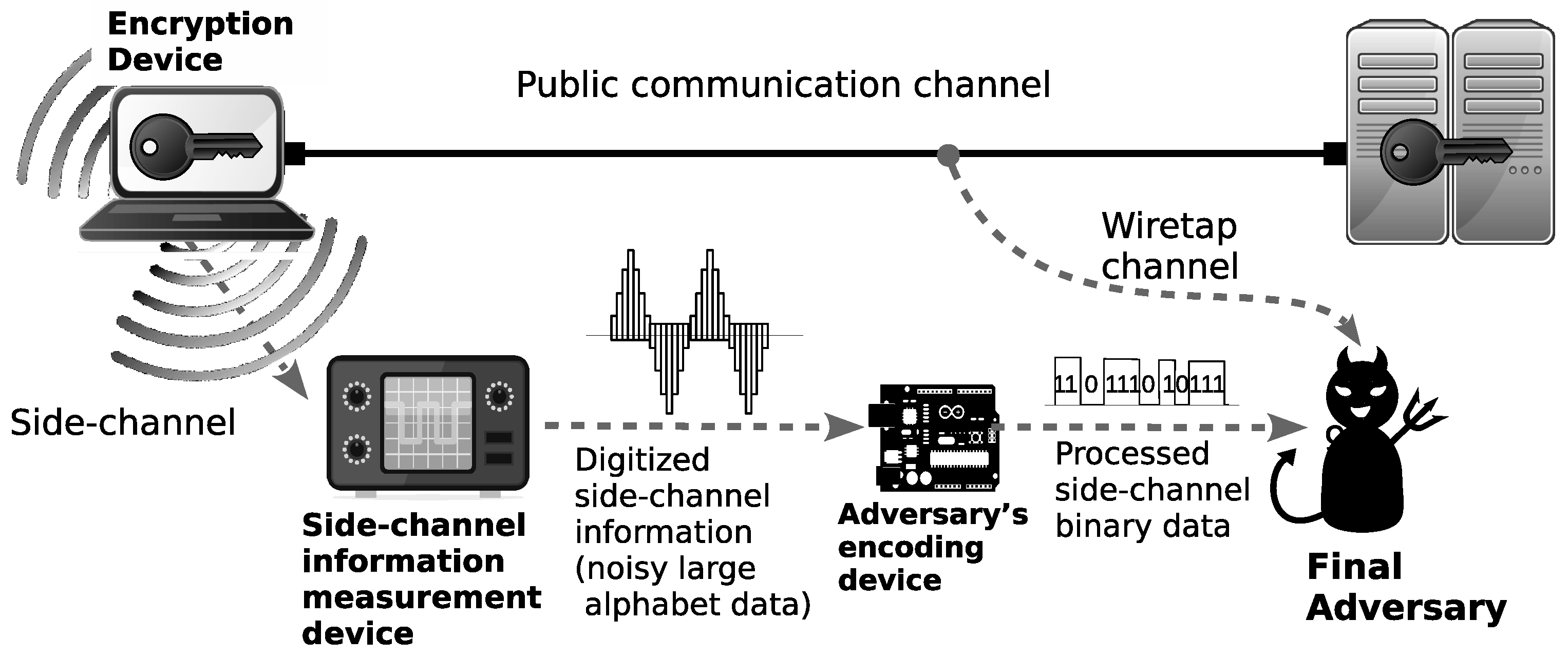
In most of theoretical security models for encryption schemes, the adversary only obtains information from the public communication channel. In such models, an adversary is often treated as an entity that tries to obtain information about the hidden source only from the ciphertexts that are sent through the public communication channel. However, in the real world, the encryption schemes are implemented on physical electronic devices, and it is widely known that any process executed in an electronic circuit will generate a certain kind of correlated physical phenomena as “side” effects, according to the type of process. For example, differences in inputs to a process in an electronic circuit can induce differences in the heat, power consumption, and electromagnetic radiation generated as byproducts by the devices. Therefore, we may consider that an adversary who has a certain degree of physical access to the devices may obtain some information on very sensitive hidden data, such as the keys used for the encryption, just by measuring the generated physical phenomena using appropriate measurement devices. More precisely, an adversary may deduce the value of the bits of the key by measuring the differences in the timing of the process of encryption or the differences in the power consumption, electromagnetic radiation, and other physical phenomena. This information channel where the adversary obtains data in the form of physical phenomena is called the side-channel, and attacks using the side-channel are known as side-channel attacks.
In the literature, there have been many works showing that adversaries have succeeded in breaking the security of cryptographic systems by exploiting side-channel information such as running time, power consumption, and electromagnetic radiation in the real physical world [
1,
2,
3,
4,
5].
1.1. Our Contributions
1.1.1. Security Model for Side-Channel Attacks
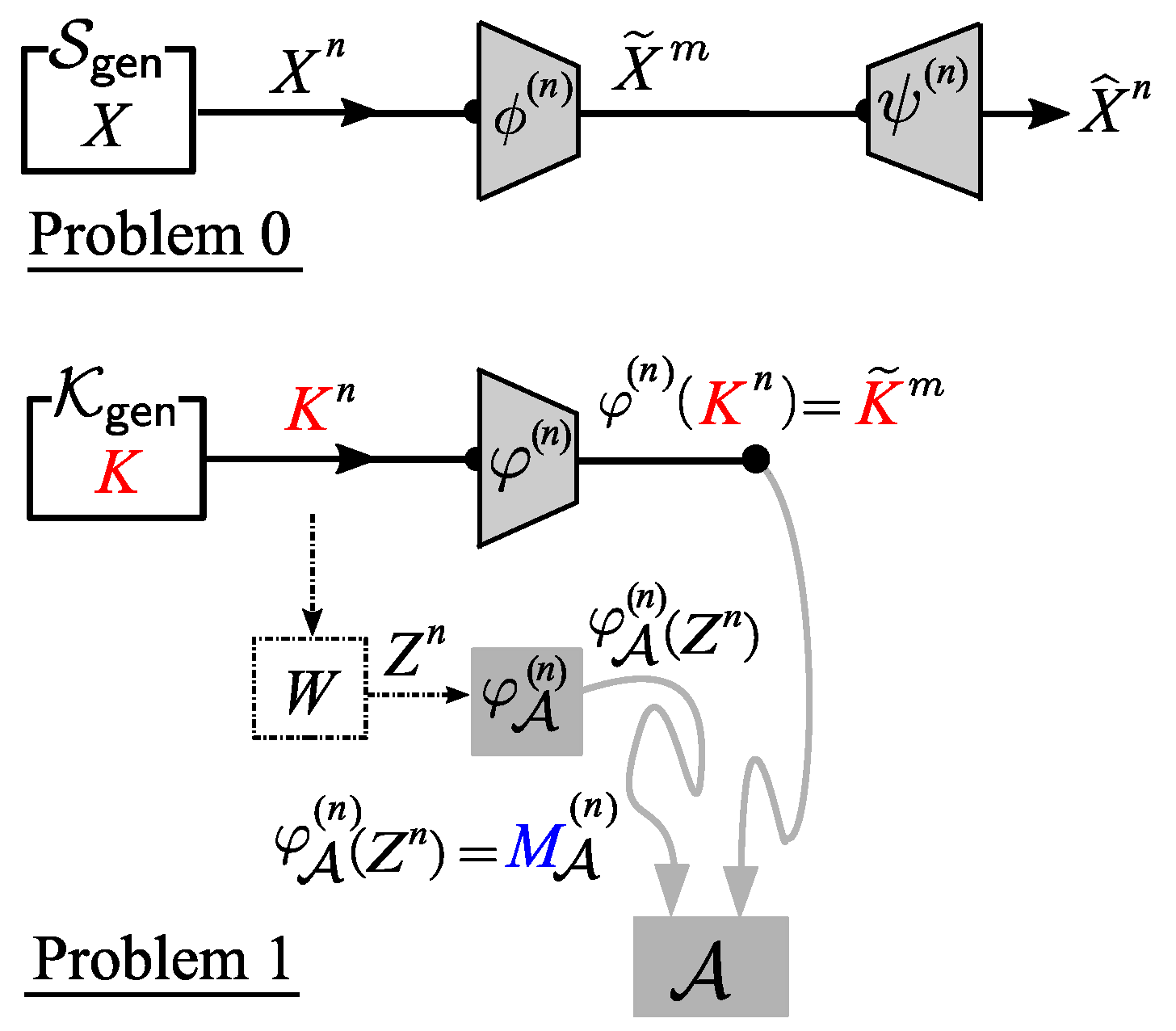
In this paper, we propose a security model where the adversary attempts to obtain information about the hidden source by collecting data from (1) the public communication channel in the form of ciphertexts, and (2) the side-channel in the form of some physical data related to the encryption keys. Our proposed security model is illustrated in
Figure 1.
Based on the security model illustrated above, we formulate a security problem of strengthening the security of Shannon cipher system where the encryption is implemented on a physical encryption device and the adversary attempts to obtain some information on the hidden source by collecting ciphertexts and performing side-channel attacks.
We describe our security model in a more formal way as follows. The source X is encrypted using an encryption device with secret key K installed. The result of the encryption, i.e., ciphertext C, is sent through a public communication channel to a data center where C is decrypted back into the source X using the same key K. The adversary is allowed to obtain C from the public communication channel and is also equipped with an encoding device that encodes and processes the noisy large alphabet data Z, i.e., the measurement result of the physical information obtained from the side-channel, into the appropriate binary data . It should be noted that in our model, we do not put any limitation on the kind of physical information measured by the adversary. Hence, any theoretical result based on this model automatically applies to any kind of side-channel attack, including timing analysis, power analysis, and electromagnetic (EM) analysis. In addition, the measurement device may just be a simple analog-to-digital converter that converts the analog data representing physical information leaked from the device into “noisy” digital data Z. In our model, we represent the measurement process as a communication channel W.
1.1.2. Main Result
As the main theoretical result, we show that we can strengthen the secrecy/security of the Shannon cipher implemented on a physical device against an adversary who collects the ciphertexts and launches side-channel attacks by a simple method of compressing the ciphertext C from a Shannon cipher using an affine encoder into before releasing it into the public communication channel.
We prove that in the case of one-time pad encryption, we can strengthen the secrecy/security of the cipher system by using an appropriate affine encoder. More precisely, we prove that for any distribution of the secret key K and any measurement device (used to convert the physical information from a side-channel into the noisy large alphabet data Z), we can derive an achievable rate region for such that if we compress the ciphertext C into using the affine encoder , which has an encoding rate R inside the achievable region, then we can achieve reliability and security in the following sense:
anyone with secret key K can construct an appropriate decoder that decrypts and encodes with exponentially decaying error probability, but
the amount of information gained by any adversary who obtains the compressed ciphertext and encoded physical information is exponentially decaying to zero as long as the encoding device encodes the side physical information into with a rate within the achievable rate region.
By utilizing the homomorphic property of one-time-pad and affine encoding, we are able to separate the theoretical analysis of reliability and security such that we can deal with each issue independently. For reliability, we mainly obtain our result by using the result of Csizár [
6] on the universal coding for a single source using linear codes. For the security analysis, we derive our result by adapting the framework of the one helper source coding problem posed and investigated by Ahlswede, Körner [
7] and Wyner [
8]. Specifically, in order to derive the secrecy exponent, we utilize the exponential strong converse theorem of Oohama [
9] for the one helper source coding problem. In [
10], Watanabe and Oohama deal with a similar source coding problem, but their result is insufficient for deriving the lower bound of the secrecy exponent. We will explain the relation between our method and previous related works in more detail in
Section 4.
1.2. Comparison to Existing Models of Side-Channel Attacks
The most important feature of our model is that we do not make any assumption about the type or characteristics of the physical information that is measured by the adversary. Several theoretical models analyzing the security of a cryptographic system against side-channel attacks have been proposed in the literature. However, most of the existing works are applicable only for specific characteristics of the leaked physical information. For example, Brier et al. [
1] and Coron et al. [
11] propose a statistical model for side-channel attacks using the information from power consumption and the running time, whereas Agrawal et al. [
5] propose a statistical model for side-channel attacks using electromagnetic (EM) radiations. A more general model for side-channel attacks is proposed by Köpf et al. [
12] and Backes et al. [
13], but they are heavily dependent upon implementation on certain specific devices. Micali et al. [
14] propose a very general security model to capture the side-channel attacks, but they fail to offer any hint of how to build a concrete countermeasure against the side-channel attacks. The closest existing model to ours is the general framework for analyzing side-channel attacks proposed by Standaert et al. [
15]. The authors of [
15] propose a countermeasure against side-channel attacks that is different from ours, i.e., noise insertion on implementation. It should be noted that the noise insertion countermeasure proposed by [
15] is dependent on the characteristics of the leaked physical information. On the other hand, our countermeasure, i.e., compression using an affine encoder, is independent of the characteristics of the leaked physical information.
1.3. Comparison to Encoding before Encryption
In this paper, our proposed solution is to perform additional encoding in the form of compression after the encryption process. Our aim is that by compressing the ciphertext, we compress the key “indirectly” and increase the “flatness” of the key used in the compressed ciphertext () such that the adversary will not get much additional information from eavesdropping on the compressed ciphertext (). Instead of performing the encoding after encryption, one may consider performing the encoding before encryption, i.e., encoding the source and the key “directly” before performing the encryption. However, since we need to apply two separate encodings on the source and the key, we can expect that the implementation cost is more expensive than our proposed solution, i.e., approximately double the cost of applying our proposed solution. Moreover, it is not completely clear whether our security analysis still applies for this case. For example, if the adversary performs the side-channel attacks on the key after it is encoded (before encryption), we need a complete remodeling of the security problem.
1.4. Organization of this Paper
This paper is structured as follows. In
Section 2, we show the basic notations and definitions that we use throughout this paper, and we also describe the formal formulations of our model and the security problem. In
Section 3, we explain the idea and the formulation of our proposed solution. In
Section 4, we explain the relation between our formulation and previous related works. Based on this, we explain the theoretical challenge which we have to overcome to prove that our proposed solution is sound. In
Section 5, we state our main theorem on the reliability and security of our solution. In
Section 6, we show the proof of our main theorem. We put the proofs of other related propositions, lemmas, and theorems in the appendix.
2. Problem Formulation
In this section, we will introduce the general notations used throughout this paper and provide a description of the basic problem we are focusing on, i.e., side-channel attacks on Shannon cipher systems. We also explain the basic framework of the solution that we consider to solve the problem. Finally, we state the formulation of the reliability and security problem that we consider and aim to solve in this paper.
2.1. Preliminaries
In this subsection, we show the basic notations and related consensus used in this paper.
Random Source of Information and Key: Let X be a random variable from a finite set . Let be a stationary discrete memoryless source (DMS) such that for each , takes values in the finite set and obeys the same distribution as that of X denoted by . The stationary DMS is specified with . In addition, let K be a random variable taken from the same finite set and representing the key used for encryption. Similarly, let be a stationary discrete memoryless source such that for each , takes values in the finite set and obeys the same distribution as that of K denoted by . The stationary DMS is specified with . In this paper, we assume that is the uniform distribution over .
Random Variables and Sequences: We write the sequence of random variables with length
n from the information source as follows:
. Similarly, strings with length
n of
are written as
. For
,
stands for the probability of the occurrence of
. When the information source is memoryless, specified with
, the following equation holds:
In this case, we write as . Similar notations are used for other random variables and sequences.
Consensus and Notations: Without loss of generality, throughout this paper, we assume that is a finite field. The notation ⊕ is used to denote the field addition operation, while the notation ⊖ is used to denote the field subtraction operation, i.e., , for any elements . Throughout this paper, all logarithms are taken to the natural basis.
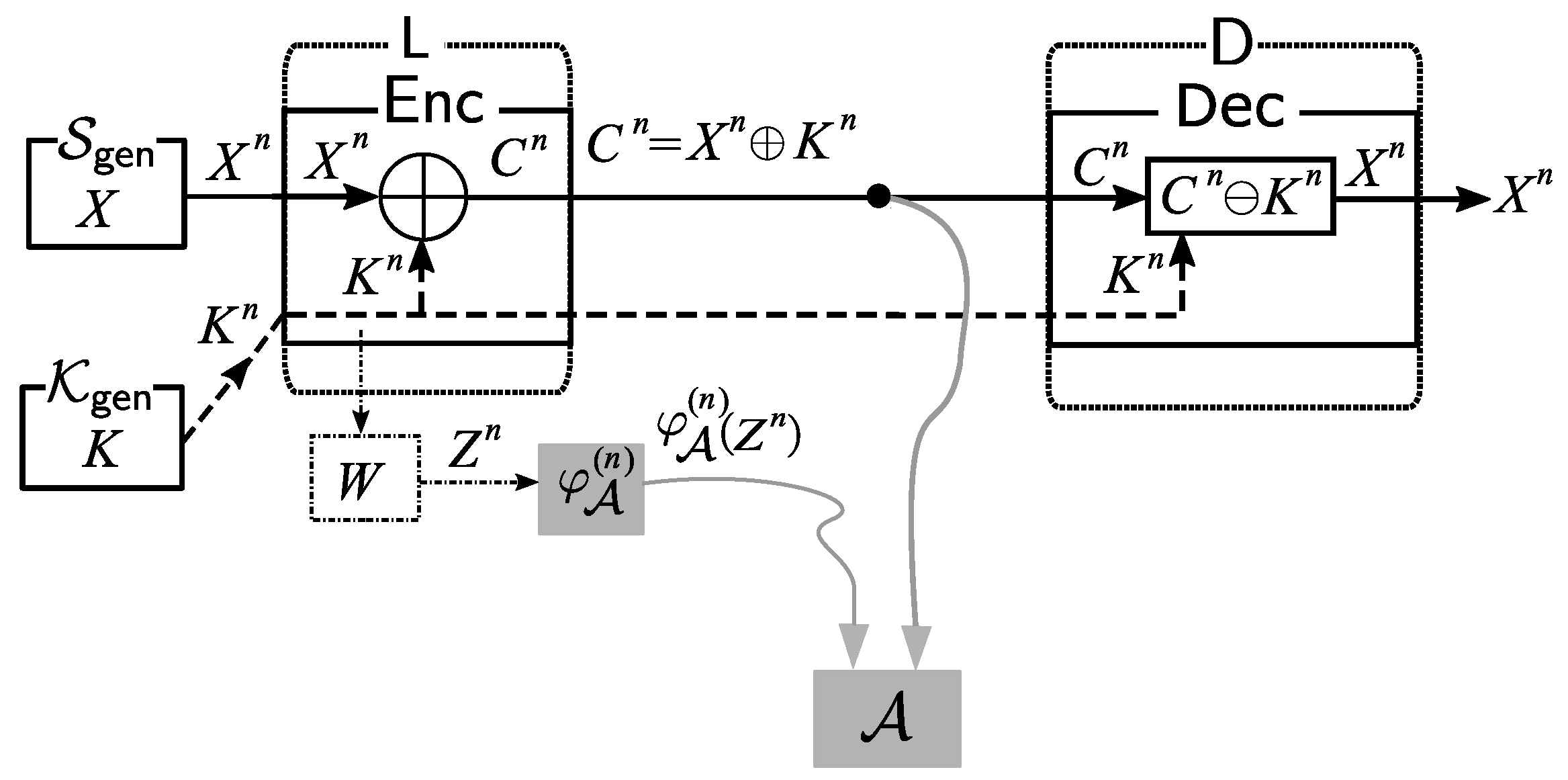
2.2. Basic System Description
In this subsection, we explain the basic system setting and the basic adversarial model we consider in this paper. First, let the information source and the key be generated independently by different parties and , respectively. In our setting, we assume the following:
Next, let the random source
from
be sent to the node
, and let the random key
from
also be sent to
. Further settings of our system are described as follows and are also shown in
Figure 2.
Source Processing: At the node
,
is encrypted with the key
using the encryption function
. The ciphertext
of
is given by
Transmission: Next, the ciphertext is sent to the information processing center through a public communication channel. Meanwhile, the key is sent to through a private communication channel.
Sink Node Processing: In , we decrypt the ciphertext using the key through the corresponding decryption procedure defined by . It is obvious that we can correctly reproduce the source output from and with the decryption function .
Side-Channel Attacks by Eavesdropper Adversary: An (eavesdropper) adversary
eavesdrops on the public communication channel in the system. The adversary
also uses side information obtained by side-channel attacks. In this paper, we introduce a new theoretical model of side-channel attacks that is described as follows. Let
be a finite set and let
be a noisy channel. Let
Z be a channel output from
W for the random input variable
K. We consider the discrete memoryless channel specified with
W. Let
be a random variable obtained as the channel output by connecting
to the input channel. We write a conditional distribution on
given
as
Since the channel is memoryless, we have
On the above output of for the input , we assume the following:
The three random variables X, K, and Z satisfy , which implies that .
W is given in the system and the adversary cannot control W.
Through side-channel attacks, the adversary can access .
We next formulate the side information the adversary
obtains by side-channel attacks. For each
, let
be an encoder function. Set
Let
be a rate of the encoder function
. For
, we set
For the encoded side information the adversary obtains, we assume the following.
The adversary , having accessed , obtains the encoded additional information . For each , the adversary can design .
The sequence must be upper-bounded by a prescribed value. In other words, the adversary must use such that for some and for any sufficiently large n, .
On the Scope of Our Theoretical Model: When the is not so large, the adversary may directly access . In contrast, in a real situation of side-channel attacks, often the noisy version of can be regarded as very close to an analog random signal. In this case, is sufficiently large and the adversary cannot obtain in a lossless form. Our theoretical model can address such situations of side-channel attacks.
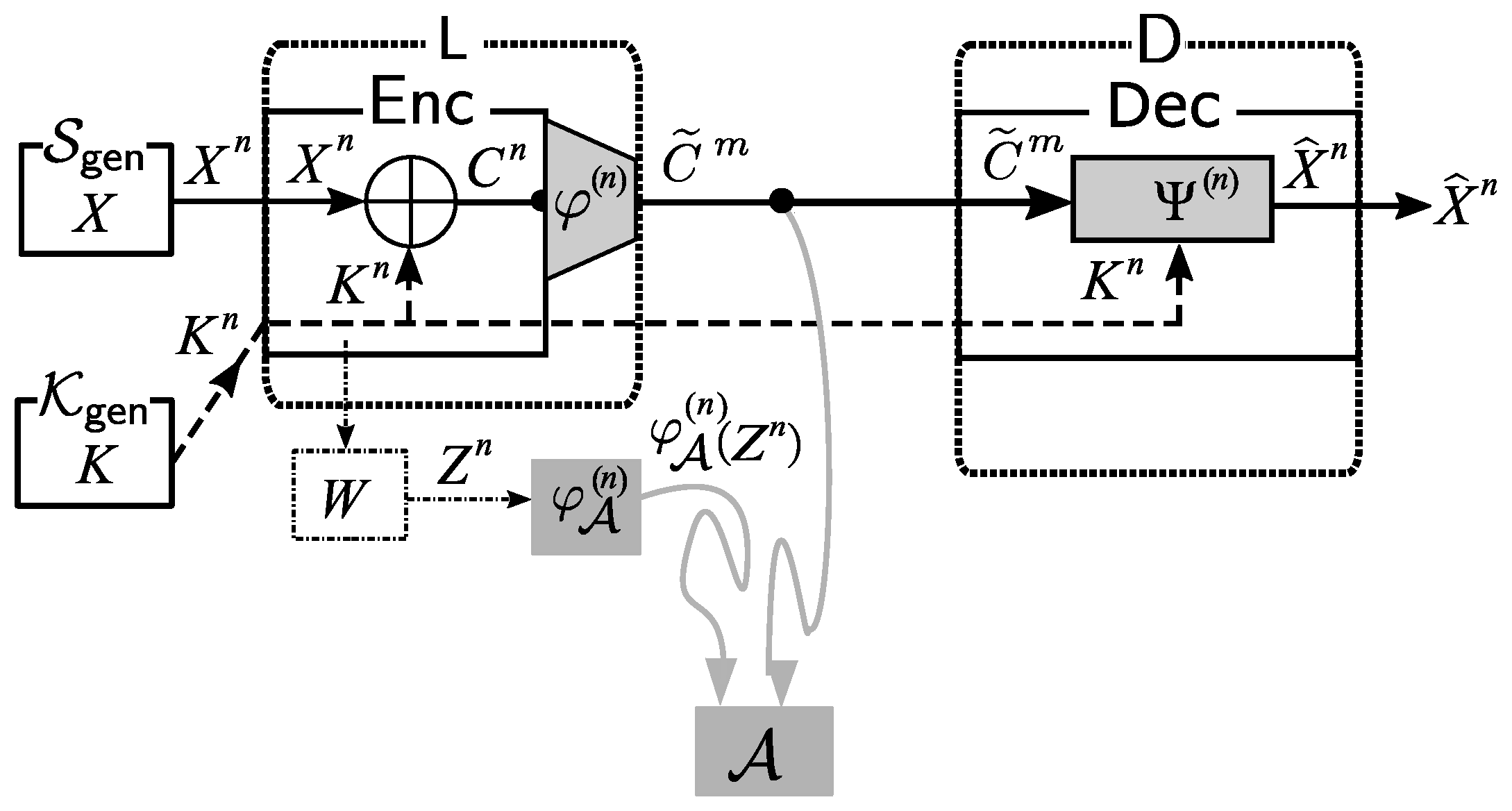
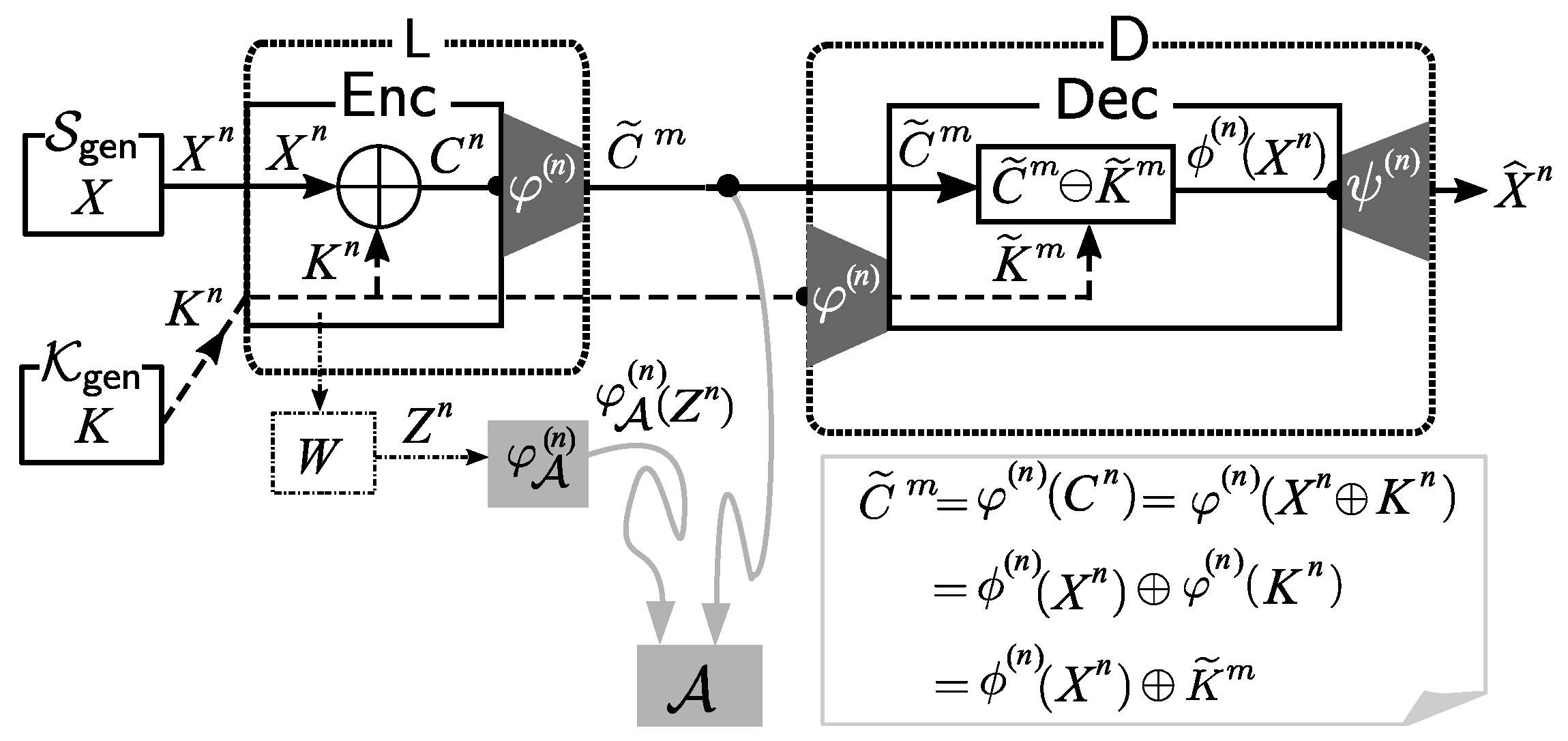
2.3. Solution Framework
As the basic solution framework, we consider applying a post-encryption-compression coding system. The application of this system is illustrated in
Figure 3.
Encoding at Source node: We first use to encode the ciphertext . The formal definition of is . Let . Instead of sending , we send to the public communication channel.
Decoding at Sink Nodes: receives from the public communication channel. Using the common key and the decoder function , outputs an estimation of .
On Reliability and Security: From the description of our system in the previous section, the decoding process in our system above is successful if
holds. Combining this and (
6), it is clear that the decoding error probabilities
are as follows:
Set
. The information leakage
on
from
is measured by the mutual information between
and
. This quantity is formally defined by
Reliable and Secure Framework:
Definition 1. A quantity R is achievable underfor the systemif there exists a sequencesuch that,
,
,
we haveand for any eavesdropperwithsatisfying,
Definition 2. [Reliable and Secure Rate Region] Letdenote the set of allsuch that R is achievable under. We callthe reliable and secure rate region.
Definition 3. A tripleis achievable underfor the systemif there exists a sequencesuch that,
,
,
we haveand for any eavesdropperwithsatisfying,
we have Definition 4 (Rate, Reliability, and Security Region)
. Letdenote the set of allsuch thatis achievable under. We callthe rate, reliability and security region.
Our aim in this paper is to find the explicit inner bounds of and .
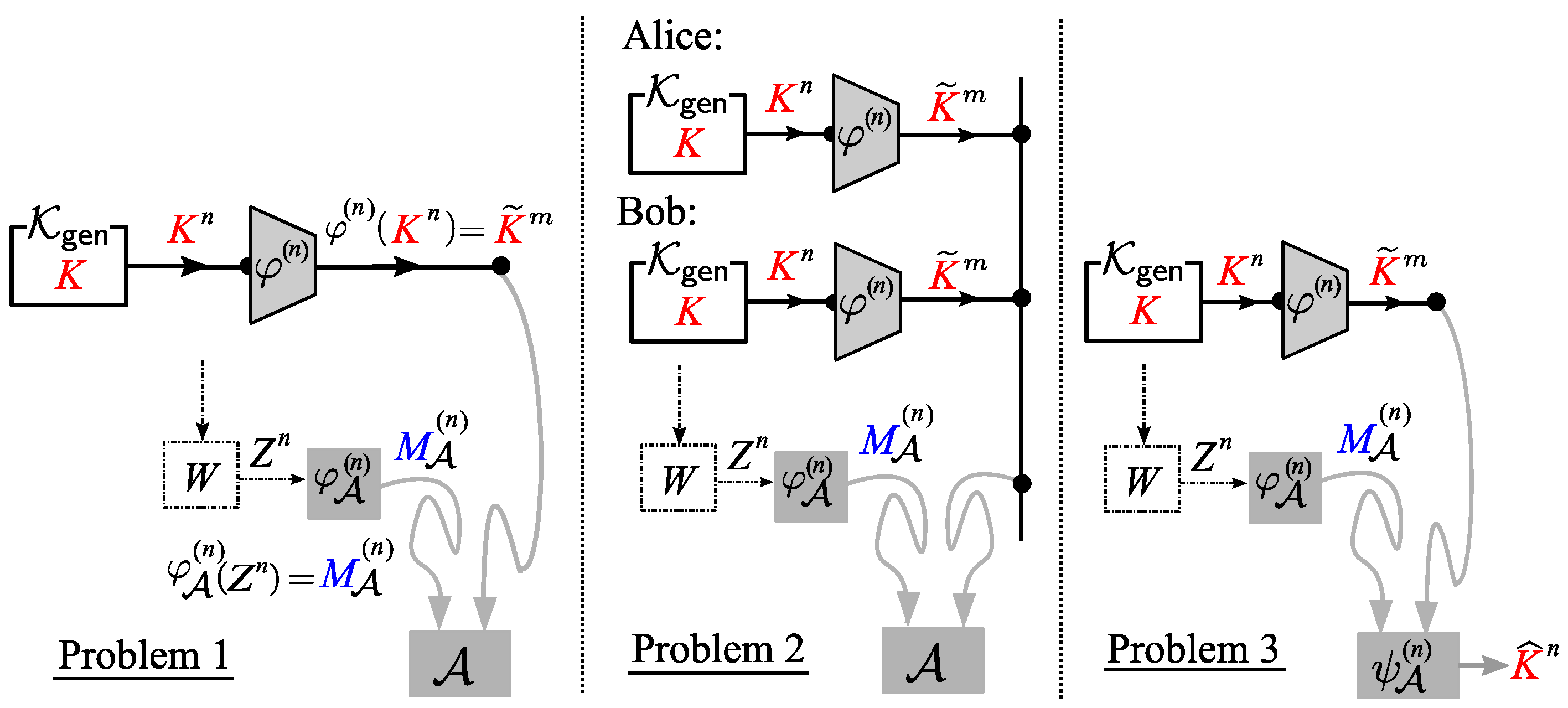
4. Previous Related Works
In this section, we introduce approaches from previous existing work related to Problem 0 (reliability) and Problem 1 (security). Our goal is that by showing these previous approaches, it will be easier to understand our approach to analyzing reliability and security. In particular, for Problem 1 (security), we explain approaches used in similar problems in previous works and highlight their differences from Problem 1.
We first state a previous result related to Problem 0. Let
be an affine encoder and
be a linear encoder induced by
. We define a function related to an exponential upper bound of
. Let
be an arbitrary random variable over
that has a probability distribution
. Let
denote the set of all probability distributions on
. For
and
, we define the following function:
By simple computation, we can prove that takes positive values if and only if . We have the following result.
Theorem 1. (Csiszár [
6]).
There exists a sequence such that for any ,
we havewhere is defined by Note that as .
It follows from Theorem 1 that if , then the error probability of decoding decays exponentially, and its exponent is lower bounded by the quantity . Furthermore, the code is a universal code that depends only on the rate R and not on the value of .
We next state two coding problems related to Problem 1. One is a problem on the privacy amplification for the bounded storage eavesdropper posed and investigated by Watanabe and Oohama [
10]. The other is the one helper source coding problem posed and investigated by Ashlswede and Körner [
7] and Wyner [
16]. We hereafter call the former and latter problems, respectively, Problem 2 and Problem 3. Problems 1–3 are shown in
Figure 6. As we can see from this figure, these three problems are based on the same communication scheme. The classes of encoder functions and the security criteria on
are different between these three problems. In Problem 1, the sequence of encoding functions
is restricted to the class of affine encoders to satisfy the homomorphic property. On the other hand, in Problems 2 and 3, we have no such restriction on the class of encoder functions. In descriptions of Problems 2 and 3, we state the difference in security criteria between Problems 1, 2, and 3. A comparison of three problems in terms of
and security criteria is summarized in
Table 1.
In Problem 2, Alice and Bob share a random variable
of block length
n, and an eavesdropper adversary
has a random variable
that is correlated to
. In such a situation, Alice and Bob try to distill a secret key as long as possible. In [
10], they considered a situation such that the adversary’s random variable
is stored in a storage that is obtained as a function value of
, and the rate of the storage size is bounded. This situation makes sense when the alphabet size of the adversary’s observation
is too huge to be stored directly in a storage. In such a situation, Watanabe and Oohama [
10] obtained an explicit characterization of the region
indicating the trade-off between the key rate
and the rate
of the storage size. In Problem 2, the variational distance
between
and
is used as a security criterion instead of
in Problem 1. Define
Then the formal definition of the region
is given by the following:
In Problem 3, the adversary outputs an estimation
of
from
and
. Let
be a decoder function of the adversary. Then
is given by
Let
be the error probability of decoding for Problem 3. The quantity
serves as a helper for the decoding of
from
. In Problem 3, Ahlswede and Körner [
7] and Wyner [
16] investigated an explicit characterization of the rate region
indicating the trade-off between
and
R under the condition that
vanishes asymptotically. The region
is formally defined by
The region
was determined by Ashlswede and Körner [
7] and Wyner [
16]. To state their result, we define several quantities. Let U be an auxiliary random variable taking values in a finite set
. We assume that the joint distribution of
is
The above condition is equivalent to
. Define the set of probability distribution
by
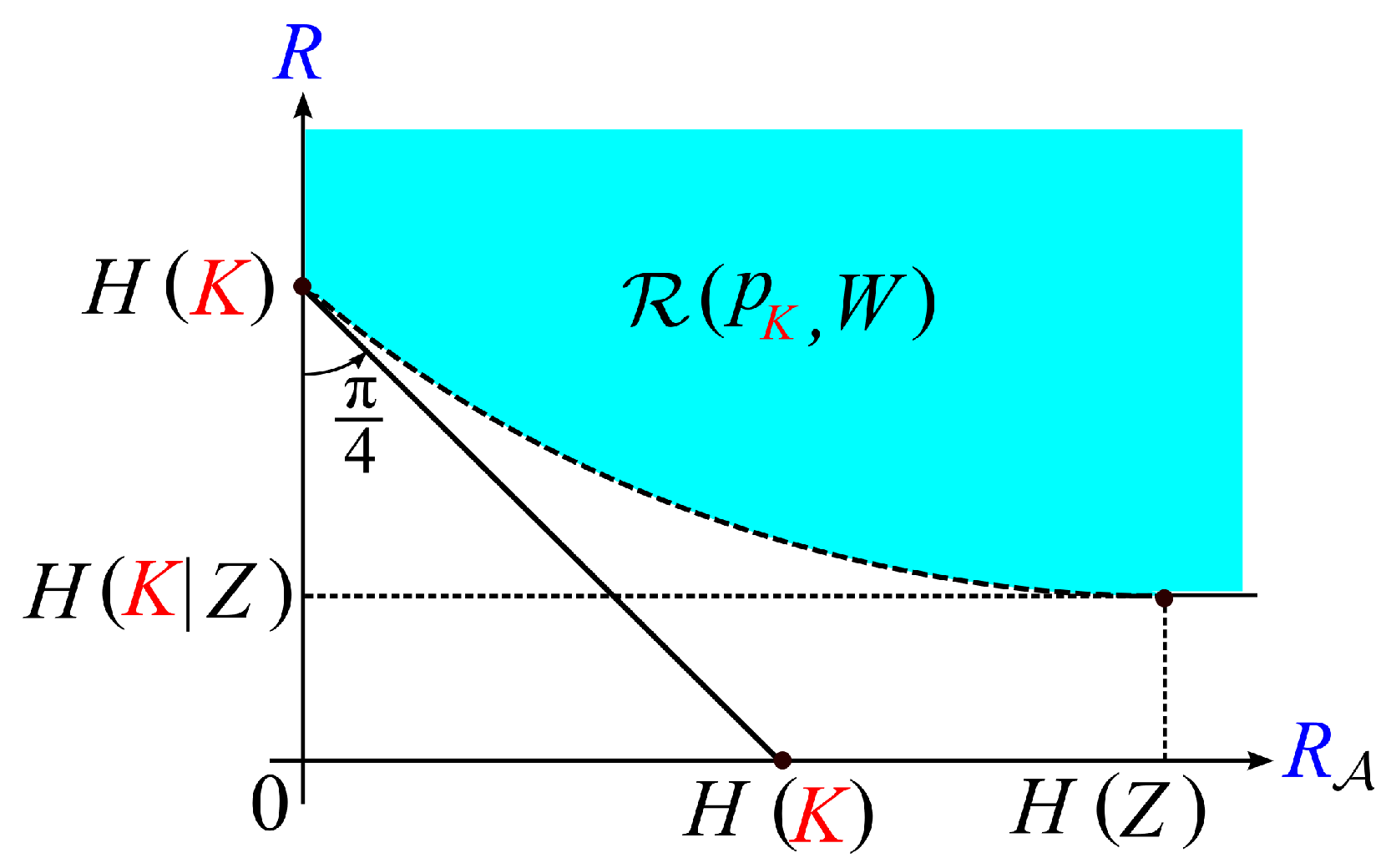
We can show that the region satisfies the following property.
Property
1. - (a)
The regionis a closed convex subset of.
- (b)
For any,
we have The minimum is attained by.
This result implies that Furthermore, the pointalways belongs to.
Property 1 part (a) is a well-known property. Proof of Property 1 part (b) is easy. Proofs of Property 1 parts (a) and (b) are omitted. Typical shape of the region
is shown in
Figure 7.
The rate region
was determined by Ahlswede and Körner [
7] and Wyner [
16]. Their result is the following.
Theorem 2. (Ahlswede, Körner [
7] andWyner [
16])
Watanabe and Oohama [
10] investigated an explicit form of
to show that it is equal to
, that is, we have the following result.
Theorem 3. (Watanabe and Oohama [
10])
In the remaining part of this section, we investigate a relationship between Problems 2 and 3 to give an outline of the proof of this theorem. Let
be the correct probability of decoding for Problem 3. The following lemma provides an important inequality to examine a relationship between these two problems.
Lemma 3. For any,
we have the following: Proof of this lemma is given in
Appendix A. Using Lemma 3, we can easily prove the inclusion
, which corresponds to the converse part of Theorem 3.
Proof of:
We assume that
. Then there exists
such that
,
From the above sequence
, we can construct the sequence
such that
Set
. Then from (14) and Lemma 3, we have
from which we have
for sufficiently large
n. From (13), (15), and the definition of
, we can see that
, or equivalent to
where we set
. Since
is arbitrary, we have that
By letting in (17) and considering that is an open set, we have that . □
To prove
, we examine an upper bound of
. For
, we define
According to Watanabe and Oohama [
10], we have the following two propositions.
Proposition 1. (Watanabe and Oohama [
10]).
Fix any positive . satisfying , we have Proposition 2. (Watanabe and Oohama [
10]).
If ,
then for any and any ,
we havewhich implies that The inclusion immediately follows from Propositions 1 and 2.
5. Reliability and Security Analysis
In this section, we state our main results. We use the affine encoder defined in the previous section. We upper bound and to obtain inner bounds of and .
Then we have the following proposition.
Proposition 3. For anyand any,
there exists a sequence of mappingssuch that for any,
we haveand for any eavesdropperwithsatisfying,
we have This proposition can be proved by several tools developed by previous works. The detail of the proof is given in the next section. As we stated in Proposition 2, Watanabe and Oohama [
10] proved that if
, then the quantity for any
and any
, the quantity
. Their method can not be applied to the analysis of
since the quantity
is multiplied with the quantity
in the definition of
. In this paper, we derive an upper bound of
that decays exponentially as
if
. To derive the upper bound, we use a new method that is developed by Oohama to prove strong converse theorems in multi-terminal source or channel networks [
9,
17,
18,
19,
20].
We define several functions and sets to describe the upper bound of
. Set
For
and for
, define
We next define a function serving as a lower bound of
. For each
, define
We can show that the above functions satisfy the following property.
Property 2. - (a)
The cardinality boundinis sufficient to describe the quantity. Furthermore, the cardinality boundinis sufficient to describe the quantity.
- (b)
For any,
we have - (c)
For anyand any,
we have - (d)
Fix anyand.
For,
we define a probability distributionby Then for,
is twice differentiable. Furthermore, for,
we have The second equality implies thatis a concave function of.
- (e)
For,
defineand set Then we have.
Furthermore, for any,
we have - (f)
For every,
the conditionimplieswhere g is the inverse function of.
Proof of this property is found in Oohama [
9] (extended version). On the upper bound of
, we have the following:
Proposition 4. For any,
we have Proof of this proposition is given in the next section. Proposition 4 has a close connection with the one helper source coding problem, which is explained as Problem 3 in the previous section. In fact, for the proof we use the result Oohama [
9] obtained for an explicit lower bound of the optimal exponent on the exponential decay of
for
. By Propositions 3 and 4, we obtain our main result shown below.
Theorem 4. For any
and any
, there exists a sequence of mappings
such that for any
, we have
and for any eavesdropper
with
satisfying
, we have
where
are defined by
Note that for , as .
The functions
and
take positive values if and only if
belongs to the set
Thus, by Theorem 4, under we have the following:
In terms of reliability, goes to zero exponentially as n tends to infinity, and its exponent is lower bounded by the function .
In terms of security, for any satisfying , the information leakage on goes to zero exponentially as n tends to infinity, and its exponent is lower bounded by the function .
The code that attains the exponent functions is the universal code that depends only on R and not on the value of the distribution .
From Theorem 4, we immediately obtain the following corollary.
A typical shape of
is shown in
Figure 8.