Stabilization of All Bell States in a Lossy Coupled-Cavity Array
Abstract
1. Introduction
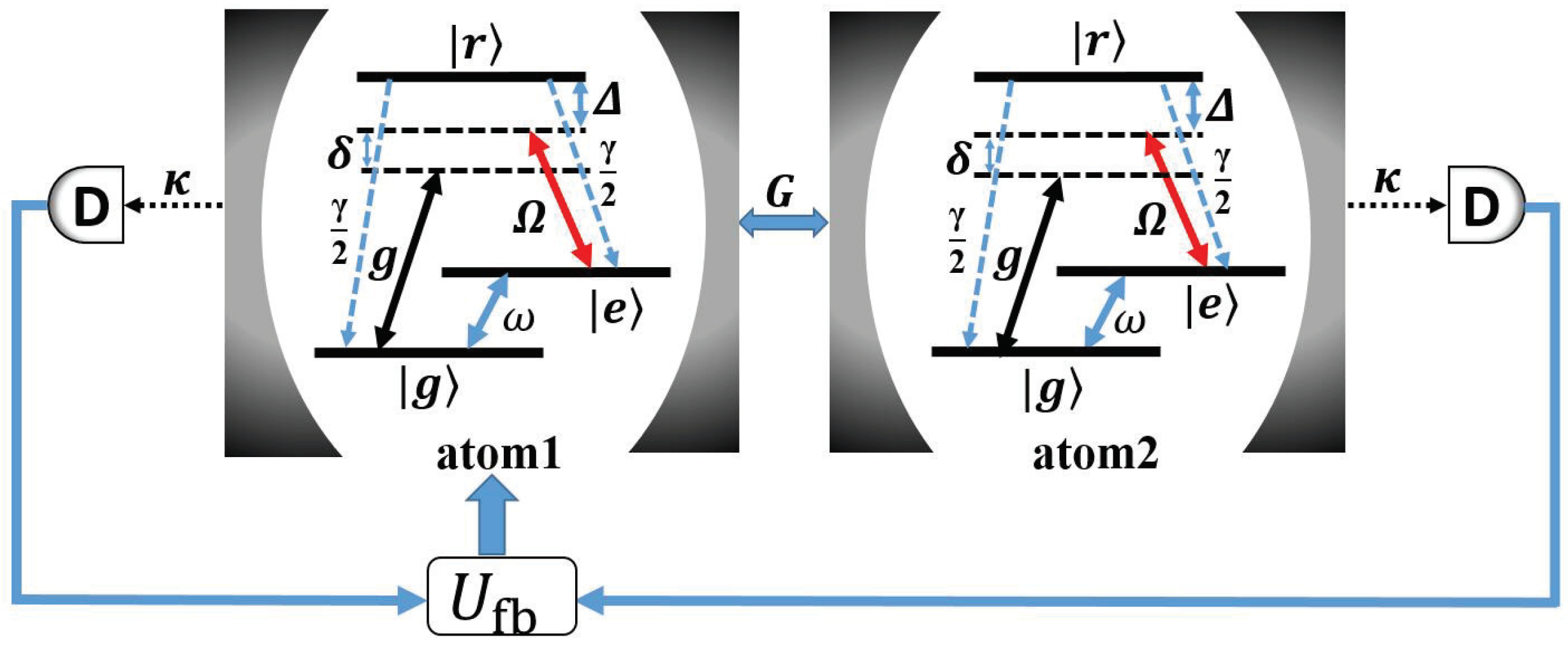
2. Effective Master Equation of the Coupled-Cavity Array System
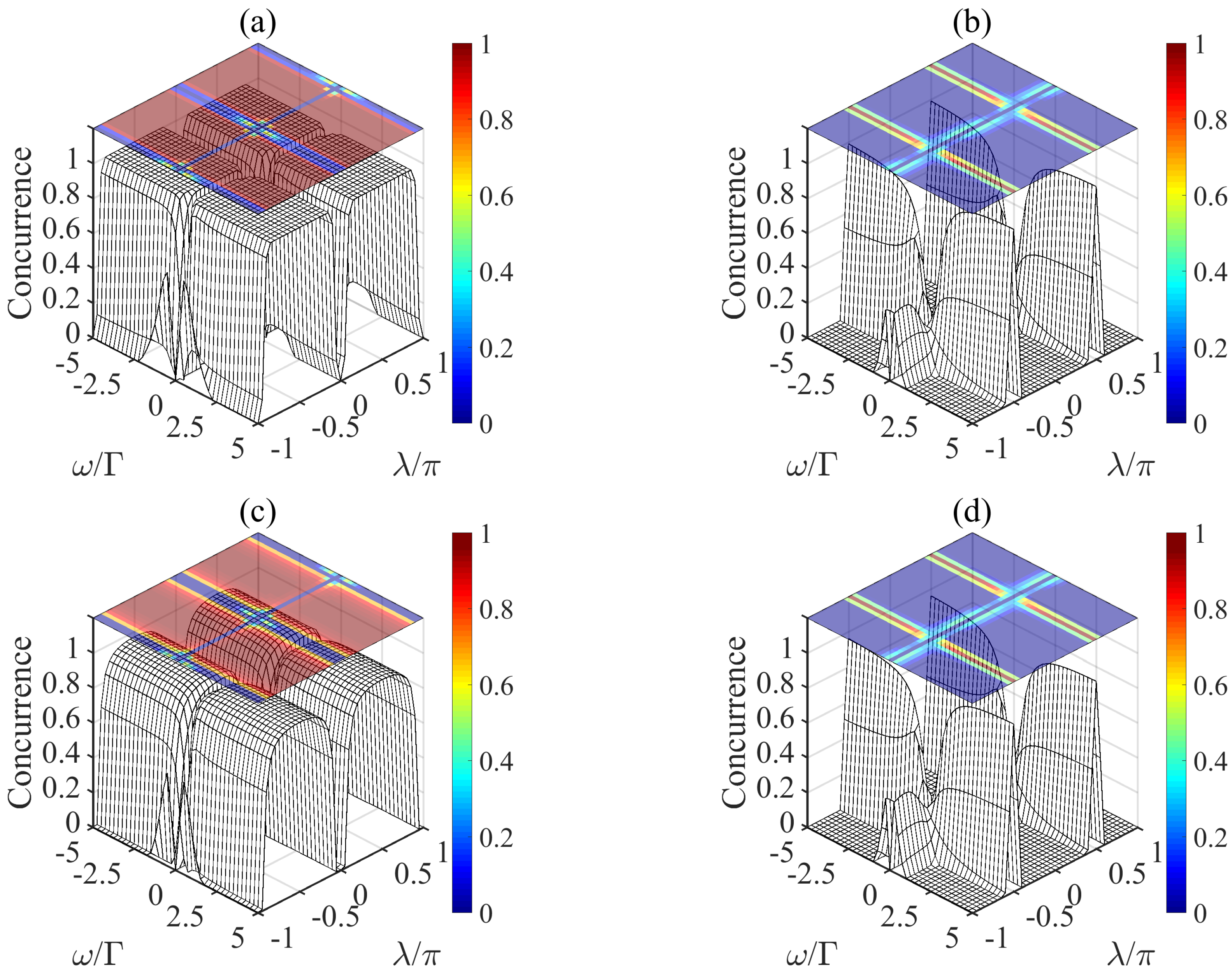
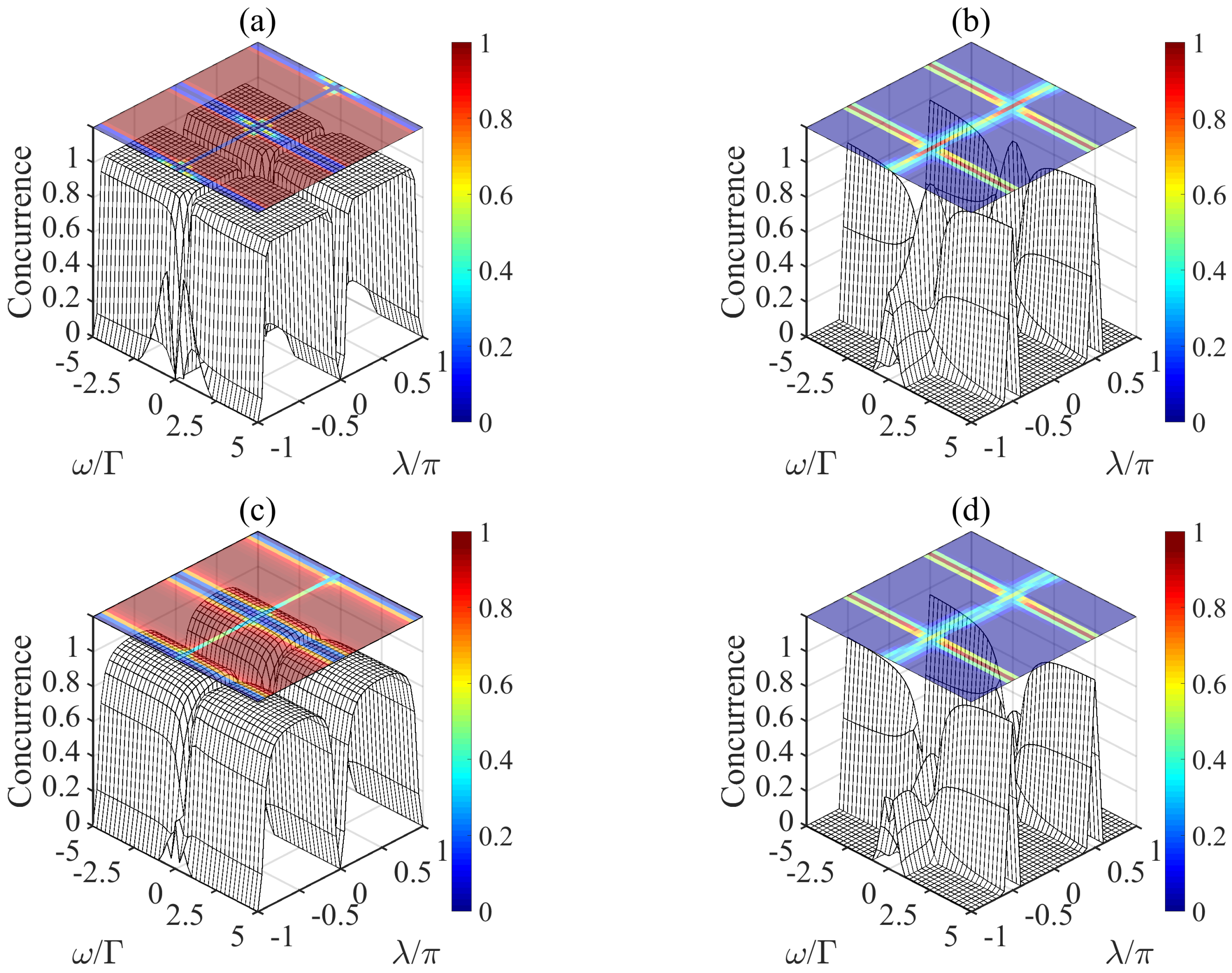
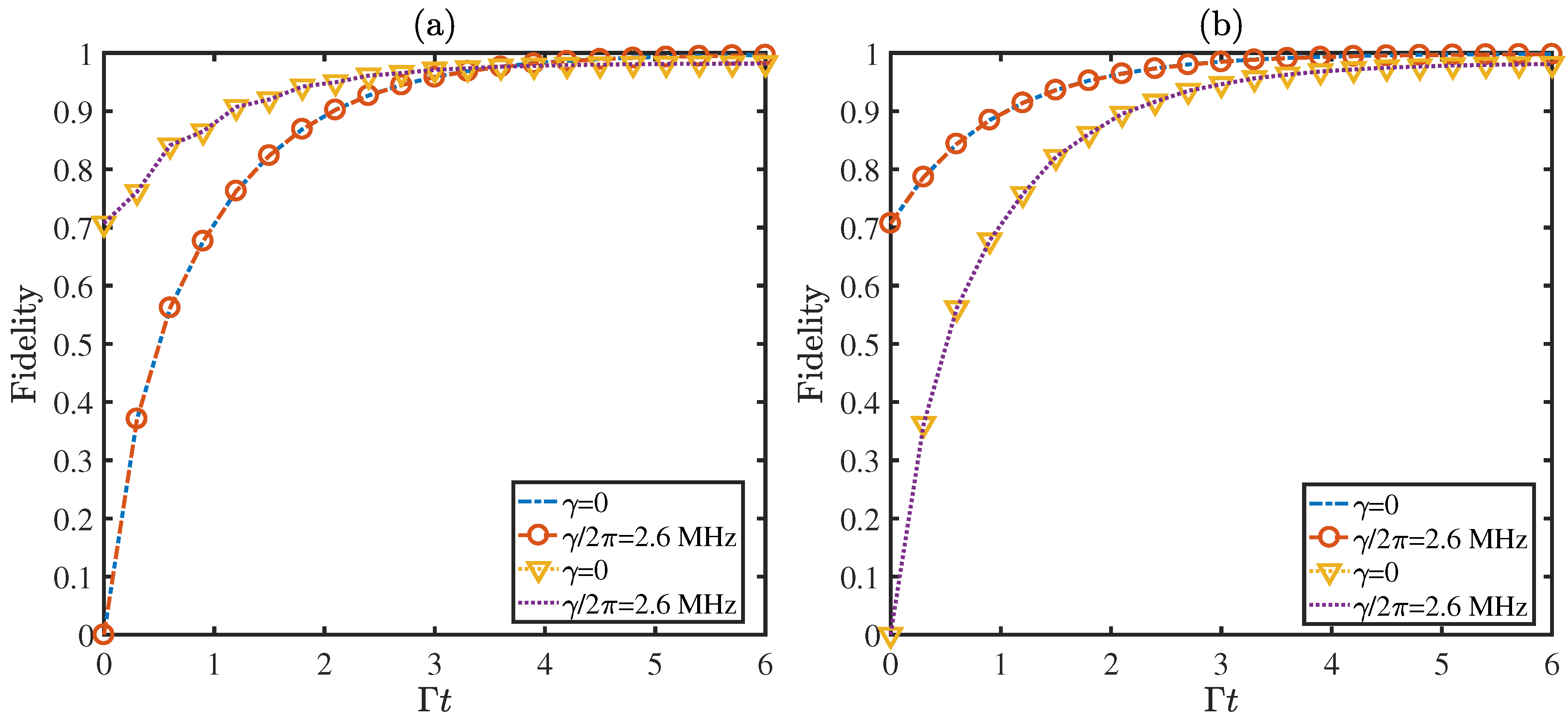
3. Stabilization of Different Bell States via Quantum Feedback Control
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Effective Master Equation
Appendix B. Generation of the Other Two Triplet States
References
- Bruß, D.; Macchiavello, C. Multipartite entanglement in quantum algorithms. Phys. Rev. 2011, 83, 052313. [Google Scholar] [CrossRef]
- Deng, F.G.; Ren, B.C.; Li, X.H. Quantum hyperentanglement and its applications in quantum information processing. Sci. Bull. 2017, 62, 46–68. [Google Scholar] [CrossRef]
- Ye, S.Y.; Zhong, Z.R.; Zheng, S.B. Deterministic generation of three-dimensional entanglement for two atoms separately trapped in two optical cavities. Phys. Rev. 2008, 77, 014303. [Google Scholar] [CrossRef]
- Yang, C.P.; Su, Q.P.; Zheng, S.B.; Nori, F.; Han, S. Entangling two oscillators with arbitrary asymmetric initial states. Phys. Rev. 2017, 95, 052341. [Google Scholar] [CrossRef]
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. 2002, 65, 032302. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef]
- Vinay, S.E.; Kok, P. Practical repeaters for ultralong-distance quantum communication. Phys. Rev. 2017, 95, 052336. [Google Scholar] [CrossRef]
- Felicetti, S.; Fedortchenko, S.; Rossi, R.; Ducci, S.; Favero, I.; Coudreau, T.; Milman, P. Quantum communication between remote mechanical resonators. Phys. Rev. 2017, 95, 022322. [Google Scholar] [CrossRef]
- Niu, P.H.; Zhou, Z.R.; Lin, Z.S.; Sheng, Y.B.; Yin, L.G.; Long, G.L. Measurement-device-independent quantum communication without encryption. Sci. Bull. 2018, 63, 1345–1350. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F. Entangled light from white noise. Phys. Rev. Lett. 2002, 88, 197901. [Google Scholar] [CrossRef]
- Yi, X.X.; Yu, C.S.; Zhou, L.; Song, H.S. Noise-assisted preparation of entangled atoms. Phys. Rev. 2003, 68, 052304. [Google Scholar] [CrossRef]
- Lambert, N.; Aguado, R.; Brandes, T. Nonequilibrium entanglement and noise in coupled qubits. Phys. Rev. B 2007, 75, 045340. [Google Scholar] [CrossRef]
- Galve, F.; Pachón, L.A.; Zueco, D. Bringing entanglement to the high temperature limit. Phys. Rev. Lett. 2010, 105, 180501. [Google Scholar] [CrossRef] [PubMed]
- Fischbach, J.; Freyberger, M. Steady-state entanglement enhanced by a dissipative ancilla. Phys. Rev. 2015, 92, 052327. [Google Scholar] [CrossRef]
- Li, D.X.; Shao, X.Q.; Wu, J.H.; Yi, X.X. Engineering steady-state entanglement via dissipation and quantum Zeno dynamics in an optical cavity. Opt. Lett. 2017, 42, 3904–3907. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.Q.; Wu, J.H.; Yi, X.X.; Long, G.L. Dissipative preparation of steady Greenberger-Horne-Zeilinger states for Rydberg atoms with quantum Zeno dynamics. Phys. Rev. 2017, 96, 062315. [Google Scholar] [CrossRef]
- Tacchino, F.; Auffèves, A.; Santos, M.F.; Gerace, D. Steady state entanglement beyond thermal limits. Phys. Rev. Lett. 2018, 120, 063604. [Google Scholar] [CrossRef] [PubMed]
- Paz, J.P.; Zurek, W.H. Continuous error correction. Proc. R. Soc. Lond. Ser. A 1998, 454, 355–364. [Google Scholar] [CrossRef]
- Ahn, C.; Doherty, A.C.; Landahl, A.J. Continuous quantum error correction via quantum feedback control. Phys. Rev. 2002, 65, 042301. [Google Scholar] [CrossRef]
- Fujii, K.; Negoro, M.; Imoto, N.; Kitagawa, M. MeasurementFree Topological Protection Using Dissipative Feedback. Phys. Rev. X 2014, 4, 041039. [Google Scholar]
- Leghtas, Z.; Touzard, S.; Pop, I.M.; Kou, A.; Vlastakis, B.; Petrenko, A.; Sliwa, K.M.; Narla, A.; Shankar, S.; Hatridge, M.J.; et al. Confining the state of light to a quantum manifold by engineered two-photon loss. Science 2015, 347, 853–857. [Google Scholar] [CrossRef] [PubMed]
- Kapit, E. Hardware-efficient and fully autonomous quantum error correction in superconducting circuits. Phys. Rev. Lett. 2016, 116, 150501. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Noh, K.; Albert, V.V.; Krastanov, S.; Devoret, M.H.; Schoelkopf, R.J.; Girvin, S.M.; Jiang, L. Quantum channel construction with circuit quantum electrodynamics. Phys. Rev. B 2017, 95, 134501. [Google Scholar] [CrossRef]
- Reiter, F.; Sørensen, A.S.; Zoller, P.; Muschik, C.A. Dissipative quantum error correction and application to quantum sensing with trapped ions. Nat. Commun. 2017, 8, 1822. [Google Scholar] [CrossRef] [PubMed]
- Li, D.X.; Shao, X.Q. Unconventional Rydberg pumping and applications in quantum information processing. Phys. Rev. 2018, 98, 062338. [Google Scholar] [CrossRef]
- Wang, C.; Gertler, J.M. Autonomous quantum state transfer by dissipation. arXiv, 2019; arXiv:1809.03571. [Google Scholar]
- Matsuzaki, Y.; Bastidas, V.M.; Takeuchi, Y.; Munro, W.J.; Saito, S. One-way transfer of quantum states via decoherence. arXiv, 2019; arXiv:1810.02995. [Google Scholar]
- Li, D.X.; Shao, X.Q. Directional quantum state transfer in a dissipative Rydberg-atom-cavity system. Phys. Rev. A 2019, 99, 032348. [Google Scholar] [CrossRef]
- Wang, J.; Wiseman, H.M.; Milburn, G.J. Dynamical creation of entanglement by homodyne-mediated feedback. Phys. Rev. 2005, 71, 042309. [Google Scholar] [CrossRef]
- Mancini, S. Markovian feedback to control continuous-variable entanglement. Phys. Rev. 2006, 73, 010304. [Google Scholar] [CrossRef]
- Carvalho, A.R.R.; Hope, J.J. Stabilizing entanglement by quantum-jump-based feedback. Phys. Rev. 2007, 76, 010301. [Google Scholar] [CrossRef]
- Carvalho, A.R.R.; Reid, A.J.S.; Hope, J.J. Controlling entanglement by direct quantum feedback. Phys. Rev. 2008, 78, 012334. [Google Scholar] [CrossRef]
- Stevenson, R.N.; Hope, J.J.; Carvalho, A.R.R. Engineering steady states using jump-based feedback for multipartite entanglement generation. Phys. Rev. 2011, 84, 022332. [Google Scholar] [CrossRef]
- Li, D.X.; Shao, X.Q.; Wu, J.H.; Yi, X.X. Noise-induced distributed entanglement in atom-cavity-fiber system. Opt. Express 2017, 25, 33359–33378. [Google Scholar] [CrossRef]
- Rafiee, M.; Nourmandipour, A.; Mancini, S. Universal feedback control of two-qubit entanglement. Phys. Rev. A 2017, 96, 012340. [Google Scholar] [CrossRef]
- Stevenson, R.N.; Carvalho, A.R.R.; Hope, J.J. Production of entanglement in Raman three-level systems using feedback. Eur. Phys. J. D 2011, 61, 523–529. [Google Scholar] [CrossRef][Green Version]
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281. [Google Scholar] [CrossRef]
- Trupke, M.; Hinds, E.A.; Eriksson, S.; Curtis, E.A.; Moktadir, Z.; Kukharenka, E.; Kraft, M. Microfabricated high-finesse optical cavity with open access and small volume. Appl. Phys. Lett. 2005, 87, 211106. [Google Scholar] [CrossRef]
- Miroshnychenko, Y.; Alt, W.; Dotsenko, I.; Förster, L.; Khudaverdyan, M.; Meschede, D.; Rauschenbeutel, A. Quantum engineering: An atom-sorting machine. Nature 2006, 442, 151. [Google Scholar] [CrossRef]
- Metz, J.; Beige, A. Macroscopic quantum jumps and entangled-state preparation. Phys. Rev. 2007, 76, 022331. [Google Scholar] [CrossRef]
- Khudaverdyan, M.; Alt, W.; Kampschulte, T.; Reick, S.; Thobe, A.; Widera, A.; Meschede, D. Quantum jumps and spin dynamics of interacting atoms in a strongly coupled atom-cavity system. Phys. Rev. Lett. 2009, 103, 123006. [Google Scholar] [CrossRef] [PubMed]
- Ficek, Z.; Tanaś, R. Entangled states and collective nonclassical effects in two-atom systems. Phys. Rep. 2002, 372, 369–443. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Li, D.-X.; Shao, X.-Q. Stabilization of All Bell States in a Lossy Coupled-Cavity Array. Entropy 2019, 21, 402. https://doi.org/10.3390/e21040402
Liu B, Li D-X, Shao X-Q. Stabilization of All Bell States in a Lossy Coupled-Cavity Array. Entropy. 2019; 21(4):402. https://doi.org/10.3390/e21040402
Chicago/Turabian StyleLiu, Bing, Dong-Xiao Li, and Xiao-Qiang Shao. 2019. "Stabilization of All Bell States in a Lossy Coupled-Cavity Array" Entropy 21, no. 4: 402. https://doi.org/10.3390/e21040402
APA StyleLiu, B., Li, D.-X., & Shao, X.-Q. (2019). Stabilization of All Bell States in a Lossy Coupled-Cavity Array. Entropy, 21(4), 402. https://doi.org/10.3390/e21040402




