Approximating Ground States by Neural Network Quantum States
Abstract
1. Introduction
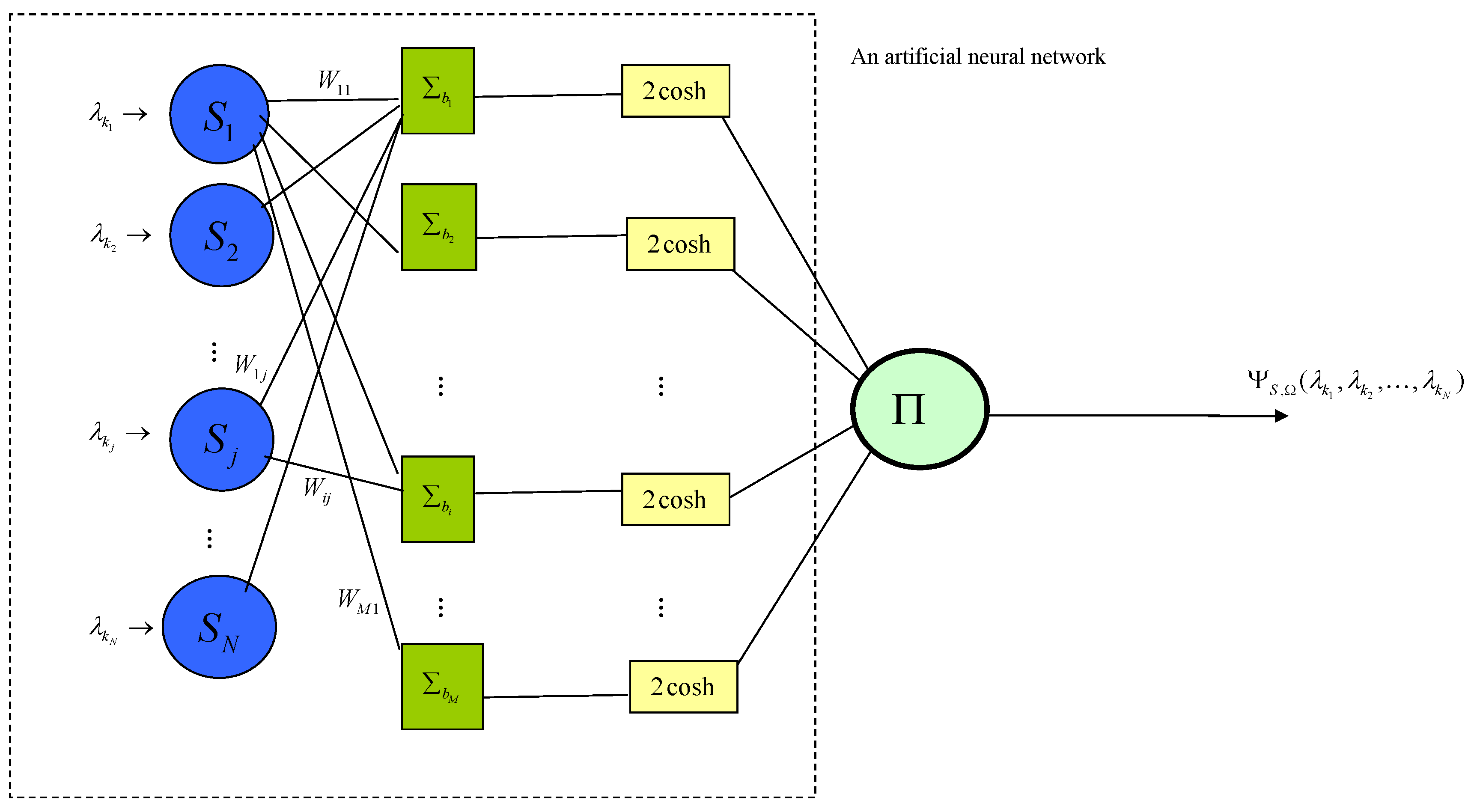
2. Neural Network Quantum States
3. Approximating Ground States by Neural Network Quantum States
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luo, S.L. Using measurement-induced disturbance to characterize correlations as classical or quantum. Phys. Rev. A 2008, 77, 022301. [Google Scholar] [CrossRef]
- Guo, Z.H.; Cao, H.X.; Qu, S.X. Partial correlations in multipartite quantum systems. Inf. Sci. 2014, 289, 262. [Google Scholar] [CrossRef]
- Zhang, T.G.; Yang, H.; Lijost, X. Uniform Quantification of Correlations for Bipartite Systems. Phys. Rev. A 2017, 95, 042316. [Google Scholar] [CrossRef]
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying entanglement. Phys. Rev. Lett. 1997, 78, 2275. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. A computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Amico, L.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2007, 80, 517. [Google Scholar] [CrossRef]
- Luo, S.L.; Fu, S.S. Measurement-induced nonlocality. Phys. Rev. Lett. 2011, 106, 120401. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Hou, J.C. Local channels preserving the states without measurement-induced nonlocality. J. Phys. A Math. Theor. 2013, 46, 325301. [Google Scholar] [CrossRef]
- Cao, H.X.; Guo, Z.H. Characterizing Bell nonlocality and EPR steering. Sci. China-Phys. Mech. Astron. 2019, 62, 030311. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Navascues, M.; Cavalcanti, D. Quantifying Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 2014, 112, 180404. [Google Scholar] [CrossRef]
- Sun, K.; Ye, X.J.; Xu, J.S.; Xu, X.Y.; Tang, J.S.; Wu, Y.C.; Chen, J.L.; Li, C.F.; Guo, G.C. Experimental quantification of asymmetric Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 2016, 116, 160404. [Google Scholar] [CrossRef]
- Cavalcanti, D.; Skrzypczyk, P. Quantum steering: A review with focus on semidefinite programming. Rep. Prog. Phys. 2017, 80, 024001. [Google Scholar] [CrossRef] [PubMed]
- Gordon, R.G. Error bounds for the energy and overlap of approximate wavefunctions. J. Chem. Phys. 1968, 48, 4984. [Google Scholar] [CrossRef]
- Wang, P.S.C. Lower bounds for the overlap of approximate wave functions. J. Chem. Phys. 1970, 52, 4464. [Google Scholar] [CrossRef]
- Merkel, R.R. A study of a lower bounding formula for the overlap between the exact and an approximate wavefunction. J. Chem. Phys. 1975, 62, 3198. [Google Scholar] [CrossRef]
- Cioslowski, J. Estimation of the overlap between the approximate and exact wave function of the ground state from the connected-moments expansion. Phys. Rev. A 1987, 36, 3441. [Google Scholar] [CrossRef]
- Hornik, M.; Snajdr, M.; Rothstein, S.M. Estimating the overlap of an approximate with the exact wave function by quantum Monte Carlo methods. J. Chem. Phys. 2000, 113, 3496. [Google Scholar] [CrossRef]
- Marmorino, M.G. Upper bounds to the overlap of approximate and exact wavefunctions. Int. J. Theor. Phys. 2000, 39, 2439. [Google Scholar] [CrossRef]
- Nomura, Y.; Darmawan, A.; Yamaji, Y.; Imada, M. Restricted-Boltzmann-machine learning for solving strongly correlated quantum systems. Phys. Rev. B 2006, 96, 205152. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition. Am. Math. Soc. Transl. 1963, 28, 55. [Google Scholar]
- Cybenko, G. Approximation by superposition of a sigmoidal function. Math. Control Signal 1989, 2, 303. [Google Scholar] [CrossRef]
- Funahashi, K. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251. [Google Scholar] [CrossRef]
- Le Roux, N.; Bengio, Y. Representational power of restricted boltzmann machines and deep belief networks. Neural Comput. 2008, 20, 1631. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602. [Google Scholar] [CrossRef] [PubMed]
- Ackley, D.H.; Hinton, G.E.; Sejnowski, T.J. A learning algorithm for Boltzmann machines. Cogn. Sci. 1985, 9, 147. [Google Scholar] [CrossRef]
- Cai, Z. Approximating quantum many-body wave functions using artificial neural networks. arXiv, 2017; arXiv:1704.05148. [Google Scholar] [CrossRef]
- Saito, H. Solving the bose-hubbard model with machine learning. J. Phys. Soc. Jpn. 2017, 86, 093001. [Google Scholar] [CrossRef]
- Gao, X.; Duan, L.M. Efficient representation of quantum many-body states with deep neural networks. Nat. Commun. 2017, 8, 662. [Google Scholar] [CrossRef]
- Huang, Y.; Moore, J.E. Neural network representation of tensor network and chiral states. arXiv, 2017; arXiv:1701.06246. [Google Scholar]
- Deng, D.L.; Li, X.P.; Das Sarma, S. Machine learning topological states. Phys. Rev. B 2017, 96, 195145. [Google Scholar] [CrossRef]
- Glasser, I.; Pancotti, N.; August, M.; Rodriguez, I.D.; Cirac, J.I. Neural-network quantum states, string-bond states, and Chiral topological states. Phys. Rev. X 2018, 8, 011006. [Google Scholar] [CrossRef]
- Gardas, B.; Rams, M.M.; Dziarmaga, J. Quantum neural networks to simulate many-body quantum systems. Phys. Rev. B 2018, 98, 184304. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, J.G. Approximating quantum many-body wave-functions using artificial neural network. Phys. Rev. B 2018, 97, 035116. [Google Scholar] [CrossRef]
- Saito, H.; Kato, M. Machine learning technique to find quantum many-body ground states of bosons on a lattice. J. Phys. Soc. Jpn. 2018, 87, 014001. [Google Scholar] [CrossRef]
- Clark, S.R. Unifying neural-network quantum states and correlator product states via tensor networks. arXiv, 2017; arXiv:1710.03545. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, H.X.; Zhang, Z.J. Neural network representations of ground states. Sci. China-Phys. Mech. Astron. 2019. submitted. [Google Scholar]


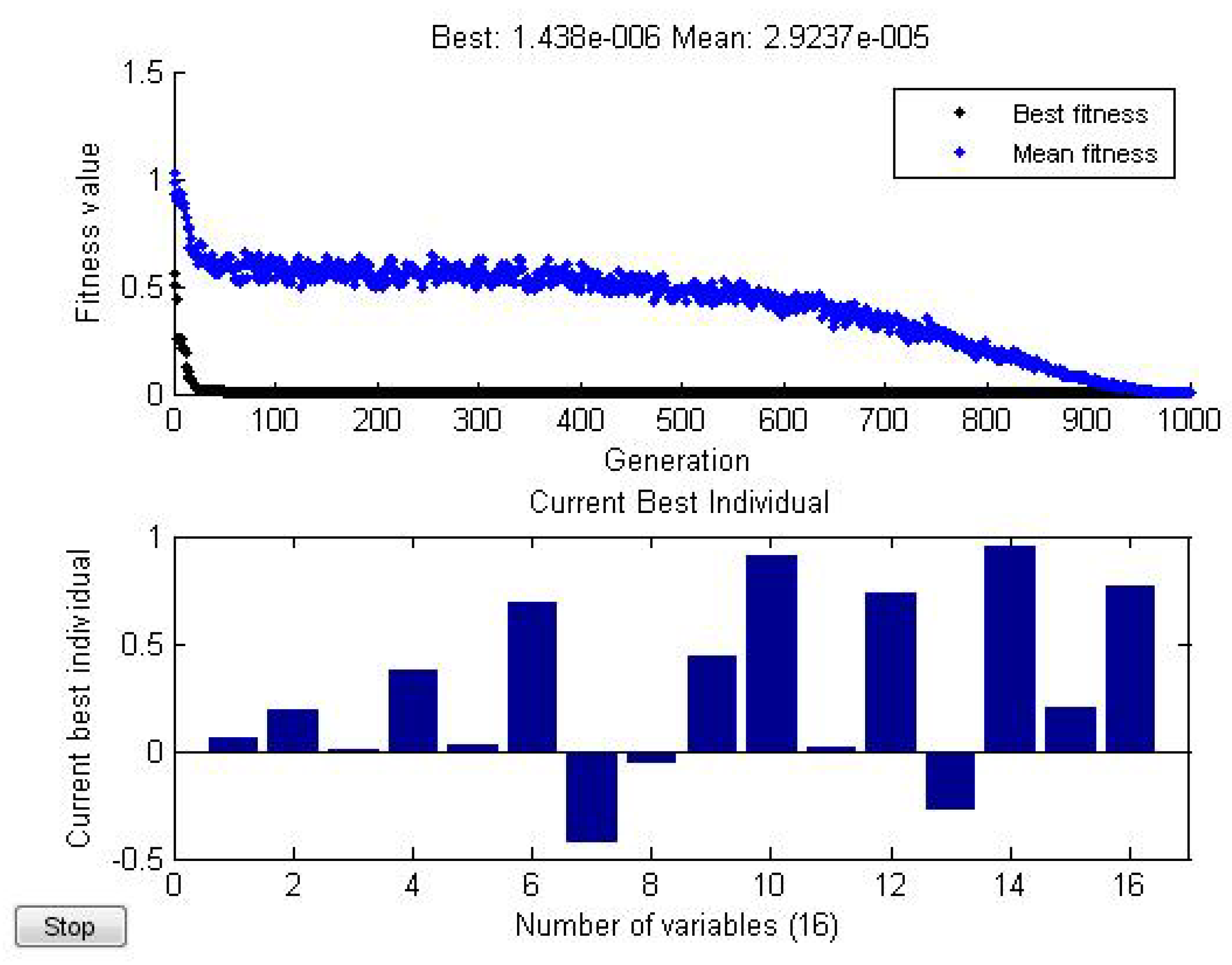
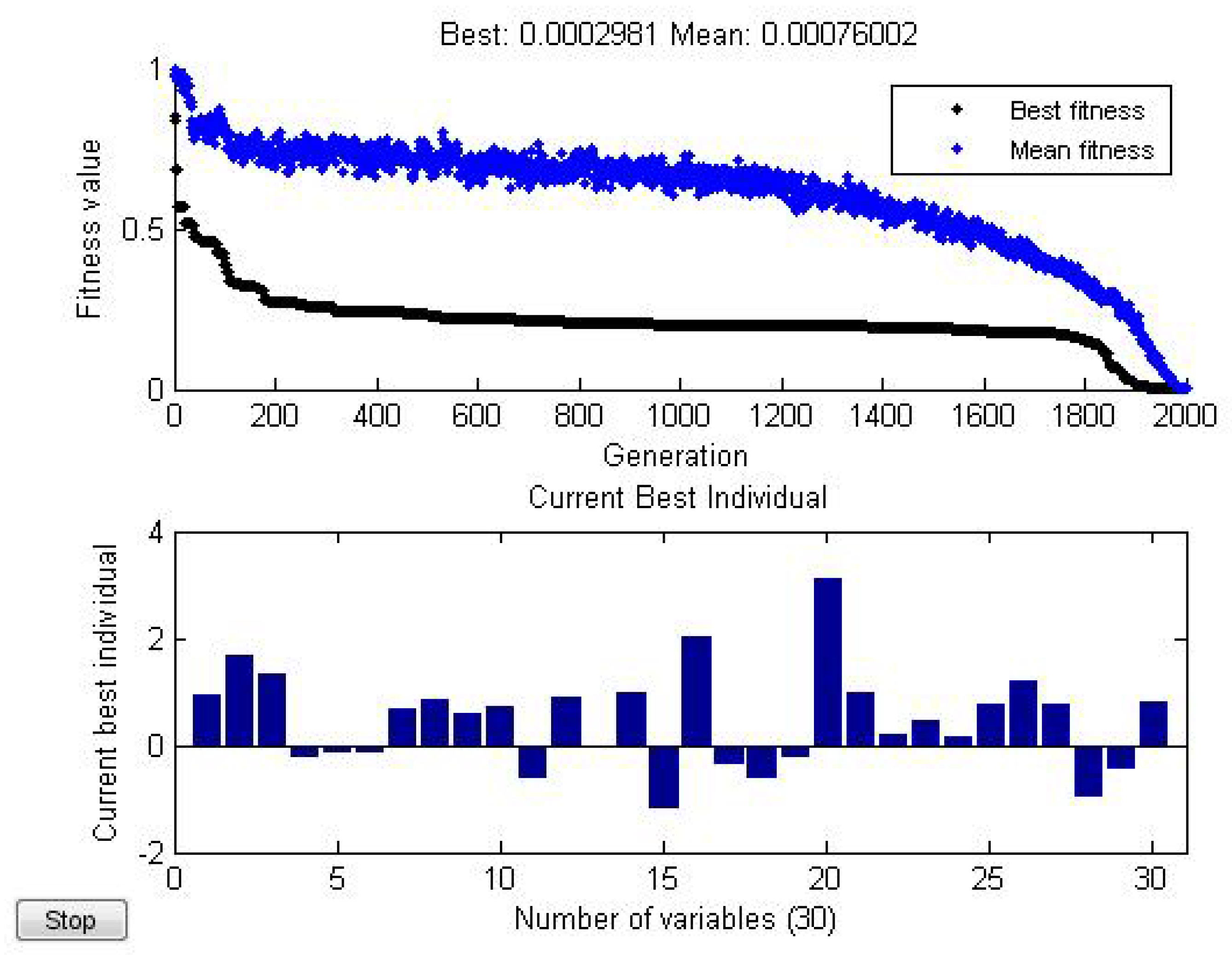
| N | M | |
|---|---|---|
| 2 | 2 | |
| 2 | 4 | |
| 2 | 6 | |
| 2 | 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, C.; Cao, H. Approximating Ground States by Neural Network Quantum States. Entropy 2019, 21, 82. https://doi.org/10.3390/e21010082
Yang Y, Zhang C, Cao H. Approximating Ground States by Neural Network Quantum States. Entropy. 2019; 21(1):82. https://doi.org/10.3390/e21010082
Chicago/Turabian StyleYang, Ying, Chengyang Zhang, and Huaixin Cao. 2019. "Approximating Ground States by Neural Network Quantum States" Entropy 21, no. 1: 82. https://doi.org/10.3390/e21010082
APA StyleYang, Y., Zhang, C., & Cao, H. (2019). Approximating Ground States by Neural Network Quantum States. Entropy, 21(1), 82. https://doi.org/10.3390/e21010082





