Bogdanov Map for Modelling a Phase-Conjugated Ring Resonator
Abstract
1. Introduction
2. Material and Methods
2.1. Bogdanov Map
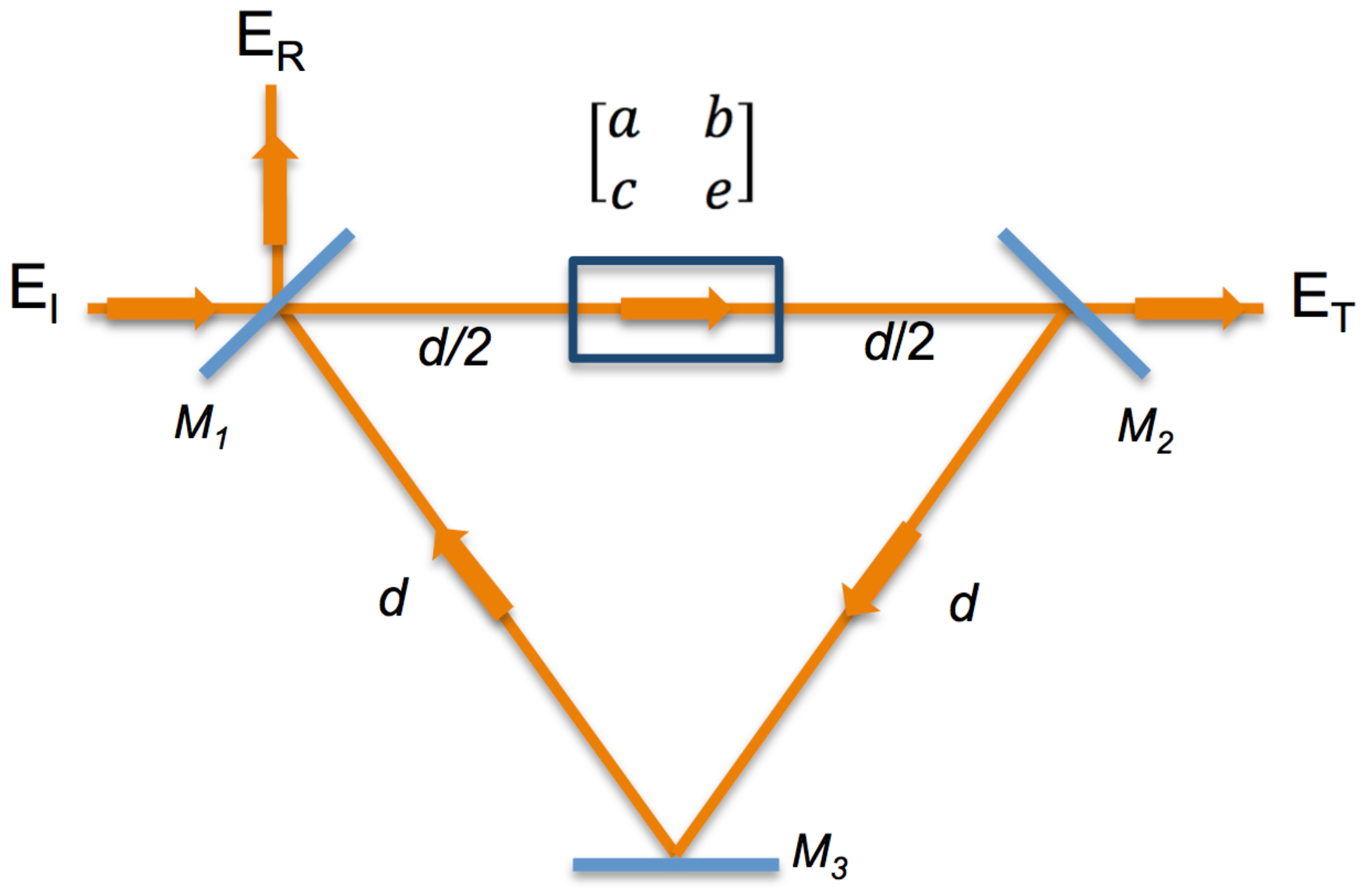
2.2. Paraxial Matrix Analysis
2.3. Bogdanov Beams
2.4. General Case for Bogdanov Beams
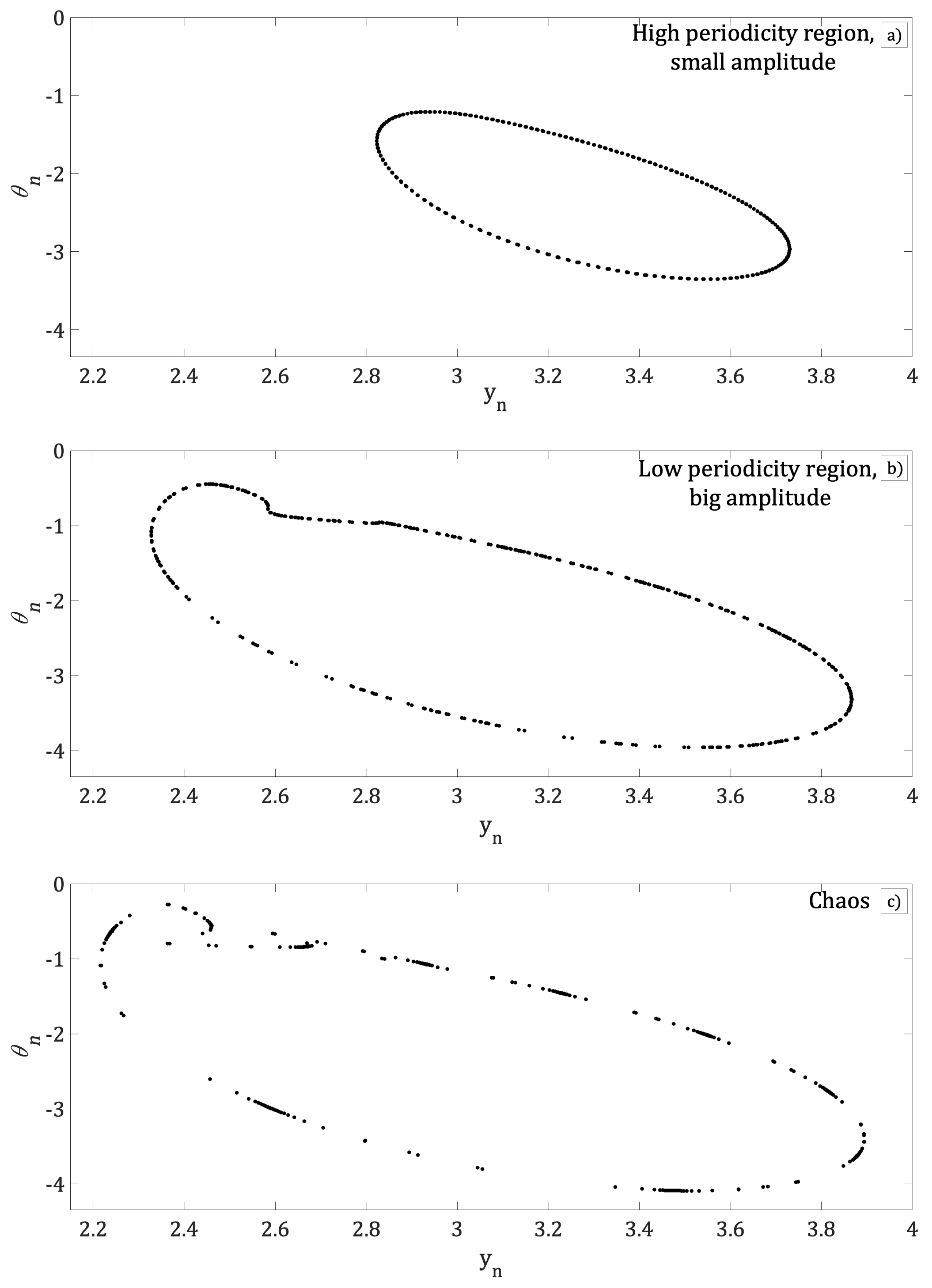
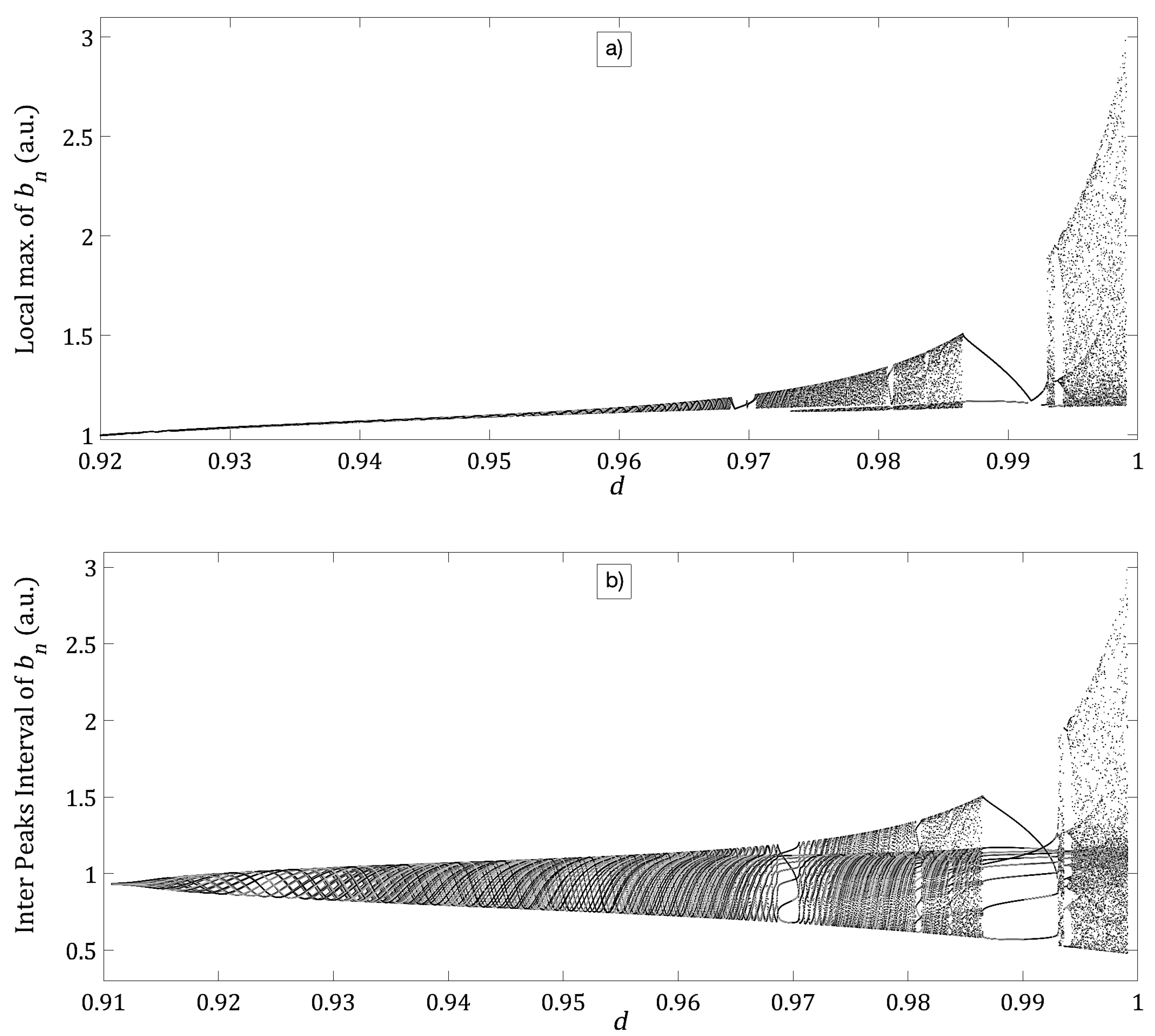
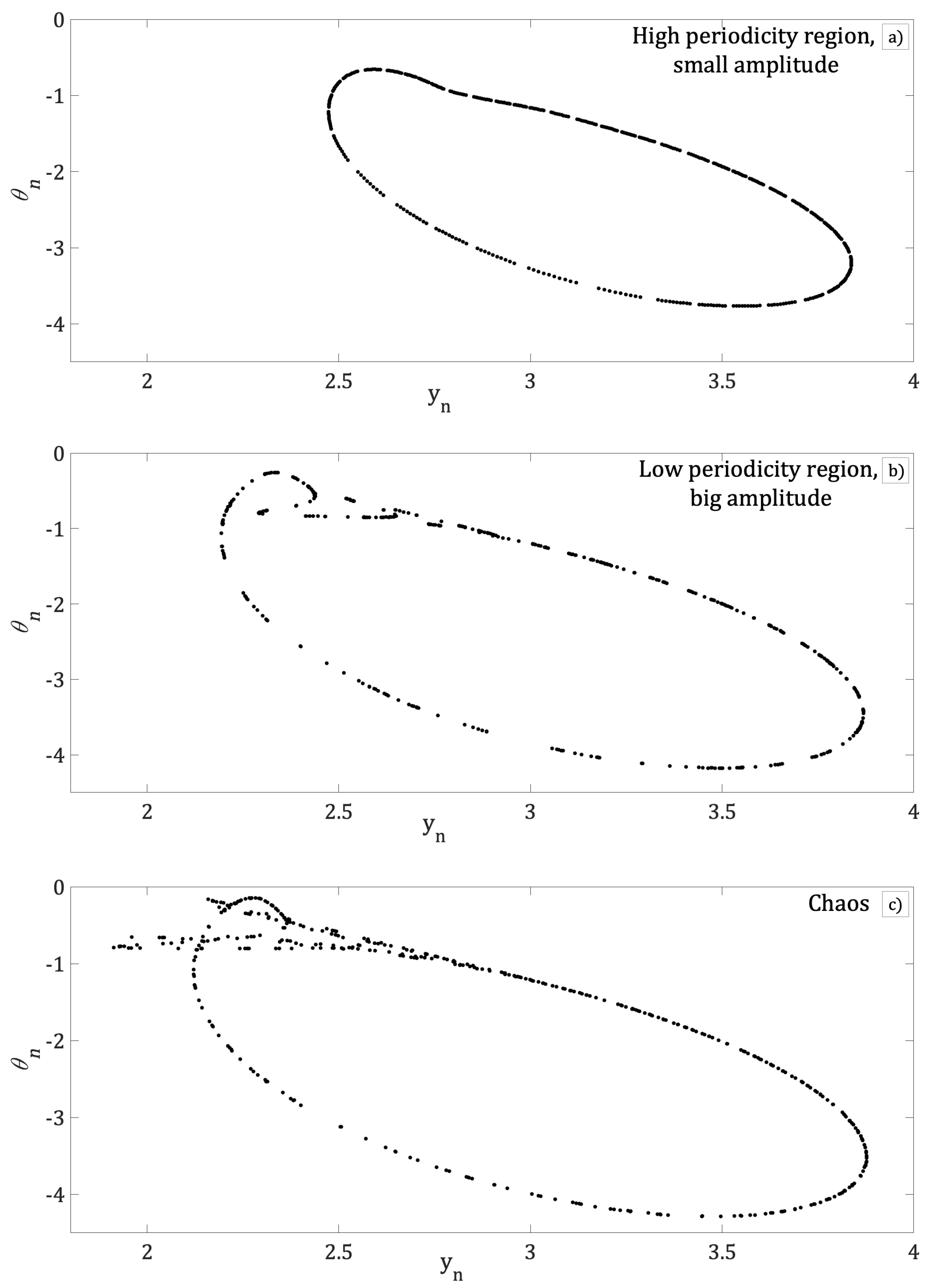
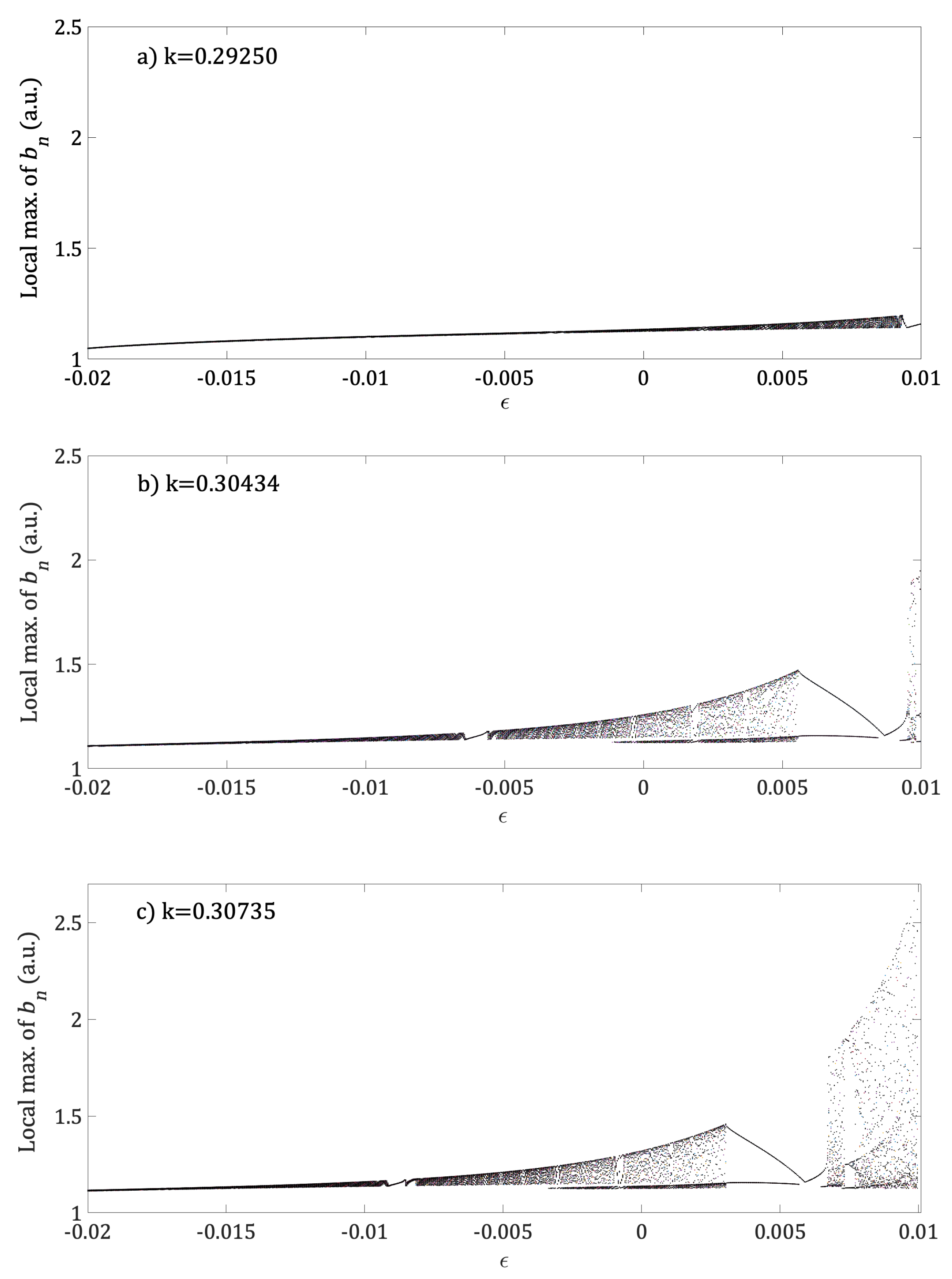
3. Results
Computer Calculations
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bélanger, P.A. Beam propagation and the ABCD ray matrices. Opt. Lett. 1991, 16, 196–198. [Google Scholar] [CrossRef] [PubMed]
- Onciul, D. ABCD propagation law for misaligned general astigmatic Gaussian beams. J. Opt. 1992, 23, 163. [Google Scholar] [CrossRef]
- Bastiaans, M. ABCD law for partially coherent Gaussian light, propagating through first-order optical systems. Opt. Quantum Electron. 1992, 24, S1011–S1019. [Google Scholar] [CrossRef]
- Tian, L. Iterative nonlinear beam propagation using Hamiltonian ray tracing and Wigner distribution function. Opt. Lett. 2010, 35, 4148–4150. [Google Scholar]
- Siegman, A.E. Lasers; University Science Books: Herndon, VA, USA, 1986. [Google Scholar]
- Tarasov, L. Physique Des Processus Dans Les Generaeurs De Rayonnement Optique Coherent; (trans. from Russian); Mir, Moscu: Gent, Belgium, 1981. [Google Scholar]
- Aboites, V.; Liceaga, D.; Kir’yanov, A.; Wilson, M. Ikeda Map and Phase Conjugated Ring Resonator Chaotic Dynamics. Appl. Math. Inf. Sci. 2016, 10, 1–6. [Google Scholar] [CrossRef]
- Aboites, V.; Wilson, M.; Lomeli, K. Standard Map Spatial Dynamics in a Ring-Phase Conjugated Resonator. Appl. Math. Inf. Sci. 2015, 9, 2823–2827. [Google Scholar]
- Aboites, V.; Barmenkov, Y.; Kiryanov, A.; Wilson, M. Tinkerbell beams in a non-linear ring resonator. Results Phys. 2012, 2, 216–220. [Google Scholar] [CrossRef][Green Version]
- Aboites, V.; Wilson, M. Tinkerbell chaos in a ring phase-conjugated resonator. Int. J. Pure Appl. Math. 2009, 54, 429–435. [Google Scholar]
- Aboites, V.; Barmenkov, Y.; Kiryanov, A.; Wilson, M. Bidimensional dynamics maps in optical resonators. Rev. Mex. Fis. 2014, 60, 13–23. [Google Scholar]
- Dignowity, D.; Wilson, M.; Rangel-Fonseca, P.; Aboites, V. Duffing spatial dynamics induced in a double phase-conjugated resonator. Laser Phys. 2013, 23, 076002. [Google Scholar] [CrossRef]
- Aboites, V. Dynamics of a LASER Resonator. Int. J. Pure Appl. Math. 2007, 36, 345–352. [Google Scholar]
- Aboites, V.; Huicochea, M. Henon beams. Int. J. Pure Appl. Math. 2010, 65, 129–136. [Google Scholar]
- Arrowsmith, D.K.; Cartwright, J.H.; Lansbury, A.N.; Place, C.M. The Bogdanov Map: Bifurcations, Mode Locking, and Chaos in a Dissipative System. Int. J. Bifurc. Chaos 1993, 3, 803–842. [Google Scholar] [CrossRef]
- Hallbach, K. Matrix Representation of Gaussian Optics. Am. J. Phys. 1964, 32, 90. [Google Scholar] [CrossRef]
- Bogdanov, R.I. Versal deformations of a singularity of a vector field on the plane in the case of zero eigenvalues. Sel. Math. Sov. 1981, 1, 373–388. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aboites, V.; Liceaga, D.; Jaimes-Reátegui, R.; García-López, J.H. Bogdanov Map for Modelling a Phase-Conjugated Ring Resonator. Entropy 2019, 21, 384. https://doi.org/10.3390/e21040384
Aboites V, Liceaga D, Jaimes-Reátegui R, García-López JH. Bogdanov Map for Modelling a Phase-Conjugated Ring Resonator. Entropy. 2019; 21(4):384. https://doi.org/10.3390/e21040384
Chicago/Turabian StyleAboites, Vicente, David Liceaga, Rider Jaimes-Reátegui, and Juan Hugo García-López. 2019. "Bogdanov Map for Modelling a Phase-Conjugated Ring Resonator" Entropy 21, no. 4: 384. https://doi.org/10.3390/e21040384
APA StyleAboites, V., Liceaga, D., Jaimes-Reátegui, R., & García-López, J. H. (2019). Bogdanov Map for Modelling a Phase-Conjugated Ring Resonator. Entropy, 21(4), 384. https://doi.org/10.3390/e21040384






