An Urban Scaling Estimation Method in a Heterogeneity Variance Perspective
Abstract
1. Introduction
2. Study Area and Data
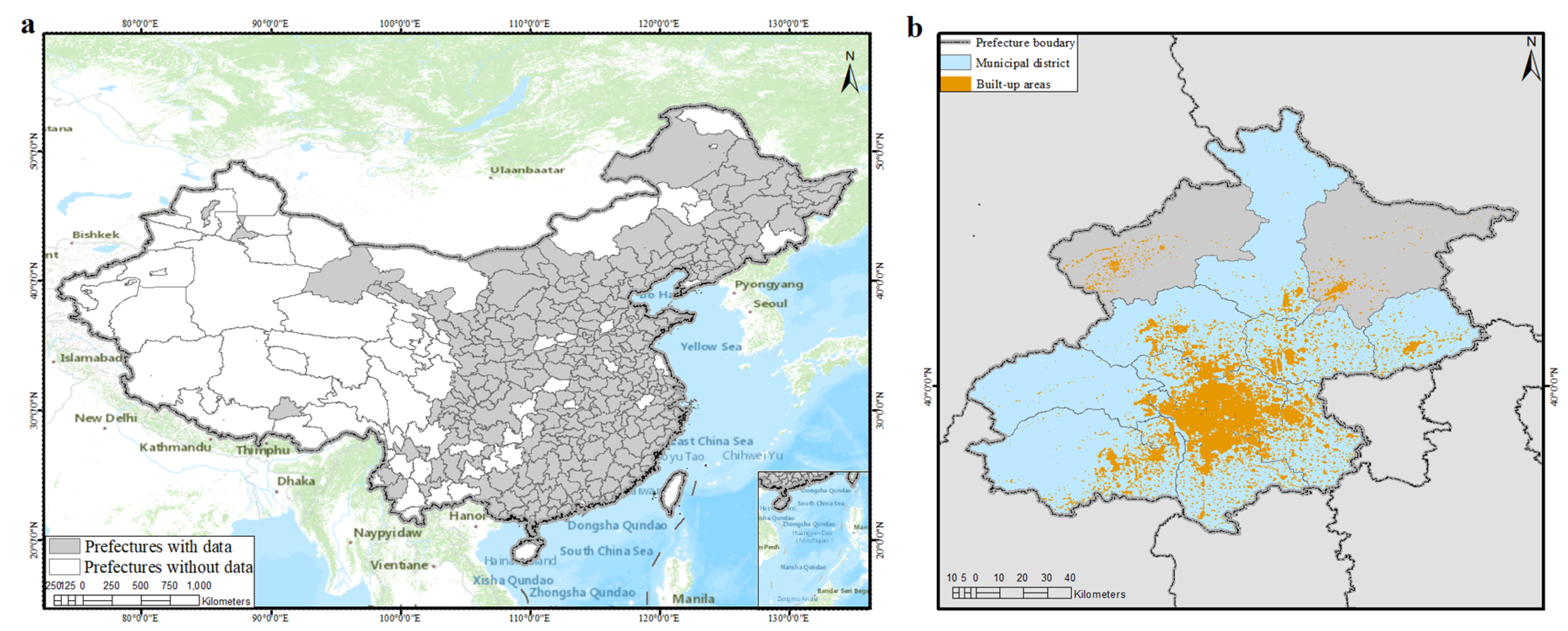
2.1. Study Area
2.2. Demographic Data
2.3. Urban Attributes Data
3. Urban Scaling Laws: Principles and Problems with Estimation
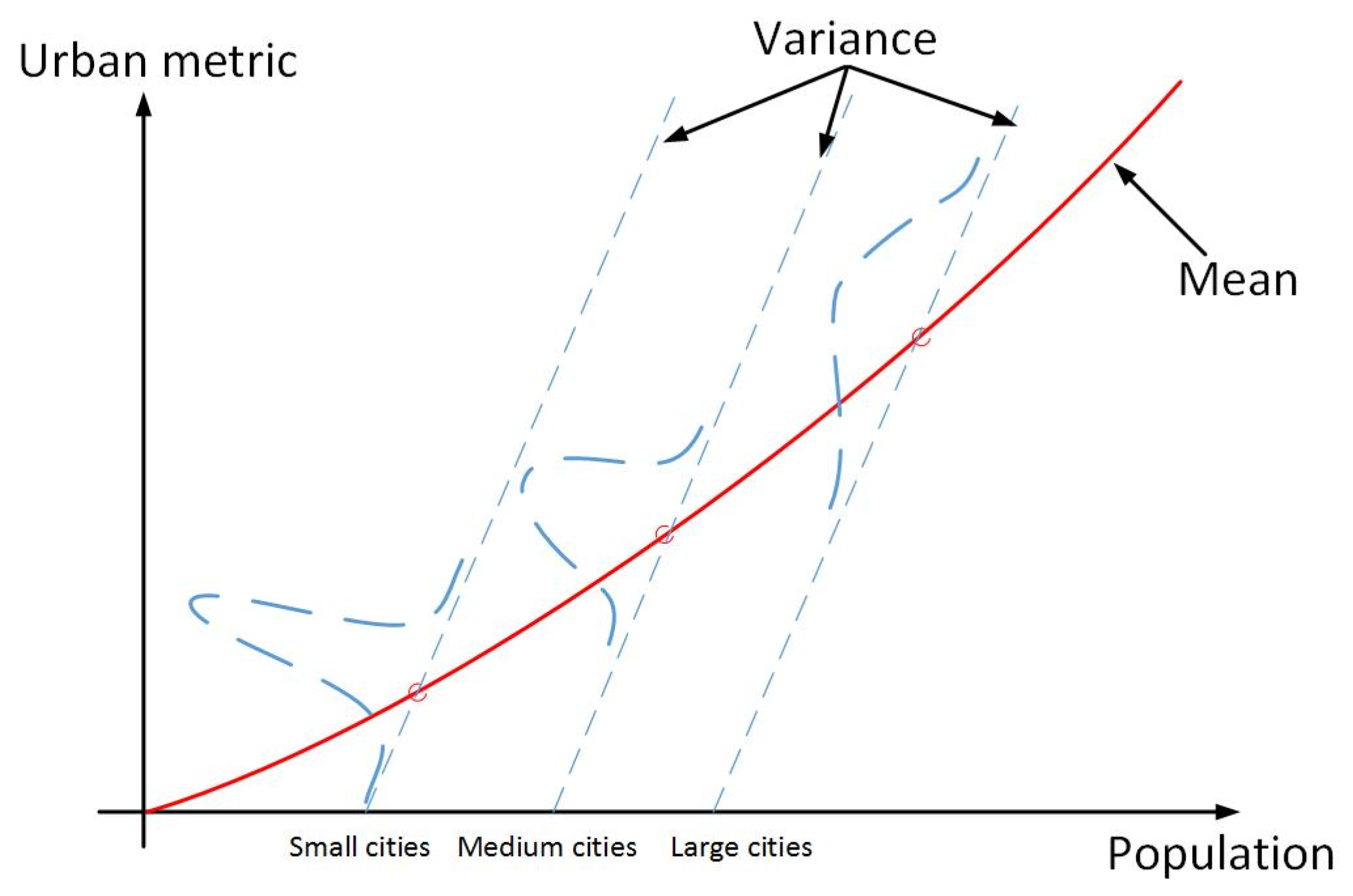
3.1. Principles of Urban Scaling Laws
- shows a super-linear scaling regime associated with social currencies (e.g., GDP, and the number of patents [45]), describing the agglomeration effect. For example, although the population of Beijing is double that of Wuhan, the GDP of Beijing is more than double that of Wuhan.
- denotes a linear scaling regime associated with individual human needs (e.g., jobs and household water consumption).
- means a sub-linear scaling regime associated with infrastructural variables (e.g., urban areas and road length), describing economies of scale.
3.2. Traditional Urban Scaling Statistic Methods
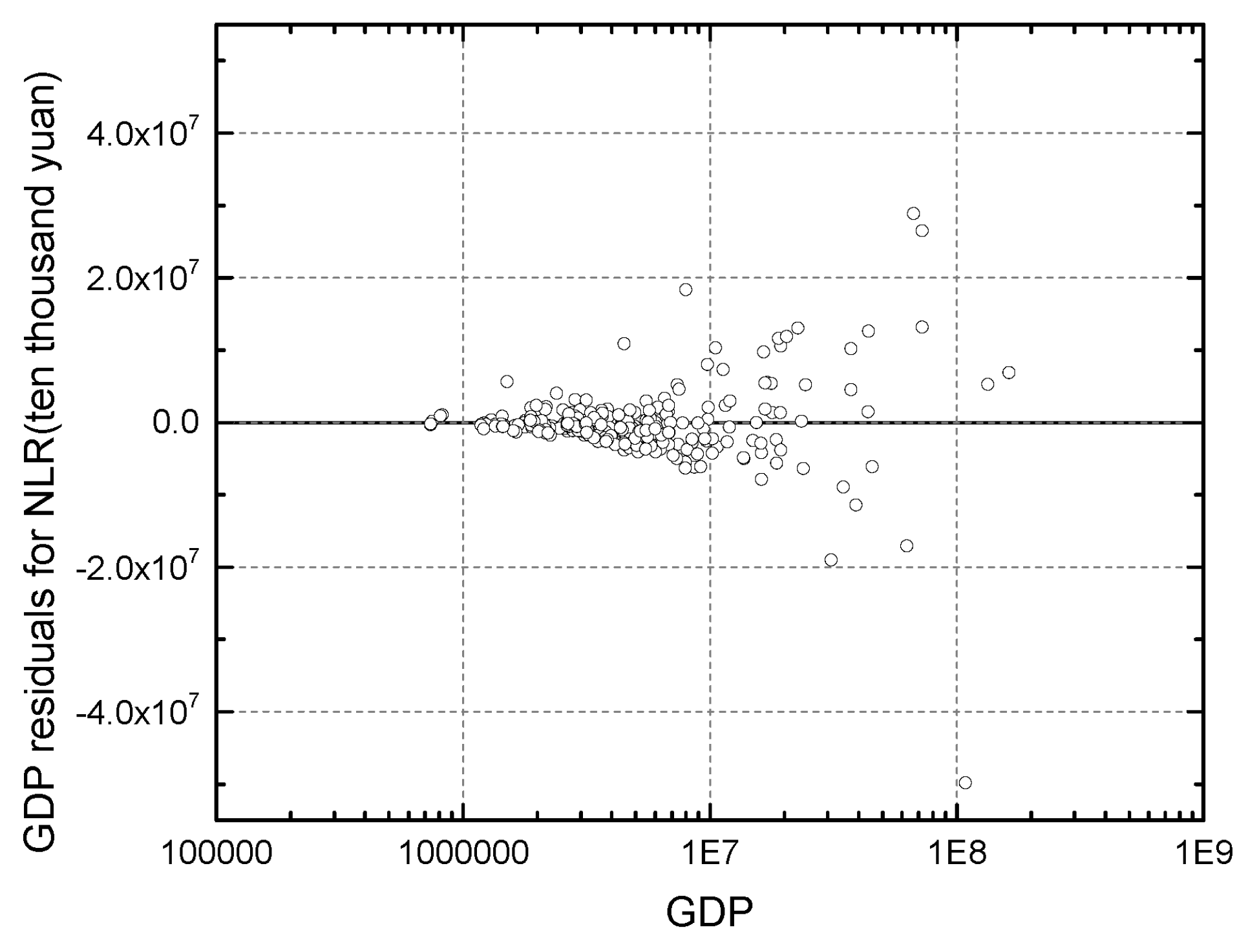
3.3. Limitations
3.4. Variance Homogeneity of the Fitting Method
4. The CHVR Method
4.1. Maximum-Likelihood Fitting Method Based on Variance Function
4.2. Meeting the Lower Bound Constraints
4.3. Defining a Self-Starter Function
5. Method Evaluation Criteria
6. Method Evaluations and Results
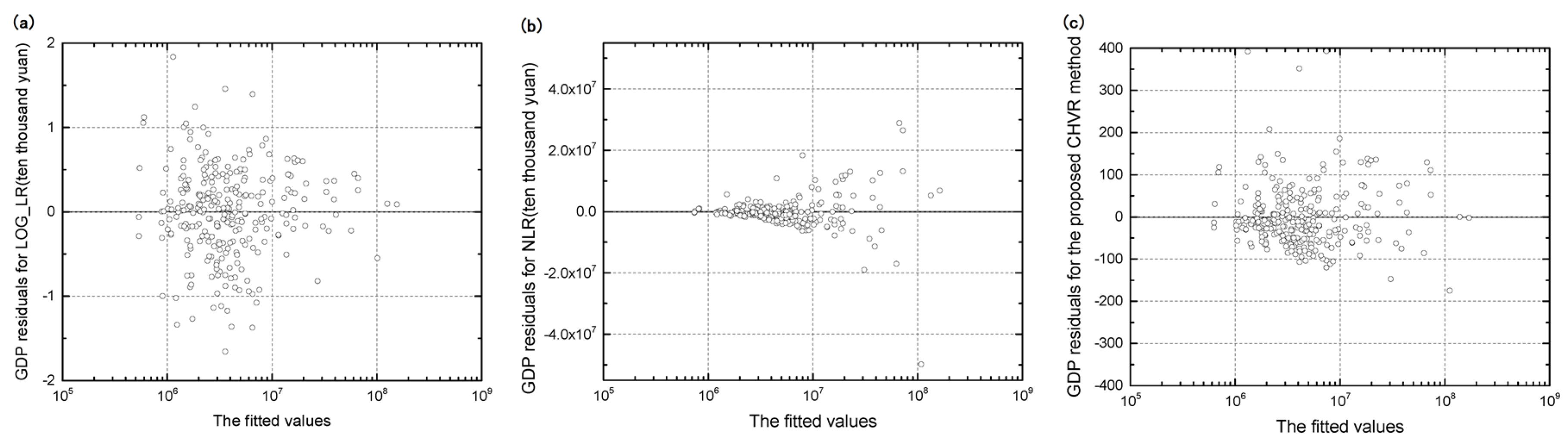
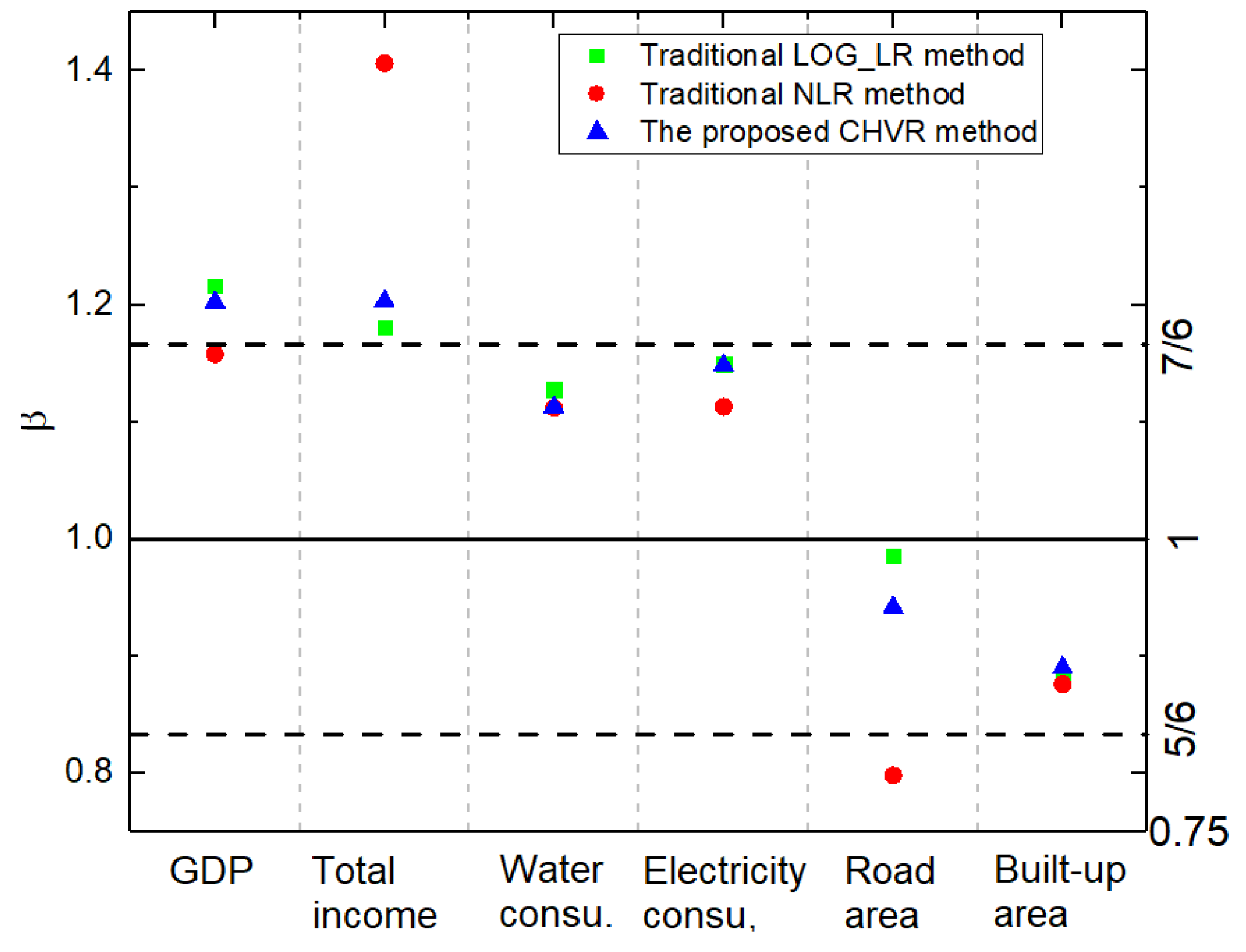
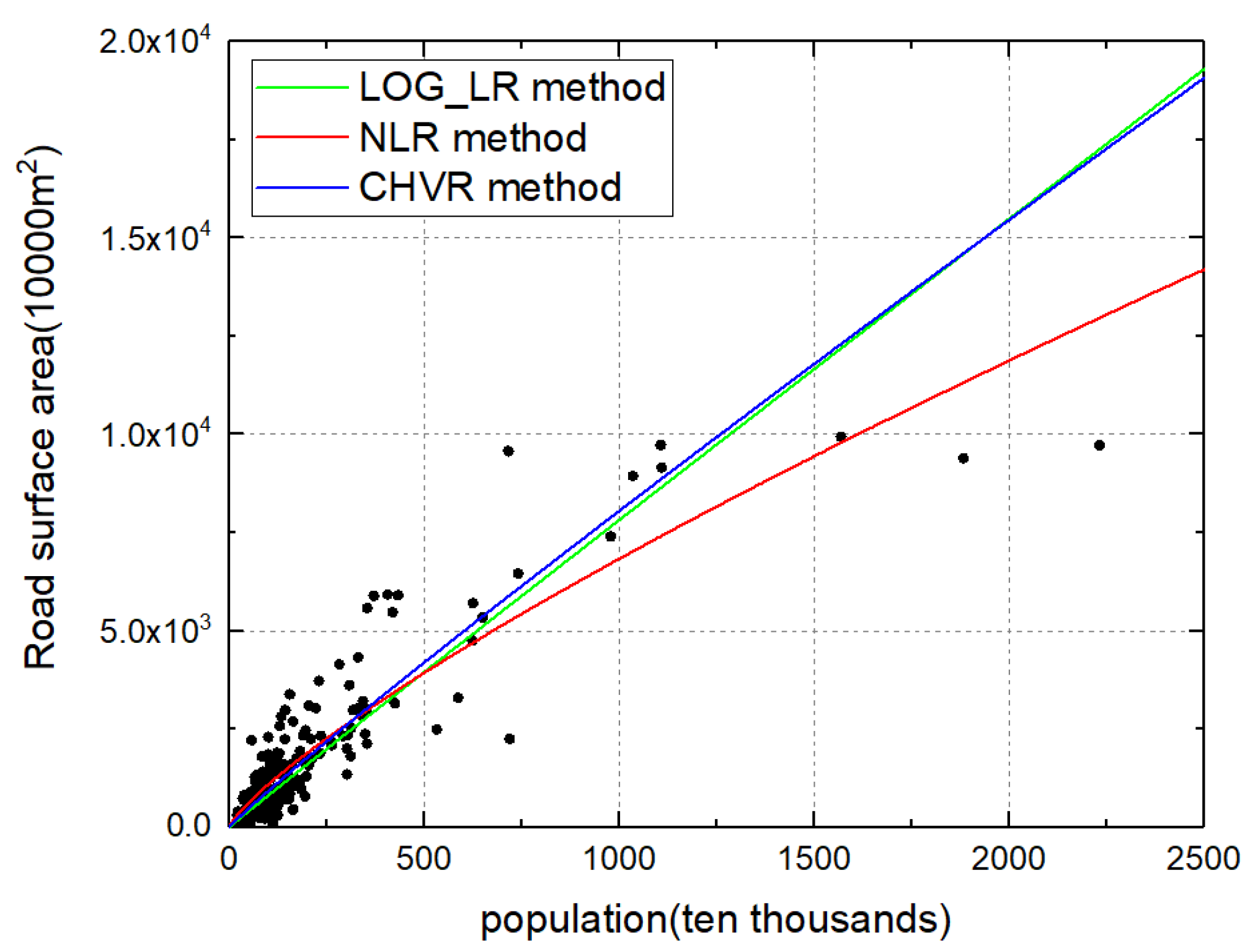
6.1. Method Evaluation Results of the LOG_LR, NLR, and CHVR Methods
6.2. Heterogeneity Results of the LOG_LR, NLR, and CHVR Methods
7. Discussions
7.1. Urban Scaling Law in CHINA Based on the CHVR Method
7.2. Dependence of the Estimated Exponent on the Method
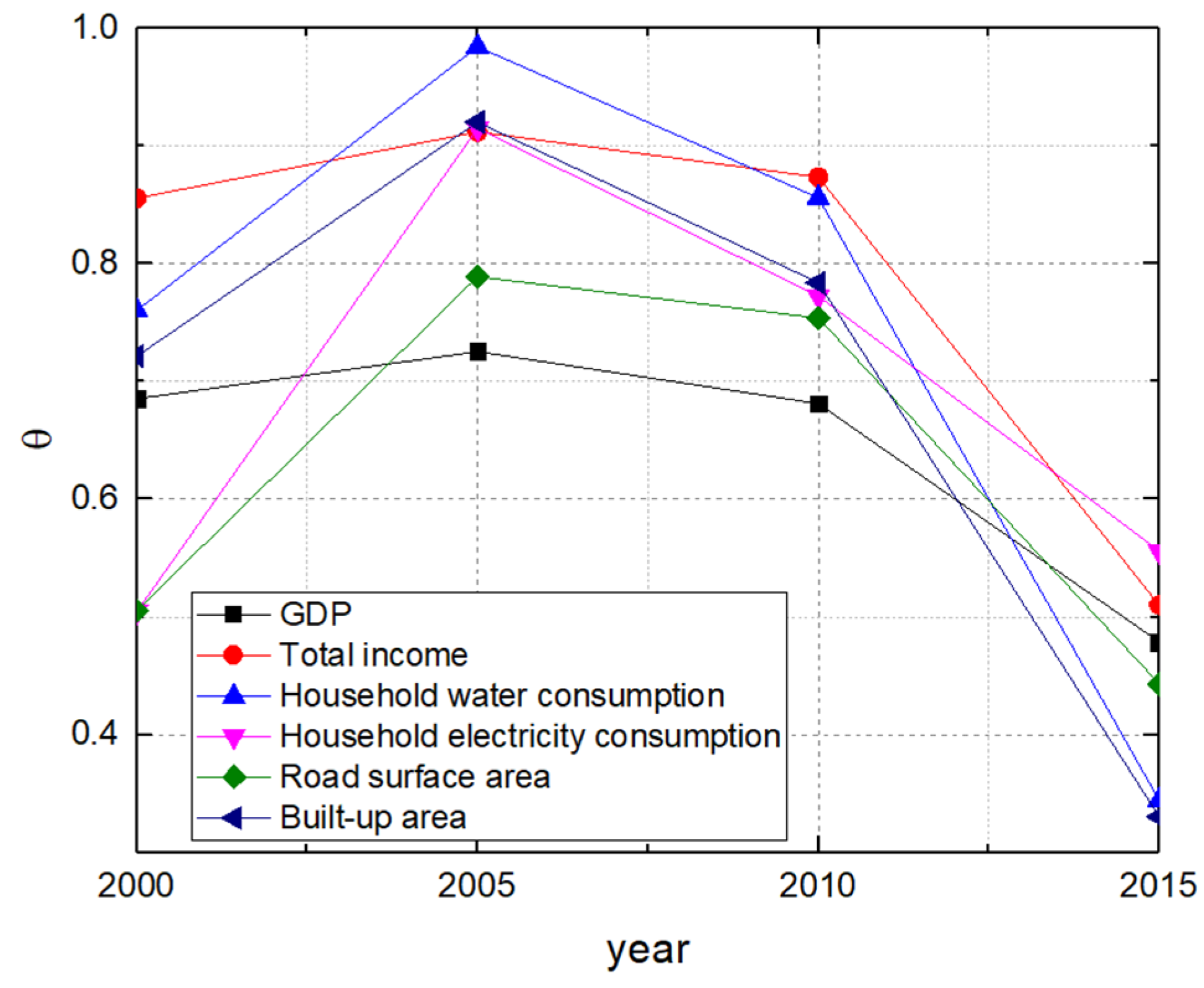
7.3. Urban Interpretations of from a Dynamic Perspective
8. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Batty, M. A theory of city size. Science 2013, 340, 1418–1419. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef]
- Bettencourt, L.M. The origins of scaling in cities. Science 2013, 340, 1438–1441. [Google Scholar] [CrossRef]
- Pumain, D.; Paulus, F.; Vacchiani-Marcuzzo, C.; Lobo, J. An evolutionary theory for interpreting urban scaling laws. Cybergeo Eur. J. Geogr. 2006. [Google Scholar] [CrossRef]
- Chen, Y.G. and Liu, M.H. Study on fractal dimension of size distribution of cities. Bull. Sci. Technol. 1998, 14, 395–400. [Google Scholar]
- Nordbeck, S. Urban allometric growth. Geogr. Ann. Ser. B Hum. Geogr. 1971, 53, 54–67. [Google Scholar] [CrossRef]
- Kleiber, M. Body size and metabolism. Hilgardia 1932, 6, 315–353. [Google Scholar] [CrossRef]
- West, G.B.; Woodruff, W.H.; Brown, J.H. Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc. Natl. Acad. Sci. USA 2002, 99, 2473–2478. [Google Scholar] [CrossRef] [PubMed]
- Batty, M. The New Science of Cities; The MIT Press: Cambridge, MA, USA, 2013; pp. 123–126. [Google Scholar]
- Bettencourt, L.; West, G. A unified theory of urban living. Nature 2010, 467, 912–913. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Lobo, J.; Strumsky, D.; West, G.B. Urban scaling and its deviations: Revealing the structure of wealth, innovation and crime across cities. PLoS ONE 2010, 5, e13541. [Google Scholar] [CrossRef] [PubMed]
- Louf, R.; Barthelemy, M. How congestion shapes cities: From mobility patterns to scaling. Sci. Rep. 2014, 4, 5561. [Google Scholar] [CrossRef] [PubMed]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Alves, L.G.; Ribeiro, H.V.; Lenzi, E.K.; Mendes, R.S. Distance to the scaling law: A useful approach for unveiling relationships between crime and urban metrics. PLoS ONE 2013, 8, e69580. [Google Scholar] [CrossRef]
- Chen, Y. Characterizing growth and form of fractal cities with allometric scaling exponents. Discret. Dyn. Nat. Soc. 2010, 2010, 194715. [Google Scholar] [CrossRef]
- Li, R.; Dong, L.; Zhang, J.; Wang, X.; Wang, W.-X.; Di, Z.; Stanley, H.E. Simple spatial scaling rules behind complex cities. Nat. Commun. 2017, 8, 1841. [Google Scholar] [CrossRef]
- Pumain, D.; Rozenblat, C. Two metropolisation gradients in the European system of cities revealed by scaling laws. Environ. Plan. B Urban Anal. City Sci. 2018. [Google Scholar] [CrossRef]
- Arbabi, H.; Mayfield, M.; Dabinett, G. Urban performance at different boundaries in England and wales through the settlement scaling theory. Reg. Stud. 2018. [Google Scholar] [CrossRef]
- Louf, R. Wandering in cities: A statistical physics approach to urban theory. arXiv, 2015; arXiv:1511.08236. [Google Scholar]
- Oliveira, E.A.; Andrade, J.S., Jr.; Makse, H.A. Large cities are less green. Sci. Rep. 2014, 4, 4235. [Google Scholar] [CrossRef]
- Cottineau, C.; Hatna, E.; Arcaute, E.; Batty, M. Diverse cities or the systematic paradox of urban scaling laws. Comput. Environ. Urban Syst. 2017, 63, 80–94. [Google Scholar] [CrossRef]
- Dong, L.; Wang, H.; Zhao, H. The definition of city boundary and scaling law. Acta Geogr. Sin. 2017, 72, 213–223. [Google Scholar]
- Finance, O.; Cottineau, C. Are the absent always wrong? Dealing with zero values in urban scaling. Environ. Plan. B Urban Anal. City Sci. 2018. [Google Scholar] [CrossRef]
- Stumpf, M.P.; Porter, M.A. Critical truths about power laws. Science 2012, 335, 665–666. [Google Scholar] [CrossRef] [PubMed]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-law distributions in empirical data. Siam Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Lobo, J. Urban scaling in Europe. J. R. Soc. Interface 2016, 13. [Google Scholar] [CrossRef] [PubMed]
- Packard, G.C. On the use of logarithmic transformations in allometric analyses. J. Theor. Biol. 2009, 257, 515–518. [Google Scholar] [CrossRef]
- Packard, G.C.; Birchard, G.F.; Boardman, T.J. Fitting statistical models in bivariate allometry. Biol. Rev. 2011, 86, 549–563. [Google Scholar] [CrossRef]
- Xiao, X.; White, E.P.; Hooten, M.B.; Durham, S.L. On the use of log-transformation vs. Nonlinear regression for analyzing biological power laws. Ecology 2011, 92, 1887–1894. [Google Scholar] [CrossRef]
- Packard, G.C.; Birchard, G.F. Traditional allometric analysis fails to provide a valid predictive model for mammalian metabolic rates. J. Exp. Biol. 2008, 211, 3581–3587. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, G.; Xu, X. Urban allometric growth in China: Theory and facts. Acta Geogr. Sin. 2009, 64, 399–407. [Google Scholar]
- Alain, F.; Zuur, E.N.L. Mixed Effects Models and Extensions in Ecology with R; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Leitão, J.C.; Miotto, J.M.; Gerlach, M.; Altmann, E.G. Is this scaling nonlinear? R. Soc. Open Sci. 2016, 3, 150649. [Google Scholar] [CrossRef]
- Eisler, Z.; Bartos, I.; Kertész, J. Fluctuation scaling in complex systems: Taylor’s law and beyond. Adv. Phys. 2008, 57, 89–142. [Google Scholar] [CrossRef]
- Gao, P.; Liu, Z.; Tian, K.; Liu, G. Characterizing traffic conditions from the perspective of spatial-temporal heterogeneity. ISPRS Int. J. Geo-Inf. 2016, 5, 34. [Google Scholar] [CrossRef]
- Greig, A.; Dewhurst, J.; Horner, M. An application of Taylor’s Power Law to measure overdispersion of the unemployed in English labor markets. Geogr. Anal. 2015, 47, 121–133. [Google Scholar] [CrossRef]
- Hanley, Q.S.; Khatun, S.; Yosef, A.; Dyer, R.-M. Fluctuation scaling, Taylor’s law, and crime. PLoS ONE 2014, 9, e109004. [Google Scholar] [CrossRef] [PubMed]
- Nomaler, Ö.; Frenken, K.; Heimeriks, G. On scaling of scientific knowledge production in US metropolitan areas. PLoS ONE 2014, 9, e110805. [Google Scholar] [CrossRef] [PubMed]
- UN. World Urbanization Prospects: The 2014 Revision; UN: New York, NY, USA, 2014. [Google Scholar]
- Deng, X.; Huang, J.; Rozelle, S.; Uchida, E. Growth, population and industrialization, and urban land expansion of China. J. Urban Econ. 2008, 63, 96–115. [Google Scholar] [CrossRef]
- Ye, X.; Xie, Y. Re-examination of Zipf’s law and urban dynamic in China: A regional approach. Ann. Reg. Sci. 2012, 49, 135–156. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y. Scaling laws and indications of self-organized criticality in urban systems. Chaos Solitons Fractals 2008, 35, 85–98. [Google Scholar] [CrossRef]
- Ramaswami, A.; Jiang, D.; Tong, K.; Zhao, J. Impact of the economic structure of cities on urban scaling factors: Implications for urban material and energy flows in China. J. Ind. Ecol. 2018, 22, 392–405. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Pumain, D.; Paulus, F.; Vacchiani-Marcuzzo, C. Innovation cycles and urban dynamics. In Complexity Perspectives in Innovation and Social Change; Springer: Berlin/Heidelberg, Germany, 2009; pp. 237–260. [Google Scholar]
- Cristelli, M.; Batty, M.; Pietronero, L. There is more than a power law in Zipf. Sci. Rep. 2012, 2, 812. [Google Scholar] [CrossRef]
- Ritz, C.; Streibig, J.C. Nonlinear Regression with R; Springer: Berlin/Heidelberg, Germany, 2008; p. 473. [Google Scholar]
- Gastwirth, J.L.; Gel, Y.R.; Miao, W. The impact of Levene’s test of equality of variances on statistical theory and practice. Stat. Sci. 2009, 24, 343–360. [Google Scholar] [CrossRef]
- Breusch, T.S.; Pagan, A.R. A simple test for heteroscedasticity and random coefficient variation. Econometrica 1979, 47, 1287–1294. [Google Scholar] [CrossRef]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-Plus, corrected third printing; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Taylor, L. Aggregation, variance and the mean. Nature 1961, 189, 732–735. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, B. Hierarchical scaling in systems of natural cities. Entropy 2018, 20, 432. [Google Scholar] [CrossRef]
- Chen, Y. The mathematical relationship between Zipf’s law and the hierarchical scaling law. Phys. A Stat. Mech. Its Appl. 2012, 391, 3285–3299. [Google Scholar] [CrossRef]
- Wen, H.; Wei, D. Urban Economics; Tsinghua University Press: Beijing, China, 2008. [Google Scholar]
- See e.G. Available online: https://obamawhitehouse.Archives.Gov/sites/default/files/omb/assets/fedreg_|2010/06282010_metro_standards-complete.Pdf (accessed on 17 November 2018).
- See e.G. Available online: http://www.Census.Gov/population/metro/ (accessed on 17 November 2018).
- Kohavi, R. In A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the IJCAI, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145. [Google Scholar]
- Cawley, G.C.; Talbot, N.L. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Greene, W.H. Econometric Analysis; Pearson Education India: Noida, India, 2003. [Google Scholar]
- Rice, W.R. Analyzing tables of statistical tests. Evolution 1989, 43, 223–225. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Lievano, A.; Patterson-Lomba, O.; Hausmann, R. Explaining the prevalence, scaling and variance of urban phenomena. Nat. Hum. Behav. 2016, 1, 0012. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.; Jing, L. Derivation of relations between urbanization level and velocity from logistic growth model. Geogr. Res. 2006, 25, 1063–1072. [Google Scholar]
- West, G. Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies; Penguin: London, UK, 2017; p. 26. [Google Scholar]
- Petri, G.; Expert, P.; Jensen, H.J.; Polak, J.W. Entangled communities and spatial synchronization lead to criticality in urban traffic. Sci. Rep. 2013, 3, 1798. [Google Scholar] [CrossRef] [PubMed]
| Urban Attributes | Methods | SE | MCI | ||||
|---|---|---|---|---|---|---|---|
| GDP | LOG_LR | 1.2162 | 0.0345 | / | 0.7814 | ||
| NLR | 1.1580 | 0.0591 | / | 0.9099 | |||
| CHVR | 1.2022 | 0.0300 | 0.6813 | 0.9342 | 3.3173 × 1013 | 1.2806 × 108 | |
| Total income | LOG_LR | 1.1809 | 0.0397 | / | 0.7367 | ||
| NLR | 1.4063 | 0.2401 | / | 0.8145 | |||
| CHVR | 1.2032 | 0.0395 | 0.8737 | 0.9625 | 2.4320 × 1012 | 3.0365 × 107 | |
| Household water consumption | LOG_LR | 1.1278 | 0.0377 | / | 0.7283 | ||
| NLR | 1.1121 | 0.0727 | / | 0.8389 | |||
| CHVR | 1.1131 | 0.0332 | 0.8561 | 0.9346 | 2.0520 × 107 | 1.0287 × 105 | |
| Household electricity consumption | LOG_LR | 1.1493 | 0.0331 | / | 0.8278 | ||
| NLR | 1.1130 | 0.0518 | / | 0.9371 | |||
| CHVR | 1.1484 | 0.0310 | 0.7539 | 0.9574 | 2.2693 × 109 | 1.0758 × 106 | |
| Road surface area | LOG_LR | 0.9862 | 0.0287 | / | 0.7034 | ||
| NLR | 0.7984 | 0.0430 | / | 0.8155 | 6.7414 × 105 | ||
| CHVR | 0.9417 | 0.0236 | 0.7727 | 0.8573 | 8.8028 × 105 | 2.0146 × 104 | |
| Built-up area | LOG_LR | 0.8790 | 0.0287 | / | 0.7544 | ||
| NLR | 0.8758 | 0.0544 | / | 0.8790 | |||
| CHVR | 0.8900 | 0.0273 | 0.7840 | 0.8882 | 2.9697 × 103 | 1.2085 × 103 |
| Parameter | LOG_LR | NLR | CHVR | |||||
|---|---|---|---|---|---|---|---|---|
| F-Value | p-Value | F-Value | p-Value | F-Value | p-Value | |||
| GDP | 3.3241 | 0.0694 | 48.9939 | 1.99 × * | 0.6134 | 0.4341 | ||
| Total income | 0.0237 | 0.8778 | 35.2855 | 8.64 × * | 3.3044 | 0.0702 | ||
| Water consumption | 6.5394 | 0.0111* | 40.9598 | 6.74 × * | 0.7598 | 0.3842 | ||
| Electricity consumption | 5.6067 | 0.0186* | 46.8604 | 5.15 × * | 0.0579 | 0.8101 | ||
| Road surface area | 2.2672 | 0.1333 | 91.3284 | 7.44 × * | 0.2567 | 0.6128 | ||
| Built-up area | 0.3846 | 0.5357 | 81.3017 | 3.51 × * | 0.1677 | 0.6825 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Zhao, H.; Tan, Q.; Gao, P. An Urban Scaling Estimation Method in a Heterogeneity Variance Perspective. Entropy 2019, 21, 337. https://doi.org/10.3390/e21040337
Wu W, Zhao H, Tan Q, Gao P. An Urban Scaling Estimation Method in a Heterogeneity Variance Perspective. Entropy. 2019; 21(4):337. https://doi.org/10.3390/e21040337
Chicago/Turabian StyleWu, Wenjia, Hongrui Zhao, Qifan Tan, and Peichao Gao. 2019. "An Urban Scaling Estimation Method in a Heterogeneity Variance Perspective" Entropy 21, no. 4: 337. https://doi.org/10.3390/e21040337
APA StyleWu, W., Zhao, H., Tan, Q., & Gao, P. (2019). An Urban Scaling Estimation Method in a Heterogeneity Variance Perspective. Entropy, 21(4), 337. https://doi.org/10.3390/e21040337






