Information Thermodynamics for Time Series of Signal-Response Models
Abstract
1. Introduction
2. Introduction to Continuous Information Thermodynamics
2.1. Entropy Production in Heat Baths
2.2. Feedbacks and Information
2.3. Irreversible Entropy Production
3. Bivariate Time Series Information Thermodynamics
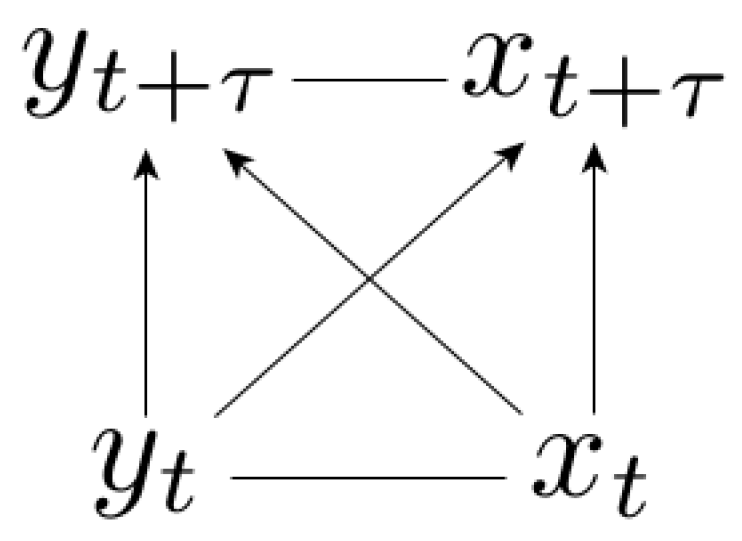
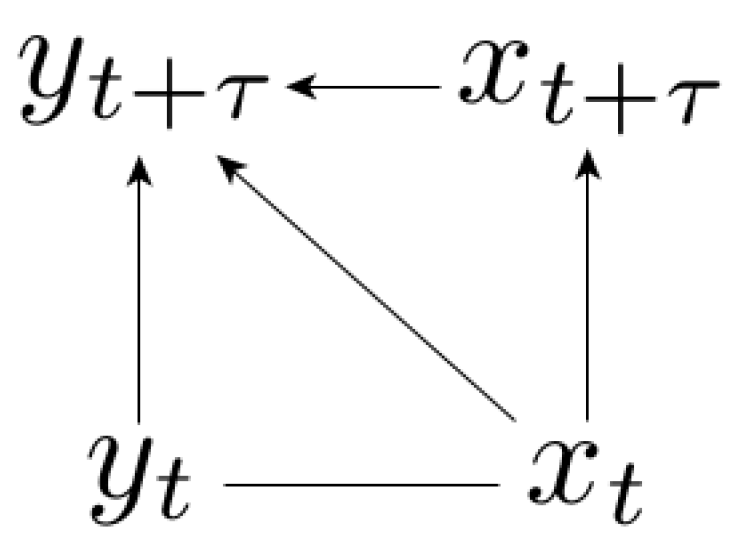
3.1. Setting and Definition of Causal Representations
3.2. Definition of Mapping Irreversibility and the Standard Integral Fluctuation Theorem
3.3. Ito Inequality for Time Series
3.4. The Mapping Irreversibility Density
4. The Fluctuation Theorem for Time Series of Signal-Response Models
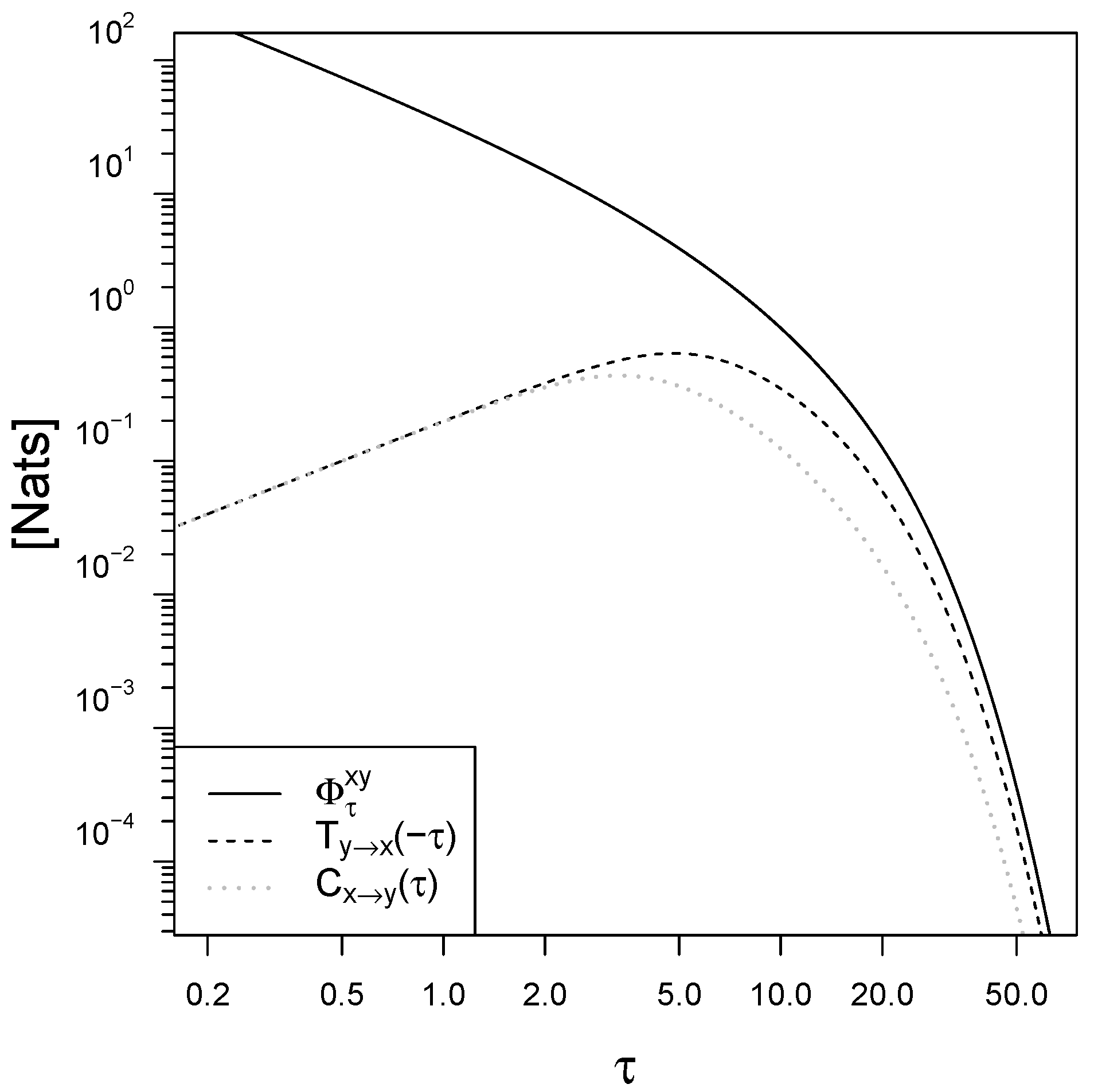
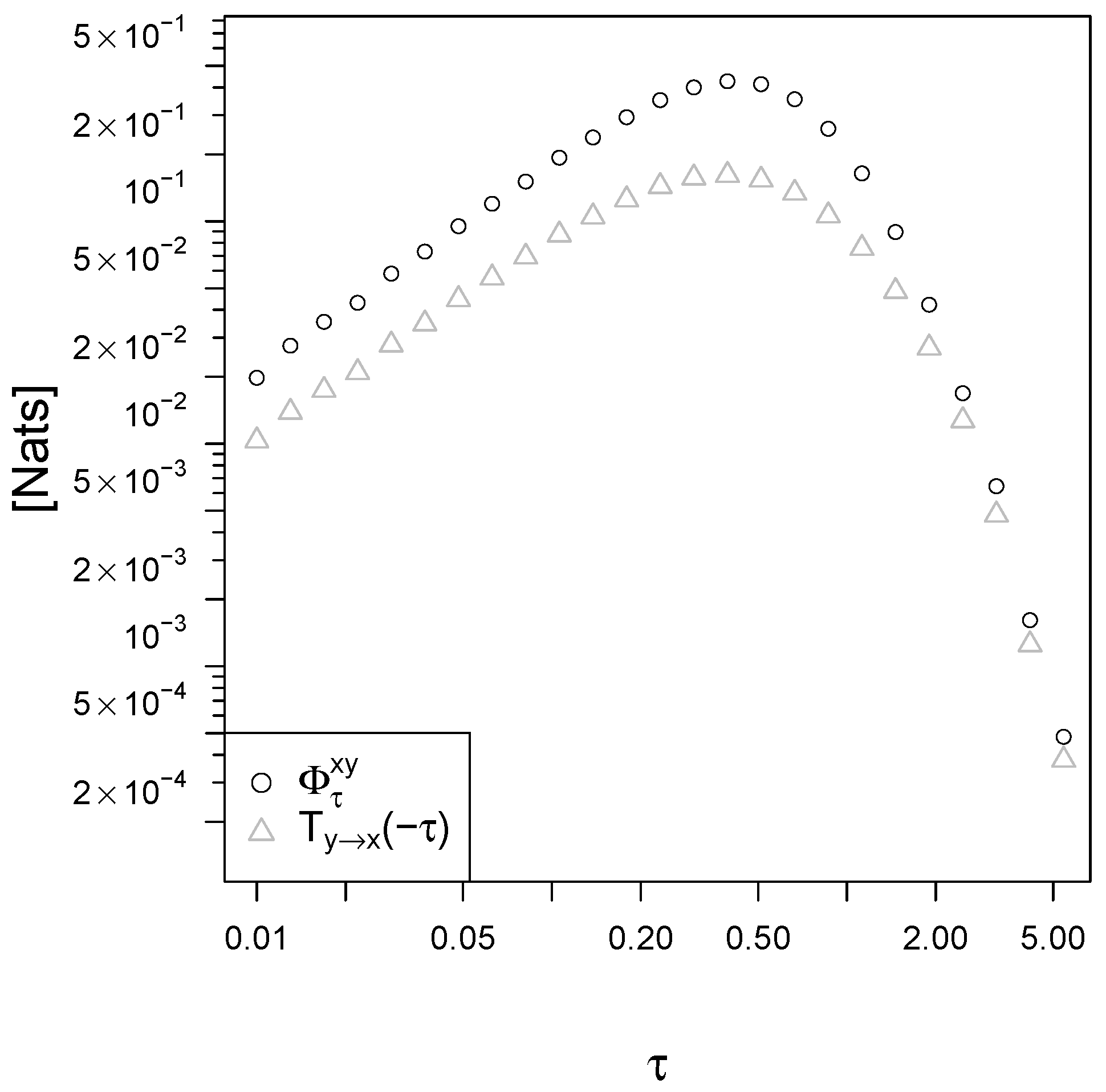
5. Applications
5.1. The Basic Linear Response Model
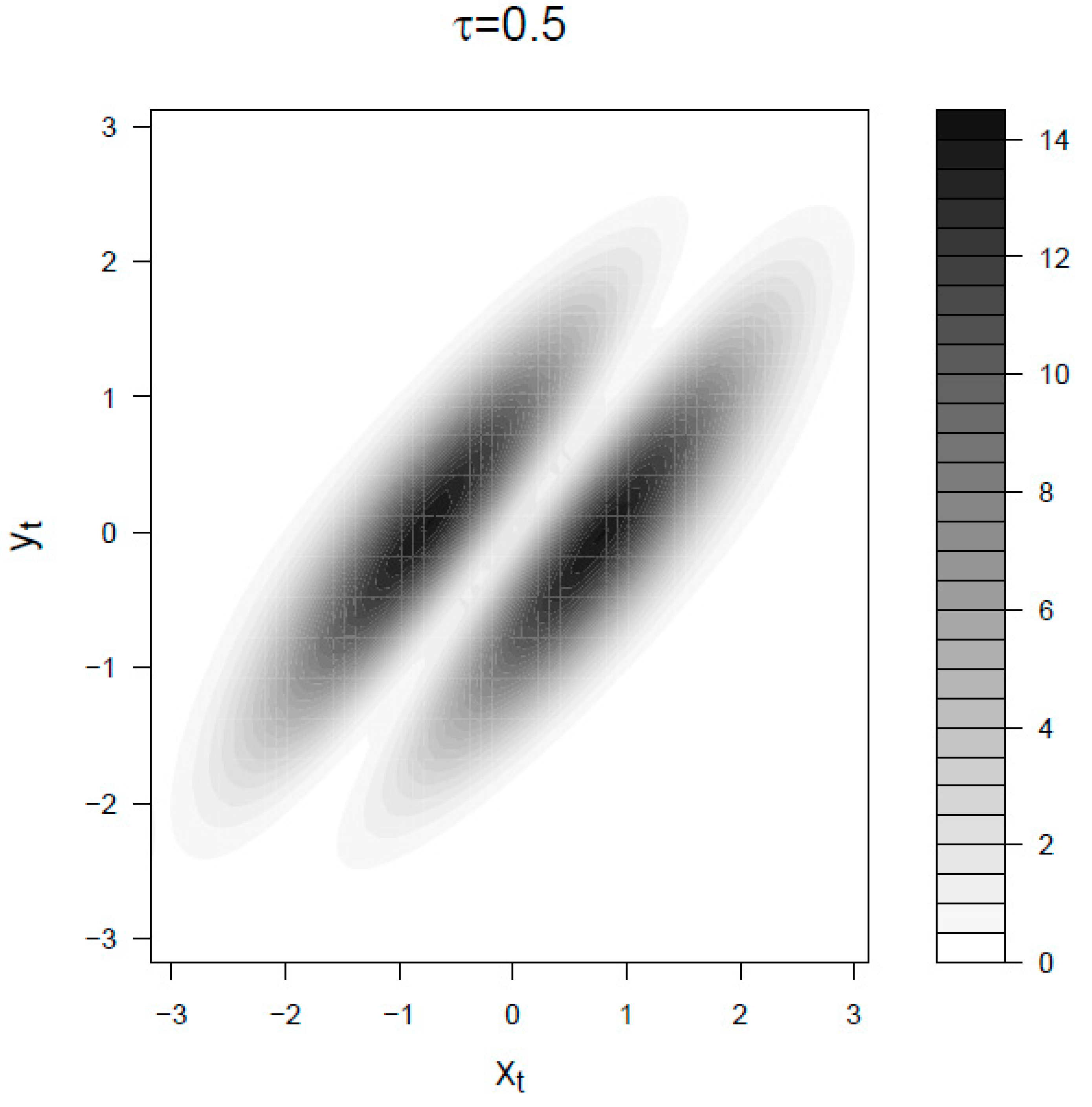
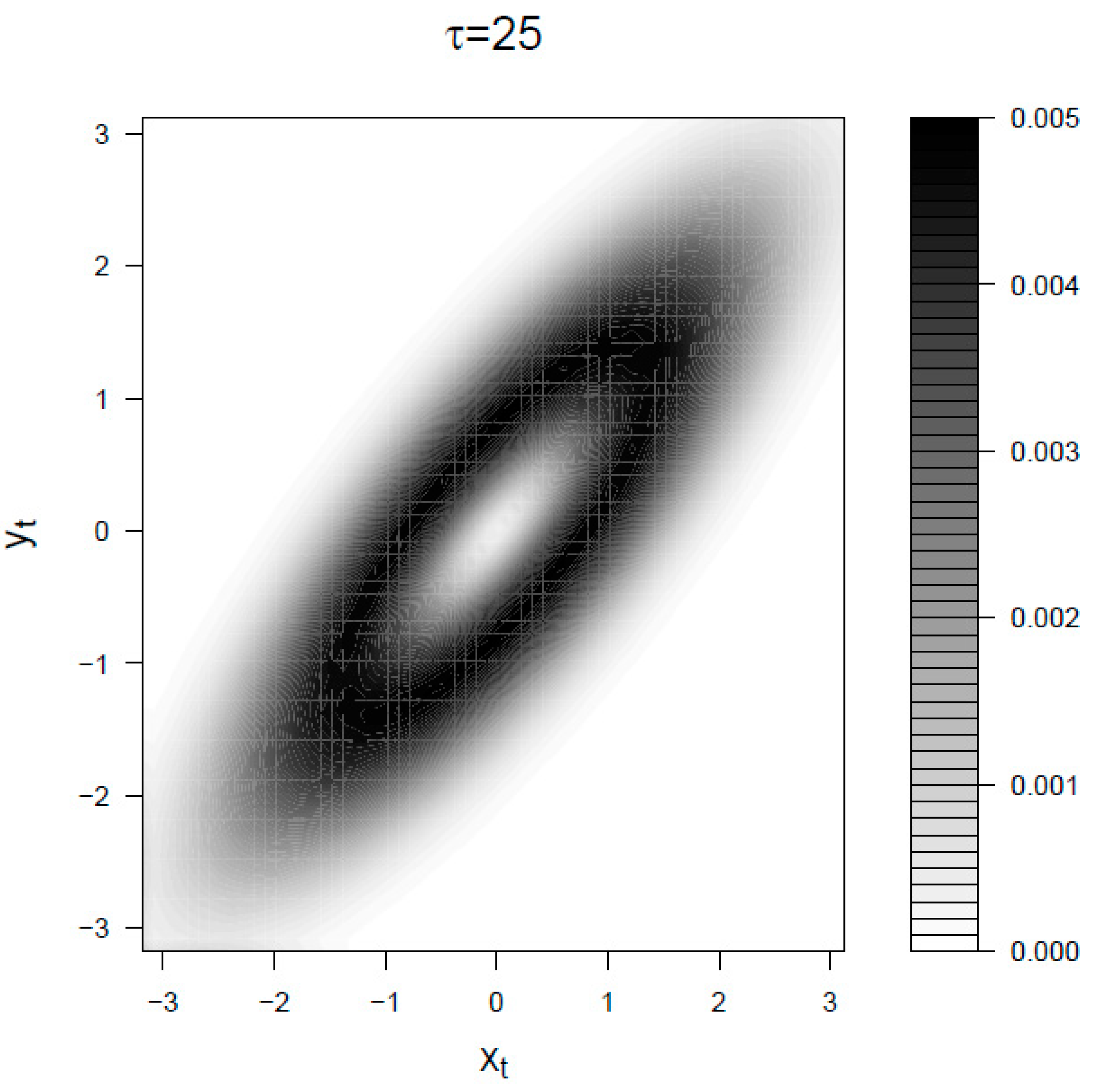
5.2. Receptor-Ligand Systems
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OU | Ornstein-Uhlenbeck process |
| BLRM | basic linear signal-response model |
Appendix A. Mapping Irreversibility in the BLRM
Appendix B. Backward Transfer Entropy in the BLRM
Appendix C. The Causal Influence Rate Converges to the Horowitz-Esposito Information Flow in the BLRM
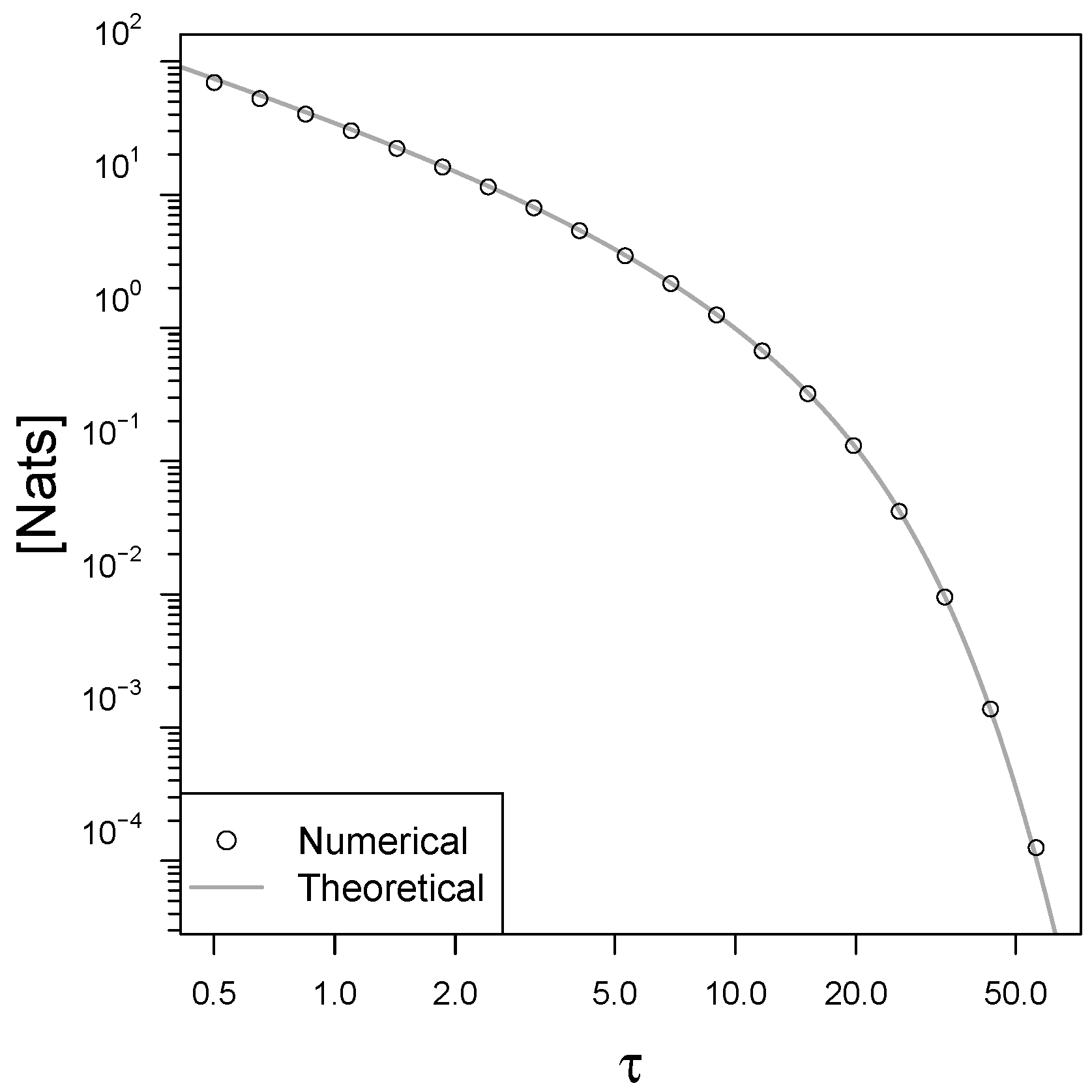
Appendix D. Numerical Convergence of the Mapping Irreversibility to the Entropy Production in the Feedback Cooling Model
Appendix E. Numerical Estimation of the Entropy Production in the Bivariate Gaussian Approximation
References
- Jarzynski, C. Equalities and inequalities: Irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter Phys. 2011, 2, 329–351. [Google Scholar] [CrossRef]
- Parrondo, J.M.; van den Broeck, C.; Kawai, R. Entropy production and the arrow of time. New J. Phys. 2009, 11, 073008. [Google Scholar] [CrossRef]
- Feng, E.H.; Crooks, G.E. Length of time’s arrow. Phys. Revi. Lett. 2008, 101, 090602. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. The fluctuation theorem. Adv. Phys. 2002, 51, 1529–1585. [Google Scholar] [CrossRef]
- Kawai, R.; Parrondo, J.; van den Broeck, C. Dissipation: The phase-space perspective. Phys. Rev. Lett. 2007, 98, 080602. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Hamiltonian derivation of a detailed fluctuation theorem. J. Stat. Phys. 2000, 98, 77–102. [Google Scholar] [CrossRef]
- Chernyak, V.Y.; Chertkov, M.; Jarzynski, C. Path-integral analysis of fluctuation theorems for general Langevin processes. J. Stat. Mech. Theory Exp. 2006, 2006, P08001. [Google Scholar] [CrossRef]
- Ito, S.; Sagawa, T. Information thermodynamics on causal networks. Phys. Rev. Lett. 2013, 111, 180603. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Nonequilibrium thermodynamics of feedback control. Phys. Rev. E 2012, 85, 021104. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Generalized Jarzynski equality under nonequilibrium feedback control. Phys. Rev. Lett. 2010, 104, 090602. [Google Scholar] [CrossRef]
- Szilard, L. On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Syst. Res. Behav. Sci. 1964, 9, 301–310. [Google Scholar] [CrossRef]
- Martínez, I.A.; Roldán, É.; Dinis, L.; Petrov, D.; Parrondo, J.M.; Rica, R.A. Brownian carnot engine. Nat. Phys. 2016, 12, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Ciliberto, S. Experiments in stochastic thermodynamics: Short history and perspectives. Phys. Rev. X 2017, 7, 021051. [Google Scholar] [CrossRef]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyuki, E.; Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nat. Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Koski, J.V.; Maisi, V.F.; Pekola, J.P.; Averin, D.V. Experimental realization of a Szilard engine with a single electron. Proc. Natl. Acad. Sci. USA 2014, 111, 13786–13789. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, J.M.; Esposito, M. Thermodynamics with continuous information flow. Phys. Rev. X 2014, 4, 031015. [Google Scholar] [CrossRef]
- Rosinberg, M.L.; Horowitz, J.M. Continuous information flow fluctuations. EPL (Europhysics Letters) 2016, 116, 10007. [Google Scholar] [CrossRef]
- Horowitz, J.M. Multipartite information flow for multiple Maxwell demons. J. Stat. Mech. Theory Exp. 2015, 2015, P03006. [Google Scholar] [CrossRef]
- Ito, S. Backward transfer entropy: Informational measure for detecting hidden Markov models and its interpretations in thermodynamics, gambling and causality. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Spinney, R.E.; Lizier, J.T.; Prokopenko, M. Transfer entropy in physical systems and the arrow of time. Phys. Rev. E 2016, 94, 022135. [Google Scholar] [CrossRef] [PubMed]
- Parrondo, J.M.; Horowitz, J.M.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Ito, S. Unified framework for the second law of thermodynamics and information thermodynamics based on information geometry. arXiv, 2018; arXiv:1810.09545. [Google Scholar]
- Ito, S. Stochastic thermodynamic interpretation of information geometry. Phys. Rev. Lett. 2018, 121, 030605. [Google Scholar] [CrossRef] [PubMed]
- Roldán, É.; Parrondo, J.M. Entropy production and Kullback-Leibler divergence between stationary trajectories of discrete systems. Phys. Rev. E 2012, 85, 031129. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Sekimoto, K. Langevin equation and thermodynamics. Prog. Theor. Phys. Supp. 1998, 130, 17–27. [Google Scholar] [CrossRef]
- Crooks, G.E.; Still, S.E. Marginal and conditional second laws of thermodynamics. arXiv, 2016; arXiv:1611.04628. [Google Scholar]
- Auconi, A.; Giansanti, A.; Klipp, E. Causal influence in linear Langevin networks without feedback. Phys. Rev. E 2017, 95, 042315. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Shreve, S.E. Stochastic Calculus for Finance II: Continuous-Time Models; Springer Science & Business Media: New York, NY, USA, 2004; Volume 11. [Google Scholar]
- Taniguchi, T.; Cohen, E. Onsager-Machlup theory for nonequilibrium steady states and fluctuation theorems. J. Stat. Phys. 2007, 126, 1–41. [Google Scholar] [CrossRef]
- Seifert, U. Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef]
- Risken, H. Fokker-planck equation. In The Fokker-Planck Equation; Springer: Berlin, Germany, 1996; pp. 63–95. [Google Scholar]
- Horowitz, J.M.; Sandberg, H. Second-law-like inequalities with information and their interpretations. New J. Phys. 2014, 16, 125007. [Google Scholar] [CrossRef]
- Gomez-Marin, A.; Parrondo, J.M.; van den Broeck, C. Lower bounds on dissipation upon coarse graining. Phys. Rev. E 2008, 78, 011107. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Sagawa, T. Information flow and entropy production on Bayesian networks. In Mathematical Foundations and Applications of Graph Entropy; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 63–100. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact numerical simulation of the Ornstein-Uhlenbeck process and its integral. Phys. Rev. E 1996, 54, 2084. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: www.r-project.org (accessed on 14 February 2019).
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Klipp, E.; Liebermeister, W.; Wierling, C.; Kowald, A.; Herwig, R. Systems Biology: A Textbook; John Wiley & Sons; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016. [Google Scholar]
- Kholodenko, B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 2006, 7, 165. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W.; Setayeshgar, S. Physical limits to biochemical signaling. Proc. Natl. Acad. Sci. USA 2005, 102, 10040–10045. [Google Scholar] [CrossRef]
- Tkačik, G.; Callan, C.G.; Bialek, W. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. USA 2008, 105, 12265–12270. [Google Scholar] [CrossRef]
- Crisanti, A.; de Martino, A.; Fiorentino, J. Statistics of optimal information flow in ensembles of regulatory motifs. Phys. Rev. E 2018, 97, 022407. [Google Scholar] [CrossRef]
- Waltermann, C.; Klipp, E. Information theory based approaches to cellular signaling. Biochimica et Biophysica Acta (BBA)-General Subjects 2011, 1810, 924–932. [Google Scholar] [CrossRef]
- Di Talia, S.; Wieschaus, E.F. Short-term integration of Cdc25 dynamics controls mitotic entry during Drosophila gastrulation. Dev. Cell 2012, 22, 763–774. [Google Scholar] [CrossRef] [PubMed]
- Nemenman, I. Gain control in molecular information processing: Lessons from neuroscience. Phys. Biol. 2012, 9, 026003. [Google Scholar] [CrossRef] [PubMed]
- Di Talia, S.; Wieschaus, E.F. Simple biochemical pathways far from steady state can provide switchlike and integrated responses. Biophys. J. 2014, 107, L1–L4. [Google Scholar] [CrossRef] [PubMed]
- Tkačik, G.; Walczak, A.M.; Bialek, W. Optimizing information flow in small genetic networks. Phys. Rev. E 2009, 80, 031920. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Rare events and the convergence of exponentially averaged work values. Phys. Rev. E 2006, 73, 046105. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Sagawa, T. Maxwell’s demon in biochemical signal transduction with feedback loop. Nat. Commun. 2015, 6, 7498. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- Duchi, J. Derivations for Linear Algebra and Optimization. Available online: https://docplayer.net/30887339-Derivations-for-linear-algebra-and-optimization.html (accessed on 11 February 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auconi, A.; Giansanti, A.; Klipp, E. Information Thermodynamics for Time Series of Signal-Response Models. Entropy 2019, 21, 177. https://doi.org/10.3390/e21020177
Auconi A, Giansanti A, Klipp E. Information Thermodynamics for Time Series of Signal-Response Models. Entropy. 2019; 21(2):177. https://doi.org/10.3390/e21020177
Chicago/Turabian StyleAuconi, Andrea, Andrea Giansanti, and Edda Klipp. 2019. "Information Thermodynamics for Time Series of Signal-Response Models" Entropy 21, no. 2: 177. https://doi.org/10.3390/e21020177
APA StyleAuconi, A., Giansanti, A., & Klipp, E. (2019). Information Thermodynamics for Time Series of Signal-Response Models. Entropy, 21(2), 177. https://doi.org/10.3390/e21020177




