Criticality as a Determinant of Integrated Information Φ in Human Brain Networks
Abstract
:1. Introduction
2. Methods
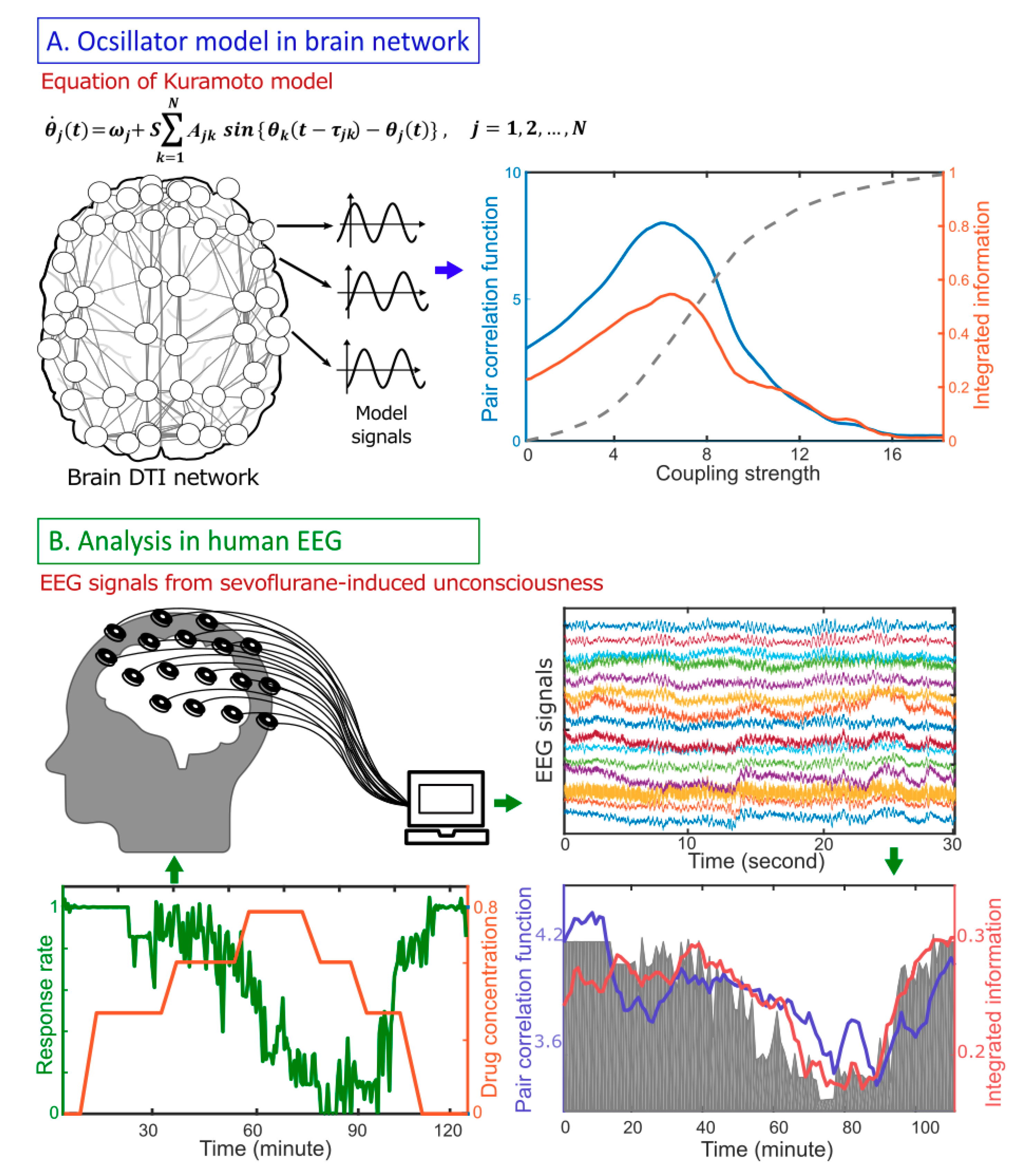
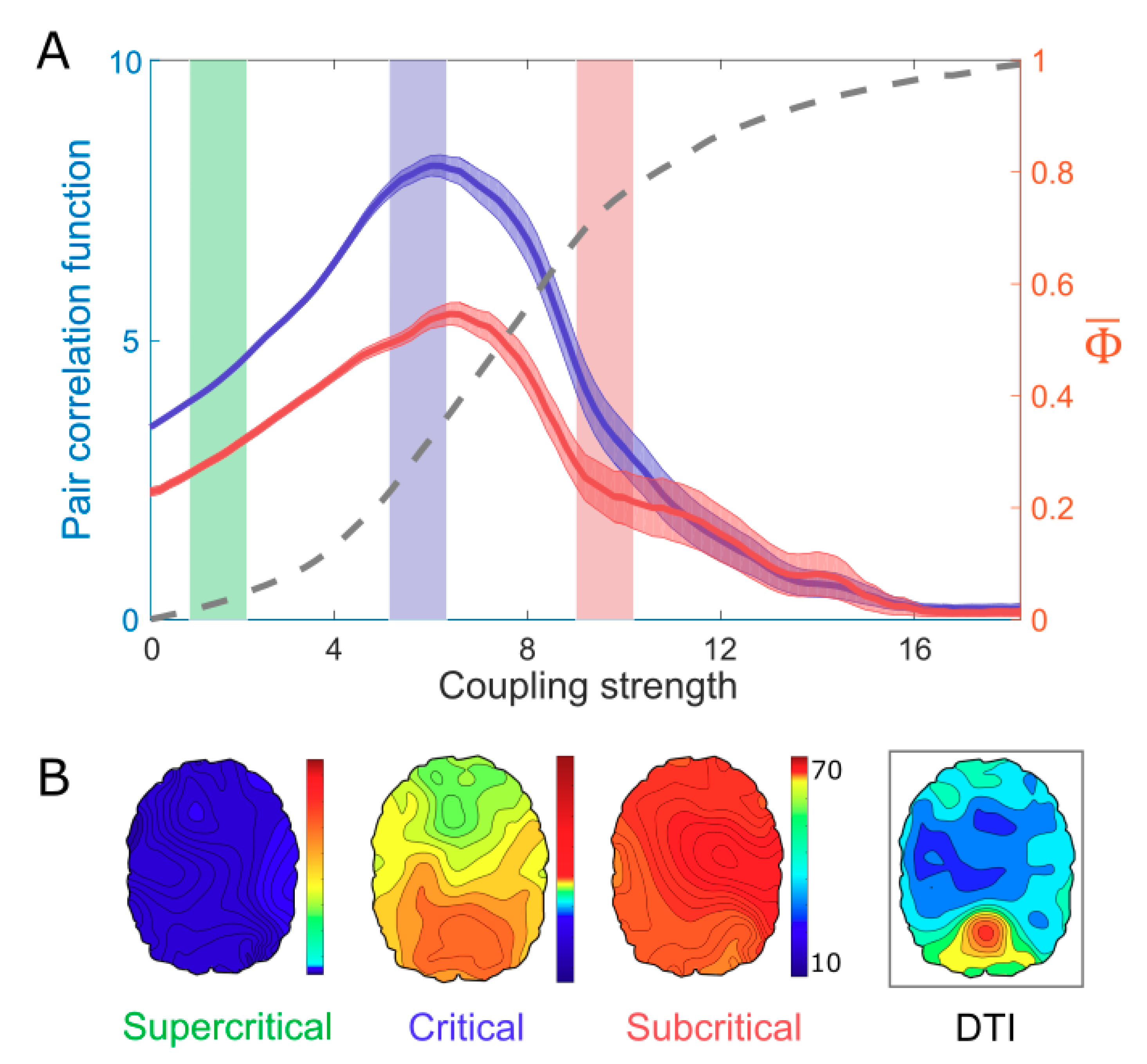
3. Results Model Study: Correlation Between Criticality and
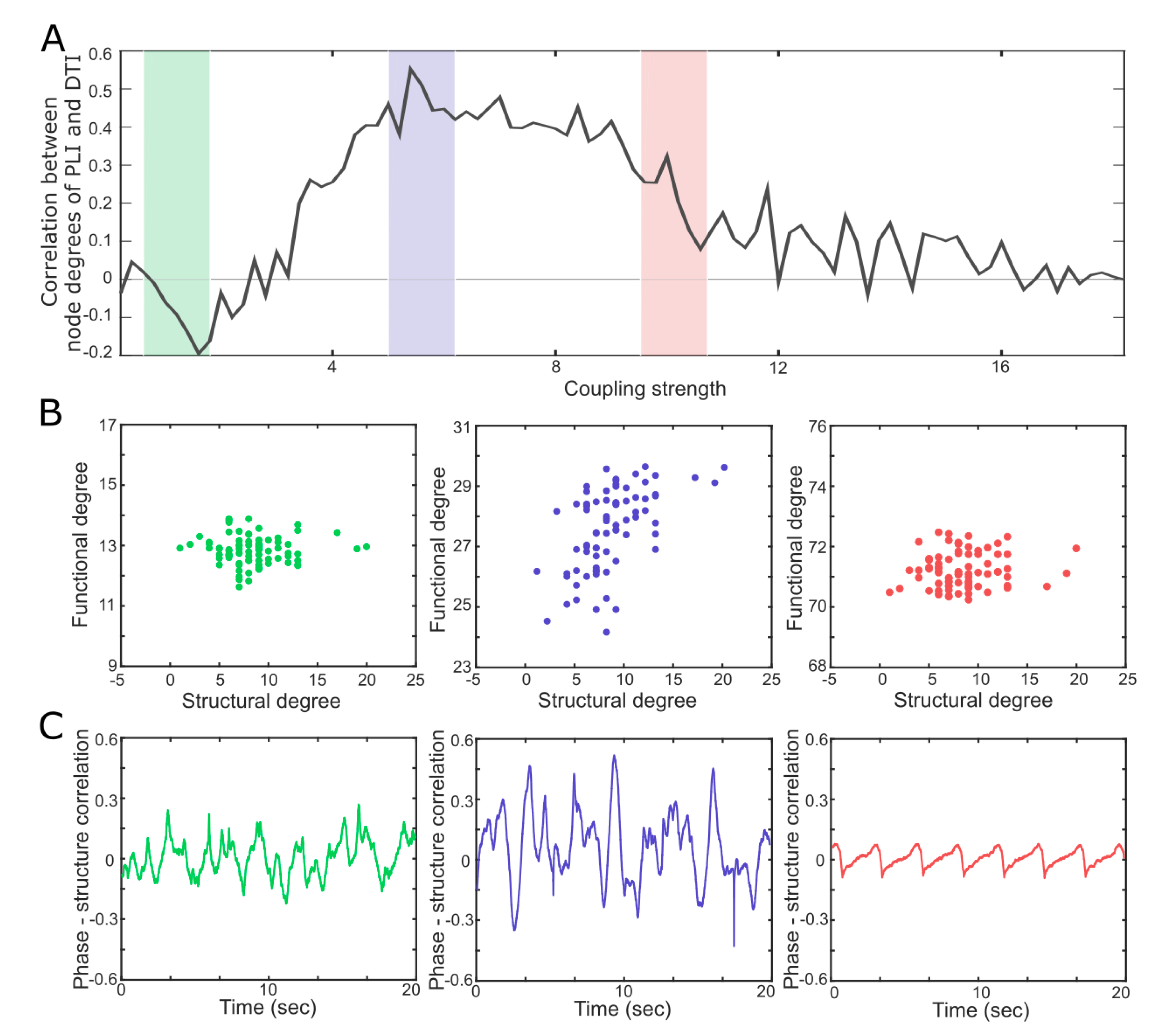
4. A Network Mechanism of the Maximal in a Critical State
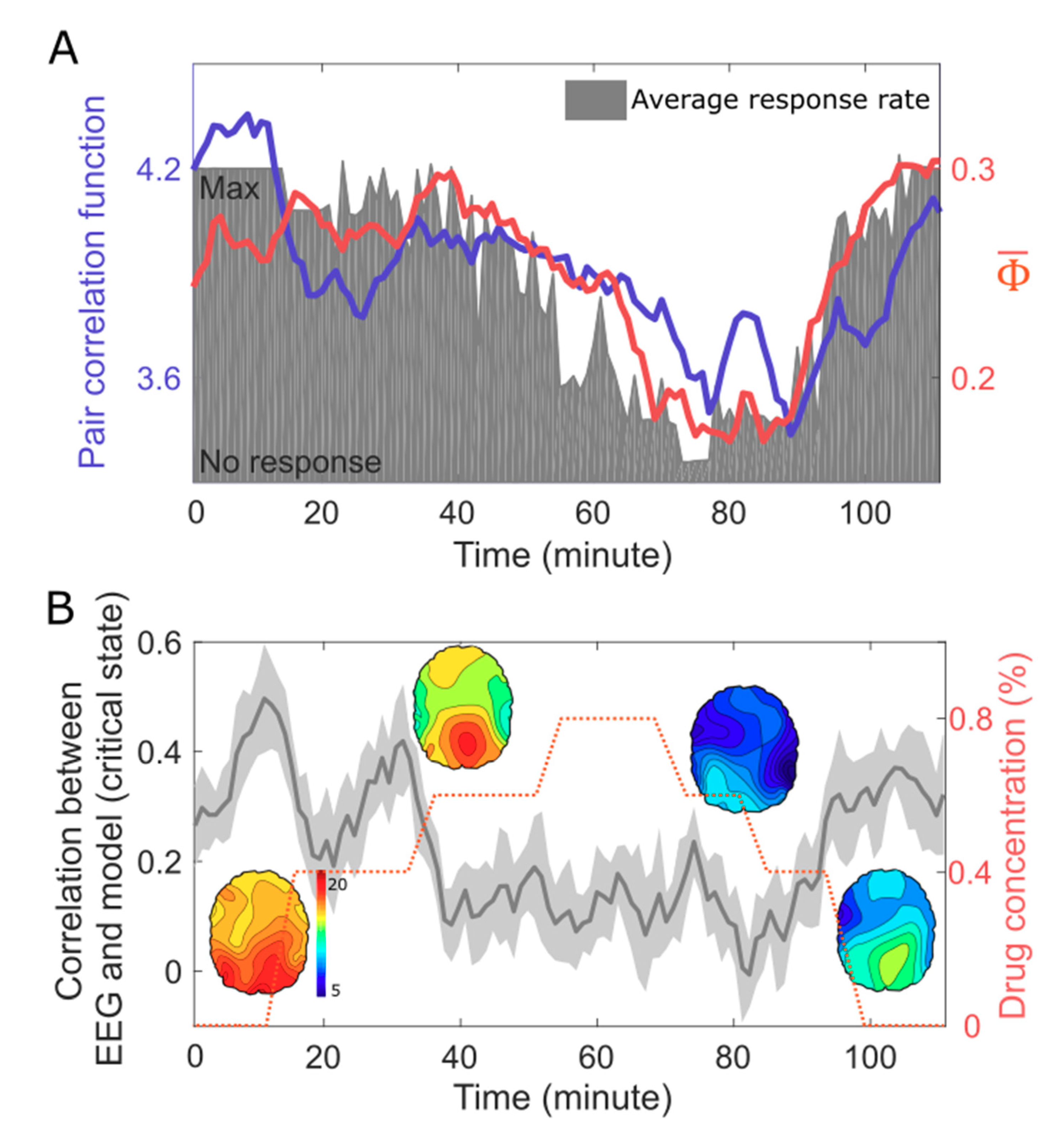
5. EEG Study: Correlation Between Criticality, , and Human Consciousness
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oizumi, M.; Albantakis, L.; Tononi, G. From the phenomenology to the mechanisms of consciousness: Integrated Information Theory 3.0. PLoS Comput Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G. An information integration theory of consciousness. BMC Neurosci. 2004, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Koch, C. The neural correlates of consciousness: An update. Ann. N. Y. Acad. Sci. 2008, 1124, 239–261. [Google Scholar] [CrossRef]
- Tononi, G. Integrated information theory of consciousness: An updated account. Arch. Ital. Biol. 2012, 150, 56–90. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G. Information integration: Its relevance to brain function and consciousness. Arch. Ital. Biol. 2010, 148, 299–322. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality. Phys. Rev. A 1988, 38, 364–374. [Google Scholar] [CrossRef]
- Bak, P.; Paczuski, M. Complexity, contingency, and criticality. Proc. Natl. Acad. Sci. USA 1995, 92, 6689–6696. [Google Scholar] [CrossRef]
- Kitzbichler, M.G.; Smith, M.L.; Christensen, S.R.; Bullmore, E. Broadband Criticality of human brain network synchronization. PLoS Comput. Biol. 2009, 5, e1000314. [Google Scholar] [CrossRef]
- Werner, G. Metastability, criticality and phase transitions in brain and its models. Biosystems 2007, 90, 496–508. [Google Scholar] [CrossRef] [Green Version]
- Hesse, J.; Gross, T. Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci. 2014, 8, 166. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, E.; Balenzuela, P.; Fraiman, D.; Chialvo, D.R. Criticality in large-scale brain FMRI dynamics unveiled by a novel point process analysis. Front. Physiol. 2012, 3, 15. [Google Scholar] [CrossRef] [PubMed]
- Hidalgo, J.; Grilli, J.; Suweis, S.; Muñoz, M.A.; Banavar, J.R.; Maritan, A. Information-based fitness and the emergence of criticality in living systems. Proc. Natl. Acad. Sci. USA 2014, 111, 10095–10100. [Google Scholar] [CrossRef] [Green Version]
- Haimovici, A.; Tagliazucchi, E.; Balenzuela, P.; Chialvo, D.R. Brain organization into resting state networks emerges at criticality on a model of the human connectome. Phys. Rev. Lett. 2013, 110, 178101. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Pellicoro, M.; Wu, G.; Angelini, L.; Cortés, J.M.; Stramaglia, S. Information transfer and criticality in the Ising model on the human connectome. PLoS ONE 2014, 9, e93616. [Google Scholar] [CrossRef]
- Moon, J.-Y.; Lee, U.; Blain-Moraes, S.; Mashour, G.A. General relationship of global topology, local dynamics, and directionality in large-scale brain networks. PLoS Comput. Biol. 2015, 11, e1004225. [Google Scholar] [CrossRef] [PubMed]
- Cocchi, L.; Gollo, L.L.; Zalesky, A.; Breakspear, M. Criticality in the brain: A synthesis of neurobiology, models and cognition. Prog. Neurobiol. 2017, 158, 132–152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beggs, J.M. The criticality hypothesis: How local cortical networks might optimize information processing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 329–343. [Google Scholar] [CrossRef] [PubMed]
- Khajehabdollahi, S.; Abeyasinghe, P.M.; Owen, A.M.; Soddu, A. The emergence of integrated information, complexity, and consciousness at criticality. bioRxiv 2019. [Google Scholar] [CrossRef]
- Kim, M.; Mashour, G.A.; Moraes, S.-B.; Vanini, G.; Tarnal, V.; Janke, E.; Hudetz, A.G.; Lee, U. Functional and Topological Conditions for Explosive Synchronization Develop in Human Brain Networks with the Onset of Anesthetic-Induced Unconsciousness. Front. Comput. Neurosci. 2016, 10. [Google Scholar] [CrossRef]
- Kim, M.; Kim, S.; Mashour, G.A.; Lee, U. Relationship of topology, multiscale phase synchronization, and state transitions in human brain networks. Front. Comput. Neurosci. 2017, 11, 55. [Google Scholar] [CrossRef] [PubMed]
- Beggs, J.M.; Timme, N. Being critical of criticality in the brain. Front. Physiol. 2012, 3, 163. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Golkowski, D.; Jordan, D.; Berger, S.; Ilg, R.; Lee, J.; Mashour, G.A.; Lee, U.; Avidan, M.S.; Blain-Moraes, S.; et al. Relationship of critical dynamics, functional connectivity, and states of consciousness in large-scale human brain networks. Neuroimage 2019, 188, 228–238. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.; Sorbaro Sindaci, M.; Goltsev, A.V.; Mendes, J.F.F. Critical behavior of the relaxation rate, the susceptibility, and a pair correlation function in the Kuramoto model on scale-free networks. Phys. Rev. E 2015, 91, 32814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moretti, P.; Muñoz, M.A. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun. 2013, 4, 2521. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.-Y.; Kim, J.; Ko, T.-W.; Kim, M.; Iturria-Medina, Y.; Choi, J.-H.; Lee, J.; Mashour, G.A.; Lee, U. Structure shapes dynamics and directionality in diverse brain networks: Mathematical principles and empirical confirmation in three species. Sci. Rep. 2017, 7, 46606. [Google Scholar] [CrossRef] [PubMed]
- Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
- Gong, G.; He, Y.; Concha, L.; Lebel, C.; Gross, D.W.; Evans, A.C.; Beaulieu, C. Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb. Cortex 2008, 19, 524–536. [Google Scholar] [CrossRef]
- Hoppensteadt, F.C.; Izhikevich, E.M. Weakly Connected Neural Networks, 1st ed.; Springer-Verlag: New York, NY, USA, 1997. [Google Scholar]
- Breakspear, M.; Heitmann, S.; Daffertshofer, A. Generative models of cortical oscillations: Neurobiological implications of the kuramoto model. Front. Hum. Neurosci. 2010, 4, 190. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, T.T.; Woolrich, M.; Luckhoo, H.; Joensson, M.; Mohseni, H.; Kringelbach, M.L.; Jirsa, V.; Deco, G. How delays matter in an oscillatory whole-brain spiking-neuron network model for MEG alpha-rhythms at rest. Neuroimage 2014, 87, 383–394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flores, F.J.; Hartnack, K.E.; Fath, A.B.; Kim, S.-E.; Wilson, M.A.; Brown, E.N.; Purdon, P.L. Thalamocortical synchronization during induction and emergence from propofol-induced unconsciousness. Proc. Natl. Acad. Sci. USA 2017, 114, E6660–E6668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deco, G.; Cabral, J.; Saenger, V.M.; Boly, M.; Tagliazucchi, E.; Laufs, H.; Van Someren, E.; Jobst, B.; Stevner, A.; Kringelbach, M.L. Perturbation of whole-brain dynamics in silico reveals mechanistic differences between brain states. Neuroimage 2018, 169, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Cabral, J.; Woolrich, M.W.; Stevner, A.B.A.; van Hartevelt, T.J.; Kringelbach, M.L. Single or multiple frequency generators in on-going brain activity: A mechanistic whole-brain model of empirical MEG data. Neuroimage 2017, 152, 538–550. [Google Scholar] [CrossRef]
- Jobst, B.M.; Hindriks, R.; Laufs, H.; Tagliazucchi, E.; Hahn, G.; Ponce-Alvarez, A.; Stevner, A.B.A.; Kringelbach, M.L.; Deco, G. Increased stability and breakdown of brain effective connectivity during slow-wave sleep: Mechanistic insights from whole-brain computational modelling. Sci. Rep. 2017, 7, 4634. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Watrous, A.J.; Patel, A.; Jacobs, J. Theta and alpha oscillations are traveling waves in the human neocortex. Neuron 2018, 98, 1269–1281.e4. [Google Scholar] [CrossRef]
- Naruse, Y.; Matani, A.; Miyawaki, Y.; Okada, M. Influence of coherence between multiple cortical columns on alpha rhythm: A computational modeling study. Hum. Brain Mapp. 2009, 31, 703–715. [Google Scholar] [CrossRef]
- Caminiti, R.; Ghaziri, H.; Galuske, R.; Hof, P.R.; Innocenti, G.M. Evolution amplified processing with temporally dispersed slow neuronal connectivity in primates. Proc. Natl. Acad. Sci. USA 2009, 106, 19551–19556. [Google Scholar] [CrossRef] [Green Version]
- Blain-Moraes, S.; Tarnal, V.; Vanini, G.; Alexander, A.; Rosen, D.; Shortal, B.; Janke, E.; Mashour, G.A. Neurophysiological correlates of sevoflurane-induced unconsciousness. Anesthesiol. J. Am. Soc. Anesthesiol. 2015, 122, 307–316. [Google Scholar] [CrossRef]
- Beggs, J.M.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [CrossRef]
- Brochini, L.; de Andrade Costa, A.; Abadi, M.; Roque, A.C.; Stolfi, J.; Kinouchi, O. Phase transitions and self-organized criticality in networks of stochastic spiking neurons. Sci. Rep. 2016, 6, 35831. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Moon, J.-Y.; Mashour, G.A.; Lee, U. Mechanisms of hysteresis in human brain networks during transitions of consciousness and unconsciousness: Theoretical principles and empirical evidence. PLoS Comput. Biol. 2018, 14, e1006424. [Google Scholar] [CrossRef] [PubMed]
- Lv, P.; Guo, L.; Hu, X.; Li, X.; Jin, C.; Han, J.; Li, L.; Liu, T. Modeling dynamic functional information flows on large-scale brain networks. In Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI 2013); Springer: Berlin/Heidelberg, Germany, 2013; pp. 698–705. [Google Scholar]
- Schmidt, R.; LaFleur, K.J.R.; de Reus, M.A.; van den Berg, L.H.; van den Heuvel, M.P. Kuramoto model simulation of neural hubs and dynamic synchrony in the human cerebral connectome. BMC Neurosci. 2015, 16, 54. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Kringelbach, M.L.; Jirsa, V.K.; Ritter, P. The dynamics of resting fluctuations in the brain: Metastability and its dynamical cortical core. Sci. Rep. 2017, 7, 3095. [Google Scholar] [CrossRef] [PubMed]
- Stanley, H.E.; Wong, V.K. Introduction to phase transitions and critical phenomena. Am. J. Phys. 1972, 40, 927–928. [Google Scholar] [CrossRef]
- Oizumi, M.; Tsuchiya, N.; Amari, S. Unified framework for information integration based on information geometry. Proc. Natl. Acad. Sci. USA 2016, 113, 14817–14822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrett, A.B.; Seth, A.K. Practical measures of integrated information for time-series data. PLoS Comput. Biol. 2011, 7, e1001052. [Google Scholar] [CrossRef] [PubMed]
- Kitazono, J.; Kanai, R.; Oizumi, M. Efficient algorithms for searching the minimum information partition in Integrated Information Theory. Entropy 2018, 20, 173. [Google Scholar] [CrossRef]
- Kim, H.; Hudetz, A.G.; Lee, J.; Mashour, G.A.; Lee, U.; the ReCCognition Study Group. Estimating the integrated information measure Phi from high-density electroencephalography during states of consciousness in humans. Front. Hum. Neurosci. 2018, 12. [Google Scholar] [CrossRef]
- Stam, C.J.; Nolte, G.; Daffertshofer, A. Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum. Brain Mapp. 2007, 28, 1178–1193. [Google Scholar] [CrossRef]
- Lee, U.; Lee, H.; Müller, M.; Noh, G.-J.; Mashour, G.A. Genuine and spurious phase synchronization strengths during consciousness and general anesthesia. PLoS ONE 2012, 7, e46313. [Google Scholar] [CrossRef] [PubMed]
- Wen, P.; Li, Y. EEG human head modelling based on heterogeneous tissue conductivity. Australas. Phys. Eng. Sci. Med. 2006, 29, 235–240. [Google Scholar] [CrossRef] [PubMed]
- Oostenveld, R.; Fries, P.; Maris, E.; Schoffelen, J.-M. FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 2011, 156869. [Google Scholar] [CrossRef]
- Deco, G.; Jirsa, V.K. Ongoing cortical activity at rest: Criticality, multistability, and ghost attractors. J. Neurosci. 2012, 32, 3366–3375. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, E.; Chialvo, D.R.; Siniatchkin, M.; Amico, E.; Brichant, J.-F.; Bonhomme, V.; Noirhomme, Q.; Laufs, H.; Laureys, S. Large-scale signatures of unconsciousness are consistent with a departure from critical dynamics. J. R. Soc. Interface 2016, 13, 20151027. [Google Scholar] [CrossRef] [PubMed]
- Hudetz, A.G.; Humphries, C.J.; Binder, J.R. Spin-glass model predicts metastable brain states that diminish in anesthesia. Front. Syst. Neurosci. 2014, 8, 234. [Google Scholar] [CrossRef] [Green Version]
- Lee, U.; Mashour, G.A.; Kim, S.; Noh, G.-J.; Choi, B.-M. Propofol induction reduces the capacity for neural information integration: Implications for the mechanism of consciousness and general anesthesia. Conscious. Cogn. 2009, 18, 56–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tagliazucchi, E. The signatures of conscious access and its phenomenology are consistent with large-scale brain communication at criticality. Conscious. Cogn. 2017, 55, 136–147. [Google Scholar] [CrossRef] [Green Version]
- Arsiwalla, X.D.; Verschure, P.F.M.J. The global dynamical complexity of the human brain network. Appl. Netw. Sci. 2016, 1, 16. [Google Scholar] [CrossRef] [Green Version]
- Mediano, P.A.M.; Farah, J.C.; Shanahan, M. Integrated Information and Metastability in Systems of Coupled Oscillators. Arxiv Prepr. 2016, arXiv:1606.08313. [Google Scholar]
- Hu, X.; Boccaletti, S.; Huang, W.; Zhang, X.; Liu, Z.; Guan, S.; Lai, C.-H. Exact solution for first-order synchronization transition in a generalized Kuramoto model. Sci. Rep. 2014, 4, 7262. [Google Scholar] [CrossRef] [Green Version]
- Ko, T.-W.; Ermentrout, G.B. Partially locked states in coupled oscillators due to inhomogeneous coupling. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2008, 78, 16203. [Google Scholar] [CrossRef] [Green Version]
- Bédard, C.; Destexhe, A. Macroscopic models of local field potentials and the apparent 1/f noise in brain activity. Biophys. J. 2009, 96, 2589–2603. [Google Scholar] [CrossRef]
- Liang, Z.; King, J.; Zhang, N. Intrinsic organization of the anesthetized brain. J. Neurosci. 2012, 32, 10183–10191. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Ward, B.D.; Binder, J.R.; Li, S.-J.; Hudetz, A.G. Scale-free functional connectivity of the brain is maintained in anesthetized healthy participants but not in patients with unresponsive wakefulness syndrome. PLoS ONE 2014, 9, e92182. [Google Scholar] [CrossRef]
- Lee, U.; Mashour, G.A. Role of network science in the study of anesthetic state transitions. Anesthesiology 2018, 129, 1029–1044. [Google Scholar] [CrossRef] [PubMed]
- Priesemann, V.; Valderrama, M.; Wibral, M.; Le Van Quyen, M. Neuronal avalanches differ from wakefulness to deep sleep—evidence from intracranial depth recordings in humans. PLoS Comput. Biol. 2013, 9, e1002985. [Google Scholar] [CrossRef]
- Lee, U.; Oh, G.; Kim, S.; Noh, G.; Choi, B.; Mashour, G.A. Brain networks maintain a scale-free organization across consciousness, anesthesia, and recovery: Evidence for adaptive reconfiguration. Anesthesiology 2010, 113, 1081–1091. [Google Scholar] [CrossRef]
- Krzemiński, D.; Kamiński, M.; Marchewka, A.; Bola, M. Breakdown of long-range temporal correlations in brain oscillations during general anesthesia. Neuroimage 2017, 159, 146–158. [Google Scholar] [CrossRef] [PubMed]
- Meisel, C.; Storch, A.; Hallmeyer-Elgner, S.; Bullmore, E.; Gross, T. Failure of adaptive self-organized criticality during epileptic seizure attacks. PLoS Comput. Biol. 2012, 8, e1002312. [Google Scholar] [CrossRef] [PubMed]
- Bonachela, J.A.; de Franciscis, S.; Torres, J.J.; Muñoz, M.A. Self-organization without conservation: Are neuronal avalanches generically critical? J. Stat. Mech. Theory Exp. 2010, 2010, P02015. [Google Scholar] [CrossRef]
- Mediano, P.; Seth, A.; Barrett, A.; Mediano, P.A.M.; Seth, A.K.; Barrett, A.B. Measuring integrated information: Comparison of candidate measures in theory and simulation. Entropy 2018, 21, 17. [Google Scholar] [CrossRef]
- Huang, Z.; Vlisides, P.E.; Tarnal, V.C.; Janke, E.L.; Keefe, K.M.; Collins, M.M.; McKinney, A.M.; Picton, P.; Harris, R.E.; Mashour, G.A.; et al. Brain imaging reveals covert consciousness during behavioral unresponsiveness induced by propofol. Sci. Rep. 2018, 8, 13195. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Lee, U. Criticality as a Determinant of Integrated Information Φ in Human Brain Networks. Entropy 2019, 21, 981. https://doi.org/10.3390/e21100981
Kim H, Lee U. Criticality as a Determinant of Integrated Information Φ in Human Brain Networks. Entropy. 2019; 21(10):981. https://doi.org/10.3390/e21100981
Chicago/Turabian StyleKim, Hyoungkyu, and UnCheol Lee. 2019. "Criticality as a Determinant of Integrated Information Φ in Human Brain Networks" Entropy 21, no. 10: 981. https://doi.org/10.3390/e21100981
APA StyleKim, H., & Lee, U. (2019). Criticality as a Determinant of Integrated Information Φ in Human Brain Networks. Entropy, 21(10), 981. https://doi.org/10.3390/e21100981



